MetaTrader 5 / 指标
English Русский Español Deutsch 日本語 Português
preview
数据科学与机器学习（第22部分）：利用自编码器神经网络实现更智能的交易——从噪声中提炼信号

数据科学与机器学习（第22部分）：利用自编码器神经网络实现更智能的交易——从噪声中提炼信号

MetaTrader 5 — 指标 | 6 一月 2025, 10:09
380 0
Omega J Msigwa
Omega J Msigwa

什么是自动编码器？

自动编码器是无监管的人工神经网络。在其最简单的形式中，自动编码器是一个神经网络，它尝试做两件事。首先将输入数据压缩到较低的维度，然后尝试使用这个较低维度的数据表示来重新创建原始输入。

假设你有一张模糊的猫的图片传递给自动编码器，这张图片将被压缩然后再解压回其原始状态，在这个过程中会丢失一些噪声/模糊的像素，最终得到一张清晰的猫的图片。

模糊的猫图片 vs 非模糊的猫图片

在本文中，我们将探讨如何在金融领域使用自动编码器神经网络来帮助我们去除市场噪音，从而发现交易机会。

如果您对ONNX、PCA和神经网络有基本了解，那么阅读本文会很轻松。

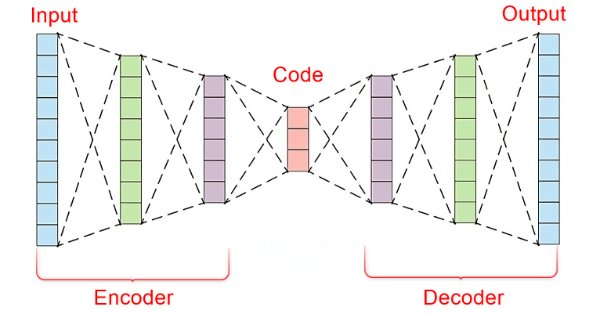
自编码器由两部分组成：

  1. 编码器 接收输入数据并将其压缩成低维的隐性表征，以捕捉数据的主要特征。
  2. 解码器接收隐性表征并尝试尽可能准确地重建原始输入数据。

自动编码器的优势：

  • 它们对于降维任务非常有用，因为它们能够获取外汇交易数据的压缩表征，这对于特征提取、数据压缩和高维数据集中的可视化等任务非常有用。
  • 通过尝试重构输入数据，自编码器可以获取关键特征并去除噪声或不相关信息。这些获取到的特征对其他机器学习任务（如分类或异常检测）也非常有用。
  • 由于它们是无监管的，因此可以在没有人工干预的情况下发现交易数据中的隐藏模式。
  • 自编码器获取到的潜在表征可以用作其他模型的预训练特征，可能会提高这些模型的性能。


它们由什么构成？

让我们剖析一下自动编码器，看看它们是由什么构成的，以及它们有什么特别之处。

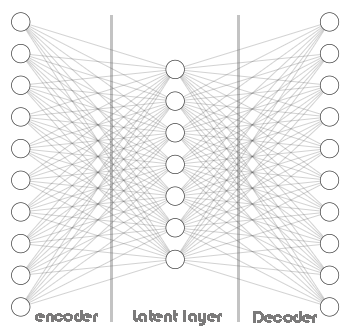
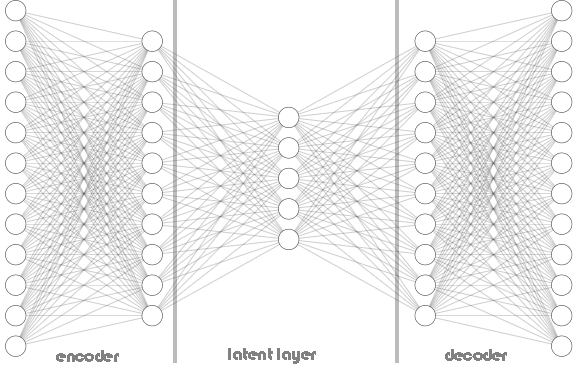
自动编码器的核心是一个由三部分组成的人工神经网络。

  1. 编码器
  2. 嵌入向量/潜在层
  3. 解码器

简单自动编码器架构

神经网络的左半部分被称为编码器。它的工作是将原始输入数据转换为低维表征。

神经网络的中间部分被称为潜在层或嵌入向量，它的作用是将输入数据压缩为低维数据。这一层的神经元数量预期会少于编码器和解码器中的神经元数量。

这个神经网络的右半部分被称为解码器。它的工作是利用编码器的输出来重新创建原始输入。换句话说，它在试图逆转编码过程。

这非常有趣，因为解码器试图从编码器返回的较低维度的数据中重新创建出较高维度的数据。这有点像通过看一张房子的照片来建造这座房子。

1D房子 vs 3D房子

这个过程的关键在于它强制性地造成了信息丢失，这是整个机制能够运作的核心。通过让解码器获得不完整的信息，并训练整个网络以达到最小化构造误差。在训练过程中，编码器和解码器被迫协同工作，以达到最小化构造误差。

构造误差是指尝试重建的数据与原始输入数据之间的差异。

如果编码器和解码器之间没有信息丢失，那么网络将简单地将输入乘以1，从而得到一个完美的重建，这将使自动编码器变得毫无用处。在这个机器学习技术中，拥有一个允许有一定程度错误的编码器是至关重要的，确保不要过度拟合您的模型。

编码器和解码器都不局限于单层，如上面展示的自编码器架构图像所示。它可以包含多个层，如下面的Python代码所示，我们有一个名为hidden_dims的列表，用于存储编码器和解码器层的神经元。

Python:

class Autoencoder(Model):
  def __init__(self, input_dim, latent_dim, hidden_dims=[]):
    super(Autoencoder, self).__init__()

    self.encoder = tf.keras.Sequential()
    # Add hidden layers to the encoder (if any)
    for dim in hidden_dims:
      self.encoder.add(layers.Dense(dim, activation='relu'))
      self.encoder.add(layers.Dropout(0.5))

    # Define the latent layer
    self.encoder.add(layers.Dense(latent_dim, activation='relu'))

    # Decoder ( mirrored structure )
    self.decoder = tf.keras.Sequential()
    # Add hidden layers to the decoder (in reverse order)
    for dim in hidden_dims[::-1]:
      self.decoder.add(layers.Dense(dim, activation='relu'))
      self.decoder.add(layers.Dropout(0.5))

    # Define the output layer
    self.decoder.add(layers.Dense(input_dim, activation='sigmoid'))  #the output layer with dimensions matching the original input data

  def call(self, x):
    encoded = self.encoder(x)
    decoded = self.decoder(encoded)
    return decoded

调用类Autoencoder：

Python:

input_dim = dataset.shape[1]  # number of columns in the data
latent_dim = 5  # Dimension of latent layer
hidden_dims = [12, 10]

autoencoder = Autoencoder(input_dim, latent_dim, hidden_dims)

以下是自动编码器架构：

12,10 自动编码器架构

在Autoencoder类中，您已经了解到在编码器和解码器中广泛使用ReLU（Rectified Linear Unit，修正线性单元）作为激活函数。在大多数您会接触的Autoencoder中，ReLU之所以被广泛使用，是有其重要原因的。

ReLU计算效率高，能够避免梯度消失，并且能够学习到稀疏表征，通常在交易数据中很常见。ReLU的其他变体，如GELU和Leaky ReLU，在处理金融数据时可能会很有帮助。

其他流行的激活函数，如S型生长曲线（Sigmoid）和双曲正切函数（TANH）也可能有用，但在将它们应用于交易数据之前，必须了解它们的优缺点。

Sigmoid:

  • 优点： 常用于图像重建任务，其中输出需要介于0和1之间（代表像素强度）。
  • 缺点： 对于金融数据可能不太理想，因为在反向传播过程中可能会引入梯度消失问题，特别是在深层架构中。
    当在Autoencoder中使用Sigmoid激活函数时，网络无法收敛，因为它一直朝着局部最小值振荡。
    Epoch 1/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 3s 5ms/step - loss: 0.4001 - val_loss: 0.3753
Epoch 2/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3733 - val_loss: 0.3745
Epoch 3/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3724 - val_loss: 0.3746
Epoch 4/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3758 - val_loss: 0.3746
Epoch 5/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3692 - val_loss: 0.3745
Epoch 6/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3747 - val_loss: 0.3746
Epoch 7/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3716 - val_loss: 0.3746
Epoch 8/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3740 - val_loss: 0.3745
Epoch 9/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3698 - val_loss: 0.3745
Epoch 10/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3713 - val_loss: 0.3745
Epoch 11/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3726 - val_loss: 0.3745
Epoch 12/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3739 - val_loss: 0.3745
Epoch 13/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3725 - val_loss: 0.3746
Epoch 14/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.3749 - val_loss: 0.3746

Tanh（双曲正切）：

  • 优点： 输出范围在-1和1之间，与Sigmoid类似，但梯度更陡峭，可能导致更快的收敛速度。
  • 缺点： 在非常深度的网络中，仍然可能陷入梯度消失的问题。

这些Sigmoid和TANH激活函数以及其他类似函数，在解码器的输出层中使用时效果最佳，以便尽可能准确地重建输入数据。在这种情况下，Autoencoder的输出应该与原始输入相似。由于输入数据通常根据预处理被归一化到[0, 1]或[-1, 1]的范围内，因此Sigmoid激活函数常被用来将输出值缩放到这个范围内。

Python:

# Define the output layer
self.decoder.add(layers.Dense(input_dim, activation='sigmoid'))  #the output layer of the decoder with dimensions matching the original input data


Min-Max Scaler是您的得力助手

Autoencoder的编码和部署相对简单，然而，为了使它们能够很好地运作，需要为它们提供正确的信息和工具。正如我们了解到的，对于这种神经网络类型来说，选择激活函数是至关重要的，缩放技术也是如此。

由于我们使用的是ReLU激活函数，当给它一个小于或等于零的值时，它会返回零，否则会返回给定的值。(x = 0 when x<=0 else x = x).

当您使用StandardScaler（标准缩放器）时，它会通过减去均值来使数据偏中心，并将其缩放到单位方差。这可能会在标准化过程中，将具有数值较大正值的异常值转换成负值（可能是-1）。如果一个异常值的标准化值变为-1，当这个负值传递给编码器中的ReLU激活函数时，该特定特征的输出将始终为0。

这可能导致一种称为“ReLU神经元死亡”的现象，即编码器中的一些神经元由于这些负输入值而永远不会被激活。这些死亡的ReLU神经元会阻碍编码器的运行，因为它们基本上变得不活跃，并且对编码过程没有贡献，因此大多数异常值或交易数据中的尖峰都会被预测为平坦：请参见下面的StandardScaler图像。

 

StandardScaler自动编码器

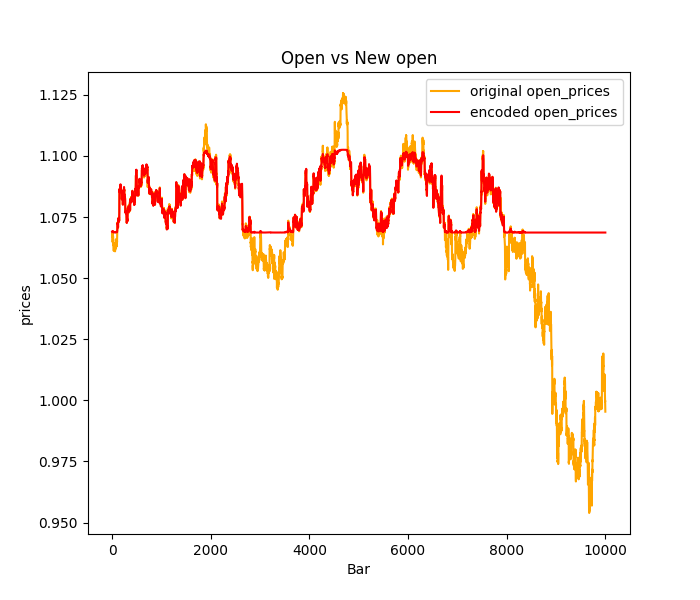
解决此问题：

尝试其他归一化技术，比如Min-Max缩放器，它将数据缩放到0和1之间的特定范围，这样可以避免产生导致RELU问题的-1值。然而，考虑到Min-Max缩放器的局限性，您也可以了解鲁棒缩放器，它相比标准缩放器对异常值不那么敏感，可能为RELU激活提供更好的缩放效果。

此外，您可能还想考虑使用Leaky RELU（对于x <= 0，leaky_relu = 0.01x；对于x > 0，relu = x）来替代标准的RELU。Leaky RELU允许负输入有一个小的非零梯度，从而缓解了RELU失效的问题。


训练自动编码器

现在我们已经简要探讨了自动编码器的基础知识，让我们来训练一个自动编码器，看看它如何帮助我们进行交易。

Python: 

import sklearn
from sklearn.model_selection import train_test_split
from keras import optimizers
from keras.callbacks import EarlyStopping

x_train, x_test = train_test_split(dataset, test_size=0.3, random_state=42) #train test the data

# Normalizing the input data 

scaler = sklearn.preprocessing.MinMaxScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

print(f"x_train {x_train.shape}.dtype({x_train.dtype}) x_test {x_test.shape}.dtype({x_test.dtype})")

# compile the autoencoder

input_dim = dataset.shape[1]
latent_dim = 32  # Dimension of latent space
hidden_dims = [256, 128, 64]

autoencoder = Autoencoder(input_dim, latent_dim, hidden_dims)

optimizer = optimizers.Adam(learning_rate=1e-5)
autoencoder.compile(optimizer=optimizer, loss=losses.MeanSquaredError())

early_stopping = EarlyStopping(monitor='val_loss', patience = 5, restore_best_weights=True) //stop the training process if 5 epochs have no change in loss
history = autoencoder.fit(x_train, x_train, epochs=50, shuffle=True, callbacks=[early_stopping], validation_data=(x_test, x_test), batch_size=64, verbose=1)

我选择了具有复杂神经网络架构的编码器[256, 128, 64]，而解码器将采用其反向排列[64, 128, 256]，同时潜在层有32个神经元。

这样一个复杂的神经网络有较高的过拟合训练数据的风险，可以从更简单的架构开始尝试，这只是一个示例。 

输出：

x_train (7000, 4).dtype(float64) x_test (3000, 4).dtype(float64)
Epoch 1/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 3s 5ms/step - loss: 0.0669 - val_loss: 0.0636
Epoch 2/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0648 - val_loss: 0.0608
Epoch 3/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0624 - val_loss: 0.0550

....
....
....

Epoch 46/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.2096e-04 - val_loss: 1.0195e-04
Epoch 47/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.0758e-04 - val_loss: 9.7759e-05
Epoch 48/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.0923e-04 - val_loss: 9.4798e-05
Epoch 49/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - loss: 1.0243e-04 - val_loss: 9.0442e-05
Epoch 50/50
110/110 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - loss: 1.0222e-04 - val_loss: 8.7384e-05

损耗 vs 迭代图：

损耗 vs 迭代曲线：

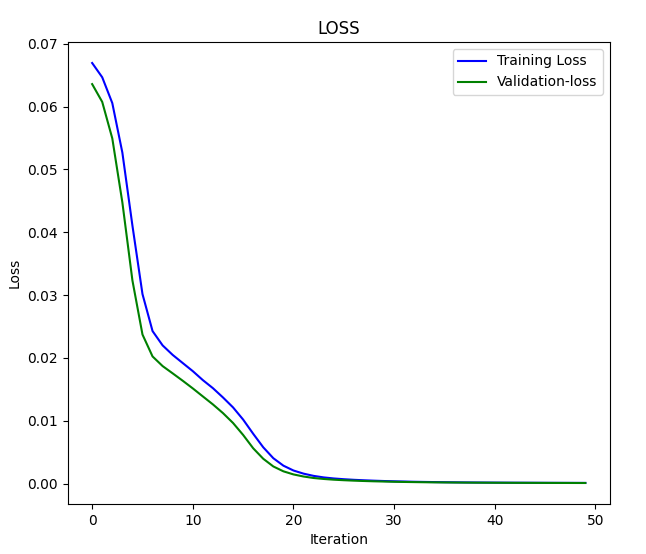
让我们将数据传输给自动编码器并观察结果：

Python: 

original_norm_data = scaler.transform(dataset)

new_data = autoencoder.call(original_norm_data)

new_data = scaler.inverse_transform(new_data) #return data to the original form 

print("original data\n",dataset,"\nnew data\n",new_data)

输出：

原始数据
 [[1.06507 1.06633 1.06497 1.06538]
 [1.06628 1.06685 1.06463 1.06508]
 [1.06771 1.06797 1.06599 1.06627]
 ...
 [0.99941 0.99996 0.9991  0.99916]
 [0.99687 0.99999 0.99646 0.99941]
 [0.99536 0.99724 0.99444 0.99687]] 
new data
 [[1.06612682 1.06676685 1.06537819 1.06605109]
 [1.06617137 1.06679912 1.06541834 1.06609218]
 [1.06742607 1.06804771 1.06668032 1.06736937]
 ...
 [0.99906356 1.00121275 0.9980908  0.99980352]
 [0.998204   1.00034005 0.9972261  0.99893805]
 [0.99581326 0.99789913 0.99494114 0.99651365]]

我决定将收盘价进行可视化：

收盘价与自动编码后的价格对比

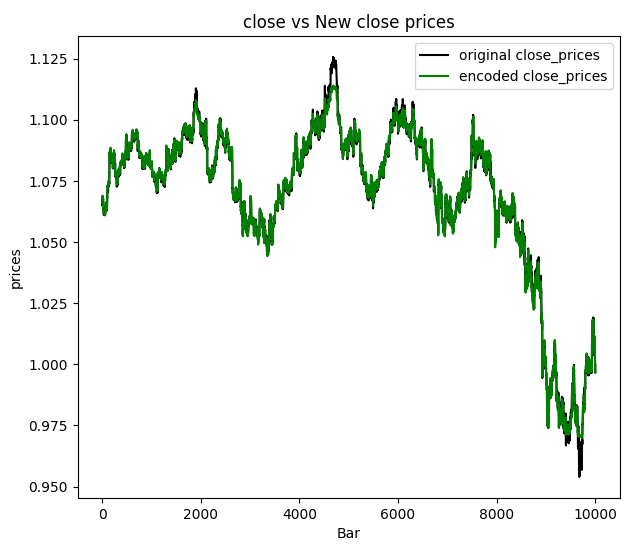
我们可以得出结论，通过自动编码器传递的新数据已经过滤掉了一些噪声，并且仅通过观察图表就很容易检测到异常值。既然我们已经确认有效，那么让我们来探讨一下自动编码器的应用，以及我们如何在基于MQL5的程序中使用它们。


自动编码器的应用

自动编码器已被广泛应用于工程、医学、娱乐等多个领域和行业，用于降维、特征学习、异常检测、推荐系统以及图像去噪等。

降维

自动编码器擅长将高维数据压缩到低维的潜在空间。在处理包含大量特征的数据集时，这一点很有价值，因为它们能够以一种更紧凑的表示形式捕获关键特征，这可以：

  • 通过减少需要处理的特征数量，提高后续机器学习任务的计算效率。 
  • 通过应用如主成分分析（PCA）等降维技术到潜在空间中，可以增强高维数据的可视化效果。

为了完成这项任务，我们只需要使用神经网络中的编码器部分 

我们需要修改Autoencoder类，通过添加一个build函数，该函数应在Autoencoder类实例化后不久被调用。这个方法对于基于输入数据的形状动态创建层很有用，它允许我们推迟层的构建，直到它们的形状已知。

Python: 

class Autoencoder(Model):
  def __init__(self, input_dim, latent_dim, hidden_dims=[]):
    super(Autoencoder, self).__init__()
    self.hidden_dims = hidden_dims
    self.input_dim = input_dim
    
    # Encoder
    self.encoder = tf.keras.Sequential(name='encoder') #give the encoder Sequential layer name=encoder
    # Decoder ( mirrored structure )
    self.decoder = tf.keras.Sequential(name='decoder') #give the decoder Sequential layer name=decoder
    
  def build(self):

    # Add hidden layers to the encoder (if any)
    for dim in hidden_dims:
      self.encoder.add(layers.Dense(dim, activation='relu'))
      self.encoder.add(layers.Dropout(0.5))

    # Define the latent layer
    self.encoder.add(layers.Dense(latent_dim, activation='relu'))
        
    # Add hidden layers to the decoder (in reverse order)
    for dim in hidden_dims[::-1]:
      self.decoder.add(layers.Dense(dim, activation='relu'))
      self.decoder.add(layers.Dropout(0.5))

    # Define the output layer
    self.decoder.add(layers.Dense(self.input_dim, activation='sigmoid'))  #the output layer with dimensions matching the original input data

  def call(self, x):
    encoded = self.encoder(x)
    decoded = self.decoder(encoded)
    return decoded

我们还需要稍微改变一下调用类函数的方式，如前所述，我们应该在编译和训练神经网络模型之前调用build函数。调用类方法的顺序很重要！

Python: 

# Instantiate the autoencoder and build the model
autoencoder = Autoencoder(input_dim, latent_dim, hidden_dims)
autoencoder.build()

optimizer = optimizers.Adam(learning_rate=1e-5)
autoencoder.compile(optimizer=optimizer, loss=losses.MeanSquaredError())

既然我们已经有了build函数，那么在自动编码器成功且无误地完成训练之后不久，我们就可以分别提取出编码器和解码器神经网络了。

Python: 

# Extract Encoder
encoder_input = autoencoder.encoder.layers[0].input
encoder_output = autoencoder.encoder.get_layer(index=-1).output # the layer at index -1 is the last layer

# Define the encoder model
encoder_model = tf.keras.Model(inputs=encoder_input, outputs=encoder_output)

# Extract Decoder
decoder_input = autoencoder.decoder.layers[0].input
decoder_output = autoencoder.decoder.get_layer(index=-1).output # the layer at index -1 is the last layer

# Define the decoder model
decoder_model = tf.keras.Model(inputs=decoder_input, outputs=decoder_output)

一旦我们有了编码器，就可以传递信息，并通过潜在层（空间）获得输出矩阵。

Python: 

from sklearn.decomposition import PCA

# Fit & transform the encoded data 
encoded_data = encoder_model.predict(original_norm_data)
print("decoded data.shape: ",encoded_data.shape)

# Create PCA object
pca = PCA(n_components=encoded_data.shape[1])

reduced_data = pca.fit_transform(encoded_data)
print("pca reduced data.shape: ",reduced_data.shape)

print("explained var:\n",np.cumsum(pca.explained_variance_ratio_))

# Plotting the scree plot
plt.figure(figsize=(10, 6))
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance')
plt.title('Scree Plot')
plt.grid(True)
plt.show()

通过将列数encoded_data.shape[1]分配给PCA组件，我们可以测量每个特征所解释的方差，并绘制一个碎石图（scree plot），这有助于我们了解在PCA中应用多少个组件来缩减数据维度是最优的。

313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step
decoded data.shape:  (10000, 32)
pca reduced data.shape:  (10000, 32)
explained var:
 [0.99623495 0.9989214  0.99982804 0.9999363  0.99996614 0.9999872
 0.99999297 0.9999953  0.9999972  0.9999982  0.9999987  0.9999991
 0.9999994  0.9999996  0.9999997  0.9999998  0.99999994 1.
 1.         1.         1.         1.         1.         1.
 1.         1.         1.         1.         1.         1.
 1.         1.        ]

PCA碎石图

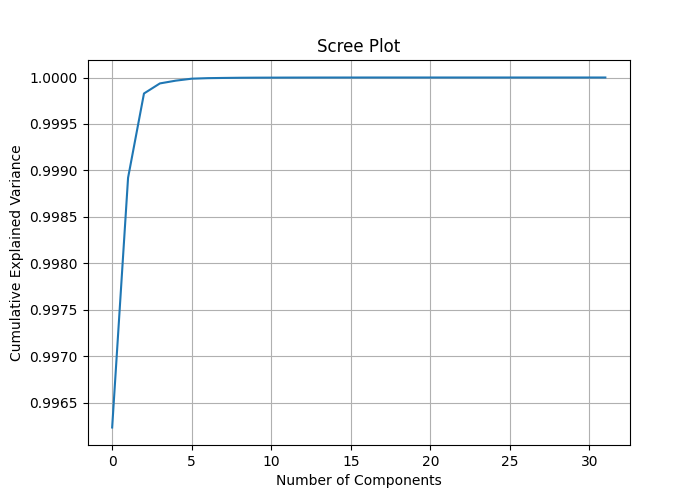
通过观察累积解释方差，我们可以发现大部分特征的解释方差比接近于1，有些甚至等于1。这意味着我们也许能够在不明显丢失信息的情况下实现大幅度的降维。碎石图显示在大约两个组件时出现了拐点，这两个组件解释了约0.9989的总方差，这是降低数据维度的最佳组件数量。即使使用一个组件也应该可以很好地工作，因为当我在一个轴上绘制这些组件时，我没有看到它们之间有显著的差异。

下次调用PCA类时，应该使用值2来调用它，以便从中获得2个组件。

# Create PCA object
pca = PCA(n_components=2)

reduced_data = pca.fit_transform(encoded_data)
print("pca reduced data.shape: ",reduced_data.shape)

结果：

pca降维后的数据形状为：(10000, 2)

我决定将潜在层的所有32个组件绘制在同一个轴上。只有一个特征与其他特征明显不同，而其他特征在图表上看起来几乎相同。这进一步证实了在这个降维后的数据中，少数几个组件是有意义的。

bar = [count+1 for count in range(reduced_data.shape[0])]

plt.figure(figsize = (7,10))
for col in range(reduced_data.shape[1]):
    plt.plot(bar,  reduced_data[:, col],label=f'feature {col}')
    
plt.xlabel("index")
plt.ylabel("feature")
plt.title("PCA encoded features")
plt.legend()
plt.savefig("pca-encoded features")

组件 vs 指数图

PCA组件图

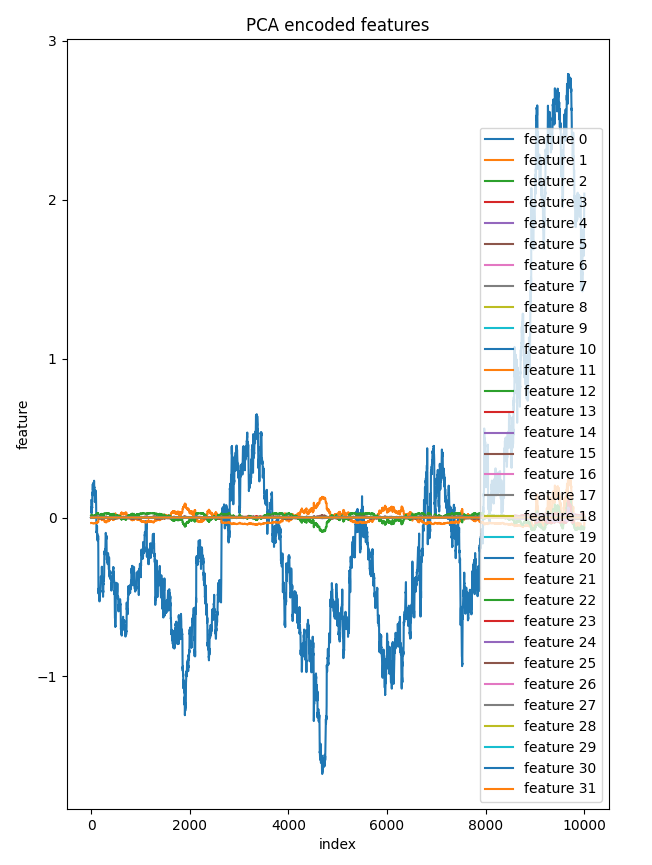
与直接将PCA应用于原始高维数据相比，将PCA应用于自动编码器的潜在空间为降维过程提供了更多的控制，同时在此过程中还有助于减少数据中的不必要噪声。

一个不容忽视的问题：

在讨论的示例中，我们对所有输入数据进行了降维，这在您想将PCA降维后的数据应用于预测模型时可能并不理想。在此情况下，您可能只需要对自变量应用PCA。


但是，在我们能够使用我们创建的自动编码器来减少MetaTrader 5中交易数据的噪声（作为自动编码器的另一个应用）之前，我们需要将其保存为ONNX格式。


将自动编码器模型保存为ONNX格式

在之前的应用中，我们已经分别提取了编码器和解码器，因此将它们转换为ONNX格式并保存应该很容易。让我们从编码器模型开始，将它们分别保存。

Python: 

import tf2onnx
import onnx
import os

output_path = os.path.join('/kaggle/working/',"encoder.eurusd.h1.onnx")

# saving the encoder for MetaTrader 5

input_signature = [tf.TensorSpec(encoder_input.shape, tf.float16, name='x_inputs')] #onnx input signature
# Use from_function for tf functions
onnx_model, _ = tf2onnx.convert.from_keras(encoder_model, input_signature, opset=13)
onnx.save(onnx_model, output_path)

在MetaTrader 5中加载ONNX格式的模型时，ONNX的input_signature有助于避免与最新版本的TensorFlow和ONNX相关的错误，因为它可以明确我们.onnx文件的输入名称。

保存解码器模型：

Python: 

# saving the decoder

output_path = os.path.join('/kaggle/working/',"decoder.eurusd.h1.onnx")

input_signature = [tf.TensorSpec(decoder_input.shape, tf.float16, name='decoder_inputs')] #onnx input signature

onnx_model, _ = tf2onnx.convert.from_keras(decoder_model, input_signature, opset=13) #conver keras model to onnx
onnx.save(onnx_model, output_path)

在文章克服ONNX集成挑战中，我解决了将同样适用于Python和mql5编程语言的降维和缩放技术整合起来以提高精度的问题，但我又发现了一个简单的解决方案来缓解缩放问题。

保存缩放器：

在Python和mql5中使用相同的缩放器至关重要。我必须一再强调这一点的重要性。

Python: 

scaler.data_min_.tofile("minmax_min.bin")
scaler.data_max_.tofile("minmax_max.bin")

我们将Min-Max缩放器的信息数组保存到简单的二进制文件中，这些文件可以包含在我们的MetaTrader 5指标中。之后将它们保存在MQL5\Files文件夹下。

MQL5 (AutoEncoder Indicator.mq5): 

//Load both the encoder_model and the decoder_model
#resource "\\Files\\encoder.eurusd.h1.onnx" as uchar encoder_onnx[];
#resource "\\Files\\decoder.eurusd.h1.onnx" as uchar decoder_onnx[];

// Load the MinMax scaler also
#resource "\\Files\\minmax_min.bin" as double min_values[];
#resource "\\Files\\minmax_max.bin" as double max_values[];


减少交易数据中的噪声

自动编码器可以从数据中去除噪声，这一点在图像去噪等多个方面已经得到验证，但我们尚未在金融数据中证明这一点。通过比较原始收盘价和自动编码器生成的新收盘价图像，可以明显看出，自动编码器生成的收盘价数据的噪声更少。接下来，我们制作一个指标，帮助我们绘制由自动编码器提供的新OHLC（开盘价、最高价、最低价、收盘价）数据所形成的K线图。

MQL5 (AutoEncoder Indicator.mq5):

#property indicator_chart_window
#property indicator_plots 1
#property indicator_buffers 5

input bool show_bars = true;
input bool show_bullish_bearish = false;

//--- plot Candle
#property indicator_label1  "autoencoded open; high; low; close"
#property indicator_type1   DRAW_COLOR_CANDLES
#property indicator_color1  clrRed, clrGray
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

我们需要创建一个Autoencoder类，以便在MQL5中更容易使用加载的ONNX模型，就像在Python中使用一样。

MQL5(Autoencoder-onnx.mqh):

class CAutoEncoderONNX
  {
protected:

   bool initialized;
   long onnx_handle;
   void PrintTypeInfo(const long num,const string layer,const OnnxTypeInfo& type_info);
   long inputs[], outputs[];
   
   void replace(long &arr[]) { for (uint i=0; i<arr.Size(); i++) if (arr[i] <= -1) arr[i] = UNDEFINED_REPLACE; }
   
public:
                     CAutoEncoderONNX(void);
                    ~CAutoEncoderONNX(void);
                     
                     bool Init(const uchar &onnx_buff[], ulong flags=ONNX_DEFAULT); //load the onnx model from a resource uchar array
                     bool Init(string onnx_filename, uint flags=ONNX_DEFAULT); //load the onnx model from a .onnx file 
                     
                     matrix predict(const matrix &x); //passing inputs for either the encoder or the decoder to the outputs in matrix form
                     vector predict(const vector &x); //passing inputs for either the encoder or the decoder to the outputs in matrix form
  };

为每个模型分别实例化CAutoEncoderONNX类，具体如下：

MQL5 (AutoEncoder Indicator.mq5): 

#include <Autoencoder-onnx.mqh>
#include <MALE5\preprocessing.mqh>

CAutoEncoderONNX encoder_model; //for the encoder model
CAutoEncoderONNX decoder_model; //for the decoder model
MinMaxScaler *scaler; //Python-like MinMax scaler

初始化模型：

MQL5 (AutoEncoder Indicator.mq5): 

//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   if (!encoder_model.Init(encoder_onnx)) //initializing the encoder
     return INIT_FAILED;
   
   if (!decoder_model.Init(decoder_onnx)) //initializing the decoder
     return INIT_FAILED;
   
   scaler = new MinMaxScaler(min_values, max_values); //Load the Minmax scaler saved in python
     
//---
   return(INIT_SUCCEEDED);
  }

为了从模型中获取预测结果，我们将原始数据传递给编码器，然后将编码器的输出结果传递给解码器以获得最终输出。注意！在Python中，我们在call函数中依次传递了两个独立的模型。

Python:

class Autoencoder(Model):
...
...

  def call(self, x):
    encoded = self.encoder(x)
    decoded = self.decoder(encoded)
    return decoded

让我们在mql5中看一下：

MQL5 (AutoEncoder Indicator.mq5): 

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime& time[],
                const double& open[],
                const double& high[],
                const double& low[],
                const double& close[],
                const long& tick_volume[],
                const long& volume[],
                const int& spread[])
  {
//---
   
   int start = prev_calculated;
   if(start>=rates_total)
      start = rates_total-1;
   
   
   vector encoded_data = {}, decoded_data = {};
   for(int i = start; i<rates_total; i++)
     {
        vector x_inputs = {open[i], high[i], low[i], close[i]};
        
        x_inputs = scaler.transform(x_inputs); //Normalize the input data, important!
        encoded_data = encoder_model.predict(x_inputs); //encode the data
        decoded_data = decoder_model.predict(encoded_data); //decode the data
        
        decoded_data = scaler.inverse_transform(decoded_data); //return data to its original state  
          
        open_candle[i]= decoded_data[0];
        high_candle[i]= decoded_data[1];
        low_candle[i]=  decoded_data[2];
        close_candle[i]=decoded_data[3];
        
        // Set upper and lower body colors based on the gradient
        
        if (close_candle[i]>open_candle[i])
         {
           color_buffer[i] = 1.0; //Draw gray for bullish candle
         }
        else
         {
          color_buffer[i] = 0.0; //draw red when there was a bearish candle
         }
                         
        if (MQLInfoInteger(MQL_DEBUG))
         Comment(StringFormat("plotting [%d/%d] OPEN[%.5f] HIGH[%.5f] LOW[%.5f] CLOSE[%.5f]",i,rates_total,open_candle[i],high_candle[i],low_candle[i],close_candle[i]));
     }
     
//--- return value of prev_calculated for next call
   return(rates_total);
  }

指标图

自动编码器doji很像蜡烛

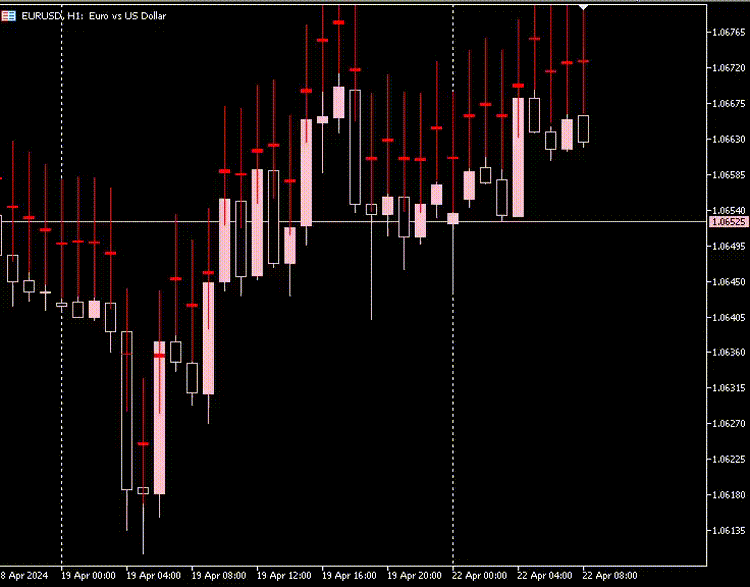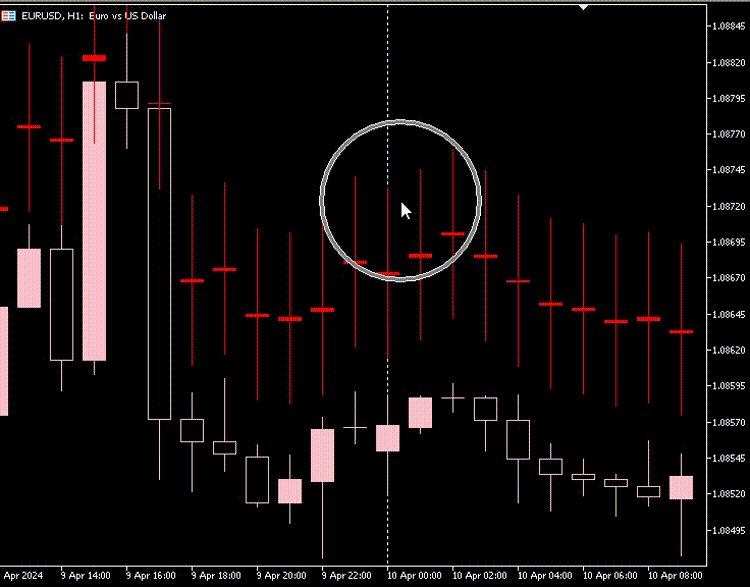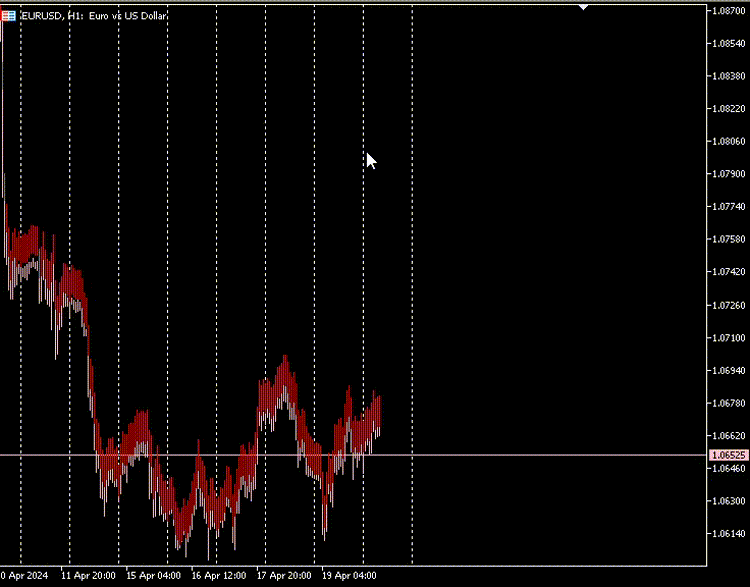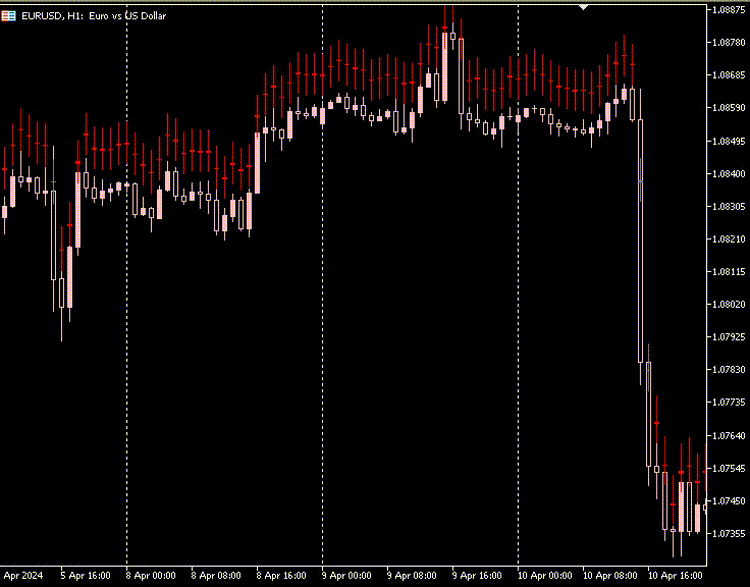
根据我的观察，由自动编码器生成的K线图中，K线的实体部分大小几乎相同，且所有K线的最低价和最高价之间的差异都很大且几乎一致。

大多数K线代表空头市场，用红色表示，而只有极少数K线代表多头市场，用灰色表示。

为了使这个指标在图表上更清晰地显示出来，我们可以填充K线最低价和最高价之间的空间。这对于多头K线和空头K线都适用。

MQL5 (AutoEncoder Indicator.mq5): 

  if (close_candle[i]>open_candle[i])
   {
     color_buffer[i] = 1.0; //Draw gray for bullish candle

     close_candle[i] = high_candle[i];
     open_candle[i] = low_candle[i];
   }
  else
   {
     color_buffer[i] = 0.0; //draw red when there was a bearish candle
    
     close_candle[i] = low_candle[i];
     open_candle[i] = high_candle[i];
   }

指标图

自动编码的新柱形

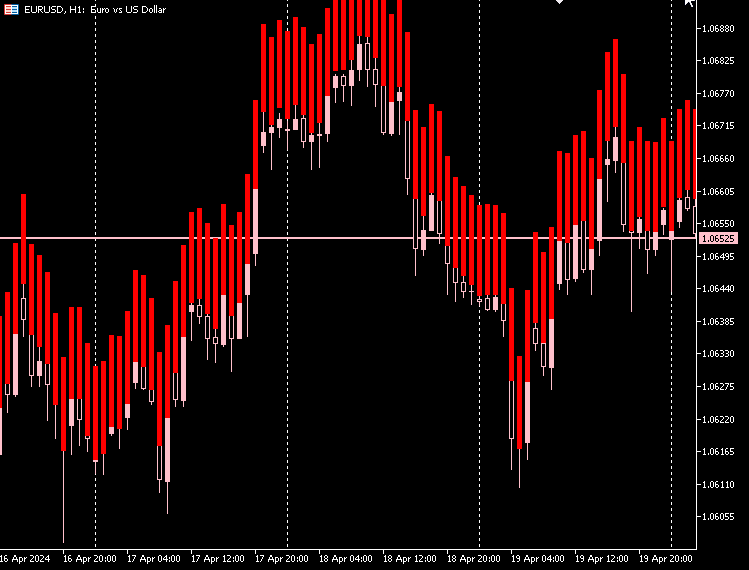
我们可以为指标提供一个选项，根据市场上的实际开盘价和收盘价来区分多头K线和空头K线。

MQL5 (AutoEncoder Indicator.mq5): 

if (show_bullish_bearish)
 {
  if (close[i]>open[i])
   color_buffer[i] = 1.0;
  else
    color_buffer[i] = 0.0;
 }

指标图

自动编码OHLCE URUSD彩色K线

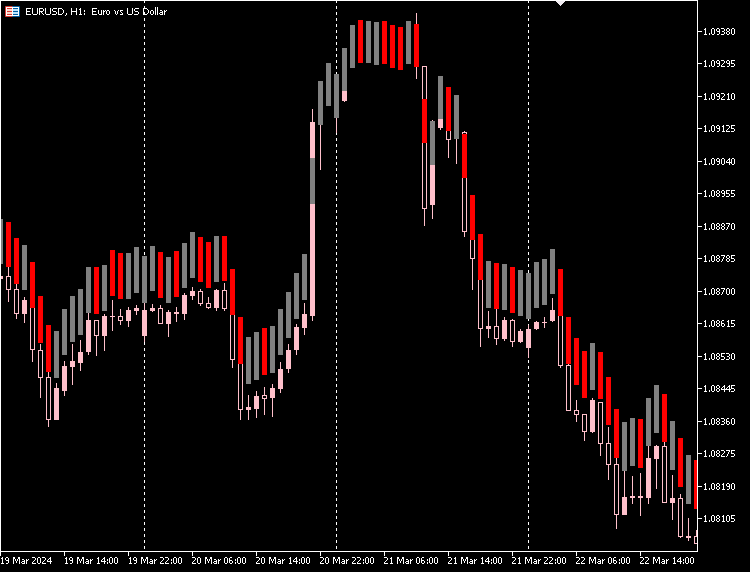
我们也可以选择隐藏原始K线图，而仅使用自编码器生成的新K线图的选项

自动编码器指示器显示条=false


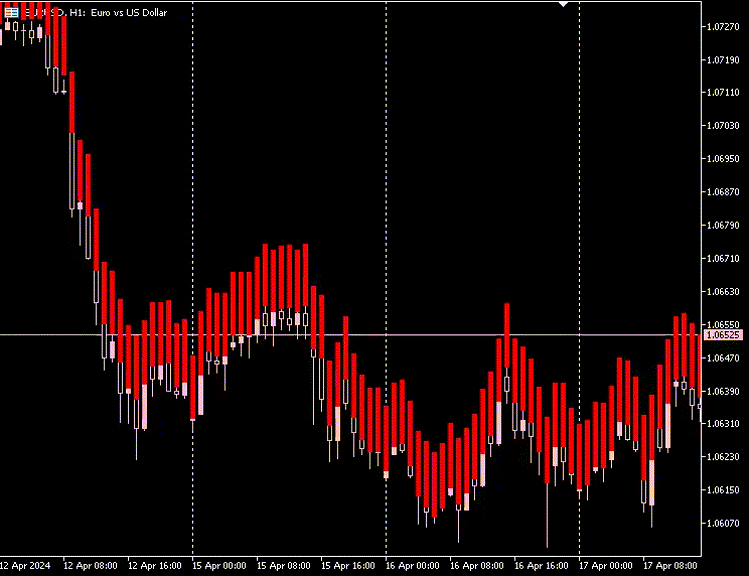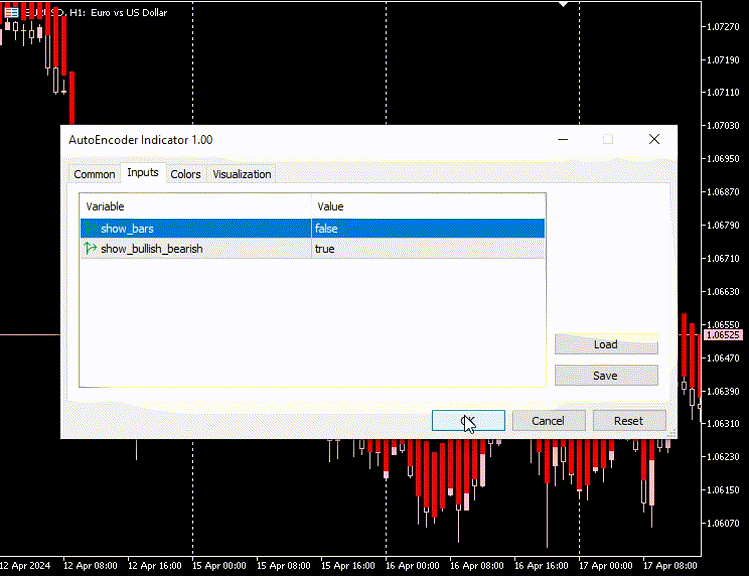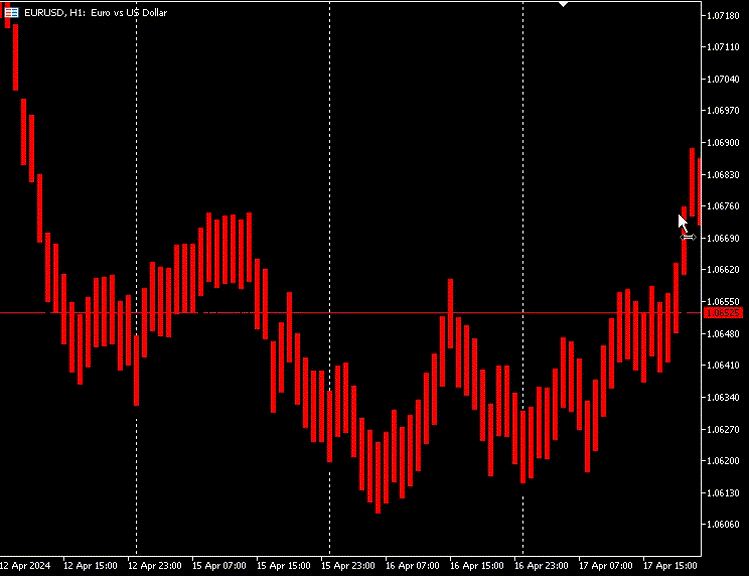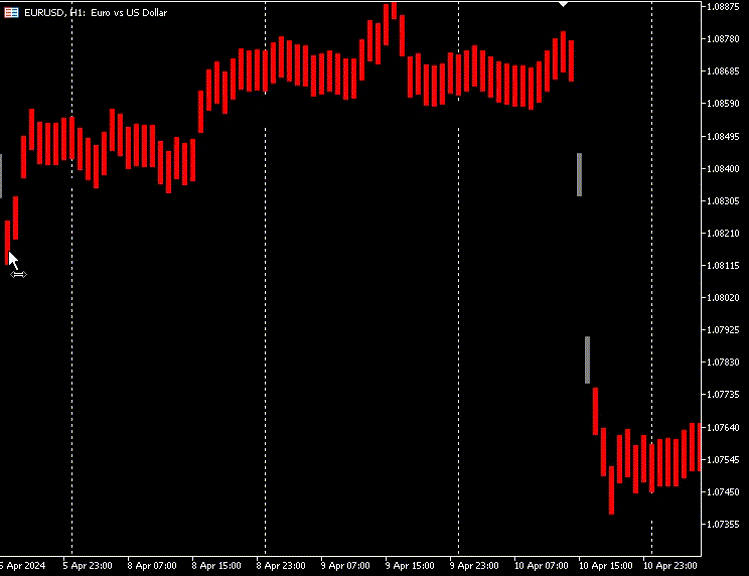
自动编码器的缺点

自动编码器像所有机器学习模型一样，都伴随着一系列的挑战：

  1. 数据重建方面的瑕疵
    自动编码器在压缩数据后尝试重新创建数据。有时，它们在这一方面的表现并不出色，导致在重建原始数据时会出现误差。如果您需要非常准确地重建原始数据，那么这就是一个问题。

  2. 很难理解
    自动编码器生成的压缩数据格式可能很难解释。如果不清楚自动编码器成功地捕捉到了数据的哪些特征，就很难解释模型的工作原理。

  3. 对噪声敏感
    自动编码器旨在突出数据的主要模式，但可能难以应对噪声和异常值。这可能导致重建效果不佳和特征有偏差，这不是理想的结果。

  4. 维度瓶颈
    自动编码器的中间层，即数据被压缩的那一层，有时空间会太小。如果这一层的维度不够，它可能无法捕获您为了完成任务所需的所有重要信息。为这一层选择合适的空间大小至关重要，具体取决于您想要实现的目标。

  5. 训练成本高
    训练深度自动编码器，尤其是在大型数据集上，会消耗大量的计算资源。如果您的资源或时间有限，了解这一点非常重要。

  6. 并非适用于所有任务
    自动编码器可能不是分类或回归等任务的最佳选择，因为对于这些任务而言，直接处理输入数据可能更为有效。

  7. 过拟合风险
    使用复杂模型解决简单问题可能导致过拟合，即模型对于现有数据的训练过于充分，但在新的、未见过的数据上却表现不佳。



总结

自动编码器是减少外汇市场噪声的一个强大工具，从我们最终得到的指标中可以看出，生成的K线图噪声更少，但仍能反映市场的情况。这些新的K线图可能比原始的蜡烛图表现更好或更差。这些新的K线图为我们提供了观察市场的不同视角。

您可以自由地从这些K线图的模式中提取信号，并在此基础上构建交易策略，以探索新的K线图。

告一段落。

附件表： 

文件 说明/用法
Include\MatrixExtend.mqh
 具有矩阵操作的附加功能。
Include\ preprocessing.mqh
 用于预处理原始输入数据，使其适合机器学习模型的库。
Indicators\ AutoEncoder Indicator.mq5 主要指标文件。用于部署探讨的自动编码器，并在预测结果上绘制K线图。
Include\ Autoencoder-onnx.mqh  用于加载ONNX格式的机器学习模型并解析输出结果的库。
Files\...  将这些文件保存在MQL5\files文件夹下
autoencoders.ipynb 用于运行所有讨论的Python代码的Python Jupyter笔记本 




本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/14760

附加的文件 |
下载ZIP
Code_6_Files.zip (689.5 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
数据科学与机器学习（第23部分）：为什么LightGBM和XGBoost能超越许多AI模型？ 数据科学与机器学习（第23部分）：为什么LightGBM和XGBoost能超越许多AI模型？
这些先进的梯度提升决策树技术提供了卓越的性能和灵活性，使其成为金融建模和算法交易的理想选择。了解如何利用这些工具来优化您的交易策略、提高预测准确性，并在金融市场中获得竞争优势。
MQL5 简介（第 7 部分）：在 MQL5 中构建 EA 交易和使用 AI 生成代码的初级指南 MQL5 简介（第 7 部分）：在 MQL5 中构建 EA 交易和使用 AI 生成代码的初级指南
在我们的综合文章中，了解使用 MQL5 构建 EA 交易的终极初学者指南。逐步学习如何使用伪代码构建 EA，并利用 AI（人工智能）生成代码的强大功能。无论你是算法交易的新手，还是想提高自己的技能，本指南都为你提供了创建有效 EA 的清晰路径。
获取市场优势的秘诀（第二部分）：预测技术指标 获取市场优势的秘诀（第二部分）：预测技术指标
你知道吗？与预测交易标的的基础价格相比，我们预测某些技术指标时能获得更高的准确性。加入我们，一起探索如何利用这一想法来制定更好的交易策略。
开发多币种 EA 交易 (第 10 部分):从字符串创建对象 开发多币种 EA 交易 (第 10 部分):从字符串创建对象
EA 开发计划包括几个阶段，中间结果保存在数据库中，它们只能作为字符串或数字而不是对象再次从那里读取。因此，我们需要一种方法来根据从数据库读取的字符串重新创建 EA 中的所需对象。