поиска закономерностей, описывающие основные закономерности
Все основные положения теории корреляции и регресии разработаны исходя из предположения о нормальном законе распределения исследуемых данных. А у вас входящие параметры (цена) имеют нормальное распределение?
Все основные положения теории корреляции и регресии разработаны исходя из предположения о нормальном законе распределения исследуемых данных. А у вас входящие параметры (цена) имеют нормальное распределение?
не понял
В принципе, покажу, что РМС выявляет любую закономерность, заложенную в ряде цифр, включая временной ряд (ВР), думаю, независимо от природы появления этих цифр в ряду. Все этие и другие тонкости будем обсуждать на конкретных примерах, включая анализ случайного ряда.
РМС то действительную или вымышленную закономерность находить будет, но из-за отсутствия нормальности распределения прогностицеская ценность модели будет равна 0. Это не тонкости, это - фундамент.
Что, конкретно, не поняли?
РМС то действительную или вымышленную закономерность находить будет, но из-за отсутствия нормальности распределения прогностицеская ценность модели будет равна 0. Это не тонкости, это - фундамент.
РМС будет находить не вымешленную, а наиболее адекватную зависимость. А насчет отсутствия или присутствия нормальности распределения исходных данных откроем отдельную ветьв дискусси и пусть здесь паралельно выскажутся знатоки этого фундамента.
Понял..... И правильно - да ну ее, нормальность! Только мешается
P.S. прогностическая ценность модели будет близка к 0
Пожалуй, начнем с линейной функции.
Представим себе, что ряд задан цифрами Yi = a+bxi:
xi Yi
0,00000001 10,0000
1,00000001 15,0000
2,00000001 20,0000
3,00000001 25,0000
4,00000001 30,0000
5,00000001 35,0000
6,00000001 40,0000
7,00000001 45,0000
8,00000001 50,0000
9,00000001 55,0000
10,00000001 60,0000
11,00000001 65,0000
12,00000001 70,0000
13,00000001 75,0000
14,00000001 80,0000
15,00000001 85,0000
16,00000001 90,0000
17,00000001 95,0000
18,00000001 100,0000
Вот график фактических и расчетных значений, ошибка модели 2,78163E-14%:
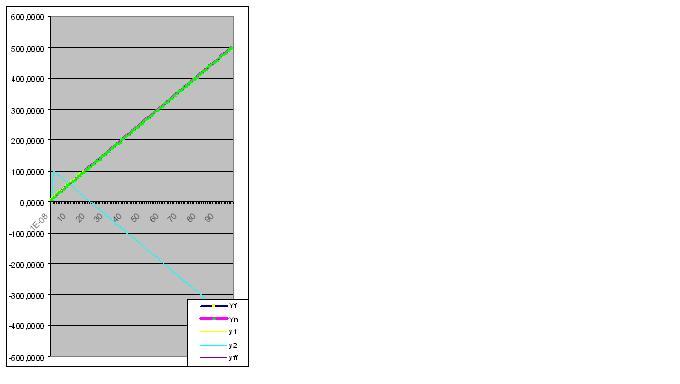
Понял..... И правильно - да ну ее, нормальность! Только мешается
P.S. прогностическая ценность модели будет близка к 0
В звязи с Вашим упорством, я вынужден начать с демонстрации прогностических способностей модели на примере анализа функции Y=tg(0,1x)+2 и введем первые 8 пар цифр:
xi Yi
0,00000001 2,0000
1,00000001 2,1003
2,00000001 2,2027
3,00000001 2,3093
4,00000001 2,4228
5,00000001 2,5463
6,00000001 2,6841
7,00000001 2,8423
Ошибка 0,427140953%:
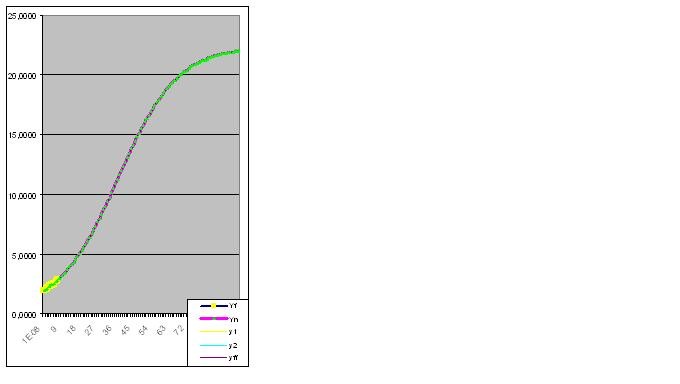
Однако, стоит ввести 9-ую пару цифр, как модель сразу прогнозирует о "странном" поведения объекта в будущем:
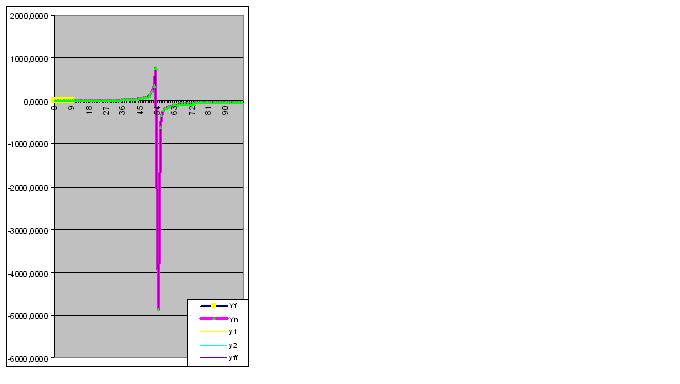
Дальнейшее введение данных приближает прогнозную "аномалию" к исходным данным:
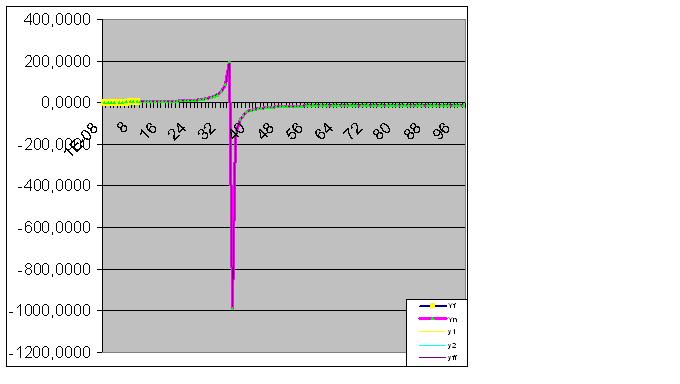
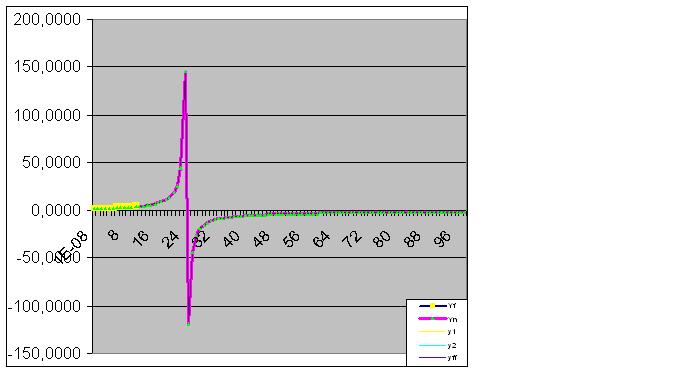
Вот и исходные данные также начали осуществлять спрогозированный "финт":
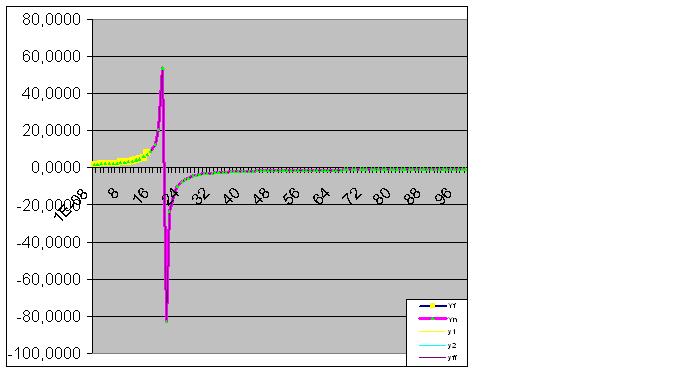
И наконец, прогноз идеально осущесвился:
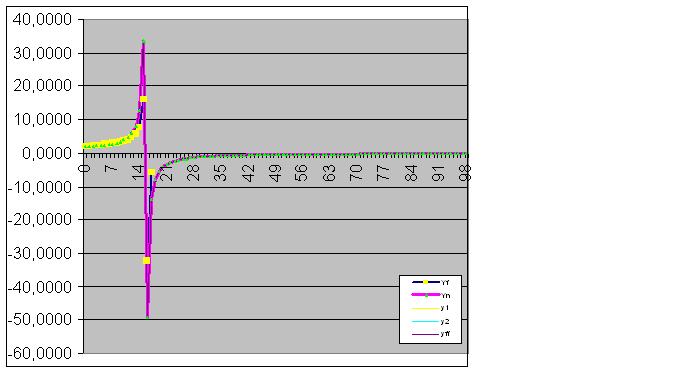
Дальше модель идеально ловит конечное состояние объекта, так, что сумма фактических значений функции равна расчетной по РМС с компьютерной точностью
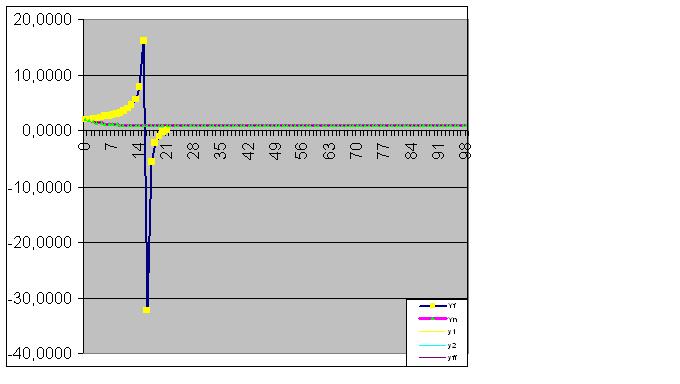
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Уважаемые форумчане, не секрет. что актуальным является вопрос поиска зависимостей, описывающие основные закономерности рынка. Здесь попытаемся приблизиться к решению этого вопроса всеми доступными средствами анализа, включая различные предложения участников по этому поводу и накопленный к этому моменту теоретический и практический материал из всевозможных источников. В результате этой работы если мы остановимся даже только на виде этой функции, думаю, будем считать, что времени и сил затрачены не зря.
Я начну с демонстрации возможностей РМС на простых примерах описания известных закономерностей : линейной зависимости, параболы, гиперболы, экспоненты, синуса, косинуса, тангенса, котангенса и других, а также их сочетании, которые, несомненно, присутствуют на рынке. Прошу поддержать меня в этом порыве с конструктивными предложениями и здоровой критикой, если потребуется.