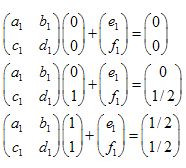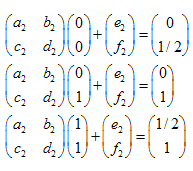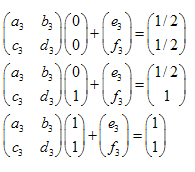Ставь лайки и следи за новостями
Поставь на него ссылку - пусть другие тоже оценят
Оцени его работу в терминале MetaTrader 5

Построение фрактальных множеств в MQL5 при помощи системы итерированных функций (IFS) - эксперт для MetaTrader 5
- Просмотров:
- 9437
- Рейтинг:
- Опубликован:
- Обновлен:
-
Нужен робот или индикатор на основе этого кода? Закажите его на бирже фрилансеров Перейти на биржу
Введение
В настоящее время существует несколько программ для отображения самоподобных множеств, заданных при помощи системы итерированных функций (Iterated Function System, IFS), например, Fractint и Fractal Designer, для пакета Matlab разработан IFS Matlab Generator. Изучение этих множеств можно осуществлять и в терминале MetaTrader 5 благодаря высокой скорости расчетов языка MQL5 и возможностью работы с графическими объектами.
Библиотека для создания изображений cIntBMP, разработанная Дмитрием (Integer), открывает новые возможности работы с графикой и значительно упрощает создание собственных графических изображений. Разработка была отмечена специальным призом от компании MetaQuotes Software Corp.
В данной работе мы приведем пример использования библиотеки cIntBMP, а также рассмотрим принцип и алгоритмы построения фрактальных множеств при помощи системы итерированных функций.
1. Aффинные преобразования плоскости
Аффинные преобразование (АП) представляет собой отображение плоскости ![]() и описывается при помощи некоторой матрицы
и описывается при помощи некоторой матрицы ![]() и вектора
и вектора ![]() , т.е. каждая точка плоскости (x,y) переводится в некоторую точку
, т.е. каждая точка плоскости (x,y) переводится в некоторую точку ![]() по правилу:
по правилу:
![]()
Для того чтобы преобразование было однозначным, необходимо, чтобы ![]() . АП производит изменение площади множества на плоскости в
. АП производит изменение площади множества на плоскости в ![]() раз.
раз.
Аффинные преобразования сохраняют природу основных геометрических образов (прямые переводят в прямые), с их помощью можно описывать "деформации" объекта на плоскости, например вращение + масштабирование + параллельный перенос.
Примеры АП плоскости:
1) Вращение плоскости на угол:
2) "Масштабирование" плоскости c коэффициентами
и
(по осям X и Y соответственно):
3) Параллельный перенос плоскости на вектор
:
Нас будут интересовать сжимающие отображения (см. также свойства IFS). Пусть точки ![]() и
и ![]() имеют координаты
имеют координаты ![]() и
и ![]() . Пусть
. Пусть ![]() - метрика (например, евклидова:
- метрика (например, евклидова: ![]() ). Аффинное преобразование называется сжимающим, если
). Аффинное преобразование называется сжимающим, если ![]() , где
, где ![]() .
.
Пример сжимающего АП:
![]()
Результат действия данного АП:
Обычно фракталы строятся следующим образом: берется некоторый (простой) геометрический объект (отрезок, треугольник, квадрат), делится на N частей (для простоты будем считать их одинаковыми), затем M из них берется для дальнейшего "конструирования" множества. (Если M=N, то никакой "фрактальности" не будет). Далее подобную процедуру применяют к каждому из полученных кусков объекта и т.д.
Примеры (классические):
Отрезок:
- Триадная кривая Koch (Triadic Koch Curve), N=3, M=4;
- Канторова пыль (Cantor Dust), N=3, M=2;
Треугольник:
- Треугольная салфетка (набивка) Серпинского (Sierpinski Gasket) N=4, M=3;
Квадрат:
- Ковер Серпинского (Sierpinski Carpet), N=9, M=8;
- Фрактал Вичека (Vichek), N=9, M=5.
и т.д.
Поскольку фрактальные множества имеют самоподобную структуру, они могут быть описаны при помощи нескольких аффинных преобразований "подобия", при которых исходное множество содержит копии самого себя. Структура преобразований зависит от способа построения фрактала. Для описания структуры фрактального множества нам достаточно описать лишь 1-й этап построения фрактала и "закодировать" его в набор аффинных преобразований.
Пусть имеется некоторое исходное множество. Пусть алгоритм требует уменьшить его, повернуть и "поставить на определенное место". Надо описать этот процесс при помощи аффинного преобразования, т.е. найти матрицу и вектор.
Как легко убедиться, достаточно взять 3 точки исходного множества, не лежащие на одной прямой и "перевести" их в 3 соответствующие точки "уменьшенного" множества. При этом получается система из 6 уравнений на неизвестные a,b,c,d,e,f, которую можно решить.
Действительно, пусть треугольник ![]() переходит в треугольник
переходит в треугольник ![]() . Записав преобразования вершин треугольника в виде аффинных преобразований общего вида, получим систему линейных уравнений, в решив которую, получим коэффициенты аффинного преобразования: коэффициенты a,b,c и d матрицы преобразования и компоненты e и f вектора сдвига:
. Записав преобразования вершин треугольника в виде аффинных преобразований общего вида, получим систему линейных уравнений, в решив которую, получим коэффициенты аффинного преобразования: коэффициенты a,b,c и d матрицы преобразования и компоненты e и f вектора сдвига:
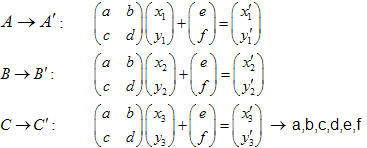
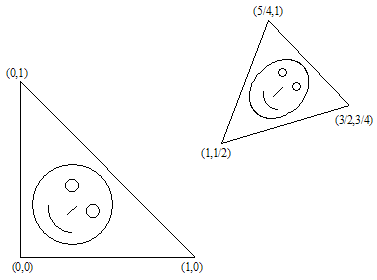
Пример: Треугольная салфетка Серпинского (Sierpinski Gasket):
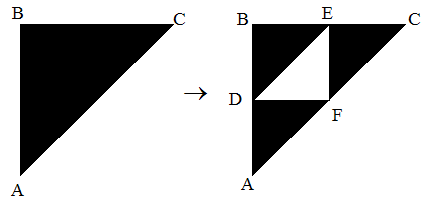
Координаты точек:
- A (0,0)
- B (0,1)
- C (1,1)
- D(0,1/2)
- E (1/2,1)
- F(1/2,1/2)
Имеем 3 преобразования:
- ABC -> ADF
- ABC -> DBE
- ABC -> FEC
Системы уравнений для каждого из преобразований:
Решения: 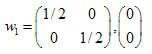 ,
, 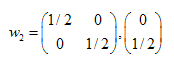 ,
, 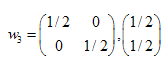
Таким образом, мы получили коэффициенты трех аффинных преобразований. Используя эти коэффициенты, можно осуществить построение фрактального множества, причем не предфрактал N-го порядка, а само множество.
3. Построение фрактальных множеств при помощи системы итерированных функций (IFS)
Система итерированных функций (Iterated Function System) представляет собой набор аффинных сжимающих отображений. Каждая из функций задается набором 7 чисел: ![]() , где
, где![]() - веса, которые будут использоваться при построении множества (они представляют "вероятность" выполнения n-го преобразования). Обычно их выбирают пропорционально "площадям":
- веса, которые будут использоваться при построении множества (они представляют "вероятность" выполнения n-го преобразования). Обычно их выбирают пропорционально "площадям": 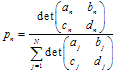 :
:
Алгоритм построения множества при помощи IFS заключается в следующем.
Берется начальная точка на плоскости с координатами ![]() . Далее случайным образом выбирается одно из преобразований строится точка
. Далее случайным образом выбирается одно из преобразований строится точка ![]() . Затем снова случайно выбираем одно из преобразований
. Затем снова случайно выбираем одно из преобразований ![]() и строим
и строим ![]() . Таким образом строится множество точек
. Таким образом строится множество точек ![]()
Преобразования выбираем случайным образом с вероятностями, пропорциональными для данного преобразования. Если этот процесс повторять достаточно долго (построить~30000 точек), то в итоге обнаружим, что полученное множество обладает структурой, несмотря на "случайность" выбора преобразований.
Пример построения треугольной салфетки Серпинского (Sierpinski Gasket):
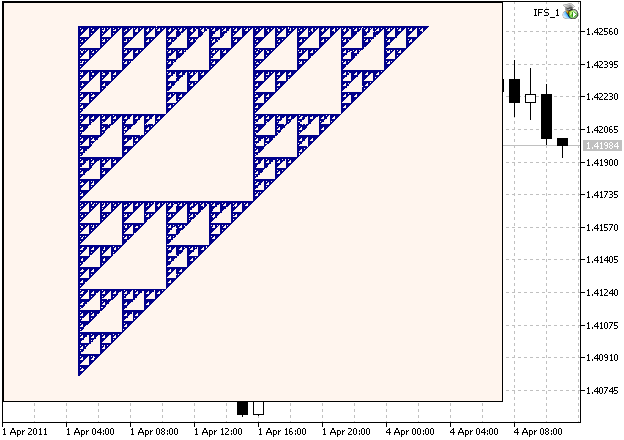
Рисунок 1. Треугольная салфетка Серпинского, построенная на базе IFS-функций раздела 2
Код:
//+------------------------------------------------------------------+ //| IFS_Sierpinski_Gasket.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" //-- включаем файл с классом cIntBMP #include <cIntBMP.mqh> //-- коэффициенты IFS для треугольной салфетки Серпинского //-- матрицы (a,b,c,d) double IFS_a[3] = {0.50, 0.50, 0.50}; double IFS_b[3] = {0.00, 0.00, 0.00}; double IFS_c[3] = {0.00, 0.00, 0.00}; double IFS_d[3] = {0.50, 0.50, 0.50}; //-- векторы сдвига (e,f) double IFS_e[3] = {0.00, 0.00, 0.50}; double IFS_f[3] = {0.00, 0.50, 0.50}; //-- "вероятности" преобразований, умноженные на 1000 double IFS_p[3]={333,333,333}; double Probs[3]; // массив Probs - используется для удобства выбора преобразований cIntBMP bmp; // экземпляр класса cIntBMP int scale=1350; // масштабный множитель //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //-- подготавливаем массив для удобной работы с вероятностями double m=0; for(int i=0; i<ArraySize(IFS_p); i++) { Probs[i]=IFS_p[i]+m; m=m+IFS_p[i]; } //-- размеры изображения BMP на экране графика int XSize=500; int YSize=400; //-- создаем bmp-картинку размером XSizexYSize c фоном цвета clrSeashell bmp.Create(XSize,YSize,clrSeashell); //-- рисуем рамку bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack); //-- координаты точек (будут испольться при построении множества) double x0=0; double y0=0; double x,y; //-- количество точек для расчета (чем больше точек, тем подробнее множество) int points=1500000; //-- расчет points точек for(int i=0; i<points; i++) { // с вероятностями, пропорциональными IFS_p // выбираем преобразование и выполняем его double prb=1000*(rand()/32767.0); for(int k=0; k<ArraySize(IFS_p); k++) { if(prb<=Probs[k]) { // осуществляем аффинное преобразование x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k]; y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k]; // обновляем предыдущие координаты x0 = x; y0 = y; // преобразуем в реальные координаты на BMP-картинке // (обратите внимание на то, как задаются ордината Y в классе cIntBMP int scX = int (MathRound(XSize/2 + (x-0.5)*scale)); int scY = int (MathRound(YSize/2 + (y-0.5)*scale)); // если координаты точки входят в размеры bmp-картинки, рисуем точку if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); } break; } } } //-- сохраняем полученную картинку в файл bmp.Save("bmpimg",true); //-- выводим ее на экран bmp.Show(0,0,"bmpimg","IFS"); //--- return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- удаляем bmp-картинку IFS с графика ObjectDelete(0,"IFS"); //--- удаляем файл bmp.Delete("bmpimg",true); } //+------------------------------------------------------------------+
Если в данном коде установить scale=1350, количество точек увеличить до 15000000, а параметры сдвига начальной точки:
int scX = int (MathRound(XSize/2 + (x-0.75)*scale)); int scY = int (MathRound(YSize/2 + (y-0.75)*scale));
то получим увеличенный фрагмент данного множества.
Как видно, оно имеет самоподобную структуру (рис. 2), т.е. содержит копии самого себя.
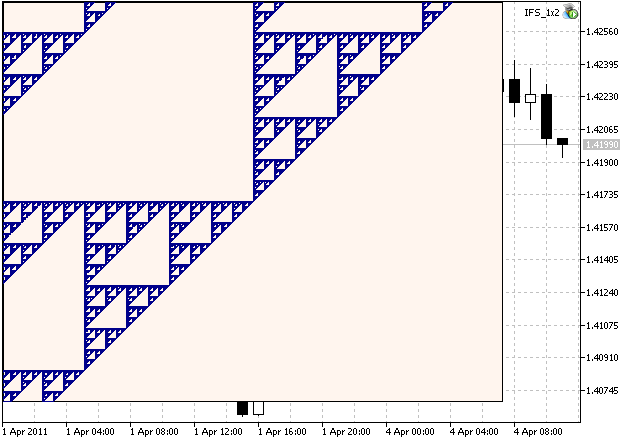
Рисунок 2. Увеличенный фрагмент треугольной салфетки Серпинского
Рассмотрим более сложный пример - фрактальный папоротник (IFS Fern), предложенный Майклом Барнсли (Michael Barnsley):
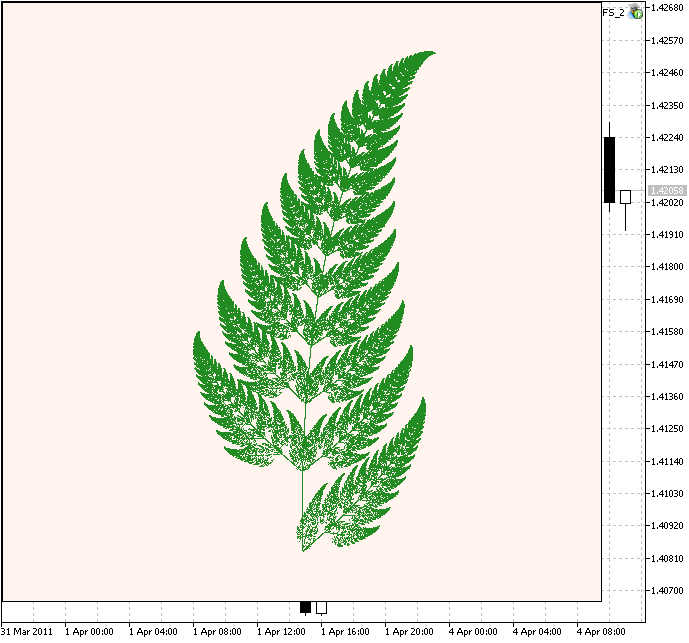
Рисунок 3. Фрактальный папоротник Барнсли
Код аналогичен, в данном случае имеем уже четыре IFS-преобразования, на этот раз с различными весами.
//+------------------------------------------------------------------+ //| IFS_fern.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include <cIntBMP.mqh> //-- коэффициенты IFS для папоротника Барнсли //-- матрицы (a,b,c,d) double IFS_a[4] = {0.00, 0.85, 0.20, -0.15}; double IFS_b[4] = {0.00, 0.04, -0.26, 0.28}; double IFS_c[4] = {0.00, -0.04, 0.23, 0.26}; double IFS_d[4] = {0.16, 0.85, 0.22, 0.24}; //-- векторы сдвига (e,f) double IFS_e[4] = {0.00, 0.00, 0.00, 0.00}; double IFS_f[4] = {0.00, 1.60, 1.60, 0.00}; //-- "вероятности" преобразований, умноженные на 1000 double IFS_p[4] = {10, 850, 70, 70}; double Probs[4]; cIntBMP bmp; int scale=50; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { double m=0; for(int i=0; i<ArraySize(IFS_p); i++) { Probs[i]=IFS_p[i]+m; m=m+IFS_p[i]; } int XSize=600; int YSize=600; bmp.Create(XSize,YSize,clrSeashell); bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack); double x0=0; double y0=0; double x,y; int points=250000; for(int i=0; i<points; i++) { double prb=1000*(rand()/32767.0); for(int k=0; k<ArraySize(IFS_p); k++) { if(prb<=Probs[k]) { x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k]; y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k]; x0 = x; y0 = y; int scX = int (MathRound(XSize/2 + (x)*scale)); int scY = int (MathRound(YSize/2 + (y-5)*scale)); if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrForestGreen); } break; } } } bmp.Save("bmpimg",true); bmp.Show(0,0,"bmpimg","IFS"); //--- return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { ObjectDelete(0,"IFS"); bmp.Delete("bmpimg",true); } //+------------------------------------------------------------------+
Обратите внимание на то, что такая сложная структура определяется небольшим набором чисел (28).
Если в данном коде величину scale увеличить до 150, а количество точек установить равным 1250000, получим увеличенный фрагмент:
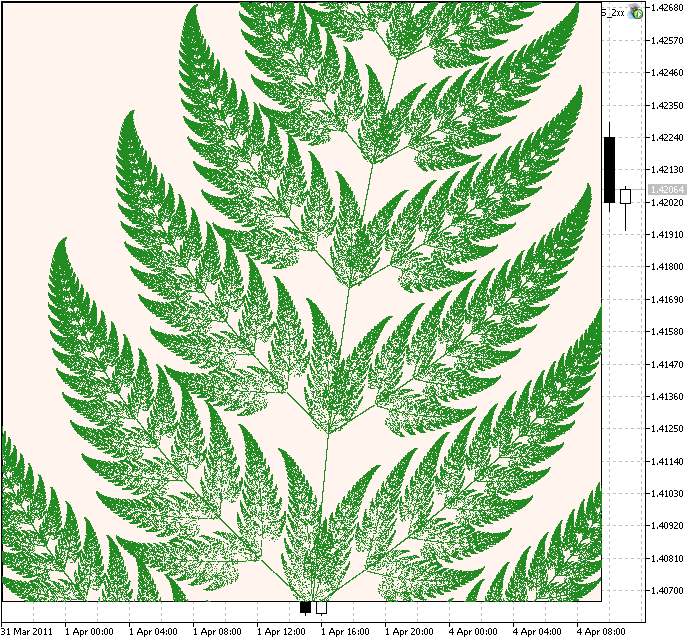
Рисунок 4. Увеличенный фрагмент фрактального папоротника Барнсли
Таким образом, при помощи IFS можно осуществлять построение различных фрактальных множеств.
Другой пример - ковер Серпинского (Sierpinski Carpet):
//-- коэффициенты IFS для ковра Серпинского double IFS_a[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333}; double IFS_b[8] = {0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00}; double IFS_c[8] = {0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00}; double IFS_d[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333}; double IFS_e[8] = {-0.125, -3.375, -3.375, 3.125, 3.125, -3.375, -0.125, 3.125}; double IFS_f[8] = {6.75, 0.25, 6.75, 0.25, 6.75, 3.5, 0.25, 3.50}; //-- "вероятности" преобразований, умноженные на 1000 double IFS_p[8]={125,125,125,125,125,125,125,125};

Рисунок 5. Ковер Серпинского
В разделе 2 была описана общая схема вычисления коэффициентов IFS-преобразований.
В качестве иллюстрации приведем пример построения самоподобной надписи "ФРАКТАЛЫ".
Заготовка выглядит следующим образом:
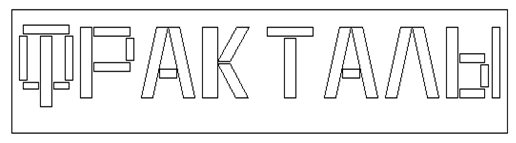
Рисунок 6. Заготовка множества "ФРАКТАЛЫ"
Для вычисления коэффициентов следует решить уравнения, описывающие преобразования заданных трех точек прямоугольника в соответствующие точки каждого из маленьких прямоугольников. Решая систему линейных уравнений, получим коэффициенты IFS:
//-- коэффициенты IFS для множества "ФРАКТАЛЫ" double IFS_a[28]= { 0.00, 0.03, 0.00, 0.09, 0.00, 0.03, -0.00, 0.07, 0.00, 0.07, 0.03, 0.03, 0.03, 0.00, 0.04, 0.04, -0.00, 0.09, 0.03, 0.03, 0.03, 0.03, 0.03, 0.00, 0.05, -0.00, 0.05, 0.00 }; double IFS_b[28]= { -0.11, 0.00, 0.07, 0.00, -0.07, 0.00, -0.11, 0.00, -0.07, 0.00, -0.11, 0.11, 0.00, -0.14, -0.12, 0.12,-0.11, 0.00, -0.11, 0.11, 0.00, -0.11, 0.11, -0.11, 0.00, -0.07, 0.00, -0.07 }; double IFS_c[28]= { 0.12, 0.00, 0.08, -0.00, 0.08, 0.00, 0.12, 0.00, 0.04, 0.00, 0.12, -0.12, 0.00, 0.12, 0.06, -0.06, 0.10, 0.00, 0.12, -0.12, 0.00, 0.12, -0.12, 0.12, 0.00, 0.04, 0.00, 0.12 }; double IFS_d[28]= { 0.00, 0.05, 0.00, 0.07, 0.00, 0.05, 0.00, 0.07, 0.00, 0.07, 0.00, 0.00, 0.07, 0.00, 0.00, 0.00, 0.00, 0.07, 0.00, 0.00, 0.07, 0.00, 0.00, 0.00, 0.07, 0.00, 0.07, 0.00 }; double IFS_e[28]= { -4.58, -5.06, -5.16, -4.70, -4.09, -4.35, -3.73, -3.26, -2.76, -3.26, -2.22, -1.86, -2.04, -0.98, -0.46, -0.76, 0.76, 0.63, 1.78, 2.14, 1.96, 3.11, 3.47, 4.27, 4.60, 4.98, 4.60, 5.24 }; double IFS_f[28]= { 1.26, 0.89, 1.52, 2.00, 1.52, 0.89, 1.43, 1.96, 1.69, 1.24, 1.43, 1.41, 1.11, 1.43, 1.79, 1.05, 1.32, 1.96, 1.43, 1.41, 1.11, 1.43, 1.41, 1.43, 1.42, 1.16, 0.71, 1.43 }; //-- "вероятности" преобразований, умноженные на 1000 double IFS_p[28]= { 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35 };
В результате получается следующая картинка:

Рисунок 7. Самоподобная надпись "ФРАКТАЛЫ"
Полный исходный код находится в файле ifs_4.mq5.
При увеличении данного множества, оно также показывает самоподобную структуру:

Рисунок 8. Увеличенный фрагмент множества "ФРАКТАЛЫ"
Программа Fractal Designer позволяет конструировать самоподобные множества на базе IFS.
Мы рассмотрели построение фрактальных множеств при помощи системы итерированных функций (IFS). Благодаря библиотеке cIntBMP рисование графических изображений получилось очень простым. Теперь обернем этот функционал в класс и реализуем отображение множеств различными цветами.
4. Класс для построения множеств IFS
Картинки, полученные при помощи IFS, можно сделать более красивыми, если учесть в цветовом построении структуру множества. Сами множества зачастую имеют нерегулярную структуру (например, см. веса преобразований папоротника Барнсли), поэтому цвет точек можно задавать в соответствии с частотой попадания точки в данную окрестность.
Данный подход удобно реализовать при помощи виртуального экрана, т.е. расчет цвета картинки производить в массиве в зависимости от текущего цвета заданного пиксела, а затем преобразовывать путем установки цветов в bmp в соответствии с палитрой.
При этом саму bmp-картинку можно рисовать на заднем фоне, установив соответствующее свойство отображения.
Код советника на базе класса CIFS:
//+------------------------------------------------------------------+ //| IFS_Fern_color.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #include <cIntBMP.mqh> //-- коэффициенты IFS папоротника Барнсли double IFS_a[4] = {0.00, 0.85, 0.20, -0.15}; double IFS_b[4] = {0.00, 0.04, -0.26, 0.28}; double IFS_c[4] = {0.00, -0.04, 0.23, 0.26}; double IFS_d[4] = {0.16, 0.85, 0.22, 0.24}; double IFS_e[4] = {0.00, 0.00, 0.00, 0.00}; double IFS_f[4] = {0.00, 1.60, 1.60, 0.00}; double IFS_p[4] = {10, 850, 70, 70}; //-- палитра uchar Palette[23*3]= { 0x00,0x00,0x00,0x02,0x0A,0x06,0x03,0x11,0x0A,0x0B,0x1E,0x0F,0x0C,0x4C,0x2C,0x1C,0x50,0x28, 0x2C,0x54,0x24,0x3C,0x58,0x20,0x4C,0x5C,0x1C,0x70,0x98,0x6C,0x38,0xBC,0xB0,0x28,0xCC,0xC8, 0x4C,0xB0,0x98,0x5C,0xA4,0x84,0xBC,0x68,0x14,0xA8,0x74,0x28,0x84,0x8C,0x54,0x94,0x80,0x40, 0x87,0x87,0x87,0x9F,0x9F,0x9F,0xC7,0xC7,0xC7,0xDF,0xDF,0xDF,0xFC,0xFC,0xFC }; //+------------------------------------------------------------------+ //| Класс CIFS | //+------------------------------------------------------------------+ class CIFS { protected: cIntBMP m_bmp; int m_xsize; int m_ysize; uchar m_virtual_screen[]; double m_scale; double m_probs[8]; public: ~CIFS() { m_bmp.Delete("bmpimg",true); }; void Create(int x_size,int y_size,uchar col); void Render(double scale,bool back); void ShowBMP(bool back); protected: void VS_Prepare(int x_size,int y_size,uchar col); void VS_Fill(uchar col); void VS_PutPixel(int px,int py,uchar col); uchar VS_GetPixel(int px,int py); int GetPalColor(uchar index); int RGB256(int r,int g,int b) const {return(r+256*g+65536*b); } void PrepareProbabilities(); void RenderIFSToVirtualScreen(); void VirtualScreenToBMP(); }; //+------------------------------------------------------------------+ //| Метод создания | //+------------------------------------------------------------------+ void CIFS::Create(int x_size,int y_size,uchar col) { m_bmp.Create(x_size,y_size,col); VS_Prepare(x_size,y_size,col); PrepareProbabilities(); } //+------------------------------------------------------------------+ //| Подготовка виртуального экрана | //+------------------------------------------------------------------+ void CIFS::VS_Prepare(int x_size,int y_size,uchar col) { m_xsize=x_size; m_ysize=y_size; ArrayResize(m_virtual_screen,m_xsize*m_ysize); VS_Fill(col); } //+------------------------------------------------------------------+ //| Метод заполнения виртуального экрана заданным цветом | //+------------------------------------------------------------------+ void CIFS::VS_Fill(uchar col) { for(int i=0; i<m_xsize*m_ysize; i++) {m_virtual_screen[i]=col;} } //+------------------------------------------------------------------+ //| Метод возвращает цвет с заданным индексом из палитры Palette | //+------------------------------------------------------------------+ int CIFS::GetPalColor(uchar index) { int ind=index; if(ind<=0) {ind=0;} if(ind>22) {ind=22;} uchar r=Palette[3*(ind)]; uchar g=Palette[3*(ind)+1]; uchar b=Palette[3*(ind)+2]; return(RGB256(r,g,b)); } //+------------------------------------------------------------------+ //| Метод "рисует" пиксел в массиве виртуального экрана | //+------------------------------------------------------------------+ void CIFS::VS_PutPixel(int px,int py,uchar col) { if (px<0) return; if (py<0) return; if (px>m_xsize) return; if (py>m_ysize) return; int pos=m_xsize*py+px; if(pos>=ArraySize(m_virtual_screen)) return; m_virtual_screen[pos]=col; } //+------------------------------------------------------------------+ //| Метод получает значение пиксела из массива виртуального экрана | //+------------------------------------------------------------------+ uchar CIFS::VS_GetPixel(int px,int py) { if (px<0) return(0); if (py<0) return(0); if (px>m_xsize) return(0); if (py>m_ysize) return(0); int pos=m_xsize*py+px; if(pos>=ArraySize(m_virtual_screen)) return(0); return(m_virtual_screen[pos]); } //+------------------------------------------------------------------+ //| Метод подготовки массива для вероятностей | //+------------------------------------------------------------------+ void CIFS::PrepareProbabilities() { double m=0; for(int i=0; i<ArraySize(IFS_p); i++) { m_probs[i]=IFS_p[i]+m; m=m+IFS_p[i]; } } //+------------------------------------------------------------------+ //| Метод отображения IFS в виртуальный экран | //+------------------------------------------------------------------+ void CIFS::RenderIFSToVirtualScreen() { double x=0,y=0; double x0=0; double y0=0; uint iterations= uint (MathRound(100000+100*MathPow(m_scale,2))); for(uint i=0; i<iterations; i++) { double prb=1000*(rand()/32767.0); for(int k=0; k<ArraySize(IFS_p); k++) { if(prb<=m_probs[k]) { x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k]; y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k]; int scX = int (MathRound(m_xsize/2 + (x-0)*m_scale)); int scY = int (MathRound(m_ysize/2 + (y-5)*m_scale)); if(scX>=0 && scX<m_xsize && scY>=0 && scY<m_ysize) { uchar c=VS_GetPixel(scX,scY); if(c<255) c=c+1; VS_PutPixel(scX,scY,c); } break; } x0 = x; y0 = y; } } } //+------------------------------------------------------------------+ //| Метод копирования виртуального экрана в bmp | //+------------------------------------------------------------------+ void CIFS::VirtualScreenToBMP() { for(int i=0; i<m_xsize; i++) { for(int j=0; j<m_ysize; j++) { uchar colind=VS_GetPixel(i,j); int xcol=GetPalColor(colind); if(colind==0) xcol=0x00; //if(colind==0) xcol=0xFFFFFF; m_bmp.DrawDot(i,j,xcol); } } } //+------------------------------------------------------------------+ //| Метод показывает bmp-картинку на заднем фоне графика | //+------------------------------------------------------------------+ void CIFS::ShowBMP(bool back) { m_bmp.Save("bmpimg",true); m_bmp.Show(0,0,"bmpimg","Fern"); ObjectSetInteger(0,"Fern",OBJPROP_BACK,back); } //+------------------------------------------------------------------+ //| Метод расчета и вывода изображения на график (на заднем фоне) | //+------------------------------------------------------------------+ void CIFS::Render(double scale,bool back) { m_scale=scale; VS_Fill(0); RenderIFSToVirtualScreen(); VirtualScreenToBMP(); ShowBMP(back); } static int gridmode; CIFS fern; int currentscale=50; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { //-- запрашиваем текущий режим отображения сетки gridmode= int (ChartGetInteger(0,CHART_SHOW_GRID,0)); //-- выключаем отображение сетки ChartSetInteger(0,CHART_SHOW_GRID,0); //-- создаем картинку fern.Create(800,800,0x00); //-- выводим на экран (как фоновую) fern.Render(currentscale,true); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int r) { //-- восстанавливаем ранее отображение сетки ChartSetInteger(0,CHART_SHOW_GRID,gridmode); //-- удаляем объект Fern ObjectDelete(0,"Fern"); } //+------------------------------------------------------------------+ //| Expert OnChart event handler | //+------------------------------------------------------------------+ void OnChartEvent(const int id, // Event identifier const long& lparam, // Event parameter of long type const double& dparam, // Event parameter of double type const string& sparam // Event parameter of string type ) { //--- клик мыши на графическом объекте if(id==CHARTEVENT_OBJECT_CLICK) { Print("Клик на графическом объекте с именем '"+sparam+"'"); if(sparam=="Fern") { // увеличиваем масштабный множитель currentscale=int (currentscale*1.1); fern.Render(currentscale,true); } } } //+------------------------------------------------------------------+
Результат:
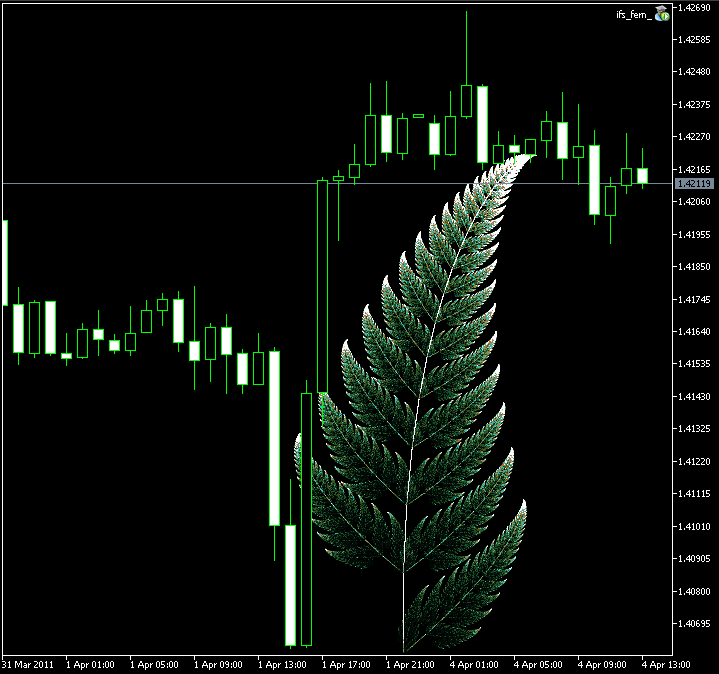
Рисунок 9. Фрактальный папоротник Барнсли, построенный при помощи класса CIFS
Рисунок 10. Увеличенный фрагмент фрактального папоротника Барнсли
Рисунок 11. Увеличенный фрагмент фрактального папоротника Барнсли

Рисунок 12. Увеличенный фрагмент фрактального папоротника Барнсли
Упражнения
1. В программе Fractint есть много других множеств, например:
// Binary double IFS_a[3] = { 0.5, 0.5, 0.0}; double IFS_b[3] = { 0.0, 0.0, -0.5}; double IFS_c[3] = { 0.0, 0.0, 0.5}; double IFS_d[3] = { 0.5, 0.5, 0.5}; double IFS_e[3] = {-2.563477, 2.436544, 4.873085}; double IFS_f[3] = {-0.000000, -0.000003, 7.563492}; double IFS_p[3] = {333, 333, 333}; // Coral double IFS_a[3] = { 0.307692, 0.307692, 0.000000}; double IFS_b[3] = {-0.531469, -0.076923, 0.54545}; double IFS_c[3] = {-0.461538, 0.153846, 0.692308}; double IFS_d[3] = {-0.293706, -0.447552, -0.195804}; double IFS_e[3] = {5.4019537, -1.295248, -4.893637}; double IFS_f[3] = { 8.655175, 4.152990, 7.269794}; double IFS_p[3] = {400, 150, 450}; // Crystal double IFS_a[2] = { 0.696970, 0.090909}; double IFS_b[2] = {-0.481061, -0.443182}; double IFS_c[2] = {-0.393939, 0.515152}; double IFS_d[2] = {-0.662879, -0.094697}; double IFS_e[2] = { 2.147003, 4.286558}; double IFS_f[2] = {10.310288, 2.925762}; double IFS_p[2] = {750, 250}; // Dragon double IFS_a[2] = { 0.824074, 0.088272}; double IFS_b[2] = { 0.281482, 0.520988}; double IFS_c[2] = {-0.212346, -0.463889}; double IFS_d[2] = { 0.864198, -0.377778}; double IFS_e[2] = {-1.882290, 0.785360}; double IFS_f[2] = {-0.110607, 8.095795}; double IFS_p[2] = {780, 220}; // Floor double IFS_a[3] = { 0, 0.52, 0}; double IFS_b[3] = {-0.5, 0, 0.5}; double IFS_c[3] = { 0.5, 0, -0.5}; double IFS_d[3] = { 0, 0.5, 0}; double IFS_e[3] = {-1.732366, -0.027891, 1.620804}; double IFS_f[3] = { 3.366182, 5.014877, 3.310401}; double IFS_p[3] = {333, 333, 333}; // Koch3 double IFS_a[5] = {0.307692, 0.192308, 0.192308, 0.307692, 0.384615}; double IFS_b[5] = { 0,-0.205882, 0.205882, 0, 0}; double IFS_c[5] = { 0, 0.653846, -0.653846, 0, 0}; double IFS_d[5] = {0.294118, 0.088235, 0.088235, 0.294118, -0.294118}; double IFS_e[5] = {4.119164,-0.688840, 0.688840, -4.136530, -0.007718}; double IFS_f[5] = {1.604278, 5.978916, 5.962514, 1.604278, 2.941176}; double IFS_p[5] = {151, 254, 254, 151, 190}; //Spiral double IFS_a[3] = { 0.787879, -0.121212, 0.181818}; double IFS_b[3] = {-0.424242, 0.257576, -0.136364}; double IFS_c[3] = { 0.242424, 0.151515, 0.090909}; double IFS_d[3] = { 0.859848, 0.053030, 0.181818}; double IFS_e[3] = { 1.758647, -6.721654, 6.086107}; double IFS_f[3] = { 1.408065, 1.377236, 1.568035}; double IFS_p[3] = {896, 52, 52}; //Swirl5 double IFS_a[2] = { 0.74545, -0.424242}; double IFS_b[2] = {-0.459091, -0.065152}; double IFS_c[2] = { 0.406061, -0.175758}; double IFS_d[2] = { 0.887121, -0.218182}; double IFS_e[2] = { 1.460279, 3.809567}; double IFS_f[2] = { 0.691072, 6.741476}; double IFS_p[2] = {920, 80}; //Zigzag2 double IFS_a[2] = {-0.632407, -0.036111}; double IFS_b[2] = {-0.614815, 0.444444}; double IFS_c[2] = {-0.545370, 0.210185}; double IFS_d[2] = { 0.659259, 0.037037}; double IFS_e[2] = { 3.840822, 2.071081}; double IFS_f[2] = { 1.282321, 8.330552}; double IFS_p[2] = {888, 112};
Постройте эти множества. Как восстановить схему построения данных множеств по коэффициентам IFS?
2. Сконструируйте свои самоподобные множества и найдите коэффициенты (раздел 2).
3. Попробуйте изменить цвета палитры (массив uchar Palette), расширьте палитру и реализуйте градиентный переход между цветами.
4. Чему равна фрактальная размерность папоротника Барнсли? Приведите идею расчета и общую формулу расчета фрактальной размерности по коэффициентам IFS*.
5. Добавьте возможность увеличения заданного участка множества, используя информацию о координатах клика мышки в обработчике события OnChartEvent:
void OnChartEvent(const int id, // Event identifier const long& lparam, // Event parameter of long type const double& dparam, // Event parameter of double type const string& sparam // Event parameter of string type ) { //--- клик левой кнопки мышки if(id==CHARTEVENT_CLICK) { Print("Координаты графика: x=",lparam," y=",dparam); } }
Заключение
Мы рассмотрели способ построения самоподобных множеств при помощи системы итерированных функций (IFS).
Использование библиотеки cIntBMP значительно упрощает работу с графическими изображениями. Помимо метода DrawDot(x,y,color), существуют другие полезные методы, их мы рассмотрим позже.
 DRAW_HISTOGRAM2
DRAW_HISTOGRAM2
Стиль DRAW_HISTOGRAM2 рисует заданным цветом гистограмму – вертикальные отрезки по значениям двух индикаторных буферов.
 DRAW_HISTOGRAM
DRAW_HISTOGRAM
Стиль DRAW_HISTOGRAM рисует заданным цветом гистограмму столбиками от нуля до указанного значения. Значения берутся из индикаторного буфера.
 RouletteGame
RouletteGame
Игрушка "Рулетка".
 DRAW_CANDLES
DRAW_CANDLES
Стиль DRAW_CANDLES рисует японские свечи по значениям четырех индикаторных буферов, в которых содержатся цены Open, High, Low и Close.