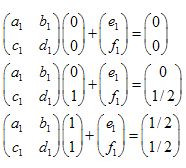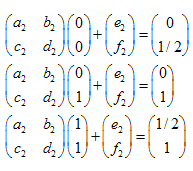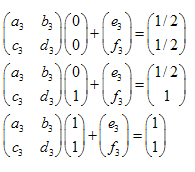Creazione di frattali in MQL5 usando la Iterated Function Systems (IFS) - sistema esperto per MetaTrader 5

Introduzione

Esistono molti programmi che consentono la creazione di insiemi autosimili, definiti con Iterated Function System (IFS). Vedi, per esempio Fractint, Fractal Designer o IFS Matlab Generator. Grazie alla velocità del linguaggio MQL5 e alla possibilità di lavorare con oggetti grafici, questi meravigliosi insiemi possono essere studiati nel terminale MetaTrader5.

La libreria cIntBMP, sviluppata da Dmitry (interamente) offre nuove opportunità grafiche e semplifica notevolmente la creazione di immagini grafiche. Questa libreria è stata insignita di un premio speciale da MetaQuotes Software Corp.

In questa pubblicazione considereremo gli esempi di lavoro con la libreria cIntBMP. Inoltre, tratteremo gli algoritmi di creazione di insiemi frattali utilizzando la Iterated Function Systems.

1. Trasformazione Affine del Piano

La trasformazione affine del piano è una mappatura . Generalmente, la trasformazione 2-D affine può essere definita con qualche matrice e , vettore. Il punto con coordinate (x,y) si trasforma in qualche altro punto usando la trasformazione lineare:

La trasformazione deve essere non singola, la . La trasformazione affine cambia la dimensione volte.

Le affini trasformate non modificano la struttura degli oggetti geometrici (le linee trasformate in linee), l'AT permette di descrivere semplici "deformazioni" degli oggetti, come rotazione, ridimensionamento e traslazione.

Esempi di piano affine trsformato:

1) <Rotazione del piano su angolo:

2) "Ridimensionamento" di un piano con e coefficenti (assi X e Y):

3) Traslazione di un piano con vettore:

Le mappature di contrazione è la chiave (vedere i risultati di Hutchinson).

Se e hanno coordinate e e è una metrica ( per esempio, metrica di Euclide:). La trasformazione affine chiamata contrazione se , quando.

Qui un esempio di trasformazione affine:

Il risultato è:

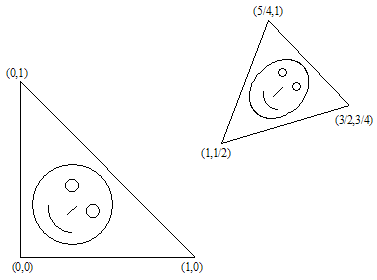
2. Trasformazioni Similari

I frattali sono costruiti nel modo seguente: alcuni (semplici) oggetti geometrici (sezione,triangolo,quadrato) suddiviso in N pezzi e M di essi utilizzato per l'ulteriore "costruzione" dell'insieme (se N=M, otterremo il risultato della dimensione intera dell'insieme). Inoltre questo processo si è ripetuto più e più volte per ciascuno dei pezzi.

Frattali classici:

Sezioni:

• Triadic Koch Curve, N=3, M=4;
• Cantor Dust, N=3, M=2;

Triangolo:

• Sierpinski Gasket, N=4, M=3;

Quadrato:

• Sierpinski Carpet, N=9, M=8;
• Vichek fractal, N=9, M=5.
  

e così via.

I frattali hanno una struttura auto-simile, alcuni di essi possono essere definiti con diverse trasformazioni di similarità. La struttura dell' affine trasformata dipende dal modo in cui si costruisce il frattale.

Come vedrai più avanti, è molto semplice, e l'unico problema che dobbiamo risolvere è descrivere solo la prima iterazione della costruzione frattale e trovare l'insieme corrispondente delle affini trasformate.

Supponiamo di avere un insieme. Secondo l'algoritmo di creazione del frattale, dobbiamo ridurlo, ruotarlo e "metterlo in un certo posto". Il problema è descrivere il processo usando le trasformazioni affini, i.e. abbiamo bisogno di trovare la matrice e il vettore.

È facile dimostrare che basta prendere 3 punti dell'insieme iniziale (non banale) e trasformarli in 3 punti corrispondenti dell'insieme "ridotto". Questa trasformazione porterà a 6 equazioni lineari, permettendoci di trovare come soluzione a,b,c,d,e,f.

Vediamolo. Supponiamo triangolo trasformato in triangolo.

Risolvendo il sistema di equazioni lineari potremo ottenere i coefficienti a,b,c,d,e e f:

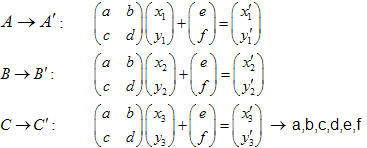
Esempio: Sierpinski Gasket:

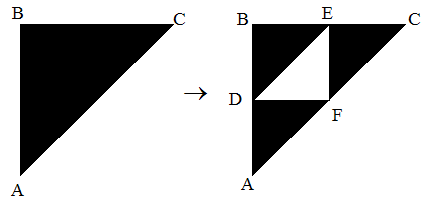
Le coordinate dei punti sono:

• A (0,0)
• B (0,1)
• C (1,1)
• D(0,1/2)
• E (1/2,1)
• F(1/2,1/2)
  

Abbiamo 3 trasformazioni:

1. ABC -> ADF
2. ABC -> DBE
3. ABC -> FEC
   

Il sistema di equazioni lineari si presenta come segue:

1. 
   
2. 
   
3. 
   

Le soluzioni sono:, ,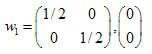

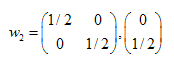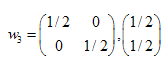
Abbiamo trovato i coefficenti di tre trasformazioni affini. In seguito li useremo per creare insiemi auto-similari.

3. Creazione di Frattali Utilizzando la Iterated Function Systems

La Iterated Function System (IFS) è un insieme di contrazioni affini dove _è il "peso". Ognuna delle funzioni IFS è definita con 7 numeri: , dove pesi è usato quando il processo di iterazione come una probabilità di n-th trasformazione. È meglio definire i loro valori, proporzionali alla contrazione: .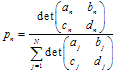

Consideriamo l'algoritmo di costruzione frattale utilizzando l' Iterated Function System (vedi anche Chaos Game).

La prima cosa di cui abbiamo bisogno è prendere dei punti iniziali con coordinate . Successivamente, scegliamo casualmente alcune delle contrazioni e tracciamo il punto . E ancora, scegliamo a caso una delle contrazioni e tracciamo . Finalmente avremo il come un insieme di punti.

La scelta della contrazione dipende dalla sua "probabilità". Se ripetiamo il processo (ad esempio, a ~30000 punti) e tracciamo l'insieme risultante, vedremo la sua struttura nonostante il processo casuale.

Qui è un esempio di Sierpinski Gasket:

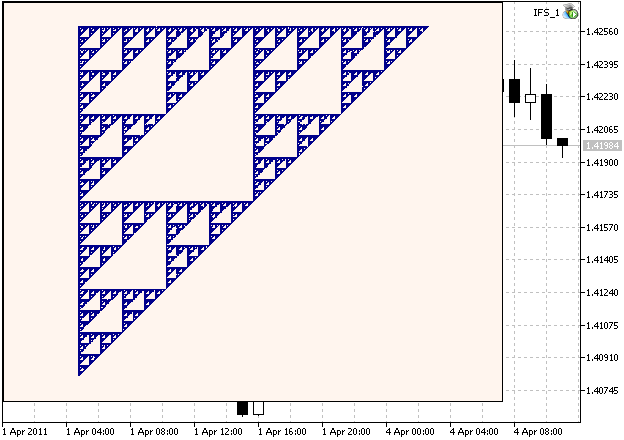
Figure 1. Il Sierpinski Gasket, generato con IFS coefficenti calcolati nel capitolo 2

Il codice:

//+------------------------------------------------------------------+
//|                                        IFS_Sierpinski_Gasket.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

//-- include file with cIntBMP class
#include <cIntBMP.mqh>

//-- Sierpinski Gasket IFS coefficients
//-- (a,b,c,d) matricies
double IFS_a[3] = {0.50,  0.50,  0.50};
double IFS_b[3] = {0.00,  0.00,  0.00};
double IFS_c[3] = {0.00,  0.00,  0.00};
double IFS_d[3] = {0.50,  0.50,  0.50};
//-- (e,f) vectors
double IFS_e[3] = {0.00,  0.00,  0.50};
double IFS_f[3] = {0.00,  0.50,  0.50};
//-- "probabilities" of transforms, multiplied by 1000
double IFS_p[3]={333,333,333};

double Probs[3]; // Probs array - used to choose IFS transforms
cIntBMP bmp;     // cIntBMP class instance
int scale=350;  // scale coefficient
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//-- Prepare Probs array
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
//-- size of BMP image
   int XSize=500;
   int YSize=400;
//-- create bmp image XSizexYSize with clrSeashell background color
   bmp.Create(XSize,YSize,clrSeashell);
//-- image rectangle
   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

//-- point coordinates (will be used in construction of set)
   double x0=0;
   double y0=0;
   double x,y;
//-- number of points to calculate (more points - detailed image)
   int points=1500000;
//-- calculate set
   for(int i=0; i<points; i++)
     {
      // choose IFS tranform with probabilities, proportional to defined
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            // affine transformation
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            // update previous coordinates
            x0 = x;
            y0 = y;
            // convert to BMP image coordinates
            // (note the Y axis in cIntBMP)
            int scX = int (MathRound(XSize/2 + (x-0.5)*scale));
            int scY = int (MathRound(YSize/2 + (y-0.5)*scale));
            // if the point coordinates inside the image, draw the dot
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); }
            break;
           }
        }
     }
//-- save image to file
   bmp.Save("bmpimg",true);
//-- plot image on the chart
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- delete image from the chart
   ObjectDelete(0,"IFS");
//--- delete file
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------+

Se impostiamo la scala a 1350, aumentiamo il numero di iterazioni a 15000000 e cambiamo lo spostamento del punto iniziale:

int scX = MathRound(XSize/2 + (x-0.75)*scale);
int scY = MathRound(YSize/2 + (y-0.75)*scale);

potremo vedere la zona ingrandita dell'insieme. Si può vedere (Fig. 2), che ha una struttura autosimile:

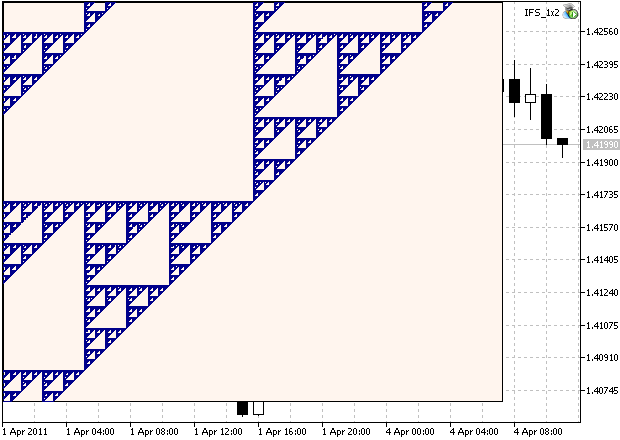
Figure 2. Zona ingrandita di Sierpinski Gasket

Consideriamo la famosa Felce di Barnsley, proposta da Michael Barnsley. E' più complessa.

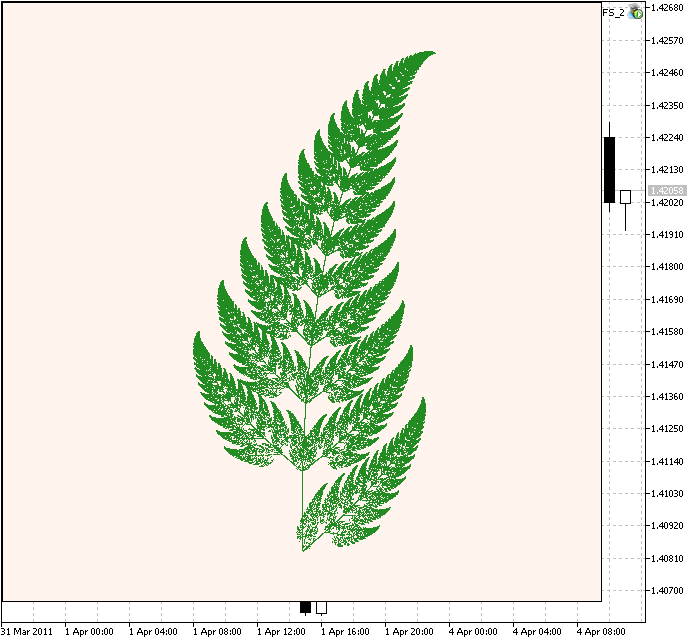
Figure 3. Felce di Barnsley

Il codice è simile, ma in questo caso abbiamo 4 contrazioni IFS con differenti pesi.

//+------------------------------------------------------------------+
//|                                                     IFS_fern.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <cIntBMP.mqh>
//-- Barnsley Fern IFS coefficients
//-- (a,b,c,d) matricies
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
//-- (e,f) vectors
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
//-- "probabilities" of transforms, multiplied by 1000
double IFS_p[4] = {10,     850,    70,     70};

double Probs[4];
cIntBMP bmp;
int scale=50;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }

   int XSize=600;
   int YSize=600;

   bmp.Create(XSize,YSize,clrSeashell);

   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

   double x0=0;
   double y0=0;
   double x,y;

   int points=250000;

   for(int i=0; i<points; i++)
     {
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            x0 = x;
            y0 = y;
            int scX = int (MathRound(XSize/2 + (x)*scale));
            int scY = int (MathRound(YSize/2 + (y-5)*scale));
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrForestGreen); }
            break;
           }
        }
     }
   bmp.Save("bmpimg",true);
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ObjectDelete(0,"IFS");
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------+ 

È notevole che una struttura così complessa possa essere definita da soli 28 numeri.

Se aumentiamo la scala a 150 e impostiamo le iterazioni a 1250000 vedremo il frammento ingrandito:

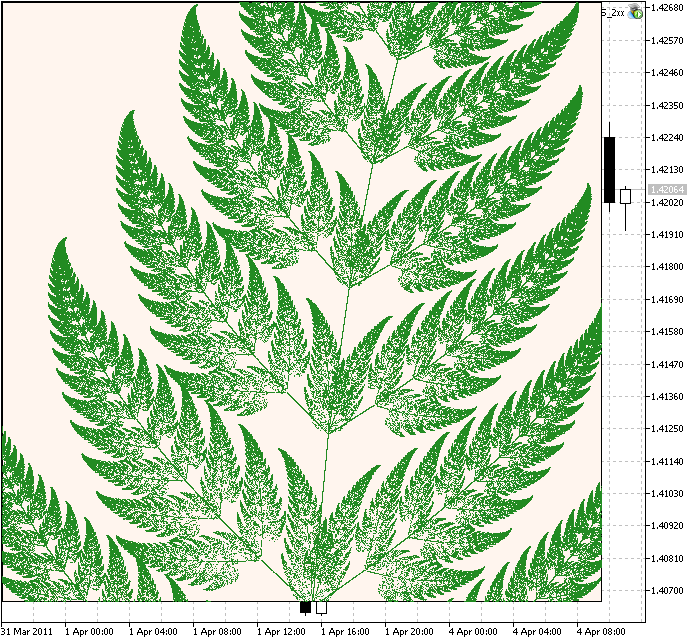
Figure 4. Un frammento della Felce di Barnsley

Come vedi l'algoritmo è universale, ti consente di generare diversi insiemi di frattali.

Il prossimo esempio è Sierpinski Carpet, definito con i seguenti coefficenti IFS:

//-- Sierpinski Gasket IFS coefficients
double IFS_a[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333};
double IFS_b[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_c[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_d[8] = {0.333, 0.333,  0.333,  0.333, 0.333,  0.333,  0.333, 0.333};
double IFS_e[8] = {-0.125, -3.375, -3.375,  3.125, 3.125, -3.375, -0.125, 3.125};
double IFS_f[8] = {6.75, 0.25, 6.75,  0.25, 6.75, 3.5, 0.25, 3.50};
//-- "probabilities", multiplied by 1000
double IFS_p[8]={125,125,125,125,125,125,125,125};

Figure 5. Sierpinski Carpet

Nel capitolo 2 abbiamo considerato l'algoritmo di calcolo dei coefficienti delle contrazioni IFS.

Consideriamo come creare le "parole frattali". In Russo, la parola "Frattale" assomiglia:

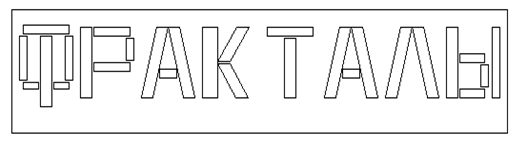
Figure 6. La parola "Frattale" in Russo

Per trovare i coefficienti IFS, dobbiamo risolvere i corrispondenti sistemi lineari. Le soluzioni sono:

//-- IFS coefficients of the "Fractals" word in Russian
double IFS_a[28]=
  {
   0.00, 0.03,  0.00, 0.09, 0.00, 0.03, -0.00, 0.07, 0.00, 0.07, 0.03,  0.03,  0.03,  0.00,
   0.04, 0.04, -0.00, 0.09, 0.03, 0.03,  0.03, 0.03, 0.03, 0.00, 0.05, -0.00,  0.05,  0.00
  };

double IFS_b[28]=
  {
   -0.11, 0.00, 0.07, 0.00, -0.07, 0.00, -0.11,  0.00, -0.07,  0.00, -0.11,  0.11, 0.00, -0.14,
   -0.12, 0.12,-0.11, 0.00, -0.11, 0.11,  0.00, -0.11,  0.11, -0.11,  0.00, -0.07, 0.00, -0.07
  };

double IFS_c[28]=
  {
   0.12,  0.00,  0.08,  -0.00,  0.08,  0.00,  0.12,  0.00,  0.04,  0.00,  0.12,  -0.12, 0.00,  0.12,
   0.06,  -0.06,  0.10,  0.00,  0.12,  -0.12,  0.00,  0.12,  -0.12,  0.12, 0.00,  0.04,  0.00,  0.12
  };

double IFS_d[28]=
  {
   0.00,  0.05,  0.00,  0.07,  0.00,  0.05,  0.00,  0.07,  0.00,  0.07,  0.00,  0.00,  0.07,  0.00,
   0.00,  0.00,  0.00,  0.07,  0.00,  0.00,  0.07,  0.00,  0.00,  0.00,  0.07,  0.00,  0.07,  0.00
  };

double IFS_e[28]=
  {
   -4.58,  -5.06, -5.16, -4.70, -4.09, -4.35, -3.73, -3.26, -2.76,  -3.26, -2.22, -1.86, -2.04, -0.98,
   -0.46,  -0.76,  0.76,  0.63,  1.78,  2.14,  1.96,  3.11,  3.47,  4.27,  4.60,  4.98,   4.60, 5.24
  };

double IFS_f[28]=
  {
   1.26,  0.89,  1.52,  2.00,  1.52,  0.89,  1.43,  1.96,  1.69,  1.24,  1.43,  1.41,  1.11,  1.43,
   1.79,  1.05,  1.32,  1.96,  1.43,  1.41,  1.11,  1.43,  1.41,  1.43,  1.42,  1.16,  0.71,  1.43
  };

//-- "probabilities", multiplied by 1000
double IFS_p[28]=
  {
   35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  
   35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35
  };

Come risultato, avremo l'immagine seguente:

Figure 7. Parola auto-similare

Il codice sorgente completo può essere trovato in ifs_fractals.mq5.

Se zoomiamo l'insieme, vediamo la struttura auto_simile:

Figure 8. Parte zoomata dell'insieme

The self-similar sets, based on IFS, can be constructed using the Fractal Designer.

Abbiamo trattato l'argomento della creazione di insiemi frattali usando l' Iterated Function Systems. Grazie alla libreria cIntBMP, il processo è molto semplice Ora è il momento di creare una classe e aggiungere alcune funzionalità per migliorare le immagini.

Puoi notare che la corretta costruzione degli insiemi è guidata dalle probabilità. La differenza di probabilità significa che l'insieme ha una struttura irregolare (vedi pesi di Barnsley Fern IFS). Questo può essere utilizzato per la creazione di bellissime immagini. Dobbiamo impostare il colore, proporzionale alla frequenza di un punto vicino.

Può essere fatto usando lo schermo virtuale (solo un array), se il colore dei pixel dipenderà dai valori precedenti. Infine, lo schermo virtuale verrà renderizzato nel bmp usando la Palette. L'immagine bmp stessa può essere disegnata come immagine di sfondo del grafico.

Qui c'è il codice dell'Expert Advisor, basato sulla classe CIFS:

//+------------------------------------------------------------------+
//|                                               IFS_Fern_color.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#include <cIntBMP.mqh>
//-- Barnsley Fern IFS coefficients
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
double IFS_p[4] = {10,     850,    70,     70};
//-- Palette
uchar Palette[23*3]=
  {
   0x00,0x00,0x00,0x02,0x0A,0x06,0x03,0x11,0x0A,0x0B,0x1E,0x0F,0x0C,0x4C,0x2C,0x1C,0x50,0x28,
   0x2C,0x54,0x24,0x3C,0x58,0x20,0x4C,0x5C,0x1C,0x70,0x98,0x6C,0x38,0xBC,0xB0,0x28,0xCC,0xC8,
   0x4C,0xB0,0x98,0x5C,0xA4,0x84,0xBC,0x68,0x14,0xA8,0x74,0x28,0x84,0x8C,0x54,0x94,0x80,0x40,
   0x87,0x87,0x87,0x9F,0x9F,0x9F,0xC7,0xC7,0xC7,0xDF,0xDF,0xDF,0xFC,0xFC,0xFC
  };
//+------------------------------------------------------------------+
//| CIFS class                                                       |
//+------------------------------------------------------------------+
class CIFS
  {
protected:
   cIntBMP           m_bmp;
   int               m_xsize;
   int               m_ysize;
   uchar             m_virtual_screen[];
   double            m_scale;
   double            m_probs[8];

public:
                    ~CIFS()                          { m_bmp.Delete("bmpimg",true); };
   void              Create(int x_size,int y_size,uchar col);
   void              Render(double scale,bool back);
   void              ShowBMP(bool back);
protected:
   void              VS_Prepare(int x_size,int y_size,uchar col);
   void              VS_Fill(uchar col);
   void              VS_PutPixel(int px,int py,uchar col);
   uchar             VS_GetPixel(int px,int py);
   int               GetPalColor(uchar index);
   int               RGB256(int r,int g,int b) const {return(r+256*g+65536*b);      }
   void              PrepareProbabilities();
   void              RenderIFSToVirtualScreen();
   void              VirtualScreenToBMP();
  };
//+------------------------------------------------------------------+
//| Create method                                                    |
//+------------------------------------------------------------------+
void CIFS::Create(int x_size,int y_size,uchar col)
  {
   m_bmp.Create(x_size,y_size,col);
   VS_Prepare(x_size,y_size,col);
   PrepareProbabilities();
  }
//+------------------------------------------------------------------+
//| Prepares virtual screen                                          |
//+------------------------------------------------------------------+
void CIFS::VS_Prepare(int x_size,int y_size,uchar col)
  {
   m_xsize=x_size;
   m_ysize=y_size;
   ArrayResize(m_virtual_screen,m_xsize*m_ysize);
   VS_Fill(col);
  }
//+------------------------------------------------------------------+
//| Fills the virtual screen with specified color                    |
//+------------------------------------------------------------------+
void CIFS::VS_Fill(uchar col)
  {
   for(int i=0; i<m_xsize*m_ysize; i++) {m_virtual_screen[i]=col;}
  }
//+------------------------------------------------------------------+
//| Returns the color from palette                                   |
//+------------------------------------------------------------------+
int CIFS::GetPalColor(uchar index)
  {
   int ind=index;
   if(ind<=0) {ind=0;}
   if(ind>22) {ind=22;}
   uchar r=Palette[3*(ind)];
   uchar g=Palette[3*(ind)+1];
   uchar b=Palette[3*(ind)+2];
   return(RGB256(r,g,b));
  }
//+------------------------------------------------------------------+
//| Draws a pixel on the virtual screen                              |
//+------------------------------------------------------------------+
void CIFS::VS_PutPixel(int px,int py,uchar col)
  {
   if (px<0) return;
   if (py<0) return;
   if (px>m_xsize) return;
   if (py>m_ysize) return;
    int pos=m_xsize*py+px;
   if(pos>=ArraySize(m_virtual_screen)) return;
   m_virtual_screen[pos]=col;
  }
//+------------------------------------------------------------------+
//| Gets the pixel "color" from the virtual screen                   |
//+------------------------------------------------------------------+
uchar CIFS::VS_GetPixel(int px,int py)
  {
   if (px<0) return(0);
   if (py<0) return(0);
   if (px>m_xsize) return(0);
   if (py>m_ysize) return(0);
    int pos=m_xsize*py+px;
   if(pos>=ArraySize(m_virtual_screen)) return(0);
   return(m_virtual_screen[pos]);
  }
//+------------------------------------------------------------------+
//| Prepare the cumulative probabilities array                       |
//+------------------------------------------------------------------+
void CIFS::PrepareProbabilities()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      m_probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
  }
//+------------------------------------------------------------------+
//| Renders the IFS set to the virtual screen                        |
//+------------------------------------------------------------------+
void CIFS::RenderIFSToVirtualScreen()
  {
   double x=0,y=0;
   double x0=0;
   double y0=0;
   uint iterations= uint (MathRound(100000+100*MathPow(m_scale,2)));

   for(uint i=0; i<iterations; i++)
     {
      double prb=1000*(rand()/32767.0);

      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=m_probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];

            int scX = int (MathRound(m_xsize/2 + (x-0)*m_scale));
            int scY = int (MathRound(m_ysize/2 + (y-5)*m_scale));

            if(scX>=0 && scX<m_xsize && scY>=0 && scY<m_ysize)
              {
               uchar c=VS_GetPixel(scX,scY);
               if(c<255) c=c+1;
               VS_PutPixel(scX,scY,c);
              }
            break;
           }
         x0 = x;
         y0 = y;
        }
     }
  }
//+------------------------------------------------------------------+
//| Copies virtual screen to BMP                                     |
//+------------------------------------------------------------------+
void CIFS::VirtualScreenToBMP()
  {
   for(int i=0; i<m_xsize; i++)
     {
      for(int j=0; j<m_ysize; j++)
        {
         uchar colind=VS_GetPixel(i,j);
         int xcol=GetPalColor(colind);
         if(colind==0) xcol=0x00;
         //if(colind==0) xcol=0xFFFFFF;
         m_bmp.DrawDot(i,j,xcol);
        }
     }
  }
//+------------------------------------------------------------------+
//| Shows BMP image on the chart                                     |
//+------------------------------------------------------------------+
void CIFS::ShowBMP(bool back)
  {
   m_bmp.Save("bmpimg",true);
   m_bmp.Show(0,0,"bmpimg","Fern");
   ObjectSetInteger(0,"Fern",OBJPROP_BACK,back);
  }
//+------------------------------------------------------------------+
//| Render method                                                    |     
//+------------------------------------------------------------------+
void CIFS::Render(double scale,bool back)
  {
   m_scale=scale;
   VS_Fill(0);
   RenderIFSToVirtualScreen();
   VirtualScreenToBMP();
   ShowBMP(back);
  }

static int gridmode;
CIFS fern;
int currentscale=50;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
void OnInit()
  {
//-- get grid mode
   gridmode= int (ChartGetInteger(0,CHART_SHOW_GRID,0));
//-- disable grid
   ChartSetInteger(0,CHART_SHOW_GRID,0);
//-- create bmp
   fern.Create(800,800,0x00);
//-- show as backround image
   fern.Render(currentscale,true);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int r)
  {
//-- restore grid mode
   ChartSetInteger(0,CHART_SHOW_GRID,gridmode); 
//-- delete Fern object
   ObjectDelete(0,"Fern");
 }
//+------------------------------------------------------------------+
//| Expert OnChart event handler                                     |
//+------------------------------------------------------------------+
void OnChartEvent(const int id,           // Event identifier  
                const long& lparam,   // Event parameter of long type
                const double& dparam, // Event parameter of double type
                const string& sparam  // Event parameter of string type
                )
  {
//--- click on the graphic object
   if(id==CHARTEVENT_OBJECT_CLICK)
     {
      Print("Click event on graphic object with name '"+sparam+"'");
      if(sparam=="Fern")
        {
         // increase scale coefficient (zoom)
         currentscale=int (currentscale*1.1);
         fern.Render(currentscale,true);
        }
     }
  }
//+------------------------------------------------------------------+

Il risultato è:

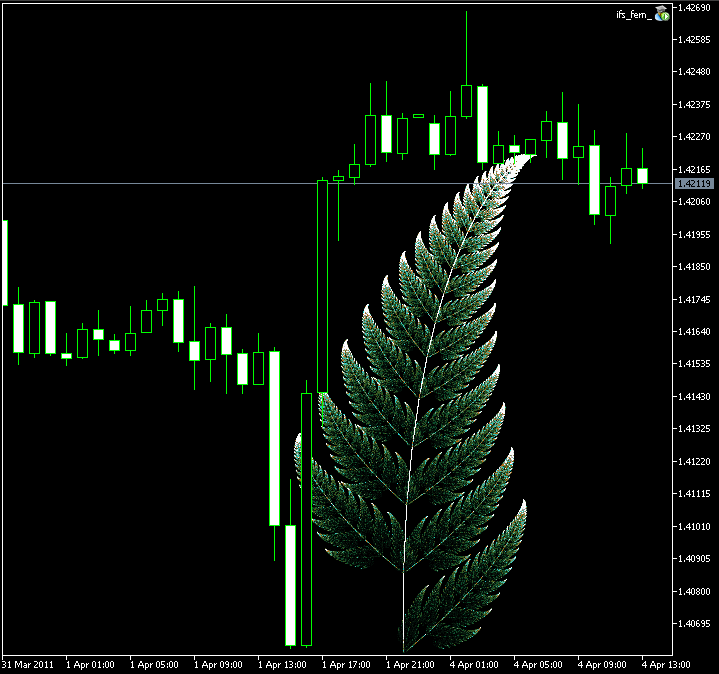
Figure 9. Immagine della felce di Barnsley,creata con la classe CIFS

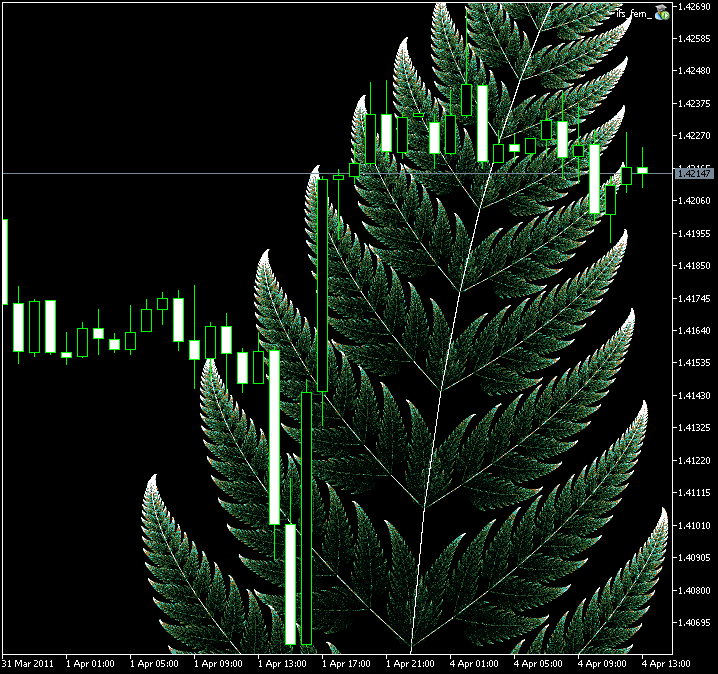
Figure 10. Parte zoomata della Felce di Barnsley

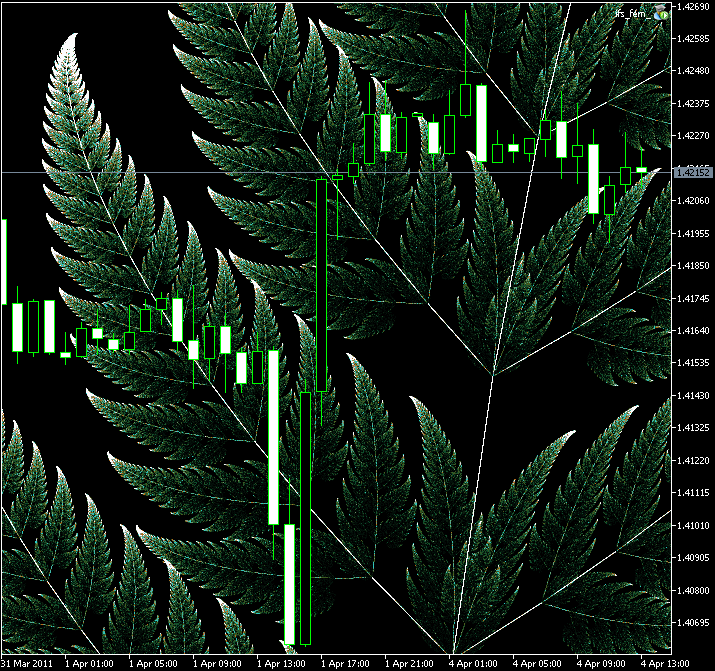
Figure 11. Parte zoomata della Felce di Barnsley

Figure 12. Parte zoomata della Felce di Barnsley

Fallo da solo

1. Ci sono molti frattali IFS in Factint, ad esempio:

// Binary
double IFS_a[3] = { 0.5,  0.5,  0.0};
double IFS_b[3] = { 0.0,  0.0, -0.5};
double IFS_c[4] = { 0.0,  0.0,  0.5};
double IFS_d[4] = { 0.5,  0.5,  0.5};
double IFS_e[4] = {-2.563477,  2.436544, 4.873085};
double IFS_f[4] = {-0.000000, -0.000003, 7.563492};
double IFS_p[4] = {333, 333, 333};

// Coral
double IFS_a[3] = { 0.307692,  0.307692,  0.000000};
double IFS_b[3] = {-0.531469, -0.076923,  0.54545};
double IFS_c[3] = {-0.461538,  0.153846,  0.692308};
double IFS_d[3] = {-0.293706, -0.447552, -0.195804};
double IFS_e[3] = {5.4019537, -1.295248, -4.893637};
double IFS_f[3] = { 8.655175,  4.152990,  7.269794};
double IFS_p[3] = {400, 150, 450};

// Crystal
double IFS_a[2] = { 0.696970,  0.090909};
double IFS_b[2] = {-0.481061, -0.443182};
double IFS_c[2] = {-0.393939,  0.515152};
double IFS_d[2] = {-0.662879, -0.094697};
double IFS_e[2] = { 2.147003,  4.286558};
double IFS_f[2] = {10.310288,  2.925762};
double IFS_p[2] = {750, 250};

// Dragon
double IFS_a[2] = { 0.824074,  0.088272};
double IFS_b[2] = { 0.281482,  0.520988};
double IFS_c[2] = {-0.212346, -0.463889};
double IFS_d[2] = { 0.864198, -0.377778};
double IFS_e[2] = {-1.882290,  0.785360};
double IFS_f[2] = {-0.110607,  8.095795};
double IFS_p[2] = {780, 220};

// Floor
double IFS_a[3] = { 0,  0.52,  0};
double IFS_b[3] = {-0.5,   0,  0.5};
double IFS_c[3] = { 0.5,   0, -0.5};
double IFS_d[3] = { 0,   0.5,  0};
double IFS_e[3] = {-1.732366, -0.027891,  1.620804};
double IFS_f[3] = { 3.366182,  5.014877,  3.310401};
double IFS_p[3] = {333, 333, 333};

// Koch3
double IFS_a[5] = {0.307692, 0.192308,  0.192308,  0.307692,  0.384615};
double IFS_b[5] = {      0,-0.205882,  0.205882,         0,        0};
double IFS_c[5] = {      0, 0.653846, -0.653846,         0,         0};
double IFS_d[5] = {0.294118, 0.088235,  0.088235,  0.294118, -0.294118};
double IFS_e[5] = {4.119164,-0.688840,  0.688840, -4.136530, -0.007718};
double IFS_f[5] = {1.604278, 5.978916,  5.962514,  1.604278,  2.941176};
double IFS_p[5] = {151, 254, 254, 151, 190};

//Spiral
double IFS_a[3] = { 0.787879, -0.121212,  0.181818};
double IFS_b[3] = {-0.424242,  0.257576, -0.136364};
double IFS_c[3] = { 0.242424,  0.151515,  0.090909};
double IFS_d[3] = { 0.859848,  0.053030,  0.181818};
double IFS_e[3] = { 1.758647,  -6.721654,  6.086107};
double IFS_f[3] = { 1.408065,   1.377236,  1.568035};
double IFS_p[3] = {896, 52, 52};

//Swirl5
double IFS_a[2] = {  0.74545, -0.424242};
double IFS_b[2] = {-0.459091, -0.065152};
double IFS_c[2] = { 0.406061, -0.175758};
double IFS_d[2] = { 0.887121, -0.218182};
double IFS_e[2] = { 1.460279,  3.809567};
double IFS_f[2] = { 0.691072,  6.741476};
double IFS_p[2] = {920, 80};

//Zigzag2
double IFS_a[2] = {-0.632407, -0.036111};
double IFS_b[2] = {-0.614815, 0.444444};
double IFS_c[2] = {-0.545370, 0.210185};
double IFS_d[2] = { 0.659259, 0.037037};
double IFS_e[2] = { 3.840822, 2.071081};
double IFS_f[2] = { 1.282321, 8.330552};
double IFS_p[2] = {888, 112};

Disegna questi insiemi. Come trovare le iniziali similarità trasformate usando i coefficienti IFS?

2. Crea i tuoi insiemi di frattali e calcola i loro coefficienti (capitolo 2).

3. Prova a giocare con i colori della palette (uchar Palette array), estendi la palette e aggiungi colori sfumati.

4. E la dimensione frattale (Hausdorff-Besicovitch) di Barnsley's Fern? Esiste una formula per il calcolo della dimensione frattale utilizzando i coefficienti IFS*.

5. Aggiungi lo zoom di una determinata parte, utilizzando le informazioni sulle coordinate del clic del mouse in OnChartEvent:

void OnChartEvent(const int id,         // Event identifier  
                const long& lparam,   // Event parameter of long type
                const double& dparam, // Event parameter of double type
                const string& sparam  // Event parameter of string type
                )
  {
//--- left button click
   if(id==CHARTEVENT_CLICK)
     {
      Print("Coordinates: x=",lparam,"  y=",dparam);
     }
  }

Conclusioni

Abbiamo considerato l'algoritmo di creazione di insiemi autosimili utilizzando l' Iterated Function System.

L'uso della libreria cIntBMP semplifica altamente il lavoro con le immagini grafiche. Oltre al metodo DrawDot(x,y,color) che abbiamo usato, la classe cIntBMP contiene molti altri metodi utili. Ma è un'altra storia.