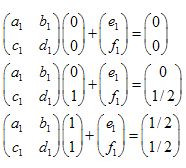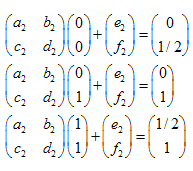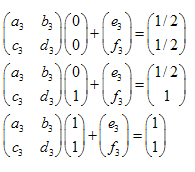Criando fractais em MQL5 utilizando os Sistemas de Funções Iteradas (IFS) - expert para MetaTrader 5

Introdução

Existem muitos programas que permitem criar conjuntos auto-similares, definido pelo Sistema de Função Iterada (IFS). Veja, por exemplo, Fractint, Fractal Designer ou IFS Matlab Generator. Graças a velocidade da linguagem MQL5 e a possibilidade de trabalhar com objetos gráficos, podemos estudar estes belos conjuntos no terminal cliente MetaTrader 5.

A biblioteca cIntBMP, desenvolvida por Dmitry (Integer) oferece novas oportunidades gráficas e simplifica enormemente a criação de imagens gráficas. Esta biblioteca foi premiada com um prêmio especial pela MetaQuotes Software Corp.

Nesta publicação, vamos considerar os exemplos de como trabalhar com a biblioteca cIntBMP. Além disso, vamos cobrir os algoritmos de criação dos conjuntos fractais que utilizam os Sistemas de Funções Iteradas.

1. Transformação afim no plano

A transformação afim no plano é uma aplicação . Geralmente, a transformação afim 2D se define com uma matriz e um vetor . O ponto de coordenadas (x,y) se transforma em outro ponto mediante a uma transformação linear:

A transformação deve ser não-singular, o .  A transformação afim muda de tamanho vezes.

As transformações afins não alteram a estrutura dos objetos geométricos (linhas transformadas em linhas), a AT permite descrever uma simples "deformação" dos objetos, tais como rotação, escala e translação.

Exemplos de transformações afins no plano:

1) Rotação do plano a um certo ângulo:

2) Mudança de escala de um plano com coeficientes e (do eixo X e Y):

3) Translação do plano pelo vetor :

O mapeamento de contração é o fator-chave (ver os resultados de Hutchinson).

Se e possuem coordenadas e e é métrico (por exemplo, Métrica Euclidiana: ). A transformação afim se chama contração se , onde .

A seguir há um exemplo de transformação afim:

Cujo resultado é:

2. Transformações de Similaridade

Os fractais se constroem da seguinte maneira: Toma-se um objeto geométrico simples (seção, triângulo, quadrado) dividido em N pedaços, dos quais M deles são utilizados posteriormente para continuar com a construção do conjunto (se N=M, obteremos a dimensão inteira do conjunto resultante). Este processo se repete novamente para cada um dos pedaços.

Fractais clássicos:

Seções:

• Curva de Koch, N=3, M=4;
• Poeira de Cantor, N=3, M=2;

Triângulo:

• Triângulo de Sierpinski, N=4, M=3;

Quadrados:

• Tapete de Sierpinski, N=9, M=8;
• Fractal de Vichek, N=9, M=5.
  

e assim por diante.

Os fractais possuem estrutura auto-semelhante, alguns deles podem ser definidos por várias transformações de similaridade. A estrutura da transformação afim depende da maneira de como o fractal é construído.

Como você verá mais adiante, é muito simples, e o único problema que temos que resolver é descrever apenas a primeira iteração de construção do fractal e encontrar o conjunto correspondente de transformações afins.

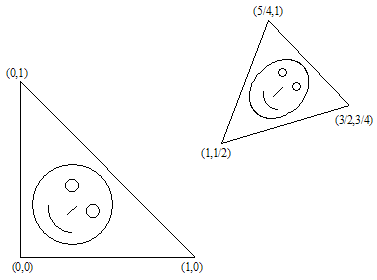
Suponha que temos um conjunto. De acordo com o algoritmo de criação do fractal, precisamos reduzi-lo, girá-lo e "colocar ele em um determinado lugar". O problema está em descrever este processo usando as transformações afins, ou seja, temos de encontrar a matriz e o vetor.

É fácil demonstrar que é o suficiente tomar apenas 3 pontos do conjunto inicial (não trivial) e transformá-lo em 3 pontos correspondentes ao conjunto "reduzido". Esta transformação nos levará a 6 equações lineares, permitindo encontrar as soluções de a,b,c,d,e,f.

Vamos a demonstração. Suponha o triângulo transformado no triângulo .

Resolvendo o sistema de equações lineares, seremos capazes de obter os coeficientes a,b,c,d,e e f:

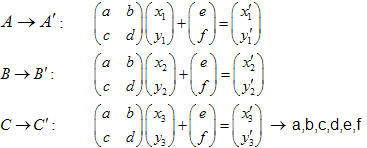
Exemplo: Triângulo de Sierpinski:

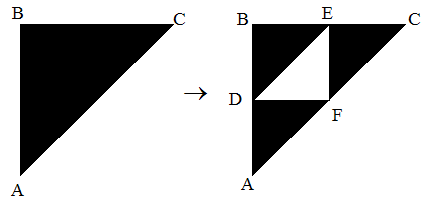
As coordenadas dos pontos são:

• A (0,0)
• B (0,1)
• C (1,1)
• D(0,1/2)
• E (1/2,1)
• F(1/2,1/2)
  

Temos 3 transformações:

1. ABC -> ADF
2. ABC -> DBE
3. ABC -> FEC
   

O sistema de equações lineares tem o seguinte aspecto:

1. 
   
2. 
   
3. 
   

As soluções são: , ,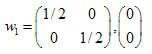

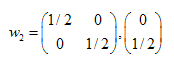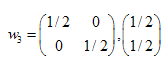
Encontramos os coeficientes de três transformações afins. Mais adiante usaremos elas para a criação de conjuntos auto-semelhantes.

3. Criando Fractais utilizando os Sistemas de Funções Iteradas

O Sistema de Funções Iteradas (IFS) é um conjunto de contrações afim onde - é o "peso". Cada uma das funções IFS são definidas por 7 números: , onde os pesos são usados quando há um processo iterativo com probabilidade de transformação enésima. É melhor definir seus valores, proporcionais a contração: .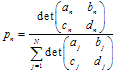

Vamos considerar o algoritmo de construção fractal utilizando o Sistema de Funções Iteradas (veja também Chaos Game).

Primeiramente precisamos tomar algum ponto inicial com coordenadas . A seguir, escolhemos aleatoriamente algumas das contrações e plotamos no ponto . E novamente, escolhemos aleatoriamente uma das contrações e plotamos . Finalmente, teremos como um conjunto de pontos.

A escolha da contração depende de sua "probabilidade". Se repetirmos o processo (por exemplo, para ~30000 pontos) e plotarmos o conjunto resultante, veremos a sua estrutura, apesar do processo aleatório.

Segue um exemplo do Triângulo de Sierpinski:

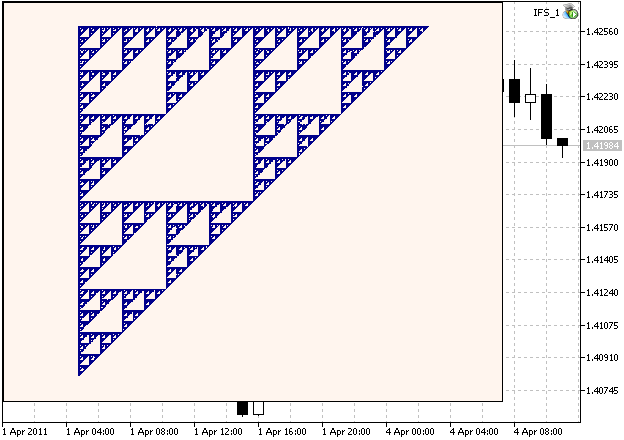
Figura 1. O triângulo de Sierpinski, gerado com os coeficientes IFS, calculados no capítulo 2

O código:

//+------------------------------------------------------------------+
//|                                        IFS_Sierpinski_Gasket.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

//-- arquivo include com a classe cIntBMP
#include <cIntBMP.mqh>

//-- coeficientes IFS do Triângulo de Sierpinski
//-- matrizes (a,b,c,d)
double IFS_a[3] = {0.50,  0.50,  0.50};
double IFS_b[3] = {0.00,  0.00,  0.00};
double IFS_c[3] = {0.00,  0.00,  0.00};
double IFS_d[3] = {0.50,  0.50,  0.50};
//-- vetores (e,f)
double IFS_e[3] = {0.00,  0.00,  0.50};
double IFS_f[3] = {0.00,  0.50,  0.50};
//-- "probabilidades" de transformações, multiplicadas por 1000
double IFS_p[3]={333,333,333};

double Probs[3]; // array Probs - usado para escolher as transformações IFS
cIntBMP bmp;     // instância da classe cIntBMP
int scale=350;  // coeficiente de escala
//+------------------------------------------------------------------+
//| Função de inicialização do Expert                                |
//+------------------------------------------------------------------+
int OnInit()
  {
//-- preparando o array Probs
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
//-- tamanho da imagem BMP
   int XSize=500;
   int YSize=400;
//-- criando a imagem bmp XSizexYSize com a cor de fundo clrSeashell
   bmp.Create(XSize,YSize,clrSeashell);
//-- imagem retangular
   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

//-- coordenada de pontos (será usado na construção dos conjuntos)
   double x0=0;
   double y0=0;
   double x,y;
//-- número de pontos para calcular (mais pontos - mais detalhada a imagem)
   int points=1500000;
//-- calculando o conjunto
   for(int i=0; i<points; i++)
     {
      // escolhendo a transformação IFS com probabilidade, proporcional a definir
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            // transformação afim
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            // atualizando coordenadas anteriores
            x0 = x;
            y0 = y;
            // convertendo para coodenadas de imagem BMP
            // (note o eixo Y em cIntBMP)
            int scX = int (MathRound(XSize/2 + (x-0.5)*scale));
            int scY = int (MathRound(YSize/2 + (y-0.5)*scale));
            // se o ponto de coordenadas está dentro da imagem, desenhe o ponto
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); }
            break;
           }
        }
     }
//-- salvar imagem para o arquivo
   bmp.Save("bmpimg",true);
//-- plotar imagem no gráfico
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Função de desinicialização do Expert                             |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- removendo a imagem do gráfico
   ObjectDelete(0,"IFS");
//--- removendo o arquivo
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------+

Se definirmos a escala para 1350, aumente o número de interações para 15000000, e mude o deslocamento do ponto inicial:

int scX = MathRound(XSize/2 + (x-0.75)*scale);
int scY = MathRound(YSize/2 + (y-0.75)*scale);

seremos capazes de ver a região ampliada do conjunto. Observe a (Fig. 2), que possui uma estrutura auto semelhante:

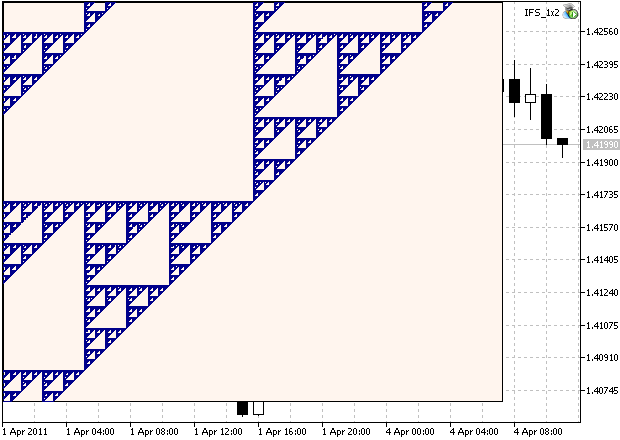
Figura 2. Região ampliada do Triângulo de Sierpinski

Vamos considerar a famosa Samambaia de Barnsley, proposta por Michael Barnsley. Ela é mais complexa.

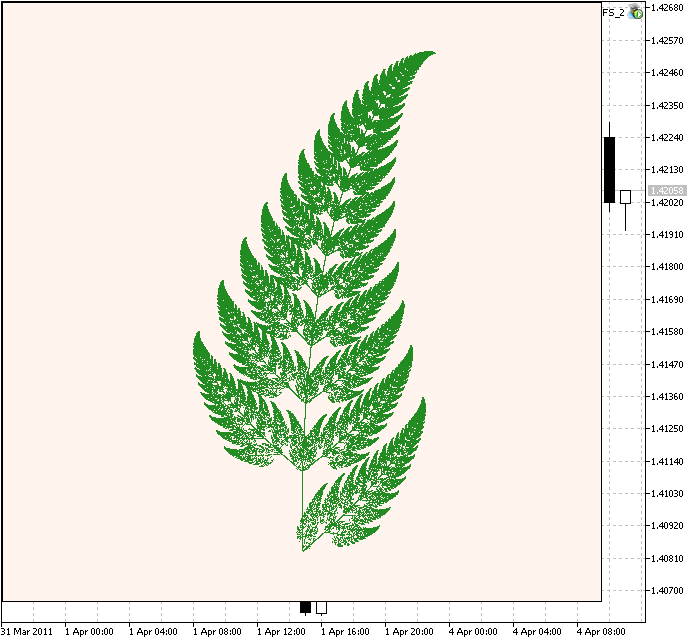
Figura 3. Samambaia de Barnsley

O código é semelhante, mas neste caso temos 4 contrações IFS com diferentes pesos.

//+------------------------------------------------------------------+
//|                                                     IFS_fern.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <cIntBMP.mqh>
//--Coeficientes IFS da Samambaia de Barnsley
//-- matrizes (a,b,c,d) 
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
//-- vetores (e,f)
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
//-- "probabilidades" de transformações, multiplicadas por 1000
double IFS_p[4] = {10,     850,    70,     70};

double Probs[4];
cIntBMP bmp;
int scale=50;
//+------------------------------------------------------------------+
//| Função de inicialização do Expert                                |
//+------------------------------------------------------------------+
int OnInit()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }

   int XSize=600;
   int YSize=600;

   bmp.Create(XSize,YSize,clrSeashell);

   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

   double x0=0;
   double y0=0;
   double x,y;

   int points=250000;

   for(int i=0; i<points; i++)
     {
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            x0 = x;
            y0 = y;
            int scX = int (MathRound(XSize/2 + (x)*scale));
            int scY = int (MathRound(YSize/2 + (y-5)*scale));
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrForestGreen); }
            break;
           }
        }
     }
   bmp.Save("bmpimg",true);
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Função de desinicialização do Expert                             |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ObjectDelete(0,"IFS");
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------+ 

É notável que tal estrutura complexa pode ser definida por apenas 28 números.

Se aumentarmos a escala para 150 e definirmos para 1250000 iterações, veremos o fragmento ampliado:

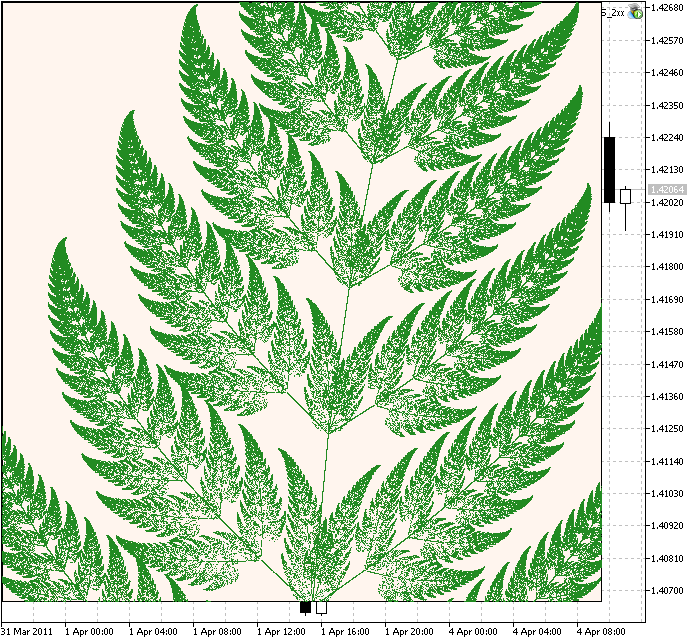
Figura 4. Fragmento da Samambaia de Barnsley

Como você pode ver, o algoritmo é universal, permitindo gerar diferentes conjuntos fractais.

O próximo exemplo é o Tapete de Sierpinski, definido pelos seguintes coeficientes IFS:

//-- coeficientes IFS do Triângulo de Sierpinski
double IFS_a[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333};
double IFS_b[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_c[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_d[8] = {0.333, 0.333,  0.333,  0.333, 0.333,  0.333,  0.333, 0.333};
double IFS_e[8] = {-0.125, -3.375, -3.375,  3.125, 3.125, -3.375, -0.125, 3.125};
double IFS_f[8] = {6.75, 0.25, 6.75,  0.25, 6.75, 3.5, 0.25, 3.50};
//-- "probabilidades", multiplicadas por 1000
double IFS_p[8]={125,125,125,125,125,125,125,125};

Figura 5. Tapete de Sierpinski

No capítulo 2, consideramos o algoritmo de cálculo dos coeficientes de contrações IFS.

Vamos considerar como criar a palavra "fractal". Em Russo, a palavra "Fractal" se parece como:

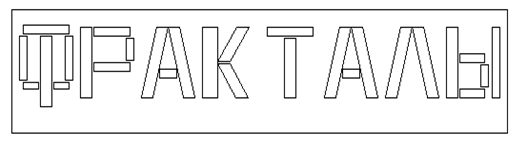
Figura 6. Palavra "Fractais" em Russo

Para encontrar os coeficientes IFS, precisamos resolver os sistemas lineares correspondentes As soluções são:

//-- coeficientes IFS da palavra "Fractais" em Russo
double IFS_a[28]=
  {
   0.00, 0.03,  0.00, 0.09, 0.00, 0.03, -0.00, 0.07, 0.00, 0.07, 0.03,  0.03,  0.03,  0.00,
   0.04, 0.04, -0.00, 0.09, 0.03, 0.03,  0.03, 0.03, 0.03, 0.00, 0.05, -0.00,  0.05,  0.00
  };

double IFS_b[28]=
  {
   -0.11, 0.00, 0.07, 0.00, -0.07, 0.00, -0.11,  0.00, -0.07,  0.00, -0.11,  0.11, 0.00, -0.14,
   -0.12, 0.12,-0.11, 0.00, -0.11, 0.11,  0.00, -0.11,  0.11, -0.11,  0.00, -0.07, 0.00, -0.07
  };

double IFS_c[28]=
  {
   0.12,  0.00,  0.08,  -0.00,  0.08,  0.00,  0.12,  0.00,  0.04,  0.00,  0.12,  -0.12, 0.00,  0.12,
   0.06,  -0.06,  0.10,  0.00,  0.12,  -0.12,  0.00,  0.12,  -0.12,  0.12, 0.00,  0.04,  0.00,  0.12
  };

double IFS_d[28]=
  {
   0.00,  0.05,  0.00,  0.07,  0.00,  0.05,  0.00,  0.07,  0.00,  0.07,  0.00,  0.00,  0.07,  0.00,
   0.00,  0.00,  0.00,  0.07,  0.00,  0.00,  0.07,  0.00,  0.00,  0.00,  0.07,  0.00,  0.07,  0.00
  };

double IFS_e[28]=
  {
   -4.58,  -5.06, -5.16, -4.70, -4.09, -4.35, -3.73, -3.26, -2.76,  -3.26, -2.22, -1.86, -2.04, -0.98,
   -0.46,  -0.76,  0.76,  0.63,  1.78,  2.14,  1.96,  3.11,  3.47,  4.27,  4.60,  4.98,   4.60, 5.24
  };

double IFS_f[28]=
  {
   1.26,  0.89,  1.52,  2.00,  1.52,  0.89,  1.43,  1.96,  1.69,  1.24,  1.43,  1.41,  1.11,  1.43,
   1.79,  1.05,  1.32,  1.96,  1.43,  1.41,  1.11,  1.43,  1.41,  1.43,  1.42,  1.16,  0.71,  1.43
  };

//-- "probabilidades", multiplicadas por 1000
double IFS_p[28]=
  {
   35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  
   35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35
  };

Como resultado, teremos a seguinte imagem:

Figura 7. Palavra auto-semelhante

O código fonte inteiro pode ser encontrado em ifs_fractals.mq5.

Se ampliarmos o conjunto, veremos a estrutura auto-semelhante:

Figura 8. Ampliando a região do conjunto

Os conjuntos auto-semelhantes, baseado em IFS, podem ser construídos usando o Fractal Designer.

Nós abordamos o tópico de criação de conjuntos fractais utilizando os Sistemas de função iterada. Graças a biblioteca cIntBMP, o processo é muito simples. Agora é hora de criar uma classe e adicionar alguns recursos para melhorar as imagens.

4. Classe de construção de imagens IFS

Você deve ter notado que a construção correta dos conjuntos são dirigidos pelas probabilidades. A diferença de probabilidades significa que esse conjunto tem uma estrutura irregular (ver pesos do IFS da Samambaia de Barnsley). Este fato pode ser usado para a criação de belas imagens. Precisamos definir a cor, proporcional à frequência do ponto em alguma vizinhança.

Isto pode ser feito utilizando a tela virtual (apenas um array), se o pixel de cor irá depender dos valores anteriores. Finalmente, a tela virtual será renderizada para bmp mediante a Paleta. A imagem bmp em si pode ser desenhada como uma imagem de fundo do gráfico.

Segue o código do Expert Advisor, baseado na classe CIFS:

//+------------------------------------------------------------------+
//|                                               IFS_Fern_color.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#include <cIntBMP.mqh>
//-- Coeficientes IFS da Samambaia de Barnsley
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
double IFS_p[4] = {10,     850,    70,     70};
//-- Paleta
uchar Palette[23*3]=
  {
   0x00,0x00,0x00,0x02,0x0A,0x06,0x03,0x11,0x0A,0x0B,0x1E,0x0F,0x0C,0x4C,0x2C,0x1C,0x50,0x28,
   0x2C,0x54,0x24,0x3C,0x58,0x20,0x4C,0x5C,0x1C,0x70,0x98,0x6C,0x38,0xBC,0xB0,0x28,0xCC,0xC8,
   0x4C,0xB0,0x98,0x5C,0xA4,0x84,0xBC,0x68,0x14,0xA8,0x74,0x28,0x84,0x8C,0x54,0x94,0x80,0x40,
   0x87,0x87,0x87,0x9F,0x9F,0x9F,0xC7,0xC7,0xC7,0xDF,0xDF,0xDF,0xFC,0xFC,0xFC
  };
//+------------------------------------------------------------------+
//| Classe CIFS                                                      |
//+------------------------------------------------------------------+
class CIFS
  {
protected:
   cIntBMP           m_bmp;
   int               m_xsize;
   int               m_ysize;
   uchar             m_virtual_screen[];
   double            m_scale;
   double            m_probs[8];

public:
                    ~CIFS()                          { m_bmp.Delete("bmpimg",true); };
   void              Create(int x_size,int y_size,uchar col);
   void              Render(double scale,bool back);
   void              ShowBMP(bool back);
protected:
   void              VS_Prepare(int x_size,int y_size,uchar col);
   void              VS_Fill(uchar col);
   void              VS_PutPixel(int px,int py,uchar col);
   uchar             VS_GetPixel(int px,int py);
   int               GetPalColor(uchar index);
   int               RGB256(int r,int g,int b) const {return(r+256*g+65536*b);      }
   void              PrepareProbabilities();
   void              RenderIFSToVirtualScreen();
   void              VirtualScreenToBMP();
  };
//+------------------------------------------------------------------+
//| Criando o método                                                 |
//+------------------------------------------------------------------+
void CIFS::Create(int x_size,int y_size,uchar col)
  {
   m_bmp.Create(x_size,y_size,col);
   VS_Prepare(x_size,y_size,col);
   PrepareProbabilities();
  }
//+------------------------------------------------------------------+
//| Preparando a tela virtual                                        |
//+------------------------------------------------------------------+
void CIFS::VS_Prepare(int x_size,int y_size,uchar col)
  {
   m_xsize=x_size;
   m_ysize=y_size;
   ArrayResize(m_virtual_screen,m_xsize*m_ysize);
   VS_Fill(col);
  }
//+------------------------------------------------------------------+
//| Preenchendo a tela virtual com cores específicas                 |
//+------------------------------------------------------------------+
void CIFS::VS_Fill(uchar col)
  {
   for(int i=0; i<m_xsize*m_ysize; i++) {m_virtual_screen[i]=col;}
  }
//+------------------------------------------------------------------+
//| Retorna a cor da paleta                                          |
//+------------------------------------------------------------------+
int CIFS::GetPalColor(uchar index)
  {
   int ind=index;
   if(ind<=0) {ind=0;}
   if(ind>22) {ind=22;}
   uchar r=Palette[3*(ind)];
   uchar g=Palette[3*(ind)+1];
   uchar b=Palette[3*(ind)+2];
   return(RGB256(r,g,b));
  }
//+------------------------------------------------------------------+
//| Desenha o pixel na tela virtual                                  |
//+------------------------------------------------------------------+
void CIFS::VS_PutPixel(int px,int py,uchar col)
  {
   if (px<0) return;
   if (py<0) return;
   if (px>m_xsize) return;
   if (py>m_ysize) return;
    int pos=m_xsize*py+px;
   if(pos>=ArraySize(m_virtual_screen)) return;
   m_virtual_screen[pos]=col;
  }
//+------------------------------------------------------------------+
//| Obtém a "cor" do pixel da tela virtual                           |
//+------------------------------------------------------------------+
uchar CIFS::VS_GetPixel(int px,int py)
  {
   if (px<0) return(0);
   if (py<0) return(0);
   if (px>m_xsize) return(0);
   if (py>m_ysize) return(0);
    int pos=m_xsize*py+px;
   if(pos>=ArraySize(m_virtual_screen)) return(0);
   return(m_virtual_screen[pos]);
  }
//+------------------------------------------------------------------+
//| Prepara o array cumulativo probabilidades                        |
//+------------------------------------------------------------------+
void CIFS::PrepareProbabilities()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      m_probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
  }
//+------------------------------------------------------------------+
//| Renderiza os conjuntos IFS para a tela virtual                   |
//+------------------------------------------------------------------+
void CIFS::RenderIFSToVirtualScreen()
  {
   double x=0,y=0;
   double x0=0;
   double y0=0;
   uint iterations= uint (MathRound(100000+100*MathPow(m_scale,2)));

   for(uint i=0; i<iterations; i++)
     {
      double prb=1000*(rand()/32767.0);

      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=m_probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];

            int scX = int (MathRound(m_xsize/2 + (x-0)*m_scale));
            int scY = int (MathRound(m_ysize/2 + (y-5)*m_scale));

            if(scX>=0 && scX<m_xsize && scY>=0 && scY<m_ysize)
              {
               uchar c=VS_GetPixel(scX,scY);
               if(c<255) c=c+1;
               VS_PutPixel(scX,scY,c);
              }
            break;
           }
         x0 = x;
         y0 = y;
        }
     }
  }
//+------------------------------------------------------------------+
//| Copia a tela virtual para BMP                                    |
//+------------------------------------------------------------------+
void CIFS::VirtualScreenToBMP()
  {
   for(int i=0; i<m_xsize; i++)
     {
      for(int j=0; j<m_ysize; j++)
        {
         uchar colind=VS_GetPixel(i,j);
         int xcol=GetPalColor(colind);
         if(colind==0) xcol=0x00;
         //if(colind==0) xcol=0xFFFFFF;
         m_bmp.DrawDot(i,j,xcol);
        }
     }
  }
//+------------------------------------------------------------------+
//| Mostra a imagem BMP no gráfico                                   |
//+------------------------------------------------------------------+
void CIFS::ShowBMP(bool back)
  {
   m_bmp.Save("bmpimg",true);
   m_bmp.Show(0,0,"bmpimg","Fern");
   ObjectSetInteger(0,"Fern",OBJPROP_BACK,back);
  }
//+------------------------------------------------------------------+
//| Método de renderização                                           |     
//+------------------------------------------------------------------+
void CIFS::Render(double scale,bool back)
  {
   m_scale=scale;
   VS_Fill(0);
   RenderIFSToVirtualScreen();
   VirtualScreenToBMP();
   ShowBMP(back);
  }

static int gridmode;
CIFS fern;
int currentscale=50;
//+------------------------------------------------------------------+
//| Função de inicialização do Expert                                |
//+------------------------------------------------------------------+
void OnInit()
  {
//-- obtêm o modo grade
   gridmode= int (ChartGetInteger(0,CHART_SHOW_GRID,0));
//-- desabilita a grade
   ChartSetInteger(0,CHART_SHOW_GRID,0);
//-- cria o bmp
   fern.Create(800,800,0x00);
//-- mostra como imagem de fundo
   fern.Render(currentscale,true);
  }
//+------------------------------------------------------------------+
//| Função de desinicialização do Expert                             |
//+------------------------------------------------------------------+
void OnDeinit(const int r)
  {
//-- restaura o modo grade
   ChartSetInteger(0,CHART_SHOW_GRID,gridmode); 
//-- remove o objeto Samambaia
   ObjectDelete(0,"Fern");
 }
//+------------------------------------------------------------------+
//| Manipulador de evento OnChart do Expert                          |
//+------------------------------------------------------------------+
void OnChartEvent(const int id,           // Identificador do Evento  
                const long& lparam,   // Parâmetro de Evento do tipo long
                const double& dparam, // Parâmetro de Evento do tipo double
                const string& sparam  // Parâmetro de Evento do tipo string
                )
  {
//--- clique no objeto do gráfico
   if(id==CHARTEVENT_OBJECT_CLICK)
     {
      Print("Evento clique no objeto do gráfico de nome '"+sparam+"'");
      if(sparam=="Fern")
        {
         // aumenta o coeficiente de escala (zoom)
         currentscale=int (currentscale*1.1);
         fern.Render(currentscale,true);
        }
     }
  }
//+------------------------------------------------------------------+

Cujo resultado é:

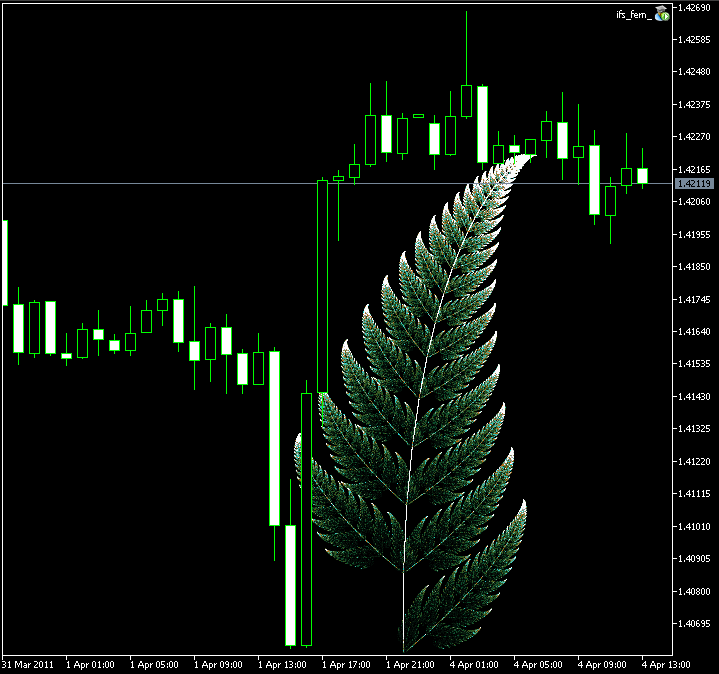
Figura 9. Imagem da Samambaia de Barnsley, criado com a classe CIFS

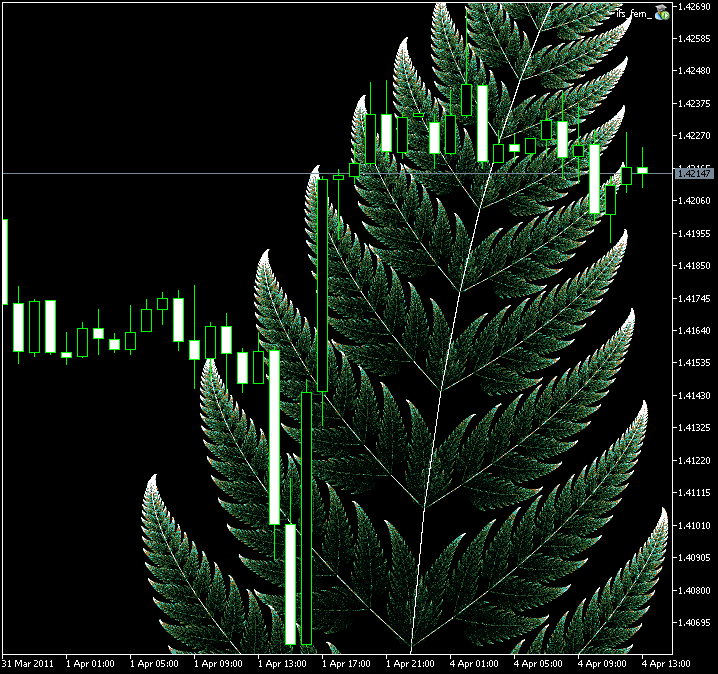
Figura 10. A região ampliada da Samambaia de Barnsley

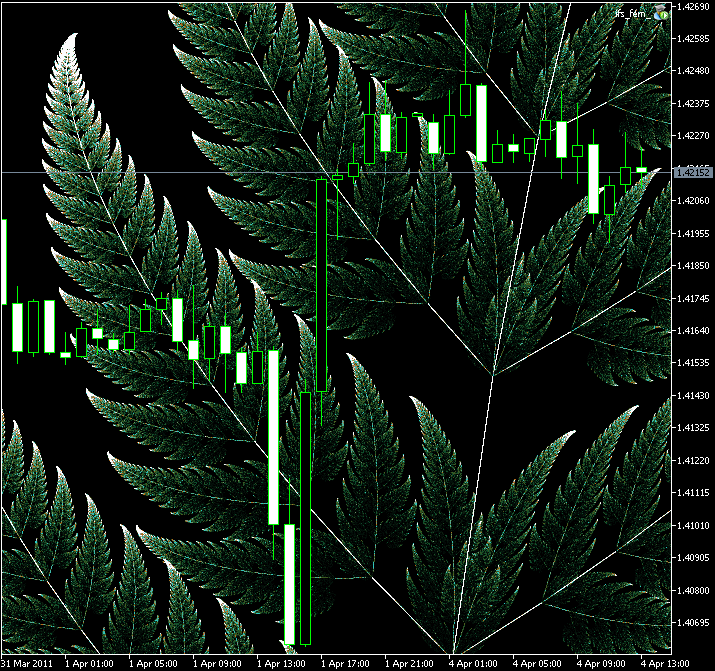
Figura 11. A região ampliada da Samambaia de Barnsley

Figura 12. A região ampliada da Samambaia de Barnsley

Faça você mesmo

1. Há vários fractais IFS em Fractint, por exemplo:

// Binary
double IFS_a[3] = { 0.5,  0.5,  0.0};
double IFS_b[3] = { 0.0,  0.0, -0.5};
double IFS_c[4] = { 0.0,  0.0,  0.5};
double IFS_d[4] = { 0.5,  0.5,  0.5};
double IFS_e[4] = {-2.563477,  2.436544, 4.873085};
double IFS_f[4] = {-0.000000, -0.000003, 7.563492};
double IFS_p[4] = {333, 333, 333};

// Coral
double IFS_a[3] = { 0.307692,  0.307692,  0.000000};
double IFS_b[3] = {-0.531469, -0.076923,  0.54545};
double IFS_c[3] = {-0.461538,  0.153846,  0.692308};
double IFS_d[3] = {-0.293706, -0.447552, -0.195804};
double IFS_e[3] = {5.4019537, -1.295248, -4.893637};
double IFS_f[3] = { 8.655175,  4.152990,  7.269794};
double IFS_p[3] = {400, 150, 450};

// Crystal
double IFS_a[2] = { 0.696970,  0.090909};
double IFS_b[2] = {-0.481061, -0.443182};
double IFS_c[2] = {-0.393939,  0.515152};
double IFS_d[2] = {-0.662879, -0.094697};
double IFS_e[2] = { 2.147003,  4.286558};
double IFS_f[2] = {10.310288,  2.925762};
double IFS_p[2] = {750, 250};

// Dragon
double IFS_a[2] = { 0.824074,  0.088272};
double IFS_b[2] = { 0.281482,  0.520988};
double IFS_c[2] = {-0.212346, -0.463889};
double IFS_d[2] = { 0.864198, -0.377778};
double IFS_e[2] = {-1.882290,  0.785360};
double IFS_f[2] = {-0.110607,  8.095795};
double IFS_p[2] = {780, 220};

// Floor
double IFS_a[3] = { 0,  0.52,  0};
double IFS_b[3] = {-0.5,   0,  0.5};
double IFS_c[3] = { 0.5,   0, -0.5};
double IFS_d[3] = { 0,   0.5,  0};
double IFS_e[3] = {-1.732366, -0.027891,  1.620804};
double IFS_f[3] = { 3.366182,  5.014877,  3.310401};
double IFS_p[3] = {333, 333, 333};

// Koch3
double IFS_a[5] = {0.307692, 0.192308,  0.192308,  0.307692,  0.384615};
double IFS_b[5] = {      0,-0.205882,  0.205882,         0,        0};
double IFS_c[5] = {      0, 0.653846, -0.653846,         0,         0};
double IFS_d[5] = {0.294118, 0.088235,  0.088235,  0.294118, -0.294118};
double IFS_e[5] = {4.119164,-0.688840,  0.688840, -4.136530, -0.007718};
double IFS_f[5] = {1.604278, 5.978916,  5.962514,  1.604278,  2.941176};
double IFS_p[5] = {151, 254, 254, 151, 190};

// Spiral
double IFS_a[3] = { 0.787879, -0.121212,  0.181818};
double IFS_b[3] = {-0.424242,  0.257576, -0.136364};
double IFS_c[3] = { 0.242424,  0.151515,  0.090909};
double IFS_d[3] = { 0.859848,  0.053030,  0.181818};
double IFS_e[3] = { 1.758647,  -6.721654,  6.086107};
double IFS_f[3] = { 1.408065,   1.377236,  1.568035};
double IFS_p[3] = {896, 52, 52};

// Swirl5
double IFS_a[2] = {  0.74545, -0.424242};
double IFS_b[2] = {-0.459091, -0.065152};
double IFS_c[2] = { 0.406061, -0.175758};
double IFS_d[2] = { 0.887121, -0.218182};
double IFS_e[2] = { 1.460279,  3.809567};
double IFS_f[2] = { 0.691072,  6.741476};
double IFS_p[2] = {920, 80};

// Zigzag2
double IFS_a[2] = {-0.632407, -0.036111};
double IFS_b[2] = {-0.614815, 0.444444};
double IFS_c[2] = {-0.545370, 0.210185};
double IFS_d[2] = { 0.659259, 0.037037};
double IFS_e[2] = { 3.840822, 2.071081};
double IFS_f[2] = { 1.282321, 8.330552};
double IFS_p[2] = {888, 112};

Plote esses conjuntos. Como encontrar transformações de similaridade iniciais usando os coeficientes IFS?

2. Criando seus próprios conjuntos de fractais e calculando seus coeficientes (capítulo 2).

3. Tente brincar com a paleta de cores (array uchar Palette), extenda a paleta e adicione cores gradientes.

4. E sobre a dimensão do fractal (Hausdorf-Bezikovitch) da Samambaia de Barnsley? Existe uma fórmula para calcular a dimensão do fractal utilizando os coeficientes IFS?

5. Amplie uma certa região, utilizando a informação das coordenadas do clique do mouse no OnChartEvent:

void OnChartEvent(const int id,         // Identificador de Evento  
                const long& lparam,   // Parâmetro de Evento do tipo long
                const double& dparam, // Parâmetro de Evento do tipo double
                const string& sparam  // Parâmetro de Evento do tipo string
                )
  {
//--- Clique com o botão esquerdo
   if(id==CHARTEVENT_CLICK)
     {
      Print("Coordenadas: x=",lparam,"  y=",dparam);
     }
  }

Conclusão

Nós consideramos o algoritmo de criação de conjuntos auto-semelhantes, usando o Sistema de Função Iterada.

O uso da biblioteca cIntBMP simplifica bastante o trabalho com imagens gráficas. Além do método DrawDot(x,y,color) que temos utilizado, a classe cIntBMP contém muitos outros métodos úteis. Mas isto é outra história.