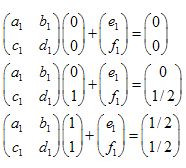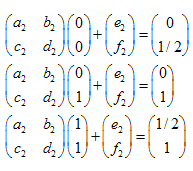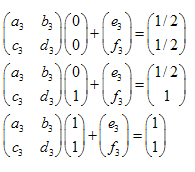在 MQL5 中使用 Iterated Function Systems (IFS - 迭代函数系统) 创建分形 - MetaTrader 5EA

有许多程序, 允许创建自相似集合, 它们的定义均依赖 Iterated Function System (IFS - 迭代函数系统)。比如, Fractint, Fractal Designer 或 IFS Matlab Generator。感谢 MQL5 语言的速度，它将处理图像对象变为可能, 这些漂亮的集合可在 MetaTrader 5 客户端中学到。

这个 cIntBMP 库, 由 Dmitry (Integer) 开发，提供新的图形操作以便极其简单的创建图形图像。这个库曾经 荣获 由 MetaQuotes Software Corp 公司授予的特别奖。

在本篇中我们将讨论使用 cIntBMP 库的例子。进一步, 我们将囊括利用 Iterated Function System (IFS - 迭代函数系统) 创建自相似分形集合的算法。

1. 平面仿射变换

平面仿射变换是一种映射 。通常, 仿射 2-D 变换可使用一些  矩阵和  , 向量来定义。坐标点 (x,y) 变换至其它点 使用线形变换:

这个变换必须是非奇异的, 即 .  这个仿射变换改变大小 倍。

这个仿射变换不能改变几何对象的结构 (线性至线性变换), 这个AT允许描述物体的简单"变形", 例如旋转, 缩放和平移。

平面仿射变换的例子:

1) 平面旋转 至 角度:

2) 平面缩放 以 及 为系数 (X 和 Y 轴):

3) 平面平移 参数  向量:

这个 收缩映射 是关键 (参见 Hutchinson 结果)。

如果 和 由坐标点 和 以及 是一个距离 (例如, 欧几里得距离: ). 这个仿射变换称为 收缩 如果 , 则 .

这是仿射变换的例子:

这是结果:

2. 相似变换

构建分形有如下方式: 一些 (简单的) 几何对象 (线段, 三角, 正方形) 分裂成 N 片，并且它们中的 M 片用于将来 "构建" 集合 (如果 N=M, 我们将得到整数维度的结果集合)。之后，重复处理每一片。

典型分形:

线段:

• Triadic Koch Curve（三元科赫曲线）, N=3, M=4;
• Cantor Dust, N=3, M=2;

三角:

• Sierpinski Gasket, N=4, M=3;

正方形:

• Sierpinski Carpet, N=9, M=8;
• Vichek fractal, N=9, M=5.
  

以及其它。

这些分形有自相似结构, 它们当中的一些可由少数相似变换定义。仿射变换的结构依赖于分形构建的方式。

正如您即将看到的, 它十分简单, 而且我们需要解决的仅有问题是描述分形构造的第一个迭代，并且找到仿射变换的相应集合。

假设我们有一些集合。根据分形创建算法，我们需要减少它，旋转并 "放于确定的地方"。问题是用仿射变换来描述这个处理过程, 如, 我们需要找到矩阵和向量。

很容易证明，选取初始集合的3个点 (非三元) 并将之变换为 "减少的" 集合中的 3个相应点是足够的。这个变换将引申出 6 个线性方程组, 允许我们找到 a,b,c,d,e,f 作为答案。

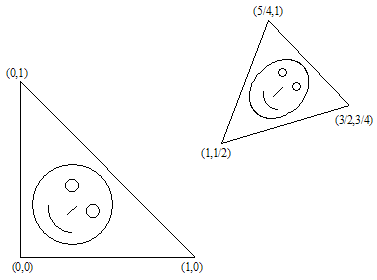
让我们来看看。假设 三角变换至 三角。

解线性方程组，我们可以得到 a,b,c,d,e 和 f 系数:

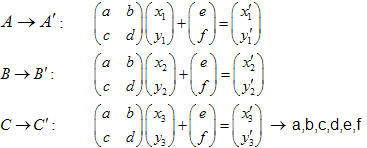
例子:Sierpinski Gasket:

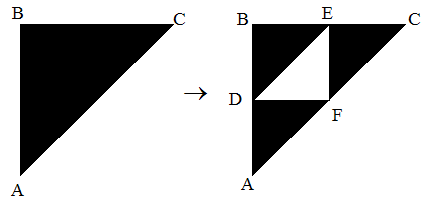
这些坐标是:

• A (0,0)
• B (0,1)
• C (1,1)
• D(0,1/2)
• E (1/2,1)
• F(1/2,1/2)
  

我们有 3 个变换:

1. ABC -> ADF
2. ABC -> DBE
3. ABC -> FEC
   

这个线性方程组看起来像这样:

1. 
   
2. 
   
3. 
   

这个答案是: , ,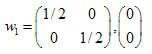

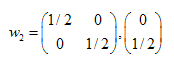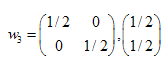
我们已经发现这三个仿射变换的系数。之后我们将用它们创建自相似集合。

3. 利用迭代函数系统创建分形

这个 Iterated Function System (IFS - 迭代函数系统) 是一组仿射收缩 此处 - 是 "权重"。每一个 IFS 函数由 7 个数字定义: , 此处权重用于当迭代处理作为第n个变换的概率。最好定义它们的值, 按比例收缩: 。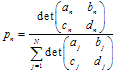

让我们来考虑一下利用迭代函数系统构造分形的算法 (参见 Chaos Game（混沌游戏）)。

首先我们要取一些初始点的坐标 。接着，我们随机选取一些收缩并绘制点 。再次, 我们随机选取一些收缩 并绘制 。最终我们将拥有 作为点集合。

收缩的选择依赖于它的 "概率"。如果我们重复处理 (例如, 至 ~30000 点) 并绘制结果集合, 我们将会看到结构，即使处理是随机的。

这是一个 Sierpinski Gasket 例子:

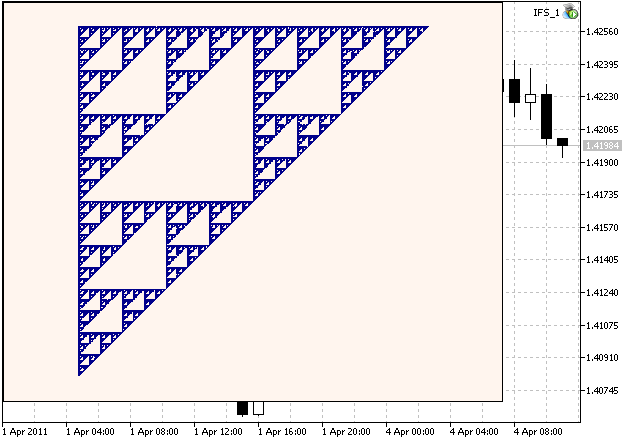
图例 1. 这个 Sierpinski Gasket, 由 IFS 生成，系数的计算见章节 2

代码:

//+------------------------------------------------------------------+
//|                                        IFS_Sierpinski_Gasket.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

//-- 包含文件 cIntBMP 类
#include <cIntBMP.mqh>

//-- Sierpinski Gasket IFS 系数
//-- (a,b,c,d) 矩阵
double IFS_a[3] = {0.50,  0.50,  0.50};
double IFS_b[3] = {0.00,  0.00,  0.00};
double IFS_c[3] = {0.00,  0.00,  0.00};
double IFS_d[3] = {0.50,  0.50,  0.50};
//-- (e,f) 向量
double IFS_e[3] = {0.00,  0.00,  0.50};
double IFS_f[3] = {0.00,  0.50,  0.50};
//-- 变换"概率", 乘以 1000
double IFS_p[3]={333,333,333};

double Probs[3]; // Probs 数组 - 用于选择 IFS 变换
cIntBMP bmp;     // cIntBMP 类实例
int scale=350;  // 缩放系数
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//-- 准备 Probs 数组
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
//-- BMP 图像尺寸
   int XSize=500;
   int YSize=400;
//-- 创建 bmp 图像 XSizexYSize 以及 clrSeashell 背景颜色
   bmp.Create(XSize,YSize,clrSeashell);
//-- 图像长方形
   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

//-- 坐标点 (将被用于构建集合)
   double x0=0;
   double y0=0;
   double x,y;
//-- 计算点的数量 (更多的点 - 图像细节)
   int points=1500000;
//-- 计算集合
   for(int i=0; i<points; i++)
     {
      // 以概率选择 IFS 变换, 按比例定义
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            // 仿射变换
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            // 更新之前的坐标
            x0 = x;
            y0 = y;
            // 转换至 BMP 图像坐标
            // (注：cIntBMP 中的 Y 轴)
            int scX = int (MathRound(XSize/2 + (x-0.5)*scale));
            int scY = int (MathRound(YSize/2 + (y-0.5)*scale));
            // 如果坐标点位于图像内, 画点
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); }
            break;
           }
        }
     }
//-- 保存图像至文件
   bmp.Save("bmpimg",true);
//-- 在图表中画图
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- 从图表中删除图像
   ObjectDelete(0,"IFS");
//--- 删除文件e
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------+

如果我们设置缩放至 1350, 增加迭代次数至 15000000, 并且改变初始点的平移:

int scX = MathRound(XSize/2 + (x-0.75)*scale);
int scY = MathRound(YSize/2 + (y-0.75)*scale);

我们将可能看到集合的伸缩区域。其一看到 (图例. 2), 它有自相似结构:

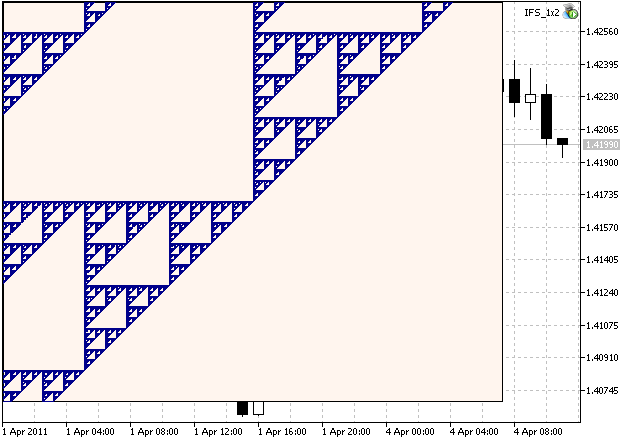
图例 2. 伸缩区域 Sierpinski Gasket

让我们考虑著名的 Barnsley's Fern, 是由 Michael Barnsley 提出。它有些复杂。

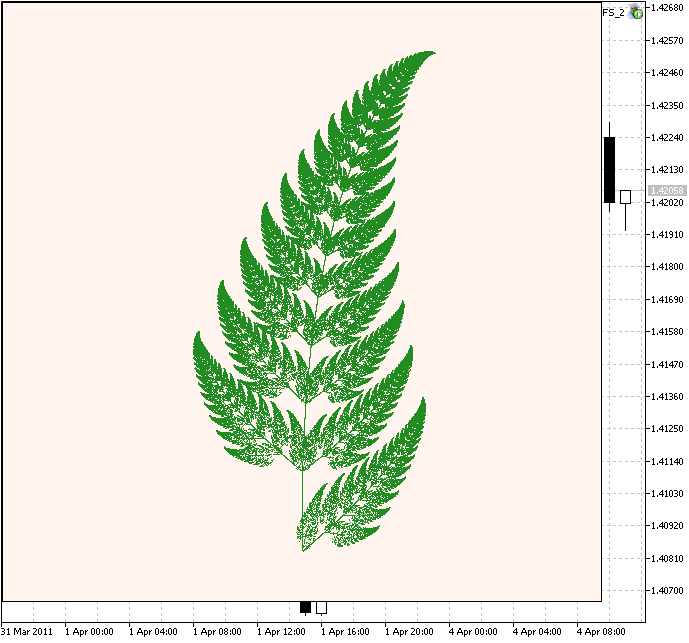
图例 3. Barnsley's Fern

代码类似, 但在这个例子中我们用了 4 个 IFS 不同权重的收缩。

//+------------------------------------------------------------------+
//|                                                     IFS_fern.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <cIntBMP.mqh>
//-- Barnsley Fern IFS 系数
//-- (a,b,c,d) 矩阵
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
//-- (e,f) 向量
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
//-- 变换"概率", 乘以 1000
double IFS_p[4] = {10,     850,    70,     70};

double Probs[4];
cIntBMP bmp;
int scale=50;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }

   int XSize=600;
   int YSize=600;

   bmp.Create(XSize,YSize,clrSeashell);

   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

   double x0=0;
   double y0=0;
   double x,y;

   int points=250000;

   for(int i=0; i<points; i++)
     {
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            x0 = x;
            y0 = y;
            int scX = int (MathRound(XSize/2 + (x)*scale));
            int scY = int (MathRound(YSize/2 + (y-5)*scale));
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrForestGreen); }
            break;
           }
        }
     }
   bmp.Save("bmpimg",true);
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ObjectDelete(0,"IFS");
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------+ 

显著的是，如此复杂的结构仅由 28 个数字定义。

如果我们增加伸缩至 150, 并且设迭代至 1250000 我们将看到拉伸的片段:

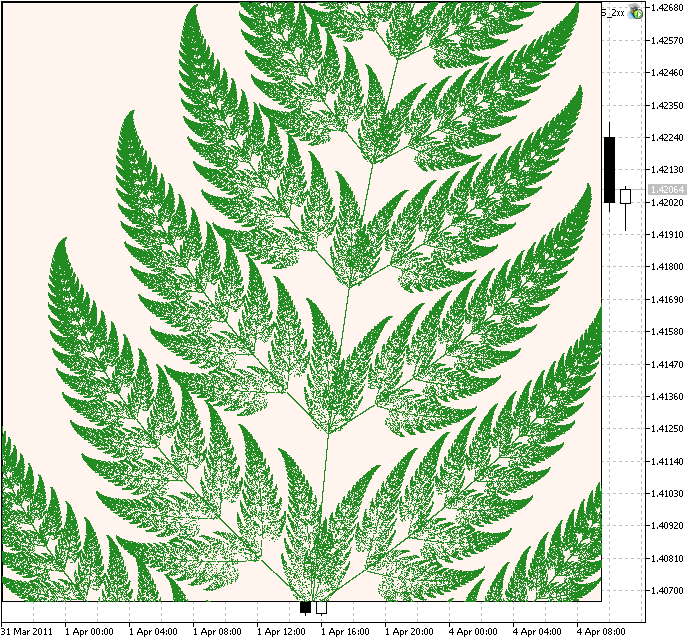
图例 4. 片段 Barnsley's Fern

如您所看到的，算法是通用的, 它允许您生成不同的分形集合。

下个例子是 Sierpinski Carpet, 定义如下 IFS 系数:

//-- Sierpinski Gasket IFS 系数
double IFS_a[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333};
double IFS_b[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_c[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_d[8] = {0.333, 0.333,  0.333,  0.333, 0.333,  0.333,  0.333, 0.333};
double IFS_e[8] = {-0.125, -3.375, -3.375,  3.125, 3.125, -3.375, -0.125, 3.125};
double IFS_f[8] = {6.75, 0.25, 6.75,  0.25, 6.75, 3.5, 0.25, 3.50};
//-- "概率", 乘以 1000
double IFS_p[8]={125,125,125,125,125,125,125,125};

图例 5. Sierpinski Carpet

在章节 2，我们已经讨论了利用 IFS 计算收缩系数的算法。

让我们来考虑创建 "分形单词"。在俄语中, "分形" 一词看上去像:

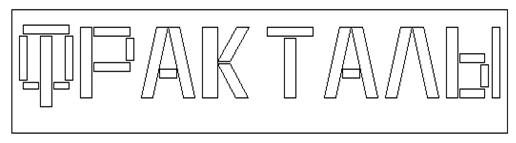
图例 6. 俄语的 "分形" 一词

为找到 IFS 系数, 我们需要解决相关的线性系统。这个方案是:

//-- IFS 系数: 俄语 "分形"
double IFS_a[28]=
  {
   0.00, 0.03,  0.00, 0.09, 0.00, 0.03, -0.00, 0.07, 0.00, 0.07, 0.03,  0.03,  0.03,  0.00,
   0.04, 0.04, -0.00, 0.09, 0.03, 0.03,  0.03, 0.03, 0.03, 0.00, 0.05, -0.00,  0.05,  0.00
  };

double IFS_b[28]=
  {
   -0.11, 0.00, 0.07, 0.00, -0.07, 0.00, -0.11,  0.00, -0.07,  0.00, -0.11,  0.11, 0.00, -0.14,
   -0.12, 0.12,-0.11, 0.00, -0.11, 0.11,  0.00, -0.11,  0.11, -0.11,  0.00, -0.07, 0.00, -0.07
  };

double IFS_c[28]=
  {
   0.12,  0.00,  0.08,  -0.00,  0.08,  0.00,  0.12,  0.00,  0.04,  0.00,  0.12,  -0.12, 0.00,  0.12,
   0.06,  -0.06,  0.10,  0.00,  0.12,  -0.12,  0.00,  0.12,  -0.12,  0.12, 0.00,  0.04,  0.00,  0.12
  };

double IFS_d[28]=
  {
   0.00,  0.05,  0.00,  0.07,  0.00,  0.05,  0.00,  0.07,  0.00,  0.07,  0.00,  0.00,  0.07,  0.00,
   0.00,  0.00,  0.00,  0.07,  0.00,  0.00,  0.07,  0.00,  0.00,  0.00,  0.07,  0.00,  0.07,  0.00
  };

double IFS_e[28]=
  {
   -4.58,  -5.06, -5.16, -4.70, -4.09, -4.35, -3.73, -3.26, -2.76,  -3.26, -2.22, -1.86, -2.04, -0.98,
   -0.46,  -0.76,  0.76,  0.63,  1.78,  2.14,  1.96,  3.11,  3.47,  4.27,  4.60,  4.98,   4.60, 5.24
  };

double IFS_f[28]=
  {
   1.26,  0.89,  1.52,  2.00,  1.52,  0.89,  1.43,  1.96,  1.69,  1.24,  1.43,  1.41,  1.11,  1.43,
   1.79,  1.05,  1.32,  1.96,  1.43,  1.41,  1.11,  1.43,  1.41,  1.43,  1.42,  1.16,  0.71,  1.43
  };

//-- "概率", 乘以 1000
double IFS_p[28]=
  {
   35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  
   35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35
  };

作为结果, 我们得到如下图像:

图例 7. 自相似单词

完整代码可在 ifs_fractals.mq5 文件中找到。

如果我们拉伸这个集合, 我们看到自相似结构:

图例 8. 集合的拉伸区域

基于 IFS 的自相似集合, 可由 Fractal Designer（分形设计者）构建。

我们的话题已经包扩了如何使用 IFS 创建分形集合。感谢 cIntBMP 库, 它极大简化了处理过程。现在是时候创建一个类并加入一些特性来制作更佳图像了。

您也许注意到正确的构造集合是以概率来驱动。不同的概率意味着集合具有不规则的结构 (参见 Barnsley Fern IFS 的权重)。这个事实用于创建漂亮的图像。我们需要设置颜色, 相邻点的频率比例。

它可以利用虚拟屏幕完成 (仅仅一个数组), 如果点的颜色依赖之前的数值。最后, 用调色板将虚拟屏幕的颜色涂染至图像。这个 bmp 图像自己可以画上去作为图表的背景照片。

这是交易程序的代码, 基于 CIFS 类:

//+------------------------------------------------------------------+
//|                                               IFS_Fern_color.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#include <cIntBMP.mqh>
//-- Barnsley Fern IFS 系数
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
double IFS_p[4] = {10,     850,    70,     70};
//-- Palette
uchar Palette[23*3]=
  {
   0x00,0x00,0x00,0x02,0x0A,0x06,0x03,0x11,0x0A,0x0B,0x1E,0x0F,0x0C,0x4C,0x2C,0x1C,0x50,0x28,
   0x2C,0x54,0x24,0x3C,0x58,0x20,0x4C,0x5C,0x1C,0x70,0x98,0x6C,0x38,0xBC,0xB0,0x28,0xCC,0xC8,
   0x4C,0xB0,0x98,0x5C,0xA4,0x84,0xBC,0x68,0x14,0xA8,0x74,0x28,0x84,0x8C,0x54,0x94,0x80,0x40,
   0x87,0x87,0x87,0x9F,0x9F,0x9F,0xC7,0xC7,0xC7,0xDF,0xDF,0xDF,0xFC,0xFC,0xFC
  };
//+------------------------------------------------------------------+
//| CIFS class                                                       |
//+------------------------------------------------------------------+
class CIFS
  {
protected:
   cIntBMP           m_bmp;
   int               m_xsize;
   int               m_ysize;
   uchar             m_virtual_screen[];
   double            m_scale;
   double            m_probs[8];

public:
                    ~CIFS()                          { m_bmp.Delete("bmpimg",true); };
   void              Create(int x_size,int y_size,uchar col);
   void              Render(double scale,bool back);
   void              ShowBMP(bool back);
protected:
   void              VS_Prepare(int x_size,int y_size,uchar col);
   void              VS_Fill(uchar col);
   void              VS_PutPixel(int px,int py,uchar col);
   uchar             VS_GetPixel(int px,int py);
   int               GetPalColor(uchar index);
   int               RGB256(int r,int g,int b) const {return(r+256*g+65536*b);      }
   void              PrepareProbabilities();
   void              RenderIFSToVirtualScreen();
   void              VirtualScreenToBMP();
  };
//+------------------------------------------------------------------+
//| Create method                                                    |
//+------------------------------------------------------------------+
void CIFS::Create(int x_size,int y_size,uchar col)
  {
   m_bmp.Create(x_size,y_size,col);
   VS_Prepare(x_size,y_size,col);
   PrepareProbabilities();
  }
//+------------------------------------------------------------------+
//| Prepares virtual screen                                          |
//+------------------------------------------------------------------+
void CIFS::VS_Prepare(int x_size,int y_size,uchar col)
  {
   m_xsize=x_size;
   m_ysize=y_size;
   ArrayResize(m_virtual_screen,m_xsize*m_ysize);
   VS_Fill(col);
  }
//+------------------------------------------------------------------+
//| Fills the virtual screen with specified color                    |
//+------------------------------------------------------------------+
void CIFS::VS_Fill(uchar col)
  {
   for(int i=0; i<m_xsize*m_ysize; i++) {m_virtual_screen[i]=col;}
  }
//+------------------------------------------------------------------+
//| Returns the color from palette                                   |
//+------------------------------------------------------------------+
int CIFS::GetPalColor(uchar index)
  {
   int ind=index;
   if(ind<=0) {ind=0;}
   if(ind>22) {ind=22;}
   uchar r=Palette[3*(ind)];
   uchar g=Palette[3*(ind)+1];
   uchar b=Palette[3*(ind)+2];
   return(RGB256(r,g,b));
  }
//+------------------------------------------------------------------+
//| Draws a pixel on the virtual screen                              |
//+------------------------------------------------------------------+
void CIFS::VS_PutPixel(int px,int py,uchar col)
  {
   if (px<0) return;
   if (py<0) return;
   if (px>m_xsize) return;
   if (py>m_ysize) return;
    int pos=m_xsize*py+px;
   if(pos>=ArraySize(m_virtual_screen)) return;
   m_virtual_screen[pos]=col;
  }
//+------------------------------------------------------------------+
//| Gets the pixel "color" from the virtual screen                   |
//+------------------------------------------------------------------+
uchar CIFS::VS_GetPixel(int px,int py)
  {
   if (px<0) return(0);
   if (py<0) return(0);
   if (px>m_xsize) return(0);
   if (py>m_ysize) return(0);
    int pos=m_xsize*py+px;
   if(pos>=ArraySize(m_virtual_screen)) return(0);
   return(m_virtual_screen[pos]);
  }
//+------------------------------------------------------------------+
//| Prepare the cumulative probabilities array                       |
//+------------------------------------------------------------------+
void CIFS::PrepareProbabilities()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      m_probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
  }
//+------------------------------------------------------------------+
//| Renders the IFS set to the virtual screen                        |
//+------------------------------------------------------------------+
void CIFS::RenderIFSToVirtualScreen()
  {
   double x=0,y=0;
   double x0=0;
   double y0=0;
   uint iterations= uint (MathRound(100000+100*MathPow(m_scale,2)));

   for(uint i=0; i<iterations; i++)
     {
      double prb=1000*(rand()/32767.0);

      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=m_probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];

            int scX = int (MathRound(m_xsize/2 + (x-0)*m_scale));
            int scY = int (MathRound(m_ysize/2 + (y-5)*m_scale));

            if(scX>=0 && scX<m_xsize && scY>=0 && scY<m_ysize)
              {
               uchar c=VS_GetPixel(scX,scY);
               if(c<255) c=c+1;
               VS_PutPixel(scX,scY,c);
              }
            break;
           }
         x0 = x;
         y0 = y;
        }
     }
  }
//+------------------------------------------------------------------+
//| Copies virtual screen to BMP                                     |
//+------------------------------------------------------------------+
void CIFS::VirtualScreenToBMP()
  {
   for(int i=0; i<m_xsize; i++)
     {
      for(int j=0; j<m_ysize; j++)
        {
         uchar colind=VS_GetPixel(i,j);
         int xcol=GetPalColor(colind);
         if(colind==0) xcol=0x00;
         //if(colind==0) xcol=0xFFFFFF;
         m_bmp.DrawDot(i,j,xcol);
        }
     }
  }
//+------------------------------------------------------------------+
//| Shows BMP image on the chart                                     |
//+------------------------------------------------------------------+
void CIFS::ShowBMP(bool back)
  {
   m_bmp.Save("bmpimg",true);
   m_bmp.Show(0,0,"bmpimg","Fern");
   ObjectSetInteger(0,"Fern",OBJPROP_BACK,back);
  }
//+------------------------------------------------------------------+
//| Render method                                                    |     
//+------------------------------------------------------------------+
void CIFS::Render(double scale,bool back)
  {
   m_scale=scale;
   VS_Fill(0);
   RenderIFSToVirtualScreen();
   VirtualScreenToBMP();
   ShowBMP(back);
  }

static int gridmode;
CIFS fern;
int currentscale=50;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
void OnInit()
  {
//-- 得到栅格模式
   gridmode= int (ChartGetInteger(0,CHART_SHOW_GRID,0));
//-- 禁止栅格
   ChartSetInteger(0,CHART_SHOW_GRID,0);
//-- 创建 bmp
   fern.Create(800,800,0x00);
//-- 显示作为背景图像
   fern.Render(currentscale,true);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int r)
  {
//-- 恢复栅格模式
   ChartSetInteger(0,CHART_SHOW_GRID,gridmode); 
//-- 删除对象 Fern
   ObjectDelete(0,"Fern");
 }
//+------------------------------------------------------------------+
//| Expert OnChart event handler                                     |
//+------------------------------------------------------------------+
void OnChartEvent(const int id,           // 事件识别符  
                const long& lparam,   // 事件参数 长整形
                const double& dparam, // 事件参数 浮点形
                const string& sparam  // 事件参数 字符形
                )
  {
//--- 点击图形对象
   if(id==CHARTEVENT_OBJECT_CLICK)
     {
      Print("Click event on graphic object with name '"+sparam+"'");
      if(sparam=="Fern")
        {
         // 增加伸缩系数 (拉伸)
         currentscale=int (currentscale*1.1);
         fern.Render(currentscale,true);
        }
     }
  }
//+------------------------------------------------------------------+

这是结果:

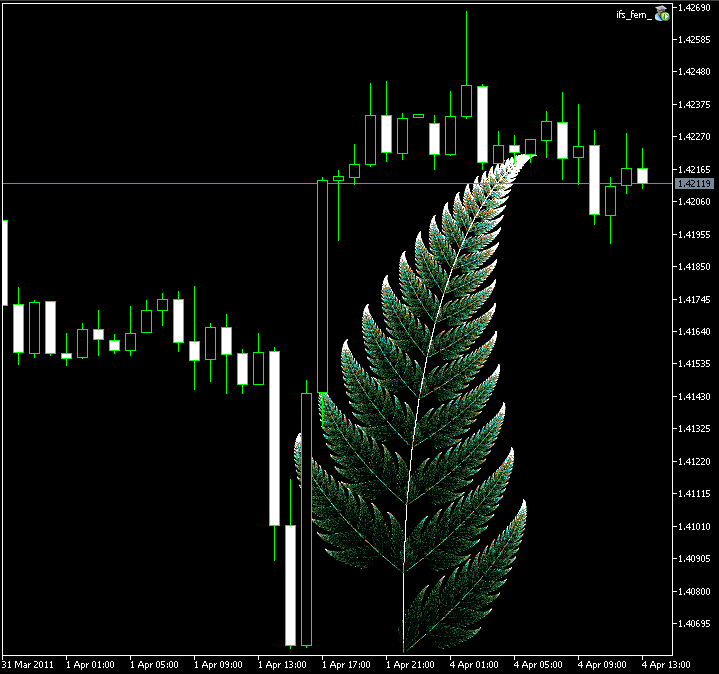
图例 9. Barnsley's fern 图像, 创建 CIFS 类

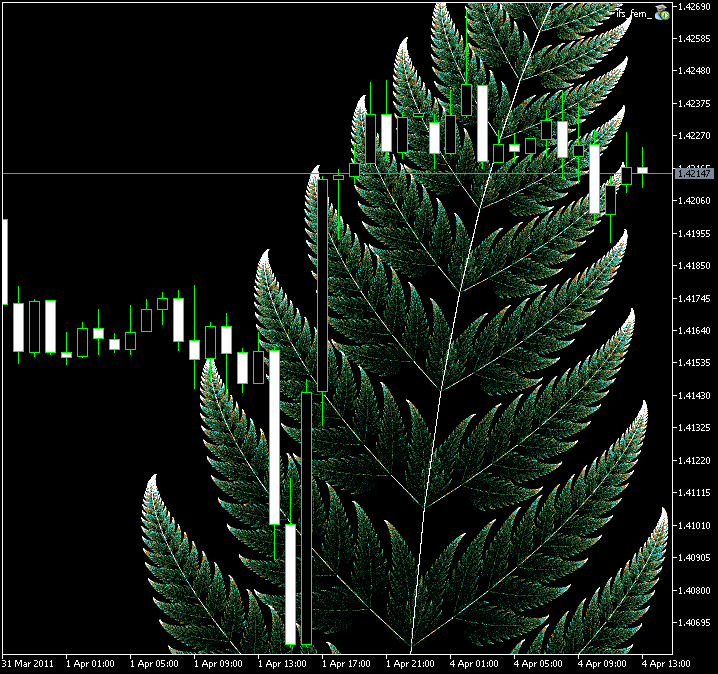
图例 10. 拉伸区域 Barnsley's Fern

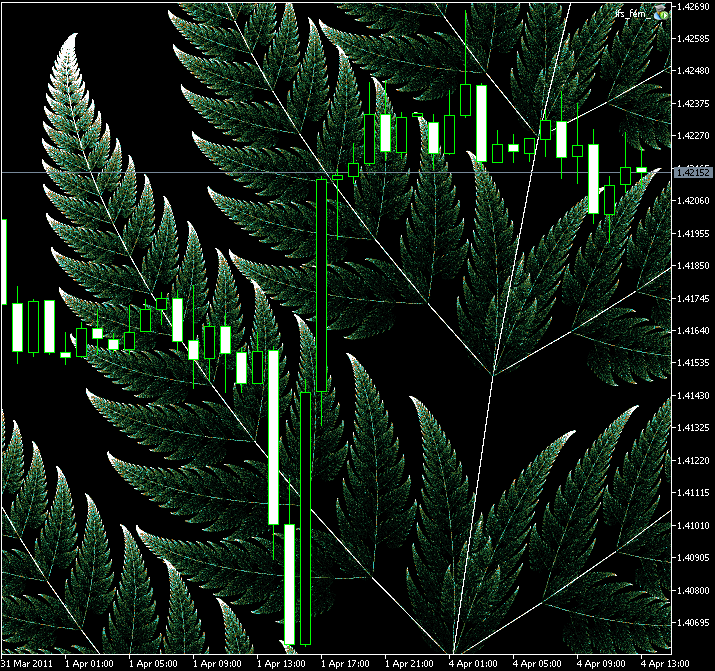
图例 11. 拉伸区域 Barnsley's Fern

图例 12. 拉伸区域 Barnsley's Fern

您亲手来做

1. 这里有许多 IFS 分形 Fractint, 例如:

// Binary
double IFS_a[3] = { 0.5,  0.5,  0.0};
double IFS_b[3] = { 0.0,  0.0, -0.5};
double IFS_c[4] = { 0.0,  0.0,  0.5};
double IFS_d[4] = { 0.5,  0.5,  0.5};
double IFS_e[4] = {-2.563477,  2.436544, 4.873085};
double IFS_f[4] = {-0.000000, -0.000003, 7.563492};
double IFS_p[4] = {333, 333, 333};

// Coral
double IFS_a[3] = { 0.307692,  0.307692,  0.000000};
double IFS_b[3] = {-0.531469, -0.076923,  0.54545};
double IFS_c[3] = {-0.461538,  0.153846,  0.692308};
double IFS_d[3] = {-0.293706, -0.447552, -0.195804};
double IFS_e[3] = {5.4019537, -1.295248, -4.893637};
double IFS_f[3] = { 8.655175,  4.152990,  7.269794};
double IFS_p[3] = {400, 150, 450};

// Crystal
double IFS_a[2] = { 0.696970,  0.090909};
double IFS_b[2] = {-0.481061, -0.443182};
double IFS_c[2] = {-0.393939,  0.515152};
double IFS_d[2] = {-0.662879, -0.094697};
double IFS_e[2] = { 2.147003,  4.286558};
double IFS_f[2] = {10.310288,  2.925762};
double IFS_p[2] = {750, 250};

// Dragon
double IFS_a[2] = { 0.824074,  0.088272};
double IFS_b[2] = { 0.281482,  0.520988};
double IFS_c[2] = {-0.212346, -0.463889};
double IFS_d[2] = { 0.864198, -0.377778};
double IFS_e[2] = {-1.882290,  0.785360};
double IFS_f[2] = {-0.110607,  8.095795};
double IFS_p[2] = {780, 220};

// Floor
double IFS_a[3] = { 0,  0.52,  0};
double IFS_b[3] = {-0.5,   0,  0.5};
double IFS_c[3] = { 0.5,   0, -0.5};
double IFS_d[3] = { 0,   0.5,  0};
double IFS_e[3] = {-1.732366, -0.027891,  1.620804};
double IFS_f[3] = { 3.366182,  5.014877,  3.310401};
double IFS_p[3] = {333, 333, 333};

// Koch3
double IFS_a[5] = {0.307692, 0.192308,  0.192308,  0.307692,  0.384615};
double IFS_b[5] = {      0,-0.205882,  0.205882,         0,        0};
double IFS_c[5] = {      0, 0.653846, -0.653846,         0,         0};
double IFS_d[5] = {0.294118, 0.088235,  0.088235,  0.294118, -0.294118};
double IFS_e[5] = {4.119164,-0.688840,  0.688840, -4.136530, -0.007718};
double IFS_f[5] = {1.604278, 5.978916,  5.962514,  1.604278,  2.941176};
double IFS_p[5] = {151, 254, 254, 151, 190};

//Spiral
double IFS_a[3] = { 0.787879, -0.121212,  0.181818};
double IFS_b[3] = {-0.424242,  0.257576, -0.136364};
double IFS_c[3] = { 0.242424,  0.151515,  0.090909};
double IFS_d[3] = { 0.859848,  0.053030,  0.181818};
double IFS_e[3] = { 1.758647,  -6.721654,  6.086107};
double IFS_f[3] = { 1.408065,   1.377236,  1.568035};
double IFS_p[3] = {896, 52, 52};

//Swirl5
double IFS_a[2] = {  0.74545, -0.424242};
double IFS_b[2] = {-0.459091, -0.065152};
double IFS_c[2] = { 0.406061, -0.175758};
double IFS_d[2] = { 0.887121, -0.218182};
double IFS_e[2] = { 1.460279,  3.809567};
double IFS_f[2] = { 0.691072,  6.741476};
double IFS_p[2] = {920, 80};

//Zigzag2
double IFS_a[2] = {-0.632407, -0.036111};
double IFS_b[2] = {-0.614815, 0.444444};
double IFS_c[2] = {-0.545370, 0.210185};
double IFS_d[2] = { 0.659259, 0.037037};
double IFS_e[2] = { 3.840822, 2.071081};
double IFS_f[2] = { 1.282321, 8.330552};
double IFS_p[2] = {888, 112};

绘制这些集合。如何找到初始相似变换的 IFS 系数?

2. 创建您自己的分形集合并且计算它们的系数 (章节 2).

3. 尝试用调色板着色 (uchar Palette array), 扩展调色板并且加入阶梯颜色。

4. 有关 Barnsley's Fern 分形 (Hausdorf-Bezikovitch) 的维度?有没有公式来计算使用 IFS 系数的分形维度*。

5. 在确定区域加入拉伸, 使用鼠标点击坐标 OnChartEvent:

void OnChartEvent(const int id,         // 事件识别符  
                const long& lparam,   // 事件参数长整型
                const double& dparam, // 事件参数浮点型
                const string& sparam  // 事件参数字符型
                )
  {
//--- 左键点击
   if(id==CHARTEVENT_CLICK)
     {
      Print("坐标: x=",lparam,"  y=",dparam);
     }
  }

结论

我们已经讨论了使用 IFS 创建分形集合的算法。

使用 cIntBMP 库极大简化图形图像工作。除了 DrawDot(x,y,color) 方法我们已经用过, 这个 cIntBMP 类还包括许多有用的方法。但它们是另外的故事了。