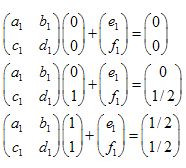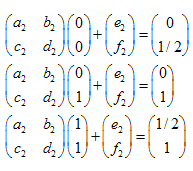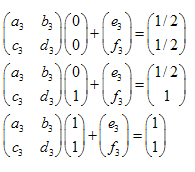Creación de fractales en MQL5 con un Sistema iterativo de funciones (SIF) - Asesor Experto para MetaTrader 5

Introducción

Hay muchos programas de creación de conjuntos autosimilares que satisfacen la definición de Sistema iterativo de funciones (SIF). Por ejemplo, Fractint, Fractal Designer o IFS Matlab Generator. Gracias a la velocidad del lenguaje MQL5 y a la posibilidad de trabajar con objetos gráficos, también podemos estudiar estos bellos conjuntos en el terminal cliente MetaTrader 5.

La librería cIntBMP, desarrollada por Dmitry (Integer), proporciona nuevas oportunidades gráficas y simplifica enormemente la creación de imágenes. Esta librería ha sido galardonada por MetaQuotes Software Corp con un premio especial.

En esta publicación vamos a tratar varios ejemplos que ilustran el funcionamiento de la librería cIntBMP, y también vamos a cubrir algunos algoritmos de creación de conjuntos fractales mediante el Sistema iterativo de funciones.

1. Transformación afín del plano

La transformación afín del plano es una aplicación . Generalmente, la transformación afín 2D se define con una matriz  y un vector  . El punto de coordenadas (x,y) se tranforma en otro punto mediante la transformación lineal:

Esta transformación debe ser no singular, es decir, .  La transformación afín cambia el tamaño veces.

Las transformaciones afines no cambian la estructura de los objetos geométricos -las líneas se transforman en líneas-, sino que describen deformaciones simples de dichos objetos, por ejemplo, rotaciones, cambios de escala y traslaciones.

Ejemplos de transformaciones afines del plano:

1) Rotación del plano un ángulo :

2) Cambio de escala de un plano con coeficientes y (ejes x e y):

3) Traslación del plano según el vector  :

La función de contracción es la clave (ver los resultados de Hutchinson).

Si y tienen coordenadas y y es una métrica (por ejemplo, la métrica euclídea: ). La transformación afín se llama contracción si , donde .

El siguiente es un ejemplo de transformación afín:

Cuyo resultado es:

2. Transformaciones de similaridad

Los fractales se construyen de la siguiente manera. Se toma un objeto geométrico simple -por ejemplo, un segmento, un triángulo o un cuadrado- y se divide en N piezas, de las cuales se tomarán M para continuar con la construcción del conjunto (si N=M, obtendremos la dimensión entera del conjunto resultante). Este proceso se repite una y otra vez para cada una de las piezas.

Fractales clásicos:

Segmentos:

• Curva de Koch, N=3, M=4;
• Polvo de Cantor, N=3, M=2;

Triángulo:

• Triángulo de Sierpinski, N=4, M=3;

Cuadrado:

• Alfombra de Sierpinski, N=9, M=8;
• Fractal de Vicsek, N=9, M=5.
  

y así sucesivamente.

Los fractales tienen una estructura autosimilar, algunos de ellos pueden definirse con varias transformaciones de similaridad. La estructura de la transformación afín depende de la forma en que se construye el fractal.

Como veremos más adelante, esto es muy sencillo, el problema que tenemos que resolver consiste en describir la primera iteración de la construcción del fractal, y encontrar el conjunto correspondiente de transformaciones afines.

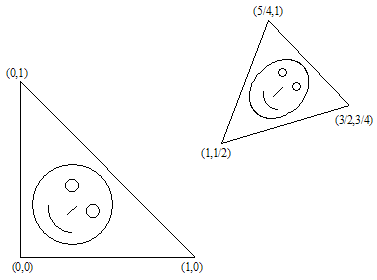
Supongamos que tenemos un conjunto. Según el algoritmo de creación del fractal tenemos que reducirlo, girarlo y "ponerlo en un lugar determinado". El problema es describir este proceso utilizando transformaciones afines; o dicho de otro modo, tenemos que encontrar la matriz y el vector.

Es fácil demostrar que es suficiente tomar 3 puntos del conjunto inicial (no trivial) y transformarlos en 3 puntos correspondientes al conjunto "reducido". Esta transformación nos lleva a 6 ecuaciones lineales que nos permiten encontrar la solución a, b, c, d, e, f.

Vamos a demostrarlo. Supongamos el triángulo transformado al triángulo .

Al resolver el sistema de ecuaciones lineales obtenemos los coeficientes a, b, c, d, e y f:

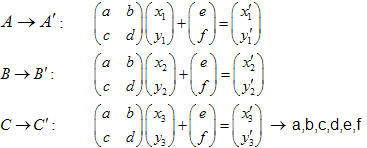
Ejemplo:Triángulo de Sierpinski:

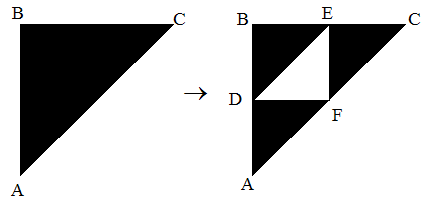
Las coordenadas de los puntos son:

• A (0,0)
• B (0,1)
• C (1,1)
• D(0,1/2)
• E (1/2,1)
• F(1/2,1/2)
  

Hay 3 transformaciones:

1. ABC -> ADF
2. ABC -> DBE
3. ABC -> FEC
   

El sistema de ecuaciones lineales es como sigue:

1. 
   
2. 
   
3. 
   

Las soluciones son: , ,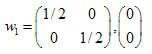

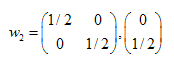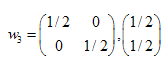
Hemos encontrado los coeficientes de tres transformaciones afines. Más adelante los utilizaremos en la creación de conjuntos autosimilares.

3. Creación de fractales con el sistema iterativo de funciones

El Sistema iterativo de funciones (SIF) -en inglés, Iterated Function System (IFS)- es un conjunto de contracciones afines donde - es el "peso". Cada una de las funciones SIF se define por 7 números: , donde hace de probabilidad de transformación n-ésima en el proceso de iteración. Es mejor definir sus valores de forma proporcional a la contracción: .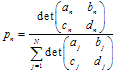

Consideremos el algoritmo de construcción del fractal usando el sistema de iterativo de funciones (ver también Chaos Game).

En primer lugar necesitamos tomar algún punto inicial con coordenadas . A continuación elegimos al azar algunas de las contracciones, trazamos el punto , y, de nuevo, elegimos al azar una de las contracciones y trazamos . Finalmente obtendremos el conjunto de puntos .

La elección de la contracción depende de su "probabilidad". Si repetimos el proceso (por ejemplo, hasta ~30000 puntos) y dibujamos el conjunto resultante, veremos su estructura a pesar del proceso aleatorio.

Este es un ejemplo de Triángulo de Sierpinski:

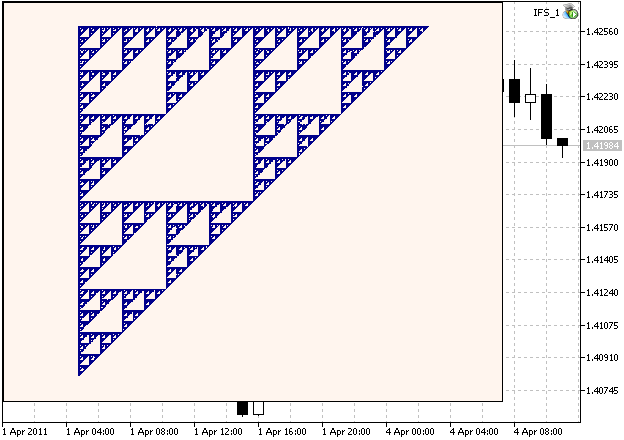
Figura 1. Triángulo de Sierpinski generado con los coeficientes SIF calculados en el capítulo 2

El código:

//+------------------------------------------------------------------------+
//|                                              IFS_Sierpinski_Gasket.mq5 |
//|                              Copyright 2011, MetaQuotes Software Corp. |
//|                                                    https://www.mql5.com |
//+------------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

//-- incluimos el archivo con la clase cIntBMP
#include <cIntBMP.mqh>

//-- Coeficientes SIF del Triángulo de Sierpinski
//-- matrices (a,b,c,d)
double IFS_a[3] = {0.50,  0.50,  0.50};
double IFS_b[3] = {0.00,  0.00,  0.00};
double IFS_c[3] = {0.00,  0.00,  0.00};
double IFS_d[3] = {0.50,  0.50,  0.50};
//-- vectores (e,f)
double IFS_e[3] = {0.00,  0.00,  0.50};
double IFS_f[3] = {0.00,  0.50,  0.50};
//-- "probabilidades" de las transformaciones, multiplicadas por 1000
double IFS_p[3]={333,333,333};

double Probs[3]; // array Probs - se utiliza para elegir las transformaciones SIF
cIntBMP bmp;     // instancia de la clase cIntBMP
int scale=350;  // coeficiente de escala
//+------------------------------------------------------------------------+
//| Función de inicialización del Asesor Experto                           |
//+------------------------------------------------------------------------+
int OnInit()
  {
//-- preparamos el array Probs
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
//-- tamaño de la imagen BMP
   int XSize=500;
   int YSize=400;
//-- creamos la imagen bmp XSizexYSize con color de fondo clrSeashell
   bmp.Create(XSize,YSize,clrSeashell);
//-- imagen rectangular
   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

//-- puntos de coordenadas (se utilizarán en la construcción del conjunto)
   double x0=0;
   double y0=0;
   double x,y;
//-- número de puntos a calcular (cuantos más puntos, más detallada es la imagen)
   int points=1500000;
//-- cálculo del conjunto
   for(int i=0; i<points; i++)
     {
      // elegimos transformación SIF con probabilidades, de forma proporcional
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            // transformación afín
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            // actualizamos las coordenadas anteriores
            x0 = x;
            y0 = y;
            // convertimos a coordenadas de imagen BMP
            // (obsérvese el eje Y en cIntBMP)
            int scX = int (MathRound(XSize/2 + (x-0.5)*scale));
            int scY = int (MathRound(YSize/2 + (y-0.5)*scale));
            // si el punto de coordenadas está dentro de la imagen, dibujamos el punto.
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); }
            break;
           }
        }
     }
//-- guardamos la imagen en el archivo
   bmp.Save("bmpimg",true);
//-- dibujamos la imagen en el gráfico
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------------+
//| Función de deinicialización del Asesor Experto                         |
//+------------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- borramos la imagen del gráfico
   ObjectDelete(0,"IFS");
//--- borramos el gráfico
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------------+

Si establecemos la escala a 1350, incrementamos el número de iteraciones a 15000000, y modificamos el desplazamiento del punto inicial:

int scX = MathRound(XSize/2 + (x-0.75)*scale);
int scY = MathRound(YSize/2 + (y-0.75)*scale);

podremos ver la región ampliada del conjunto. Obsérvese (Fig. 2), se trata de una estructura autosimilar:

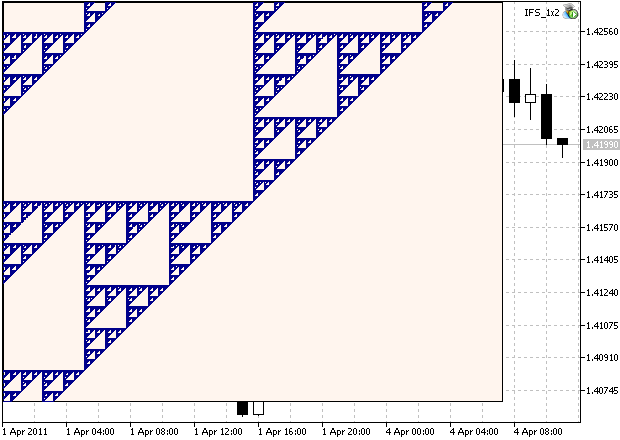
Figura 2. Región ampliada del Triángulo de Sierpinski

Veamos ahora el conocido Helecho de Barnsley -en inglés, Barnsley's Fern-, propuesto por Michael Barnsley. Es algo más complejo.

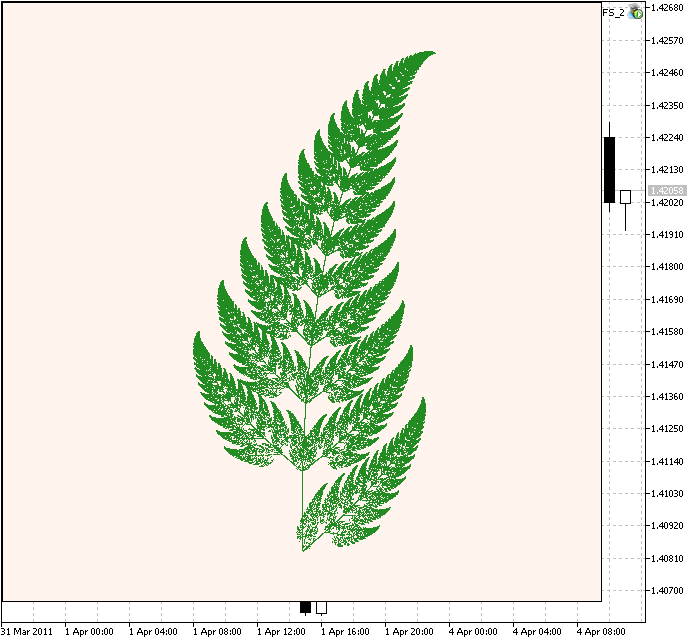
Figura 3. Helecho de Barnsley

El código es parecido, pero ahora tenemos 4 contracciones SIF con diferentes pesos.

//+------------------------------------------------------------------------+
//|                                                           IFS_fern.mq5 |
//|                              Copyright 2011, MetaQuotes Software Corp. |
//|                                                    https://www.mql5.com |
//+------------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <cIntBMP.mqh>
//-- Coeficientes SIF del Helecho de Barnsley
//-- matrices (a,b,c,d)
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
//-- vectores (e,f)
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
//-- "probabilidades" de las transformaciones, multiplicadas por 1000
double IFS_p[4] = {10,     850,    70,     70};

double Probs[4];
cIntBMP bmp;
int scale=50;
//+------------------------------------------------------------------------+
//| Función de inicialización del Asesor Experto                           |
//+------------------------------------------------------------------------+
int OnInit()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }

   int XSize=600;
   int YSize=600;

   bmp.Create(XSize,YSize,clrSeashell);

   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

   double x0=0;
   double y0=0;
   double x,y;

   int points=250000;

   for(int i=0; i<points; i++)
     {
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            x0 = x;
            y0 = y;
            int scX = int (MathRound(XSize/2 + (x)*scale));
            int scY = int (MathRound(YSize/2 + (y-5)*scale));
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrForestGreen); }
            break;
           }
        }
     }
   bmp.Save("bmpimg",true);
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------------+
//| Función de deinicialización del Asesor Experto                         |
//+------------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ObjectDelete(0,"IFS");
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------------+ 

Es notable que estructuras de esta complejidad puedan definirse con tan sólo 28 números.

Si aumentamos la escala a 150 y fijamos las iteraciones a 1250000 veremos el fragmento ampliado:

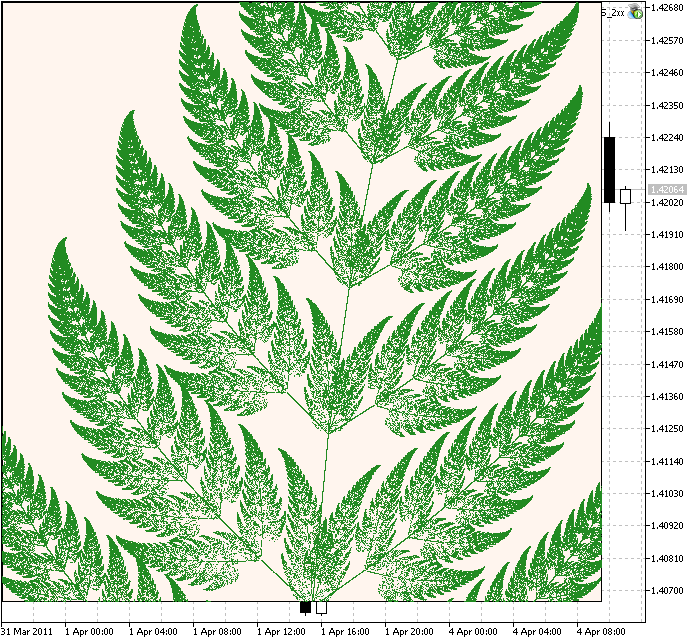
Figura 4. Fragmento del Helecho de Barnsley

Como vemos el algoritmo es universal en tanto que puede generar varios conjuntos fractales.

El siguiente ejemplo es la Alfombra de Sierpinski, definida por los siguientes coeficientes SIF:

//-- Coeficientes SIF del Triángulo de Sierpinski
double IFS_a[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333};
double IFS_b[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_c[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_d[8] = {0.333, 0.333,  0.333,  0.333, 0.333,  0.333,  0.333, 0.333};
double IFS_e[8] = {-0.125, -3.375, -3.375,  3.125, 3.125, -3.375, -0.125, 3.125};
double IFS_f[8] = {6.75, 0.25, 6.75,  0.25, 6.75, 3.5, 0.25, 3.50};
//-- "probabilidades", multiplicadas por 1000
double IFS_p[8]={125,125,125,125,125,125,125,125};

Figura 5. Alfombra de Sierpinski

En el capítulo 2 hemos visto el algoritmo que calcula los coeficientes de las contracciones SIF.

Veamos ahora cómo crear palabras fractales. En ruso, la palabra "fractales" tiene este aspecto:

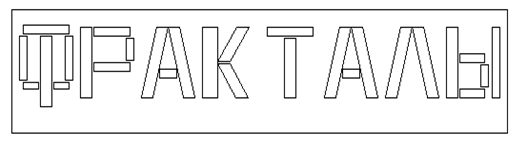
Figura 6. Palabra "fractales" en ruso

Para encontrar los coeficientes SIF tenemos que resolver los sistemas lineales correspondientes. Las soluciones son:

//-- Coeficientes SIF de la palabra "fractales" en ruso
double IFS_a[28]=
  {
   0.00, 0.03,  0.00, 0.09, 0.00, 0.03, -0.00, 0.07, 0.00, 0.07, 0.03,  0.03,  0.03,  0.00,
   0.04, 0.04, -0.00, 0.09, 0.03, 0.03,  0.03, 0.03, 0.03, 0.00, 0.05, -0.00,  0.05,  0.00
  };

double IFS_b[28]=
  {
   -0.11, 0.00, 0.07, 0.00, -0.07, 0.00, -0.11,  0.00, -0.07,  0.00, -0.11,  0.11, 0.00, -0.14,
   -0.12, 0.12,-0.11, 0.00, -0.11, 0.11,  0.00, -0.11,  0.11, -0.11,  0.00, -0.07, 0.00, -0.07
  };

double IFS_c[28]=
  {
   0.12,  0.00,  0.08,  -0.00,  0.08,  0.00,  0.12,  0.00,  0.04,  0.00,  0.12,  -0.12, 0.00,  0.12,
   0.06,  -0.06,  0.10,  0.00,  0.12,  -0.12,  0.00,  0.12,  -0.12,  0.12, 0.00,  0.04,  0.00,  0.12
  };

double IFS_d[28]=
  {
   0.00,  0.05,  0.00,  0.07,  0.00,  0.05,  0.00,  0.07,  0.00,  0.07,  0.00,  0.00,  0.07,  0.00,
   0.00,  0.00,  0.00,  0.07,  0.00,  0.00,  0.07,  0.00,  0.00,  0.00,  0.07,  0.00,  0.07,  0.00
  };

double IFS_e[28]=
  {
   -4.58,  -5.06, -5.16, -4.70, -4.09, -4.35, -3.73, -3.26, -2.76,  -3.26, -2.22, -1.86, -2.04, -0.98,
   -0.46,  -0.76,  0.76,  0.63,  1.78,  2.14,  1.96,  3.11,  3.47,  4.27,  4.60,  4.98,   4.60, 5.24
  };

double IFS_f[28]=
  {
   1.26,  0.89,  1.52,  2.00,  1.52,  0.89,  1.43,  1.96,  1.69,  1.24,  1.43,  1.41,  1.11,  1.43,
   1.79,  1.05,  1.32,  1.96,  1.43,  1.41,  1.11,  1.43,  1.41,  1.43,  1.42,  1.16,  0.71,  1.43
  };

//-- "probabilidades", multiplicadas por 1000
double IFS_p[28]=
  {
   35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  
   35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35,  35
  };

El resultado es esta imagen:

Figura 7. Palabra autosimilar

El código completo se encuentra en ifs_fractals.mq5.

Si ampliamos el conjunto veremos esta estructura autosimilar:

Figura 8. Región ampliada del conjunto

Los conjuntos autosimilares basados en SIF se pueden construir con el Fractal Designer.

Hemos estudiado la creación de conjuntos fractales con sistemas iterativos de funciones. Gracias a la librería cIntBMP hemos podido simplificar mucho este proceso. Ahora vamos a crear una clase con varias características que mejorarán las imágenes que hemos pintado hasta este momento.

4. Clase para construir imágenes SIF

Las probabilidades dirigen la construcción de los conjuntos. La diferencia en las probabilidades significa que el conjunto tiene una estructura irregular (ver los pesos del SIF Helecho de Barnsley), lo que se puede utilizar para crear imágenes bonitas. Para ello tenemos que definir el color proporcional a la frecuencia del punto en los alrededores.

Esto se consigue mediante el uso de la pantalla virtual (una matriz), si el color del píxel depende de los valores anteriores. Por último, la pantalla virtual se renderizará en el bmp mediante la paleta -Palette-. Este bmp puede hacer de imagen de fondo del gráfico.

El código del Asesor Experto basado en la clase CIFS es el siguiente:

//+------------------------------------------------------------------------+
//|                                                     IFS_Fern_color.mq5 |
//|                              Copyright 2011, MetaQuotes Software Corp. |
//|                                                    https://www.mql5.com |
//+------------------------------------------------------------------------+
#include <cIntBMP.mqh>
//-- Coeficientes SIF del Helecho de Barnsley
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
double IFS_p[4] = {10,     850,    70,     70};
//-- Paleta
uchar Palette[23*3]=
  {
   0x00,0x00,0x00,0x02,0x0A,0x06,0x03,0x11,0x0A,0x0B,0x1E,0x0F,0x0C,0x4C,0x2C,0x1C,0x50,0x28,
   0x2C,0x54,0x24,0x3C,0x58,0x20,0x4C,0x5C,0x1C,0x70,0x98,0x6C,0x38,0xBC,0xB0,0x28,0xCC,0xC8,
   0x4C,0xB0,0x98,0x5C,0xA4,0x84,0xBC,0x68,0x14,0xA8,0x74,0x28,0x84,0x8C,0x54,0x94,0x80,0x40,
   0x87,0x87,0x87,0x9F,0x9F,0x9F,0xC7,0xC7,0xC7,0xDF,0xDF,0xDF,0xFC,0xFC,0xFC
  };
//+------------------------------------------------------------------------+
//| Clase CIFS                                                             |
//+------------------------------------------------------------------------+
class CIFS
  {
protected:
   cIntBMP           m_bmp;
   int               m_xsize;
   int               m_ysize;
   uchar             m_virtual_screen[];
   double            m_scale;
   double            m_probs[8];

public:
                    ~CIFS()                          { m_bmp.Delete("bmpimg",true); };
   void              Create(int x_size,int y_size,uchar col);
   void              Render(double scale,bool back);
   void              ShowBMP(bool back);
protected:
   void              VS_Prepare(int x_size,int y_size,uchar col);
   void              VS_Fill(uchar col);
   void              VS_PutPixel(int px,int py,uchar col);
   uchar             VS_GetPixel(int px,int py);
   int               GetPalColor(uchar index);
   int               RGB256(int r,int g,int b) const {return(r+256*g+65536*b);      }
   void              PrepareProbabilities();
   void              RenderIFSToVirtualScreen();
   void              VirtualScreenToBMP();
  };
//+------------------------------------------------------------------------+
//| Método Create                                                          |
//+------------------------------------------------------------------------+
void CIFS::Create(int x_size,int y_size,uchar col)
  {
   m_bmp.Create(x_size,y_size,col);
   VS_Prepare(x_size,y_size,col);
   PrepareProbabilities();
  }
//+------------------------------------------------------------------------+
//| Prepara la pantalla virtual                                            |
//+------------------------------------------------------------------------+
void CIFS::VS_Prepare(int x_size,int y_size,uchar col)
  {
   m_xsize=x_size;
   m_ysize=y_size;
   ArrayResize(m_virtual_screen,m_xsize*m_ysize);
   VS_Fill(col);
  }
//+------------------------------------------------------------------------+
//| Llena la pantalla virtual con el color especificado                    |
//+------------------------------------------------------------------------+
void CIFS::VS_Fill(uchar col)
  {
   for(int i=0; i<m_xsize*m_ysize; i++) {m_virtual_screen[i]=col;}
  }
//+------------------------------------------------------------------------+
//| Devuelve el color de la paleta                                         |
//+------------------------------------------------------------------------+
int CIFS::GetPalColor(uchar index)
  {
   int ind=index;
   if(ind<=0) {ind=0;}
   if(ind>22) {ind=22;}
   uchar r=Palette[3*(ind)];
   uchar g=Palette[3*(ind)+1];
   uchar b=Palette[3*(ind)+2];
   return(RGB256(r,g,b));
  }
//+------------------------------------------------------------------------+
//| Dibuja un píxel en la pantalla virtual                                 |
//+------------------------------------------------------------------------+
void CIFS::VS_PutPixel(int px,int py,uchar col)
  {
   if (px<0) return;
   if (py<0) return;
   if (px>m_xsize) return;
   if (py>m_ysize) return;
    int pos=m_xsize*py+px;
   if(pos>=ArraySize(m_virtual_screen)) return;
   m_virtual_screen[pos]=col;
  }
//+------------------------------------------------------------------------+
//| Obtiene el color del píxel de la pantalla virtual                      |
//+------------------------------------------------------------------------+
uchar CIFS::VS_GetPixel(int px,int py)
  {
   if (px<0) return(0);
   if (py<0) return(0);
   if (px>m_xsize) return(0);
   if (py>m_ysize) return(0);
    int pos=m_xsize*py+px;
   if(pos>=ArraySize(m_virtual_screen)) return(0);
   return(m_virtual_screen[pos]);
  }
//+------------------------------------------------------------------------+
//| Prepara el array de probabilidades acumulativas                        |
//+------------------------------------------------------------------------+
void CIFS::PrepareProbabilities()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      m_probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
  }
//+------------------------------------------------------------------------+
//| Renderiza el conjunto SIF en la pantalla virtual                       |
//+------------------------------------------------------------------------+
void CIFS::RenderIFSToVirtualScreen()
  {
   double x=0,y=0;
   double x0=0;
   double y0=0;
   uint iterations= uint (MathRound(100000+100*MathPow(m_scale,2)));

   for(uint i=0; i<iterations; i++)
     {
      double prb=1000*(rand()/32767.0);

      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=m_probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];

            int scX = int (MathRound(m_xsize/2 + (x-0)*m_scale));
            int scY = int (MathRound(m_ysize/2 + (y-5)*m_scale));

            if(scX>=0 && scX<m_xsize && scY>=0 && scY<m_ysize)
              {
               uchar c=VS_GetPixel(scX,scY);
               if(c<255) c=c+1;
               VS_PutPixel(scX,scY,c);
              }
            break;
           }
         x0 = x;
         y0 = y;
        }
     }
  }
//+------------------------------------------------------------------------+
//| Copia la pantalla virtual a BMP                                        |
//+------------------------------------------------------------------------+
void CIFS::VirtualScreenToBMP()
  {
   for(int i=0; i<m_xsize; i++)
     {
      for(int j=0; j<m_ysize; j++)
        {
         uchar colind=VS_GetPixel(i,j);
         int xcol=GetPalColor(colind);
         if(colind==0) xcol=0x00;
         //if(colind==0) xcol=0xFFFFFF;
         m_bmp.DrawDot(i,j,xcol);
        }
     }
  }
//+------------------------------------------------------------------------+
//| Muestra la imagen BMP en el gráfico                                    |
//+------------------------------------------------------------------------+
void CIFS::ShowBMP(bool back)
  {
   m_bmp.Save("bmpimg",true);
   m_bmp.Show(0,0,"bmpimg","Fern");
   ObjectSetInteger(0,"Fern",OBJPROP_BACK,back);
  }
//+------------------------------------------------------------------------+
//| Método de renderizado                                                  |     
//+------------------------------------------------------------------------+
void CIFS::Render(double scale,bool back)
  {
   m_scale=scale;
   VS_Fill(0);
   RenderIFSToVirtualScreen();
   VirtualScreenToBMP();
   ShowBMP(back);
  }

static int gridmode;
CIFS fern;
int currentscale=50;
//+------------------------------------------------------------------------+
//| Función de inicialización del Asesor Experto                           |
//+------------------------------------------------------------------------+
void OnInit()
  {
//-- obtención del modo cuadrícula -grid mode-
   gridmode= int (ChartGetInteger(0,CHART_SHOW_GRID,0));
//-- deshabilitamos el grid
   ChartSetInteger(0,CHART_SHOW_GRID,0);
//-- creación del bmp
   fern.Create(800,800,0x00);
//-- mostramos como imagen de fondo
   fern.Render(currentscale,true);
  }
//+------------------------------------------------------------------------+
//| Función de deinicialización del Asesor Experto                         |
//+------------------------------------------------------------------------+
void OnDeinit(const int r)
  {
//-- restablecemos el modo cuadrícula -modo grid-
   ChartSetInteger(0,CHART_SHOW_GRID,gridmode); 
//-- eliminamos el objeto Fern
   ObjectDelete(0,"Fern");
 }
//+------------------------------------------------------------------------+
//| Manejador del evento OnChart del Asesor Experto                        |
//+------------------------------------------------------------------------+
void OnChartEvent(const int id,           // Identificador del evento  
                const long& lparam,   // Parámetro del evento de tipo long
                const double& dparam, // Parámetro del evento de tipo double
                const string& sparam  // Parámetro del evento de tipo string
                )
  {
//--- clic sobre el objeto gráfico
   if(id==CHARTEVENT_OBJECT_CLICK)
     {
      Print("Evento clic sobre el objeto gráfico llamado '"+sparam+"'");
      if(sparam=="Fern")
        {
         // incremento del coeficiente de la escala (zoom)
         currentscale=int (currentscale*1.1);
         fern.Render(currentscale,true);
        }
     }
  }
//+------------------------------------------------------------------------+

Cuyo resultado es:

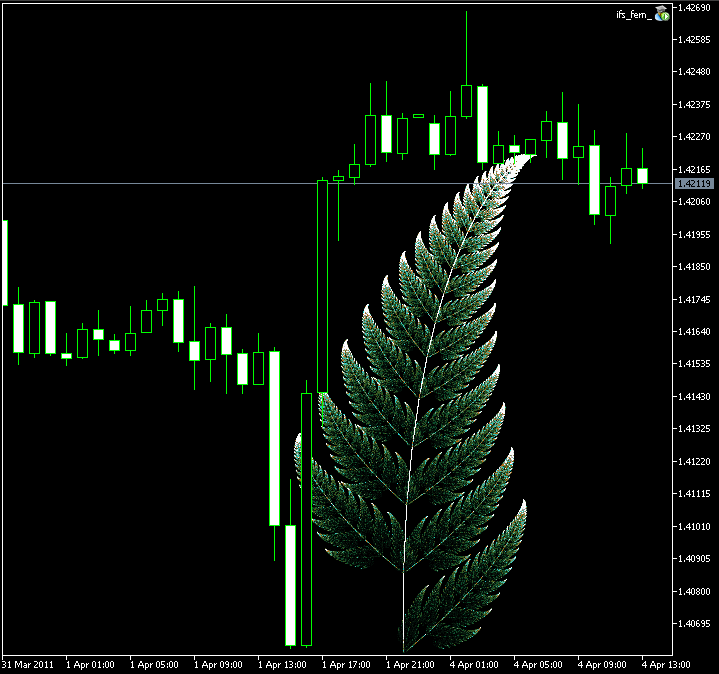
Figura 9. Imagen de Barnsley creada con la clase CIFS

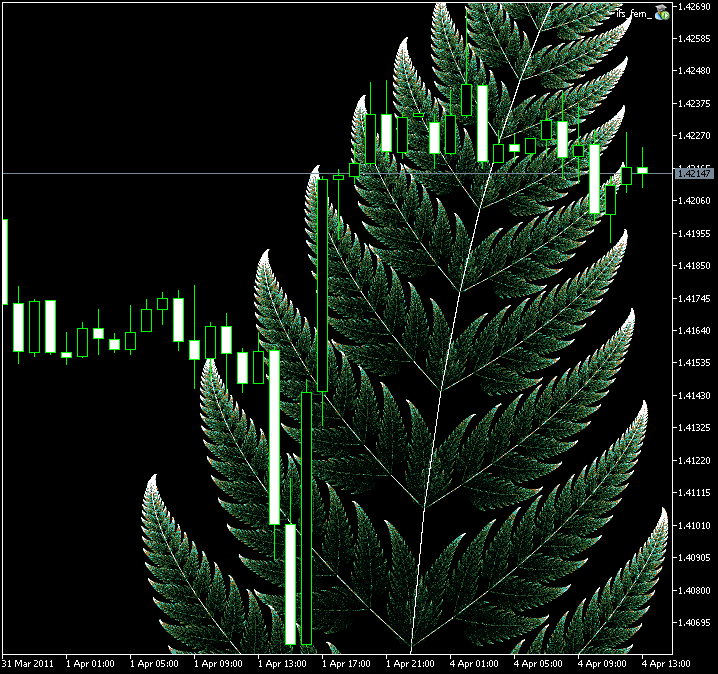
Figura 10. Región ampliada del Helecho de Barnsley

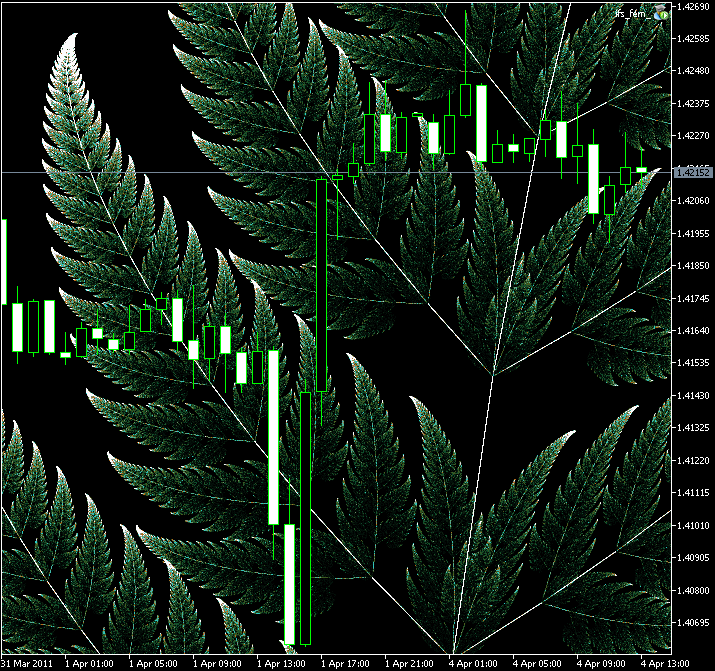
Figura 11. Región ampliada del Helecho de Barnsley

Figura 12. Región ampliada del Helecho de Barnsley

Hazlo tú mismo

1. En Fractint hay muchos fractales SIF, por ejemplo:

// Binary
double IFS_a[3] = { 0.5,  0.5,  0.0};
double IFS_b[3] = { 0.0,  0.0, -0.5};
double IFS_c[4] = { 0.0,  0.0,  0.5};
double IFS_d[4] = { 0.5,  0.5,  0.5};
double IFS_e[4] = {-2.563477,  2.436544, 4.873085};
double IFS_f[4] = {-0.000000, -0.000003, 7.563492};
double IFS_p[4] = {333, 333, 333};

// Coral
double IFS_a[3] = { 0.307692,  0.307692,  0.000000};
double IFS_b[3] = {-0.531469, -0.076923,  0.54545};
double IFS_c[3] = {-0.461538,  0.153846,  0.692308};
double IFS_d[3] = {-0.293706, -0.447552, -0.195804};
double IFS_e[3] = {5.4019537, -1.295248, -4.893637};
double IFS_f[3] = { 8.655175,  4.152990,  7.269794};
double IFS_p[3] = {400, 150, 450};

// Crystal
double IFS_a[2] = { 0.696970,  0.090909};
double IFS_b[2] = {-0.481061, -0.443182};
double IFS_c[2] = {-0.393939,  0.515152};
double IFS_d[2] = {-0.662879, -0.094697};
double IFS_e[2] = { 2.147003,  4.286558};
double IFS_f[2] = {10.310288,  2.925762};
double IFS_p[2] = {750, 250};

// Dragon
double IFS_a[2] = { 0.824074,  0.088272};
double IFS_b[2] = { 0.281482,  0.520988};
double IFS_c[2] = {-0.212346, -0.463889};
double IFS_d[2] = { 0.864198, -0.377778};
double IFS_e[2] = {-1.882290,  0.785360};
double IFS_f[2] = {-0.110607,  8.095795};
double IFS_p[2] = {780, 220};

// Floor
double IFS_a[3] = { 0,  0.52,  0};
double IFS_b[3] = {-0.5,   0,  0.5};
double IFS_c[3] = { 0.5,   0, -0.5};
double IFS_d[3] = { 0,   0.5,  0};
double IFS_e[3] = {-1.732366, -0.027891,  1.620804};
double IFS_f[3] = { 3.366182,  5.014877,  3.310401};
double IFS_p[3] = {333, 333, 333};

// Koch3
double IFS_a[5] = {0.307692, 0.192308,  0.192308,  0.307692,  0.384615};
double IFS_b[5] = {      0,-0.205882,  0.205882,         0,        0};
double IFS_c[5] = {      0, 0.653846, -0.653846,         0,         0};
double IFS_d[5] = {0.294118, 0.088235,  0.088235,  0.294118, -0.294118};
double IFS_e[5] = {4.119164,-0.688840,  0.688840, -4.136530, -0.007718};
double IFS_f[5] = {1.604278, 5.978916,  5.962514,  1.604278,  2.941176};
double IFS_p[5] = {151, 254, 254, 151, 190};

//Spiral
double IFS_a[3] = { 0.787879, -0.121212,  0.181818};
double IFS_b[3] = {-0.424242,  0.257576, -0.136364};
double IFS_c[3] = { 0.242424,  0.151515,  0.090909};
double IFS_d[3] = { 0.859848,  0.053030,  0.181818};
double IFS_e[3] = { 1.758647,  -6.721654,  6.086107};
double IFS_f[3] = { 1.408065,   1.377236,  1.568035};
double IFS_p[3] = {896, 52, 52};

//Swirl5
double IFS_a[2] = {  0.74545, -0.424242};
double IFS_b[2] = {-0.459091, -0.065152};
double IFS_c[2] = { 0.406061, -0.175758};
double IFS_d[2] = { 0.887121, -0.218182};
double IFS_e[2] = { 1.460279,  3.809567};
double IFS_f[2] = { 0.691072,  6.741476};
double IFS_p[2] = {920, 80};

//Zigzag2
double IFS_a[2] = {-0.632407, -0.036111};
double IFS_b[2] = {-0.614815, 0.444444};
double IFS_c[2] = {-0.545370, 0.210185};
double IFS_d[2] = { 0.659259, 0.037037};
double IFS_e[2] = { 3.840822, 2.071081};
double IFS_f[2] = { 1.282321, 8.330552};
double IFS_p[2] = {888, 112};

Dibuja estos conjuntos. ¿Cómo encontrarías las transformaciones de similaridad iniciales mediante los coeficientes SIF?

2. Crea tus propios conjuntos fractales y calcula sus coeficientes (capítulo 2).

3. Juega con la paleta de colores (array uchar Palette), extiéndela y añade colores degradados.

4. ¿Qué sucede con la dimensión fractal (Hausdorf-Bezikovitch) del Helecho de Barnsley? ¿Existe una fórmula para calcular la dimensión fractal utilizando los coeficientes* SIF?.

5. Hacer zoom en una región determinada usando la información de las coordenadas del clic del ratón en OnChartEvent:

void OnChartEvent(const int id,         // Identificador del evento  
                const long& lparam,   // Parámetro del evento de tipo long
                const double& dparam, // Parámetro del evento de tipo double
                const string& sparam  // Parámetro del evento de tipo string
                )
  {
//--- clic del botón izquierdo
   if(id==CHARTEVENT_CLICK)
     {
      Print("Coordenadas: x=",lparam,"  y=",dparam);
     }
  }

Conclusión

En esta publicación hemos estudiado el algoritmo de creación de conjuntos autosimilares mediante el sistema iterativo de funciones.

La librería cIntBMP simplifica considerablemente el trabajo con imágenes gráficas. Además del método DrawDot(x,y,color) que nosotros hemos utilizado, la clase cIntBMP contiene otros muchos métodos de utilidad. Pero eso es otra historia.