MetaTrader 5 / Statistiques et analyses
English Русский 中文 Español Deutsch 日本語 Português 한국어 Italiano Türkçe
La transformation de Box-Cox

La transformation de Box-Cox

MetaTrader 5 — Statistiques et analyses | 12 janvier 2022, 17:10
789 0
Victor
Victor

Introduction

Alors que les capacités des PC augmentent, les traders et analystes du Forex ont davantage de possibilités d'utiliser des algorithmes mathématiques complexes et très élaborés qui nécessitent des ressources informatiques considérables. Mais l'adéquation des ressources informatiques ne peut à elle seule résoudre les problèmes des traders. Des algorithmes efficaces d'analyse des cotations du marché sont également nécessaires.

Actuellement, des domaines tels que la statistique mathématique, l'économie et l'économétrie fournissent un grand nombre de méthodes, de modèles et d'algorithmes efficaces et performants utilisés activement par les traders pour l'analyse du marché. Le plus souvent, il s'agit de méthodes paramétriques standard créées avec une hypothèse de stabilité des séquences recherchées et de normalité de leur loi de distribution.

Mais ce n'est pas un secret que les cotations Forex sont des séquences qui ne peuvent pas être classées comme étant stables et ayant une loi de distribution normale loi de répartition normale. Par conséquent, nous ne pouvons pas utiliser les méthodes paramétriques « standard » de statistiques mathématiques, d'économétrie, etc. lors de l'analyse des devis.

Dans l'article "Box-Cox La transformation et l'illusion de la macroéconomie Série « Normalité » [1] A.N. Porunov écrit comme suit : 

« Les analystes économiques doivent souvent traiter des données statistiques qui ne passent pas le test de normalité pour une raison ou une autre. Dans cette situation, il y a deux choix : soit se tourner vers des méthodes non paramétriques qui nécessitent une bonne formation mathématique, soit utiliser des techniques spéciales qui permettent de convertir les « statistiques anormales » d'origine en « normales », ce qui est également assez une tâche complexe ».

Bien que la citation d'A.N.Porunov se réfère à des analystes économiques, elle peut être entièrement attribuée aux tentatives d'analyse des cotations « anormales » du Forex à l'aide de méthodes paramétriques de statistiques mathématiques et d'économétrie. La grande majorité de ces méthodes a été développée pour analyser des séquences ayant la loi de distribution normale. Mais dans la plupart des cas, le fait que les données initiales soient « anormales » est simplement ignoré. En outre, les méthodes mentionnées nécessitent souvent non seulement une distribution normale, mais aussi des séquences initiales stationnarité.

La régression, dispersion (ANOVA) et certains autres types d'analyse peuvent être appelés méthodes « standard » nécessitant la normalité des données initiales. Il n'est pas possible d'énumérer toutes les méthodes paramétriques qui ont des limitations concernant la normalité de la loi de distribution, car elles occupent tout le domaine, disons, de l'économétrie, à l'exception de ses méthodes non paramétriques.

Pour être juste, il faut ajouter que les méthodes paramétriques « standard » ont une sensibilité différente à l'écart de la loi de distribution des données initiale par rapport à la valeur normale. Par conséquent, l'écart par rapport à la « normalité » lors de l'utilisation de telles méthodes n'entraîne pas nécessairement des conséquences désastreuses mais, bien sûr, cela n'augmente pas la précision et la fiabilité des résultats obtenus.

Tout cela pose la question de la nécessité de passer à des méthodes non paramétriques d'analyse et de prévision des cotations. Cependant, les méthodes paramétriques restent très attrayantes. Cela peut s'expliquer par leur prévalence et une quantité suffisante de données, d'algorithmes prêts à l'emploi et d'exemples de leur application. Pour utiliser correctement ces méthodes, il est nécessaire de faire face au moins à deux problèmes liés aux séquences initiales - l'instabilité et « l'anormalité ».

Bien que nous ne puissions pas influencer la stabilité des séquences initiales, nous pouvons essayer de rapprocher leur loi de distribution de la normale. Pour résoudre ce problème, il existe différentes transformations. Les plus connues sont brièvement décrites dans l'article « L'utilisation de la technique de transformation Box-Cox dans les analyses économiques et statistiques » [2]. Dans cet article, nous ne considérerons qu'une seule d'entre elles - la transformation de Box-Cox [1], [2], [3].

Nous devons souligner ici que l'utilisation de la transformation de Box-Cox, comme tout autre type de transformation, ne peut que rapprocher plus ou moins la loi de distribution de la séquence initiale de la loi normale. Cela signifie que l'utilisation de cette transformation ne garantit pas que la séquence résultante aura la loi de distribution normale.


1. La transformation de Box-Cox

Pour la séquence originale X de longueur N

La transformation de Box-Cox à un paramètre se trouve comme suit :


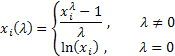
où .

Comme vous pouvez le voir, cette transformation n'a qu'un seul paramètre - lambda. Si la valeur lambda est égale à zéro, la transformation logarithmique de la séquence initiale est effectuée, au cas où la valeur lambda diffère de zéro, la transformation est de type puissance-loi. Si le paramètre lambda est égal à un, la loi de distribution de séquence initiale reste inchangée, bien que la séquence se déplace, car l'unité est soustraite de chacune de ses valeurs.

Selon la valeur lambda, la transformation de Box-Cox inclut les cas particuliers suivants :


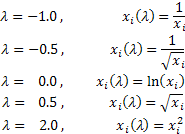
L'utilisation de la transformation de Box-Cox nécessite que toutes les valeurs de séquence d'entrée soient positives et différentes de zéro. Si la séquence d'entrée ne satisfait pas à ces exigences, elle peut être déplacée dans la zone positive par le volume qui garantit la « positivité » de toutes ses valeurs.

Pour l'instant, nous n'examinerons que la transformation de Box-Cox à un paramètre, en préparant les données d'entrée de manière appropriée. Afin d'éviter des valeurs négatives ou nulles dans les données d'entrée, nous trouverons toujours la valeur la plus basse de la séquence d'entrée et la déduirons de chaque élément de la séquence en effectuant en plus un petit décalage égal à 1e-5. Ce décalage supplémentaire est nécessaire pour garantir un déplacement de la séquence vers la zone positive, au cas où sa valeur la plus basse serait égale à zéro.

En fait, il n'est pas nécessaire d'appliquer ce déplacement à des suites « positives ». Mais nous utiliserons néanmoins le même algorithme pour réduire la probabilité d'obtenir des valeurs excessivement élevées lors de l'élévation à une puissance pendant la transformation. Ainsi, toute séquence d'entrée sera située dans la zone positive après le décalage et aura la valeur la plus basse proche de zéro.

La figure 1 montre les courbes de transformation de Box-Cox avec différentes valeurs du paramètre lambda. La figure 1 est tirée de l'article « Box-Cox Transformations » [3]. La grille horizontale sur le graphique est donnée sur une échelle logarithmique.

Fig. 1. La transformation de Box-Cox en fonction des différentes valeurs du paramètre lambda

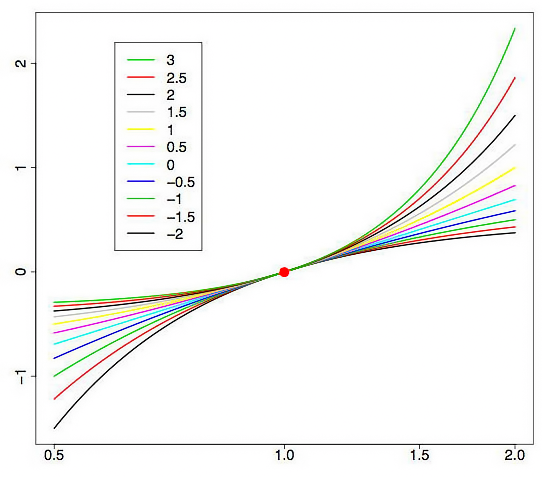
Fig. 1. La transformation de Box-Cox en fonction des différentes valeurs du paramètre lambda

Comme on peut le voir, les « queues » de la distribution initiale peuvent être « étirées » ou « pincées ». La courbe supérieure de la figure 1 correspond à lambda=3, tandis que la courbe inférieure - à lambda=-2.

Pour que la loi de distribution de séquence résultante soit aussi proche que possible de la loi normale, la valeur optimale du paramètre lambda doit être sélectionnée.

Une façon de déterminer la valeur optimale de ce paramètre est de maximiser le logarithme de la fonction de vraisemblance :

où

Cela signifie que nous devons sélectionner le paramètre lambda, auquel cette fonction atteint sa valeur maximale.

L'article « Box-Cox Transformations » [3] traite brièvement d'une autre façon de déterminer la valeur optimale de ce paramètre en fonction de la recherche de la valeur la plus élevée du coefficient de corrélation entre les quantiles de la fonction de distribution normale et la séquence transformée. Il est très probablement possible de trouver d'autres méthodes d'optimisation des paramètres lambda, mais abordons d'abord la recherche du maximum logarithmique de la fonction de vraisemblance mentionnée plus haut.

Il existe différentes manières de le trouver. Nous pouvons par exemple utiliser une recherche simple. Pour ce faire, nous devons calculer la valeur de la fonction de vraisemblance dans un intervalle sélectionné en modifiant la valeur du paramètre lambda dans un écartement plus bas. Nous devons également sélectionner le paramètre lambda optimal, pour lequel la fonction de vraisemblance a la valeur la plus élevée.

La distance d'écartement déterminera la précision du calcul de la valeur optimale du paramètre lambda. Plus l’écartement est bas, plus la précision est élevée, bien que le nombre de calculs requis soit augmenté proportionnellement dans ce cas. Divers algorithmes de recherche de la fonction maximum/minimum, des algorithmes génétiques et quelques autres méthodes peuvent être utilisés pour augmenter l'efficacité des calculs.


2. Transformation en loi de distribution normale

L'une des tâches les plus importantes de la transformation de Box-Cox est la réduction de la loi de distribution des séquences d'entrée à une forme « normale ». Essayons de voir dans quelle mesure ce problème peut être résolu à l'aide de cette transformation.

Pour éviter toute distraction et répétition inutile, nous utiliserons l'algorithme de recherche du minimum de la fonction par la méthode de Powell. Cet algorithme a été décrit dans les articles « Prévision des séries temporelles à l'aide du lissage exponentiel » et « Prévision des séries temporelles à l'aide du lissage exponentiel (suite) ».

Nous devons créer la classe CBoxCox pour rechercher la valeur optimale du paramètre de transformation. Dans cette classe, la fonction de vraisemblance mentionnée ci-dessus sera réalisée comme un objectif. La classe PowellsMethod [4], [5]] est utilisée comme base pour réaliser directement l'algorithme de recherche.

//+------------------------------------------------------------------+
//|                                                      CBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| CBoxCox class                                                    |
//+------------------------------------------------------------------+
class CBoxCox:public PowellsMethod
  {
protected:
   double            Dat[];          // Input data
   double            BCDat[];        // Box-Cox data
   int               Dlen;          // Data size
   double            Par[1];         // Parameters
   double            LnX;            // ln(x) sum
public:
   void   CBoxCox(void) { }
   void              CalcPar(double &dat[]);
   double GetPar(int n) { return(Par[n]); }
private:
   virtual double    func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CBoxCox::CalcPar(double &dat[])
  {
   int i;
   double a;
   //--- Lambda initial value
   Par[0]=1.0;                
   Dlen=ArraySize(dat);
   ArrayResize(Dat,Dlen);
   ArrayResize(BCDat,Dlen);
   LnX=0;
   for(i=0;i<Dlen;i++)
     {
    //--- input data
      a=dat[i]; Dat[i]=a;
     //--- ln(x) sum
     LnX+=MathLog(a);        
     }
    //--- Powell optimization
    Optimize(Par);            
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CBoxCox::func(const double &p[])
  {
   int i;
   double a,lamb,var,mean,k,ret;

   lamb=p[0]; var=0; mean=0; k=0;
   if(lamb>5.0){k=(lamb-5.0)*400; lamb=5.0;}         // Lambda >  5.0
   else if(lamb<-5.0){k=-(lamb+5.0)*400; lamb=-5.0;} // Lambda < -5.0

   //--- Lambda != 0.0
   if(lamb!=0)                                     
     {
      for(i=0;i<Dlen;i++)
        {
          //--- Box-Cox transformation
         BCDat[i]=(MathPow(Dat[i],lamb)-1.0)/lamb;  
          //--- average value calculation
         mean+=BCDat[i]/Dlen;
        }
     }
    //--- Lambda == 0.0
    else                                            
     {
      for(i=0;i<Dlen;i++)
        {
          //--- Box-Cox transformation
         BCDat[i]=MathLog(Dat[i]);
          //--- average value calculation
         mean+=BCDat[i]/Dlen;
        }
     }
   for(i=0;i<Dlen;i++)
     {
      a=BCDat[i]-mean;
       //--- variance
      var+=a*a/Dlen;
     }
   //--- log-likelihood
   ret=Dlen*MathLog(var)/2.0-(lamb-1)*LnX;         
   return(k+ret);
  }
//------------------------------------------------------------------------------------

Maintenant, tout ce que nous avons à faire pour trouver la valeur optimale du paramètre lambda est de se référer à la méthode CalcPar de la classe mentionnée en lui fournissant le lien vers le tableau contenant les données d'entrée. Nous pouvons obtenir la valeur optimale du paramètre obtenu en nous référant à la méthode GetPar. Comme il a été dit précédemment, les données d'entrée doivent être positives.

La classe PowellsMethod met en œuvre l'algorithme de recherche du minimum de la fonction de beaucoup de variables, mais dans notre cas, seul un seul paramètre est optimisé. Cela conduit au fait que la dimension du tableau Par[] est égale à un. Cela signifie que le tableau ne contient qu'une seule valeur. En théorie, nous pouvons utiliser une variable standard à la place du tableau de paramètres dans ce cas, mais cela nécessiterait de modifier le code de la classe de base PowellsMethod. On peut supposer qu'il n'y aura aucun problème si nous compilons le code source MQL5 en utilisant des tableaux ne contenant qu'un seul élément.

Nous devons tenir compte du fait que la fonction CBoxCox::func() contient une limitation de l’intervalle des valeurs admissibles du paramètre lambda. Dans notre cas, cet intervalle est limité aux valeurs de -5 à 5. Ceci afin d'éviter d'obtenir des valeurs trop grandes ou trop petites en élevant les données d'entrée au degré lambda.

En outre, si nous obtenons des valeurs lambda excessivement grandes ou trop petites pendant l'optimisation, cela peut indiquer que la séquence est peu utile pour le type de transformation sélectionné. Il serait donc judicieux, dans tous les cas, de ne pas dépasser un certain intervalle raisonnable lors du calcul de la valeur lambda.


3. Séquences aléatoires

Écrivons un script de test qui effectuera la transformation Box-Cox de la séquence pseudo-aléatoire formée par nous en utilisant la classe CBoxCox.

Vous trouverez ci-dessous le code source d'un tel script.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest1.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- data size
   n=1600;
//--- input array preparation
   ArrayResize(dat,n);
//--- transformed data array
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- random sequence generation
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Exp();

//--- input data shift
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- optimization by lambda  
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- input data
//--- bcdat[] <-- transformed data
  }
//-----------------------------------------------------------------------------------

Une séquence pseudo-aléatoire avec la loi de distribution exponentielle est utilisée comme données transformées d'entrée dans le script affiché. La longueur de la séquence est définie dans n variable et est égale à 1600 valeurs dans ce cas.

La classe RNDXor128 (George Marsaglia, Xorshift RNG) est utilisée pour la génération d'une séquence pseudo-aléatoire. Cette classe a été décrite dans l'article « Analyse des principales caractéristiques des séries chronologiques » [6]. Tous les fichiers nécessaires à la compilation du script BoxCoxTest1.mq5 se trouvent dans l'archive Box-Cox-Tranformation_MQL5.zip. Ces fichiers doivent se trouver dans un répertoire pour une compilation réussie.

Lorsque le script affiché est exécuté, la séquence d'entrée est formée, déplacée vers la zone des valeurs positives et la recherche de la valeur optimale du paramètre lambda est effectuée. Ensuite, le message contenant la valeur lambda obtenue et le nombre de passages de l'algorithme de recherche sont affichés. En conséquence, la séquence transformée sera créée dans le tableau de sortie bcdat[].

Ce script dans sa forme actuelle permet uniquement de préparer la séquence transformée pour son utilisation ultérieure et ne met en œuvre aucun changement. Lors de la rédaction de cet article, le type d'analyse décrit dans l'article « Analyse des principales caractéristiques des séries chronologiques » [6] a été sélectionné pour l'évaluation des résultats de la transformation. Les scripts utilisés pour cela ne sont pas présentés dans cet article pour réduire le volume de codes publiés. Seuls les résultats graphiques d'analyse prêts à l'emploi sont présentés ci-dessous.

La figure 2 montre l'histogramme et le graphique fournis par l'échelle de distribution normale pour la séquence pseudo-aléatoire avec la loi de distribution exponentielle utilisée dans le script BoxCoxTest1.mq5. Résultat du test de Jarque-Bera JB=3241.73, p= 0.000. Comme nous pouvons le voir, la séquence d'entrée n'est pas du tout « normale » et, comme prévu, sa distribution est similaire à celle exponentielle.

Fig. 2

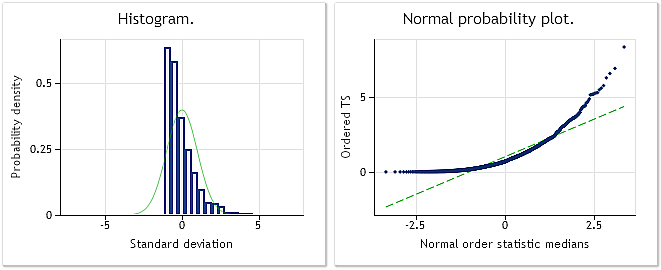
Fig. 2. Séquence pseudo-aléatoire avec la loi de distribution exponentielle. Test de Jarque-Bera JB=3241.73, р=0.000.

 Fig. 3

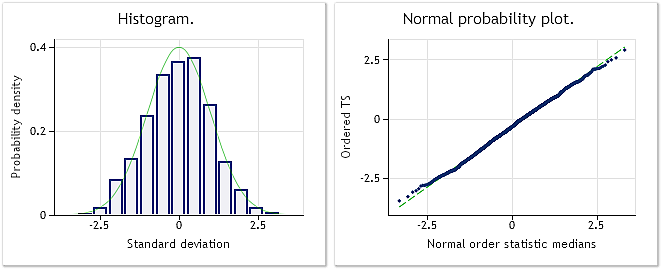
Fig. 3. Séquence transformée. Paramètre Lambda=0.2779, test de Jarque-Bera JB=4.73, р=0.094

La figure 3 montre le résultat de l'analyse de séquence transformée (BoxCoxTest1.mq5 script, bcdat[] array). La loi de distribution des séquences transformées est beaucoup plus proche de la loi normale, qui est également confirmé par les résultats du test de Jarque-Bera JB=4.73, p=0.094. La valeur du paramètre lambda obtenue = 0.2779.

La transformation Box-Cox s'est avérée suffisamment adaptée dans cet exemple. Il semble que la séquence résultante soit devenue beaucoup plus proche de la séquence « normale » et le résultat du test de Jarque-Bera a diminué de JB=3241.73 à JB=4.73. Ce n'est pas surprenant, puisque la séquence choisie s'adapte bien évidemment assez bien à ce type de transformation.

Examinons un autre exemple de la transformation de Box-Cox de la séquence pseudo-aléatoire. Nous devrions créer une séquence d'entrée « appropriée » pour la transformation de Box-Cox compte tenu de sa nature en loi de puissance. Pour y parvenir, nous devons générer une séquence pseudo-aléatoire (dont la loi de distribution est déjà proche de la normale), puis la déformer en élevant toutes ses valeurs à la puissance 0,35. Nous pouvons nous attendre à ce que la transformation Box-Cox renvoie la distribution normale originale à la séquence d'entrée avec une grande précision.

Vous trouverez ci-dessous le code source du script de texte BoxCoxTest2.mq5.

Ce script ne diffère du précédent que par le fait qu'une autre séquence d'entrée y est générée.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest2.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- data size
   n=1600;
//--- input data array
   ArrayResize(dat,n);
//--- transformed data array
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- random sequence generation
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Norm();

//--- input data shift
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;
   for(i=0;i<n;i++)dat[i]=MathPow(dat[i],0.35);

//--- optimization by lambda
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);

   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0) { for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;   }
   else          { for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);  }     // Lambda == 0.0

//-- dat[]   <-- input data
//-- bcdat[] <-- transformed data
  }
//-----------------------------------------------------------------------------------

La séquence pseudo-aléatoire d'entrée avec la loi de distribution normale est générée dans le script affiché. Elle est déplacée vers la zone des valeurs positives, puis tous les éléments de cette séquence sont élevés à la puissance 0,35. Une fois l'opération de script terminée, le tableau dat[] contient la séquence d'entrée, tandis que le tableau bcdat[] contient la séquence transformée.

La figure 4 montre les caractéristiques de la séquence d'entrée qui a perdu sa distribution normale d'origine en raison de l'élévation à la puissance de 0,35. Dans ce cas, le test de Jarque-Bera montre JB=3609.29, p= 0.000.

Fig. 4

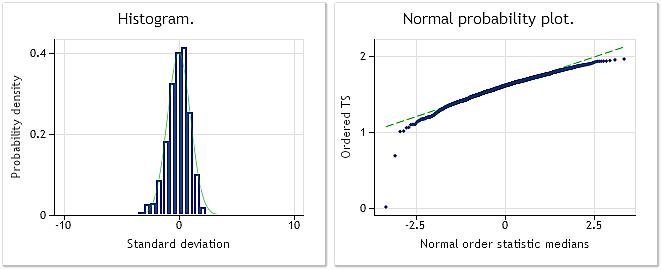
Fig. 4. Séquence pseudo-aléatoire d'entrée. Test de Jarque-Bera JB=3609.29, p=0.000.

Fig. 5

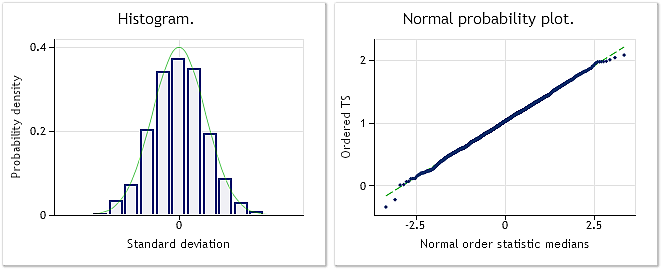
Fig. 5. Séquence transformée. Paramètre lambda=2.9067, test de Jarque-Bera JB=0.30, p=0.859

Comme le montre la figure 5, la séquence transformée a une loi de distribution suffisamment proche de la loi normale, ce qui est également confirmé par la valeur de test de Jarque-Bera JB=0,30, p=0,859.

Ces exemples d'utilisation de la transformation de Box-Cox ont donné de très bons résultats. Mais il ne faut pas oublier que dans les deux cas, nous avons traité les séquences qui convenaient le mieux à cette transformation. Par conséquent, ces résultats peuvent être considérés comme une simple confirmation de la performance de l'algorithme que nous avons créé.


4. Cotations

Après avoir confirmé la performance normale de l'algorithme mettant en œuvre la transformation de Box-Cox, nous devrions essayer de l'appliquer aux cotations réelles du Forex, car nous voulons les ramener à la loi de distribution normale.

Nous utiliserons les séquences décrites dans l'article « Prévisions des séries temporelles à l'aide du lissage exponentiel (suite) » [5] comme cotations de test. Elles sont placées dans le répertoire \Dataset2 de l'application Box-Cox-Tranformation_MQL5.zip archive et fournit de vraies cotations, dont les 1200 valeurs qui ont été enregistrées dans les fichiers appropriés. Extrait Le dossier \Dataset2 doit être placé dans le répertoire \MQL5\Files du terminal pour permettre l'accès à ces fichiers.

Supposons que ces cotations ne soient pas des séquences stationnaires. Par conséquent, nous n'étendrons pas les résultats de l'analyse à la population dite générale, mais les considérerons uniquement comme des caractéristiques de cette séquence particulière de longueur finie.

En outre, il convient de mentionner à nouveau que s'il n'y a pas de stationnarité, différents fragments de cotations d'une même paire de devises suivent des lois de distribution très différentes.

Créons un script permettant de lire les valeurs de séquence d'un fichier et d'effectuer sa transformation de Box-Cox. Par rapport aux scripts de test présentés ci-dessus, il ne diffère que par la formation de la séquence d'entrée. Vous trouverez ci-dessous le code source d'un tel script, tandis que le script BoxCoxTest3.mq5 est placé dans l'archive jointe.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest3.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
CBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
   string fname;
//--- input data file
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- data reading
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- data size
   n=ArraySize(dat);
//--- transformed data array
   ArrayResize(bcdat,n);

//--- input data array
   min=dat[ArrayMinimum(dat)]-1e-5;
   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- lambda parameter optimization
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- input data
//--- bcdat[] <-- transformed data
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//-----------------------------------------------------------------------------------

Toutes les valeurs (il y en a 1200 dans notre cas) sont importées dans le tableau dat[] de ce script à partir du fichier cotations, dont le nom est défini dans la variable fname. Ensuite, le décalage de la séquence initiale, la recherche de la valeur optimale du paramètre et la transformation de Box-Cox sont effectués, de la manière décrite ci-dessus. Après l'exécution du script, le résultat de la transformation est situé dans le tableau bcdat[].

Comme on peut le voir dans le code source montré, la séquence de cotation de l'EURUSD M1 a été sélectionnée dans le script pour la transformation. Le résultat de l'analyse de la séquence originale et de la séquence transformée est présenté dans les figures 6 et 7.

Fig. 6

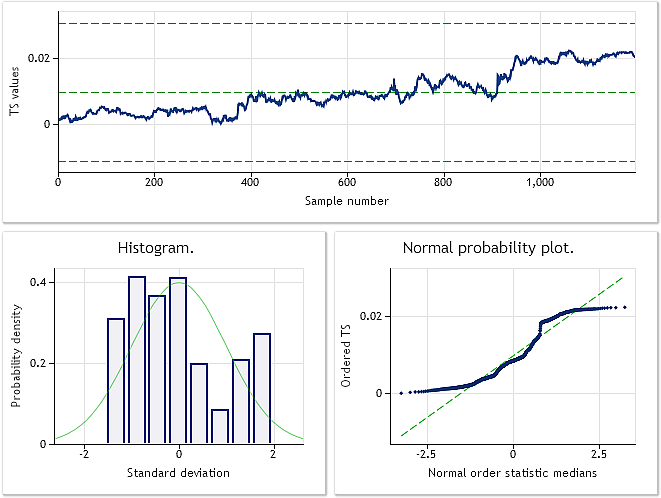
Fig. 6. Séquence d'entrée EURUSD M1. Test de Jarque-Bera JB=100.94, p=0.000.

Fig. 7

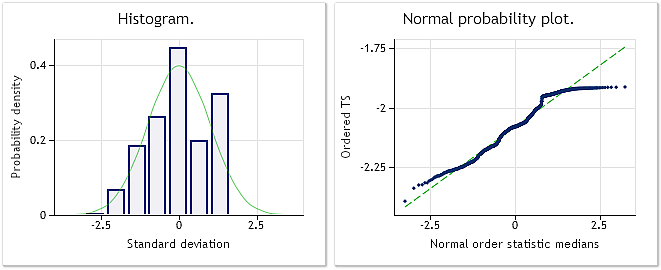
Fig. 7. Séquence transformée. Paramètre Lambda=0.4146, test de Jarque-Bera JB=39.30, p=0.000

Selon les caractéristiques montrées dans la figure 7, le résultat de la transformation des cotations EURUSD M1 n'est pas aussi impressionnant que les résultats de la transformation des séquences pseudo-aléatoires montrés précédemment. La transformation de Box-Cox n'est pas capable de gérer tous les types de séquences d'entrée, bien qu'elle soit considérée comme suffisamment universelle. Par exemple, il est impensable d'attendre de la transformation en loi de puissance qu'elle transforme la distribution à deux sommets en distribution normale.

Bien que la loi de distribution présentée à la figure 7 puisse difficilement être considérée comme normale, nous pouvons tout de même constater une diminution considérable des valeurs du test de Jarque-Bera comme dans les exemples précédents. Alors que JB=100.94 pour la séquence d'origine, il montre JB=39.30 après la transformation. Cela signifie que la loi de distribution a réussi à se rapprocher des valeurs normales dans une certaine mesure après la transformation.

On a obtenu à peu près les mêmes résultats en transformant différents fragments d'autres cotations. A chaque fois, la transformation de Box-Cox a plus ou moins rapproché la loi de distribution de la normale. Cependant, elle n'est jamais devenue normale.

Une série d'expériences avec différentes transformations des cotations permet de tirer une conclusion tout à fait prévisible - la transformation de Box-Cox permet de rapprocher la loi de distribution des cotations Forex de la normale, mais elle ne peut pas garantir l'obtention de la véritable normalité de la loi de distribution des données transformées.

Est-il raisonnable de procéder à la transformation, qui ne ramène toujours pas la séquence originale à la séquence normale ? Il n'y a pas de réponse définitive à cette question. Dans chaque cas spécifique, nous devons prendre une décision individuelle concernant la nécessité de la transformation de Box-Cox. Dans ce cas, beaucoup dépendra du type de méthodes paramétriques utilisées dans l'analyse des cotations et de la sensibilité de ces méthodes à l'écart des données initiales par rapport à la loi de distribution normale.


5. Suppression de la tendance

La partie supérieure de la figure 6 affiche le graphique de la séquence originale EURUSD M1 utilisée dans le script BCTransform.mq5. On peut facilement voir que ses valeurs augmentent presque uniformément tout au long de la séquence. En première approximation, on peut conclure que la séquence contient la tendance linéaire. La présence d'une telle « tendance » suggère que nous devrions essayer d'exclure la tendance avant d'effectuer diverses transformations et d'analyser la séquence reçue.

La suppression d'une tendance des séquences d'entrée analysées ne devrait probablement pas être considérée comme une méthode adaptée à absolument tous les cas. Mais supposons que nous allons analyser la séquence représentée sur la figure 6 pour y trouver des composantes périodiques (ou cycliques). Dans ce cas, nous pouvons sûrement soustraire la tendance linéaire de la séquence d'entrée après avoir défini les paramètres de la tendance.

La suppression d'une tendance linéaire n'affectera pas la détection des composantes périodiques. Cela peut même être utile et rendre les résultats d'une telle analyse plus précis ou plus fiables dans une certaine mesure, selon la méthode d'analyse choisie.

Si nous avons décidé que la suppression d'une tendance peut être utile dans certains cas, il est probablement logique d'examiner comment la transformation de Box-Cox traite une séquence après qu'une tendance en ait été exclue.

Dans n'importe quelle situation, lors de la suppression d'une tendance, nous devrons décider quelle courbe doit être utilisée pour l'approximation de la tendance ? Il peut s'agir d'une ligne droite, de courbes d'ordre supérieur, de moyennes mobiles, etc. Dans ce cas, choisissons, si je puis dire, la version extrême afin de ne pas se laisser distraire par le problème de sélection de courbe optimale. Nous utiliserons les incréments de la séquence originale, c'est-à-dire les différences entre ses valeurs actuelles et précédentes, au lieu de la séquence originale elle-même.

Dès lors que nous abordons l'analyse des incréments, il est impossible de ne pas commenter certains points connexes.

Dans divers articles et forums, la nécessité de la transition à l'analyse des incréments est justifiée de telle manière qu'elle peut laisser une impression erronée sur les propriétés d'une telle transition. L'analyse de transition vers des incréments est souvent décrite comme une sorte de transformation capable de transformer une séquence originale en une séquence stationnaire ou de normaliser sa loi de distribution. Mais est-ce vrai ? Essayons de répondre à cette question.

Nous devons partir du fait que l'essence de l'analyse de transition vers des incréments est constituée d'une idée très simple de diviser une séquence originale en deux composants. Nous pouvons le démontrer comme suit.

Supposons que nous ayons la séquence d'entrée

Et nous avons décidé de la diviser, pour une raison quelconque, en une tendance et quelques éléments restants qui sont apparus après la soustraction des valeurs de la tendance des éléments de la séquence originale. Supposons que nous ayons décidé d'utiliser une moyenne mobile simple avec une période de lissage égale à deux éléments de séquence pour une approximation de tendance.

Une telle moyenne mobile peut être calculée comme la somme de deux éléments de séquence adjacents divisée par deux. Dans ce cas, le résidu de la soustraction de la moyenne de la séquence originale sera égal à la différence entre les mêmes éléments adjacents divisée par deux.

Désignons la valeur moyenne mentionnée ci-dessus comme S, tandis que le résidu sera D. Si nous déplaçons le facteur permanent 2 vers la partie gauche de l'équation pour plus de clarté, nous obtiendrons ce qui suit :


Après avoir terminé nos transformations assez simples, nous avons divisé notre séquence originale en deux composantes, dont l'une est la somme des valeurs des séquences adjacentes, et l'autre est constituée des différences. Ce sont exactement les séquences que nous appelons incréments, tandis que les sommes forment la tendance.

À cet égard, il serait plus raisonnable de considérer les incréments comme une partie de la séquence originale. Il ne faut donc pas oublier que, si l'on passe à l'analyse des incréments, l'autre partie de la séquence définie par les sommes est souvent tout simplement ignorée, sauf si on ne l'analyse pas séparément, bien sûr.

Le moyen le plus simple d'avoir une idée des avantages que nous pouvons retirer de cette division de la séquence est d'appliquer la méthode spectrale.

Directement à partir des expressions données ci-dessus, nous pouvons déduire que la composante S est le résultat du filtrage de séquence d'origine avec l'utilisation du filtre basse fréquence ayant les caractéristiques d'impulsion h=1,1. Par conséquent, la composante D est le résultat du filtrage avec l'utilisation du filtre haute fréquence ayant les caractéristiques d'impulsion h = -1,1. La figure 8 présente nominalement les caractéristiques de fréquence de tels filtres.

Fig. 8

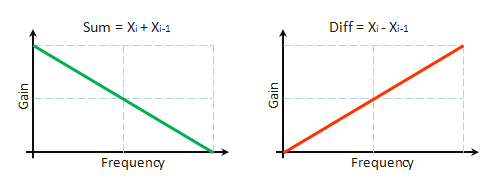
Fig. 8. Caractéristiques amplitude-fréquence

Supposons que nous soyons passés de l'analyse directe de la séquence elle-même à l'analyse de ses différences. Que pouvons-nous attendre ici ? Il existe différentes options dans ce cas. Nous n'examinerons brièvement que certains d'entre eux.

  1. Si l'énergie de base du processus analysé est concentrée dans la région basse fréquence de la séquence originale, le passage à l'analyse des différences ne fera que supprimer cette énergie, ce qui rendra plus complexe, voire impossible de poursuivre l'analyse ;
  2. Dans le cas où l'énergie de base du processus analysé est concentrée dans la région haute fréquence de la séquence originale, le passage à l'analyse des différences peut conduire à des effets positifs en raison de la filtration des composantes basse fréquence interférentes. Mais cela n'est possible que si une telle filtration n'affecte pas de manière significative les propriétés du processus analysé ;
  3. Nous pouvons également mentionner le cas où l'énergie du processus analysé est uniformément distribuée sur toute l’intervalle de fréquences de la séquence. Dans ce cas, nous déformerons irréversiblement le processus après le passage à l'analyse de ses différences en supprimant sa partie basse fréquence.

De même, nous pouvons tirer des conclusions sur les résultats de la transition vers l'analyse des différences pour toute autre combinaison de tendances, tendance à court terme, bruit parasite, etc. Mais dans tous les cas, le passage à l'analyse des différences ne conduira pas à une forme stationnaire du processus analysé et ne normalisera pas le processus de distribution.

Sur la base de ce qui précède, nous pouvons conclure qu'une séquence ne « s'améliore » pas automatiquement après la transition vers l'analyse des différences. Nous pouvons supposer que dans certains cas, il est préférable d'analyser à la fois la séquence d'entrée et les différences avec les sommes de ses valeurs adjacentes pour obtenir une connaissance plus claire de la séquence d'entrée, tandis que les conclusions finales sur les propriétés de cette séquence doivent être tirées sur la base de l'examen conjoint de tous les résultats obtenus.

Revenons au sujet de notre article et voyons comment se comporte la transformation de Box-Cox en cas de transition vers l'analyse des incréments de la séquence EURUSD M1 illustrée à la Fig.6. Pour ce faire, nous utiliserons le script BoxCoxTest3.mq5 présenté précédemment, dans lequel nous remplacerons les valeurs de séquence par des différences (incréments) après avoir calculé ces valeurs de séquence à partir du fichier. Étant donné qu'aucune autre modification du code source du script n'est mise en œuvre, il est inutile de le publier. Nous nous contenterons de montrer les résultats de son analyse de fonctionnement.

EURUSD M1 incréments. Test de Jarque-Bera JB=32494,8, p=0,000

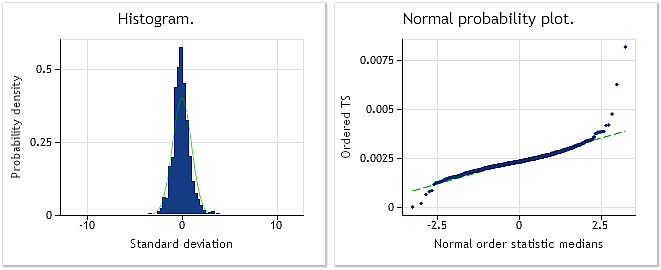
Fig. 9. EURUSD M1 incréments. Test de Jarque-Bera JB=32494,8, p=0,000

Fig. 10. Séquence transformée. Paramètre lambda=0.6662, test de Jarque-Bera JB=10302.5, p=0.000

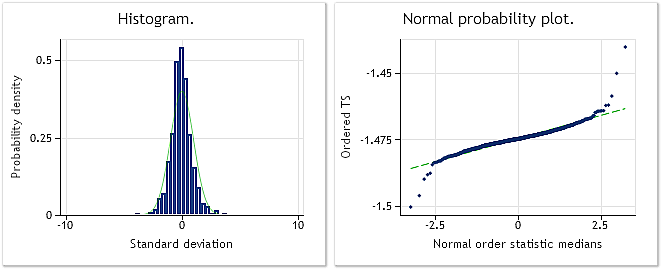
Fig. 10. Séquence transformée. Paramètre lambda=0.6662, test de Jarque-Bera JB=10302.5, p=0.000

La figure 9 montre les caractéristiques de la séquence constituée d'incréments EURUSD M1 (différences), tandis que la figure 10 montre ses caractéristiques obtenues après la transformation de Box-Cox. Malgré le fait que la valeur du test de Jarque-Bera a diminué de plus de trois fois passant de JB = 32494,8 à JB = 10302,5 après la transformation, la loi de distribution de séquence transformée est encore loin d'être normale.

Cependant, il ne faut pas tirer de conclusions hâtives en pensant que la transformation de Box-Cox ne peut pas gérer correctement la transformation par incréments. Nous n'avons considéré qu'un cas particulier. En traitant d'autres séquences d'entrée, nous pouvons obtenir des résultats complètement différents.


6. Exemples cités

Tous les exemples précédemment cités de la transformation de Box-Cox concernent le cas où la loi de distribution de séquence originale est supposée être réduite à la loi normale ou, peut-être, à la loi la plus proche possible de la normale. Comme il a été mentionné au début, une telle transformation peut être nécessaire lors de l'utilisation des méthodes d'analyse paramétrique, qui peuvent être assez sensibles à l'écart d'une loi de distribution de séquence examinée par rapport à la loi normale.

Les exemples montrés ont démontré que dans tous les cas après la transformation, selon les résultats du test de Jarque-Bera, nous avons effectivement reçu les séquences dont la loi de distribution est plus proche de la normale par rapport aux séquences originales. Ce fait montre clairement la polyvalence et l'efficacité de la transformation de Box-Cox.

Mais il ne faut pas surestimer les possibilités de la transformation de Box-Cox et supposer que toute séquence d'entrée sera transformée en une séquence strictement normale. Comme le montrent les exemples ci-dessus, c'est loin d'être vrai. Ni la séquence originale ni la séquence transformée ne peuvent être considérées comme normales pour les cotations réelles.

Jusqu'à présent, la transformation de Box-Cox n'a été considérée que sous sa forme plus visuelle, à un paramètre. Cela a été fait afin de simplifier la première rencontre avec le produit. Cette approche est justifiée pour démontrer les capacités de cette transformation, mais à des fins pratiques, il serait probablement préférable d'utiliser une forme plus générale de sa présentation.


7. La forme générale de la transformation de Box-Cox

Il convient de rappeler que la transformation de Box-Cox n'est applicable qu'aux séquences ayant des valeurs positives et non nulles. En pratique, cette exigence est facilement satisfaite par un simple décalage d'une séquence vers la zone positive, mais l'ampleur du décalage dans la zone positive peut avoir un impact direct sur le résultat de la transformation.

Par conséquent, la valeur de décalage peut être considérée comme un paramètre de transformation supplémentaire et l'optimiser avec le paramètre lambda, ne permettant pas aux valeurs de séquence d'entrer dans la zone négative.

Pour la séquence originale X de longueur N :

les expressions déterminant la forme plus générale de la transformation de Box-Cox à deux paramètres sont les suivantes :

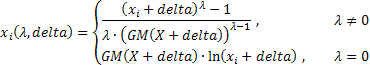
où :

;

GM() - moyenne géométrique.

La moyenne géométrique de la séquence peut être calculée de la manière suivante :

Comme nous pouvons le voir, deux paramètres sont déjà utilisés dans les expressions affichées - lambda et delta. Maintenant, nous devons optimiser ces deux paramètres simultanément lors de la transformation. Malgré la légère complication de l'algorithme, l'introduction d'un paramètre supplémentaire peut certainement augmenter l'efficacité de la transformation. De plus, les facteurs de normalisation supplémentaires sont apparus dans les expressions par rapport à la transformation utilisée précédemment. Avec ces facteurs, le résultat de la transformation conservera sa dimension pendant la modification du paramètre lambda.

Plus d'informations sur la transformation de Box-Cox peuvent être trouvées dans [7], [8]. D'autres transformations du même type sont brièvement décrites dans [8].

Voici les principales caractéristiques de la forme de transformation actuelle, plus générale :

  1. La transformation elle-même exige que la séquence d'entrée ne contienne que des valeurs positives. L'inclusion d'un paramètre delta supplémentaire permet d'effectuer automatiquement le décalage requis de la séquence lorsque certaines conditions précises sont remplies ;
  2. Lors de la sélection de la valeur optimale du paramètre delta, son amplitude doit garantir la « positivité » de toutes les valeurs de séquence ;
  3. La transformation est continue en cas de modification du paramètre lambda y compris les changements proches de sa valeur zéro ;
  4. Le résultat de la transformation conserve sa dimension en cas de modification de la valeur du paramètre lambda.

Le critère logarithmique de la fonction de vraisemblance a été utilisé dans tous les exemples cités précédemment lors de la recherche de la valeur optimale du paramètre lambda. Bien entendu, ce n'est pas le seul moyen d'estimer la valeur optimale des paramètres de transformation.

A titre d'exemple, on peut citer la méthode d'optimisation des paramètres, à laquelle on recherche la valeur maximale du coefficient de corrélation entre une séquence transformée triée de manière ascendante et une séquence des quantiles de fonction de distribution normale. Cette variante a déjà été mentionnée dans l'article. Les valeurs des quantiles de la fonction de distribution normale peuvent être calculées selon les expressions suggérées par James J. Filliben [9].

Les expressions qui déterminent la forme générale de la transformation à deux paramètres sont certainement plus lourdes que celles considérées précédemment. C'est peut-être la raison pour laquelle ce type de transformation est assez rarement utilisé dans les paquets mathématiques et statistiques. Les expressions citées ont été réalisées en MQL5 pour avoir la possibilité d'utiliser la transformation de Box-Cox sous une forme plus générale au besoin.

Le fichier CFullBoxCox.mqh contient le code source de la classe CFullBoxCox qui effectue la recherche de la valeur optimale des paramètres de transformation. Comme cela a déjà été mentionné, le processus d'optimisation est basé sur le calcul du coefficient de corrélation.

//+------------------------------------------------------------------+
//|                                                  CFullBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+

#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| CFullBoxCox class                                                |
//+------------------------------------------------------------------+
class CFullBoxCox:public PowellsMethod
  {
protected:
  int    Dlen;                     // data size
  double Dat[];                    // input data array
  double Shift[];                  // input data array with the shift
  double BCDat[];                  // transformed data (Box-Cox)
  double Mean;                     // transformed data average value
  double Cdf[];                    // Quantile of the distribution cumulative function
  double Scdf;                     // Square root of summ of Quantile^2
  double R;                        // correlation coefficient 
  double DeltaMin;                 // Delta minimum value
  double DeltaMax;                 // Delta maximum value
  double Par[2];                   // parameters array
public:
  void   CFullBoxCox(void)       { }
  void   CalcPar(double &dat[]);
  double GetPar(int n)           { return(Par[n]); }
private:
  double ndtri(double y0);         // the function opposite to the normal distribution function
  virtual double func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CFullBoxCox::CalcPar(double &dat[])
  {
  int i;
  double a,max,min;
  
  Dlen=ArraySize(dat);
  ArrayResize(Dat,Dlen);
  ArrayResize(Shift,Dlen);
  ArrayResize(BCDat,Dlen);
  ArrayResize(Cdf,Dlen);
//--- copy the input data array
  ArrayCopy(Dat,dat);
  
  Scdf=0;
  a=MathPow(0.5,1.0/Dlen);
  Cdf[Dlen-1]=ndtri(a); Scdf+=Cdf[Dlen-1]*Cdf[Dlen-1];
  Cdf[0]=ndtri(1.0-a); Scdf+=Cdf[0]*Cdf[0];
  a=Dlen+0.365;
  for(i=1;i<(Dlen-1);i++)
    {
    //--- calculation of the distribution cumulative function Quantile
    Cdf[i]=ndtri((i+0.6825)/a);
    //--- calculation of the sum of Quantile^2
    Scdf+=Cdf[i]*Cdf[i];
    }

//--- square root of the sum of Quantile^2
  Scdf=MathSqrt(Scdf);             
  
  min=dat[0]; max=min;
  for(i=0;i<Dlen;i++)
    {
//--- copy the input data
    a=dat[i]; Dat[i]=a;
    if(min>a)min=a;
    if(max<a)max=a;
    }
  
//--- Delta minimum value
  DeltaMin=1e-5-min;
//--- Delta maximum value
  DeltaMax=(max-min)*200-min;
//--- Lambda initial value
  Par[0]=1.0;
//--- Delta initial value
  Par[1]=(max-min)/2-min;
//--- optimization using Powell method
  Optimize(Par);             
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CFullBoxCox::func(const double &p[])
  {
  int i;
  double a,b,c,lam,del,k1,k2,gm,gmpow,mean,ret;
  
  lam=p[0]; del=p[1]; k1=0; k2=0;
  if (lam>5.0){k1=(lam-5.0)*400; lam=5.0;}                    // Lambda >  5.0
  else if(lam<-5.0){k1=-(lam+5.0)*400; lam=-5.0;}             // Lambda < -5.0
  if (del>DeltaMax){k2=(del-DeltaMax)*400; del=DeltaMax;}    // Delta > DeltaMax
  else if(del<DeltaMin){k2=(DeltaMin-del)*400; del=DeltaMin; // Delta < DeltaMin
  
  gm=0;
  for(i=0;i<Dlen;i++)
    {
    Shift[i]=Dat[i]+del;
    gm+=MathLog(Shift[i]);
    }

//--- geometric mean
  gm=MathExp(gm/Dlen);
  gmpow=lam*MathPow(gm,lam-1);
  mean=0;
//--- Lambda != 0.0
   if(lam!=0)                                  
    {
    for(i=0;i<Dlen;i++)
      {
      a=(MathPow(Shift[i],lam)-1.0)/gmpow;
       //--- transformed data (Box-Cox)
      BCDat[i]=a;
       //--- average value
      mean+=a;
      }
    }
  //--- Lambda == 0.0
  else                                        
     {
    for(i=0;i<Dlen;i++)
      {
      a=gm*MathLog(Shift[i]);
       //--- transformed data (Box-Cox)
      BCDat[i]=a;
      //--- average value
      mean+=a;
      }
    }
  mean=mean/Dlen;
  //--- sorting of the transformed data array
  ArraySort(BCDat);
  a=0; b=0;
  for(i=0;i<Dlen;i++)
    {
    c=(BCDat[i]-mean);
    a+=Cdf[i]*c;
    b+=c*c;
    }
  //--- correlation coefficient
  ret=a/(Scdf*MathSqrt(b)); 
  return(k1+k2-ret);
  }
//+------------------------------------------------------------------+
//| The function opposite to the normal distribution function        |
//| Prototype:                                                       |
//| Cephes Math Library Release 2.8: June, 2000                      |
//| Copyright 1984, 1987, 1989, 2000 by Stephen L. Moshier           |
//+------------------------------------------------------------------+
double CFullBoxCox::ndtri(double y0)
  {
  static double s2pi =2.50662827463100050242E0; // sqrt(2pi)
  static double P0[5]={-5.99633501014107895267E1,  9.80010754185999661536E1,
                       -5.66762857469070293439E1,  1.39312609387279679503E1,
                       -1.23916583867381258016E0};
  static double Q0[8]={ 1.95448858338141759834E0,  4.67627912898881538453E0,
                        8.63602421390890590575E1, -2.25462687854119370527E2,
                        2.00260212380060660359E2, -8.20372256168333339912E1,
                        1.59056225126211695515E1, -1.18331621121330003142E0};
  static double P1[9]={ 4.05544892305962419923E0,  3.15251094599893866154E1,
                        5.71628192246421288162E1,  4.40805073893200834700E1,
                        1.46849561928858024014E1,  2.18663306850790267539E0,
                       -1.40256079171354495875E-1,-3.50424626827848203418E-2,
                       -8.57456785154685413611E-4};
  static double Q1[8]={ 1.57799883256466749731E1,  4.53907635128879210584E1,
                        4.13172038254672030440E1,  1.50425385692907503408E1,
                        2.50464946208309415979E0, -1.42182922854787788574E-1,
                       -3.80806407691578277194E-2,-9.33259480895457427372E-4};
  static double P2[9]={ 3.23774891776946035970E0,  6.91522889068984211695E0,
                        3.93881025292474443415E0,  1.33303460815807542389E0,
                        2.01485389549179081538E-1, 1.23716634817820021358E-2,
                        3.01581553508235416007E-4, 2.65806974686737550832E-6,
                        6.23974539184983293730E-9};
  static double Q2[8]={ 6.02427039364742014255E0,  3.67983563856160859403E0,
                        1.37702099489081330271E0,  2.16236993594496635890E-1,
                        1.34204006088543189037E-2, 3.28014464682127739104E-4,
                        2.89247864745380683936E-6, 6.79019408009981274425E-9};
  double x,y,z,y2,x0,x1,a,b;
  int i,code;
  if(y0<=0.0){Print("Function ndtri() error!"); return(-DBL_MAX);}
  if(y0>=1.0){Print("Function ndtri() error!"); return(DBL_MAX);}
  code=1; y=y0;
  if(y>(1.0-0.13533528323661269189)){y=1.0-y; code=0;}  // 0.135... = exp(-2)
  if(y>0.13533528323661269189)                         // 0.135... = exp(-2)
    {
    y=y-0.5; 
    y2=y*y;
    a=P0[0]; for(i=1;i<5;i++)a=a*y2+P0[i];
    b=y2+Q0[0]; for(i=1;i<8;i++)b=b*y2+Q0[i];
    x=y+y*(y2*a/b);
    x=x*s2pi; 
    return(x);
    }
  x=MathSqrt(-2.0*MathLog(y));
  x0=x-MathLog(x)/x;
  z=1.0/x;
//--- y > exp(-32) = 1.2664165549e-14
  if(x<8.0)
    {
    a=P1[0]; for(i=1;i<9;i++)a=a*z+P1[i];
    b=z+Q1[0]; for(i=1;i<8;i++)b=b*z+Q1[i];
    x1=z*a/b;
    }
  else
    {
    a=P2[0]; for(i=1;i<9;i++)a=a*z+P2[i];
    b=z+Q2[0]; for(i=1;i<8;i++)b=b*z+Q2[i];
    x1=z*a/b;
    }
  x=x0-x1;
  if(code!=0)x=-x;
  return(x);
  }
//------------------------------------------------------------------------------------

Certaines limitations sont appliquées à l’intervalle de modification des paramètres de transformation pendant l'optimisation. La valeur du paramètre lambda est limitée par les valeurs 5,0 et -5,0. Les limitations des paramètres delta sont spécifiées par rapport à la valeur minimale de la séquence d'entrée. Ce paramètre est limité par les valeurs DeltaMin=(0,00001-min) et DeltaMax=(max-min)*200-min, où min et max sont les valeurs minimale et maximale des éléments de séquence d'entrée.

Le script FullBoxCoxTest.mq5 illustre l'utilisation de la classe CFullBoxCox. Le code source de ce script est présenté ci-dessous.

//+------------------------------------------------------------------+
//|                                               FullBoxCoxTest.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include  "CFullBoxCox.mqh"
CFullBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],shift[],bcdat[],lambda,delta,gm,gmpow;
   string fname;

//--- input file name
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- reading the data
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- data size
   n=ArraySize(dat);
//--- shifted input data array
   ArrayResize(shift,n);
//--- transformed data array
   ArrayResize(bcdat,n);

//--- lambda and delta parameters optimization
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   delta=Bc.GetPar(1);

   PrintFormat("Iterations= %i,   lambda= %.4f,   delta= %.4f",
               Bc.GetIter(),lambda,delta);
   gm=0;
   for(i=0;i<n;i++)
     {
      shift[i]=dat[i]+delta;
      gm+=MathLog(shift[i]);
     }
//--- geometric mean
   gm=MathExp(gm/n);
   gmpow=lambda*MathPow(gm,lambda-1);
   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(shift[i],lambda)-1.0)/gmpow;}
   else         {for(i=0;i<n;i++)bcdat[i]=gm*MathLog(shift[i]);}
//--- dat[]   <-- input data
//--- shift[] <-- input data with the shift
//--- bcdat[] <-- transformed data
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//------------------------------------------------------------------------------------

La séquence d'entrée est téléchargée dans le tableau dat[] à partir du fichier au début du script, puis la recherche des valeurs optimales des paramètres de transformation est effectuée. Ensuite, la transformation elle-même est effectuée à l'aide des paramètres obtenus. Par conséquent, le tableau dat[] contient la séquence originale, le tableau shift[] contient la séquence originale décalée de la valeur delta et le tableau bcdat[] contient le résultat de la transformation de Box-Cox.

Tous les fichiers nécessaires à la compilation du script FullBoxCoxTest.mq5 se trouvent dans l'archive Box-Cox-Tranformation_MQL5.zip.

La transformation des séquences de test que nous utilisons est effectuée à l'aide du script FullBoxCoxTest.mq5. Comme prévu, lors de l'analyse des données obtenues, nous pouvons conclure que ce type de transformation à deux paramètres donne de meilleurs résultats que le type à un paramètre. Par exemple, pour la séquence EURUSD M1, dont les résultats d'analyse sont présentés sur la figure 6, la valeur du test de Jarque-Bera comprenait JB=100,94. JB=39,30 après la transformation à un paramètre (voir Fig. 7), mais après la transformation à deux paramètres (script FullBoxCoxTest.mq5) cette valeur est descendue à JB=37,49.


Conclusion

Dans cet article, nous avons examiné les cas où les paramètres de transformation de Box-Cox ont été optimisés pour que la loi de distribution de séquence résultante soit aussi proche que possible de la normale. Mais dans la pratique, il peut arriver que la transformation de Box-Cox doive être utilisée d'une manière légèrement différente. Par exemple, l'algorithme suivant peut être utilisé lors de la prévision des séquences temporelles :

  1. Des valeurs préliminaires des valeurs des paramètres de transformation de Box-Cox et des modèles de prévision sont sélectionnés ;
  2. La transformation de Box-Cox des données d'entrée est effectuée ;
  3. La prévision est réalisée en fonction des paramètres actuels ;
  4. La transformation inverse de Box-Cox est effectuée pour les résultats de la prévision ;
  5. L'erreur de prévision est évaluée par la séquence d'entrée non transformée ;
  6. Les valeurs des paramètres sont modifiées pour minimiser l'erreur de prévision et l'algorithme revient à l'étape 2.

Dans l'algorithme ci-dessus, les paramètres de transformation doivent être minimisés, ainsi que ceux du modèle de prévision, par le critère de l'erreur de prévision minimale. Dans ce cas, l'objectif de la transformation de Box-Cox n'est déjà pas la transformation de la séquence d'entrée en loi de distribution normale.

Maintenant, il est nécessaire de transformer la séquence d'entrée pour recevoir la loi de distribution fournissant l'erreur de prévision minimale. Selon la méthode de prévision choisie, cette loi de distribution ne doit pas nécessairement être normale.

La transformation de Box-Cox n'est applicable qu'aux séquences avec des valeurs positives et non nulles. Le décalage de la séquence d'entrée doit être effectué dans tous les autres cas. Cette caractéristique de la transformation peut certainement être qualifiée comme l'un de ses inconvénients. Mais malgré cela, la transformation Box-Cox est probablement l'outil le plus polyvalent et le plus efficace parmi d'autres transformations du même genre.


Liste de références

  1. А.N. Porunov. Transformation de Box-Сox et l'illusion de la « normalité » des séries macroéconomiques. Revue « Business Informatics », 2(12)-2010, pp. 3-10.
  2. Mohammad Zakir Hossain, L'utilisation de la technique de transformation de Box-Cox dans les analyses économiques et statistiques. Journal des tendances émergentes en sciences économiques et de gestion (JETEMS) 2 (1) : 32-39.
  3. Transformations de Box-Cox.
  4. L'article « Prévision de séries chronologiques à l'aide du lissage exponentiel ».
  5. L'article « Prévision de séries chronologiques à l'aide du lissage exponentiel (suite) ».
  6. Analyse des principales caractéristiques des séries chronologiques.
  7. Power transform.
  8. Draper NR et H. Smith, Analyse de régression appliquée, 3e édition, 1998, John Wiley & Sons, New York.
  9. Q-Q plot.

Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/363

Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.

Autres articles par cet auteur

Aller à la discussion
Se débarrasser des DLL auto-produites Se débarrasser des DLL auto-produites
Si la fonctionnalité du langage MQL5 n'est pas suffisante pour accomplir les tâches, un programmeur MQL5 doit utiliser des outils supplémentaires. Il doit passer à un autre langage de programmation et créer une DLL intermédiaire. MQL5 a la possibilité de présenter différents types de données et de les transférer vers l'API mais, malheureusement, MQL5 ne peut pas résoudre le problème concernant l'extraction de données à partir du pointeur accepté. Dans cet article, nous allons parsemer tous les « i » et montrer des mécanismes simples d'échange et de travail avec des types de données complexes.
Quelques conseils pour les nouveaux clients Quelques conseils pour les nouveaux clients
Une sagesse proverbiale souvent attribuée à diverses personnes célèbres dit : « Celui qui ne fait pas d'erreurs ne fait jamais rien. » À moins que vous ne considériez l'oisiveté comme une erreur, cette affirmation est difficile à contredire. Mais vous pouvez toujours analyser les erreurs passées (les vôtres et celles des autres) pour minimiser le nombre de vos erreurs futures. Nous allons tenter de passer en revue les situations qui peuvent se présenter lors de l'exécution de travaux dans le service du même nom.
Qui est qui dans MQL5.community ? Qui est qui dans MQL5.community ?
Le site MQL5.com se souvient très bien de vous tous ! Combien de vos fils de discussion sont épiques, quelle est la popularité de vos articles et combien de fois vos programmes dans la base de code sont téléchargés - ce n'est qu'une petite partie de ce qui est retenu sur MQL5.com. Vos réalisations sont disponibles dans votre profil, mais qu'en est-il de l'image globale ? Dans cet article, nous allons montrer le tableau général des réalisations de tous les membres de la MQL5.community.
Analyse de régression multiple. Générateur et testeur de stratégie en un Analyse de régression multiple. Générateur et testeur de stratégie en un
L'article donne une description des méthodes d'utilisation de l'analyse de régression multiple pour le développement de systèmes de trading. Il démontre l'utilisation de l'analyse de régression pour l'automatisation de la recherche de stratégies. Une équation de régression générée et intégrée dans un EA sans nécessiter une grande maîtrise de la programmation est donnée à titre d'exemple.