MetaTrader 5 / Estadística y análisis
English Русский 中文 Deutsch 日本語 Português 한국어 Français Italiano Türkçe
La transformación Box-Cox

La transformación Box-Cox

MetaTrader 5 — Estadística y análisis | 8 mayo 2014, 10:46
9 332 0
Victor
Victor

Introducción

A medida que aumentan las capacidades informáticas, los operadores y analistas de Forex disponen de más opciones a la hora de utilizar algoritmos matemáticos muy desarrollados y complejos que requieren una gran cantidad de recursos informáticos. Pero la idoneidad de los recursos informáticos por sí solo no resuelve los problemas de los operadores. También son necesarios algoritmos eficientes para analizar las cotizaciones del mercado.

Actualmente, áreas como la estadística matemática, la economía y la econometría proporcionan un gran número de métodos, modelos y algoritmos eficientes y con buenos resultados que son utilizados por los operadores para el análisis del mercado. Con frecuencia, se trata de métodos paramétricos estándar creados bajo la suposición de estabilidad de las series analizadas y la normalidad de su ley de distribución.

Pero no es un secreto que las cotizaciones Forex son series que no pueden ser clasificadas como estables y con una ley de distribución normal. Por tanto, no podemos utilizar los métodos paramétricos "estándar" de la estadística matemática, la econometría, etc., cuando analizamos las cotizaciones.

En el artículo "La transformación Box-Cox y la ilusión de la normalidad de las series macroeconómicas [1]", A. N. Porunov escribe lo siguiente: 

"A menudo, los analistas económicos tienen que trabajar con datos estadísticos que no pasan la prueba de normalidad por una u otra razón. En esta situación hay dos opciones: utilizar los métodos no paramétricos que requieren una gran cantidad de conocimientos matemáticos o utilizar técnicas especiales que permitan convertir la "estadística anormal" en otra "normal", que también constituye una tarea compleja".

A pesar de que la cita de A. N. Porunov se refiere a los analistas económicos, puede ser también aplicable a los intentos de analizar las cotizaciones "anormales" de Forex utilizando métodos paramétricos de la estadística matemática y la econometría. La inmensa mayoría de estos métodos han sido desarrollados para analizar secuencias con una ley de distribución normal. Pero en la mayoría de casos, la cuestión de la "anormalidad" inicial de los datos es simplemente ignorada. Además, los métodos mencionados requieren a menudo no solo una distribución normal, sino también de estacionariedad de las series iniciales.

La regresión, la dispersión (ANOVA) y algunos otros tipos de análisis pueden denominarse métodos "estándar" que requieren una normalidad de los datos iniciales. No es posible enumerar todos los métodos paramétricos que presentan limitaciones respecto a la normalidad de la ley de distribución, ya que ocupan todo el campo de la econometría, excepto en el caso de los métodos no paramétricos.

Para ser justos, debe añadirse que los métodos paramétricos "estándar" tienen una sensibilidad distinta a la desviación de la ley de distribución de datos inicial con respecto a valor normal. Por tanto, la desviación de la "normalidad" durante el uso de dichos métodos no lleva necesariamente a consecuencias desastrosas, aunque, por supuesto, no incrementa la precisión y fiabilidad de los resultados obtenidos.

Todo ello plantea la cuestión de la necesidad de cambiar a los métodos no paramétricos para el análisis y predicción de las cotizaciones. Sin embargo, los métodos paramétricos siguen siendo muy atractivos. Esto se debe al predominio y cantidad de datos y a los algoritmos prediseñados y ejemplos de su aplicación. Para usar adecuadamente estos métodos, es necesario hacer frente, al menos, a dos cuestiones relacionadas con las series iniciales: la inestabilidad y la "anormalidad".

Aunque no podemos influir sobre la estabilidad de las series iniciales, podemos intentar que su ley de distribución sea más próxima a una normal. Para resolver este problema existen varias transformaciones. Las más conocidas se describen brevemente en el artículo "El uso de la técnica de transformación Box-Cox en el análisis económico y estadístico" [2]. En este artículo vamos a considerar solo una de ellas: la transformación de Box-Cox [1], [2], [3].

Debemos destacar aquí que el uso de la transformación Box-Cox, como ocurre con cualquier otro tipo de transformación, solo puede llevar la ley de distribución de la serie inicial a un estado más o menos cercano al de una distribución normal. Esto significa que el uso de esta transformación no garantiza que la serie obtenida se ajuste a una ley de distribución normal.


1. La transformación Box-Cox

Para la serie original X de longitud N

La transformación Box-Cox de un parámetro es la siguiente:


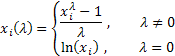
donde .

Como puede ver, esta transformación solo tiene un parámetro lambda. Si el valor de lambda es igual a cero, se lleva a cabo la transformación logarítmica de la serie inicial, y si dicho valor es distinto a cero la transformación es potencial. Si el parámetro lambda es igual a uno, la ley de distribución de la serie inicial permanece sin cambios, aunque la serie cambia, ya que se resta una unidad a cada uno de sus valores.

En función del valor de lambda, la transformación de Box-Cox incluye los siguientes casos especiales:


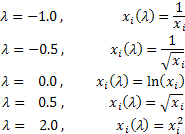
La utilización de la transformación Box-Cox requiere que todos los valores de la serie de entrada sean positivos y distintos a cero. Si la serie de entrada no satisface estos requisitos puede ser desplazada al área positiva por el volumen que garantiza un valor "positivo" de todos sus valores.

Por ahora, solo vamos a examinar la transformación de Box-Cox de un parámetro preparando los datos de entrada para la misma de forma adecuada. Para evitar valores negativos o iguales a cero en los datos de entrada, vamos a buscar siempre el valor más bajo de la serie de entrada y lo deduciremos de cada elemento de la serie realizando adicionalmente un pequeño cambio igual a 1 E-5. Es preciso realizar dicho cambio para proporcionar una garantía del desplazamiento de la serie al área positiva en caso de que el valor más bajo sea igual a cero.

De hecho, no es necesario aplicar este desplazamiento a las series "positivas". No obstante, usaremos el mismo algoritmo para disminuir la probabilidad de obtener valores demasiado altos al elevar a una potencia durante la transformación. De esta forma, cualquier serie de entrada se situará en el área positiva después del cambio y tendrá el valor más bajo cercano a cero.

La Figura 1 muestra las curvas de la transformación de Box-Cox con valores distintos del parámetro lambda. La Figura 1 se ha obtenido del artículo "Transformaciones Box-Cox" [3]. La cuadrícula horizontal en el gráfico se muestra en una escala logarítmica.

Fig. 1. Transformación Box-Cox con varios valores del parámetro lambda

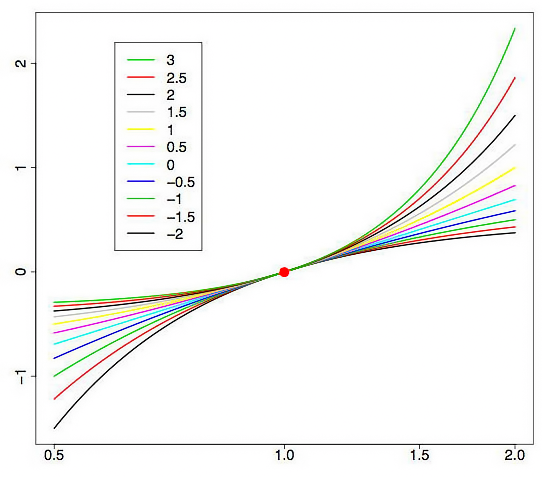
Fig. 1. Transformación Box-Cox con varios valores del parámetro lambda

Como vemos, las "colas" de la distribución inicial pueden "estirarse" o "contraerse". La curva superior de la Figura 1 se corresponde con lambda=3, mientras que la inferior lo hace con lambda=-2.

Para que la ley de distribución de la serie resultante sea tan cercana a la distribución normal como sea posible, debe seleccionarse el valor óptimo del parámetro lambda.

Una forma de obtener el valor óptimo de este parámetro es maximizar el logaritmo de la función de probabilidad:

donde:

Significa que necesitamos seleccionar el parámetro lambda en el que esta función alcanza su valor máximo.

El artículo "transformaciones Box-Cox" [3] trata brevemente sobre otras formas de determinar el valor óptimo de este parámetro en base a la búsqueda del valor más alto del coeficiente de correlación entre los cuantiles de la función de distribución normal y la serie transformada. Lo más probable es que sea posible encontrar otros métodos de optimización del parámetro lambda, pero vamos a ver primero la búsqueda del máximo del logaritmo de la función de probabilidad mencionado anteriormente.

Hay diferentes formas de encontrarlo. Por ejemplo, podemos utilizar una simple búsqueda. Para hacer esto debemos calcular el valor de la función de probabilidad dentro de un rango seleccionado cambiando el valor del parámetro lambda a un paso bajo. También debemos seleccionar el parámetro lambda óptimo al que la función de probabilidad tiene el valor más alto.

La distancia de avance determinará la precisión del cálculo del valor óptimo del parámetro lambda. Cuando más bajo sea el avance, mayor será la precisión, aunque la cantidad requerida de cálculos se incrementará proporcionalmente en dicho caso. Pueden usarse varios algoritmos de búsqueda del máximo/mínimo de la función, los algoritmos genéticos y algunos otros métodos, para incrementar la eficiencia de los cálculos.


2. Transformación en una ley de distribución normal

Una de las tareas más importantes de la transformación Box-Cox es la reducción de la ley de distribución de la serie de entrada a una forma "normal". Vamos a intentar encontrar cómo puede resolverse esta cuestión con la ayuda de esta transformación.

Para evitar cualquier distracción y repetición innecesaria usaremos el algoritmo de búsqueda del mínimo de la función por el método de Powell. Este algoritmo fue descrito en los artículos "Predicción de series de tiempo mediante el uso del ajuste exponencial" y Predicción de series de tiempo mediante el uso del ajuste exponencial (continuación)".

Debemos crear una clase CBoxCox para la búsqueda del valor óptimo del parámetro de la transformación. En esta clase obtendremos la función de probabilidad como objetivo número uno. La clase PowellsMethod [4], [5] se utiliza como clase básica para obtener directamente el algoritmo de búsqueda.

//+------------------------------------------------------------------+
//|                                                      CBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| CBoxCox class                                                    |
//+------------------------------------------------------------------+
class CBoxCox:public PowellsMethod
  {
protected:
   double            Dat[];          // Input data
   double            BCDat[];        // Box-Cox data
   int               Dlen;          // Data size
   double            Par[1];         // Parameters
   double            LnX;            // ln(x) sum
public:
   void   CBoxCox(void) { }
   void              CalcPar(double &dat[]);
   double GetPar(int n) { return(Par[n]); }
private:
   virtual double    func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CBoxCox::CalcPar(double &dat[])
  {
   int i;
   double a;
   //--- Lambda initial value
   Par[0]=1.0;                
   Dlen=ArraySize(dat);
   ArrayResize(Dat,Dlen);
   ArrayResize(BCDat,Dlen);
   LnX=0;
   for(i=0;i<Dlen;i++)
     {
    //--- input data
      a=dat[i]; Dat[i]=a;
     //--- ln(x) sum
     LnX+=MathLog(a);        
     }
    //--- Powell optimization
    Optimize(Par);            
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CBoxCox::func(const double &p[])
  {
   int i;
   double a,lamb,var,mean,k,ret;

   lamb=p[0]; var=0; mean=0; k=0;
   if(lamb>5.0){k=(lamb-5.0)*400; lamb=5.0;}         // Lambda >  5.0
   else if(lamb<-5.0){k=-(lamb+5.0)*400; lamb=-5.0;} // Lambda < -5.0

   //--- Lambda != 0.0
   if(lamb!=0)                                     
     {
      for(i=0;i<Dlen;i++)
        {
          //--- Box-Cox transformation
         BCDat[i]=(MathPow(Dat[i],lamb)-1.0)/lamb;  
          //--- average value calculation
         mean+=BCDat[i]/Dlen;
        }
     }
    //--- Lambda == 0.0
    else                                            
     {
      for(i=0;i<Dlen;i++)
        {
          //--- Box-Cox transformation
         BCDat[i]=MathLog(Dat[i]);
          //--- average value calculation
         mean+=BCDat[i]/Dlen;
        }
     }
   for(i=0;i<Dlen;i++)
     {
      a=BCDat[i]-mean;
       //--- variance
      var+=a*a/Dlen;
     }
   //--- log-likelihood
   ret=Dlen*MathLog(var)/2.0-(lamb-1)*LnX;         
   return(k+ret);
  }
//------------------------------------------------------------------------------------

Ahora, todo lo que tenemos que hacer para encontrar el valor óptimo del parámetro lambda es hacer referencia al método CalcPar de la clase mencionada proporcionándole el enlace a la matriz que contiene los datos de entrada. Podemos obtener el valor óptimo del parámetro haciendo referencia al método GetPar. Como se ha mencionado anteriormente, los datos de entrada deben ser positivos.

La clase PowellsMethod implementa el algoritmo de búsqueda del mínimo de la función de muchas variables, pero en nuestro caso solo se optimiza un único parámetro. Esto conduce al hecho de que la dimensión de la matriz sea igual a uno. Significa que la matriz contiene un solo valor. En teoría, podemos usar una variable estándar en lugar de la matriz de parámetros en este caso, aunque esto requeriría implementar cambios en el código de la clase básica PowellsMethod. Lo más probable es que no surjan problemas si compilamos el código fuente de MQL5 utilizando matrices con solo un elemento.

Debemos tener en cuenta el hecho de que la función CBoxCox::func() contiene una limitación del rango de los valores admisibles del parámetro lambda. En nuestro caso, este rango se limita a los valores de -5 a 5. Esto se hace para evitar obtener valores demasiado grandes o demasiado pequeños al elevar los datos de entrada al grado lambda.

Además, si obtenemos valores de lambda demasiado grandes o demasiado pequeños durante la optimización, esto puede indicar que la serie es de poca utilidad para el tipo de transformación seleccionada. Por tanto, sería una buena idea en cualquier caso no excederse de un rango razonable a la hora de calcular el valor lambda.


3. Series aleatorias

Vamos a escribir un script de prueba que realizará la transformación de Box-Cox de la serie seudoaleatoria que hemos creado usando la clase CBoxCox.

A continuación se muestra el código fuente del script al que nos referimos.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest1.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- data size
   n=1600;
//--- input array preparation
   ArrayResize(dat,n);
//--- transformed data array
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- random sequence generation
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Exp();

//--- input data shift
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- optimization by lambda  
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- input data
//--- bcdat[] <-- transformed data
  }
//-----------------------------------------------------------------------------------

En dicho script se usa una serie seudoaletoria con una ley de distribución exponencial como datos transformados. La longitud de la serie se establece en la variable n y es igual a 1.600 valores en este caso.

Se utiliza la clase RNDXor128 (George Marsaglia, Xorshift RNG) para la generación de una serie seudoaleatoria. Esta clase fue descrita en el artículo "Análisis de las principales características de las series de tiempo" [6]. Todos los archivos necesarios para la compilación del script BoxCoxTest1.mq5 se encuentran en el archivo Box-Cox-Tranformation_MQL5.zip. Esto archivos deben ubicarse en un directorio para su correcta compilación.

Cuando se ejecuta el script mostrado anteriormente, se crea la serie de entrada, se desplaza al área de los valores positivos y se lleva a cabo la búsqueda del valor óptimo del parámetro lambda. A continuación se muestran en pantalla en mensaje con el valor de lambda obtenido y el número de las pasadas del algoritmo de búsqueda. Como resultado, se creará la serie transformada en la matriz de salida bcdat[].

En su forma actual, este script permite solo preparar la serie transformada para su posterior uso y no lleva incorporado ningún cambio. Al escribir este artículo se seleccionó el tipo de análisis descrito en el artículo "Análisis de las principales características de las series de tiempo" [6] para la evaluación de los resultados de la transformación. Los scripts utilizados no se muestran en este artículo para reducir el volumen del código publicado. A continuación solo se muestran los resultados gráficos del análisis realizado.

La Figura 2 muestra el histograma y el gráfico proporcionados por la escala de distribución normal para la serie seudoaleatoria con una ley de distribución exponencial en el script BoxCoxTest1.mq5. La prueba de Jarque-Bera da como resultado JB=3.241,73 y p=0,000. Como podemos ver, la serie de entrada no es normal en absoluto y, tal y como era de esperar, su distribución es similar a la exponencial.

Fig. 2.

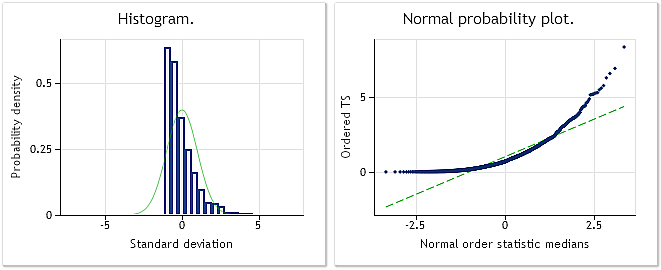
Fig. 2. Serie seudoaleatoria con una ley de distribución exponencial. La prueba de Jarque-Bera da como resultado JB=3.241,73 y p=0,000.

 Fig. 3.

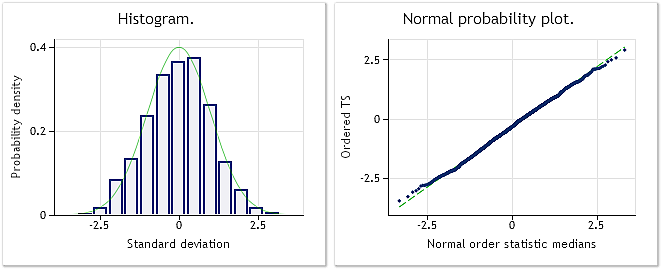
Fig. 3. Serie transformada. Parámetro lambda=0,2779 y la prueba de Jarque-Bera da como resultado JB=4,73 y p=0,094.

La Figura 3 muestra el resultado del análisis de la serie transformada (script BoxCoxTest1.mq5, matriz bcdat[]). La ley de distribución de la serie transformada está mucho más cerca de la norma, lo que también se confirma a partir los resultados de la prueba de Jarque-Bera JB=4.73, р=0.094. El valor del parámetro lambda obtenido es 0,2779.

La transformación Box-Cox ha demostrado ser lo suficientemente adecuada en este ejemplo. Parece que la serie resultante se aproxima mucho más a la normal y que el resultado de la prueba de Jarque-Bera ha disminuido de JB=3.241,73 to JB=4,73. Estos resultados no son una sorpresa ya que la serie elegida se ajusta bastante bien a este tipo de transformación.

Vamos a examinar otro ejemplo de transformación Box-Cox de la serie seudoaleatoria. Debemos crear una serie de entrada "adecuada" para la transformación de Box-Cox teniendo en cuenta su naturaleza de ley exponencial. Para conseguir esto necesitamos generar una serie seudoaleatoria (que ya tenga una ley de distribución cercana a la normal) y luego modificarla elevando todos sus valores a la potencia 0,35. Podemos esperar que la transformación de Box-Cox devuelva la distribución normal original a la serie de entrada con gran precisión.

A continuación se muestra el código fuente del script de texto BoxCoxTest2.mq5 al que nos referimos.

Este script difiere del previo solo en el hecho de que en el mismo se genera otra serie de entrada.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest2.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- data size
   n=1600;
//--- input data array
   ArrayResize(dat,n);
//--- transformed data array
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- random sequence generation
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Norm();

//--- input data shift
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;
   for(i=0;i<n;i++)dat[i]=MathPow(dat[i],0.35);

//--- optimization by lambda
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);

   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0) { for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;   }
   else          { for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);  }     // Lambda == 0.0

//-- dat[]   <-- input data
//-- bcdat[] <-- transformed data
  }
//-----------------------------------------------------------------------------------

La serie seudoaleatoria de entrada con la ley de distribución normal se genera en el script mostrado. Se cambia al área de valores positivos y luego todos los elementos de esta serie se elevan a la potencia 0,35. Después de completar la operación del script, la matriz dat[] contiene la serie de entrada, mientras que la matriz bcdat[] contiene la transformada.

La Figura 4 muestra las características de la serie de entrada que ha perdido su distribución normal debido a la elevación a la potencia 0,35. En dicho caso, la prueba de Jarque-Bera da como resultado JB=3.609,29, p= 0,000.

Fig. 4.

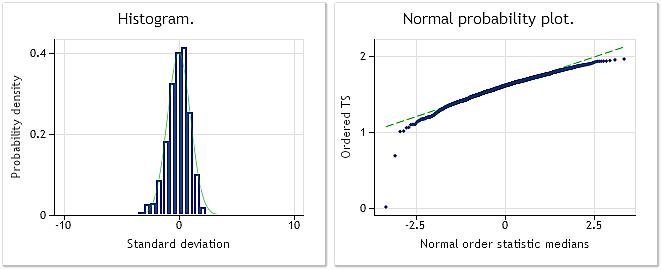
Fig. 4. Serie seudoaleatoria de entrada. La prueba de Jarque-Bera da como resultado JB=3.609,29 y p=0,000.

Fig. 5.

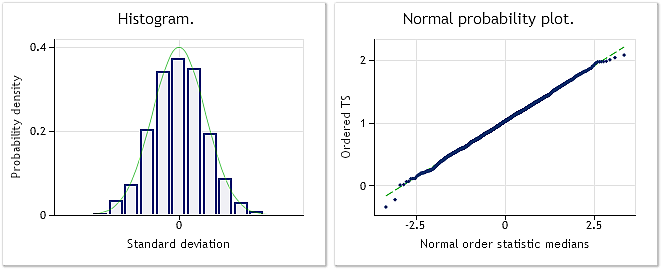
Fig. 5. Serie transformada. Parámetro lambda=2,9067 y la prueba de Jarque-Bera da como resultado JB=0,30 y p=0,859.

Como se muestra en la Figura 5, la serie transformada tiene una ley de distribución lo suficientemente cercana a la normal, lo que se confirma también por los resultados de la prueba de Jarque-Bera JB=0,30 y p=0,859.

Estos ejemplos de uso de la transformación Box-Cox han dado muy buenos resultados. Pero no debemos olvidar que en ambos casos hemos trabajado con series que eran las más adecuadas para este tipo de transformación. Por tanto, estos resultados pueden considerarse simplemente como una confirmación del funcionamiento del algoritmo que hemos creado.


4. Cotizaciones

Después de confirmar el funcionamiento normal del algoritmo que implementa la transformación Box-Cox debemos intentar aplicarlo a las cotizaciones Forex reales, ya que queremos ajustarlas a una ley de distribución normal.

Usaremos como cotizaciones de prueba las series descritas en el artículo "Predicción de series de tiempo usando el ajuste exponencial (continuación)"[5]. Se encuentran en el directorio \Dataset2 del archivo Box-Cox-Tranformation_MQL5.zip y proporcionan cotizaciones reales, 1.200 valores guardados en los archivos correspondientes. La carpeta extraída \Dataset2 debe ubicarse en el directorio \MQL5\Files del terminal para proporcionar acceso a estos archivos.

Vamos a asumir que estas cotizaciones no son series estacionarias. Por tanto, no ampliaremos los resultados del análisis a la población general, sino que solo los consideraremos como características de esta serie de longitud finita.

Además, debe mencionarse de nuevo que si no hay estacionariedad, cada fragmento de cotización distinto para el mismo par seguirá un ley de distribución muy distinta.

Vamos a crear un script que permita leer valores de la serie de un archivo y realizar una transformación Box-Cox. Solo se diferenciará de los scripts de prueba anteriores en la forma de creación de la serie de entrada. A continuación se muestra el código fuente de dicho script mientras que el script BoxCoxTest3.mq5 se sitúa en el archivo adjunto.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest3.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
CBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
   string fname;
//--- input data file
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- data reading
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- data size
   n=ArraySize(dat);
//--- transformed data array
   ArrayResize(bcdat,n);

//--- input data array
   min=dat[ArrayMinimum(dat)]-1e-5;
   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- lambda parameter optimization
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- input data
//--- bcdat[] <-- transformed data
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//-----------------------------------------------------------------------------------

Todos los valores (hay 1.200 en nuestro caso) se importan a la matriz dat[] en este script a partir del archivo de cotizaciones cuyo nombre se establece en la variable fname. Más adelante, se realiza el cambio de la serie inicial, la búsqueda del valor del parámetro óptimo y la transformación Box-Cox en forma descrita anteriormente. Después de la ejecución del script el resultado de la transformación se ubica en la matriz bcdat[].

Como puede verse en el código fuente mostrado, se ha elegido en el script para la transformación la serie de cotizaciones EURUSD M1. El resultado del análisis de la serie original y transformada se muestra en las figuras 6 y 7.

Fig. 6.

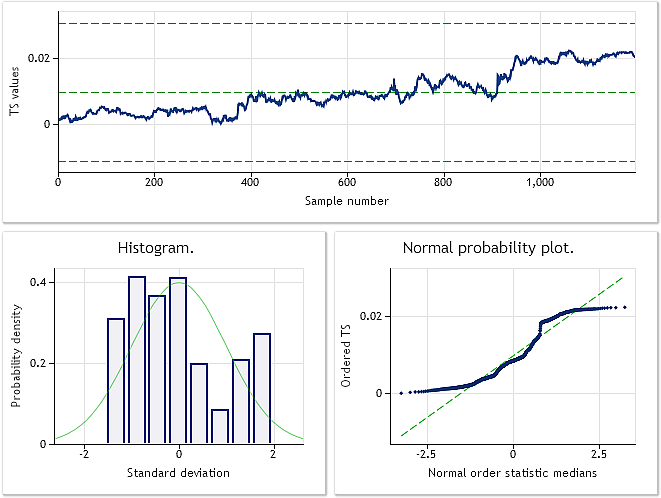
Fig. 6. Serie de entrada EURUSD M1. La prueba de Jarque-Bera da como resultado JB=100,94 y p=0,000.

Fig. 7.

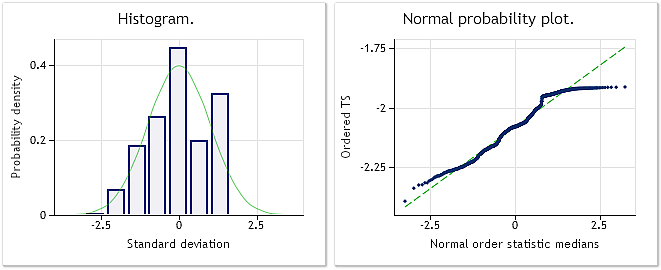
Fig. 7. Serie transformada. Parámetro lambda=0,4146 y la prueba de Jarque-Bera da como resultado JB=39,30 y p=0,000.

Según las características mostradas en la Figura 7, el resultado de la transformación de las cotizaciones EURUSD M1 no es tan impresionante como los resultados de la transformación de las series seudoaleatorias mostrado anteriormente. La transformación Box-Cox no es capaz de hacer frente a todos los tipos de series de entrada, aunque se considera lo suficientemente universal. Por ejemplo, es imposible esperar que la transformación de la ley exponencial convierta la distribución con dos máximos en una normal.

Aunque la ley de distribución mostrada en la Figura 7 no puede ser fácilmente considerada como normal, aún podemos apreciar un considerable descenso de los valores de la prueba de Jarque-Bera como en los ejemplos anteriores. Mientras que JB=100,94 para la serie original, después de la transformación muestra un valor de JB=39,30. Esto significa que la ley de distribución ha logrado acercarse a los valores normales hasta cierto punto después de la transformación.

Cuando se transformaron varios fragmentos de otras cotizaciones se obtuvieron, aproximadamente, los mismos resultados. En todos los casos la transformación Box-Cox llevó la ley de distribución cerca de la normal en mayor o menor medida. Sin embargo, nunca llegó a ser normal.

Una serie de experimentos con diferentes transformaciones en las cotizaciones permiten sacar una conclusión muy esperada: la transformación Box-Cox permite llevar la ley de distribución de las cotizaciones Forex cerca de la normal, aunque no garantiza alcanzar una auténtica normalidad de la ley de distribución de los datos transformados.

¿Es razonable realizar una transformación que no es capaz de ajustar la serie original a una normal? No hay una respuesta definitiva a esta pregunta. En cada caso específico debemos tomar una decisión individual en relación a la necesidad de la transformación Box-Cox. En este caso dependerá mucho del tipo de métodos paramétricos usados en el análisis de las cotizaciones y la sensibilidad del estos métodos a la desviación de los datos iniciales de la ley de distribución normal.


5. Eliminación de la tendencia

La parte superior de la Figura 6 muestra el gráfico de la serie original EURUSD M1 utilizada en el script BCTransform.mq5. Puede verse fácilmente que su valor se incrementa casi uniformemente en toda la serie. En una primera aproximación podemos concluir que la serie contiene una tendencia lineal. La presencia de dicha "tendencia" sugiere que debemos intentar excluirla antes de realizar las distintas transformaciones y analizar la serie obtenida.

La eliminación de una tendencia de las series de entrada analizadas no debe considerarse en absoluto un método adecuado para todos los casos posibles. Pero supongamos que vamos a analizar la serie mostrada en el Figura 6 para encontrar en ella componentes periódicos (o cíclicos). En este caso, es seguro que podemos eliminar la tendencia lineal de la serie de entrada después de definir los parámetros de la tendencia.

La eliminación de una tendencia lineal no afectará a la eliminación de los componentes periódicos. Incluso puede ser útil y hacer que los resultados de dicho análisis sean más precisos o fiables hasta cierto grado, según el método de análisis elegido.

Si hemos decidido que la eliminación de la tendencia puede ser útil en algunos casos, es probable que tenga sentido examinar cómo se comporta una transformación Box-Cox con una serie después de excluir una tendencia de esta.

En cualquier caso, al eliminar una tendencia tendremos que decidir qué curva debe utilizarse para el ajuste de la tendencia. Puede ser una línea recta, curvas de orden mayor, medias móviles, etc. En este caso, vamos a elegir, si es posible, la versión extrema para no distraernos por la elección de la curva óptima. Usaremos los incrementos de la serie original, es decir, las diferencias entre sus valores actuales y previos, en lugar de la propia secuencia original.

Cuando trabajamos con el análisis de incrementos, es imposible no hacer comentarios sobre algunos puntos relacionados con dicha cuestión.

En varios artículos y foros, la necesidad de transición al análisis de incrementos se justifica de tal forma que puede dar una impresión equivocada sobre las propiedades de dicha transición. La transición al análisis de incrementos se describe a menudo como un tipo de transformación capaz de convertir una serie original en una estacionaria o normalizar su ley de distribución. Pero ¿es esto cierto? Vamos a intentar responder a esta pregunta.

Debemos partir del hecho de que la esencia de la transición al análisis de incrementos consta de la simple idea de dividir una serie original en dos componentes. Podemos demostrar esto de la siguiente forma.

Asumimos que tenemos la serie de entrada.

Y que hemos decidido dividirla por las razones que sean en una tendencia y en algunos elementos más que aparecieron después de sustraer los valores de la tendencia de los elementos de la serie original. Supongamos que hemos decidido utilizar una simple media móvil con un periodo de ajuste igual a dos elementos de la serie para una aproximación de la tendencia.

Dicha media móvil puede calcularse como la suma de dos elementos de la serie adyacentes dividida por dos. En tal caso, el residuo resultante de sustraer el promedio de la serie original será igual a la diferencia entre los mismos elementos adyacentes dividida por dos.

Vamos a denominar al valor del promedio anterior S, mientras que el residuo será D. Si desplazamos el factor permanente 2 al lado izquierdo de la ecuación para mayor claridad, obtendremos lo siguiente:


Después de completar nuestras simples transformaciones, hemos dividido nuestra serie original en dos componentes, uno de los cuales es la suma de los valores de las series adyacentes y el otro comprende las diferencias. Estas son, exactamente, las series a las que llamamos incrementos, mientras que las sumas constituyen la tendencia.

A este respecto, sería más razonable considerar los incrementos como parte de la serie original. Por tanto, no debemos olvidar que si cambiamos al análisis de incrementos la otra parte de la serie definida por las sumas es a menudo simplemente obviada, a menos que no las analicemos separadamente, por supuesto.

La forma más sencilla de hacernos una idea de qué clase de beneficios podemos obtener con esta división de la serie, es aplicar el método espectral.

Podemos deducir, directamente de las expresiones anteriores, que el componente S es el resultado del filtrado de la serie original usando el filtro de menor frecuencia con el impulso h=1,1. Por consiguiente, el componente D es el resultado del filtrado mediante un filtro de alta frecuencia con un impulso h=-1,1. La Figura 8 muestra las características de frecuencia de dichos filtros.

Fig. 8.

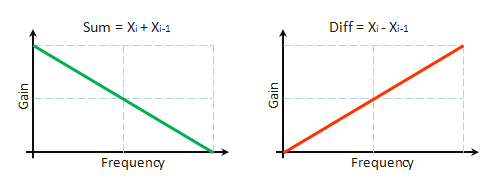
Fig. 8. Características de amplitud-frecuencia

Supongamos que hemos ido del análisis directo de la propia serie al análisis de sus diferencias. ¿Qué podemos esperar aquí? Hay varias opciones en este caso. Veremos brevemente tan solo algunas de ellas.

  1. En caso de que la energía básica del proceso analizado se concentre en la región de baja frecuencia de la serie original, la transición al análisis de las diferencias suprimirá esa energía, haciendo que seguir con el análisis sea más complejo o incluso imposible.
  2. En caso de que la energía básica del proceso analizado se concentre en la región de alta frecuencia de la serie original, la transición al análisis de las diferencias puede provocar efectos debido al filtrado de los componentes de baja frecuencia que interfieren. Pero esto solo es posible si dicha filtración no afecta demasiado a las propiedades del proceso analizado;
  3. También es posible mencionar el caso en el que la energía del proceso analizado se distribuye uniformemente sobre todo el rango de frecuencia de la serie. En dicho caso modificaremos de forma irreversible el proceso después de la transición al análisis de sus diferencias suprimiendo su parte de baja frecuencia.

De forma similar, podemos sacar conclusiones sobre los resultados de la transición hacia el análisis de las diferencias para cualquier otra combinación de tendencias, tendencia a corto plazo, ruido de interferencia y demás. Pero en cualquier caso, la transición hacia el análisis de las diferencias no conducirá a una forma estacionaria del proceso analizado y no normalizará el proceso de distribución.

Según lo dicho anteriormente, podemos concluir que una serie no "mejora" automáticamente después de la transición al análisis de diferencias. Podemos asumir que, en algunos casos, es mejor analizar la serie de entrada y las diferencias junto con las sumas de sus valores adyacentes para conocer con mayor claridad la serie de entrada, mientras que las conclusiones finales sobre las propiedades de esta serie deben obtenerse en base a la revisión conjunta de todos los resultados obtenidos.

Vamos a volver al tema de nuestro artículo y vamos a ver cómo se comporta la transformación Box-Cox en caso de transición al análisis de incrementos de la serie EURUSD M1 mostrada en la Fig. 6. Para hacer esto, usaremos el script mostrado anteriormente en el que vamos a reemplazar los valores de la serie con las diferencias (incrementos) después de tener en cuenta estos valores de la serie a partir del archivo. Como no se han implementado ningún cambio adicional al código fuente del script, no hay razón para publicarlo. En lugar de ello, mostraremos los resultados del análisis de su funcionamiento.

Incrementos de EURUSD M1. La prueba de Jarque-Bera da como resultado JB=32.494,8 y p=0,000.

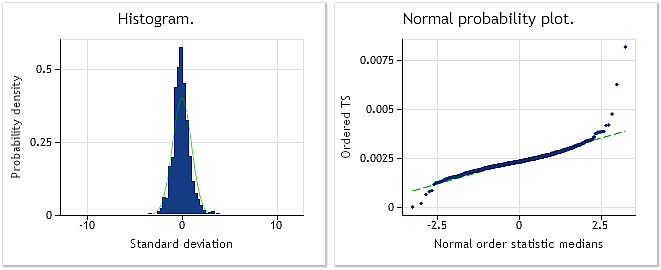
Fig. 9. Incrementos de EURUSD M1. La prueba de Jarque-Bera da como resultado JB=32.494,8 y p=0,000.

Fig. 10. Serie transformada. Parámetro lambda=0,6662 y la prueba de Jarque-Bera da como resultado JB=10.302,5 y p=0,000.

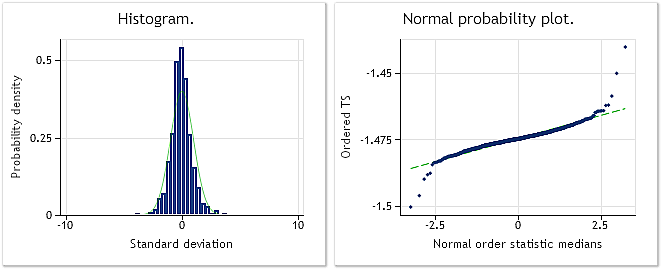
Fig. 10. Serie transformada. Parámetro lambda=0,6662 y la prueba de Jarque-Bera da como resultado JB=10.302,5 y p=0,000.

La Fig. 9 muestra las características de la serie que consta de EURUSD M1 incrementos (diferencias), mientras que la Fig. 10 muestra sus características obtenidas después de la transformación Box-Cox. A pesar del que el valor de la prueba de Jarque-Bera ha disminuido más de tres veces desde JB = 32.494,8 hasta JB = 10.302,5 después de la transformación, la ley de distribución de la serie transformada está aún lejos de la normal.

Sin embargo, no debemos sacar conclusiones prematuras y pensar que la transformación Box-Cox no puede hacer frente a la transformación de los incrementos adecuadamente. Hemos considerado solo un caso especial. Al trabajar con otras series de entrada podemos obtener resultados completamente distintos.


6. Ejemplos citados

Todos los ejemplos de la transformación Box-Cox citados anteriormente están relacionados con el caso en el que la ley de distribución de la serie original se considera reducida a una normal o, quizás, a una ley tan cercana a la normal como sea posible. Como se ha mencionado al principio, dicha transformación puede ser necesaria al utilizar los métodos de análisis paramétricos que pueden ser muy sensitivos a la desviación de la normal de una ley de distribución de la serie en cuestión.

Los ejemplos que hemos visto han mostrado que en todos los casos después de la transformación, de acuerdo con los resultados de la prueba de Jarque-Bera, hemos recibido realmente series con una ley de distribución más cercana a la norma al compararlas con las series originales. Este hecho muestra claramente la versatilidad y eficiencia de la transformación Box-Cox.

Pero no debemos sobreestimar las posibilidades de la transformación Box-Cox y asumir que cualquier serie de entrada puede transformarse estrictamente en una normal. Como puede verse en los ejemplos anteriores, esto está muy lejos de ser cierto. Ni la serie original ni la transformada pueden considerarse normales para las cotizaciones reales.

La transformación Box-Cox se ha considerado hasta ahora, solo en su forma más visual y con un parámetro. Esto se ha hecho así para simplificar el primer trabajo con ella. Este enfoque se justifica para demostrar las capacidades de esta transformación, aunque por razones prácticas sería probablemente mejor utilizar una forma más general en su presentación.


7. Forma general de la transformación Box-Cox

Debe recordarse que la transformación Box-Cox solo es aplicable a las series con valores positivos o cero. En la práctica, este requisito se satisface con facilidad con un simple cambio de una serie al área positiva, pero el tamaño del cambio dentro de dicha área puede afectar directamente al resultado de la transformación.

Por tanto, el valor de cambio puede considerarse un parámetro adicional de la transformación y se puede optimizar junto con el parámetro lambda, sin permitir que los valores de la serie entren en el área negativa.

Para la serie original X de longitud N:

las expresiones que determinan una forma más general de la transformación Box-Cox de dos parámetros son las siguientes:

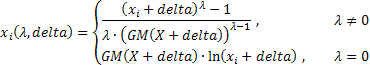
donde:

;

GM() - media geométrica.

La media geométrica de la serie puede calcularse de la siguiente forma:

Como podemos ver, los dos parámetros ya se utilizan en las expresiones mostradas: lambda y delta. Ahora, tenemos que optimizar estos parámetros simultáneamente durante la transformación. A pesar de la ligera complicación del algoritmo, la introducción de un parámetro adicional puede incrementar ciertamente la eficiencia de la transformación. Además, han aparecido factores de normalización adicionales en las expresiones, si se compara con la transformación anterior. Con estos factores, el resultado de la transformación conserva su dimensión durante la modificación del parámetro lambda.

Puede consultarse más información sobre la transformación Box-Cox en [7] y [8]. En [8] se describen brevemente algunas transformaciones adicionales del mismo tipo.

Estas son las características principales de la transformación actual, más general:

  1. La propia transformación requiere que la serie de entrada contenga solo valores positivos. La inclusión de parámetros delta adicionales permite realizar automáticamente el cambio necesario de la serie al cumplir algunas condiciones concretas;
  2. Al seleccionar el valor óptimo del parámetro delta, su magnitud debe garantizar la "positividad" de todos los valores de la serie;
  3. La transformación es continua en caso de que la alteración del parámetro lambda incluya cambios cercanos a su valor cero;
  4. El resultado de la transformación conserva su dimensión en caso de modificación del valor del parámetro lambda.

Se utilizó el criterio del logaritmo de la función de probabilidad en todos los ejemplos citados anteriormente al buscar el valor óptimo del parámetro lambda. Por supuesto, esta no es la única forma de estimar el valor óptimo de los parámetros de la transformación.

Como ejemplo, podemos mencionar el método de la optimización de parámetros en el que se busca el valor máximo del coeficiente de correlación entre una serie transformada ordenada de forma ascendente y una serie cuantiles de la función de distribución normal. Esta variante ha sido mencionada con anterioridad en el artículo. Los valores de los cuantiles de la función de distribución normal pueden calcularse según las expresiones recomendadas por James J. Filliben [9].

Las expresiones que determinan la forma general de la transformación de dos parámetros son en realidad más farragosas que las consideradas anteriormente. Quizás sea esa la razón de que este tipo de transformación se utilice muy raramente en los paquetes matemáticos y estadísticos. Las expresiones mencionadas se han elaborado en MQL5 para poder utilizar la transformación Box-Cox en una forma más general si es necesario.

El archivo CFullBoxCox.mqh contiene el código fuente de la clase CFullBoxCox que realiza la búsqueda del valor óptimo de los parámetros de la transformación. Como se ha mencionado anteriormente, el proceso de optimización se basa en el cálculo del coeficiente de correlación.

//+------------------------------------------------------------------+
//|                                                  CFullBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+

#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| CFullBoxCox class                                                |
//+------------------------------------------------------------------+
class CFullBoxCox:public PowellsMethod
  {
protected:
  int    Dlen;                     // data size
  double Dat[];                    // input data array
  double Shift[];                  // input data array with the shift
  double BCDat[];                  // transformed data (Box-Cox)
  double Mean;                     // transformed data average value
  double Cdf[];                    // Quantile of the distribution cumulative function
  double Scdf;                     // Square root of summ of Quantile^2
  double R;                        // correlation coefficient 
  double DeltaMin;                 // Delta minimum value
  double DeltaMax;                 // Delta maximum value
  double Par[2];                   // parameters array
public:
  void   CFullBoxCox(void)       { }
  void   CalcPar(double &dat[]);
  double GetPar(int n)           { return(Par[n]); }
private:
  double ndtri(double y0);         // the function opposite to the normal distribution function
  virtual double func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CFullBoxCox::CalcPar(double &dat[])
  {
  int i;
  double a,max,min;
  
  Dlen=ArraySize(dat);
  ArrayResize(Dat,Dlen);
  ArrayResize(Shift,Dlen);
  ArrayResize(BCDat,Dlen);
  ArrayResize(Cdf,Dlen);
//--- copy the input data array
  ArrayCopy(Dat,dat);
  
  Scdf=0;
  a=MathPow(0.5,1.0/Dlen);
  Cdf[Dlen-1]=ndtri(a); Scdf+=Cdf[Dlen-1]*Cdf[Dlen-1];
  Cdf[0]=ndtri(1.0-a); Scdf+=Cdf[0]*Cdf[0];
  a=Dlen+0.365;
  for(i=1;i<(Dlen-1);i++)
    {
    //--- calculation of the distribution cumulative function Quantile
    Cdf[i]=ndtri((i+0.6825)/a);
    //--- calculation of the sum of Quantile^2
    Scdf+=Cdf[i]*Cdf[i];
    }

//--- square root of the sum of Quantile^2
  Scdf=MathSqrt(Scdf);             
  
  min=dat[0]; max=min;
  for(i=0;i<Dlen;i++)
    {
//--- copy the input data
    a=dat[i]; Dat[i]=a;
    if(min>a)min=a;
    if(max<a)max=a;
    }
  
//--- Delta minimum value
  DeltaMin=1e-5-min;
//--- Delta maximum value
  DeltaMax=(max-min)*200-min;
//--- Lambda initial value
  Par[0]=1.0;
//--- Delta initial value
  Par[1]=(max-min)/2-min;
//--- optimization using Powell method
  Optimize(Par);             
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CFullBoxCox::func(const double &p[])
  {
  int i;
  double a,b,c,lam,del,k1,k2,gm,gmpow,mean,ret;
  
  lam=p[0]; del=p[1]; k1=0; k2=0;
  if (lam>5.0){k1=(lam-5.0)*400; lam=5.0;}                    // Lambda >  5.0
  else if(lam<-5.0){k1=-(lam+5.0)*400; lam=-5.0;}             // Lambda < -5.0
  if (del>DeltaMax){k2=(del-DeltaMax)*400; del=DeltaMax;}    // Delta > DeltaMax
  else if(del<DeltaMin){k2=(DeltaMin-del)*400; del=DeltaMin; // Delta < DeltaMin
  
  gm=0;
  for(i=0;i<Dlen;i++)
    {
    Shift[i]=Dat[i]+del;
    gm+=MathLog(Shift[i]);
    }

//--- geometric mean
  gm=MathExp(gm/Dlen);
  gmpow=lam*MathPow(gm,lam-1);
  mean=0;
//--- Lambda != 0.0
   if(lam!=0)                                  
    {
    for(i=0;i<Dlen;i++)
      {
      a=(MathPow(Shift[i],lam)-1.0)/gmpow;
       //--- transformed data (Box-Cox)
      BCDat[i]=a;
       //--- average value
      mean+=a;
      }
    }
  //--- Lambda == 0.0
  else                                        
     {
    for(i=0;i<Dlen;i++)
      {
      a=gm*MathLog(Shift[i]);
       //--- transformed data (Box-Cox)
      BCDat[i]=a;
      //--- average value
      mean+=a;
      }
    }
  mean=mean/Dlen;
  //--- sorting of the transformed data array
  ArraySort(BCDat);
  a=0; b=0;
  for(i=0;i<Dlen;i++)
    {
    c=(BCDat[i]-mean);
    a+=Cdf[i]*c;
    b+=c*c;
    }
  //--- correlation coefficient
  ret=a/(Scdf*MathSqrt(b)); 
  return(k1+k2-ret);
  }
//+------------------------------------------------------------------+
//| The function opposite to the normal distribution function        |
//| Prototype:                                                       |
//| Cephes Math Library Release 2.8: June, 2000                      |
//| Copyright 1984, 1987, 1989, 2000 by Stephen L. Moshier           |
//+------------------------------------------------------------------+
double CFullBoxCox::ndtri(double y0)
  {
  static double s2pi =2.50662827463100050242E0; // sqrt(2pi)
  static double P0[5]={-5.99633501014107895267E1,  9.80010754185999661536E1,
                       -5.66762857469070293439E1,  1.39312609387279679503E1,
                       -1.23916583867381258016E0};
  static double Q0[8]={ 1.95448858338141759834E0,  4.67627912898881538453E0,
                        8.63602421390890590575E1, -2.25462687854119370527E2,
                        2.00260212380060660359E2, -8.20372256168333339912E1,
                        1.59056225126211695515E1, -1.18331621121330003142E0};
  static double P1[9]={ 4.05544892305962419923E0,  3.15251094599893866154E1,
                        5.71628192246421288162E1,  4.40805073893200834700E1,
                        1.46849561928858024014E1,  2.18663306850790267539E0,
                       -1.40256079171354495875E-1,-3.50424626827848203418E-2,
                       -8.57456785154685413611E-4};
  static double Q1[8]={ 1.57799883256466749731E1,  4.53907635128879210584E1,
                        4.13172038254672030440E1,  1.50425385692907503408E1,
                        2.50464946208309415979E0, -1.42182922854787788574E-1,
                       -3.80806407691578277194E-2,-9.33259480895457427372E-4};
  static double P2[9]={ 3.23774891776946035970E0,  6.91522889068984211695E0,
                        3.93881025292474443415E0,  1.33303460815807542389E0,
                        2.01485389549179081538E-1, 1.23716634817820021358E-2,
                        3.01581553508235416007E-4, 2.65806974686737550832E-6,
                        6.23974539184983293730E-9};
  static double Q2[8]={ 6.02427039364742014255E0,  3.67983563856160859403E0,
                        1.37702099489081330271E0,  2.16236993594496635890E-1,
                        1.34204006088543189037E-2, 3.28014464682127739104E-4,
                        2.89247864745380683936E-6, 6.79019408009981274425E-9};
  double x,y,z,y2,x0,x1,a,b;
  int i,code;
  if(y0<=0.0){Print("Function ndtri() error!"); return(-DBL_MAX);}
  if(y0>=1.0){Print("Function ndtri() error!"); return(DBL_MAX);}
  code=1; y=y0;
  if(y>(1.0-0.13533528323661269189)){y=1.0-y; code=0;}  // 0.135... = exp(-2)
  if(y>0.13533528323661269189)                         // 0.135... = exp(-2)
    {
    y=y-0.5; 
    y2=y*y;
    a=P0[0]; for(i=1;i<5;i++)a=a*y2+P0[i];
    b=y2+Q0[0]; for(i=1;i<8;i++)b=b*y2+Q0[i];
    x=y+y*(y2*a/b);
    x=x*s2pi; 
    return(x);
    }
  x=MathSqrt(-2.0*MathLog(y));
  x0=x-MathLog(x)/x;
  z=1.0/x;
//--- y > exp(-32) = 1.2664165549e-14
  if(x<8.0)
    {
    a=P1[0]; for(i=1;i<9;i++)a=a*z+P1[i];
    b=z+Q1[0]; for(i=1;i<8;i++)b=b*z+Q1[i];
    x1=z*a/b;
    }
  else
    {
    a=P2[0]; for(i=1;i<9;i++)a=a*z+P2[i];
    b=z+Q2[0]; for(i=1;i<8;i++)b=b*z+Q2[i];
    x1=z*a/b;
    }
  x=x0-x1;
  if(code!=0)x=-x;
  return(x);
  }
//------------------------------------------------------------------------------------

Durante la optimización se aplican algunas limitaciones al rango de alteración de los parámetros de la transformación. El valor del parámetro lambda se limita a los valores 5 y -5. Las limitaciones de los parámetros delta se especifican con relación al valor mínimo de la serie de entrada. Este parámetro se limita por los valores DeltaMin=(0.00001-min) y DeltaMax=(max-min)*200-min, donde min y max son los valores mínimos y máximos de los elementos de la serie de entrada.

El script FullBoxCoxTest.mq5 muestra el uso de la clase CFullBoxCox. El código fuente de este script se muestra más abajo.

//+------------------------------------------------------------------+
//|                                               FullBoxCoxTest.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include  "CFullBoxCox.mqh"
CFullBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],shift[],bcdat[],lambda,delta,gm,gmpow;
   string fname;

//--- input file name
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- reading the data
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- data size
   n=ArraySize(dat);
//--- shifted input data array
   ArrayResize(shift,n);
//--- transformed data array
   ArrayResize(bcdat,n);

//--- lambda and delta parameters optimization
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   delta=Bc.GetPar(1);

   PrintFormat("Iterations= %i,   lambda= %.4f,   delta= %.4f",
               Bc.GetIter(),lambda,delta);
   gm=0;
   for(i=0;i<n;i++)
     {
      shift[i]=dat[i]+delta;
      gm+=MathLog(shift[i]);
     }
//--- geometric mean
   gm=MathExp(gm/n);
   gmpow=lambda*MathPow(gm,lambda-1);
   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(shift[i],lambda)-1.0)/gmpow;}
   else         {for(i=0;i<n;i++)bcdat[i]=gm*MathLog(shift[i]);}
//--- dat[]   <-- input data
//--- shift[] <-- input data with the shift
//--- bcdat[] <-- transformed data
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//------------------------------------------------------------------------------------

La serie de entrada se carga en la matriz dar[] a partir del archivo al principio del script y luego se realiza la búsqueda de los valores óptimos de los parámetros de la transformación. A continuación se realiza la propia transformación usando los parámetros obtenidos. Como resultado, la matriz dat[] contiene la serie original, la matriz shift[] contiene la serie original cambiada por el valor delta y la matriz bcdat[] contiene el resultado de la transformación Box-Cox.

Todos los archivos necesarios para la compilación del script FullBoxCoxTest.mq5 se encuentran en el archivo Box-Cox-Tranformation_MQL5.zip.

La transformación de las series de prueba que usamos se realiza con la ayuda del script FullBoxCoxTest.mq5. Como era de esperar, durante el análisis de los datos obtenidos podemos concluir que este tipo de transformación de dos parámetros da un mejor resultado cuando se compara con el tipo de un parámetro. Por ejemplo, para la serie EURUSD M1, cuyos resultados de los análisis se muestran en la Fig. 6, el valor de la prueba de Jarque-Bera fue JB=100,94. JB=39,30 después de la transformación de un parámetro (ver Fig. 7), pero después de la transformación de dos parámetros (script FullBoxCoxTest.mq5) este valor descendió a JB=37,49.


Conclusión

En este artículo hemos examinado los casos en los que se han optimizado los parámetros de la transformación de Box-Cox de forma que la ley de distribución resultante sea tan cercana a la norma como sea posible. Pero en la práctica, los casos pueden surgir cuando deba usarse la transformación Box-Cox de una forma ligeramente distinta. Por ejemplo, puede usarse el siguiente algoritmo al predecir las series de tiempo:

  1. Se seleccionan los valores preliminares de los parámetros de la transformación Box-Cox y los modelos de predicción;
  2. Se realiza la transformación Box-Cox de los datos de entrada;
  3. Se realiza la predicción según los parámetros actuales;
  4. Se realiza la inversa de la transformación de Box-Cox para los resultados de la predicción;
  5. El error de predicción es evaluado por la serie no transformada de entrada;
  6. Se modifican los valores de los parámetros para minimizar el error de predicción y el algoritmo vuelve al paso 2.

En el algoritmo anterior, los parámetros de la transformación y los del modelo de predicción deben ser minimizados por el criterio mínimo del error de predicción. En este caso, el objetivo de la transformación Box-Cox ya no es la transformación de la serie de entrada en una ley de distribución normal.

Ahora es necesario transformar la serie de entrada para recibir la ley de distribución con el error de predicción mínimo. Dependiendo del método de predicción seleccionado, esta ley de distribución no tiene por qué ser necesariamente la normal.

La transformación Box-Cox solo es aplicable a las series con valores positivos o distintos a cero. El cambio de la serie de entrada debe realizarse en todos los demás casos. Esta característica de la transformación puede considerarse en realidad uno de sus inconvenientes. Pero a pesar de esto, la transformación Box-Cox es probablemente la herramienta más versátil y eficiente entre las todas las de este tipo.


Bibliografía

  1. А.N. Porunov. Box-Сox Transformation and the Illusion of «Normality» of Macroeconomic Series. "Business Informatics" journal, №2(12)-2010, pp. 3-10.
  2. Mohammad Zakir Hossain, The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses. Journal of Emerging Trends in Economics and Management Sciences (JETEMS) 2(1):32-39.
  3. Box-Cox Transformations.
  4. The article "Time Series Forecasting Using Exponential Smoothing".
  5. The article "Time Series Forecasting Using Exponential Smoothing (continued)".
  6. Analysis of the Main Characteristics of Time Series.
  7. Power transform.
  8. Draper N.R. and H. Smith, Applied Regression Analysis, 3rd ed., 1998, John Wiley & Sons, New York.
  9. Q-Q plot.

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/363

Archivos adjuntos |
Descargar ZIP
box-cox-transformation_mql5.zip (91.48 KB)
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
Estimación de la densidad del kernel de la función de densidad de probabilidad desconocida Estimación de la densidad del kernel de la función de densidad de probabilidad desconocida
Este artículo trata sobre la creación de un programa en el que se permite la estimación de la densidad del kernel de la función de densidad de probabilidad desconocida. Se ha elegido el método de estimación de la densidad del kernel para realizar la tarea. El artículo contiene códigos fuente de la implementación del software del método y ejemplos de su uso e ilustraciones.
Análisis de regresión múltiple, generador y probador de estrategias en una sola aplicación Análisis de regresión múltiple, generador y probador de estrategias en una sola aplicación
El artículo ofrece una descripción de las formas de utilización del análisis de regresión múltiple para el desarrollo de sistemas de trading. Muestra el uso del análisis de regresión para la automatización de la búsqueda de estrategias. Se proporciona como ejemplo una ecuación de regresión generada e integrada en un asesor experto sin necesidad de disponer de habilidades de programación.
Aplicación del método de coordenadas de Eigen al análisis estructural de distribuciones estadísticas no extensivas Aplicación del método de coordenadas de Eigen al análisis estructural de distribuciones estadísticas no extensivas
El mayor problema de la estadística aplicada es la aceptación de hipótesis estadísticas. Durante mucho tiempo se consideró un problema imposible de resolver. La situación cambió con la aparición del método de las coordenadas de Eigen. Es una refinada y potente herramienta para el estudio estructural de una señal, permitiendo ver más de lo que es posible utilizando métodos de la estadística moderna aplicada. El artículo se centra en la utilización práctica de este método y plantea distintos programas en MQL5. También trata sobre el problema de la identificación de la función usando como ejemplo la distribución de Hilhorst y Schehr.
MQL5-RPC. Llamadas a procedimientos remotos desde MQL5: acceso al servicio web y analizador XML-RPC ATC para divertirse y conseguir beneficios MQL5-RPC. Llamadas a procedimientos remotos desde MQL5: acceso al servicio web y analizador XML-RPC ATC para divertirse y conseguir beneficios
Este artículo describe el esquema conceptual de MQL5-RPC que permite las llamadas a procedimientos remotos desde MQL5. Comienza con los fundamentos de XML-RPC, la implementación de MQL5 y continúa con dos ejemplos de uso real. El primer ejemplo es el uso de un servicio web externo y el segundo es un cliente del servicio del analizador XML-RPC ATC 2011 simple. Si está interesado en conocer cómo se implementan y analizan las distintas estadísticas de ATC 2011 en tiempo real, este es su artículo.