박스-칵스(Box-Cox) 변환
1 339
0
개요
컴퓨터의 기능이 점점 발달하면서 외환 투자자와 분석가들은 상당한 계산 리소스를 필요로 하는, 보다 복잡하고 섬세한 알고리즘을 이용할 수 있게 되었습니다. 하지만 계산 리소스가 크다고 해서 투자자가 겪는 문제가 해결되는 건 아니죠. 시장 가격을 분석하는 효과적인 알고리즘이 필요합니다.
현재 통계학, 경제학 및 계량 경제학 등을 적용한 다양한 메소드, 모델 그리고 아주 효과적으로 작동하는 알고리즘이 시장 분석에 널리 사용되고 있습니다. 대부분의 경우 시퀀스의 안정성과 그 분포의 정규성을 추정해 생성된 모수 통계를 기반으로 하죠.
하지만 여러분도 아시다시피 외환 시세는 안정적이라거나 정규 분포를 따른다고는 할 수 없는 시퀀스들입니다. 따라서 시세 분석 시에 '표준' 모수 통계를 이용할 수 없죠.
'Box-Cox Transformation and the Illusion of Macroeconomic Series "Normality' [1]에서 A.N. Porunov은 다음과 같이 이야기합니다.
"경제학자들은 정상성 테스트를 통과하지 못하는 통계 자료를 상대해야 할 때가 있다. 이 경우 두 가지 선택지가 있는데, 하나는 꽤 높은 수학적 지식이 요구되는 비모수 통계를 이용하는 것이고, 또 하나는 기존의 '비정상적인 통계'를 '정상적'인 자료로 바꾸어 주는 꽤 복잡한 특수 테크닉을 이용하는 것이다."
Porunov가 경제학자들에 대해 이야기하고 있긴 하지만 이는 모수 통계와 계량 경제학을 이용해 '비정상적인' 외환 시세를 분석하려는 시도에도 적용됩니다. 대부분이 정규 분포를 따르는 시퀀스 분석을 위해 개발되었죠. 초기 데이터가 '비정상성'을 띤다는 사실은 반영되지 않은 겁니다. 게다가 위의 방법들은 초기 시퀀스가 정규 분포를 따라야할 뿐 아니라 시퀀스의 안정성을 요구합니다.
회귀 분석, 분산 분석(ANOVA)을 포함하는 몇 가지 분석법이 초기 데이터의 정상성을 필요로 하는 '표준' 분석법에 포함됩니다. 정규 분포와 정상성에 관한 한계점을 갖는 모수 통계법 전체를 다룰 수는 없습니다. 비모수 통계를 제외한 계량 경제학 전체가 이에 해당하니까요.
'표준' 모수 통계는 초기 데이터의 편차 값에 대한 민감도 자체가 다릅니다. 따라서 '정상성'으로부터의 편차가 획득 결과의 정확도나 안정성을 증가시키지 않죠.
이 때문에 시세 분석 및 예측에 비모수 통계를 적용하게 된 겁니다. 물론 모수 통계는 그 장점이 많습니다. 알고리즘, 적용 예제 등 모수 통계와 관련된 자료의 양만 봐도 알 수 있죠. 해당 자료를 잘 이용하려면 초기 시퀀스의 불안정성과 '비정상성'을 해결해야 하는데요.
초기 시퀀스의 안정성을 바꿀 수는 없지만 분포를 정규 분포에 가깝게 만들 수는 있습니다. 다양한 변환법을 이용해 이 문제를 해결할 수 있는데요. 'The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses' [2]에 가장 잘 알려진 방법들이 소개되어 있습니다. 본문에서는 박스-칵스 변환 [1], [2], [3]에 대해서만 알아볼 겁니다.
다시 한번 강조하지만 박스-칵스 변환은 초기 시퀀스 분포를 정규 분포에 가깝게 만드는 것 뿐입니다. 결과 시퀀스가 정규 분포를 따를 것이라는 보장은 없는 거죠.
1. 박스-칵스(Box-Cox) 변환
길이가 N인 초기 시퀀스 X에 대한
1개 매개 변수 박스-칵스 변환은 다음과 같습니다.
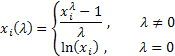
읽는 법
해당 변환은 단 하나의 매개 변수인 '람다'를 갖습니다. 람다 값이 0인 경우 초기 시퀀스에 대한 로그 변형이 실행되며 람다 값이 0이 아닌 경우 멱법칙을 따릅니다. 람다 변수가 1인 경우, 초기 시퀀스가 이동하여도 그 분포는 그대로 유지됩니다.
람다 값에 따라 박스-칵스 변환은 다음의 경우를 포함할 수 있습니다.
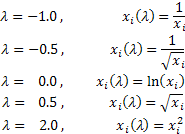
박스-칵스 변환을 적용하려면 모든 시퀀스 값이 0이 아닌 양수여야 합니다. 인풋 시퀀스가 위의 조건을 충족하지 못하는 경우 시퀀스 값이 모두 0이 아닌 양수가 되도록 이동해도 됩니다.
적절한 인풋 데이터를 갖는 1개 매개 변수 박스-칵스 변환을 살펴보겠습니다. 인풋 데이터 내 0 또는 음수 값을 피하기 위해 시퀀스의 각 엘리먼트에서 인풋 시퀀스의 가장 작은 값만큼을 빼고 1e-5에 해당하는 시프트를 실행합니다. 해당 시프트는 시퀀스의 가장 작은 값이 0일 경우 모든 값이 양수가 되도록 이동할 수 있게 합니다.
사실 이런 식의 시프트를 반드시 적용할 필요는 없습니다. 하지만 변형 과정에서 과도하게 큰 수치를 얻을 확률을 낮추기 위해 동일한 알고리즘을 사용하겠습니다. 따라서 모든 인풋 시퀀스는 이동 후 양수 값을 갖게 되며 0에 가까운 최소값을 가질 것입니다.
그림 1은 다양한 람다 변수가 적용된 박스-칵스 변환 곡선입니다. 그림 1은 'Box-Cox Transformations' [3]에서 발췌했습니다. 차트의 수평 그리드는 로그 눈금을 따릅니다.
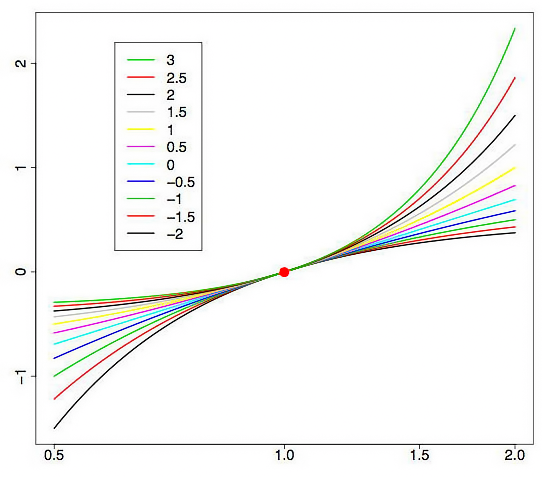
그림 1. 람다 매개 변수에 따른 박스-칵스 변환
초기 분포의 '꼬리'가 길어지거나 짧아집니다. 그림 1의 상위 곡선은 람다 값이 3인 경우, 하위 곡선은 람다 값이 -2인 경우입니다.
결과 시퀀스의 분포를 최대한 정규 분포와 가깝게 만들기 위해 최적의 람다 변수 값을 선택해야 하는데요.
함수 알고리즘의 가능도를 최대화해 최적 값을 구할 수 있습니다.
읽는 법
함수가 최대값을 갖는 람다 변수를 선택해야 합니다.
'Box-Cox Transformations' [3]에는 정규 분포 함수의 사분위수와 변환된 정렬 시퀀스 간의 가장 큰 상관 계수를 기반으로 최적 변수를 구하는 방법을 다룹니다. 또 다른 방법도 있겠지만 우선은 위에서 언급한 알고리즘 가능도를 최대화하는 방법을 찾아보죠.
여러 방법이 있는데요. 예를 들어, 단순 탐색을 할 수 있습니다.. 선택된 범위 내에서 람다 변수 값을 낮은 피치로 변경해 가며 함수 값의 가능도를 계산합니다. 함수의 가능도가 가장 높은 값을 갖는 람다 변수가 최적 변수입니다.
피치의 거리가 람다 변수 최적 값 계산의 정확도를 판단합니다. 피치가 낮을수록 정확도가 높습니다만 정확도가 높을 수록 더 많은 계산이 필요합니다. 함수의 최대값 및 최소값을 구하는 알고리즘이나 유전 알고리즘 등을 이용해 계산의 효율성을 증대시킬 수 있습니다.
2. 정규 분포로의 변환
박스-칵스 변환의 가장 중요한 포인트 중 하나는 인풋 시퀀스의 분포를 '정상적'으로 만드는 것이죠. 해당 변환법을 이용한 결과를 보겠습니다.
불필요한 반복을 피하기 위해 Powell의 방법을 이용해 함수 최소값을 구하겠습니다. 해당 알고리즘은 '지수 평활화를 이용한 시계열 예측' 및 '지수 평활화를 이용한 시계열 예측(계속)'에서 설명한 바 있습니다..
변형 변수의 최적값을 구하기 위해 CBoxCox 클래스를 생성합니다. 해당 클래스에서는 위에서 언급된 가능도 함수가 목적 함수로 실현됩니다. PowellsMethod 클래스 [4], [5]를 이용해 탐색 알고리즘을 곧바로 실행합니다.
//+------------------------------------------------------------------+ //| CBoxCox.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //+------------------------------------------------------------------+ //| CBoxCox class | //+------------------------------------------------------------------+ class CBoxCox:public PowellsMethod { protected: double Dat[]; // Input data double BCDat[]; // Box-Cox data int Dlen; // Data size double Par[1]; // Parameters double LnX; // ln(x) sum public: void CBoxCox(void) { } void CalcPar(double &dat[]); double GetPar(int n) { return(Par[n]); } private: virtual double func(const double &p[]); }; //+------------------------------------------------------------------+ //| CalcPar | //+------------------------------------------------------------------+ void CBoxCox::CalcPar(double &dat[]) { int i; double a; //--- Lambda initial value Par[0]=1.0; Dlen=ArraySize(dat); ArrayResize(Dat,Dlen); ArrayResize(BCDat,Dlen); LnX=0; for(i=0;i<Dlen;i++) { //--- input data a=dat[i]; Dat[i]=a; //--- ln(x) sum LnX+=MathLog(a); } //--- Powell optimization Optimize(Par); } //+------------------------------------------------------------------+ //| func | //+------------------------------------------------------------------+ double CBoxCox::func(const double &p[]) { int i; double a,lamb,var,mean,k,ret; lamb=p[0]; var=0; mean=0; k=0; if(lamb>5.0){k=(lamb-5.0)*400; lamb=5.0;} // Lambda > 5.0 else if(lamb<-5.0){k=-(lamb+5.0)*400; lamb=-5.0;} // Lambda < -5.0 //--- Lambda != 0.0 if(lamb!=0) { for(i=0;i<Dlen;i++) { //--- Box-Cox transformation BCDat[i]=(MathPow(Dat[i],lamb)-1.0)/lamb; //--- average value calculation mean+=BCDat[i]/Dlen; } } //--- Lambda == 0.0 else { for(i=0;i<Dlen;i++) { //--- Box-Cox transformation BCDat[i]=MathLog(Dat[i]); //--- average value calculation mean+=BCDat[i]/Dlen; } } for(i=0;i<Dlen;i++) { a=BCDat[i]-mean; //--- variance var+=a*a/Dlen; } //--- log-likelihood ret=Dlen*MathLog(var)/2.0-(lamb-1)*LnX; return(k+ret); } //------------------------------------------------------------------------------------
이제 클래스의 CalcPar 메소드를 참조하면 람다 변수 최적 값을 구할 수 있습니다. 해당 메소드에 인풋 데이터가 포함된 배열의 링크를 입력합니다. GetPar 메소드를 참조해 결과 값을 구합니다. 인풋 데이터가 양수 값을 가져야 한다는 걸 기억하세요.
PowellsMethod 클래스는 많은 변수를 갖는 함수에 대한 최소값 탐색 알고리즘을 구현하지만 우리의 경우 1개 변수만이 최적화됩니다. 따라서 Par[] 배열이 일차원 배열이 되죠. 배열이 한 개 값만을 포함함을 의미합니다. 이론상 변수 배열 대신 표준 변수를 이용할 수도 있지만 이 경우 PowellsMethod 클래스 코드에 대한 수정이 필요합니다. 한 개의 엘리먼트를 포함하는 배열을 이용해 MQL5 소스 코드를 컴파일 하는 경우 아무런 문제가 없을 겁니다.
CBoxCox::func() 함수가 람다 변수가 가질 수 있는 값의 범위에 제한을 둔다는 것에 주의해야 합니다. 우리의 경우 해당 범위는 -5와 5 사이가 되죠. 이는 인풋 데이터를 람다 값에 맞출 때 너무 크거나 너무 작은 값이 나오지 않도록 하기 위함입니다.
최적화 과정에서 너무 크거나 너무 작은 람다 값이 나오는 경우 해당 변형 방법에 선택된 시퀀스가 맞지 않음을 의미합니다. 따라서 람다 값을 구할 때에는 일정한 범위를 벗어나지 않는 것이 좋습니다.
3. 랜덤 시퀀스
CBoxCox 클래스로 형성된 유사 랜덤 시퀀스에 대한 박스-칵스 변환을 수행할 테스트 스크립트를 작성하겠습니다.
아래는 해당 스크립트의 소스 코드입니다.
//+------------------------------------------------------------------+ //| BoxCoxTest1.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CBoxCox.mqh" #include "RNDXor128.mqh" CBoxCox Bc; RNDXor128 Rnd; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],bcdat[],lambda,min; //--- data size n=1600; //--- input array preparation ArrayResize(dat,n); //--- transformed data array ArrayResize(bcdat,n); Rnd.Reset(); //--- random sequence generation for(i=0;i<n;i++)dat[i]=Rnd.Rand_Exp(); //--- input data shift min=dat[ArrayMinimum(dat)]-1e-5; for(i=0;i<n;i++)dat[i]=dat[i]-min; //--- optimization by lambda Bc.CalcPar(dat); lambda=Bc.GetPar(0); PrintFormat("Iterations= %i, lambda= %.4f",Bc.GetIter(),lambda); if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;} else {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);} // Lambda == 0.0 //--- dat[] <-- input data //--- bcdat[] <-- transformed data } //-----------------------------------------------------------------------------------
지수 분포를 따르는 유사 랜덤 시퀀스가 인풋 변환 데이터로 사용되었습니다. 시퀀스의 길이는 n 변수로 설정되며 이 경우 그 값은 1600입니다.
RNDXor128 클래스(George Marsaglia, Xorshift RNG)를 이용해 유사 랜덤 시퀀스를 생성합니다. 해당 클래스는 '시간열 주요 특성 분석' [6]에서 언급된 바 있습니다. BoxCoxTest1.mq5 스크립트를 컴파일하는 데에 필요한 모든 파일은 Box-Cox-Tranformation_MQL5.zip 아카이브에 포함되어 있습니다. 컴파일 완료를 위해서는 모든 파일이 동일한 디렉토리에 위치해야 합니다.
해당 스크립트가 실행되면 인풋 시퀀스가 형성되어 양수 값을 갖는 범위로 이동되며 람다 변수 최적 값 탐색이 시작됩니다. 탐색 알고리즘 실행 횟수와 획득된 람다 값이 포함된 메세지가 나타납니다. 변환된 시퀀스는 bcdat[] 아웃풋 배열에 저장됩니다.
해당 스크립트는 변형된 시퀀스를 다른 연산에 이용할 수 있게 만들며 다른 수정 사항을 구현하지는 않습니다. '시간열 주요 특성 분석' [6]의 분석 방식이 본문의 변형 결과 평가에 사용되었습니다. 코드의 양을 줄이기 위해 평가에 이용된 코드는 본문에 포함하지 않았습니다. 아래는 분석 결과 그래픽입니다.
그림 2는 BoxCoxTest1.mq5 스크립트에서 사용된 지수 분포를 따르는 유사 랜덤 시퀀스에 정규 분포 스케일을 적용한 차트와 히스토그램입니다. 자크-베라 검정 결과: JB=3241.73, p= 0.000. 보시다시피 인풋 시퀀스는 전혀 '정상적'이지 않으며 지수 분포에 가까운 분포르 따르고 있죠.
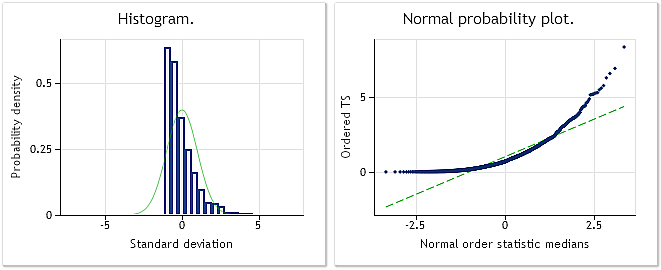
그림 2. 지수 분포를 따르는 유사 랜덤 시퀀스 자크-베라 검정 결과: JB=3241.73, р=0.000.
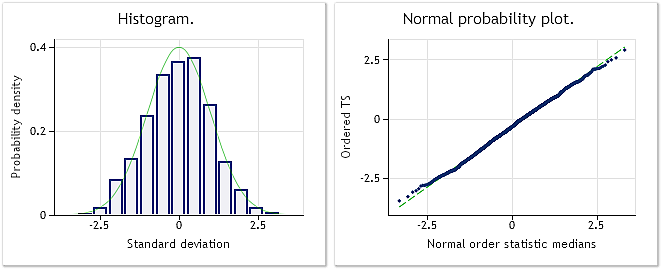
그림 3. 변환된 시퀀스 람다 변수=0.2779, 자크-베라 검정 결과: JB=4.73, р=0.094
그림 3은 변환된 시퀀스 분석 결과입니다(BoxCoxTest1.mq5 스크립트, bcdat[] 배열). 변환된 시퀀스는 정규 분포에 훨씬 가까운 분포를 따르며 자크-베라 검정 결과 또한 JB=4.73, p=0.094로 이를 뒷받침합니다. 획득된 람다 변수 값은 0.2779입니다.
박스-칵스 변환의 사용이 적절했네요. 결과 시퀀스가 '정상적인' 분포에 훨씬 가까워졌고 자크-베라 검정 결과 또한 JB=3241.73에서 JB=4.73으로 감소했습니다. 해당 변환에 알맞는 시퀀스를 선택했으니 놀랄 일은 아닙니다.
유사 랜덤 시퀀스를 적용한 박스-칵스 변환의 또 다른 예를 살펴보겠습니다. 멱법칙을 고려해 박스-칵스 변환에 '맞는' 인풋 시퀀스를 생성해야 합니다. 이미 정상 분포에 가까운 분포를 띠는 유사 랜덤 시퀀스를 생성해 모든 시퀀스 값에 0.35를 곱해 왜곡 변환을 하겠습니다. 박스-칵스 변환을 적용하면 해당 시퀀스가 정상 분포를 따르는 기존 시퀀스로 돌아갈 것이라는 걸 예측할 수 있죠.
다음은 BoxCoxTest2.mq5 스크립트의 소스 코드입니다.
이전 스크립트와 다른 점은 새로운 인풋 시퀀스가 생성되었다는 점 한 가지입니다.
//+------------------------------------------------------------------+ //| BoxCoxTest2.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CBoxCox.mqh" #include "RNDXor128.mqh" CBoxCox Bc; RNDXor128 Rnd; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],bcdat[],lambda,min; //--- data size n=1600; //--- input data array ArrayResize(dat,n); //--- transformed data array ArrayResize(bcdat,n); Rnd.Reset(); //--- random sequence generation for(i=0;i<n;i++)dat[i]=Rnd.Rand_Norm(); //--- input data shift min=dat[ArrayMinimum(dat)]-1e-5; for(i=0;i<n;i++)dat[i]=dat[i]-min; for(i=0;i<n;i++)dat[i]=MathPow(dat[i],0.35); //--- optimization by lambda Bc.CalcPar(dat); lambda=Bc.GetPar(0); PrintFormat("Iterations= %i, lambda= %.4f",Bc.GetIter(),lambda); if(lambda!=0) { for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda; } else { for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]); } // Lambda == 0.0 //-- dat[] <-- input data //-- bcdat[] <-- transformed data } //-----------------------------------------------------------------------------------
해당 스크립트에는 정규 분포를 따르는 유사 랜덤 시퀀스가 생성되었죠. 양수 값을 갖도록 이동되었으며 시퀀스의 모든 엘리먼트에 0.35가 곱해졌습니다. 스크립트를 실행하고 나면 dat[] 배열에 인풋 시퀀스가, bcdat[] 배열에 변형된 시퀀스가 저장됩니다.
그림 4은 각 값에 0.35가 곱해져 기존의 정상 분포를 더이상 따르지 않는 인풋 시퀀스의 특성을 나타냅니다. 이 경우 자크-베라 검정 결과 JB=3609.29, p= 0.000입니다.
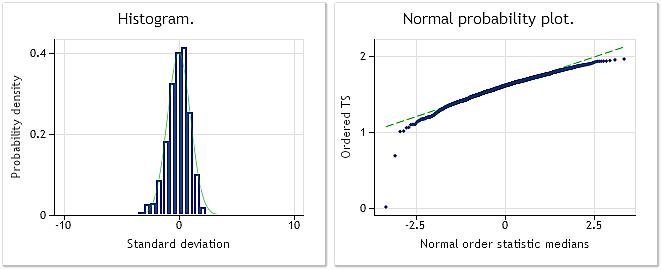
그림. 4. 인풋 유사 랜덤 시퀀스 자크-베라 검정 결과: JB=3609.29, p=0.000.
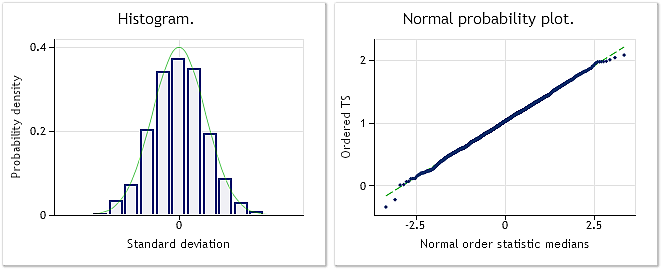
그림 5. 변환된 시퀀스 람다 변수=2.9067, 자크 베라 검정 결과: JB=0.30, p=0.859
그림 5에서 확인할 수 있듯 변환된 시퀀스는 정상에 가까운 분포를 따르며 자크-베라 검정 결과 또한 JB=0.30, p=0.859로 이를 뒷받침합니다.
박스-칵스 변환이 적용된 위의 예제들은 굉장히 좋은 결과를 낳았네요. 하지만 이는 우리가 변환에 적절한 시퀀스를 이용했기 때문입니다. 따라서 위의 결과는 우리가 생성한 알고리즘의 성능을 확인한 것이라 볼 수 있겠습니다.
4. 시세
이제 알고리즘의 성능을 확인했으니 실제 외환 시세에 적용해 보겠습니다.
'지수 평활화를 이용한 시계열 예측(계속)' [5]의 시퀀스를 테스트 시세로 적용하겠습니다. Box-Cox-Tranformation_MQL5.zip 아카이브의 /Dataset2 폴더에 저장되어 있으며 1200개의 실제 시세를 포함합니다. Extracted \Dataset2 폴더를 터미널의 \MQL5\Files 디렉토리에 저장해야 시세 파일에 액세스할 수 있습니다.
해당 시세들이 정상 시퀀스가 아니라고 가정하겠습니다. 따라서 분석 결과는 모집단에 적용되지 않으며 해당 특정 시퀀스의 특징으로 간주합니다.
또한, 정상성을 띠지 않는 경우 동일 통화쌍의 서로 다른 시세 프래그먼트는 굉장히 다른 분포 법칙을 따릅니다.
시퀀스 값을 읽어 들이고 박스-칵스 변환을 실행하는 스크립트를 작성해 보죠. 위의 테스트 스크립트와는 인풋 시퀀스 생성 방법만 상이합니다. 아래는 해당 스크립트의 소스 코드이며 BoxCoxTest3.mq5 스크립트는 본문 하단에 첨부되어 있습니다.
//+------------------------------------------------------------------+ //| BoxCoxTest3.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CBoxCox.mqh" CBoxCox Bc; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],bcdat[],lambda,min; string fname; //--- input data file fname="Dataset2\\EURUSD_M1_1200.txt"; //--- data reading if(readCSV(fname,dat)<0){Print("Error."); return;} //--- data size n=ArraySize(dat); //--- transformed data array ArrayResize(bcdat,n); //--- input data array min=dat[ArrayMinimum(dat)]-1e-5; for(i=0;i<n;i++)dat[i]=dat[i]-min; //--- lambda parameter optimization Bc.CalcPar(dat); lambda=Bc.GetPar(0); PrintFormat("Iterations= %i, lambda= %.4f",Bc.GetIter(),lambda); if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;} else {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);} // Lambda == 0.0 //--- dat[] <-- input data //--- bcdat[] <-- transformed data } //+------------------------------------------------------------------+ //| readCSV | //+------------------------------------------------------------------+ int readCSV(string fnam,double &dat[]) { int n,asize,fhand; fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI); if(fhand==INVALID_HANDLE) { Print("FileOpen Error!"); return(-1); } asize=512; ArrayResize(dat,asize); n=0; while(FileIsEnding(fhand)!=true) { dat[n++]=FileReadNumber(fhand); if(n+128>asize) { asize+=128; ArrayResize(dat,asize); } } FileClose(fhand); ArrayResize(dat,n-1); return(0); } //-----------------------------------------------------------------------------------
fname 변수로 지정된 파일 내 전체 값을 dat[] 배열로 불러오기합니다. 앞서 설명한 대로 초기 시퀀스 이동, 최적 매개 변수 탐색 및 박스-칵스 변환이 실행됩니다. 스크립트가 실행되면 변환 결과가 bcdat[] 배열에 저장됩니다.
소스 코드에서 확인할 수 있듯이 EURUSD M1 시세가 변환에 이용되었습니다. 그림 6과 7은 초기 시퀀스와 변환 시퀀스의 분석 결과입니다.
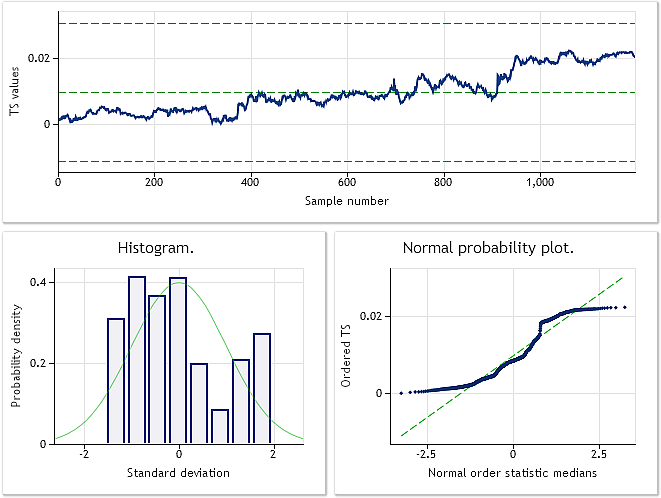
그림 6. EURUSD M1 인풋 시퀀스 자크-바라 검정 결과: JB=100.94, p=0.000.
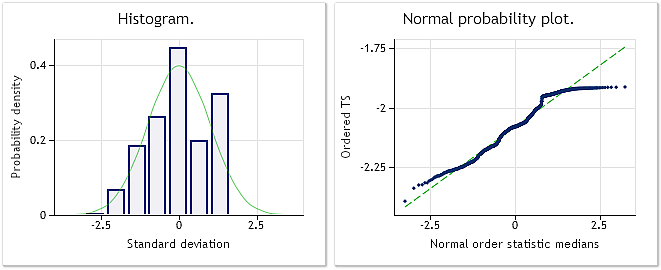
그림 7. 변환된 시퀀스 람다 변수=0.4146, 자크-바라 검정 결과: JB=39.30, p=0.000
그림 7을 보니 EURUSD M1 시세 변환 결과는 앞서 실행한 유사 랜덤 시퀀스 변환 결과를 따라가지 못하네요. 박스-칵스 변환이 꽤 보편적으로 활용되기는 하지만 모든 인풋 시퀀스에 적용되는 것은 아닙니다. 예를 들어 멱법칙 변환을 통해 두 개의 꼭지점을 갖는 분포를 정규 분포로 바꿀 수는 없겠죠.
그림 7에서 나타난 분포는 정규 분포와는 거리가 멀지만 이전 변환 결과와 동일하게 자크-베라 검정 결과 값이 상당히 감소했음을 알 수 있습니다. 초기 시퀀스의 경우 JB=100.94인 반면 변환 후에는 JB=39.30이 됐네요. 분포가 변환을 통해 어느 정도 정규 분포에 가까워졌음을 의미합니다.
다른 시세의 다른 프래그먼트를 변환했을 때도 거의 동일한 결과가 나왔습니다. 박스-칵스 변환이 프래그먼트 분포를 어느 정도 정규 분포에 가깝게 만들었죠. 하지만 완전히 정규 분포가 된 경우는 없었습니다.
여러 시세를 적용한 변환 실험 결과, 박스-칵스 변환은 외환 시세 분포 형태를 정상 분포에 가깝게 만들지만 완전한 정규 분포로 만들지는 못한다는 결론을 내릴 수 있습니다.
초기 시퀀스를 정상화시킬 수 없는데도 변환을 하는 것이 맞을까요? 여기에는 정해진 답이 없습니다. 박스-칵스 변환이 필요한지에 대해서는 각 케이스 별로 여러분이 판단을 내려야 합니다. 이 경우 시세 분석에 적용된 모수 통계법과 해당 방법의 초기 데이터의 분산에 대한 민감도에 큰 영향을 받게 됩니다.
5. 추세 제거
그림 6의 상단에 BCTransform.mq5 스크립트에서 이용된 EURUSD M1 초기 시퀀스 차트가 나타나 있습니다. 시퀀스를 따라 거의 균일하게 그 값이 증가함을 알 수 있죠. 1차 추정 후 시퀀스가 선형 추세를 포함하다는 걸 알 수 있습니다. 이러한 '추세'의 존재는 변형 실행을 통한 시퀀스 분석 이전에 추세를 제거해야함을 의미하는데요.
분석된 인풋 시퀀스에 대한 추세 제거는 절대로 모든 케이스에 적합한 방법이 아닙니다. 그림 6에 나타난 시퀀스를 분석해 주기적인 컴포넌트를 구한다고 가정하겠습니다. 이 경우 추세 매개 변수를 설정한 후 인풋 시퀀스에서 선형 추세를 제거할 수 있죠.
선형 추세 제거가 주기적인 컴포넌트 탐색에 영향을 미치지 않으니까요. 선택된 분석 방법에 따라 추세를 제거하면 분석 결과가 더 정확해질 수도 있습니다.
추세가 제거된 시퀀스에 박스-칵스 변환이 어떻게 적용되는지 보겠습니다.
추세 제거에 앞서 반드시 추세 추정 곡선을 결정해야 합니다. 직선이거나, 곡선이거나, 이동 평균일 수도 있죠. 어떤 곡선이 최적인지 판단하는 문제를 피하기 위해 조금은 극단적인 케이스를 적용하겠습니다. 초기 시퀀스 대신 초기 시퀀스의 증분을 이용할 겁니다.
증분 분석에 대해 짚고 넘어갈 사항이 있는데요.
포럼의 여러 글을 읽어 보면 증분 분석의 특징을 간과하는 경우가 많더라고요. 증분 분석이 그저 초기 시퀀스를 정상화하거나 정규 분포화하는 데에 사용되는 변환인 것처럼 설명된 경우가 많았습니다. 정말일까요? 같이 알아보죠.
증분 분석은 초기 시퀀스를 두 개의 컴포넌트로 분리하는 것에서 시작합니다. 설명해 볼게요.
다음과 같은 초기 시퀀스가 있다고 가정합니다.
해당 시퀀스를 추세와 기초 시퀀스 엘리먼트에서 추세 값을 제거한 나머지 엘리먼트로 나눕니다. 평활화 기간이 두 개의 시퀀스 엘리먼트에 해당하는 이동 평균을 이용한다고 가정합니다.
해당 이동 평균은 두 개의 인접한 시퀀스 엘리먼트를 더한 값을 2로 나누어 구해집니다. 이 경우 초기 시퀀스에서 평균 값을 제거하고 남은 잔차가 인접한 엘리먼트를 2로 나눈 값의 차이와 동일할 겁니다.
위의 평균 값을 S로, 잔차를 D로 규정합니다. 불변수 2를 방정식 좌측으로 옮겨 명확성을 높이면 다음의 결과가 나옵니다.
변환을 완료하면 초기 시퀀스가 두 개의 컴포넌트로 나뉘며 하나는 인접한 시퀀스 값의 합을, 다른 하나는 값의 차이를 포함합니다. 이 두 시퀀스가 바로 증분이라는 것이죠. 그 합은 추세를 형성합니다.
이렇게 보면 증분을 초기 시퀀스의 일부로 보는 게 더 합당해 보입니다. 따라서 증분 분석 시 합으로 나타나는 시퀀스의 나머지 부분이 고려되지 않는다는 것을 기억해야 합니다.
스펙트럼 방법을 적용해 보면 시퀀스를 나누는 것의 이점이 무엇인지 알 수 있습니다.
위의 식에서 컴포넌트 S는 h=1.1인 저주파 필터를 이용한 초기 시퀀스 필터링 값임을 알 수 있습니다.. 컴포넌트 D는 h=-1.1인 고주파 필터를 이용한 초기 시퀀스 필터링 값이죠. 그림 8은 위 필터의 주파수 특성을 나타냅니다.
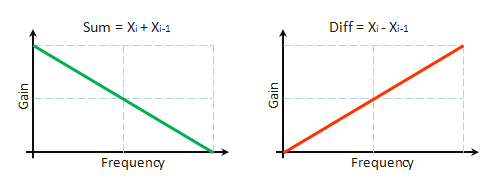
그림 8. 진폭-주파수 특징
시퀀스를 직접 분석하지 않고 그 차이를 분석하기로 했다고 합시다. 어떤 결과가 나올까요? 여러 옵션이 있는데요. 몇 가지만 살펴보도록 하죠.
- 분석 결과 에너지가 초기 시퀀스의 저주파 영역으로 몰리는 경우 증분 분석은 해당 에너지를 억압해 분석을 더 복잡하거나 불가능하게 만들 뿐입니다.
- 분석 결과 에너지가 초기 시퀀스의 고주파 영역으로 몰리는 경우 증분 분석은 방해가 되는 저주파 컴포넌트를 필터링해 긍정적인 효과를 낳을 수 있습니다. 하지만 필터링이 분석 결과의 특성에 크게 영향을 끼치지 않는 경우에만 적용 가능하죠.
- 분석 결과 에너지가 시퀀스 주파 범위에 골고루 분포되는 경우도 있습니다. 이 경우 저주파 영역을 제거해 증분 분석 결과를 왜곡합니다.
여러 추세가 결합된 경우, 단기 추세가 나타나는 경우, 방해가 되는 노이즈가 있는 경우 등도 같은 결과를 갖게 됩니다. 하지만 증분 분석이 초기 시퀀스를 정상화 시키는 것은 아니며 분포를 정규화하지도 않습니다.
따라서 증분 분석 이후 시퀀스가 자동으로 '개선된다'고 할 수는 없겠습니다. 인풋 시퀀스와 증분을 이웃하는 값의 합과 함께 분석해야 하는 경우도 있고, 모든 획득 값을 기반으로 시퀀스의 특성을 판단해야 하는 경우도 있죠.
EURUSD M1 시퀀스를 이용해 박스-칵스 변환에 증분 분석을 적용하면 어떻게 되는지 살펴보죠(그림 6). BoxCoxTest3.mq5 스크립트를 이용해 시퀀스 값을 구한 후 해당 값을 증분으로 대체합니다. 다른 수정 사항은 없으므로 따로 살펴보지는 않겠습니다. 분석 결과를 함께 보죠.
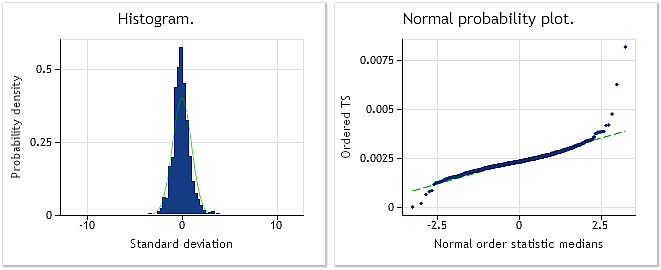
그림 9. EURUSD M1 증분 자크-베라 검정 결과: JB=32494.8, p=0.000
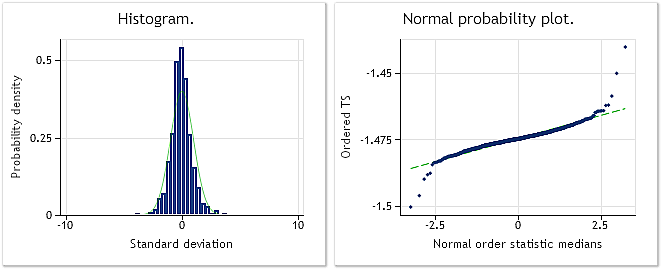
그림 10. 변환된 시퀀스 람다 변수=0.6662, 자크-베라 검정 결과 JB=10302.5, p=0.000
그림 9 EURUSD M1 증분(차이)로 구성된 시퀀스의 특징을, 그림 10은 박스-칵스 변환 후의 특징을 나타냅니다. 자크-베라 검정 결과가 JB=32494.8에서 JB=10302.5로 세 배 이상 감소했음에도 변환된 시퀀스의 분포는 정규 분포와는 거리가 멀죠.
그렇다고 해서 박스-칵스 변환이 증분에 적용될 수 없다는 성급한 결론을 내려서는 안됩니다. 하나의 특수 케이스만 알아본 거니까요. 다른 인풋 시퀀스를 이용하면 완전히 다른 결과가 나올지도 모릅니다.
6. 인용 예시
위에서 언급된 박스-칵스 변환의 예시는 초기 시퀀스 분포를 정상화하거나 최대한 정규 분포에 가까운 분포를 따르도록 해야 하는 경우입니다. 초기 데이터 편차 값에 대해 꽤 민감한 모수 통계를 이용할 때 필요하다고 말씀드린 바 있죠.
모든 변환 예시에서 자크-베라 검정 결과가 실제로 초기 시퀀스 분포가 변환 후 정규 분포에 좀 더 가까워진다는 것을 증명했습니다. 박스-칵스 변환이 얼마나 유용하고 효율적인지 알 수 있죠.
하지만 모든 인풋 시퀀스가 변환 후 정상성을 띤다고 판단해서는 안됩니다. 위에서 보셨듯이 전혀 그렇지 않죠. 실제 시세의 경우 초기 시퀀스나 변환 시퀀스 모두 정상성을 띤다고 할 수 없습니다.
박스-칵스 변환은 주로 1개 매개 변수 형식으로만 적용되었습니다. 처음 접하는 분들의 이해를 돕기 위해서죠. 실제 사용에는 보다 일반적인 형식을 적용하는 것이 좋을 겁니다.
7. 박스-칵스 변환 일반형
박스-칵스 변환은 0이 아닌 양수 값을 갖는 시퀀스에만 적용 가능합니다. 실제 적용 시 시퀀스를 이동하면 되지만 양수 범위 내 이동 크기가 변형 결과에 영향을 미칠 수 있습니다.
따라서 시프트 값을 추가 변형 매개 변수로 간주하여 람다 변수와 함께 최적화해야 합니다.
길이가 N인 초기 시퀀스 X에 대한
2개 매개 변수 박스-칵스 변환 일반형을 결정하는 방정식은 다음과 같습니다.
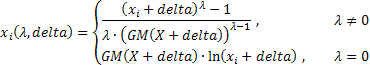
읽는 법
;
GM()-기하 평균
시퀀스의 기하 평균은 다음의 방법으로 계산합니다.
람다와 델타 변수가 보이네요. 이제 변환을 통해 동시에 두 변수를 최적화합니다. 알고리즘이 약간 복잡해지긴 하지만 추가 변수를 포함하면 변환 효율이 증가합니다. 기존의 변환 방법에 정상화 요인이 추가되었는데요. 추가된 요인들 덕분에 람다 변수가 변해도 변환 결과 배열의 차원이 유지됩니다.
박스-칵스 변환에 대한 더 많은 정보는 참고 자료 [7], [8]을 참고하세요. 동일한 형식의 다른 변환 방법 몇 가지가 [8]에 소개되어 있습니다.
보다 일반적인 변환 형식의 주요 특징은 다음과 같습니다.
- 양수 값을 갖는 인풋 시퀀스만 변환할 수 있습니다. 델타 변수를 추가하면 자동으로 시퀀스 시프팅이 수행됩니다.
- 델타 변수 최적 값 선택 시 반드시 전체 시퀀스가 양수 값을 가져야 합니다.
- 람다 변수가 변화하는 경우 변환은 계속됩니다.
- 람다 변수가 변화하는 경우 변환의 배열 차원은 유지됩니다.
로그 가능도 기준을 이용해 람다 변수 최적 값을 탐색합니다. 물론 변환 변수의 최적 값을 계산하는 다른 방법도 있습니다.
매개 변수 최적화 방법을 예로 들게요. 오름차순으로 분류된 변환 시퀀스와 정규 분포 함수 사분위수 시퀀스 간의 상관 계수의 최대값을 찾습니다. 이 방법은 앞서 언급한 바 있죠. James J. Filliben [9]의 방정식으로 정규 분포 함수의 사분위수를 구할 수 있습니다.
2개 매개 변수 변환 형식을 결정하는 방정식은 훨씬 복잡합니다. 아마 그래서 수리 및 통계 패키지에서 잘 사용되지 않는 것인지도 몰라요. 인용된 방정식은 MQL5로 구현하여 박스-칵스 변형에 사용할 수 있게 했습니다.
CFullBoxCox.mqh 파일에 CFullBoxCox 클래스 소스 코드가 포함되어 있으며 이는 변형 매개 변수의 최적 값을 구하는 데에 쓰입니다. 최적화는 상관 계수 계산을 기반으로 한다고 말씀드렸죠.
//+------------------------------------------------------------------+ //| CFullBoxCox.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //+------------------------------------------------------------------+ //| CFullBoxCox class | //+------------------------------------------------------------------+ class CFullBoxCox:public PowellsMethod { protected: int Dlen; // data size double Dat[]; // input data array double Shift[]; // input data array with the shift double BCDat[]; // transformed data (Box-Cox) double Mean; // transformed data average value double Cdf[]; // Quantile of the distribution cumulative function double Scdf; // Square root of summ of Quantile^2 double R; // correlation coefficient double DeltaMin; // Delta minimum value double DeltaMax; // Delta maximum value double Par[2]; // parameters array public: void CFullBoxCox(void) { } void CalcPar(double &dat[]); double GetPar(int n) { return(Par[n]); } private: double ndtri(double y0); // the function opposite to the normal distribution function virtual double func(const double &p[]); }; //+------------------------------------------------------------------+ //| CalcPar | //+------------------------------------------------------------------+ void CFullBoxCox::CalcPar(double &dat[]) { int i; double a,max,min; Dlen=ArraySize(dat); ArrayResize(Dat,Dlen); ArrayResize(Shift,Dlen); ArrayResize(BCDat,Dlen); ArrayResize(Cdf,Dlen); //--- copy the input data array ArrayCopy(Dat,dat); Scdf=0; a=MathPow(0.5,1.0/Dlen); Cdf[Dlen-1]=ndtri(a); Scdf+=Cdf[Dlen-1]*Cdf[Dlen-1]; Cdf[0]=ndtri(1.0-a); Scdf+=Cdf[0]*Cdf[0]; a=Dlen+0.365; for(i=1;i<(Dlen-1);i++) { //--- calculation of the distribution cumulative function Quantile Cdf[i]=ndtri((i+0.6825)/a); //--- calculation of the sum of Quantile^2 Scdf+=Cdf[i]*Cdf[i]; } //--- square root of the sum of Quantile^2 Scdf=MathSqrt(Scdf); min=dat[0]; max=min; for(i=0;i<Dlen;i++) { //--- copy the input data a=dat[i]; Dat[i]=a; if(min>a)min=a; if(max<a)max=a; } //--- Delta minimum value DeltaMin=1e-5-min; //--- Delta maximum value DeltaMax=(max-min)*200-min; //--- Lambda initial value Par[0]=1.0; //--- Delta initial value Par[1]=(max-min)/2-min; //--- optimization using Powell method Optimize(Par); } //+------------------------------------------------------------------+ //| func | //+------------------------------------------------------------------+ double CFullBoxCox::func(const double &p[]) { int i; double a,b,c,lam,del,k1,k2,gm,gmpow,mean,ret; lam=p[0]; del=p[1]; k1=0; k2=0; if (lam>5.0){k1=(lam-5.0)*400; lam=5.0;} // Lambda > 5.0 else if(lam<-5.0){k1=-(lam+5.0)*400; lam=-5.0;} // Lambda < -5.0 if (del>DeltaMax){k2=(del-DeltaMax)*400; del=DeltaMax;} // Delta > DeltaMax else if(del<DeltaMin){k2=(DeltaMin-del)*400; del=DeltaMin; // Delta < DeltaMin gm=0; for(i=0;i<Dlen;i++) { Shift[i]=Dat[i]+del; gm+=MathLog(Shift[i]); } //--- geometric mean gm=MathExp(gm/Dlen); gmpow=lam*MathPow(gm,lam-1); mean=0; //--- Lambda != 0.0 if(lam!=0) { for(i=0;i<Dlen;i++) { a=(MathPow(Shift[i],lam)-1.0)/gmpow; //--- transformed data (Box-Cox) BCDat[i]=a; //--- average value mean+=a; } } //--- Lambda == 0.0 else { for(i=0;i<Dlen;i++) { a=gm*MathLog(Shift[i]); //--- transformed data (Box-Cox) BCDat[i]=a; //--- average value mean+=a; } } mean=mean/Dlen; //--- sorting of the transformed data array ArraySort(BCDat); a=0; b=0; for(i=0;i<Dlen;i++) { c=(BCDat[i]-mean); a+=Cdf[i]*c; b+=c*c; } //--- correlation coefficient ret=a/(Scdf*MathSqrt(b)); return(k1+k2-ret); } //+------------------------------------------------------------------+ //| The function opposite to the normal distribution function | //| Prototype: | //| Cephes Math Library Release 2.8: June, 2000 | //| Copyright 1984, 1987, 1989, 2000 by Stephen L. Moshier | //+------------------------------------------------------------------+ double CFullBoxCox::ndtri(double y0) { static double s2pi =2.50662827463100050242E0; // sqrt(2pi) static double P0[5]={-5.99633501014107895267E1, 9.80010754185999661536E1, -5.66762857469070293439E1, 1.39312609387279679503E1, -1.23916583867381258016E0}; static double Q0[8]={ 1.95448858338141759834E0, 4.67627912898881538453E0, 8.63602421390890590575E1, -2.25462687854119370527E2, 2.00260212380060660359E2, -8.20372256168333339912E1, 1.59056225126211695515E1, -1.18331621121330003142E0}; static double P1[9]={ 4.05544892305962419923E0, 3.15251094599893866154E1, 5.71628192246421288162E1, 4.40805073893200834700E1, 1.46849561928858024014E1, 2.18663306850790267539E0, -1.40256079171354495875E-1,-3.50424626827848203418E-2, -8.57456785154685413611E-4}; static double Q1[8]={ 1.57799883256466749731E1, 4.53907635128879210584E1, 4.13172038254672030440E1, 1.50425385692907503408E1, 2.50464946208309415979E0, -1.42182922854787788574E-1, -3.80806407691578277194E-2,-9.33259480895457427372E-4}; static double P2[9]={ 3.23774891776946035970E0, 6.91522889068984211695E0, 3.93881025292474443415E0, 1.33303460815807542389E0, 2.01485389549179081538E-1, 1.23716634817820021358E-2, 3.01581553508235416007E-4, 2.65806974686737550832E-6, 6.23974539184983293730E-9}; static double Q2[8]={ 6.02427039364742014255E0, 3.67983563856160859403E0, 1.37702099489081330271E0, 2.16236993594496635890E-1, 1.34204006088543189037E-2, 3.28014464682127739104E-4, 2.89247864745380683936E-6, 6.79019408009981274425E-9}; double x,y,z,y2,x0,x1,a,b; int i,code; if(y0<=0.0){Print("Function ndtri() error!"); return(-DBL_MAX);} if(y0>=1.0){Print("Function ndtri() error!"); return(DBL_MAX);} code=1; y=y0; if(y>(1.0-0.13533528323661269189)){y=1.0-y; code=0;} // 0.135... = exp(-2) if(y>0.13533528323661269189) // 0.135... = exp(-2) { y=y-0.5; y2=y*y; a=P0[0]; for(i=1;i<5;i++)a=a*y2+P0[i]; b=y2+Q0[0]; for(i=1;i<8;i++)b=b*y2+Q0[i]; x=y+y*(y2*a/b); x=x*s2pi; return(x); } x=MathSqrt(-2.0*MathLog(y)); x0=x-MathLog(x)/x; z=1.0/x; //--- y > exp(-32) = 1.2664165549e-14 if(x<8.0) { a=P1[0]; for(i=1;i<9;i++)a=a*z+P1[i]; b=z+Q1[0]; for(i=1;i<8;i++)b=b*z+Q1[i]; x1=z*a/b; } else { a=P2[0]; for(i=1;i<9;i++)a=a*z+P2[i]; b=z+Q2[0]; for(i=1;i<8;i++)b=b*z+Q2[i]; x1=z*a/b; } x=x0-x1; if(code!=0)x=-x; return(x); } //------------------------------------------------------------------------------------
최적화 중에는 변환 매개 변수 변동 범위에 대한 제한이 발생합니다. 람다 매개 변수는 -5.0과 5.0 사이의 값을 갖습니다. 델타 변수 값에 대한 제한은 인풋 시퀀스 최소 값에 비례하도록 특정되어 있습니다. 해당 변수는 DeltaMin=(0.00001-min)과 DeltaMax=(max-min)*200-min 값으로 제한되는데요. 최소값과 최대값은 각각 인풋 시퀀스 엘리먼트의 최소값과 최대값입니다.
FullBoxCoxTest.mq5 스크립트에 CFullBoxCox 클래스 이용법이 포함되어 있습니다. 아래는 해당 스크립트의 소스 코드입니다.
//+------------------------------------------------------------------+ //| FullBoxCoxTest.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CFullBoxCox.mqh" CFullBoxCox Bc; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],shift[],bcdat[],lambda,delta,gm,gmpow; string fname; //--- input file name fname="Dataset2\\EURUSD_M1_1200.txt"; //--- reading the data if(readCSV(fname,dat)<0){Print("Error."); return;} //--- data size n=ArraySize(dat); //--- shifted input data array ArrayResize(shift,n); //--- transformed data array ArrayResize(bcdat,n); //--- lambda and delta parameters optimization Bc.CalcPar(dat); lambda=Bc.GetPar(0); delta=Bc.GetPar(1); PrintFormat("Iterations= %i, lambda= %.4f, delta= %.4f", Bc.GetIter(),lambda,delta); gm=0; for(i=0;i<n;i++) { shift[i]=dat[i]+delta; gm+=MathLog(shift[i]); } //--- geometric mean gm=MathExp(gm/n); gmpow=lambda*MathPow(gm,lambda-1); if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(shift[i],lambda)-1.0)/gmpow;} else {for(i=0;i<n;i++)bcdat[i]=gm*MathLog(shift[i]);} //--- dat[] <-- input data //--- shift[] <-- input data with the shift //--- bcdat[] <-- transformed data } //+------------------------------------------------------------------+ //| readCSV | //+------------------------------------------------------------------+ int readCSV(string fnam,double &dat[]) { int n,asize,fhand; fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI); if(fhand==INVALID_HANDLE) { Print("FileOpen Error!"); return(-1); } asize=512; ArrayResize(dat,asize); n=0; while(FileIsEnding(fhand)!=true) { dat[n++]=FileReadNumber(fhand); if(n+128>asize) { asize+=128; ArrayResize(dat,asize); } } FileClose(fhand); ArrayResize(dat,n-1); return(0); } //------------------------------------------------------------------------------------
스크립트가 시작하면서 인풋 시퀀스가 dat[] 배열로 업로드되며 변형 매개 변수 최적 값 탐색이 시작됩니다. 최적 값 탐색이 완료되면 획득 값을 이용한 변환이 실행됩니다. 그 결과 dat[] 배열에 초기 시퀀스가 저장되며 shift[] 배열은 델타 값만큼 이동한 초기 시퀀스를, bcdat[] 배열은 박스-칵스 변환 결과 시퀀스를 갖습니다.
Box-Cox-Tranformation_MQL5.zip 아카이브에 FullBoxCoxTest.mq5 스크립트 컴파일에 필요한 모든 파일이 포함되어 있습니다.
테스트 시퀀스 변형 또한 FullBoxCoxTest.mq5 스크립트를 이용해 실행되었습니다. 획득 값 분석을 통해 2개 매개 변수 변환이 1개 매개 변수 변환보다 나은 결과를 산출함을 알 수 있습니다. 예를 들어, 그림 6의 EURUSD M1 시퀀스의 경우 자크-베라 테스트 값 JB=100.94였습니다. 1개 매개 변수 변환 후에는 JB=39.30(그림 7), 2개 매개 변수 변환(FullBoxCoxTest.mq5 스크립트) 후에는 JB=37.49로 값이 내려갔죠.
결론
결과 시퀀스의 분포를 최대한 정상에 가깝게 만들기 위해 박스-칵스 변환 매개 변수를 최적화해 보았습니다. 하지만 실제로는 박스-칵스 변환이 약간 다르게 사용되는 경우가 있는데요. 예를 들어, 시계열 예측 시 다음의 알고리즘을 사용할 수 있습니다.
- 예비 박스-칵스 변환 매개 변수 값과 예측 모델을 선택합니다.
- 인풋 데이터에 대한 박스-칵스 변환을 실행합니다.
- 현재 매개 변수에 따라 예측 값이 생산됩니다.
- 역 박스-칵스 변환을 실행해 예측 결과를 얻습니다.
- 변환 전 인풋 시퀀스로 예측 오류를 평가합니다.
- 오류가 최소화되도록 변수 값을 수정한 후 2단계로 돌아갑니다.
위의 알고리즘에서는 오류 최소화 기준에 따라 변형 매개 변수와 예측 모델 변수는 최소화됩니다. 박스-칵스 변환의 목적이 더이상 인풋 시퀀스의 분포를 정규 분포화 시키는 것이 아니죠.
인풋 시퀀스를 변환해서 최소의 예측 에러를 포함하는 분포 규칙을 구하게 된 겁니다. 예측 방법에 따라 분포가 반드시 정규 분포를 따를 필요는 업습니다.
다시 한번 말하지만 박스-칵스 변환은 0이 아닌 양수 값을 갖는 시퀀스에만 적용 가능합니다. 다른 값을 갖는 시퀀스의 경우 인풋 시퀀스를 이동해야 합니다. 물론 이런 특성이 해당 변환의 단점 중 하나가 될 수도 있습니다. 그래도 박스-칵스 변환이 비슷한 변환법 가운데 가장 유용하고 효과적일 겁니다.
참고 자료
- А.N. Porunov. Box-Сox Transformation and the Illusion of «Normality» of Macroeconomic Series. "Business Informatics" journal, №2(12)-2010, pp. 3-10.
- Mohammad Zakir Hossain, The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses. Journal of Emerging Trends in Economics and Management Sciences (JETEMS) 2(1):32-39.
- Box-Cox Transformations.
- '지수 평활화를 이용한 시계열 예측'
- '지수 평활화를 이용한 시계열 예측(계속)'
- Analysis of the Main Characteristics of Time Series.
- Power transform.
- Draper N.R. and H. Smith, Applied Regression Analysis, 3rd ed., 1998, John Wiley & Sons, New York.
- Q-Q plot.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/363
DLL 생성이 불필요한 이유
최초 구매 고객을 위한 팁
MQL5.community 회원 활동 기록
다중 선형 회귀 분석 올인원 전략 생성기와 전략 테스터
