MetaTrader 5機械学習の設計図（第3回）：トレンドスキャンラベリング法

はじめに

「MetaTrader 5機械学習の設計図」第3回へようこそ。本連載では、第1回においてデータ整合性に関する基礎的課題を扱い、第2回では革新的なラベリング手法を導入しました。そして本記事では、適応型トレンドスキャンラベリング法の実装に踏み込みます。

金融市場は本質的に非定常です。過去に有効であった手法が将来も機能する保証はなく、強力に見えるシグナルが、実際には観測の重複によって生じた冗長なノイズである場合も少なくありません。本記事では、Marcos López de Pradoの研究に基づく実践的かつ強力な手法を用いて、これらの問題に正面から取り組みます。本記事で実装するトレンドスキャニング法は、予測期間に関する従来の考え方を根本から変革するものです。5日先や10日先といった任意の期間を事前に固定するのではなく、市場環境ごとに統計的に最も有意な予測期間を動的に決定します。これは、市場動向を最も明瞭に捉えるために焦点を自動調整する観測装置のようなものに例えることができます。

本記事は第2回で解説した概念を前提として構成されています。そのため、未読の方は先に第2回をご参照されることを強く推奨します。本記事を通じて、読者は市場環境に適応可能な実運用水準のラベリングシステムを習得できるでしょう。本記事で扱う内容は単なる理論的考察にとどまらず、実際の取引環境における現実的課題を解決するための実践的枠組みを提供するものです。

トレンドスキャンラベリング法

理論と動機

第2回で扱ったトリプルバリア法は、固定期間ラベリングに比べて大幅な改善をもたらしましたが、依然として垂直バリアの時間的制限を事前に設定する必要がありました。すなわち、ポジションを50バー、100バー、あるいはその他の任意の期間保持するかを事前に決定する必要がありました。このアプローチは、最適な予測期間がすべての市場状況において一定であるという前提に基づいています。しかし、変動の激しい市場で取引経験のある者であれば、この前提が根本的に誤っていることは容易に理解できるでしょう。たとえば、数週間にわたり勢いが持続する上昇トレンド市場と、数日ごとにトレンドが反転するレンジ相場では、同じ予測期間を適用することは、夏と冬に同じジャケットを着るようなもので、時折はうまくいくこともありますが、最適であることはほとんどありません。

トレンドスキャニング法は、この問題をエレガントに解決します。各観測点ごとにデータ自身が最適な予測期間を決定できるようにするのです。固定期間を課すのではなく、複数の先行期間を検証し、統計的に最も強いトレンドの証拠が得られる期間を選択します。

具体的には次のように機能します。各取引エントリーポイントにおいて、アルゴリズムは将来の複数期間（例：5バー、10バー、15バー、最大設定値まで）に対するリターンの線形トレンドのt統計量を計算します。そして、最も統計的に有意な結果を与える期間を選択し、「どの将来時点でトレンドが最も明確に現れるか」を判断します。

この手法には、固定期間ラベリングに対していくつかの重要な利点があります。

• 市場適応性：変動が激しい期間では、トレンドが明確な短期間を選択します。落ち着いたトレンド相場では、持続的な動きを捉えるために長期間を選択します。

• 統計的厳密性：任意のカットオフではなく、ラベルは統計的有意性に基づいて付与されます。トレンドは、厳密な統計基準を満たす場合にのみラベリングされます。

• ノイズ除去：統計的有意性を要求することで、意味のないランダムな価格変動が自然に除外されます。

• 動的応答：市場環境が変化するにつれて、最適期間は自動的に調整され、手動で介入する必要はありません。

数学的基盤は単純でありながら強力です。各候補期間hに対して、その期間におけるリターンの線形トレンドのt統計量を計算します。t統計量は、観測されたトレンドがゼロ（トレンドなし）から何標準偏差離れているかを示します。絶対値が大きいほど、トレンドの統計的証拠が強いことを意味します。

アルゴリズムは、絶対t統計量を最大化する期間を選択しますが、同時に有意性の最小閾値を満たす場合に限ります。これにより、単にランダムな変動の中で「最もノイズが少ない」選択肢を取るのではなく、真に有意なトレンドを識別することができます。

トレンドスキャニングの最も優れた点の一つは、市場行動の種類に応じて自動的に適応することです。トレンド相場では、持続的な動きを捉えるために通常は長期間を選択します。平均回帰市場では、反転が最も統計的に明確な短期間を選択します。レンジ相場では、どの期間においても統計的に有意なトレンドが存在せず、自然に「保持」シグナルが生成されます。

この適応性により、トレンドスキャニングは異なる市場環境に対応する戦略において特に価値があります。特定の条件に最適化してその持続を期待するのではなく、アルゴリズムは常に現在の市場動向に応じて分析の焦点を自動的に調整します。

実装

Marcos López de PradoのMachine Learning for Asset Managersでトレンドスキャニング法を実装したコードスニペット（セクション5.4）を以下に共有します。 

import numpy as np
import pandas as pd
import statsmodels.api as sm

from multiprocess import mp_pandas_obj


# SNIPPET 5.1 T-VALUE OF A LINEAR TREND
# ---------------------------------------------------
def tValLinR(close):
    # tValue from a linear trend
    x = np.ones((close.shape[0], 2))
    x[:, 1] = np.arange(close.shape[0])
    ols = sm.OLS(close, x).fit()
    return ols.tvalues[1]

# SNIPPET 5.2 IMPLEMENTATION OF THE TREND-SCANNING METHOD
def getBinsFromTrend(close, span, molecule):
    """
    Derive labels from the sign of t-value of linear trend
    Output includes:
    - t1: End time for the identified trend
    - tVal: t-value associated with the estimated trend coefficient
    - bin: Sign of the trend
    """
    out = pd.DataFrame(index=molecule, columns=["t1", "tVal", "bin"])
    hrzns = range(*span)

    for dt0 in molecule:
        df0 = pd.Series()
        iloc0 = close.index.get_loc(dt0)
        if iloc0 + max(hrzns) > close.shape[0]:
            continue
        for hrzn in hrzns:
            dt1 = close.index[iloc0 + hrzn - 1]
            df1 = close.loc[dt0:dt1]
            df0.loc[dt1] = tValLinR(df1.values)
        dt1 = df0.replace([-np.inf, np.inf, np.nan], 0).abs().idxmax()
        out.loc[dt0, ["t1", "tVal", "bin"]] = (
            df0.index[-1],
            df0[dt1],
            np.sign(df0[dt1]),
        )  # prevent leakage

    out["t1"] = pd.to_datetime(out["t1"])
    out["bin"] = pd.to_numeric(out["bin"], downcast="signed")
    return out.dropna(subset=["bin"])

def trendScanningLabels(close, span, num_threads=4, verbose=True):
    out = mp_pandas_obj(
        getBinsFromTrend,
        ("molecule", close.index),
        num_threads,
        verbose=verbose,
        close=close,
        span=span,
    )
    return out.astype({"bin": "int8"})

trendScanningLabelsはmp_pandas_objを用いたマルチプロセッシングエンジン（添付のmultiprocess.py参照）を利用していますが、元の実装は実取引環境へのデプロイには速度が不足していました。私が最適化したバージョンでは、Numbaを用いてコアループを高速な機械語にコンパイルすることで、Python特有のパフォーマンスボトルネックを解消しています。この改善により、関数の処理速度は約350倍に向上しました。また、元のコードに存在した制約を解消する重要な機能更新も併せて導入しています。

from numba import njit, prange


@njit(parallel=True, cache=True)
def _window_stats_numba(y, window_length):
    """
    Compute slopes, t-values, and R² for all fixed-length windows.
    This function is optimized for performance using Numba's JIT compilation.

    :param y: (np.ndarray) The input data array.
    :param window_length: (int) The length of the sliding window.
    :return: (tuple) A tuple containing:
        - t_values: (np.ndarray) The t-values for each window.
        - slopes: (np.ndarray) The slopes for each window.
        - r_squared: (np.ndarray) The R² values for each window.
    """
    n = len(y)
    num_windows = n - window_length + 1

    t_values = np.empty(num_windows)
    slopes = np.empty(num_windows)
    r_squared = np.empty(num_windows)

    t = np.arange(window_length)
    mean_t = t.mean()
    Var_t = ((t - mean_t) ** 2).sum()

    for i in prange(num_windows):
        window = y[i : i + window_length]
        mean_y = window.mean()
        sum_y = window.sum()
        sum_y2 = (window**2).sum()

        # Slope estimation
        S_ty = (window * t).sum()
        slope = (S_ty - window_length * mean_t * mean_y) / Var_t
        slopes[i] = slope

        # SSE calculation
        beta0 = mean_y - slope * mean_t
        SSE = sum_y2 - beta0 * sum_y - slope * S_ty

        # R² calculation
        SST = sum_y2 - (sum_y**2) / window_length
        epsilon = 1e-9
        r_squared[i] = max(0.0, 1.0 - SSE / (SST + epsilon)) if SST > epsilon else 0.0

        # t-value calculation
        sigma2 = SSE / (window_length - 2 + epsilon)
        se_slope = np.sqrt(sigma2 / Var_t)
        t_values[i] = slope / (se_slope + epsilon)

    return t_values, slopes, r_squared

以下の関数は、トレンドスキャニングラベルを取得する際の主要なオーケストレーターとして機能します。

from typing import List, Tuple, Union

import numpy as np
import pandas as pd

from loguru import logger

def trend_scanning_labels(
    close: pd.Series,
    span: Union[List[int], Tuple[int, int]] = (5, 20),
    volatility_threshold: float = 0.1,
    lookforward: bool = True,
    use_log: bool = True,
    verbose: bool = False,
) -> pd.DataFrame:
    """
    `Trend scanning <https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3257419>`_ is both a classification and
    regression labeling technique.
    It fits OLS regressions over multiple rolling windows and selects the one with the highest absolute t-value.
    The sign of the t-value indicates trend direction, while its magnitude reflects confidence.
    The method incorporates volatility-based masking to avoid spurious signals in low-volatility regimes.
    This implementation offers a robust, leakage-proof trend-scanning label generator with:
      - Expanding, data-adaptive volatility thresholding
      - Full feature masking (t-value, slope, R²) in low-volatility regimes
      - Boundary protection to avoid look-ahead leaks
      - Support for both look-forward and look-backward scan

    Parameters
    ----------
    close : pd.Series
        Time-indexed raw price series. Must be unique and sorted (monotonic).
    span : list[int] or tuple(int, int), default=(5, 20)
        If list, exact window lengths to scan. If tuple `(min, max)`, uses
        `range(min, max)` as horizons.
    volatility_threshold : float, default=0.1
        Quantile level (0-1) on the expanding rolling std of log-prices. Windows
        below this vol threshold are zero-masked.
    lookforward : bool, default=True
        If True, labels trend on `[t, t+L-1]`; else on `[t-L+1, t]` by reversing.
    use_log : bool, default=True
        Apply log transformation before trend analysis
    verbose : bool, default=False
        Print progress for each horizon.

    Returns
    -------
    pd.DataFrame
        Indexed by the valid subset of `close.index`. Columns:
        - t1 : pd.Timestamp
        End of the event window (lookforward) or start (lookbackward).
        - window : int
        Chosen optimal horizon (argmax |t-value|).
        - slope : float
        Estimated slope over that window.
        - t_value : float
        t-stat for the slope (clipped to ±min(var, 20)).
        - r_squared : float
        Goodness-of-fit (zero if below vol threshold).
        - ret : float
        Hold-period return over the chosen window.
        - bin : int8
        Sign of `t_value` (-1, 0, +1), zero if |t_value|≈0.

    Notes
    -----
    1. Log-transformation stabilizes variance before regression.
    2. Uses a precompiled Numba `_window_stats_numba` for the heavy sliding
       O(N·H) regressions.
    3. Boundary slices ensure no forward-looking data leak into features.
    """
    # Input validation and setup
    close = close.sort_index() if not close.index.is_monotonic_increasing else close.copy()
    hrzns = list(range(*span)) if isinstance(span, tuple) else span
    max_hrzn = max(hrzns)

    if lookforward:
        valid_indices = close.index[:-max_hrzn].to_list()
    else:
        valid_indices = close.index[max_hrzn - 1 :].to_list()

    if not valid_indices:
        return pd.DataFrame(columns=["t1", "window", "slope", "t_value", "rsquared", "ret", "bin"])

    # Log transformation
    if use_log:
        close_processed = close.clip(lower=1e-8).astype(np.float64)
        y = np.log(close_processed).values
    else:
        y = close.values.astype(np.float64)

    N = len(y)

    # Compute volatility threshold
    volatility = pd.Series(y, index=close.index).rolling(max_hrzn, min_periods=1).std().ffill()
    vol_threshold = volatility.expanding().quantile(volatility_threshold).ffill().values

    # Precompute all window stats
    window_stats = np.full((3, N, len(hrzns)), np.nan)
    for k, hrzn in enumerate(hrzns):
        if verbose:
            print(f"Processing horizon {hrzn}", end="\r", flush=True)
        y_window = y if lookforward else y[::-1]
        t_vals, slopes, r_sq = _window_stats_numba(y_window, hrzn)
        if not lookforward:
            t_vals, slopes, r_sq = t_vals[::-1], slopes[::-1], r_sq[::-1]
            start_idx = hrzn - 1
        else:
            start_idx = 0
        n = len(t_vals)
        valid_vol = volatility.iloc[start_idx : start_idx + n].values
        mask = valid_vol > vol_threshold[start_idx : start_idx + n]
        window_stats[0, start_idx : start_idx + n, k] = np.where(mask, t_vals, 0)
        window_stats[1, start_idx : start_idx + n, k] = np.where(mask, slopes, 0)
        window_stats[2, start_idx : start_idx + n, k] = np.where(mask, r_sq, 0)

    # Integer positions for events
    event_idx = close.index.get_indexer(valid_indices)

    # Extract sub-blocks for these events
    t_block = window_stats[0, event_idx, :]  # shape: (E, H)
    s_block = window_stats[1, event_idx, :]
    rsq_block = window_stats[2, event_idx, :]

    # Best horizon per event (argmax of abs t-value)
    best_j = np.nanargmax(np.abs(t_block), axis=1)  # (E,)

    # Gather optimal metrics
    opt_tval = t_block[np.arange(len(event_idx)), best_j]
    opt_slope = s_block[np.arange(len(event_idx)), best_j]
    opt_rsq = rsq_block[np.arange(len(event_idx)), best_j]
    opt_hrzn = np.array(hrzns)[best_j]

    # Compute t1 indices vectorised
    if lookforward:
        t1_idx = np.clip(event_idx + opt_hrzn - 1, 0, N - 1)
    else:
        t1_idx = np.clip(event_idx - opt_hrzn + 1, 0, N - 1)

    # Map to timestamps and returns
    t1_arr = close.index[t1_idx]
    a, b = (event_idx, t1_idx) if lookforward else (t1_idx, event_idx)
    rets = close.iloc[b].array / close.iloc[a].array - 1

    # Filter labels by t-value
    tval_abs = np.abs(opt_tval)
    mask = (tval_abs > 1e-6)
    bins = np.where(mask, np.sign(opt_tval), 0).astype("int8")

    # Assemble DataFrame
    df = pd.DataFrame(
        {
            "t1": t1_arr,
            "window": opt_hrzn,
            "slope": opt_slope,
            "t_value": opt_tval,
            "rsquared": opt_rsq,
            "ret": rets,
            "bin": bins,
        },
        index=pd.Index(valid_indices),
    )

    return df

トレンドスキャニング回帰y = α + βt + εは誤差分散が一定であることを前提としています。この前提は生の価格データでは成立しませんが、対数価格を用いることで満たされます。

元の実装からの主な改善点

1. ボラティリティレジームによるフィルタリング

従来のトレンドスキャニング法は、市場状況に関係なくすべての観測点を同等に扱っていました。私たちの実装では、動的ボラティリティ閾値設定を導入しています。

# Expanding volatility percentile calculation
vol_threshold = volatility.expanding().quantile(volatility_threshold).ffill().values

# Zero out statistics during low-volatility periods
vol_mask = valid_vol > vol_threshold[start_idx : start_idx + n]

これにより、価格変動が主にノイズである低活動期にアルゴリズムが誤ったシグナルを生成することを防ぎます。また、累積分位点(expanding quantiles)を用いることで、市場のボラティリティレジームの変化に応じて閾値が適応します。

2. 二重用途設計：ラベル生成と特徴量生成

実装は、次の2つのモードで動作できます。

• lookforward=True：各観測点から未来のトレンドをスキャンしてラベルを生成
• lookforward=False：各観測点までの過去のトレンドをスキャンして特徴量を生成

# Feature generation example (no data leakage)
trend_features = trend_scanning_labels(
    close_prices, 
    span=(5, 20),
    lookforward=False,  # Look backward for features
    verbose=True
)

# Label generation example  
trend_labels = trend_scanning_labels(
    close_prices,
    span=(5, 20), 
    lookforward=True,   # Look forward for labels
    verbose=True
)

この二重機能により、堅牢なトレンド検出ロジックを統一フレームワーク内で特徴量設計とラベル生成の両方に活用することが可能です。

3. 厳格な境界保護

元の実装とは異なり、今回の実装では厳格な境界保護をおこなっています。

# Remove observations that would require future data
iloc0 = slice(0, -max_hrzn) if lookforward else slice(max_hrzn - 1, None)
t_series = t_series.iloc[iloc0]

これにより、将来のデータを使用する必要のある観測点を除外し、時系列の整合性を維持します。これは信頼性の高いバックテストや実取引において不可欠です。

本実装の優位性

1. 実運用対応：ボラティリティレジームや数値的不安定性など現実データの課題に対応
2. リーケージ防止：時系列の厳格な境界により未来情報の漏洩を防止
3. 計算効率：NumbaによるJITコンパイルで大幅な速度向上
4. 柔軟性：単一の実装で特徴量生成とラベル生成の両方に対応
5. 堅牢性：ボラティリティマスキングやt値の上限設定によりシグナル品質を向上

この強化版トレンドスキャニング実装は、市場状況に応じて適応可能な機械学習ラベルの基盤を提供するとともに、アルゴリズム取引システムに不可欠な時系列の整合性を維持します。トレンドスキャンラベリング法は、回帰モデルにおいてt値を目的変数として設定することでトレンドの大きさを予測することができ、また分類モデルにおいてはラベルを目的変数、t値をサンプル重みとして利用することで、精度の高いトレンド判定に活用可能です。

トレンドスキャニングラベルの性能分析

ここでは、トレンドスキャニング手法を検証するために、2018年1月1日から2021年12月31日までのEURUSD M5データを使用します。基本モデルとしてMA20とMA50の移動平均クロスオーバー戦略を用い、固定期間ラベル、トリプルバリアラベル、トレンドスキャンラベリング法によって生成されたラベルにメタラベリングを適用します。triple_barrier_labelsとtrend_scanning_labelsに入力される取引イベント(t_events)は、移動平均のクロスオーバーによって決定されます。トレンドスキャニングを用いたメタラベリングでは、移動平均クロスオーバー戦略によって予測された方向とトレンドスキャニングラベルが一致した場合のみ、その取引を1として分類し、それ以外は0としています。ランダムフォレストは、トレンドフォロー型モデルに有効な特徴量を用いて学習させました。特徴量には各種移動平均やADXなどのトレンド特徴量、さらにtrend_scanning_labelsをlookforward=Falseで実行して得られる特徴量を含めています（コードは添付のma_crossover_feature_engine.py参照）。トレンドスキャニングラベルは、ウィンドウ幅5から99を走査することで生成され、span=(5, 100)を設定しました。トリプルバリアラベリング法はストップロスの閾値設定に使用し、利益確定バリアは設定せず、トレンドが水平バリアに達するまで継続する仕様としています。9のウィンドウをスキャンすることによって生成されました。 関連する設定は次のとおりです。

• ボラティリティターゲット：20日指数移動標準偏差（get_daily_vol参照、添付volatility.py）
• 利益確定バリア：0
• ストップロスバリア：2
• 水平バリア：100

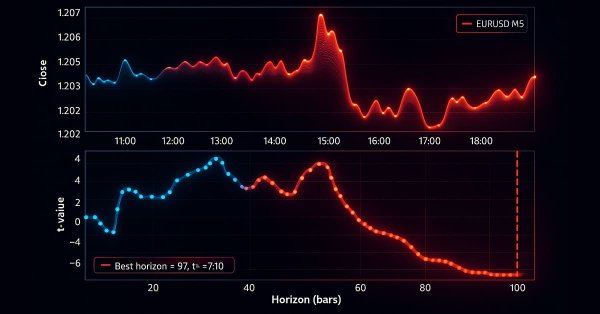
以下のチャートは、上記のパラメータに基づくトレンドスキャニングの動作例です。

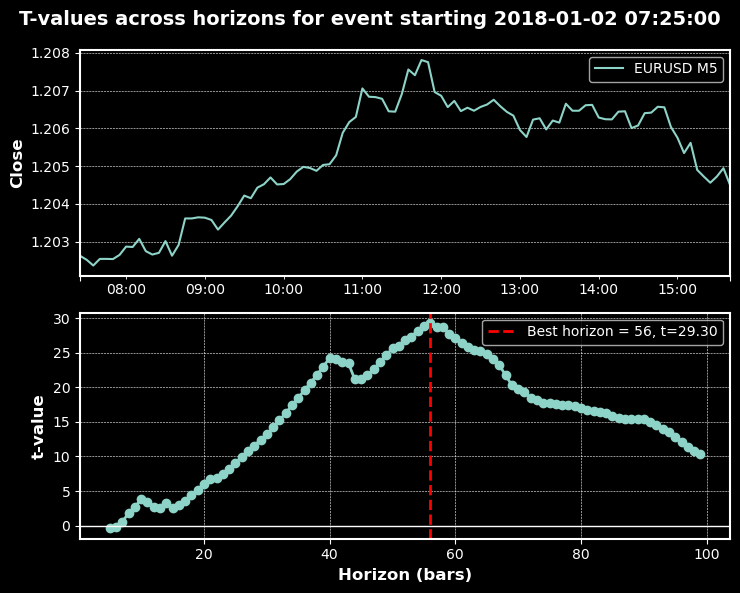
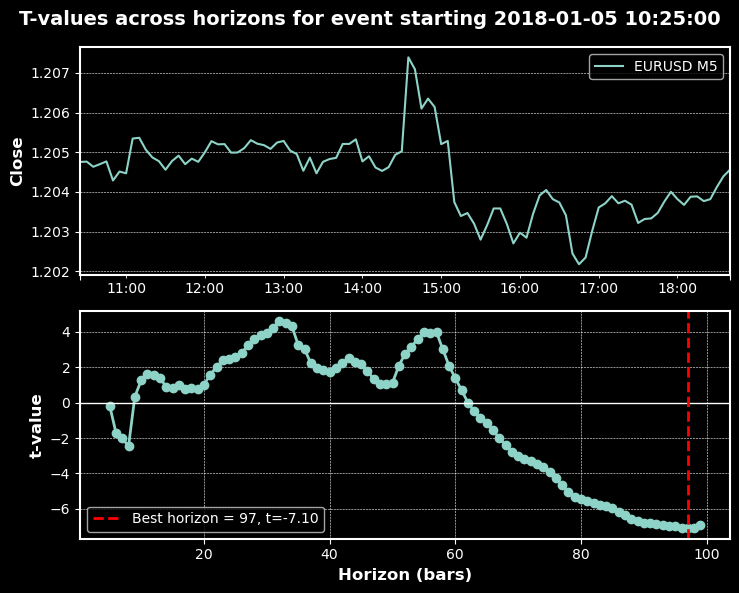
分類レポート

以下は、学習済みランダムフォレスト分類器における精度、再現率、F1スコアを、さまざまなボラティリティ閾値で評価した結果です。評価は、t値をサンプル重みとして用いた場合と、用いない場合の両方を示しています。

ボラティリティ閾値別トレンドスキャニング分類指標

		0.0	0.05	0.1	0.2	0.3
クラス
-1	精度	0.505	0.489	0.486	0.448	0.428
-1	再現率	0.545	0.382	0.408	0.440	0.413
-1	F1スコア	0.524	0.429	0.444	0.444	0.420
-1	サポート	1043	985	909	752	622
0	精度	NaN	0.176	0.297	0.525	0.658
0	再現率	NaN	1.000	0.926	0.875	0.858
0	F1スコア	NaN	0.299	0.449	0.656	0.745
0	サポート	NaN	115	256	566	840
1	精度	0.495	0.479	0.464	0.444	0.425
1	再現率	0.455	0.319	0.259	0.228	0.260
1	F1スコア	0.474	0.383	0.332	0.301	0.323
1	サポート	1022	965	900	747	603
精度		0.500	0.387	0.407	0.482	0.550

t値をサンプル重みとして用いたボラティリティ閾値別トレンドスキャニング分類指標

		0.0	0.05	0.1	0.2	0.3
クラス
-1	精度	0.514	0.514	0.509	0.502	0.490
-1	再現率	0.513	0.585	0.538	0.516	0.468
-1	F1スコア	0.513	0.548	0.523	0.509	0.479
-1	サポート	1043	945	865	721	596
1	精度	0.504	0.513	0.506	0.501	0.485
1	再現率	0.505	0.442	0.478	0.487	0.508
1	F1スコア	0.504	0.475	0.492	0.494	0.496
1	サポート	1022	935	858	719	589
精度		0.509	0.514	0.508	0.501	0.488

閾値別精度（重み付きvs非重み付き）

閾値	精度（非重み付き）	精度（重み付き）
0.0	0.500	0.509
0.05	0.387	0.514
0.1	0.407	0.508
0.2	0.482	0.501
0.3	0.550	0.488

閾値・クラス別F1スコア（重み付きvs非重み付き）

クラス	指標	0.0	0.05	0.1	0.2	0.3
非重み付きモデル
-1	F1スコア	0.524	0.429	0.444	0.444	0.420
0	F1スコア	NaN	0.299	0.449	0.656	0.745
1	F1スコア	0.474	0.383	0.332	0.301	0.323
重み付きモデル（t値をサンプル重みとして利用）
-1	F1スコア	0.513	0.548	0.523	0.509	0.479
0	F1スコア	N/A（バイナリ分類）
1	F1スコア	0.504	0.475	0.492	0.494	0.496

モデル選択の考慮点：重み付きモデルと非重み付きモデルの使い分け

重み付きモデル（t値をサンプル重みとして利用）

• 統計的に強いシグナルの強調：ノイズや弱いラベルの重みを下げ、信号の有意性を反映する
• ピークよりも安定性を重視：単一の高精度点よりも、閾値全体で一貫した性能を優先
• 実運用対応：実取引環境における堅牢性と信頼性を確保
• クラス不均衡への対応：中立またはノイズクラスの支配を緩和

非重み付きモデル

• 生シグナル品質の評価：重み付けバイアスなしで基礎的な優位性を確認
• 中立/非取引ゾーンのモデル化：決定境界上で重要なフラットクラス(0)を保持
• 研究とプロトタイピング：統計的制約を導入する前の迅速な実験に適する
• ピーク閾値の最適化：単一の運用閾値をターゲットとし、変動を許容できる場合に有効

アウトオブサンプル性能

以下の結果は、EURUSD M5のデータ（2021年12月31日～2024年12月31日）において、MA20とMA50のクロスオーバー発生時に同一のベットサイズで取引をおこなった場合のアウトオブサンプル性能を示しています。トレンドスキャニングのメタラベルは、ボラティリティ閾値0.05およびt値をサンプル重みとして使用して生成したトレンドスキャニングラベルで学習したランダムフォレストの予測を用いて作成しています。

  

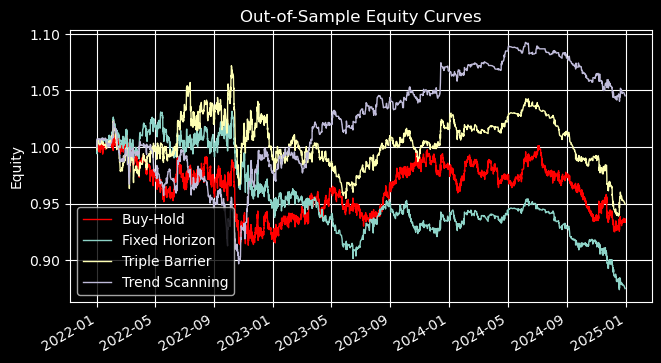
メタラベリング vs 基本モデル性能比較（MAクロスオーバー20/50）

指標	固定期間	トリプルバリア	トレンドスキャニング
総リターン	-12.49% (↓88.4%)	-5.04% (↑34.5%)	4.53% (↔ 0.0%)
年率リターン	-4.35% (↓92.4%)	-1.71% (↑35.1%)	1.49% (↔ 0.0%)
シャープレシオ	-3.72 (↓360%)	-1.66 (↓5.1%)	2.62 (↑37.3%)
ソルティノレシオ	-5.09 (↓354%)	-3.66 (↓2.2%)	4.25 (↑88.5%)
カルマーレシオ	-0.285 (↓22.3%)	-0.138 (↑28.9%)	0.121 (↔ 0.0%)
最大ドローダウン	15.27% (↓57.4%)	12.38% (↑8.8%)	12.32% (↔ 0.0%)
勝率	49.6% (↔)	40.3% (↑14.5%)	21.2% (↑88.5%)
プロフィットファクター	0.96 (↓3.0%)	0.98 (↔)	1.04 (↔)
期待値	-0.0046% (↓332%)	-0.0016% (↓18%)	-0.0762% (↑34%)
ケリー基準	-0.0206 (↓308%)	-0.0068 (↓14%)	-0.3255 (↑34%)

主要な知見

アウトオブサンプルの結果から、3つのメタラベリング手法には明確な性能差があることが示されました。

• 固定期間ラベリングは一貫してパフォーマンスを悪化させ、リターンはマイナス、シャープレシオおよびソルティノレシオも低く、ドローダウンも深くなりました。これは、時間ベースの固定出口戦略がこの手法には適していないことを示唆しています。
• トリプルバリアラベリングはリターンとドローダウンの管理においてわずかな改善をもたらしましたが、リスク調整後の指標（シャープレシオ、ソルティノレシオ）は依然として低迷していました。ある程度の安定性は提供するものの、決定的な優位性はありません。
• トレンドスキャンラベリングは、リスク調整後のリターンで最も大きな向上を示しました。シャープレシオは37%以上改善し、ソルティノレシオはほぼ倍増、ドローダウンは横ばいのままでした。これは、統計的有意性に応じてトレードの比重を決めることで、より堅牢で一貫したパフォーマンスが得られることを示しています。

実務上、固定期間はベンチマーク用にのみ有用であり、トリプルバリアは中程度のリスク管理に適し、トレンドスキャニングは安定性とリスク調整後のリターンが最重要な場合の本番運用に最適です。

拡張メタラベリングによる性能指標

	固定期間	トリプルバリア	トレンドスキャニング
total_return	-0.124942	-0.050359	0.045288
annualized_return	-0.043504	-0.017072	0.01487
volatility	0.888104	0.709836	0.521126
downside_volatility	0.649197	0.323178	0.32075
sharpe_ratio	-3.722773	-1.66439	2.616468
sortino_ratio	-5.092763	-3.655701	4.251009
var_95	-0.005302	-0.003206	-0.002467
cvar_95	-0.007848	-0.004445	-0.003576
skewness	-0.107052	1.311478	2.165464
kurtosis	3.459559	4.599455	14.055488
positive_concentration	0.000775	0.000923	0.003244
negative_concentration	0.000796	0.000342	0.000683
time_concentration	0.004943	0.004943	0.004943
max_drawdown	0.152723	0.123841	0.123154
avg_drawdown	0.021861	0.016572	0.013556
drawdown_duration	91 days 05:53:45	64 days 09:48:32	51 days 23:37:23
ulcer_index	0.04722	0.035056	0.029828
calmar_ratio	-0.284854	-0.137858	0.120745
avg_trade_duration	0 days 06:01:02	0 days 07:39:46	0 days 04:24:31
bet_frequency	26	66	33
bets_per_year	8	21	10
num_trades	2665	2665	2665
trades_per_year	888	888	888
win_rate	0.495685	0.403002	0.212383
avg_win	0.002258	0.002348	0.002342
avg_loss	-0.002311	-0.001612	-0.0016
best_trade	0.017643	0.017643	0.017643
worst_trade	-0.01916	-0.012522	-0.012522
profit_factor	0.961558	0.983383	1.038523
expectancy	-0.000046	-0.000016	-0.000762
kelly_criterion	-0.020585	-0.00681	-0.325531
consecutive_wins	6	6	3
consecutive_losses	8	12	3
ratio_of_longs	0.5	0.484375	1.0
signal_filter_rate	0.469546	0.469546	0.469546
confidence_threshold	0.5	0.5	0.5

性能概要：ラベリング戦略

トレンドスキャニングは、複数の指標において最も堅牢な戦略であることが明らかになりました。

• リターン：唯一、総リターン(+4.5%)および年率リターン(+1.5%)でプラスのリターンを示しています。
• リスク調整後パフォーマンス：シャープレシオ(2.62)およびソルティノレシオ(4.25)が最も高く、ボラティリティ(0.52)およびアルサーインデックス(0.03)が最も低いです。
• ドローダウン耐性：ドローダウン期間が最も短く（52日）、平均ドローダウンも最小(0.0136)です。
• テール特性：正の歪度(2.17)および高い尖度(14.06)により、非対称的な上昇ポテンシャルを示しています。
• 取引効率：勝率は最も低い(21.2%)ものの、プロフィットファクターは最高(1.04)です。
• バイアス：完全にロング偏重（ロング比率＝1.0）で、ポジティブ集中度も最高(0.0032)です。

一方、固定期間ラベルおよびトリプルバリア戦略は、リターンがマイナスでリスク調整後パフォーマンスも劣る結果となりました。ただし、トリプルバリアは下方ボラティリティの制御や取引頻度の面では一定の利点があります。 

結論

トレンドスキャニング法は、適切にフィルタリングすることで有効性を発揮します。ただし、その効果は評価フレームワークに依存します。すべてのトレンドシグナルが取引に値するわけではなく、高信頼期間に注目することで、はるかに良好な結果を得られます。

私たちは、従来の誤ったタイムスタンプや硬直的なラベルから、現実の取引行動を反映する適応的・確率的システムへと進化させました。重要な洞察は方法論にあります。ラベルを取引の現実に整合させることが不可欠です。設計を誤れば、複雑さは成果を救えませんが、正しく設計すれば、単純なモデルでも優れた成果を上げることが可能です。

金融機械学習の未来は、より複雑なアルゴリズムではなく、より賢明なデータ準備にあると考えます。この基盤が整ったことで、次のステップであるサンプルウェイトの設定、モデル選択、クロスバリデーション、そしてライブ運用へと進む準備が整いました。旅はまだ続きます。