知っておくべきMQL5ウィザードのテクニック（第13回）：ExpertSignalクラスのためのDBSCAN

はじめに

本連載はMQL5ウィザードに関するもので、人生の他の分野における数学の抽象的なアイデアが、取引システムとして活かされ、その前提に真剣に取り組む前にテストまたは検証されることがいかに多いかを紹介するものです。シンプルで、まだ完全には実装されていない、あるいは想定されていないアイデアを取り入れ、取引システムとしての可能性を探るこの能力は、エキスパートアドバイザー(EA)向けのMQL5ウィザードアセンブリが提供する宝石の1つです。ウィザードのEAクラスは、特に取引の開始と終了に関連するEAに必要とされる日常的な機能の多くを提供しますが、新しいバー形成でのみ意思決定を実行するなど、見落とされがちな側面も提供します。

したがって、このプロセスのライブラリをEAの別個の側面として保持することで、MQL5ウィザードを使用すると、あらゆるアイデアを独立してテストできるだけでなく、考慮されている他のアイデア（または方法）とある程度同等の立場で比較することもできます。本連載では、k平均法クラスタリングだけでなく、凝集型クラスタリングのような代替クラスタリング手法も見てきました。

これらの各アプローチでは、それぞれのクラスタを生成する前に、必要な入力パラメータの1つは、作成するクラスタの数でした。これは要するに、ユーザーがデータセットに精通しており、不慣れなデータセットを探索したり見たりしていないことを前提としています。Density Based Spatial Clustering for Applications with Noise (DBSCAN)では、形成されるクラスタ数は「重要な」未知数です。これにより、未知のデータセットを探索してその主要な分類特性を発見する際に柔軟性が高まるだけでなく、想定されるクラスタの数が検証できるかどうかについて、特定のデータセットに関する既存の「バイアス」や一般的に保持されている見解を確認することもできます。

DBSCANは、クラスタ内の点間の最大空間距離であるεと、クラスタを構成するのに必要な最小点数の2つのパラメータを取るだけで、サンプリングされたデータからクラスタを生成するだけでなく、これらのクラスタの適切な数を決定することができます。その驚くべき偉業を理解するためには、他のアプローチとは対照的なクラスタリングを見てみるのが役に立つかもしれません。

Mediumでのこの公開記事によると、DBSCANとk平均法クラスタリングは、その定義により、これらの別々のクラスタリング結果を与えます。 

k平均法クラスタリングでは次のようになります。

一方、DBSCANでは次のようになります。

これらに加えて、この記事ではDBSCANとCLARANSという別のクラスタリングアプローチとの比較もおこない、以下の結果を得ました。CLARANSの再分類は以下の通りでした。

しかし、同じフォームを使用したDBSCANでは、以下のようなグループ化がなされました。

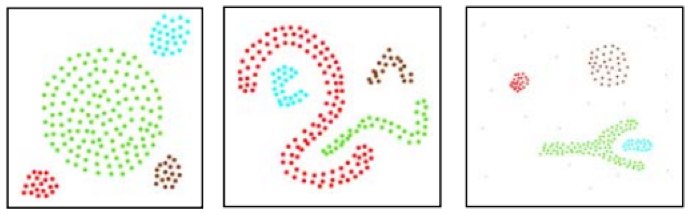
最初の例は想定内のプレゼンテーションかもしれませんが、2番目の例は決定的なものです。この背景には、分類に必要なクラスタ数を事前に設定することなく、DBSCANはポイントの密度または平均間隔を使用して、適切なグループ化、したがってクラスタを考え出すという主張があります。

上の画像から観察できるように、k平均法は領域分割に関係しており、この場合はx軸とy軸の座標に支配されています。つまり、k平均法がおこなうのは、軸の制約（この場合はxとy）内の点を最適適合として配分することです。DBSCANは、座標軸領域内に単に豊富であるだけでは十分ではなく、すべての点の内部近接性も考慮される追加の密度の「次元」を導入します。その結果、クラスタは平均軌跡または最適適合とみなされる領域を超えて拡張領域に広がる可能性があります。

そこでこの記事では、DBSCANがMQL5ウィザードで使用されるExpertSignalクラスの売買判断の精緻化にどのように役立つかを見ていくことにします。クラスタリングがこの種の判断にいかに有益であるかは、上記リンク先の2つの記事ですでに見ているので、DBSCANのシグナルクラスを構築する際には、それをベースにするつもりです。

そのため、主に異なるデータセットの処理から異なる方法でDBSCANを使用する、異なるExpertSignalクラスの3つの図解を用意します。最後に、冒頭で述べたように、これらのアイデアは予備的なテストとスクリーニングのために提示されたものであり、ライブ口座で使用されるべきものではありません。読者側の自主的な努力が常に期待されます。

DBSCANの謎を解き明かす

DBSCANの「謎を解き明かす」ためには、取引以外の、日常的に遭遇するような例をいくつか挙げるのがいいかもしれません。では、3つの例を見てみましょう。

例1：あなたがスーパーマーケットのオーナーで、買い物客のデータセットを分析し、将来的にプランニングに利用できるパターンがあるかどうかを調べなければならない状況を想像してみてください。この分析もまた、典型的にはいくつかの形をとることができますが、今回の目的では主にクラスタリングを考えることにします。k平均法の場合、まず一定の数の顧客のタイプを仮定する必要があります。例えば、セールの時だけ大物の消費財や電化製品を購入する裁量消費者と、週に1回程度家庭用の食料品を購入する店舗でよく見かける定番消費者を仮定します。このセットバッチングがあれば、あとは彼らが購入するものを箇条書きにし、今後の需要に対応できるように在庫を適切に計画することができます。クラスタ（顧客タイプ）を2つにプリセットしているため、在庫を補充するために2つの主要な支出（平均セントロイドとして時間的に位置づけられる）が発生することになります。これは、希望するほどキャッシュフローに優しくない可能性があります。より多くの、より小規模の支出は管理しやすくなる可能性があります。一方、顧客のセグメント化にDBSCANを使用した場合、顧客のタイプ数は、顧客の密度、またはこれらの顧客が買い物をする時間がどれだけ近いかによって設定されます。ε（データ点の近さ）を定量化する際に、X軸とY軸のアナロジーを使用しましたが、スーパーの顧客との時間の場合は、カレンダーで十分です。カレンダーでどれだけ離れた日にちで買い物をするかで、顧客がどれだけ「近い」かが定量化されます。これにより、効果的に顧客の柔軟なグループ分けが可能になり、在庫補充時の支出をより管理しやすくなるなどの利点があります。

例2：あなたが、ある都市の都市計画担当者として、都市の交通パターンを調査し、各自治区で許可されるべき住居の最大数を再評価する任務を負っている状況を考えてみましょう。例1では、クラスタリングの空間的領域として時間を使用しましたが、この例では、都市を横断し、おそらく行政区を結ぶ物理的な路線に限定します。K平均クラスタリングは、まず既存の行政区の数をクラスタとして使用し、その接続路線における朝と夕方の平均交通量に基づいて、各行政区の重み付けまたは人口閾値を決定します。新しい加重比率では、各行政区は居住制限を比例して増減します。しかし、行政区そのものが決まっているわけではありません。いくつかの行政区は死につつあり、他の行政区は繁栄しており、さらに重要なことに、いくつかの行政区が新興しているかもしれません。そのため、行政区の数を仮定せず、交通路線だけを用いてDBSCANを使用すれば、路線をさまざまな形のクラスタにグループ分けすることができ、そのクラスタによって新しい行政区をマッピングすることができます。この場合のεは、各路線（朝夕のピーク時間帯）に何台の車が走っているかを例えばキロ単位で追跡します。このことは、より密度の高い路線が、より密度の低い路線よりもグループ化されることを意味し、路線が異なる地理的地域に通じている場合に問題が生じます。これを回避したり、データを理解したりする方法としては、これらの路線は、たとえ物理的には異なる地域にマッピングされていても、同じ「行政区のタイプ」を表しており（所得水準などによる可能性がある）、したがって、計画目的上、同様の方法で設定することができます。

例3：最後に、SNSは、多くの企業にとって金のデータマインであり、それらをよりよく理解するための鍵は、ユーザーを異なるグループに分類する能力（私たちの場合はクラスタ化する能力）にあると考えられます。さて、SNSユーザーは、レジャーや仕事のために独自のグループを形成し、共通の関心を持っている場合もあればそうでない場合もあり、また散発的に交流することもあるため、クラスタリングプロセスを開始する際に、k平均法が直ちに許容できる数のクラスタを出すのは至難の業です。一方、DBSCANは密度に注目することで、例えば一定期間の列挙を通じて、ユーザーとのインタラクションの数に焦点を絞ることができます。このように、あるユーザーから別のユーザーへの相互作用の数は、与えられたSNSプラットフォームで可能なさまざまなクラスタを形成し定義する際に、εパラメータを導くことができます。

これらの例で指摘された点以外にも、DBSCANのように教師なし学習の場合、特にノイズの処理と異常値の識別に優れていることは注目に値します。最小ポイント数入力パラメータも、サンプリングされたデータセットに対して理想的なクラスタ数を導き出す際に重要ですが、本質的な役割は「ノイズ」閾値を設定することであるため、εほど敏感（または重要）ではありません。DBSCANでは、指定されたクラスタに入らないデータはすべてノイズとなります。

MQL5での実装

MQL5ウィザードで組み立てられたEAの基本的な構造については、すでに以前の記事で説明しました。これに関する公式の入門書はここにありますが、要約すれば、ウィザードで組み立てられたEAは、「<includeExpert.mqh>」ファイルで定義されたExpertクラスに依存します。このExpertクラスは、主にポジションのオープンとクローズに関連する典型的なEA関数がどのように処理されるかを定義します。このクラスは、ファイル <include\Expert\ExpertBase.mqh>で定義されているExpertBaseクラスに依存し、このファイルは、EAがアタッチされている銘柄の現在の価格情報の取得とバッファリングを処理します。アンカーと考えることができるExpertBaseクラスから、他の3つのクラス（ExpertSignal、ExpertTrailing、ExpertMoney）が継承されます。これらの各クラスのカスタマイズされた実装は、すでに以前の記事で共有されていますが、ExpertSignalクラスが売買の決定を処理し、ExpertTrailingクラスが未決ポジションのトレーリングストップをいつ、どれだけ動かすかを決定し、最後にExpertMoneyクラスがポジションサイジングで利用可能な証拠金の割合を設定することは、繰り返し説明する価値があります。

ライブラリの利用可能なクラスからEAを組み立てる手順は実に簡単で、上記の共有リンクのほかにも、この方法についての記事があります。データの準備はExpertBaseクラスによって処理されますが、これを銀行取引に利用するためには、理想的には、目的の証券会社の価格データを使用してテストをおこない、利用可能な限り実際のティックを証券会社のサーバーからダウンロードすべきです。

DBSCAN関数のコーディングにおいて、この航海記事は、私たちの関数を定義するために構築されたいくつかの有用なソースコードを共有しています。最も基本的なものから始めると、全部で4つの単純な関数があります。ここでは、距離関数に注目します。

//+------------------------------------------------------------------+
//| Function for Euclidean Distance between points                   |
//+------------------------------------------------------------------+
double CSignalDBSCAN::Distance(Spoint &A, Spoint &B)
{  double _d = 0.0;
   for(int i = 0; i < int(fmin(A.key.Size(), B.key.Size())); i++)
   {  _d += pow(A.key[i] - B.key[i], 2.0);
   }
   _d = sqrt(_d);
   return(_d);
}

引用された記事やDBSCANの公開されているソースコードの多くは、ユークリッド距離を、任意の点の集合において点がどの程度離れているかを定量化するための主要なメトリックとして使用しています。しかし、私たちの点はベクトル形式であるため、MQL5ではこの点間距離を測定するために、余弦類似度などの他の選択肢をいくつか提示しています。これらはベクトルデータ型のサブ関数であるため、読者はこれらを調べることができます。ユークリッド関数はLoss関数やRegression Metric関数で見つけることができなかったので、ゼロからコーディングします。

次にビルディングブロックで必要なのは、RegionQuery関数です。これは、入力パラメータεで定義された閾値の範囲内で、問題の点と同じクラスタ内にあるとみなすことができる点のリストを返します。

//+------------------------------------------------------------------+
//| Function that returns neighbouring points for an input point &P[]|
//+------------------------------------------------------------------+
void CSignalDBSCAN::RegionQuery(Spoint &P[], int Index, CArrayInt &Neighbours)
{  Neighbours.Resize(0);
   int _size = ArraySize(P);
   for(int i = 0; i < _size; i++)
   {  if(i == Index)
      {  continue;
      }
      else if(Distance(P[i], P[Index]) <= m_epsilon)
      {  Neighbours.Resize(Neighbours.Total() + 1);
         Neighbours.Add(i);
      }
   }
   P[Index].visited = true;
}

通常、検討中のデータセット内の各点について、見落としがないようにこのような点のリストを作成します。このリストは次の関数であるExpandCluster関数に役立ちます。

//+------------------------------------------------------------------+
//| Function that extends cluster for identified cluster IDs         |
//+------------------------------------------------------------------+
bool CSignalDBSCAN::ExpandCluster(Spoint &SetOfPoints[], int Index, int ClusterID)
{  CArrayInt _seeds;
   RegionQuery(SetOfPoints, Index, _seeds);
   if(_seeds.Total() < m_min_points) // no core point
   {  SetOfPoints[Index].cluster_id = -1;
      return(false);
   }
   else
   {  SetOfPoints[Index].cluster_id = ClusterID;
      for(int ii = 0; ii < _seeds.Total(); ii++)
      {  int _current_p = _seeds[ii];
         CArrayInt _result;
         RegionQuery(SetOfPoints, _current_p, _result);
         if(_result.Total() > m_min_points)
         {  for(int i = 0; i < _result.Total(); i++)
            {  int _result_p = _result[i];
               if(SetOfPoints[_result_p].cluster_id == -1)
               {  SetOfPoints[_result_p].cluster_id = ClusterID;
               }
            }
         }
      }
   }
   return(true);
}

この関数は、クラスタ IDと点インデックスを受け取り、前述の領域クエリ関数の結果に基づいて、クラスタ IDを新しい点に割り当てる必要があるかどうかを判断します。もし結果が真であれば、クラスタのサイズは増加し、そうでなければ維持されます。この関数の中では、繰り返しを避けるために、すでにクラスタ化されている点を確認し、前述のように、クラスタ化されていない点（クラスタID：-1のまま）はノイズとみなされます。

このすべてをまとめるには、現在のクラスタIDを拡張する必要があるかどうかを確立することによって、データセット内のすべての点を繰り返し処理するメインのDBSCAN関数を使用します。現在のクラスタIDは、新しいクラスタが確立されるたびにインクリメントされる整数であり、各インクリメントごとに、このクラスタに属するすべての点の近傍が、すでに述べたように、RegionQuery関数によってクエリされ、これはExpandCluster関数によって呼び出されます。コードは以下の通りです。

//+------------------------------------------------------------------+
//| Main clustering function                                         |
//+------------------------------------------------------------------+
void CSignalDBSCAN::DBSCAN(Spoint &SetOfPoints[])
{  int _cluster_id = -1;
   int _size = ArraySize(SetOfPoints);
   for(int i = 0; i < _size; i++)
   {  if(SetOfPoints[i].cluster_id == -1)
      {  if(ExpandCluster(SetOfPoints, i, _cluster_id))
         {  _cluster_id++;
            SetOfPoints[i].cluster_id = _cluster_id;
         }
      }
   }
}

同様に、上記のコードでSetOfPointsと呼ばれているデータセットを扱う構造体は、クラスヘッダで以下のように定義されています。

   struct Spoint
   {  vector            key;
      bool              visited;
      int               cluster_id;

                     Spoint()
      {              key.Resize(0);
         visited = false;
         cluster_id = -1;
      };
                    ~Spoint() {};
   };

クラスタリング手法としてのDBSCANは、データセットの大きさによってメモリの問題に直面します。また、クラスタ密度を測定する重要な入力パラメータであるεは、すべてのクラスタで一様であってはならないと考える学派もあります。この記事で使用している実装ではこれが当てはまりますが、今後の記事では、入力としてεさえ必要とせず、クラスタ内の最小数のポイントのみに依存するHDBSCANのようなDBSCANのバリアントが取り上げられる可能性があります。これは、それほど重要ではなく機密性の高いパラメータであるため、クラスタリングにおけるより汎用性の高いアプローチになります。

シグナルクラス

上記で定義したことを基に実装すれば、証券価格データをクラスタリングして売買シグナルを生成する様々なアプローチを提示できます。というわけで、冒頭でお約束した3つのアプローチ例はクラスタリングとなります。

- 生のOHLC価格バーデータ

- RSI指標データの変化

- 移動平均価格指標の変化

以前のクラスタリング記事では、クラスタ化された値に最終的な価格の変化を「死後」にラベル付けし、その変化の現在の加重平均を使用して次の予測をおこなうという粗雑なモデルを使用していました。今回は同様のアプローチを採用しますが、各手法の主な違いは、主にDBSCAN関数に供給されるデータセットです。これらのデータセットは様々であるため、各シグナルクラスの入力パラメータも異なる可能性があります。

生のOHLCデータから始めると、データセットは4つのキーポイントで構成されます。つまり、データを保持するSpoint構造体のkeyとして定義したベクトルのサイズは4になります。この4点は、始値、高値、安値、終値のそれぞれの変化となります。Spoint構造体に現在の価格情報を次のように入力します。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalDBSCAN::GetOutput()
{  double _output = 0.0;
   
...

...


   for(int i = 0; i < m_set_size; i++)
   {  for(int ii = 0; ii < m_key_size; ii++)
      {  if(ii == 0)
         {  m_model.x[i].key[ii] = (m_open.GetData(StartIndex() + i) - m_open.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
         else if(ii == 1)
         {  m_model.x[i].key[ii] = (m_high.GetData(StartIndex() + i) - m_high.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
         else if(ii == 2)
         {  m_model.x[i].key[ii] = (m_low.GetData(StartIndex() + i) - m_low.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
         else if(ii == 3)
         {  m_model.x[i].key[ii] = (m_close.GetData(StartIndex() + i) - m_close.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
      }
      if(i > 0) //assign classifier only for data points for which eventual bar range is known
      {  m_model.y[i - 1] = (m_close.GetData(StartIndex() + i - 1) - m_close.GetData(StartIndex() + i)) / m_symbol.Point();
      }
   }
   
...

   return(_output);
}

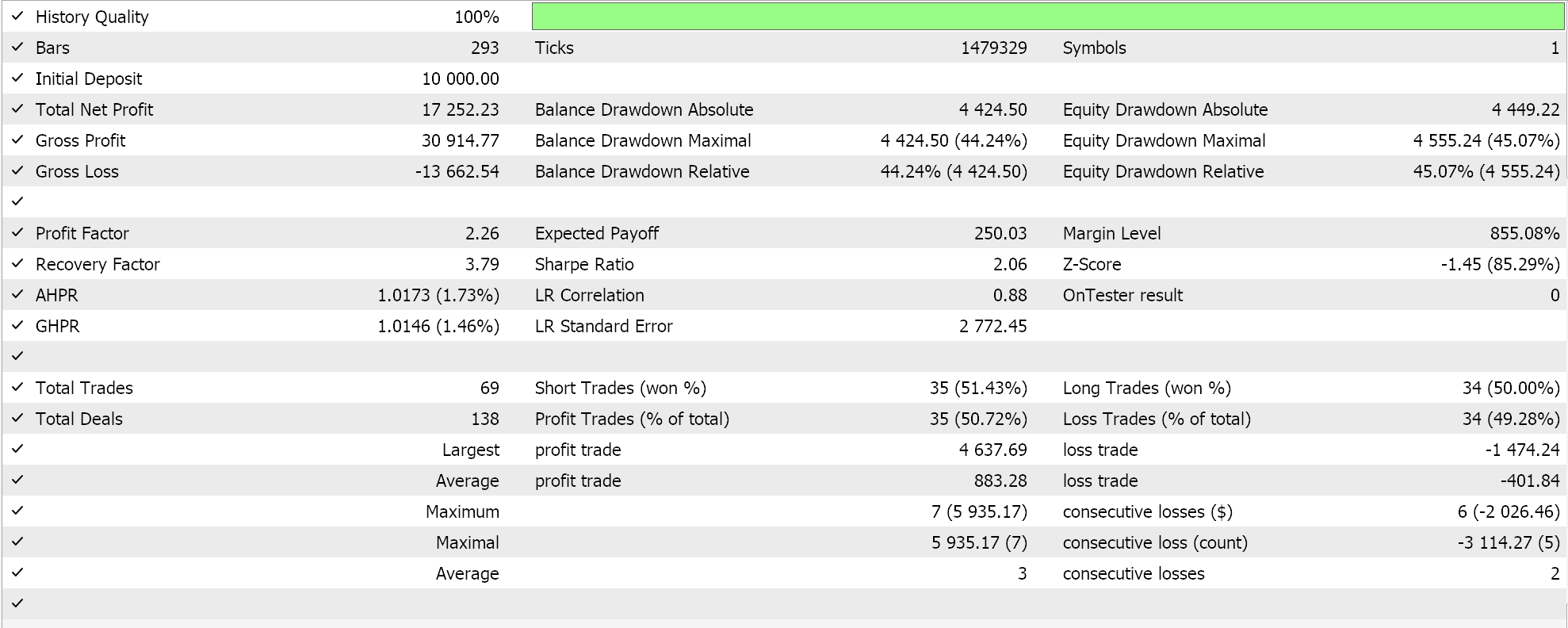
このシグナルをウィザードで組み立て、2023年のEURUSDを日足でテストすると、最良の結果は以下のレポートとエクイティ曲線のようになります。

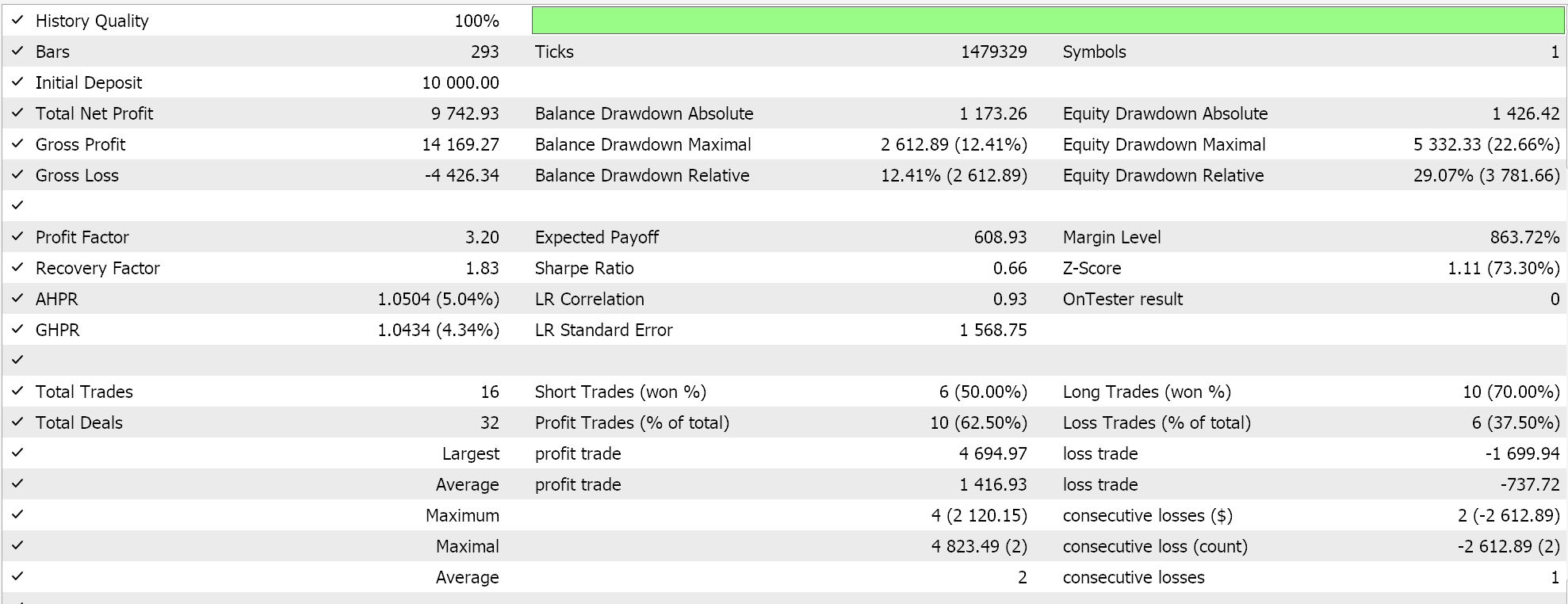
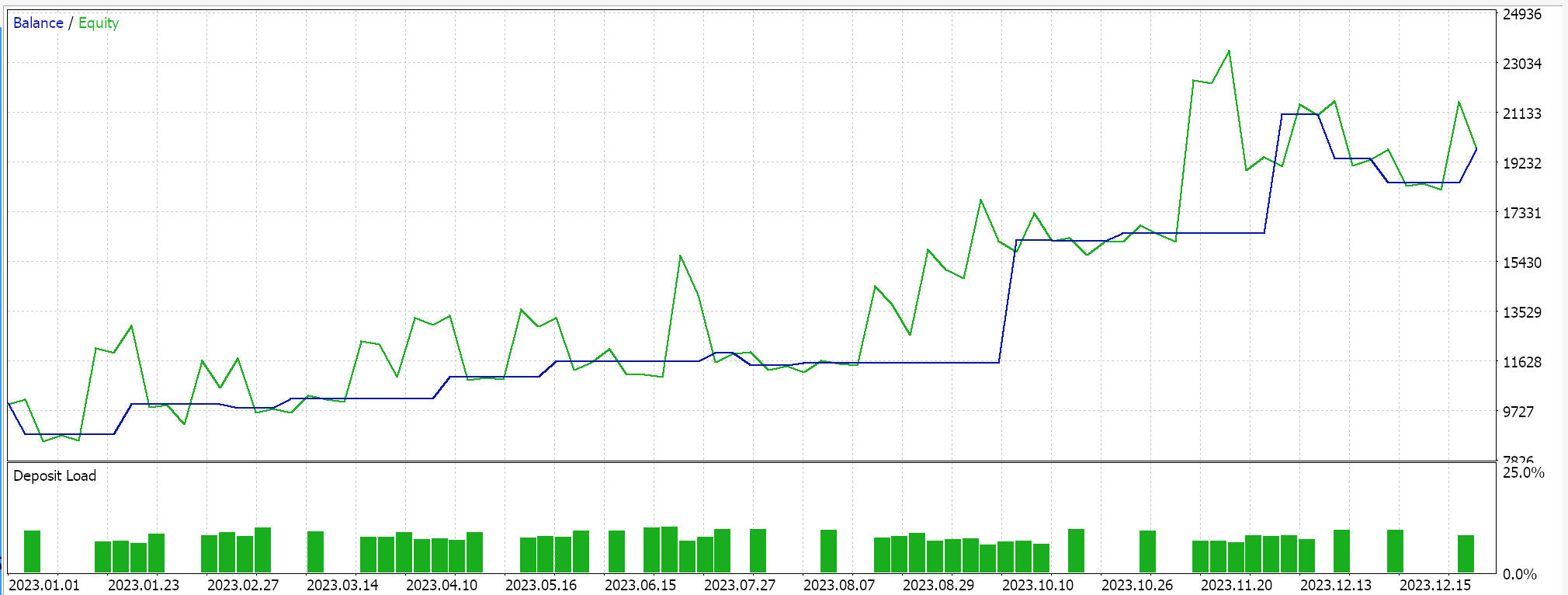
レポートからは可能性があると言えますが、今回の場合は、以前の記事で小規模に試みたようなウォークフォワードテストはおこなっていないため、これ以上進める前にはウォークフォワードテストを実行するようお勧めします。

RSIの絶対値をデータセットとして使用し続ける場合、RSIの読み取りをおこなう3つの異なるラグ期間をどのように考慮するかが主な違いですが、同様の方法で実装します。つまり、このデータセットでは、生のOHLC価格と同様に1回につき4つのデータポイントを取得していますが、これらのデータポイントはRSI指標値です。それらが取得されるラグは、A、B、C とラベル付けした3つの入力パラメータによって設定されます。データ セットは次のように設定されます。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalDBSCAN::GetOutput()
{  double _output = 0.0;

...

   RSI.Refresh(-1);
   for(int i = 0; i < m_set_size; i++)
   {  for(int ii = 0; ii < m_key_size; ii++)
      {  if(ii == 0)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i);
         }
         else if(ii == 1)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i + m_lag_a);
         }
         else if(ii == 2)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i + m_lag_a + m_lag_b);
         }
         else if(ii == 3)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i + m_lag_a + m_lag_b + m_lag_c);
         }
      }
      if(i > 0) //assign classifier only for data points for which eventual bar range is known
      {  m_model.y[i - 1] = (m_close.GetData(StartIndex() + i - 1) - m_close.GetData(StartIndex() + i)) / m_symbol.Point();
      }
   }
   int _o[];

...

...

   return(_output);
}

そこで、同じ銘柄について、同じ期間2023年に日足の時間枠でテストを実行すると、最良の実行から次のような結果が得られます。

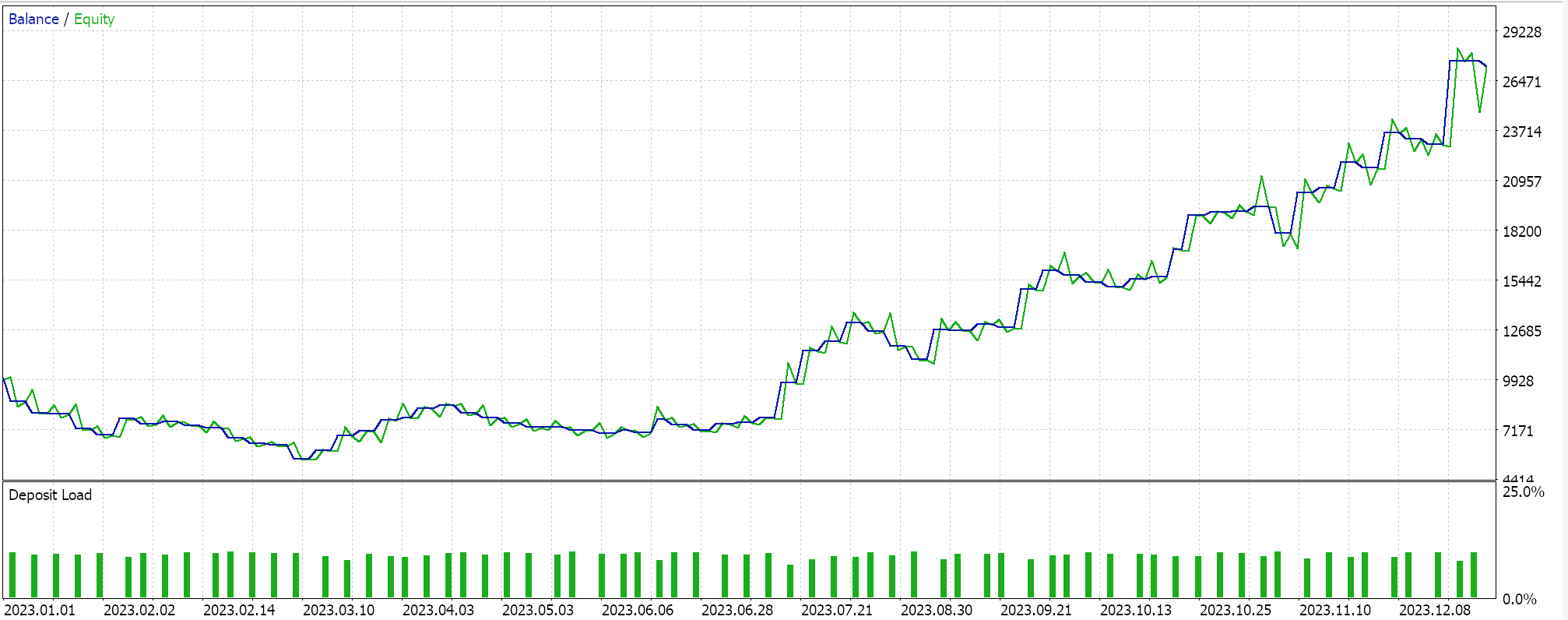
有望なレポートですが、またしても結論は出ません。本記事で紹介するすべてのEAは、指値注文で取引をおこない、ポジションを決済する際に利食い価格や損切り価格を使用しません。つまり、シグナルが反転するまでポジションを保有し、その後、逆に新しいポジションを建てます。

最後に、移動平均の変化については、RSIでおこなったのとほぼ同じようにデータセットを埋めますが、主な違いは、RSIでは絶対値に関心があったのに対して、ここではMA指標の読み値の変化を探しているということです。もう1つの大きな違いはキー値です。絶対値ではなくラグ変化に注目しているため、Spoint構造体内のkeyベクトルのサイズは3つだけで、4つではありません。

テストランを実行すると、その最良のランについて次のようなレポートが得られます。

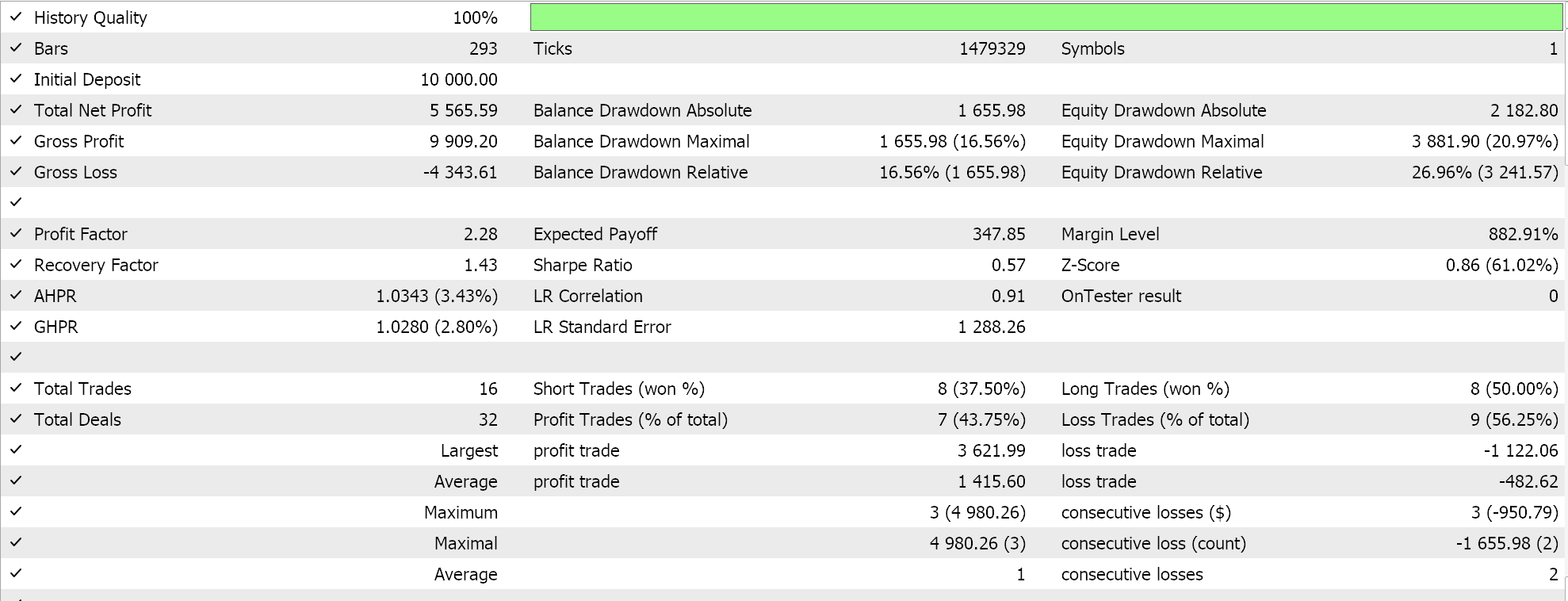
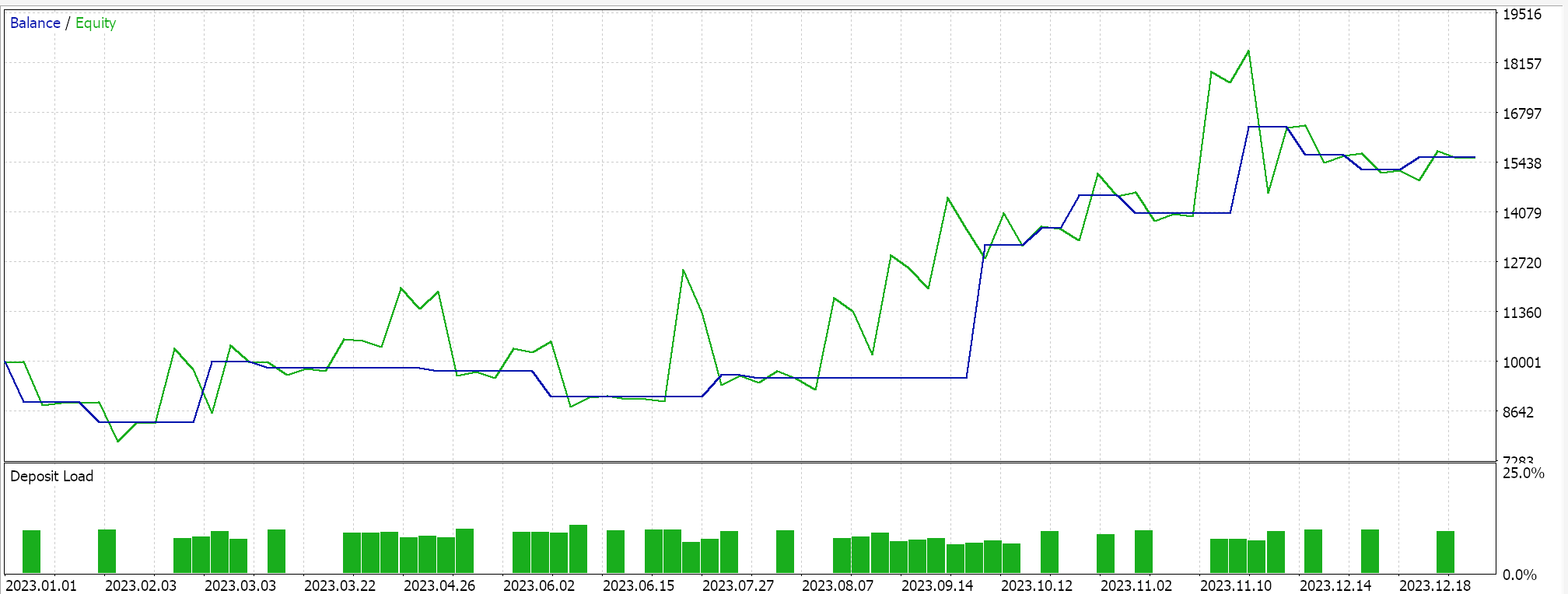
結論

結論として、DBSCANはk平均法のような従来のアプローチとは異なり、最小限の入力パラメータでデータを分類する教師なし方法です。必要なパラメータは2つだけで、そのうち1つのεだけが重要であり、これによりこの入力に対する過度の依存または敏感さが生じます。

このようにεに過度に依存しているにもかかわらず、どのような分類においてもクラスタ数が有機的に決定されるという事実によって、様々なデータセットに対して非常に汎用性が高く、ノイズをよりうまく扱うことができます。

ExpertSignalクラスのカスタムインスタンス内で使用する場合、生の価格から指標値まで、様々な入力データセットを証券分類の基礎として使用することができます。

ExpertSignalクラスのカスタムインスタンスを作成する以外にも、本連載の以前の記事で取り上げたように、読者はDBSCANを使用するExpertTrailingクラスやExpertMoneyクラスの同様のカスタム実装を作成することができます。

私がDBSCANと一般的なクラスタリングが適していると感じる、見る価値のあるもう1つの道は、データの正規化です。多くの予測モデルは、予測に使用する前に入力データの正規化を必要とする傾向があります。例えば、ランダムフォレストアルゴリズムやニューラルネットワークは、特に証券価格のデータフィードの場合、理想的には正規化されたデータを必要とします。現在流行しているTransformerアーキテクチャーを使用した大規模言語モデルでは、これに相当するステップが埋め込みです。ニューラルネットワークを介したフィードフォワード処理の目的のために、基本的に数字を含むすべてのテキストに数字が再割り当てされます。このようにテキストと数字を正規化しなければ、ネットワークがAIアルゴリズムを開発する際のような膨大な量のデータを処理することは不可能です。ただし、また、この正規化は、ネットワークを訓練し、許容できる重みとバイアスを考え出そうとするときに頭痛の種となる異常値を扱います。クラスタリングとDBSCANの適切な使い方は他にもあるかもしれませんが、これが私の意見です。頑張りましょう。