您应当知道的 MQL5 向导技术（第 13 部分）：智能信号类 DBSCAN

概述

这些关于 MQL5 向导的系列文章，是关于现实中其它领域的数学抽象概念何为何常常令交易系统充满活力，并在据其做出任何严肃承诺之前进行测试或验证。采取简单、且未完全实现、或设想中的思路，来探索它们作为交易系统潜力的能力，是由 MQL5 向导组装智能系统表现出的瑰宝之一。向导的专家类提供了智能系统所需的众多平凡功能，尤其是与开仓和平仓交易有关，但也涉及被忽视的层面，像是仅在新柱线形成时执行决策。

故此，保留该流程库作为智能交易系统的一个独立方面，依靠 MQL5 向导，不仅能够独立测试任何思路，而且在某种同等地位上与正在考虑的任何其它思路（或方法）进行比较。在这些系列中，我们查看了替代聚类方法，例如聚合聚类和 k-均值聚类。

在每种方式中，于生成相应的聚类之前，所需的输入参数之一是要创建的聚类数量。这实质上假设用户精通数据集，且不会探索或查看不熟悉的数据集。利用《基于密度的空间聚类参与噪声应用》（DBSCAN），形成的聚类数量是一个“被看重的”未知数。这不仅在探索未知数据集、和发现其主要分类特征方面提供了更大的灵活性，而且还允许检查任何给定数据集上现有的“偏差”、或普遍持有的观点，以致假设的聚类数量是否可以验证。

只需取两个参数，即 “ε（epsilon）”，其为聚类当中点位之间的最大空间距离；以及构成聚类所需的最小点位数量，DBSCAN 不仅能够从采样数据中生成聚类，还可以判定这些聚类的相应数量。为了致敬其非凡壮举，相较于替代方式，也许查看它能执行的一些聚类会有所帮助。

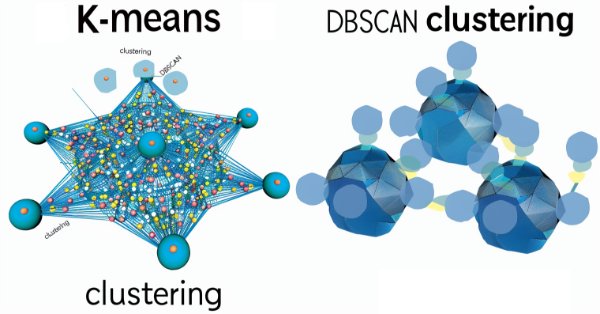
根据媒体上的这篇公开文章，DBSCAN 和 k-均值聚类能由其定义给出这些单独的聚类结果。 

对于 k-均值聚类，我们将得到：

而 DBSCAN 将给出：

除此之外，这篇论文还将 DBSCAN 与另一种名为 CLARANS 的聚类方式进行了比较，得出了以下结果。对于 CLARANS，重新分类为：

不过，具有相同形式的 DBSCAN 给出了以下分组：

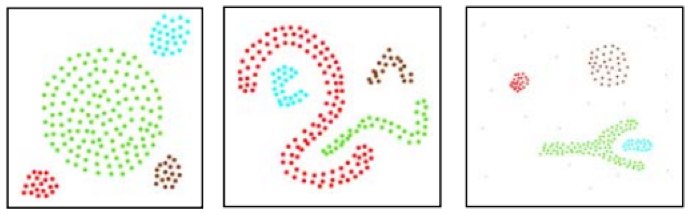
第一个例子也许是概念性表述，然而第二个例子是确定的。这背后的论点是，如果没有分类所需的预设数量的聚类，DBSCAN 会使用点位的密度或均值间距来得出相应的分组，以及聚类。

从上图中可以观察到，k-均值与地域划分有关，在这种情况下，地域划分由 x 轴和 y 轴坐标管辖。是以 k-均值所做的是将数轴约束（在本例中为 x & y）内的点位按最佳拟合分配。DBSCAN 引入了一个额外的密度“维度”，其中仅在坐标轴区域内大量存在是不够的，但还要考虑所有点位的内部接近度；其结果是聚类可以延伸到超出其所认定平均位置或最佳拟合的扩展区域。

因此对于本文来讲，我们将看到 DBSCAN 如何帮助使用 MQL5 向导中的智能信号类优调买入和卖出决策。我们已在上面链接的前两篇关于主题的文章中看到了聚类如何在这些类型的决策中提供信息，如此我们将在此基础上为 DBSCAN 构建信号类。

为此，我们将提供 3 个不同智能信号类的概述，它们以不同的方式使用 DBSCAN，主要来自处理不同的数据集。最后，正如开头提到的，这些在此表述的思路用于初步测试和筛选，与应在真实账户上使用的思路相去甚远。读者的独立勤奋总是被期望的。

揭开 DBSCAN 的神秘面纱

为了“揭开” DBSCAN 的神秘面纱，在提供一些交易之外，我们每天都会遇到的概述也许是一个好主意。故此，我们来看 3 个例子。

示例-1：想象这样一种状况：您是一位超市老板，您必须分析一些购物者的数据集，并尝试查看是否有任何模式可以收集，并在将来用于规划目的。该分析典型情况下亦能采用多种形式，不过出于我们的意图，我们主要考虑聚类。配合 k-均值，您必须首先假设客户类型数量是固定的，就是说您假设可自由支配的花销者，即大额消费者，或仅当您有售电子产品时才出手的消费者，以及您经常在店里看到的那些每周购买一次家庭杂货的主力消费者。通过这种分组批处理，您可以继续逐项列出他们购买的商品，并相应地规划您的库存，从而能够处理他们未来的供求。现在，由于您已将聚类（客户类型）预设为 2，因此您必定有 2 项主要支出费用（按时间定位作为平均质心）来补充您的库存，这样的话现金流也许不像您所愿那样友好，因为更多但规模较小的支出可能更易于管理。另一方面，如果您运用 DBSCAN 对客户进行细分，那么您得出的客户类型数量将取决于他们的密度、或这些客户购物时间倾向的接近程度。我们在上面量化 ε（数据点的接近度）中使用了 x 轴和 y 轴的类比，但对于超市客户的时间情况，日历就足够了，其中客户的“接近”程度可以由他们的购物日期在日历上的相隔时间来量化。这允许更有效、更灵活的客户分组，反过来其又能导致在补充库存时更可控的支出费用，以及其它益处。

示例-2：研究这样一种状况：作为城市规划者，您的任务是通过研究城市交通模式来重新评估城市每个行政区应允许的最大住宅数量。在 示例-1 中，我们使用时间作为聚类的空间域，而在本例中，我们仅制约穿越城市、并可能连接各行政区的物理路线。K-均值聚类一开始会用现有的行政区数量作为聚类，然后据其连接路线中早晨和晚上的平均交通量来判定每个行政区的权重、或人口阈值。按照新的加权比例，每个行政区的住宅限额将按比例减少或增加。然而，行政区本身可能并非一成不变的。有些可能正在消亡，有些可能正在蓬勃发展，更重要的是，有些可能正在崛起，因此通过运用 DBSCAN，仅对交通路线进行假设，而不假设行政区数量，我们可以将路线分组为不同形式的聚类，而后凭这些聚类划分我们的新行政区。在这种情况下，我们的 ε 将跟踪每条路线上（在早上和晚上的高峰时段）有多少辆汽车，例如每公里。这可能意味着，比之密度较低的路线，密度较高的路线更可能分组到一起，而当路线通向不同地理区域的情况下会产生问题。围绕这个问题工作、或理解数据的方式，应当是这些路线即使划分到不同的物理区域，也代表相同的“行政区类型”（可能是由于收入水平等），因此出于规划目的，可按类似的措施配置它们。

示例-3：最后，社交网络是许多公司的数据金矿，更好地理解它们的关键可能在于将用户分类、或者在我们的例子中将用户聚类到不同分组中的能力。现在，因为社交媒体用户为了休闲或工作而组建自己的群组，也许是在分享兴趣，甚至可能偶尔互动；对于 K-均值来说，在开始聚类过程时，马上得出可接受的聚类数量是一项艰巨的任务。另一方面，通过关注密度，DBSCAN 可将用户交互的数量归零，说的是通过涵盖设定时间周期的枚举。因此，从一个用户到另一个用户的交互次数可以指导 ε 参数形成，并在给定社交媒体平台上定义可能的不同聚类。

除了这些例子中提出的观点外，还值得注意的是 DBSCAN 更擅长处理噪声和识别异常值，尤其是配合 DBSCAN 的无监督学习的状况下为例。当采样数据集达到理想聚类数量时，最小点数输入参数也很重要，但是它不像 ε 那样敏感（或重要），因为它的作用本质上是设置“噪声”阈值。而配合 DBSCAN，任何未落于指定聚类的数据都是噪声。

利用 MQL5 实现

是以，MQL5 向导组装智能系统的基本结构已在之前的文章中言及。有关该内容的官方入门可在此处找到。然而，回顾向导组装智能系统，要依赖 '<include\Expert\Expert.mqh>' 文件中定义的 Expert 类。该智能类主要定义如何处理与开仓和平仓相关的典型智能系统函数。它反过来依赖文件 '<include\Expert\ExpertBase.mqh>' 中定义的智能基类，在这之后附加的是检索和缓冲品种当前价格信息的文件处理智能系统。自我们可以视为锚点的 Expert 类中，通过继承从它派生出其它 3 个类，即：智能信号类、智能尾随类、和智能资金类。这些类中的每个自定义实现均已在之前的文章中分享，不过值得重申的是，智能信号类处理买入和卖出决策， 而智能尾随类判定何时持仓的尾随止损、以及移动多少，最后智能资金类设置开仓规模的可用保证金比例。

自函数库中的可用类组装智能系统的步骤非常简单，除了上面的分享的链接外，这里还有关于如何执行该操作的文章。数据准备由智能基类处理，不过要做到这一点，理想情况下应该使用您目标经纪商的价格数据进行测试，并且应该从他们的服务器下载尽可能多的真实报价。

在编写 DBSCAN 函数的代码时，这篇公开论文分享了一些实用的源代码，我们以这些源代码为基础来定义我们的函数。如果我们从其中最基本的开始，总共有 4 个简单的函数，我们将查看距离函数。

//+------------------------------------------------------------------+
//| Function for Euclidean Distance between points                   |
//+------------------------------------------------------------------+
double CSignalDBSCAN::Distance(Spoint &A, Spoint &B)
{  double _d = 0.0;
   for(int i = 0; i < int(fmin(A.key.Size(), B.key.Size())); i++)
   {  _d += pow(A.key[i] - B.key[i], 2.0);
   }
   _d = sqrt(_d);
   return(_d);
}

DBSCAN 上引用的论文和大多数公开源代码中，都以欧几里得距离作为主要衡量值，来量化任何点位集合中的彼此距离。然而，看到我们的点是向量形式，MQL5 也提供了少量其它替代方案来测量点之间的距离，例如余弦相似度等，读者可以探索这些，因为它们是向量数据类型的子函数。我们从头开始编写 Euclidean 函数，因为我在 Loss 函数、或 Regression Metric 函数下未找到它。

接下来，在构建模块中，我们需要一个 'RegionQuery' 函数。这将返回由输入参数 ε 定义的阈值内的点列表，这些点可被视为与相关点位于同一聚类内。

//+------------------------------------------------------------------+
//| Function that returns neighbouring points for an input point &P[]|
//+------------------------------------------------------------------+
void CSignalDBSCAN::RegionQuery(Spoint &P[], int Index, CArrayInt &Neighbours)
{  Neighbours.Resize(0);
   int _size = ArraySize(P);
   for(int i = 0; i < _size; i++)
   {  if(i == Index)
      {  continue;
      }
      else if(Distance(P[i], P[Index]) <= m_epsilon)
      {  Neighbours.Resize(Neighbours.Total() + 1);
         Neighbours.Add(i);
      }
   }
   P[Index].visited = true;
}

典型情况下，对于所考虑的数据集中的每个点，我们都会尝试提出这样一个点列表，如此就不会遗漏任何内容，并且该列表对于下一个函数（即 'ExpandCluster' 函数）很有用。

//+------------------------------------------------------------------+
//| Function that extends cluster for identified cluster IDs         |
//+------------------------------------------------------------------+
bool CSignalDBSCAN::ExpandCluster(Spoint &SetOfPoints[], int Index, int ClusterID)
{  CArrayInt _seeds;
   RegionQuery(SetOfPoints, Index, _seeds);
   if(_seeds.Total() < m_min_points) // no core point
   {  SetOfPoints[Index].cluster_id = -1;
      return(false);
   }
   else
   {  SetOfPoints[Index].cluster_id = ClusterID;
      for(int ii = 0; ii < _seeds.Total(); ii++)
      {  int _current_p = _seeds[ii];
         CArrayInt _result;
         RegionQuery(SetOfPoints, _current_p, _result);
         if(_result.Total() > m_min_points)
         {  for(int i = 0; i < _result.Total(); i++)
            {  int _result_p = _result[i];
               if(SetOfPoints[_result_p].cluster_id == -1)
               {  SetOfPoints[_result_p].cluster_id = ClusterID;
               }
            }
         }
      }
   }
   return(true);
}

该函数采用聚类 ID 和点索引，基于上述区域查询函数的结果，判定是否需要将聚类 ID 分配给任何新点。如果结果为 true，则聚类增加大小，否则将保持维护状态。在该函数中，我们检查已识别的聚类点，从而避免重复，且如上所述，任何无聚类的点（保持聚类 ID：-1）都被视为噪声。

将这一切放在一起是通过主要的 DBSCAN 函数完成的，其迭代遍历数据集中的所有点，来判定是否需要扩展当前聚类 ID。当前聚类 ID 是一个整数，每当建立新聚类时，该整数都会递增，并且在每次递增时，如前所述，通过区域查询函数查询属于该聚类的所有点的邻域，其由扩展聚类函数调用。该清单如下：

//+------------------------------------------------------------------+
//| Main clustering function                                         |
//+------------------------------------------------------------------+
void CSignalDBSCAN::DBSCAN(Spoint &SetOfPoints[])
{  int _cluster_id = -1;
   int _size = ArraySize(SetOfPoints);
   for(int i = 0; i < _size; i++)
   {  if(SetOfPoints[i].cluster_id == -1)
      {  if(ExpandCluster(SetOfPoints, i, _cluster_id))
         {  _cluster_id++;
            SetOfPoints[i].cluster_id = _cluster_id;
         }
      }
   }
}

与此类似，处理数据集的结构，引用上面清单中的“点位集合”，定义如下：

   struct Spoint
   {  vector            key;
      bool              visited;
      int               cluster_id;

                     Spoint()
      {              key.Resize(0);
         visited = false;
         cluster_id = -1;
      };
                    ~Spoint() {};
   };

DBSCAN 作为一种聚类方法，会面临内存挑战，具体取决于数据集的规模。此外，有一种思想流派认为 ε 这个衡量聚类密度的关键输入参数不应该对于所有聚类都是统一的。在本文中我们所用的实现中，不过有一些 DBSCAN 的变体案例，例如 HDBSCAN，我们也许会在以后的文章中涵盖，它们甚至不需要 ε 作为输入，而只依赖于聚类中的最小点位数量，其为一个不太重要和敏感的参数，这令其成为一种更通用的聚类方式。

信号类

如果我们在实现中基于上面定义的内容进行构建，我们可以提出许多不同的方式来聚类证券价格数据，从而生成交易信号。故此，本文开头承诺的第三种示例方式将是聚类：

- 原始 OHLC 价格柱线数据，

- RSI 指标数据的变化，

- 最后是移动平均价格指标的变化。

在之前的聚类文章中，我们有一个粗糙的模型，其中我们按价格的最终变化来追加已标记聚类值，并用这些变化的当前加权平均值来做出下一次预测。我们将采用类似的方式，但每种方法之间的主要区别主要在于饲喂到 DBSCAN 函数中的数据集。因为这些数据集是变化的，是以每个信号类的输入参数也许亦不同。

如果我们从原始 OHLC 数据开始，我们的数据集将构成 4 个关键点。故此，我们在 'Spoint' 结构体中定义的 'key' 的向量，所持有的大小为 4。这 4 个点是开盘价、最高价、最低价、和收盘价的对应变化。故此，我们以当前价格信息填充 'Spoint' 结构，如下所示：

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalDBSCAN::GetOutput()
{  double _output = 0.0;
   
...

...


   for(int i = 0; i < m_set_size; i++)
   {  for(int ii = 0; ii < m_key_size; ii++)
      {  if(ii == 0)
         {  m_model.x[i].key[ii] = (m_open.GetData(StartIndex() + i) - m_open.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
         else if(ii == 1)
         {  m_model.x[i].key[ii] = (m_high.GetData(StartIndex() + i) - m_high.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
         else if(ii == 2)
         {  m_model.x[i].key[ii] = (m_low.GetData(StartIndex() + i) - m_low.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
         else if(ii == 3)
         {  m_model.x[i].key[ii] = (m_close.GetData(StartIndex() + i) - m_close.GetData(StartIndex() + ii + i + 1)) / m_symbol.Point();
         }
      }
      if(i > 0) //assign classifier only for data points for which eventual bar range is known
      {  m_model.y[i - 1] = (m_close.GetData(StartIndex() + i - 1) - m_close.GetData(StartIndex() + i)) / m_symbol.Point();
      }
   }
   
...

   return(_output);
}

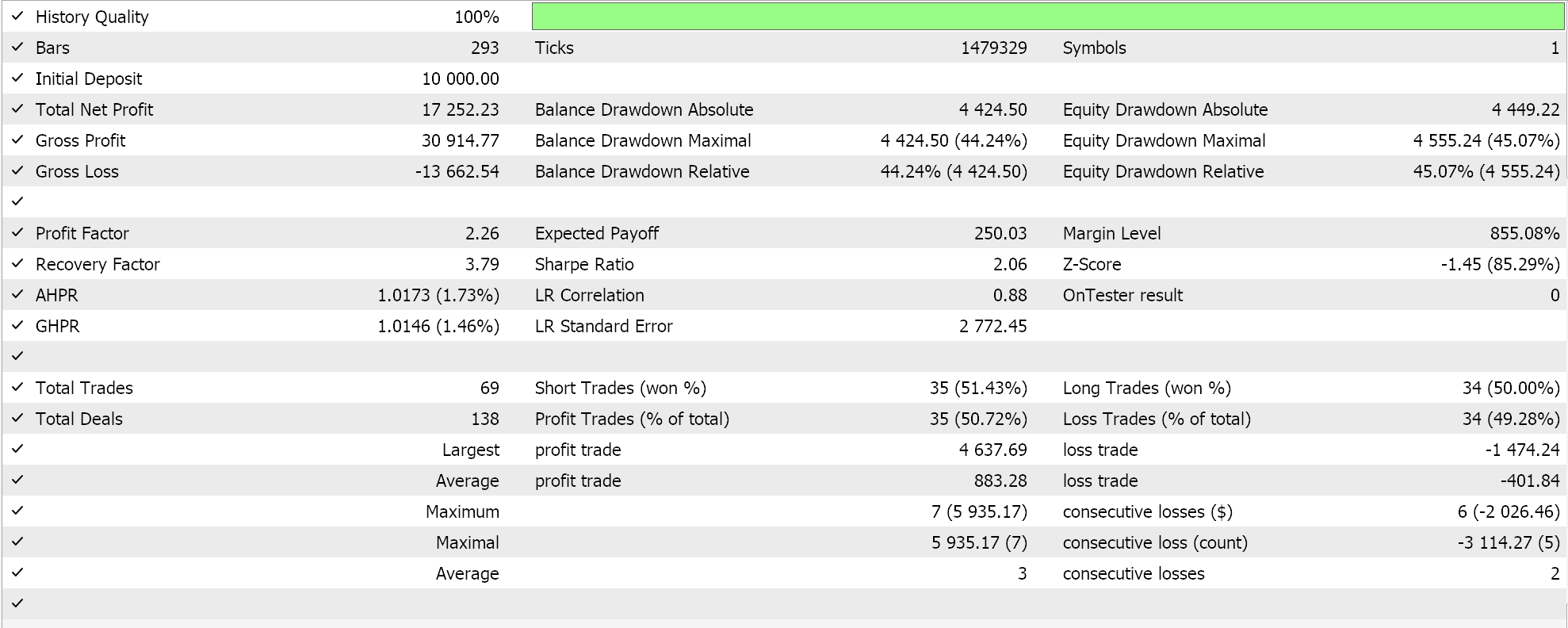
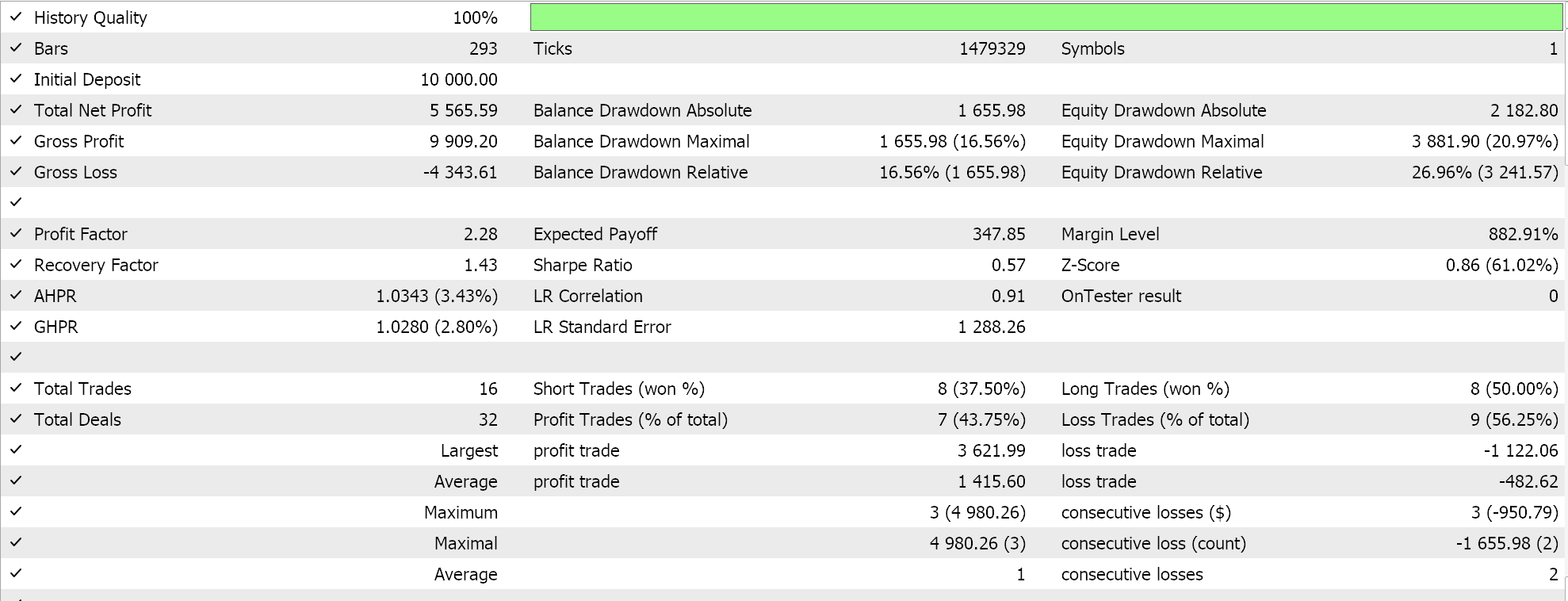
如果我们通过向导组装该信号，并在日线时间帧上依据 2023 年的 EURUSD 进行测试，我们的最佳运行会为我们提供以下报告和净值曲线。

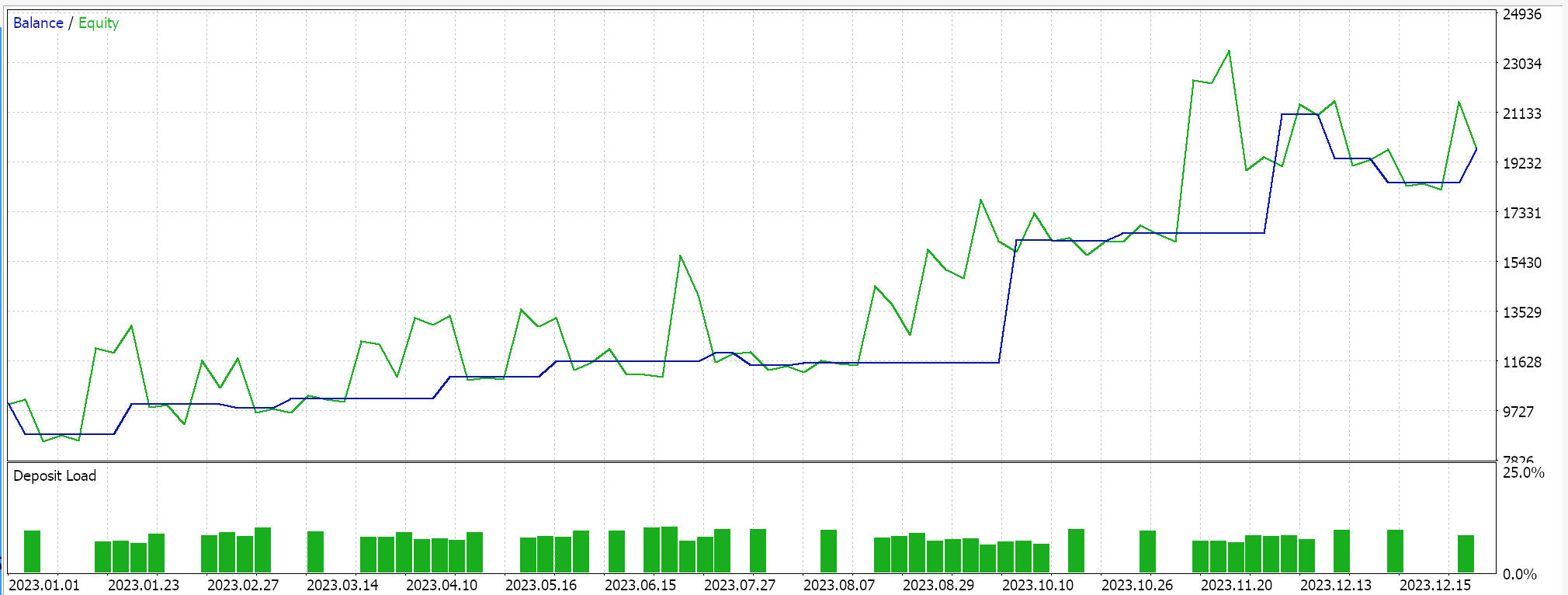
从报告中，您可以说有潜力，不过在这种情况下，我们还未像之前文章中那样进行小规模的前向测试，因此请读者在进一步讨论之前完成这样的操作。

继续以 RSI 的绝对值作为数据集，我们将以类似的措施实现这一点，主要区别在于我们如何考量取得 RSI 读数的 3 个不同的滞后周期。故此，依据这个数据集，我们与原始 OHLC 价格一样，每次获得 4 个数据点，但这些数据点是 RSI 指标值。取它们的滞后周期由我们标记为 A、B 和 C 的 3 个输入参数设置。数据集的填充方式如下：

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalDBSCAN::GetOutput()
{  double _output = 0.0;

...

   RSI.Refresh(-1);
   for(int i = 0; i < m_set_size; i++)
   {  for(int ii = 0; ii < m_key_size; ii++)
      {  if(ii == 0)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i);
         }
         else if(ii == 1)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i + m_lag_a);
         }
         else if(ii == 2)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i + m_lag_a + m_lag_b);
         }
         else if(ii == 3)
         {  m_model.x[i].key[ii] = RSI.Main(StartIndex() + i + m_lag_a + m_lag_b + m_lag_c);
         }
      }
      if(i > 0) //assign classifier only for data points for which eventual bar range is known
      {  m_model.y[i - 1] = (m_close.GetData(StartIndex() + i - 1) - m_close.GetData(StartIndex() + i)) / m_symbol.Point();
      }
   }
   int _o[];

...

...

   return(_output);
}

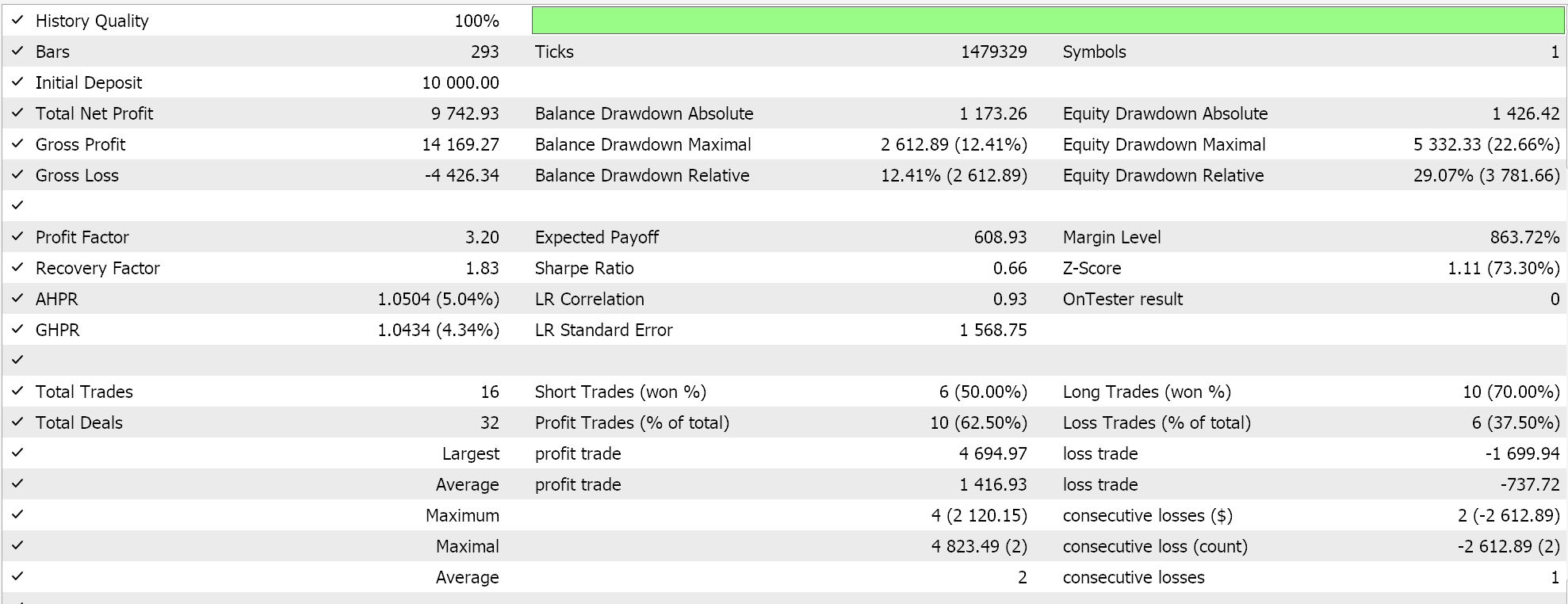
故此，当我们针对同一品种，覆盖 2023 年同期日线时间帧进行测试时，我们从最佳运行中获得以下结果：

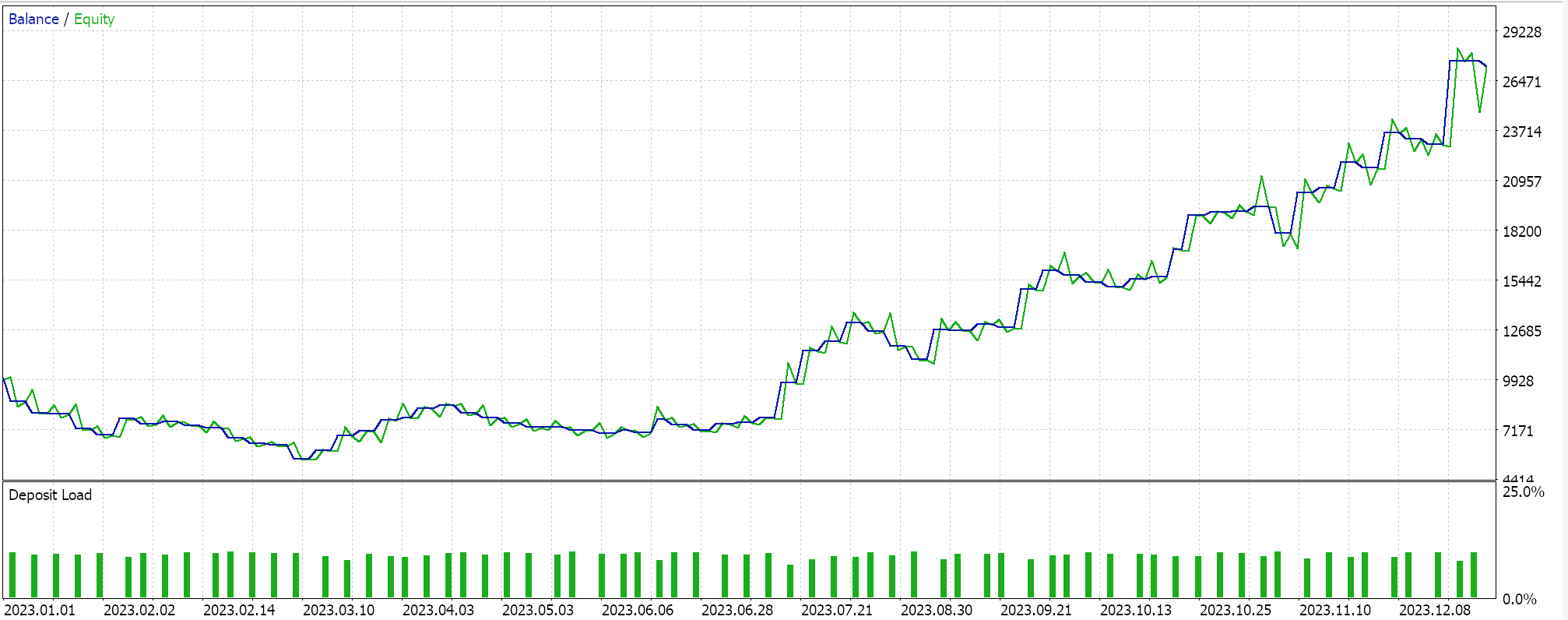
一份有前景的报告，但再一次未下定论，亟待大家自己的努力。本文所有组装的智能系统都通过限价单进行交易，并且不使用止盈或止损价格来平仓。这意味着持仓一直持有，直至信号逆转，然后逆向开新仓。

最后，随着移动平均线的变化，我们就如同采用 RSI 一样填充数据集，主要区别在于，我们正在寻找 MA 指标读数的变化，而对于 RSI，我们对绝对值感兴趣。另一个主要区别是键值，'Spoint' 结构体中 'key' 向量的大小只有 3，而非 4，因为我们关注的是滞后变化，而非绝对读数。

执行测试运行会给出以下最佳运行报告。

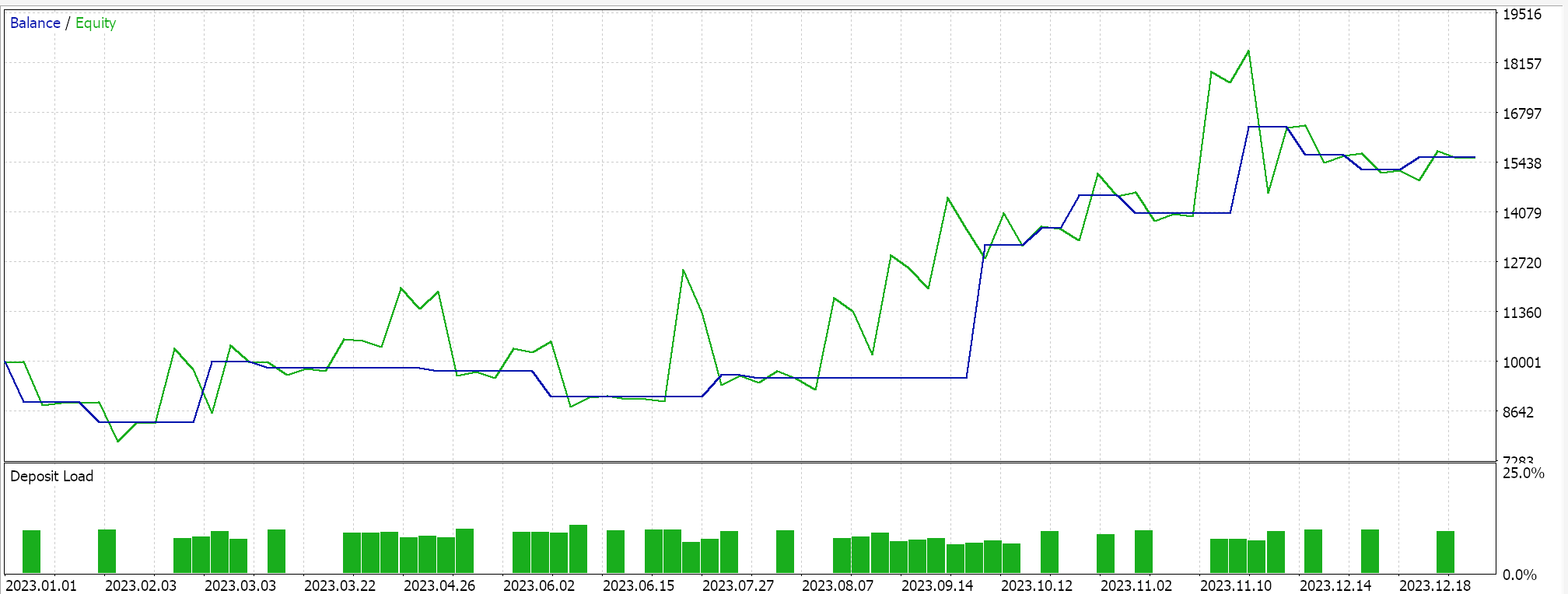
结束语

总而言之，DBSCAN 是一种无监督的数据分类方式，与更传统的方式（如 k-均值）不同，它采用最少的输入参数。它只需要两个参数，其中只有一个 ε 是关键的，这会导致对这个输入的过度依赖或敏感。

尽管过度依赖 ε，但对于任何分类，聚类的数量都是有机判定的，这一事实令其在各种数据集上具有相当的通用性，并且能够更好地处理噪声。

当用在智能信号类的自定义实例中，从原始价格到指标值的各种输入数据集都可以用作证券分类的基础。

除了创建智能信号类的自定义实例外，读者还可以创建类似的智能尾随类或智能资金类的自定义实现，它们也使用 DBSCAN，正如我们在本系列之前的文章中涵盖的那样。

我认为另一个值得关注的途径是 DBSCAN 和聚类通常准备的用途，是数据常规化。许多预测模型往往需要对输入数据进行某种形式的常规化，然后才能用于预测。举例，理想情况下，随机森林算法或神经网络理想情况下需要常规化数据，尤其当馈送的数据是证券价格。在如今流行的运用变换器架构的语言大模型中，与此等效的步骤是嵌入，其中基本上所有文本（包括数字）都被重新分配一个数字，以便通过神经网络进行前馈处理。如果没有这种文本和数字的常规化，网络就不可能切实处理它在开发 AI 算法时所做的大量数据。而且，这种常规化是与异常值打交道，其在在尝试训练网络、并得出可接受的权重和偏差时，可能会令人头疼。聚类和 DBSCAN 可能还有其它相关的用途，但这只是我的看法。祝您狩猎愉快。