Algorithmes d'optimisation de la population : Algorithme des Lucioles (Firefly Algorithm - FA)

Sommaire

1. Introduction
2. Description de l'algorithme
3. Résultats des tests

1. Introduction

La nature a toujours été une source d’inspiration pour de nombreux algorithmes métaheuristiques. Elle a réussi à trouver des solutions aux problèmes sans incitation, sur la base de l'expérience individuelle. La sélection naturelle et la survie des plus aptes ont été les principales motivations de la création des premiers algorithmes métaheuristiques. Dans la nature, les animaux communiquent entre eux de plusieurs manières. Les lucioles utilisent leur capacité à cligner des yeux pour communiquer. Il existe environ 2 000 espèces de lucioles dotées de leurs propres modèles de flash spéciaux. Elles produisent généralement un flash court avec un motif spécifique. La lumière et son intensité sont le résultat de processus biochimiques appelés bioluminescence. On pense que la fonction principale de ces éclairs est d’attirer des partenaires pour s’accoupler ou des victimes potentielles. Certaines lucioles tropicales peuvent synchroniser leurs éclairs, démontrant ainsi un exemple d'auto-organisation biologique. L'intensité de la lumière, en fonction de la distance à sa source, obéit à une loi du carré inverse, de sorte que la lumière vacillante provenant d'une luciole fait réagir les lucioles qui l'entourent et qui voient le flash.

Il existe 2 variantes d'algorithmes d'optimisation de population inspirés du comportement des lucioles : l'algorithme Firefly et l'algorithme Glowworm Swarm Optimization (GSO). La principale différence entre les lucioles et les vers luisants est que ces derniers sont sans ailes. Dans cet article, nous considérerons le premier type d’algorithme d’optimisation.

2. Description de l'algorithme

L'algorithme de Luciole (algorithme F) a été proposé par X-Sh. Yang à l'Université de Cambridge (Royaume-Uni) en 2007 et a immédiatement attiré l'attention des chercheurs en optimisation. L'algorithme Firefly fait partie d'une famille d'algorithmes d'intelligence en essaim qui ont récemment montré des résultats impressionnants dans la résolution de problèmes d'optimisation. L'algorithme Firefly, en particulier, est utilisé pour résoudre des problèmes d'optimisation continue et discrète.

L'algorithme des lucioles comporte 3 règles basées sur les caractéristiques de scintillement des vraies lucioles. Les règles sont les suivantes :

1. Toutes les lucioles se dirigeront vers des homologues plus attrayantes et plus lumineuses.
2. Le degré d'attraction d'une luciole est proportionnel à sa luminosité, qui diminue à mesure que la distance par rapport à une autre luciole augmente en raison du fait que l'air absorbe la lumière. Par conséquent, entre deux lucioles vacillantes, la moins brillante se déplacera vers la plus brillante. S’il n’existe pas d’équivalent plus brillant ou plus attrayant, une luciole se déplacera de manière aléatoire.
3. La luminosité ou l'intensité lumineuse de la luciole est déterminée par la valeur de la fonction objectif du problème.

Initialement, au début de l'algorithme, toutes les lucioles sont dispersées de manière aléatoire dans l'espace de recherche. L'algorithme détermine ensuite les partitions optimales en fonction de 2 phases :

1. Changement d'intensité lumineuse : la luminosité de la luciole dans sa position actuelle se reflète dans la valeur de sa forme physique, évoluant vers une luciole attrayante.
2. La luciole change de position en observant l'intensité lumineuse des lucioles voisines.

Nous pouvons maintenant approfondir plus en détail les subtilités de l’optimisation de Firefly. L'essence de l'algorithme est clairement illustrée dans la figure 1.

Fig. 1 : Lucioles dans l'espace de recherche. La visibilité diminue avec l'augmentation de la distance

L'idée principale derrière le principe de recherche est une diminution non linéaire de la visibilité avec l'augmentation de la distance entre les lucioles. Sans cette relation non linéaire, chaque luciole se déplacerait de manière déterministe vers une source de lumière plus brillante. Mais comme nous le voyons sur la figure 1, la luciole ne choisit pas son parent le plus brillant, car sa lumière est moins perceptible en raison de l'absorption de la lumière par l'environnement. A sa place, elle choisit un homologue moins brillant (bien que le plus brillant de son environnement). Cette fonctionnalité explique la bonne capacité de l’algorithme à se diviser en essaims plus petits. Cela se produit naturellement uniquement en raison de la fonction non linéaire d’absorption de la lumière à distance. Dans la figure 2 ci-dessous, on peut voir la fonction visibilité en fonction de la distance pour l'algorithme avec différentes valeurs du coefficient d'absorption du milieu gamma (l'un des paramètres de l'algorithme).

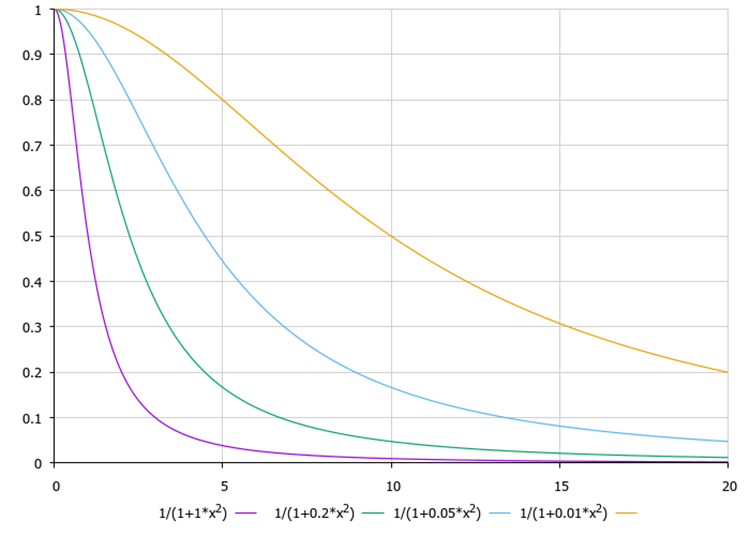
Figure 2 : Fonction de transparence du milieu à partir de la distance f(x), où le coefficient de transparence gamma est respectivement égal à 1,0, 0,2, 0,05 et 0,01

Lorsque gamma tend vers l'infini, l'environnement devient opaque. Et lorsque gamma est nul, l'environnement est complètement transparent. Chaque luciole voit l'autre à n'importe quelle distance dans l'espace de recherche. Que se passe-t-il si gamma = 0,0 ? Toutes les lucioles voleront vers le parent le plus brillant et convergeront vers un point non optimal. Ainsi, l’algorithme ne convergera pas en restant coincé dans l’un des extrema locaux. Que se passe-t-il si l’environnement est complètement opaque ? Les lucioles ne verront personne de plus attirant qu’elles. Selon le concept proposé par l'auteur de l'algorithme, ne voir personne mieux que soi, fait bouger une luciole de manière aléatoire. L'algorithme se transformera en une recherche aléatoire. Dans notre tableau de classification des algorithmes, l'algorithme de recherche aléatoire occupe la dernière place.  

Examinons plus en profondeur l'algorithme et considérons les équations qui décrivent les mouvements des lucioles. La fonction visibilité/distance sous-tend le calcul de ce que l’on appelle l’indice d’attractivité :

attractivité = lucioles [k].f / (1,0 + gamma * distance * distance);

avec :
attractivité : l’indice d’attractivité
gamma : le coefficient d'opacité de l'environnement
distance : la distance euclidienne entre les lucioles
lucioles [k].f : l’intensité lumineuse de la k-ème luciole

L'équation montre clairement que la fonction d'attractivité dépend directement de la dimension du problème et des limites de la valeur de la distance. L'auteur de l'algorithme recommande donc de sélectionner le coefficient de transparence pour un problème d'optimisation spécifique. Je pense qu'il est peu pratique et prend du temps de le faire sans savoir à l'avance comment l'algorithme se comportera. Je pense donc qu'il est nécessaire de normaliser les valeurs de distance dans la plage de 0 à 20. Pour y parvenir, appliquez la fonction Scale() que nous avons utilisée à plusieurs reprises dans d'autres algorithmes. La conversion de la « distance » avant le calcul de l’attractivité ressemble à ceci :

distance = Scale(distance, 0.0, maxDist, 0.0, 20.0, false);

avec :

maxDist : la distance euclidienne maximale entre une paire de lucioles parmi toutes les autres

Dans ce cas, l’attractivité des lucioles ne dépendra pas de la dimension du problème et il n’est pas nécessaire de sélectionner le coefficient gamma pour un problème d’optimisation spécifique. La fonction d’attractivité détermine le type de choix de partenaire que fera chaque luciole. Ce choix est strictement déterminé. L'influence de l'attractivité des lucioles les unes sur les autres détermine le coefficient bêta (le deuxième paramètre de l'algorithme). Comment les capacités de recherche de l'algorithme sont-elles assurées si le choix des lucioles est déjà déterminé à l'avance à chaque itération correspondante ? Pour y parvenir, une composante vectorielle aléatoire et le troisième paramètre d'algorithme (alpha) sont introduits. Les relations comportementales complexes des lucioles ressembleraient à ceci :

lucioles [i].c [c] = Xj + bêta * (Xi - Xj) + alpha * r * v [c];

avec :
lucioles [i].c [c] : la c-ième coordonnée de la i-ème luciole
bêta : le coefficient d'influence de l'attraction des lucioles
alpha : le coefficient qui affecte la composante aléatoire lors du déplacement des lucioles, donnant les écarts par rapport à l'objectif de mouvement
r : un nombre aléatoire dans la plage [-1,0 ; 1,0]
v[c] : la composante vectorielle caractérisant la distance entre les points extrêmes de la plage de recherche par la c-ième coordonnée
Хj : la coordonnée correspondante de la luciole dans la paire, vers laquelle il y aura du mouvement
Xi : la coordonnée correspondante de la luciole pour laquelle le mouvement est calculé

Il est maintenant temps de décrire le code de l'algorithme. C'est relativement simple. Examinons-le plus en détail.

Une luciole sera décrite avec une structure simple S_Firefly comportant 2 composantes, à savoir c[] - les coordonnées, et f - la luminosité de la luciole (fonction fitness). Puisque pour chaque luciole il n'y a qu'un seul individu à l'itération correspondante, vers lequel elle se déplacera en formant une paire, on ne risque pas d'écraser les coordonnées lors du calcul du prochain mouvement. Pour cela, je présenterai une structure spéciale ci-dessous.

//——————————————————————————————————————————————————————————————————————————————
struct S_Firefly
{
  double c  []; //coordinates
  double f;     //the value of the fitness function
};
//——————————————————————————————————————————————————————————————————————————————

La structure S_Attractiveness est destinée à stocker la valeur d'attractivité et le numéro de la luciole correspondante par paire. Chaque luciole ne se déplace pas vers les coordonnées de la plus attractive, mais vers les coordonnées où son partenaire s'est déjà déplacé. Il y a une certaine différence avec la version de l'algorithme décrite par l'auteur, mais c'est ainsi qu'il fonctionne mieux.

//——————————————————————————————————————————————————————————————————————————————
struct S_Attractiveness
{
  double a; //attractiveness
  int    i; //index of the most attractive firefly
};
//——————————————————————————————————————————————————————————————————————————————

L'algorithme Firefly est décrit à l'aide de la classe C_AO_FA. Il existe 3 méthodes publiques : Init() pour l'initialisation initiale, et deux méthodes publiques qui doivent être appelées à chaque itération : Flight() et Luminosity(), des méthodes et des membres privés pour stocker les constantes des paramètres.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_FA
{
  //----------------------------------------------------------------------------
  public: S_Firefly fireflies []; //fireflies
  public: double    rangeMax  []; //maximum search range
  public: double    rangeMin  []; //minimum search range
  public: double    rangeStep []; //step search
  public: double    cB        []; //best coordinates
  public: double    fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,  //number of opt. parameters
                     const int    sizeP,    //swarm size
                     const double alphaP,   //alpha, randomness in motion
                     const double betaP,    //beta, effect of attractiveness
                     const double gammaP);  //gamma, transparency of the environment

  public: void Flight ();
  public: void Luminosity ();

  //----------------------------------------------------------------------------
  private: S_Attractiveness att [];
  private: int    swarmSize;
  private: int    params;
  private: double maxDist;
  private: double v [];

  private: double alpha;      //randomness in motion
  private: double beta;       //effect of attractiveness
  private: double gamma;      //transparency of the environment
  private: bool   luminosity;

  private: double SeInDiSp  (double In, double inMin, double inMax, double step);
  private: double RNDfromCI (double min, double max);
  protected: double Scale   (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

La méthode Init() est utilisée pour l'initialisation et doit être appelée avant le début de chaque optimisation. Ses paramètres sont des paramètres de superstructure de l'algorithme. La méthode allouera de la mémoire aux tableaux et réinitialisera la valeur de luminosité de la luciole globale et de chaque luciole individuelle.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FA::Init (const int    paramsP, //number of opt. parameters
                    const int    sizeP,   //swarm size
                    const double alphaP,  //alpha, randomness in motion
                    const double betaP,   //beta, effect of attractiveness
                    const double gammaP)  //gamma, transparency of the environment
{
  fB = -DBL_MAX;

  params    = paramsP;
  swarmSize = sizeP;
  alpha     = alphaP;
  beta      = betaP;
  gamma     = gammaP;

  ArrayResize (rangeMax,  params);
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeStep, params);
  ArrayResize (v,         params);
  ArrayResize (att,       swarmSize);

  luminosity = false;

  ArrayResize (fireflies, swarmSize);

  for (int i = 0; i < swarmSize; i++)
  {
    ArrayResize (fireflies [i].c,  params);
    fireflies [i].f = -DBL_MAX;
  }

  ArrayResize (cB, params);
}
//——————————————————————————————————————————————————————————————————————————————

Considérons la première méthode publique appelée à chaque itération : Flight(). La logique principale de l'algorithme est concentrée dans cette méthode. Nous allons donc l'examiner plus en détail. La variable 'luminosity' sert de drapeau nous permettant de déterminer si l'algorithme s'exécute à la première itération ou aux suivantes. Si le drapeau n'est pas positionné, il est nécessaire de répartir les lucioles de manière aléatoire dans l'espace de coordonnées conformément à la répartition uniforme. En même temps, nous définissons le vecteur de déplacement pour chaque coordonnée et nous calculons immédiatement la distance euclidienne maximale possible pouvant être entre les lucioles (comme déjà mentionné, cela est nécessaire pour normaliser les distances entre les lucioles pour éviter la dépendance du coefficient de transparence de l'environnement sur la dimension du problème). Après ces opérations, nous activons le drapeau 'luminosity'.

if (!luminosity)
{
  fB = -DBL_MAX;

  //--------------------------------------------------------------------------
  double summCoordinates = 0.0;
  for (int c = 0; c < params; c++)
  {
    v [c] = rangeMax [c] - rangeMin [c];
    summCoordinates += pow (v [c], 2.0);
  }
  maxDist = pow (summCoordinates, 0.5);

  //--------------------------------------------------------------------------
  for (int s = 0; s < swarmSize; s++)
  {
    for (int k = 0; k < params; k++)
    {
      fireflies [s].c  [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      fireflies [s].c  [k] = SeInDiSp (fireflies [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    }
  }

  luminosity = true;
}

À partir de la deuxième itération et des suivantes, une fois que les lucioles ont été distribuées de manière aléatoire lors de la première itération et ont commencé à briller (la fonction de fitness a été calculée pour elles), nous pouvons calculer le degré d'attractivité de chaque luciole. Pour cela, nous devons calculer la distance euclidienne entre toutes les paires possibles de lucioles : additionnez simplement les carrés des différences de coordonnées et trouvez la racine de leur somme. La distance calculée sera utilisée dans l’équation de calcul de l’attractivité. C’est ainsi que l’on obtient la seule paire possible pour chaque luciole. Déterminez la luminosité maximale pour toutes les lucioles. Cela sera nécessaire afin de déterminer la luciole la plus brillante, pour laquelle il ne sera pas possible d'en trouver un couple et qui se déplacera seule dans l'espace. Elle aura peut être plus de chance lors de la prochaine itération.

//measure the distance between all------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  att [i].a = -DBL_MAX;

  for (int k = 0; k < swarmSize; k++)
  {
    if (i == k) continue;

    summCoordinates = 0.0;
    for (int c = 0; c < params; c++) summCoordinates += pow (fireflies [i].c [c] - fireflies [k].c [c], 2.0);

    distance = pow (summCoordinates, 0.5);
    distance = Scale (distance, 0.0, maxDist, 0.0, 20.0, false);
    attractiveness = fireflies [k].f / (1.0 + gamma * distance * distance);

    if (attractiveness > att [i].a)
    {
      att [i].a = attractiveness;
      att [i].i = k;
    }

    if (fireflies [i].f > maxF) maxF = fireflies [i].f;
  }
}

Cette partie du code de la méthode Flight() est responsable du vol des lucioles. Pour la malheureuse luciole dont la luminosité est supérieure à toutes les autres, le calcul s'effectue un peu différemment : le vecteur de mouvement est ajouté à sa position actuelle via le coefficient alpha multiplié par un nombre aléatoire [-1.0 ; 1.0]. Dans l'algorithme, cela agit théoriquement comme une étude supplémentaire de la meilleure solution dans l'espoir qu'elle soit encore meilleure. Mais comme nous le verrons plus tard, cette technique s'avérera inutile. A ce stade, nous considérons la version classique de l’algorithme.

Pour toutes les autres lucioles pour lesquelles un couple a déjà été trouvé, le calcul du mouvement consistera à se déplacer vers le couple approprié avec l'ajout d'une composante aléatoire (j'en parlais plus haut).

//flight--------------------------------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  if (fireflies [i].f >= maxF)
  {
    for (int c = 0; c < params; c++)
    {
      r  = RNDfromCI (-1.0, 1.0);
      fireflies [i].c [c] = fireflies [i].c [c] + alpha * r * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); 
    }
  }
  else
  {
    for (int c = 0; c < params; c++)
    {
      r  = RNDfromCI (-1.0, 1.0);
      Xi = fireflies [i].c [c];
      Xj = fireflies [att [i].i].c [c];
      fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Une méthode simple appelée à chaque itération. Nous mettrons ici à jour la meilleure solution.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FA::Luminosity ()
{
  for (int i = 0; i < swarmSize; i++)
  {
    if (fireflies [i].f > fB)
    {
      fB = fireflies [i].f;
      ArrayCopy (cB, fireflies [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Passons aux tests et regardons les résultats de l'algorithme sur les fonctions de test :

2022.12.16 13:39:00.102 Test_AO_FA (EURUSD, M1) ==============================
2022.12.16 13:39:05.930 Test_AO_FA (EURUSD, M1) 1 skin ; Func exécute 10 000 résultats : 4,901742065217812
2022.12.16 13:39:05.930 Test_AO_FA (EURUSD, M1) Score : 0,99603
2022.12.16 13:39:13.579 Test_AO_FA (EURUSD, M1) 20 skins ; Func exécute 10 000 résultats : 3,2208359936020665
2022.12.16 13:39:13.579 Test_AO_FA (EURUSD, M1) Score : 0,59468
2022.12.16 13:39:53.607 Test_AO_FA (EURUSD, M1) 500 Skins ; Func exécute 10 000 résultats : 0,98491319842575
2022.12.16 13:39:53.607 Test_AO_FA (EURUSD, M1) Score : 0,06082
2022.12.16 13:39:53.607 Test_AO_FA (EURUSD,M1) ==============================
2022.12.16 13:39:59.313 Test_AO_FA (EURUSD,M1) 1 Forest ; Func exécute 10 000 résultats : 1,578196881663454
2022.12.16 13:39:59.313 Test_AO_FA (EURUSD, M1) Score : 0,89271
2022.12.16 13:40:07.274 Test_AO_FA (EURUSD, M1) 20 Forest ; Func exécute 10 000 résultats : 0,3101994341994826
2022.12.16 13:40:07.274 Test_AO_FA (EURUSD, M1) Score : 0,17546
2022.12.16 13:40:49.159 Test_AO_FA (EURUSD, M1) 500 Forest ; Func exécute 10 000 résultats : 0,06829102669136165
2022.12.16 13:40:49.159 Test_AO_FA (EURUSD, M1) Score : 0,03863
2022.12.16 13:40:49.159 Test_AO_FA (EURUSD, M1) ==============================
2022.12.16 13:40:54.895 Test_AO_FA (EURUSD,M1) 1 Megacity ; Func exécute 10 000 résultats : 8,2
2022.12.16 13:40:54,895 Test_AO_FA (EURUSD, M1) Score : 0,68333
2022.12.16 13:41:02.777 Test_AO_FA (EURUSD, M1) 20 Megacity ; Func exécute 10 000 résultats : 1,5900000000000003
2022.12.16 13:41:02.777 Test_AO_FA (EURUSD, M1) Score : 0,13250
2022.12.16 13:41:43.901 Test_AO_FA (EURUSD, M1) 500 Megacity ; Func exécute 10 000 résultats : 0,2892
2022.12.16 13:41:43.901 Test_AO_FA (EURUSD, M1) Score : 0,02410
2022.12.16 13:41:43.901 Test_AO_FA (EURUSD, M1) ==============================
2022.12.16 13:41:43.901 Test_AO_FA (EURUSD, M1) Tous les scores pour C_AO_FA : 0,39980648892951776

Les résultats ne sont pas impressionnants, c’est un euphémisme. L'algorithme n'est que légèrement meilleur que PSO, FSS et GWO dans les tests individuels. Il occupe la deuxième position en partant du bas sur la note totale, ne laissant derrière lui que l’algorithme de recherche aléatoire. Compte tenu de tout cela, l'idée est née de revoir le calcul des indicateurs estimés dans les tests. Dans les articles suivants, je passerai à un schéma plus pratique de calcul des notes. J'ajouterai l'histogramme des résultats finaux dans l'article actuel. Il montrera clairement le rapport de performances entre les algorithmes individuels.

L'algorithme Firefly classique est facile à mettre en œuvre. Mais des études montrent qu’il converge lentement et tombe facilement dans le piège des extrêmes locaux pour les problèmes multimodaux. Il lui manque également des coefficients qui dépendent paramétriquement de l’itération en cours. L’un des objectifs de l’étude était de modifier l’algorithme standard de Firefly pour améliorer ses performances.

L’idée même de l’algorithme est assez originale. Il serait dommage de tout laisser tel quel et de ne pas chercher à améliorer ses caractéristiques. J'ai donc tenté de modifier l'algorithme en remplaçant la composante aléatoire par un vol de Levy. Le vol de Levy ne peut pas améliorer la capacité de recherche de chaque algorithme. Après avoir examiné l'algorithme de recherche du coucou, j'ai essayé d'améliorer d'autres algorithmes en utilisant cette méthode, mais cela n'a pas apporté les résultats escomptés. Apparemment, cela devrait être cohérent d’une certaines manière avec la stratégie de recherche interne au sein de l’algorithme qui le complète. Dans ce cas particulier, l'application du vol de Levy a produit un effet frappant : les capacités de l'algorithme ont considérablement augmenté. Nous en parlerons dans la partie de cet article sur les résultats des tests.

Voici la partie du code où la modification a été effectuée. Premièrement, dans la version classique, la luciole ayant la meilleure luminosité se déplace dans une direction aléatoire depuis sa position actuelle. Ensuite, notre meilleure luciole quitte la meilleure position globale en essayant d’améliorer non pas sa position actuelle, mais la solution dans son ensemble. Nous ajoutons ensuite un nombre aléatoire de distribution du vol de Levy (distribution avec des queues lourdes) de même coefficient alpha, prenant en compte le vecteur mouvement, aux coordonnées de la meilleure solution. Cela a réellement permis d'améliorer les coordonnées de la solution globale en affinant la zone voisine.

Comme vous pouvez le constater, le comportement du reste des lucioles obéit désormais aux mêmes règles classiques, bien qu'ajustées, pour tenir compte de la composante aléatoire du vol de Levy. C’est toute la modification apportée à l’algorithme.

//flight--------------------------------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  if (fireflies [i].f >= maxF)
  {
    for (int c = 0; c < params; c++)
    {
      r1 = RNDfromCI (0.0, 1.0);
      r1 = r1 > 0.5 ? 1.0 : -1.0;
      r2 = RNDfromCI (1.0, 20.0);

      fireflies [i].c [c] = cB [c] + alpha * r1 * pow (r2, -2.0) * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
  else
  {
    for (int c = 0; c < params; c++)
    {
      r1 = RNDfromCI (0.0, 1.0);
      r1 = r1 > 0.5 ? 1.0 : -1.0;
      r2 = RNDfromCI (1.0, 20.0);

      Xi = fireflies [i].c [c];
      Xj = fireflies [att [i].i].c [c];

      fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r1 * pow (r2, -2.0) * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Tableau des fonctions des vols de Levy sur la figure 3. Comment l’exposant dans l’équation de la fonction peut-il affecter le comportement de l’algorithme ? D'après mes recherches, à mesure que le degré augmente, le nombre de sauts longs (queues lourdes) diminue par rapport aux sauts courts. Et la capacité de l'algorithme à affiner les coordonnées à proximité de la meilleure solution s'améliore. Du fait qu'il y a peu de sauts en longueur, la probabilité de rester coincé dans les extrema locaux augmente. Cet effet sera plus visible lors de l'étude de fonctions discrètes, alors qu'il ne sera pas aussi prononcé sur les fonctions lisses. Au contraire, avec une diminution de l'exposant, le nombre de sauts longs augmente, les capacités de recherche de l'algorithme s'améliorent, mais la précision de convergence se détériore. Nous avons donc besoin d'un juste milieu entre précision et recherche. Cela peut être également différent selon le problème d’optimisation.

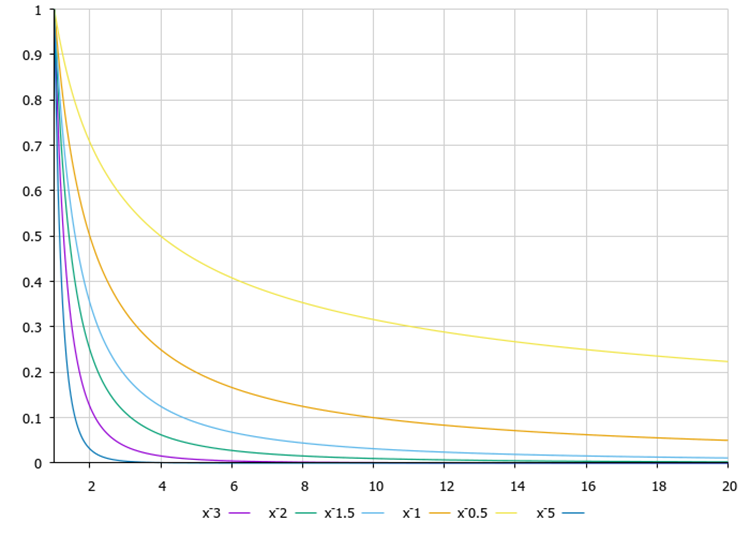
Fig. 3 : Fonction du vol de Levy, degrés 0,5 à 3,0 

Passons donc aux résultats des tests de la version modifiée de l'algorithme. Vous pouvez voir ci-dessous à quel point les performances de la version originale se sont améliorées par rapport à la version classique.

2022.12.16 13:07:15.925 Test_AO_FAm (EURUSD,M1) ==============================
2022.12.16 13:07:21.544 Test_AO_FAm (EURUSD,M1) 1 skin ; Func exécute 10 000 résultats : 4,854437214435259
2022.12.16 13:07:21.544 Test_AO_FAm (EURUSD,M1) Score : 0,98473
2022.12.16 13:07:29.518 Test_AO_FAm (EURUSD,M1) 20 skins ; Func exécute 10 000 résultats : 4,588539001298423
2022.12.16 13:07:29.518 Test_AO_FAm (EURUSD,M1) Score : 0,92124
2022.12.16 13:08:12.587 Test_AO_FAm (EURUSD, M1) 500 Skins ; Func exécute 10 000 résultats : 1,981278990090829
2022.12.16 13:08:12.587 Test_AO_FAm (EURUSD, M1) Score : 0,29872
2022.12.16 13:08:12.587 Test_AO_FAm (EURUSD,M1) ==============================
2022.12.16 13:08:18.336 Test_AO_FAm (EURUSD,M1) 1 Forest ; Func exécute 10 000 résultats : 1,7665409595127233
2022.12.16 13:08:18.336 Test_AO_FAm (EURUSD, M1) Score : 0,99924
2022.12.16 13:08:26.432 Test_AO_FAm (EURUSD,M1) 20 Forest ; Func exécute 10 000 résultats : 0,6261364994589462
2022.12.16 13:08:26.432 Test_AO_FAm (EURUSD,M1) Score : 0,35417
2022.12.16 13:09:10.587 Test_AO_FAm (EURUSD,M1) 500 Forest ; Func exécute 10 000 résultats : 0,14269062630878
2022.12.16 13:09:10.587 Test_AO_FAm (EURUSD, M1) Score : 0,08071
2022.12.16 13:09:10.587 Test_AO_FAm (EURUSD,M1) ==============================
2022.12.16 13:09:16.393 Test_AO_FAm (EURUSD,M1) 1 Megacity ; Func exécute 10 000 résultats : 10,0
2022.12.16 13:09:16.393 Test_AO_FAm (EURUSD,M1) Score : 0,83333
2022.12.16 13:09:24.373 Test_AO_FAm (EURUSD, M1) 20 Megacity ; Func exécute 10 000 résultats : 1.7899999999999998
2022.12.16 13:09:24.373 Test_AO_FAm (EURUSD,M1) Score : 0,14917
2022.12.16 13:10:09.298 Test_AO_FAm (EURUSD, M1) 500 Megacity ; Func exécute 10 000 résultats : 0,5076
2022.12.16 13:10:09.298 Test_AO_FAm (EURUSD,M1) Score : 0,04230
2022.12.16 13:10:09.298 Test_AO_FAm (EURUSD,M1) ==============================
2022.12.16 13:10:09.298 Test_AO_FAm (EURUSD, M1) Tous les scores pour C_AO_FAm : 0,5181804234713119

Comme vous pouvez le constater, l'algorithme modifié affiche non seulement de meilleurs résultats, mais occupe également une position de leader dans le tableau de notation. Nous examinerons de plus près les résultats dans la section suivante. Ci-dessous, une animation de la version modifiée de l'algorithme sur le banc d'essai.

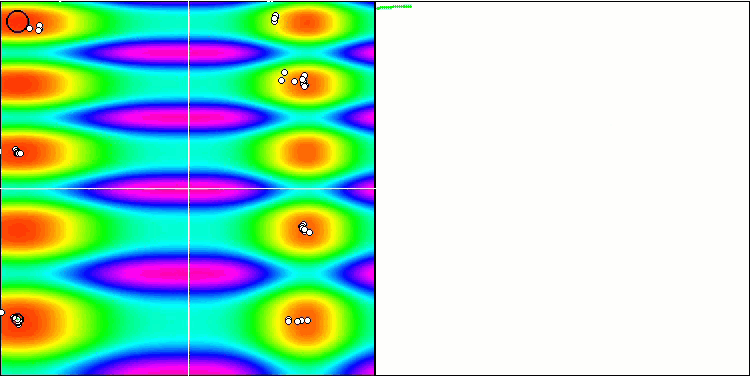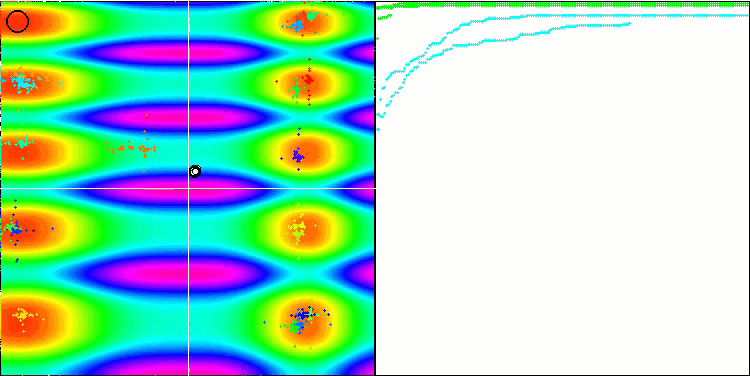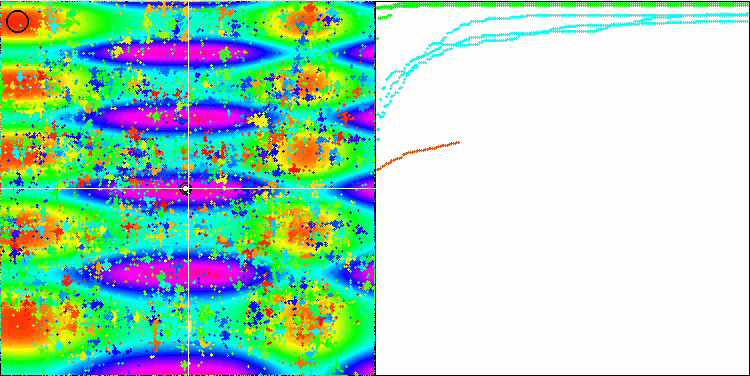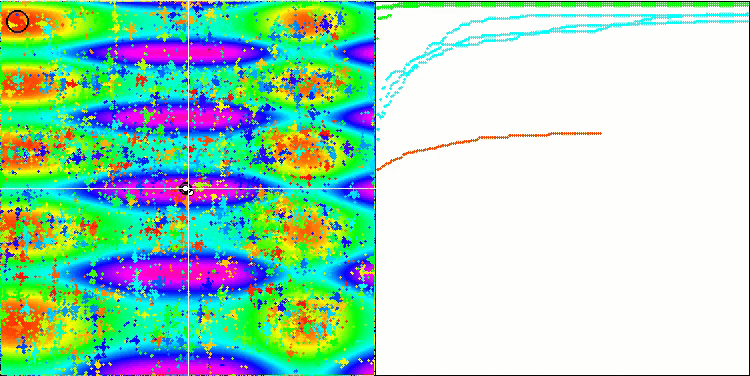
  FAm sur la fonction de test Skin.

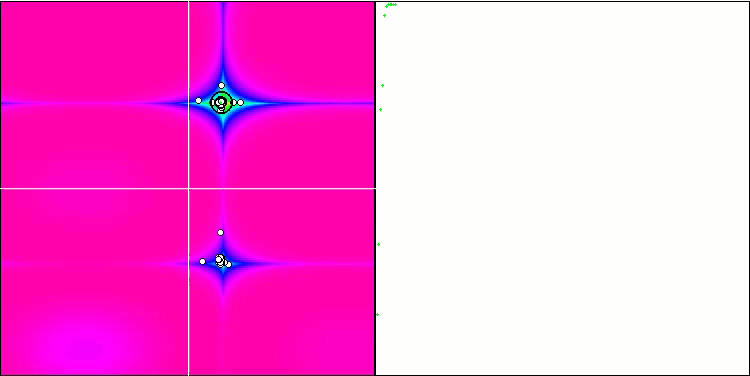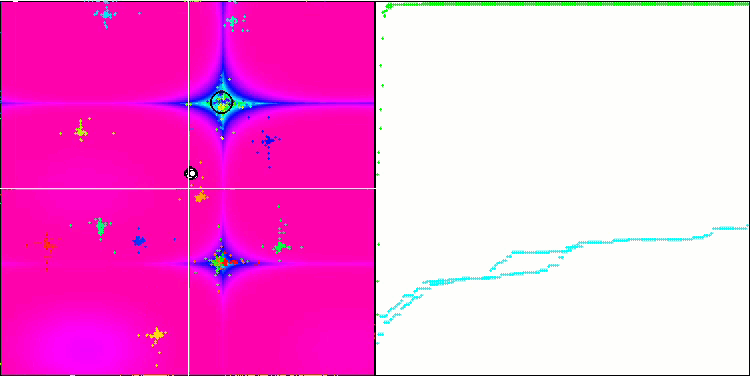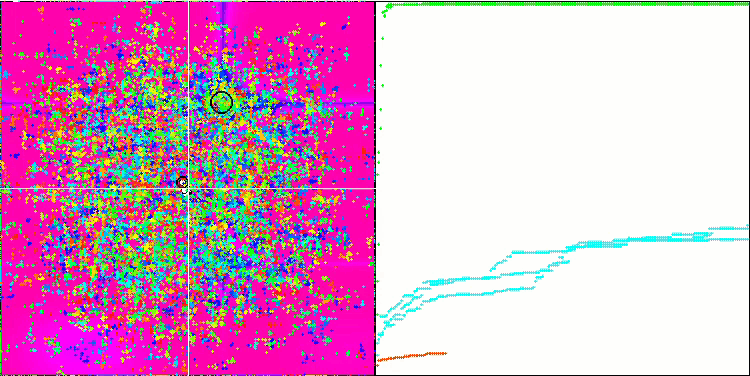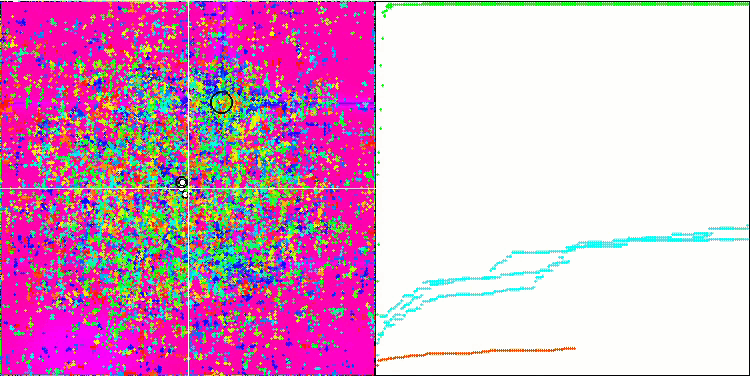
  FAm sur la fonction test Forest.

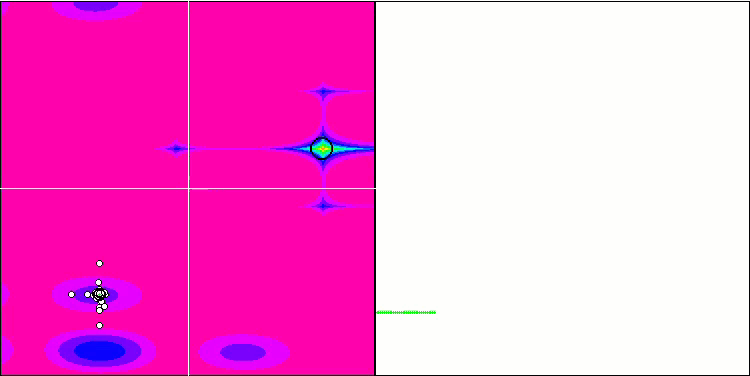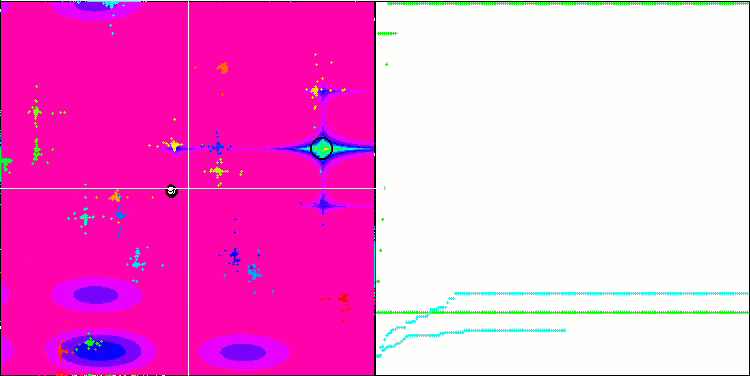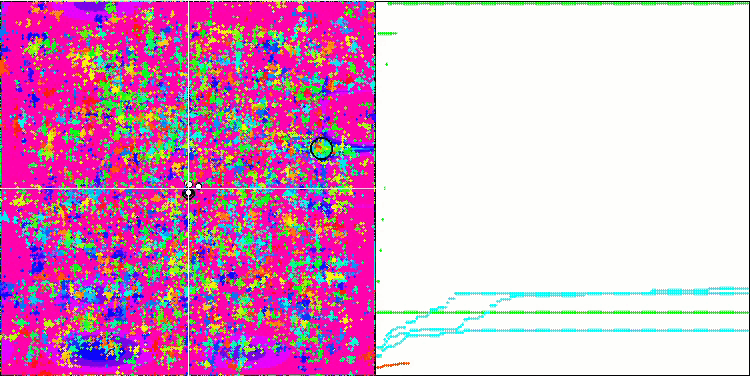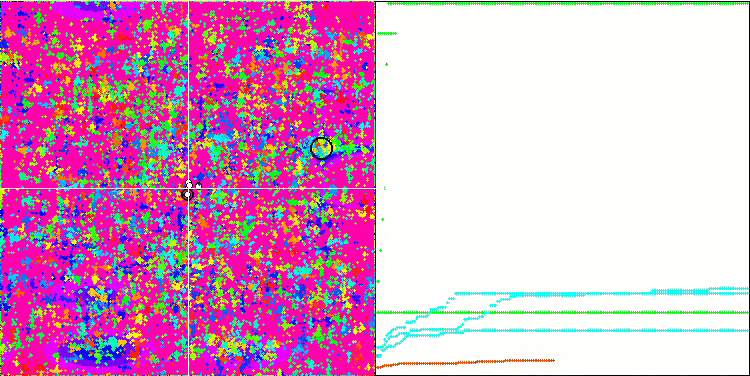
  FAm sur la fonction test Megacity .

3. Résultats des tests

L'algorithme de luciole modifié (FAm) a obtenu d'excellents résultats dans tous les tests. Les résultats dépendent généralement des paramètres de l'algorithme. Dans le cas de certains paramètres, une convergence de 100% a été obtenue sur les trois fonctions à deux variables. La grande évolutivité de l'algorithme lui confère un leadership dans les tests avec 40 et 1 000 paramètres. Les paramètres bêta et gamma ont une forte influence permettant d'obtenir à la fois une convergence élevée et une résistance au blocage dans les extrema locaux. Les résultats varient considérablement, ce qui peut généralement être attribué aux inconvénients de l’algorithme. Toutes choses étant égales par ailleurs, l’algorithme est le plus puissant parmi ceux examinés précédemment. Son utilisation peut être recommandée dans un très large éventail de tâches, notamment les tâches d’apprentissage automatique et d’intelligence artificielle, en particulier lors de la formation des réseaux de neurones.

Vous trouverez ci-dessous le tableau de notation final, dans lequel l'algorithme de luciole modifié prend la tête. Malheureusement, l’algorithme classique, malgré son originalité, n’a pas permis d’obtenir de bons résultats. La sélection des paramètres de réglage n’a pas non plus été couronnée de succès.

AO	Description	Skin			Skin final	Forest			Forest final	Megacity (discrète)			Megacity final	Résultat final
		2 paramètres (1 F)	40 paramètres (20 F)	1.000 paramètres (500 F)		2 paramètres (1 F)	40 paramètres (20 F)	1.000 paramètres (500 F)		2 paramètres (1 F)	40 paramètres (20 F)	1.000 paramètres (500 F)
Fam	algorithme de luciole M	0,98473	0,92124	0,29872	0,73490	0,99924	0,35417	0,08071	0,47804	0,83333	0,14917	0,04230	0,34160	0,51817889
COAm	algorithme d'optimisation du coucou M	1,00000	0,85911	0,14316	0,66742	0,99283	0,28787	0,04551	0,44207	1,00000	0,24917	0,03537	0,42818	0,51255778
ACOm	optimisation des colonies de fourmis M	0,98229	0,79108	0,12602	0,63313	1,00000	0,62077	0,11521	0,57866	0,38333	0,44000	0,02377	0,28237	0,49805222
ABCm	colonie d'abeilles artificielle M	1,00000	0,63922	0,08076	0,57333	0,99908	0,20112	0,03785	0,41268	1,00000	0,16333	0,02823	0,39719	0,46106556
ABC	colonie d'abeilles artificielles	0,99339	0,73381	0,11118	0,61279	0,99934	0,21437	0,04215	0,41862	0,85000	0,16833	0,03130	0,34988	0,46043000
GWO	optimiseur du loup gris	0,99900	0,48033	0,18924	0,55619	0,83844	0,08755	0,02555	0,31718	1,00000	0,10000	0,02187	0,37396	0,41577556
FSS	recherche du banc de poissons	0,99391	0,5692	0,11341	0,55884	0,85172	0,12143	0,03223	0,33513	0,91667	0,08583	0,02583	0,34278	0,41224778
PSO	optimisation des essaims de particules	0,99627	0,38080	0,05089	0,47599	0,93772	0,14540	0,04856	0,37723	1,00000	0,09333	0,02233	0,37189	0,40836667
FA	algorithme de luciole	0,99603	0,59468	0,06082	0,55051	0,89271	0,17546	0,03863	0,36893	0,68333	0,13250	0,02410	0,27998	0,39980649
RND	aléatoire	0,99932	0,44276	0,06827	0,50345	0,83126	0,11524	0,03048	0,32566	0,83333	0,09000	0,02403	0,31579	0,38163222

A partir de cet article, je publierai un histogramme, sur lequel le meilleur algorithme au moment du test aura 100 points conditionnels, alors que le pire algorithme n’aura qu’1 point. Je pense que c'est la méthode d'affichage la plus pratique en termes de perception visuelle puisque nous pouvons clairement voir l'ampleur des résultats finaux des algorithmes du tableau de notation. Nous pouvons maintenant voir à quel point l’algorithme aléatoire est en retard sur le leader.

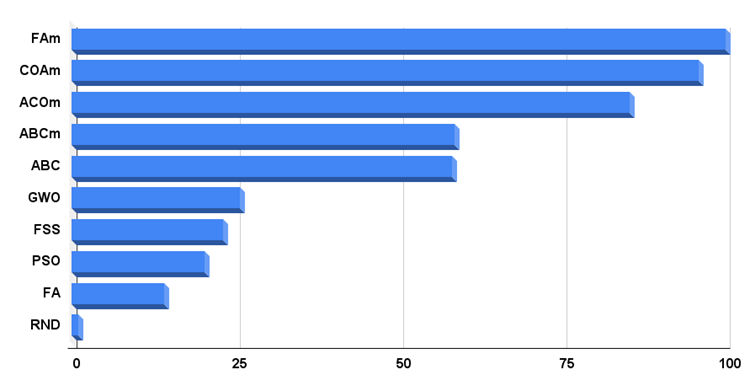
Fig. 4 : Histogramme des résultats finaux des algorithmes de test

Comme vous vous en souvenez peut-être, les algorithmes métaheuristiques sont des méthodes approximatives pour résoudre des problèmes d'optimisation qui utilisent la propriété du hasard avec une hypothèse raisonnable dans leur moteur de recherche. Ils tentent d'améliorer la qualité des solutions disponibles par le biais d'itérations à partir d'un ensemble généré aléatoirement de solutions valides en examinant et en utilisant l'espace de solution. Bien que ces algorithmes ne soient pas garantis optimaux, ils sont testés pour donner une solution raisonnable et acceptable. De plus, ils ont l’avantage que le comportement du problème ne les affecte pas beaucoup, ce qui les rend utiles dans de nombreuses tâches. La présence de nombreux algorithmes disponibles permet de choisir celui qui convient pour résoudre un problème, en fonction de son comportement.

Depuis l’avènement des algorithmes évolutionnaires, de nombreuses recherches ont été menées sur les algorithmes heuristiques. La mise en œuvre de nouveaux algorithmes a été l’un des principaux domaines de recherche. Il existe actuellement plus de 40 algorithmes métaheuristiques. La plupart d’entre eux sont créés en simulant des scénarios issus de la nature.

Les avantages et les inconvénients font référence à une version modifiée de l'algorithme Firefly (FAm).

Avantages :

• Mise en œuvre simple. Facile à modifier.
• Haute évolutivité.
• Convergence élevée (peut varier en fonction des paramètres de l'algorithme).
• La possibilité de regrouper la région de l’espace de recherche en groupes distincts autour des extrema locaux.

Inconvénients :

• Forte influence des paramètres sur les résultats d'optimisation.
• Avec certains paramètres, l’algorithme a tendance à rester bloqué dans des extrema locaux.

Chaque article présente une archive contenant les versions actuelles mises à jour des codes algorithmiques de tous les articles précédents. Chaque nouvel article est l'expérience personnelle accumulée de l'auteur. Les conclusions et les jugements sont basés sur les expériences réalisées sur un banc d'essai spécial développé à cet effet.