Automating Black-Scholes Greeks: Advanced Scalping and Microstructure Trading

Table of contents:

1. Introduction
2. Automation Overview
3. Getting Started
4. Back Results
5. Conclusion

Introduction

In the previous article, we laid the foundation by explaining the core mechanics of the Delta and Gamma Greeks under the Black‑Scholes model—how Delta captures directional sensitivity and how Gamma measures the rate of change of Delta. We showed how these parameters, originally designed for options hedging, can be reframed in the context of trading and volatility, setting the stage for algorithmic applications.

We move beyond theoretical exposition and into implementation. Furthermore, we will cover how to systematically calculate Greeks in an algorithmic environment, integrate them into your MetaTrader 5 Expert Advisor framework, and use them as real-time triggers for scalping and microstructure strategies. We’ll explore how Delta and Gamma can be used not just for hedging but as powerful input signals in high-frequency contexts: identifying ultra-short-term liquidity shifts, and automating precise entries and exits in fast‐moving markets.

Automation Overview

Our primary objective is to create an automated trading system that dynamically manages option positions through continuous delta hedging and strategic gamma scalping. The core concept revolves around maintaining a delta-neutral portfolio while capitalizing on gamma-driven price movements. Since options' delta values change as the underlying asset price moves (a phenomenon measured by gamma), we need an automated system that can continuously monitor these Greek exposures and execute trades to rebalance the portfolio. This approach aims to profit from the volatility of the underlying asset rather than its directional movement, creating a market-neutral strategy that generates returns through frequent, small adjustments rather than betting on price direction.

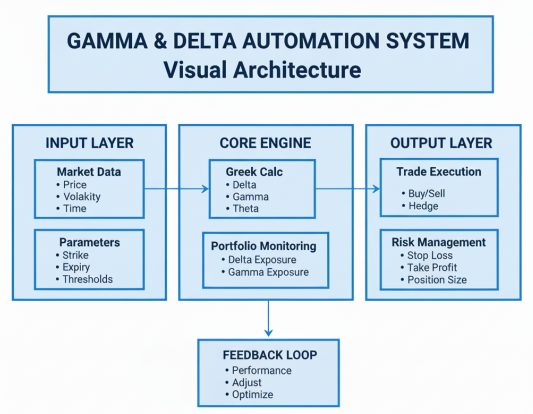
The automation process involves implementing real-time calculations of Black-Scholes Greeks, specifically delta and gamma, based on the current market price of EU50, the predetermined strike price, and time to expiration. The system will constantly track the portfolio's overall delta exposure, which combines the delta from our option positions with any hedging positions in the underlying asset. When the portfolio's net delta deviates beyond a specified threshold from zero, the system will automatically execute trades in the underlying EU50 to rebalance back to delta neutrality. Simultaneously, we'll implement gamma scalping logic that identifies periods of high gamma sensitivity—when the option's delta is most responsive to price changes—to execute strategic trades that profit from these heightened sensitivity periods.

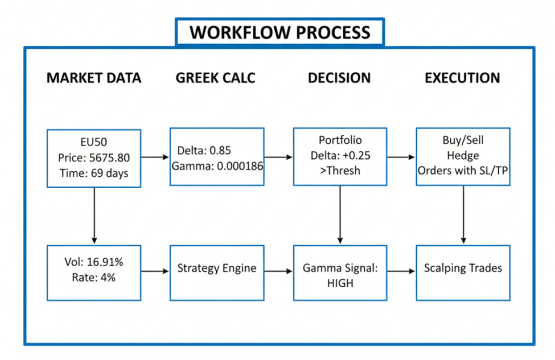
To ensure robust operation, the automated system will incorporate multiple layers of risk management, including position sizing controls, stop-loss mechanisms, and dynamic adjustment of hedging frequency based on market conditions. The system will factor in time decay as expiration approaches, adjusting its strategy for the accelerating effects of theta. By automating this complex interplay between delta hedging and gamma scalping, we create a sophisticated options trading system that can operate 24/5, responding to market movements with precision and discipline that would be challenging to maintain manually, ultimately aiming to generate consistent profits through volatility capture and dynamic position management.

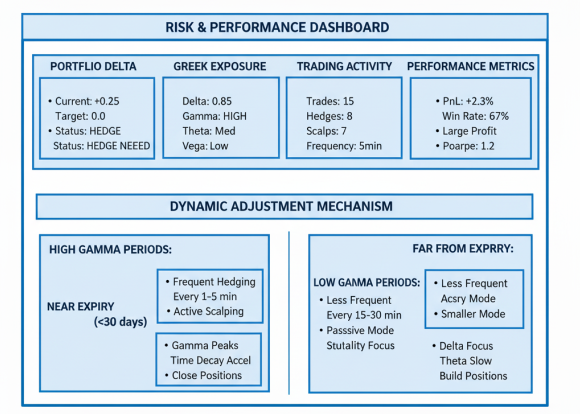
Getting Started

//+------------------------------------------------------------------+
//|                                               AutoGammaDelta.mq5 |
//|                        GIT under Copyright 2025, MetaQuotes Ltd. |
//|                     https://www.mql5.com/en/users/johnhlomohang/ |
//+------------------------------------------------------------------+
#property copyright "GIT under Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com/en/users/johnhlomohang/"
#property version   "1.00"
#include <Trade\Trade.mqh>
#include <Math\Stat\Normal.mqh>

//--- Input Parameters
input double   StrikePrice     = 5000.0;    // Option strike price
input double   Volatility      = 0.1691;    // Annual volatility (16.91%)
input double   RiskFreeRate    = 0.04;      // Risk-free interest rate
input double   DividendYield   = 0.02;      // Dividend yield
input double   OptionPosition  = 1.0;       // Option contract size (positive long, negative short)
input double   DeltaThreshold  = 0.10;      // Delta hedge threshold
input double   GammaThreshold  = 0.0001;    // Gamma hedge threshold  
input double   LotSize         = 0.1;       // Trading lot size for underlying
input int      StopLoss        = 50;        // Hedge Stop Loss (points)
input int      TakeProfit      = 30;        // Hedge Take Profit (points)
input int      HedgeFrequency  = 1;         // Hedge check frequency (minutes)
input bool     EnableTrading   = true;      // Enable actual trading

//--- Global Variables
CTrade         trade;
double         currentDelta, currentGamma;
double         portfolioDelta, targetDelta;
datetime       lastHedgeTime;
int            currentHedgeFrequency;

This block of code sets up the full parameter and infrastructure layer needed to automate Delta-Gamma hedging inside an MQL5 environment. The first two include files bring in the trading class (CTrade) and the statistical functions required for computing the cumulative normal distribution—an essential component for calculating Black-Scholes Greeks. The input parameters define all the options-related variables (strike price, volatility, interest rate, dividend yield, and option position) along with thresholds for Delta and Gamma adjustments, which determine when the system should rebalance the hedge. Additional trading parameters such as lot size, stop loss, take profit, hedge frequency, and a switch to enable or disable live trading give the user full control over how aggressively or conservatively the hedging logic should intervene in the market.

The global variables prepare the EA for real-time computation and execution. The CTrade trade object handles all buy and sell operations on the underlying instrument used for hedging. currentDelta and currentGamma store the latest calculated Greeks, while portfolioDelta and targetDelta help track how far the current exposure is from the desired hedge state (usually near zero for delta-neutral strategies). lastHedgeTime and currentHedgeFrequency are used to regulate how often the system evaluates the hedge, ensuring that the algorithm does not overtrade while still reacting quickly enough to market changes. Together, these variables form the backbone of an automated Black-Scholes hedging engine that continuously monitors risk and executes micro-adjustments in real time.

//+------------------------------------------------------------------+
//| Black-Scholes Greeks Calculator                                  |
//+------------------------------------------------------------------+
double NormalCDF(double x)
{
   double a1=0.254829592, a2=-0.284496736, a3=1.421413741;
   double a4=-1.453152027, a5=1.061405429, p=0.3275911;
   int sign = 1;
   if(x < 0) { sign = -1; x = -x; }
   double t = 1.0/(1.0 + p*x);
   double y = 1.0 - (((((a5*t + a4)*t) + a3)*t + a2)*t + a1)*t*MathExp(-x*x);
   return 0.5*(1.0 + sign*y);
}

double NormalPDF(double x)
{
   return MathExp(-0.5*x*x)/MathSqrt(2.0*M_PI);
}

void BS_d1d2(double S, double K, double sigma, double T, double r, double q, double &d1, double &d2)
{
   if(T <= 0 || sigma <= 0) { d1 = d2 = 0.0; return; }
   double sqt = sigma * MathSqrt(T);
   d1 = (MathLog(S/K) + (r - q + 0.5*sigma*sigma)*T) / sqt;
   d2 = d1 - sqt;
}

double CalculateDelta(double S, double K, double sigma, double T, double r, double q)
{
   if(T <= 0) return (S > K) ? 1.0 : 0.0;
   double d1, d2;
   BS_d1d2(S, K, sigma, T, r, q, d1, d2);
   return MathExp(-q*T) * NormalCDF(d1);
}

double CalculateGamma(double S, double K, double sigma, double T, double r, double q)
{
   if(T <= 0 || sigma <= 0) return 0.0;
   double d1, d2;
   BS_d1d2(S, K, sigma, T, r, q, d1, d2);
   double pdf = NormalPDF(d1);
   return (pdf * MathExp(-q*T)) / (S * sigma * MathSqrt(T));
}

//+------------------------------------------------------------------+
//| Time to Expiry Calculator                                        |
//+------------------------------------------------------------------+
double TimeToExpiry()
{
   datetime expiry = D'2025.12.31 23:59:59';
   datetime current = TimeCurrent();
   double days = (expiry - current) / (60.0 * 60.0 * 24.0);
   return MathMax(days / 365.0, 0.0);
}

In the previous article, these functions formed the mathematical backbone of our Delta–Gamma automation framework by implementing the essential components of the Black-Scholes model directly inside MQL5. We began by constructing NormalCDF and NormalPDF, which approximate the cumulative and probability density functions of the standard normal distribution. These functions are required for every Greek calculation in the Black-Scholes system, since the model fundamentally relies on how likely price movements are relative to the normal curve. The implementation uses a fast numerical approximation suitable for real-time trading environments where performance matters.

Building on these statistical tools, we then defined the BS_d1d2 function, which computes the core inputs d1 and d2 used throughout the Greeks. These values reflect the standardized distance between the current price and the strike price, adjusted for volatility, time, interest rate, and dividend yield. With d1 and d2 available, we implemented CalculateDelta and CalculateGamma, which are the heart of the options sensitivity model. Delta measures the rate at which the option price changes relative to the underlying, while Gamma measures the curvature—how quickly Delta itself reacts to price changes. Both functions incorporate discounting for dividends and rely directly on the normal distribution functions created earlier.

Finally, the TimeToExpiry function provides a clean, automated way to track remaining option life in years, which is critical for all option pricing and Greeks. By calculating the difference between the current server time and a fixed expiry date, and converting that into a fraction of a year, this utility enables the EA to continuously update Delta and Gamma as real time moves forward. Collectively, these functions allowed us to bridge theoretical Black-Scholes mathematics with practical, real-time algorithmic trading logic—setting the stage for the automated scalp hedging system.

//+------------------------------------------------------------------+
//| Position Management Functions                                    |
//+------------------------------------------------------------------+
double GetUnderlyingPosition()
{
   double position = 0.0;
   int total = PositionsTotal();
   
   for(int i = 0; i < total; i++)
   {
      ulong ticket = PositionGetTicket(i);
      if(PositionGetString(POSITION_SYMBOL) == _Symbol)
      {
         long type = PositionGetInteger(POSITION_TYPE);
         double volume = PositionGetDouble(POSITION_VOLUME);
         
         if(type == POSITION_TYPE_BUY)
            position += volume;
         else if(type == POSITION_TYPE_SELL)
            position -= volume;
      }
   }
   return position;
}

double CalculatePortfolioDelta()
{
   double underlyingPos = GetUnderlyingPosition();
   double optionDelta = currentDelta * OptionPosition;
   return underlyingPos + optionDelta;
}

These position management functions handle the crucial task of monitoring the trader’s current exposure in the underlying instrument and combining it with the option’s Delta to compute the overall portfolio Delta. GetUnderlyingPosition() loops through all open positions on the account and filters only those matching the current symbol. It then accumulates the net exposure by adding the volume of buy trades and subtracting the volume of sell trades. This gives a clear picture of how much of the underlying asset the trader currently holds, expressed as a positive (net long), negative (net short), or zero (flat) position.

The CalculatePortfolioDelta() function extends this by incorporating the option’s sensitivity to price changes. It multiplies the current option Delta by the option position size to compute the “option-side Delta,” then adds it to the net underlying position returned by GetUnderlyingPosition(). The result is a full portfolio Delta value that reflects both the option and hedge legs combined. This measurement is essential for Delta-neutral or Delta-targeted strategies, allowing the system to decide when a hedge adjustment is necessary based on deviations from the desired Delta state.

//+------------------------------------------------------------------+
//| Gamma Scalping Logic                                             |
//+------------------------------------------------------------------+
int CalculateDynamicFrequency()
{
   // Adjust frequency based on gamma levels
   if(currentGamma > GammaThreshold * 2)
      return 1;  // High gamma - check every minute
   else if(currentGamma > GammaThreshold)
      return HedgeFrequency; // Medium gamma - use base frequency
   else
      return 5;  // Low gamma - check every 5 minutes
}

//+------------------------------------------------------------------+
//| Execute trade with risk parameters                               |
//+------------------------------------------------------------------+
void ExecuteTrade(ENUM_ORDER_TYPE tradeType, string symbol)
{
   if(!EnableTrading) 
   {
      Print("DEMO: ", EnumToString(tradeType), " ", LotSize, " lots");
      return;
   }
   
   double point = SymbolInfoDouble(symbol, SYMBOL_POINT);
   double price = (tradeType == ORDER_TYPE_BUY) ? SymbolInfoDouble(symbol, SYMBOL_ASK) :
                                                SymbolInfoDouble(symbol, SYMBOL_BID);

   double sl_distance = StopLoss * point * 10; // Convert points to price
   double tp_distance = TakeProfit * point * 10;
   
   double sl = (tradeType == ORDER_TYPE_BUY) ? price - sl_distance : price + sl_distance;
   double tp = (tradeType == ORDER_TYPE_BUY) ? price + tp_distance : price - tp_distance;

   if(trade.PositionOpen(symbol, tradeType, LotSize, price, sl, tp, "GammaDelta Hedge"))
   {
      Print("TRADE EXECUTED: ", EnumToString(tradeType), 
            " Lots: ", LotSize, 
            " Price: ", price,
            " SL: ", sl, 
            " TP: ", tp);
   }
   else
   {
      Print("TRADE FAILED: ", EnumToString(tradeType), 
            " Error: ", GetLastError());
   }
}

//+------------------------------------------------------------------+
//| Gamma-Based Trading Strategy                                     |
//+------------------------------------------------------------------+
void ExecuteGammaStrategy()
{
   double S = SymbolInfoDouble(_Symbol, SYMBOL_BID);
   
   // Strategy 1: Gamma Scalping - Trade when gamma indicates high sensitivity
   if(currentGamma > GammaThreshold * 1.5)
   {
      Print("High Gamma detected: ", currentGamma, " - Gamma scalping opportunity");
      
      // If gamma is high and we're near the strike, consider directional trades
      if(MathAbs(S - StrikePrice) < (StrikePrice * 0.02)) // Within 2% of strike
      {
         if(currentDelta > 0.6) 
         {
            Print("Gamma Scalp: BUY signal (High Delta: ", currentDelta, ")");
            ExecuteTrade(ORDER_TYPE_BUY, _Symbol);
         }
         else if(currentDelta < 0.4)
         {
            Print("Gamma Scalp: SELL signal (Low Delta: ", currentDelta, ")");
            ExecuteTrade(ORDER_TYPE_SELL, _Symbol);
         }
      }
   }
}

//+------------------------------------------------------------------+
//| Delta Hedging Engine                                             |
//+------------------------------------------------------------------+
void ExecuteDeltaHedge()
{
   portfolioDelta = CalculatePortfolioDelta();
   targetDelta = 0.0; // Target delta-neutral
  
   double deltaDeviation = MathAbs(portfolioDelta - targetDelta);
   
   Print("Delta Check - Portfolio: ", portfolioDelta, " Deviation: ", deltaDeviation);
   
   if(deltaDeviation > DeltaThreshold)
   {
      // Determine trade direction
      ENUM_ORDER_TYPE orderType;
      if(portfolioDelta > targetDelta)
      {
         orderType = ORDER_TYPE_SELL; // Sell to reduce positive delta
         Print("DELTA HEDGE: SELL to reduce positive delta ", portfolioDelta);
      }
      else
      {
         orderType = ORDER_TYPE_BUY;  // Buy to reduce negative delta
         Print("DELTA HEDGE: BUY to reduce negative delta ", portfolioDelta);
      }
      
      ExecuteTrade(orderType, _Symbol);
   }
}

//+------------------------------------------------------------------+
//| Combined Gamma & Delta Strategy                                  |
//+------------------------------------------------------------------+
void ExecuteCombinedStrategy()
{
   double S = SymbolInfoDouble(_Symbol, SYMBOL_BID);
   double T = TimeToExpiry();
   
   // Update Greeks
   currentDelta = CalculateDelta(S, StrikePrice, Volatility, T, RiskFreeRate, DividendYield);
   currentGamma = CalculateGamma(S, StrikePrice, Volatility, T, RiskFreeRate, DividendYield);
   
   Print("Strategy Analysis - Price: ", S, " Delta: ", currentDelta, " Gamma: ", currentGamma);
   
   // 1. Execute Delta Hedging (Priority)
   ExecuteDeltaHedge();
   
   // 2. Execute Gamma Strategy (Secondary)
   ExecuteGammaStrategy();
   
   // 3. Time-based opportunities (Near expiry)
   if(T * 365 < 30) // Less than 30 days to expiry
   {
      Print("Near expiry detected: ", T*365, " days - Monitoring for time decay opportunities");
      
      // Consider closing positions or adjusting strategy near expiry
      if(currentGamma > GammaThreshold * 3)
      {
         Print("High Gamma near expiry - Potential for volatility plays");
      }
   }
}

This section of the code implements the core decision-making engine that turns Greek calculations into automated trading actions. The CalculateDynamicFrequency() function adjusts how frequently the algorithm checks for hedging opportunities based on current Gamma levels. High Gamma implies rapid changes in Delta, so the system increases monitoring to once per minute. Medium Gamma uses the base frequency defined by the user, while low Gamma relaxes the evaluation interval to five minutes. This dynamic timing control ensures responsiveness during volatile conditions and reduces unnecessary trading during calmer markets. The ExecuteTrade() function then provides a robust, risk-controlled way to place trades, applying stop-loss and take-profit levels based on the symbol’s point value and returning detailed logs for both successful and failed order executions.

The gamma-based trading logic, implemented through ExecuteGammaStrategy(), focuses on capturing opportunities when Gamma is high—an environment where price is more sensitive and intraday moves become more pronounced. When Gamma surpasses 1.5× the threshold and the underlying trades near its strike price, the system generates BUY or SELL signals depending on Delta extremes: high Delta suggests bullish bias, and low Delta suggests bearish bias. Meanwhile, the Delta hedging engine (ExecuteDeltaHedge()) works continuously to push the portfolio back to a delta-neutral state. It calculates the combined Delta of the underlying and option positions, checks for deviations beyond the allowed threshold, and executes counter-trades to rebalance risk.

The function, ExecuteCombinedStrategy(), integrates everything into a unified trading cycle. It recalculates the Greeks, outputs diagnostic information, performs Delta hedging as the primary safety mechanism, and then checks for Gamma-scalping opportunities as secondary trades. Additionally, it monitors time to expiry, highlighting scenarios where high Gamma and short maturity create elevated volatility and potential trading edges. This hierarchical structure—Delta hedge first, Gamma opportunities second, and time-based logic last—ensures that the system maintains risk control while still exploiting short-term microstructure opportunities driven by Greek dynamics.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
{
   static datetime lastCheck = 0;
   
   // Update display on every tick
   UpdateGreeksDisplay();
   
   // Execute strategy at dynamic frequency
   if(TimeCurrent() - lastCheck >= currentHedgeFrequency * 60)
   {
      lastCheck = TimeCurrent();
      
      Print("\n=== STRATEGY CYCLE ===");
      Print("Time: ", TimeToString(TimeCurrent()));
      
      // Execute combined gamma/delta strategy
      ExecuteCombinedStrategy();
      
      Print("=== CYCLE COMPLETE ===\n");
   }
}

void OnTrade()
{
   Print("Position Update - Total Positions: ", PositionsTotal());
   portfolioDelta = CalculatePortfolioDelta();
}

//+------------------------------------------------------------------+
//| Monitoring and Reporting                                         |
//+------------------------------------------------------------------+
void UpdateGreeksDisplay()
{
   double S = SymbolInfoDouble(_Symbol, SYMBOL_BID);
   double T = TimeToExpiry();
   
   currentDelta = CalculateDelta(S, StrikePrice, Volatility, T, RiskFreeRate, DividendYield);
   currentGamma = CalculateGamma(S, StrikePrice, Volatility, T, RiskFreeRate, DividendYield);
   portfolioDelta = CalculatePortfolioDelta();
   
   currentHedgeFrequency = CalculateDynamicFrequency();
   
   Comment(
      "EU50 Gamma/Delta Auto Trader\n",
      "Price: ", DoubleToString(S, 2), " | Strike: ", StrikePrice, "\n",
      "Option Delta: ", DoubleToString(currentDelta, 4), 
      " | Gamma: ", DoubleToString(currentGamma, 6), "\n",
      "Portfolio Delta: ", DoubleToString(portfolioDelta, 4), 
      " | Target: ", targetDelta, "\n",
      "Hedge Freq: ", currentHedgeFrequency, "min",
      " | Days to Expiry: ", DoubleToString(T*365, 0), "\n",
      "Trades: ", PositionsTotal(), " | Mode: ", EnableTrading ? "LIVE" : "DEMO"
   );
}

The OnTick() function acts as the main execution loop of the Expert Advisor, running every time a new market tick arrives. It begins by refreshing the on-chart display so the trader can visually monitor live Delta, Gamma, hedge frequency, and other key metrics. The function then checks whether enough time has passed since the last hedge cycle, using the dynamically adjusted frequency generated from Gamma levels. When the time condition is met, it initiates a full strategy cycle, logs the timestamp, and calls ExecuteCombinedStrategy()—which handles Delta hedging, Gamma scalping, and expiry-based logic. This structure ensures that the EA reacts with precision during high-volatility Gamma periods while avoiding unnecessary trading during stable conditions. The accompanying OnTrade() event handler provides real-time updates whenever a position changes, recalculating portfolio Delta to keep the risk model synchronized with actual market exposure.

The reporting function UpdateGreeksDisplay() consolidates all calculations and populates the on-screen dashboard. It recalculates the underlying price, time to expiry, Delta, Gamma, portfolio Delta, and the dynamic hedge frequency. These metrics are then displayed through the Comment() panel in a structured format so the trader can instantly see the system’s state—whether it's operating in live or demo mode, how many trades are open, and how close the portfolio is to Delta neutrality. By updating this panel on every tick, the EA provides continuous situational awareness, turning abstract Greek values into a real-time visualization of risk and strategy readiness.

Back Test Results

The back-testing was evaluated on the symbol 'EU50cash' on the 1H timeframe across roughly a 2-month testing window (14 February 2025 to 11 April 2025), with the following settings:

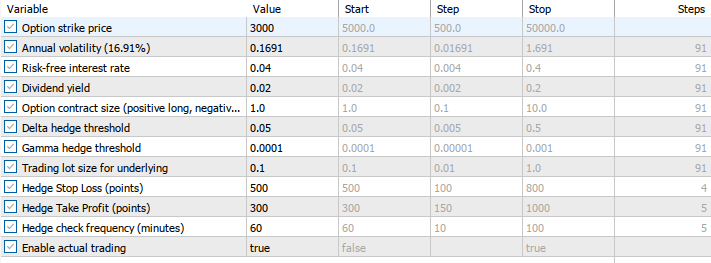
Now here is the equity curve and the backtest results:

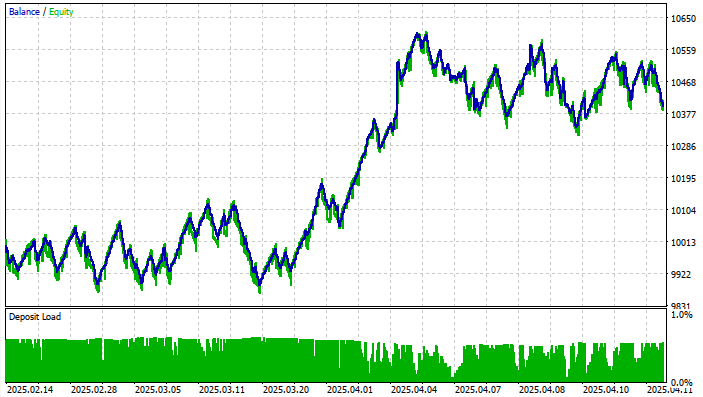
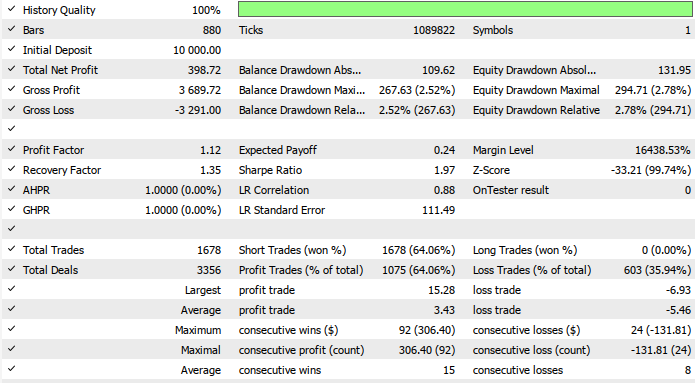
From the results, we can see that the Gamma/Delta automation is functioning correctly as both a microstructure scalper and a hedging engine, generating many small, low-risk profits while keeping risk tightly controlled. The system is ideal for traders who prioritize capital preservation, market-neutral exposure, and steady compounding rather than aggressive profit-chasing.

Conclusion

In summary, we brought the full automation pipeline of Black-Scholes Greeks into an actionable trading framework, bridging theoretical sensitivity measures with real-time market execution. We implemented fast numerical functions for Delta, Gamma, and time-to-expiry, built a dynamic frequency system driven by Gamma intensity, and developed hedge logic capable of maintaining Delta neutrality while opportunistically exploiting Gamma-scalping conditions. By combining Delta hedging, Gamma-based microstructure signals, expiry-aware logic, and a live on-chart monitoring dashboard, we transformed Greek analytics into a complete automated engine for EU50 and similar instruments.

In conclusion, this automated Greek-driven system offers traders a powerful tool for navigating short-term volatility and microstructure shifts with precision and reduced risk. By continuously recalculating sensitivities, adjusting hedge timing based on Gamma, and executing trades only when statistically justified, the model enables disciplined, data-driven decision-making—far beyond what manual trading can achieve. Whether used for hedging, scalping, or volatility harvesting, this approach empowers traders with institutional-grade risk control and tactical responsiveness.