Developing a Trading Strategy: The Triple Sine Mean Reversion Method

Introduction

Traditional technical indicators such as the Moving Average Convergence Divergence (MACD), Money Flow Index (MFI), Stochastic Oscillator, and Awesome Oscillator (AO) have long served as the foundation for traders and analysts seeking to identify market entry and exit points. While diverse in their construction each of these indicators is built upon distinct mathematical formulations that transform price data into meaningful graphical representations, helping traders interpret market behavior and momentum.

In this article, we explore the development of a novel trading strategy that steps beyond these conventional tools. We introduce a mean-reversion strategy whose entry criteria are based on a custom-built indicator: the Triple Sine Oscillator (TSO). To achieve this, we employ a specific trigonometric function—the Sine Cube—to engineer an oscillator that uses scaled price data as its primary input. The goal is to harness the cyclical nature of trigonometric functions to identify potential mean reversion points in price movements.

Mathematical Foundation: The Sine Cube Function

At the core of the Triple Sine Indicator lies the sine cube function, mathematically expressed as:

This function, being a higher-order transformation of the basic sine wave, preserves its oscillatory behavior but with more pronounced curvature around the zero line. Like the standard sine function, it oscillates between -1 and +1, but with smoother transitions near the peaks and sharper inflection points around zero. These characteristics make it ideal for designing a mean reversion-based signal, as it captures subtle shifts in momentum and a candidate for constructing an overbought/oversold trading signal.

The sine cube function thus serves as a powerful mechanism for smoothing out price fluctuations while retaining sensitivity to directional changes. When applied to scaled price inputs, it produces an indicator that highlights overbought and oversold regions — conditions that are essential for mean reversion strategies.

Visualizing the Sine Wave Cycle

At this point, it is important to visualize the nature of the sine cube function to gain a clearer understanding of its behavior and how it can be applied within our trading framework. To achieve this, we plot the function over the range –2π to 2π. 

Figure 1: Sine Cube Plot

Figure 1 shows the structure of the sine cube function. The resulting waveform reveals the cyclical and symmetric structure of the sine cube function. Within this interval, the function completes afull oscillatory cycle, displaying two peaks and two troughs. Each half of the cycle exhibits one positive and one negative extreme — in other words, the negative inputs (-2π  to  0) produce alternating +1 and –1 outputs, and the same pattern is mirrored for the positive inputs (0 to 2π). 

This periodic symmetry highlights the balance between bullish and bearish momentum swings, a property that is essential for mean reversion analysis. By observing how the function transitions smoothly between these peaks and troughs, traders can interpret the turning points as potential zones of price exhaustion or reversal, providing a foundation for constructing reliable entry and exit rules in the Triple Sine Mean Reversion strategy. 

Exploring the MQL5 Code Structure for Plotting the Sine Cube

Before developing the Triple Sine Oscillator indicator, it is essential to understand the foundational MQL5 script structure used to plot the Sine Cube function. This process provides insight into how graphical plots are constructed and displayed within the MetaTrader 5 environment.

Importing the Graphics Library

The script begins by importing the graphics library, which provides the necessary tools for visual rendering:

#include <Graphics/Graphic.mqh>

string g_name = "SineCubePlot";

Here, the Graphic.mqh file is included to access graphical functions and classes required for plotting. The variable g_name is defined as "SineCubePlot" , serving as the name of the graphical window that will display the sine cube plot.

Creating the Graphic Object and Window

The next step involves creating an instance of the CGraphic class and initializing the plotting window:

   // Create graphic object
   CGraphic graphic;
   
   // Create graphic window
   if(!graphic.Create(0, g_name, 0, 30, 30, 1000, 600))
   {
      Print("Error creating graphic!");
      return;
   }

In this section, a graphic object named graphic is declared. The Create() method is then called to initialize a graphical window with specific parameters such as position and size (30, 30, 1000, 600). If the window creation fails, an error message — “Error creating graphic!” — is printed, and the program terminates gracefully.

Setting Up the Chart Properties for the Sine Cube Plot

It is important to define the appearance and layout of the chart. The function SetupChart() handles this task by configuring the background color, axis limits, labels, font sizes, and grid properties to ensure the final plot is clear and visually appealing.

//+------------------------------------------------------------------+
//| Set up the chart properties                                      |
//+------------------------------------------------------------------+
void SetupChart(CGraphic &graphic)
{
   // Set background color
   graphic.BackgroundColor(clrWhite);
         
   // Configure X axis
   graphic.XAxis().Min(-2*M_PI);
   graphic.XAxis().Max(2*M_PI);
   graphic.XAxis().Name("x");
   
   // Configure Y axis
   graphic.YAxis().Min(-1.2);
   graphic.YAxis().Max(1.2);
   graphic.YAxis().Name("sin(x)³");
   
   // Add grid
   graphic.XAxis().Color(clrGray);
   graphic.YAxis().Color(clrGray);
   
   // Increase font sizes
   graphic.XAxis().ValuesSize(14);
   graphic.YAxis().ValuesSize(14);
   graphic.XAxis().NameSize(20);
   graphic.YAxis().NameSize(20);
   
   // Add title
   graphic.CurvePlotAll();
   graphic.Update();
}

The SetupChart() function initializes the chart environment before plotting begins.

• The background color is set to white for a clean, professional appearance.
• The X-axis ranges from  −2π to +2π, representing two complete sine wave cycles, while the Y-axis spans from  −1.2 to +1.2, slightly beyond the function’s natural amplitude to give space for visual clarity.
• Axis labels are assigned: "x" for the horizontal axis and "sin(x)³" for the vertical axis.
• Grid lines are added in gray to improve readability without overpowering the plotted curve.
• Finally, font sizes for both axis names and numerical values are increased to enhance visibility.

Once all these parameters are configured, the chart is refreshed using graphic.Update() to apply the new settings.

Generating and Plotting the Sine Cube Function

After preparing the chart layout, the next step is to generate the data points for the Sine Cube function and display them using the PlotSinCube() function.

//+------------------------------------------------------------------+
//| Generate and plot sin(x)^3 data                                  |
//+------------------------------------------------------------------+
void PlotSinCube(CGraphic &graphic)
{
   int points = 1000;
   double x[], y[];
   ArrayResize(x, points);
   ArrayResize(y, points);
   
   // Generate data points
   for(int i = 0; i < points; i++)
   {
      x[i] = -2*M_PI + (4*M_PI)*i/(points-1);
      y[i] = MathPow(MathSin(x[i]), 3);
   }
  
   // Get the curve object and set line properties
   CCurve* curve = graphic.CurveAdd(x, y, CURVE_LINES, "sin(x)³");
   if(curve != NULL)
   {
      curve.LinesStyle(STYLE_SOLID);
      curve.LinesWidth(3);
      curve.Color(ColorToARGB(clrBlue, 255));
   }   
   graphic.CurvePlotAll();
}

This function builds the Sine Cube by:

• Defining 1,000 evenly spaced data points within the −2π to +2π interval.
• Computing each y value as sine cube and storing it alongside its corresponding x value.
• Using the CurveAdd() method to plot the resulting waveform with a solid blue line that has a width of three pixels for better visibility.
• Updating the chart with CurvePlotAll() to render the final curve.

Putting It All Together

The combination of SetupChart() and PlotSinCube() allows the MQL5 script to both configure and visualize mathematical functions efficiently. By separating chart configuration from data generation, the script maintains clarity and modularity.

Triple Sine Oscillator (TSO) Indicator

Having examined the behavior of the sine cube function, we now proceed to construct the Triple Sine Oscillator (TSO) — a technical indicator that applies the mathematical principles of the sine cube function to market price data.

The TSO aims to translate raw price movements into a bounded oscillatory signal that fluctuates between –1 and +1, making it ideal for identifying mean reversion opportunities. However, since the sine cube function operates effectively within the input range –6.284 to +6.284 (approximately equivalent to –2π to +2π for one complete cycle), the raw price data must be scaled appropriately before being applied to the function.

To achieve this, we transform the closing price into a normalized input variable as follows:

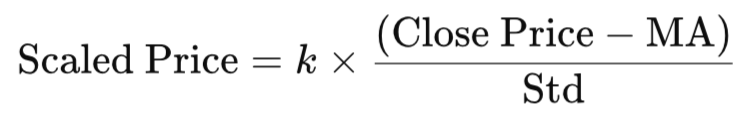
Where:

• MA = Moving Average of the price (represents the central tendency)
• Std= Standard deviation of price (measures volatility)
• k= Sensitivity factor (a scalar constant that controls the degree of oscillation)

This transformation ensures that price movements are represented in a standardized, dimensionless form, compatible with the oscillatory range of the sine cube function. This calculation is powerful because it measures how many standard deviations the current price is from its moving average. A value of +2, for instance, indicates the price is two standard deviations above the mean—a potential overbought condition. 

The sensitivity factor (k) allows traders to adjust the responsiveness of the indicator — a higher k value increases sensitivity to short-term price fluctuations, while a lower k value smooths out noise for broader trend detection.

By applying the sine cube function to this scaled price input, we derive the Triple Sine Oscillator — TSO = sin³( Scaled_Price )— a bounded and cyclic indicator capable of detecting overbought and oversold zones, and signaling potential price reversion points in the market.

TSO Indicator Code Structure

Before demonstrating how the Triple Sine Oscillator (TSO) performs in real-time trading scenarios, it is essential to first understand the code structure that governs its operation. The TSO indicator is built on a simple yet powerful framework designed to transform market price data into oscillatory signals using the sine cube function. The structure can be summarized in the following key stages:

Initialization Section

The Initialization Section defines the foundational structure and visual layout of the TSO indicator. This includes the indicator’s name, display mode, color scheme, and predefined levels that guide signal interpretation.

#property description "Triple-Sine Oscillator — (sin(x))^3"
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1

//--- plot settings
#property indicator_label1  "Triple-Sine Oscillator"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrYellowGreen
#property indicator_width1  2

//--- indicator levels
#property indicator_level1   0.7
#property indicator_level2  -0.7
#property indicator_level3   0
#property indicator_levelcolor clrGray

In this configuration:

• The indicator is labeled “Triple-Sine Oscillator — (sin(x))³” to reflect its mathematical foundation.
• It is displayed in a separate indicator window, making it independent of the main price chart.
• Only one plot bufferis used, which stores and renders the computed TSO values.
• The plotted line appears in YellowGreen with a width of two pixels for clear visibility.
• Three reference levels are added at +0.7 , –0.7 , and 0 , colored gray. These levels visually identify overbought, oversold, and neutral (mean reversion) zones.

Input Parameters

The indicator accepts two key inputs that determine its responsiveness and smoothing behavior:

//--- input parameters
input int mPeriod = 20;      // Period for SMA and StdDev
input double Ksense = 0.5;   // Sensitivity multiplier

• MA Period (mPeriod)— defines the lookback window for calculating the Simple Moving Average (SMA) and Standard Deviation (StdDev). The default period is 20 bars.

• Sensitivity Factor (Ksense) — controls how strongly the indicator reacts to price deviations. A higher value makes it more responsive, while a lower value smooths the output. By default, k = 0.5.

These parameters allow traders to adjust the indicator based on market volatility and preferred signal frequency.

Defining the Triple Sine Function

At the core of the TSO lies the Triple Sine function, which mathematically transforms normalized price deviations into a smooth oscillatory waveform.

//+------------------------------------------------------------------+
//| TripleSine function                                              |
//+------------------------------------------------------------------+
double TripleSine(double x)
  {
   return(MathPow(MathSin(x), 3));
  }

Core Calculation Logic

Within the main calculation loop, the indicator computes the scaled price for each bar and transforms it using the Triple Sine function.

   int limit =rates_total- MathMax(mPeriod, prev_calculated - 1);

   for(int i = limit; i>=0; i--)
     {
      if(sd[i] == 0) { TripleSineBuffer[i] = 0; continue; }

      double scaled = Ksense * (price[i] - ma[i]) / sd[i];
      TripleSineBuffer[i] = TripleSine(scaled);
     }

Here, the moving average and standard deviation are dynamically calculated over the specified period to normalize price action. 

The scaled price is then passed into the sine cube function. This transforms the normalized data into a bounded oscillatory signal ranging between –1 and +1.

Finally, the computed TSO values are stored in the TripleSineBuffer and plotted as a continuous line. This graphical output represents the cyclical behavior of market momentum — highlighting overbought, oversold, and mean reversion zones.

TSO indicator Demonstration

At this juncture, it is time to test the newly developed TSO on the MetaTrader 5 platform. This stage allows us to validate the indicator’s performance, visual behavior, and responsiveness to real market data.

Figure 2: Triple Sine Oscillator 

In the demonstration of the TSO, a key observation was made regarding the effect of the sensitivity factor (k) on the indicator’s responsiveness to price movement.

When the sensitivity value was increased from 0.5 to 2.3, the oscillator became more reactive to market fluctuations. This heightened sensitivity caused the TSO line to respond sharply to even minor price changes, making it ideal for short-term or highly volatile trading environments where quick signals are essential.

Conversely, when the sensitivity value was reduced to 0.1, the TSO became less responsive to price action. The oscillator appeared smoother, filtering out small market noise and emphasizing broader trends instead. This setting is often preferred in longer-term analysis, where traders aim to capture major market cycles rather than frequent reversals.

By optimizing both the sensitivity factor (k) and the moving average period (mPeriod), the TSO can be fine-tuned to adapt effectively across various financial instruments — from fast-moving currency pairs and commodities to slower, trend-oriented equities.

This flexibility makes the TSO a versatile analytical tool, capable of aligning its behavior with the volatility profile and trading characteristics of different markets.

TSO Trading Strategy: The Mean Reversion Method

Now that the TSO indicator is fully constructed, we can build upon it to develop a complete Mean Reversion Trading Strategy. Before delving into the strategy itself, it is crucial to understand the underlying concept of mean reversion in financial markets.

Mean reversion is based on the idea that prices and other financial variables tend to move back toward their historical average (mean) over time. In simpler terms, when an asset’s price deviates significantly from its long-term average — either rising too high or falling too low — it is likely to “revert” or return toward that average eventually.

This concept assumes that markets exhibit a natural equilibrium, and that extreme price movements are temporary deviations caused by short-term imbalances in buying and selling pressure. Once these pressures subside, prices often normalize, moving closer to their mean.

However, it’s important to note that mean reversion strategies typically perform poorly in strongly trending markets. In such conditions, prices may continue to move away from the average for extended periods, leading to premature or false reversal signals. Therefore, the effectiveness of a mean reversion strategy depends heavily on identifying range-bound or oscillatory market conditions.

In the following section, we will integrate the TSO with key market conditions to formulate a complete mean reversion trading framework, defining the entry and exit rules that guide profitable decision-making.

Trading Logic and Conditions

1. Sell Condition

A sell (short) position is initiated when the oscillator indicates that price momentum has moved excessively above its equilibrium zone. This occurs when:

Previous TSO< 0.7 and Current TSO> 0.7

This condition signals a potential overbought market, suggesting that prices may soon revert downward toward the mean.

2. Buy Condition

A buy (long) position is triggered when the oscillator identifies a downward deviation from the mean — a potential oversold condition. The criteria are:

Previous TSO > − 0.7 and Current TSO < − 0.7 

This crossover suggests that selling pressure may be fading, increasing the likelihood of an upward correction.

3. Exit Condition

All open positions will be closed when either the Take Profit (TP) or Stop Loss (SL) thresholds are reached. This ensures that profits are secured and downside risks are managed effectively.

4. Multiple Entry Rule

The strategy supports multiple entries in the direction of an active trade to capitalize on sustained mean reversion moves:

• When a buyposition is active, no sellpositions are opened.
• Additional buy trades may be added only if the buy condition is met again while the initial trade remains open.
• The same rule applies to sell positions — new sells are permitted only if existing ones are active and the sell condition reoccurs.

To prevent overtrading and ensure sufficient market movement between entries, the system enforces a 10-bar interval before checking for a new entry signal.

Furthermore, the maximum number of entries per direction is capped at five (5). This constraint balances profit potential with controlled risk exposure, avoiding excessive position stacking during volatile periods.

Code Structure of TSO Expert Advisor

The first operation within the OnTick() function is to determine whether a new bar (candle) has formed. This is done using the custom function IsNewBar() .

This conditional statement ensures that all computations — including indicator updates and signal checks — occur only once per completed bar, rather than on every incoming tick. This approach significantly reduces computational load and prevents repeated trade triggers within the same candle.

    if(!IsNewBar()) return;
    
    // Calculate TSO values
    CalculateTSO();
    
    // Check entry conditions
    CheckEntryConditions();

Once a new bar is confirmed, the EA calls the CalculateTSO() function. 

This function computes the most recent Triple Sine Oscillator (TSO) values based on the current price data. It performs the following operations internally:

• Updates the moving average (MA) and standard deviation (Std) of the price.
• Scales the price using the sensitivity factor (k).
• Applies the sine cube function to generate the TSO value.

The computed oscillator values (previous and current) are then stored in buffers for use in the signal evaluation phase.

After calculating the updated TSO readings, the EA proceeds to evaluate the trading logic using the CheckEntryConditions() function.

The CheckEntryConditions() function forms the decision-making core of the Triple Sine Mean Reversion Expert Advisor, responsible for validating trading signals and managing position entries based on the TSO indicator values. It integrates position tracking, trade direction control, and signal verification to ensure that each trade adheres to the system’s logic and risk parameters.

//+------------------------------------------------------------------+
//| Check entry conditions                                           |
//+------------------------------------------------------------------+
void CheckEntryConditions()
{
    // Count current positions
    CountPositions();
    
    // Check if we can open new positions
    if(buyCount + sellCount >= MaxEntries)
    {
        Print("Maximum entries reached: ", MaxEntries);
        return;
    }
    
    // Check Buy condition: PrevTSO > -0.7 && CurTSO < -0.7
    if(prevTSO > -TSO_Threshold && curTSO < -TSO_Threshold)
    {
        Print("Buy condition met");
        if(CanOpenBuy())
        {
            OpenBuyPosition();
        }
    }
    
    // Check Sell condition: PrevTSO < 0.7 && CurTSO > 0.7
    if(prevTSO < TSO_Threshold && curTSO > TSO_Threshold)
    {
        Print("Sell condition met");
        if(CanOpenSell())
        {
            OpenSellPosition();
        }
    }
}

Below is the operational breakdown of the function:

At the start of the function, the EA counts the number of active buy and sell positions currently open in the market. The information is stored in buyCount and sellCount variables, which are later used to enforce position limits and directional consistency.

Before any new trades can be opened, the EA ensures that the total number of positions does not exceed the predefined maximum.

This condition prevents overexposure by limiting the total number of open positions to five (5), as defined in the strategy. Once this threshold is reached, the EA halts any further entries until one or more positions are closed.

The system then evaluates the buy signal condition, which occurs when the previous TSO value is greater than –0.7 and the current TSO value crosses below –0.7.

If this condition is met, it signals a potential oversold state in the market.

Before executing a new buy order, the EA calls the helper function CanOpenBuy(), which ensures:

• No existing sell positions are open (to maintain one-sided trading).
• The minimum bar interval(10 bars) since the last entry has elapsed.

Once these conditions are verified, the EA executes a new buy order through OpenBuyPosition().

Similarly, the sell condition is checked when the previous TSO value is less than +0.7 and the current TSO value crosses above +0.7.

This indicates an overbought condition, suggesting that the price may revert downward. The CanOpenSell() function ensures that no buy positions are active and that the minimum bar spacing requirement is satisfied before opening a new sell trade.

Trade Filtering and Control

By combining CountPositions() , CanOpenBuy() , and CanOpenSell() , the system enforces the following safeguards:

• Directional Consistency:Only one trade direction (buy or sell) is active at any time.
• Position Control:No more than five positions can be open simultaneously.
• Timing Discipline: A minimum of 10 bars must elapse before a new position is considered.

TSO Expert Advisor Demonstration

Having walked you through the code structure and the internal logic of the EA, we now demonstrate how the system executes trades in a live market environment.

When deployed, the EA continuously monitors market data in real time and evaluating entry conditions at the opening of each new bar. Once a valid signal is detected — based on the crossover behavior of the TSO — the EA automatically triggers buy or sell orders according to the rules defined earlier.

Figure 3: TSO EA demonstration

Figure 3 illustrates how the TSO EA executes these orders in an actual market scenario. Each buy and sell execution corresponds precisely with the oscillator’s threshold crossovers. 

In addition, multiple entries in the same direction can be observed, reflecting the EA’s ability to add to existing positions when the same condition reoccurs — provided the 10-bar interval and maximum entry limit are respected.

Through this automated execution process, the TSO EA transforms mathematical signal detection into precise market actions, ensuring consistency, speed, and discipline in trade management.

Conclusion

In this article, we have successfully developed a new trading approach by integrating mathematical modeling with technical analysis. Beginning with the sine cube function, we constructed the Triple Sine Oscillator (TSO) — a unique indicator designed to capture cyclical market behavior and identify mean reversion opportunities. We further extended this concept into a complete Mean Reversion Strategy, detailing its structure, code logic, and real-time trade execution process.

The TSO’s mathematical foundation allows it to effectively detect overbought and oversold conditions, providing timely entry signals in range-bound markets. By incorporating multiple entries, the strategy enables traders to “scale in” and maximize potential profits during strong mean reversion phases. However, this same feature introduces additional exposure, meaning that while it can enhance gains, it also carries a higher risk of compounded losses when market conditions shift unexpectedly.

Through this article, we have demonstrated how a mathematical function can be transformed into a novel oscillator and then built upon to form a structured mean reversion trading strategy. The Triple Sine method showcases how creativity in mathematical design can lead to innovative trading tools with real-world applicability.

In our next article, we will evaluate the performance of the TSO when combined with trend-following indicators, testing its robustness and adaptability across various market conditions to determine its strengths, limitations, and optimization potential.

FileName	Description
SineCube.mq5	The file plots the mathematical sine function in the range of -2π to +2π. Once plotted, the template has to be updated to remove the plot
TripleSineOscillator.mq5	This file generates the oscillator indicator on the chart window.
TSO_EA.mq5	This file is an expert advisor that executes the trade in real time.