Integrate Your Own LLM into EA (Part 5): Develop and Test Trading Strategy with LLMs (III) – Adapter-Tuning

Table of contents

• Table of contents
• Introduction
• Environment Setup
• Creating the Adapter Module
• Rewriting the GPT2LMHeadModel Class
• Adapter-tuning
• Performance Comparison of Different Fine-tuning Methods
• Conclusion

Introduction

In the previous article, we introduced how to fine-tune the GPT-2 pre-trained model using the LoRA method and compared it with the fully fine-tuned model from several aspects we are concerned about, including but not limited to training overhead, inference overhead, and model performance.

In this article, we will use the Adapter-tuning method to fine-tune the GPT-2 pre-trained model and compare it with the fine-tuning methods already introduced. Of course, we will not continue to introduce various methods of fine-tuning large language models because new fine-tuning methods are constantly emerging. To reproduce each method one by one, I am afraid you will not have the patience to read them all, so I will only introduce a few of the most basic fine-tuning methods (for example, we have already introduced LoRA-tuning and will not spend a lot of space introducing QLoRA-tuning, a method extended from LoRA).

This means that this will be the last article on fine-tuning large language models. If you want to try other methods, you can refer to the logic of fine-tuning mentioned in this series of articles and apply it to other fine-tuning methods to continue exploring. Starting from the next article, we will focus on combining the trained model with EA development to develop trading strategies and conduct back testing.

In our example, we use a relatively aggressive approach, which is to input 20 data points to predict the next 40 data points. We chose this because it's difficult to compare the differences if the predicted values are too short. This is more aggressive than in practical applications, where you might use a more conservative strategy of inputting 20 values to predict the next 5 values. It is important to keep this in mind when applying these techniques to real-time trading. A more practical solution is to set these two values (input and output length) as hyperparameters, and then use a genetic algorithm to back test on different currency pairs and different periods to find the optimal parameters. We will not discuss this specifically in this series of articles, and readers can try to do it themselves.

Now let's focus on how to use Adapter-tuning to fine-tune the GPT-2 pre-trained model.

Environment Setup

The following describes the operating environment for the code examples provided in this article. Of course, this does not mean that your code environment must be the same as mine, but if you encounter problems running the code, you can refer to my environment configuration.

Operating System: Ubuntu 22.04.5 LTS (or the corresponding version of WSL)

Python Version: 3.10.14

Necessary Python Libraries:

• torch-2.4.1
• numpy-1.26.3
• pandas-2.2.3
• transformers-4.45.1
• peft-0.13.0
• matplotlib-3.9.2

If you are not familiar with how to configure the code running environment, I have described it in detail in other articles in this series:

• AMD graphics card users can refer to the previous article:  Integrate Your Own LLM into EA (Part 4): Training Your Own LLM with GPU
• NVIDIA graphics card users can refer to the second article in this series: Integrate Your Own LLM into EA (Part 2): Example of Environment Deployment

This article will not introduce this part in detail.

Creating the Adapter Module

We briefly introduced Adapter-tuning in the first article of this section. In general, Adapter-tuning is a modular fine-tuning method that achieves fine-tuning by inserting specialized adapter modules into different layers of the pre-trained model. Each Adapter module can be regarded as a small neural network, responsible for capturing the data distribution of a specific task. Moreover, the Adapter module can be trained independently of the original model, which is convenient for management and optimization.

At the same time, adapters for multiple tasks can be easily added to the same pre-trained model to achieve multi-task learning. Especially when the task is complex and the amount of data is limited, the model fine-tuned using Adapter-tuning can obtain higher performance.

Of course, compared with LoRA, the Adapter module may introduce more parameters, increasing the burden of storage and calculation, and it is necessary to design and adjust the corresponding adapter module for each task, and the design process is more complicated. LoRA-tuning focuses more on improving the adaptability of the model with a minimal number of parameters, which is suitable for scenarios with limited resources and requiring efficient fine-tuning. Adapter-tuning, on the other hand, captures task-specific information by introducing independent modules, which is suitable for scenarios that require multi-task learning or flexible adjustment.

At present, once you have determined a task goal, choosing the right method is crucial. If the trained model cannot obtain good results, no matter how you adjust the parameters, you should consider changing the model or training method instead of denying your own ideas.

Next, we will use Adapter-tuning to fine-tune the GPT-2 model step by step. First, we will create an Adapter module and a GPT2LMHeadModel module (namely the GPT2LMHeadModelWithAdapters class), and then adapt the Adapter module to the GPT2LMHeadModelWithAdapters class.

To integrate the Adapter module into GPT-2, we will create a modified version of the GPT2LMHeadModel class. This example only provides a simplified implementation. Please pay attention to the key technologies of Adapter integration. The overall implementation logic of the Adapter module is not complicated. First, we define a class that inherits from nn.Module, which contains two main operations: down-sampling (down_project) and up-sampling (up_project). down_project maps the input features to the bottleneck layer, passes through the ReLU activation function, and adds dropout to prevent overfitting; up_project maps the features of the bottleneck layer back to the original dimension and uses dropout again to prevent overfitting.

Now let's implement the code. First, define the Adapter class, inheriting from torch's nn.Module: class Adapter(nn.Module):

Define the initialization method of the class, accepting two parameters: in_features and bottleneck_features: def __init__(self, in_features, bottleneck_features=64):

1. in_features: This is the dimension of the input features. For the GPT-2 model, it is the dimension of its embedding layer.
2. bottleneck_features: This is the dimension of the bottleneck layer, that is, the feature dimension after the linear projection layer. The default is set to 64.

• Call the initialization method of the parent class (nn.Module): super(Adapter, self).__init__()
• Define a linear layer (nn.Linear) to reduce the dimension of input features to the dimension of the bottleneck layer: self.down_project = nn.Linear(in_features, bottleneck_features)
• Define another linear layer to increase the feature dimension from the bottleneck layer back to the input feature dimension: self.up_project = nn.Linear(bottleneck_features, in_features)
• Define the Dropout layer, which is used to randomly discard a part of neurons during training to prevent overfitting. The discard probability is set to 0.1: self.dropout = nn.Dropout(0.1)
• Call the weight initialization method: self.init_weights()

Define the weight initialization method init_weights():

• Initialize the weight parameters of the down_project layer using a normal distribution with a mean of 0.0 and a standard deviation of 0.02: nn.init.normal_(self.down_project.weight, mean=0.0, std=0.02)
• Initialize the bias parameters of the down_project layer with a constant of 0: nn.init.constant_(self.down_project.bias, 0)
• Similarly, initialize the weight parameters of the up_project layer using a normal distribution with a mean of 0.0 and a standard deviation of 0.02: nn.init.normal_(self.up_project.weight, mean=0.0, std=0.02)
• Initialize the bias parameters of the up_project layer with a constant of 0: nn.init.constant_(self.up_project.bias, 0)

Define the forward propagation method forward(): def forward(self, hidden_states), which accepts one parameter hidden_states

• Project the input hidden states to the dimension of the bottleneck layer through the down_project linear layer: hidden_states = self.down_project(hidden_states)
• Perform a nonlinear transformation on the hidden states of the bottleneck layer using the ReLU activation function: hidden_states = F.relu(hidden_states)
• Apply Dropout to the nonlinearly transformed hidden states, randomly discarding a portion of neurons: hidden_states = self.dropout(hidden_states)
• Increase the hidden states from the dimension of the bottleneck layer back to the dimension of the input features through the up_project linear layer: hidden_states = self.up_project(hidden_states)
• Apply Dropout again to the upsampled hidden states: hidden_states = self.dropout(hidden_states)
• Finally, return the hidden states processed by the Adapter module: return hidden_states

The complete Adapter class:

class Adapter(nn.Module):
    def __init__(self, in_features, bottleneck_features=64):
        super(Adapter, self).__init__()
        self.down_project = nn.Linear(in_features, bottleneck_features)
        self.up_project = nn.Linear(bottleneck_features, in_features)
        self.dropout = nn.Dropout(0.1)
        self.init_weights()

    def init_weights(self):
        nn.init.normal_(self.down_project.weight, mean=0.0, std=0.02)
        nn.init.constant_(self.down_project.bias, 0)
        nn.init.normal_(self.up_project.weight, mean=0.0, std=0.02)
        nn.init.constant_(self.up_project.bias, 0)

    def forward(self, hidden_states):
        hidden_states = self.down_project(hidden_states)
        hidden_states = F.relu(hidden_states)
        hidden_states = self.dropout(hidden_states)
        hidden_states = self.up_project(hidden_states)
        hidden_states = self.dropout(hidden_states)
        return hidden_states

In this way, we have simply created an Adapter module. The next step is to adapt this module to our GPT-2 model, so we need to rewrite the GPT2LMHeadModel class.

Rewriting the GPT2LMHeadModel Class

If you want to rewrite the GPT2LMHeadModel class comprehensively, it will be a huge project. We only provide a simplified version here to provide an example, and only implement the key parts. Our task here is to adapt the Adapter module to the GPT-2 network and handle various input conditions and output requirements of the model. After initialization, we also have to rewrite the forward propagation function forward(), call the transformer layer of the original GPT-2 model to obtain the hidden state hidden_states, and then apply each adapter module in turn, adding the output of the adapter module to the original hidden state. Finally, the final logits are generated through the linear layer of the language model (lm_head), and the loss is calculated. Now let's complete the code.

We define our rewritten class as GPT2LMHeadModelWithAdapters, inheriting from GPT2LMHeadModel: class GPT2LMHeadModelWithAdapters(GPT2LMHeadModel)

Define the initialization method __init__() of the GPT2LMHeadModelWithAdapters class and call the initialization method of the parent class in the initialization method to add adapters:

• Define the class method __init__(self, config), which receives a configuration parameter config: def __init__(self, config):
• Call the initialization method of the parent class: super().__init__(config)
• Initialize adapters, the type is nn.ModuleList, which contains Adapter modules that are the same as the number of layers of the GPT-2 model, where config.n_embd is the dimension of the embedding layer, and config.n_layer is the number of layers: self.adapters = nn.ModuleList([Adapter(config.n_embd) for _ in range(config.n_layer)])

Next, implement the forward propagation method forward() in the GPT2LMHeadModelWithAdapters class:

• Define the forward propagation method, accepting the parameters we need, which are used to control the behavior and input format of the model (we will not introduce these parameters one by one here, interested readers can try to optimize these parameters): def forward(self, input_ids=None, past_key_values=None, attention_mask=None, token_type_ids=None, position_ids=None, head_mask=None, inputs_embeds=None, encoder_hidden_states=None, encoder_attention_mask=None, labels=None, use_cache=None, output_attentions=None, output_hidden_states=None, return_dict=None,):
• Then call the transformer layer in the model for forward propagation, and obtain the output of the model and pass it to the variable transformer_outputs: transformer_outputs = self.transformer(input_ids, past_key_values=past_key_values, attention_mask=attention_mask, token_type_ids=token_type_ids, position_ids=position_ids, head_mask=head_mask, inputs_embeds=inputs_embeds, encoder_hidden_states=encoder_hidden_states, encoder_attention_mask=encoder_attention_mask, use_cache=use_cache, output_attentions=output_attentions, output_hidden_states=output_hidden_states, return_dict=return_dict,)

• Obtain the hidden state output hidden_states of the transformer layer, which is the input that the Adapter module needs to process: hidden_states = transformer_outputs[0]
• Next, loop through all Adapter modules using a for loop to prepare for the next step of adaptation: for i, adapter in enumerate(self.adapters):
• Add the output of each layer of the Adapter module to the original hidden state and assign it to hidden_states as the new hidden state passed to the next layer: hidden_states = hidden_states + adapter(hidden_states)
• After processing hidden_states, we also need to convert the processed hidden state (hidden_states) into the logits output of the language model through the lm_head layer of the model. Each logit corresponds to the probability of a vocabulary: lm_logits = self.lm_head(hidden_states)

After the conversion, it is the link to calculate the loss:

• Initialize the loss to empty: loss = None
• Check if labels are provided: if labels is not None:
• Remove the last token of the logits output because we need to predict the next token: shift_logits = lm_logits[..., :-1, :].contiguous()
• Remove the last token of the label because we need to predict the next token: shift_labels = labels[..., 1:].contiguous()
• Define the loss function as cross-entropy loss (CrossEntropyLoss), which is a commonly used loss function for classification tasks: loss_fct = nn.CrossEntropyLoss()
• Flatten shift_logits and shift_labels (view(-1, ...)) and then use the cross-entropy loss function: loss = loss_fct(shift_logits.view(-1, shift_logits.size(-1)), shift_labels.view(-1))    

It should be specially noted here that the language model is usually trained when predicting the next word, rather than directly predicting the current word. Therefore, the model output lm_logits and the label labels need to be staggered by one position in the time step to accurately calculate the loss. For example, if a sentence is "I love programming", then the model input may be "I love", and the model output lm_logits should be the probability distribution corresponding to "love programming". To calculate the loss, we need to align the probability distribution of "love programming" with the label of "programming".

• Check the configuration of return_dict. If it is set to False, calculate and merge the output: if not return_dict:
• Merge the logits output with other outputs of the transformer layer (except the first hidden state output) into the output output: output = (lm_logits,) + transformer_outputs[1:]
• If labels are provided and the loss is calculated, the loss is returned together with the output, otherwise only the output is returned: return ((loss,) + output) if loss is not None else output
• If return_dict is set to True, return the causal output directly: return modeling_outputs.CausalLMOutputWithCrossAttentions( loss=loss, logits=lm_logits,past_key_values=transformer_outputs.past_key_values, hidden_states=transformer_outputs.hidden_states, attentions=transformer_outputs.attentions,cross_attentions=transformer_outputs.cross_attentions,)

The complete GPT2LMHeadModelWithAdapters class:

class GPT2LMHeadModelWithAdapters(GPT2LMHeadModel):
    def __init__(self, config):
        super().__init__(config)
        self.adapters = nn.ModuleList([Adapter(config.n_embd) for _ in range(config.n_layer)])

    def forward(
        self,
        input_ids=None,
        past_key_values=None,
        attention_mask=None,
        token_type_ids=None,
        position_ids=None,
        head_mask=None,
        inputs_embeds=None,
        encoder_hidden_states=None,
        encoder_attention_mask=None,
        labels=None,
        use_cache=None,
        output_attentions=None,
        output_hidden_states=None,
        return_dict=None,
    ):
        transformer_outputs = self.transformer(
            input_ids,
            past_key_values=past_key_values,
            attention_mask=attention_mask,
            token_type_ids=token_type_ids,
            position_ids=position_ids,
            head_mask=head_mask,
            inputs_embeds=inputs_embeds,
            encoder_hidden_states=encoder_hidden_states,
            encoder_attention_mask=encoder_attention_mask,
            use_cache=use_cache,
            output_attentions=output_attentions,
            output_hidden_states=output_hidden_states,
            return_dict=return_dict,
        )
        hidden_states = transformer_outputs[0]

        # Apply adapters
        for i, adapter in enumerate(self.adapters):
            hidden_states = hidden_states + adapter(hidden_states)

        lm_logits = self.lm_head(hidden_states)

        loss = None
        if labels is not None:
            # Shift so that tokens < n predict the next token
            shift_logits = lm_logits[..., :-1, :].contiguous()
            shift_labels = labels[..., 1:].contiguous()
            # Flatten the tokens
            loss_fct = nn.CrossEntropyLoss()
            loss = loss_fct(shift_logits.view(-1, shift_logits.size(-1)), shift_labels.view(-1))

        if not return_dict:
            output = (lm_logits,) + transformer_outputs[1:]
            return ((loss,) + output) if loss is not None else output

        return modeling_outputs.CausalLMOutputWithCrossAttentions(
            loss=loss,
            logits=lm_logits,
            past_key_values=transformer_outputs.past_key_values,
            hidden_states=transformer_outputs.hidden_states,
            attentions=transformer_outputs.attentions,
            cross_attentions=transformer_outputs.cross_attentions,
        )

In this way, we have adapted the Adapter module to our GPT2LMHeadModelWithAdapters class. But please note again that this is just a simple example. In real application scenarios, please carefully design related modules according to task requirements.

Adapter-tuning

We have created the Adapter class and the GPT-2 model class GPT2LMHeadModelWithAdapters adapted with the Adapter module. Next, we load the model and data to start fine-tuning. Some codes that have been interpreted in the original article will not be interpreted in detail here. Please refer to the previous articles.

1. Preparation

Import the required libraries, nothing special to introduce here.

import pandas as pd

from transformers import GPT2LMHeadModel, GPT2Tokenizer

from transformers import TextDataset, DataCollatorForLanguageModeling

from transformers import Trainer, TrainingArguments, modeling_outputs

import torch

from torch import nn

import torch.nn.functional as F

If there is an available GPU in the system (checked by torch.cuda.is_available()), use the GPU, otherwise use the CPU. Define the loaded model and the name of the fine-tuned model.

dvc = 'cuda' if torch.cuda.is_available() else 'cpu'

print(dvc)

model_name_or_path = 'gpt2'

Tuned_model = "gpt2_Adapter-tuning"

2. Load Data and Tokenizer

Remember not to forget to put the Adapter module we created and the rewritten GPT2LMHeadModelWithAdapters class here. You can also choose to put them in other scripts and then import them in the training script.

Read the data from the llm_data.csv file and create a DataFrame object, which is used to test the fine-tuned model.

df = pd.read_csv('llm_data.csv')

Load the pre-trained GPT-2 tokenizer.

tokenizer = GPT2Tokenizer.from_pretrained(model_name_or_path)

Create a training dataset object, specify the tokenizer used with the tokenizer parameter, specify the path of the training data file with the file_path parameter, and specify the block size as 60 with block_size=60. Note that this value cannot be set arbitrarily and must correspond to the data in the dataset.

train_dataset = TextDataset(tokenizer=tokenizer,

                            file_path="train.txt",

                            block_size=60)

Combine multiple data samples into one batch, and process the masked language modeling (MLM) task at the same time. Use the parameter tokenizer to specify the tokenizer used, and use mlm=False to specify that masked language modeling (MLM) is not used, but causal language modeling (CLM) is used.

data_collator = DataCollatorForLanguageModeling(tokenizer=tokenizer, mlm=False)

3. Load the Model and Fine-tune the Model

First, use the TrainingArguments class to instantiate the training parameter object.

training_args = TrainingArguments(output_dir=Tuned_model,

                                  overwrite_output_dir=True,

                                  num_train_epochs=3,

                                  per_device_train_batch_size=32,

                                  save_strategy='no',

                                  )

• output_dir=Tuned_model: Specifies the training output directory as gpt2_Adapter-tuning.
• overwrite_output_dir=True: Whether to overwrite if the output directory already exists.
• num_train_epochs=3: Specifies the number of training epochs as 3.
• per_device_train_batch_size=32: Specifies the training batch size of each device as 32.
• save_strategy='no': Specifies not to save checkpoints.

Next, load and instantiate the pre-trained GPT-2 model object with the Adapter module:

    model = GPT2LMHeadModelWithAdapters.from_pretrained(model_name_or_path)

    trainer = Trainer(model=model,
                    args=training_args,
                    data_collator=data_collator,
                    train_dataset=train_dataset,)

• model=model: Specifies the model to be trained.
• args=training_args: Specifies the training parameters.
• data_collator=data_collator: Specifies the data collector.
• train_dataset=train_dataset: Specifies the training dataset.

Use the train() method of the Trainer object to start the training process: trainer.train()

trainer.train()

Save the fine-tuned model after training: trainer.save_model(Tuned_model)

trainer.save_model(Tuned_model)

After fine-tuning, the model will be saved in the gpt2_Adapter-tuning folder under the file where the training script is located.

4. Test the Fine-tuned Model

After fine-tuning, we need to load the fine-tuned model and perform an inference to check whether the fine-tuned model can work normally. Of course, when loading the fine-tuned model, we need to use our rewritten class GPT2LMHeadModelWithAdapters to load it. After loading the model, we also have to set it to GPU acceleration and turn the model into inference mode.

    model = GPT2LMHeadModelWithAdapters.from_pretrained(Tuned_model)
    model.to(dvc)
    model.eval()

The next step is inference testing to see if the model is working properly. This process is the same as the previous article. For a detailed code interpretation, please refer to the previous article. This article will not discuss it.

prompt = ' '.join(map(str, df.iloc[:, 1:20].values[-1]))

generated = tokenizer.decode(model.generate(tokenizer.encode(prompt, return_tensors='pt').to(dvc),

                                            do_sample=True,

                                            max_length=200)[0],

                                            skip_special_tokens=True)

print(generated)

The result is as follows:

The complete fine-tuning code script is lora-tuning.py:

import pandas as pd
from transformers import GPT2LMHeadModel, GPT2Tokenizer
from transformers import TextDataset, DataCollatorForLanguageModeling
from transformers import Trainer, TrainingArguments,modeling_outputs
import torch
from torch import nn
import torch.nn.functional as F

dvc = 'cuda' if torch.cuda.is_available() else 'cpu'
print(dvc)
model_name_or_path = 'gpt2'
Tuned_model="gpt2_Adapter-tuning"

# Define the Adapter module
class Adapter(nn.Module):
    def __init__(self, in_features, bottleneck_features=64):
        super(Adapter, self).__init__()
        self.down_project = nn.Linear(in_features, bottleneck_features)
        self.up_project = nn.Linear(bottleneck_features, in_features)
        self.dropout = nn.Dropout(0.1)
        self.init_weights()

    def init_weights(self):
        nn.init.normal_(self.down_project.weight, mean=0.0, std=0.02)
        nn.init.constant_(self.down_project.bias, 0)
        nn.init.normal_(self.up_project.weight, mean=0.0, std=0.02)
        nn.init.constant_(self.up_project.bias, 0)

    def forward(self, hidden_states):
        hidden_states = self.down_project(hidden_states)
        hidden_states = F.relu(hidden_states)
        hidden_states = self.dropout(hidden_states)
        hidden_states = self.up_project(hidden_states)
        hidden_states = self.dropout(hidden_states)
        return hidden_states

# Integrate the Adapter into the model
class GPT2LMHeadModelWithAdapters(GPT2LMHeadModel):
    def __init__(self, config):
        super().__init__(config)
        self.adapters = nn.ModuleList([Adapter(config.n_embd) for _ in range(config.n_layer)])

    def forward(
        self,
        input_ids=None,
        past_key_values=None,
        attention_mask=None,
        token_type_ids=None,
        position_ids=None,
        head_mask=None,
        inputs_embeds=None,
        encoder_hidden_states=None,
        encoder_attention_mask=None,
        labels=None,
        use_cache=None,
        output_attentions=None,
        output_hidden_states=None,
        return_dict=None,
    ):
        transformer_outputs = self.transformer(
            input_ids,
            past_key_values=past_key_values,
            attention_mask=attention_mask,
            token_type_ids=token_type_ids,
            position_ids=position_ids,
            head_mask=head_mask,
            inputs_embeds=inputs_embeds,
            encoder_hidden_states=encoder_hidden_states,
            encoder_attention_mask=encoder_attention_mask,
            use_cache=use_cache,
            output_attentions=output_attentions,
            output_hidden_states=output_hidden_states,
            return_dict=return_dict,
        )
        hidden_states = transformer_outputs[0]

        # Apply adapters
        for i, adapter in enumerate(self.adapters):
            hidden_states = hidden_states + adapter(hidden_states)

        lm_logits = self.lm_head(hidden_states)

        loss = None
        if labels is not None:
            # Shift so that tokens < n predict the next token
            shift_logits = lm_logits[..., :-1, :].contiguous()
            shift_labels = labels[..., 1:].contiguous()
            # Flatten the tokens
            loss_fct = nn.CrossEntropyLoss()
            loss = loss_fct(shift_logits.view(-1, shift_logits.size(-1)), shift_labels.view(-1))

        if not return_dict:
            output = (lm_logits,) + transformer_outputs[1:]
            return ((loss,) + output) if loss is not None else output

        return modeling_outputs.CausalLMOutputWithCrossAttentions(
            loss=loss,
            logits=lm_logits,
            past_key_values=transformer_outputs.past_key_values,
            hidden_states=transformer_outputs.hidden_states,
            attentions=transformer_outputs.attentions,
            cross_attentions=transformer_outputs.cross_attentions,
        )
if __name__=="__main__":
# Load data
    df = pd.read_csv('llm_data.csv')

    tokenizer = GPT2Tokenizer.from_pretrained(model_name_or_path)

    train_dataset = TextDataset(tokenizer=tokenizer,
                                file_path="train.txt", 
                                block_size=60)

    data_collator = DataCollatorForLanguageModeling(tokenizer=tokenizer, mlm=False)

    training_args = TrainingArguments(output_dir=Tuned_model,     
                                    overwrite_output_dir=True,    
                                    num_train_epochs=3,     
                                    per_device_train_batch_size=32,
                                    save_strategy= 'no',   
                                    )

    # Initialize model with adapters
    model = GPT2LMHeadModelWithAdapters.from_pretrained(model_name_or_path)

    trainer = Trainer(model=model,
                    args=training_args,
                    data_collator=data_collator,
                    train_dataset=train_dataset,)

    trainer.train()

    trainer.save_model(Tuned_model)

    # Load the model for inference
    model = GPT2LMHeadModelWithAdapters.from_pretrained(Tuned_model)
    model.to(dvc)
    model.eval()

    prompt = ' '.join(map(str, df.iloc[:, 1:20].values[-1])) 
    generated = tokenizer.decode(model.generate(tokenizer.encode(prompt, return_tensors='pt').to(dvc), 
                                                do_sample=True, 
                                                max_length=200)[0], 
                                                skip_special_tokens=True)

    print(f"test the model:{generated}")

The data files are attached at the end of the article. The original data file is llm_data.csv, and the preprocessed data file is train.txt.

Performance Comparison of Different Fine-tuning Methods

Next, we will compare the efficiency and performance of different fine-tuning methods. So far, we have only introduced full-parameter fine-tuning and LoRA fine-tuning. Adding Adapter-tuning in this article, there are three in total. Next, we will only compare them.

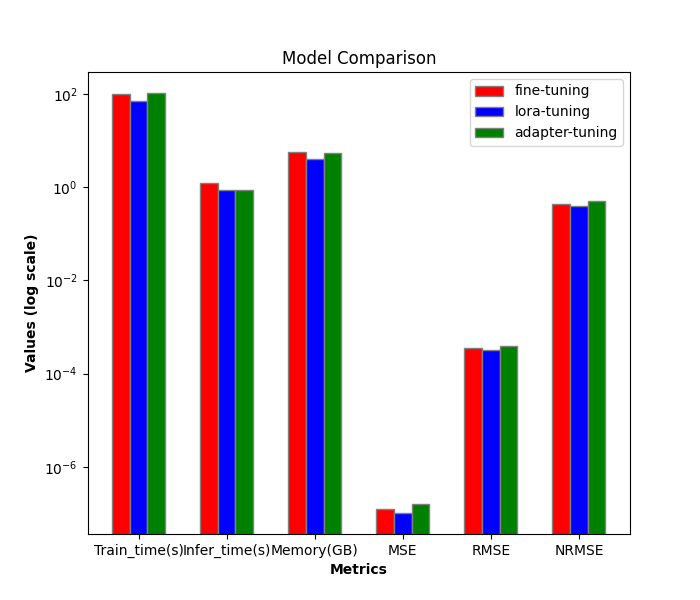
1. Efficiency Comparison

LoRA-tuning training process:

• train_runtime: 69.5605s
• VRAM: 4.1G
• generate_runtime: 1.242877s

Full-parameter fine-tuning training process:

• train_runtime: 101.7946s
• VRAM: 5.67G
• generate_runtime: 0.876525s

Adapter-tuning training process:

• train_runtime: 104.4355s
• VRAM: 5.52G
• generate_runtime: 0.882792s

	Train_runtime(s)	VRAM(GB)	Generate_runtime(s)
Full-parameter fine-tuning	101.7946	5.67	0.876525
LoRA-tuning	69.5605	4.1	1.242877
Adapter-tuning	104.4355	5.52	0.882792

2. Accuracy Comparison

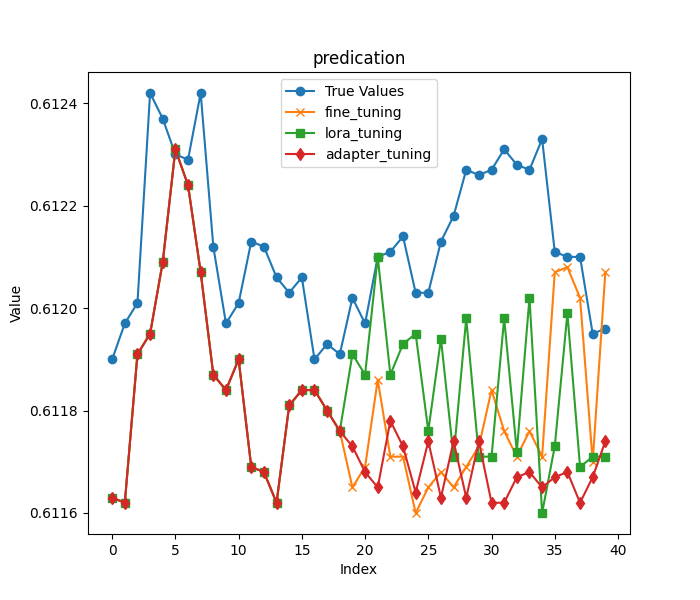
As in the previous article, we still load the first 20 columns of closing prices in the last row of the original data as input, and the remaining data as the result to evaluate the models obtained by the two training methods. It should be noted here that as mentioned at the beginning of the article, to make the comparison of results more significant, we chose a more aggressive prediction length.

The first 20 closing prices:

• input data:[0.61163 0.61162 0.61191 0.61195 0.61209 0.61231 0.61224 0.61207 0.61187 0.61184 0.6119 0.61169 0.61168 0.61162 0.61181 0.61184 0.61184 0.6118 0.61176]

The remaining closing prices:

• true prices:[0.6119, 0.61197, 0.61201, 0.61242, 0.61237, 0.6123, 0.61229, 0.61242, 0.61212, 0.61197, 0.61201, 0.61213, 0.61212, 0.61206, 0.61203, 0.61206, 0.6119, 0.61193, 0.61191, 0.61202, 0.61197, 0.6121, 0.61211, 0.61214, 0.61203, 0.61203, 0.61213, 0.61218, 0.61227, 0.61226]

Next, we load the models separately (the model parameters of full-parameter fine-tuning are saved in the gpt2_stock folder in the current directory, the model of LoRA fine-tuning is saved in the gpt2_LORA_None folder in the current directory, and the model of Adapter-tuning is stored in the gpt2_Adapter-tuning in the current directory), and run inference, and calculate their MSE, RMSE, and NRMSE according to the obtained results. These codes have been introduced in the previous article, and this article will not describe them in detail. The complete test code script is test.py:

import time
import pandas as pd
from transformers import GPT2LMHeadModel, GPT2Tokenizer, GPT2Config
from sklearn.metrics import mean_squared_error
import torch
import numpy as np
from peft import PeftModel
import matplotlib.pyplot as plt

from adapter_tuning import GPT2LMHeadModelWithAdapters

df = pd.read_csv('llm_data.csv')
dvc='cuda' if torch.cuda.is_available() else 'cpu'
base_model='gpt2'
fine_tuning_path='./gpt2_stock'
lora_tuning_path ='./gpt2_LORA_None'
adpter_tuning_path='./gpt2_Adapter-tuning'

pre_length=40
tokenizer = GPT2Tokenizer.from_pretrained(base_model)
model_fine_tuning = GPT2LMHeadModel.from_pretrained(fine_tuning_path).to(dvc)

model_lora_tuning = GPT2LMHeadModel.from_pretrained(base_model)
model_lora_tuning=PeftModel.from_pretrained(model_lora_tuning, lora_tuning_path).to(dvc)

model_adapter_tuning = GPT2LMHeadModelWithAdapters.from_pretrained(adpter_tuning_path).to(dvc)

input_data=df.iloc[:,1:20].values[-1]
true_prices= df.iloc[-1:,21:].values.tolist()[0]
prompt = ' '.join(map(str, input_data))

def generater(model):
    global true_prices
    model.eval()
    token=tokenizer.encode(prompt, return_tensors='pt').to(dvc)
    start_=time.time()
    generated = tokenizer.decode(model.generate(token, do_sample=True, max_length=200)[0], skip_special_tokens=True)
    end_=time.time()
    print(f'generate time:{end_-start_}')
    generated_prices=generated.split('\n')[0]
    generated_prices=list(map(float,generated_prices.split()))
    generated_prices=generated_prices[0:pre_length]
    # def trim_lists(a, b):
    #     min_len = min(len(a), len(b))
    #     return a[:min_len], b[:min_len]
    # true_prices,generated_prices=trim_lists(true_prices,generated_prices)
    print(f"input data:{input_data}")
    print(f"true prices:{true_prices}")
    print(f"generated prices:{generated_prices}")
    mse = mean_squared_error(true_prices[:pre_length], generated_prices)
    print('MSE:', mse)
    rmse=np.sqrt(mse)
    nrmse=rmse/(np.max(true_prices)-np.min(generated_prices))
    print(f"RMSE:{rmse},NRMSE:{nrmse}")
    return generated_prices, mse, rmse, nrmse

def plot_(a,b,c,title):
    plt.figure(figsize=(7, 6))
    if title=='predication':
        plt.plot(true_prices[:pre_length], label='True Values', marker='o')
    plt.plot(a, label='fine_tuning', marker='x')
    plt.plot(b, label='lora_tuning', marker='s')
    plt.plot(c,label='adapter_tuning',marker='d')
    plt.title(title)
    plt.xlabel('Index')
    plt.ylabel('Value')
    plt.legend()
    plt.savefig(f"{title}.png")

def groups_chart(a,b,c,models):
    metrics = ['Train_time(s)', 'Infer_time(s)', 'Memory(GB)', 'MSE', 'RMSE', 'NRMSE']
    plt.figure(figsize=(7, 6))
    a=[101.7946,1.243,5.67,a[1],a[2],a[3]]
    b=[69.5605,0.877,4.10,b[1],b[2],b[3]]
    c=[104.4355,0.883,5.52,c[1],c[2],c[3]]# 104.4355s，VRAM：5.52G  generate_runtime:0.882792s  
    bar_width = 0.2

    r1 = np.arange(len(metrics))
    r2 = [x + bar_width for x in r1]
    r3 = [x + bar_width for x in r2]

    plt.bar(r1, a, color='r', width=bar_width, edgecolor='grey', label=models[0])
    plt.bar(r2, b, color='b', width=bar_width, edgecolor='grey', label=models[1])
    plt.bar(r3, c, color='g', width=bar_width, edgecolor='grey', label=models[2])

    plt.yscale('log')
    plt.xlabel('Metrics', fontweight='bold')
    plt.xticks([r + bar_width for r in range(len(metrics))], metrics)
    plt.ylabel('Values (log scale)', fontweight='bold')
    plt.title('Model Comparison')
    plt.legend()
    # plt.show()
    plt.savefig('Comparison.png')
    
fine_tuning_result = generater(model_fine_tuning)
lora_tuning_result = generater(model_lora_tuning)
adapter_tuning_result=generater(model_adapter_tuning)

plot_(fine_tuning_result[0],lora_tuning_result[0],adapter_tuning_result[0],title='predication')
groups_chart(fine_tuning_result,lora_tuning_result,adapter_tuning_result,models=['fine-tuning','lora-tuning','adapter-tuning'])

Note:

There is a problem to note here that the order of magnitude of the indicators we are measuring is not the same, so I used a logarithmic scale here: plt.yscale('log'), this can effectively deal with the situation where the data magnitude differs greatly.

The inference result of the full-parameter fine-tuning model:

• generated prices:[0.61163, 0.61162, 0.61191, 0.61195, 0.61209, 0.61231, 0.61224, 0.61207, 0.61187, 0.61184, 0.6119, 0.61169, 0.61168, 0.61162, 0.61181, 0.61184, 0.61184, 0.6118, 0.61176, 0.61165, 0.61169, 0.61186, 0.61171, 0.61171, 0.6116, 0.61165, 0.61168, 0.61165, 0.61169, 0.61173, 0.61184, 0.61176, 0.61171, 0.61176, 0.61171, 0.61207, 0.61208, 0.61202, 0.6117, 0.61207]
• MSE: 1.257374999999991e-07
• RMSE:0.00035459483921794336
• NRMSE:0.43243273075362537

LoRA fine-tuning model inference results:

• generated prices:[0.61163, 0.61162, 0.61191, 0.61195, 0.61209, 0.61231, 0.61224, 0.61207, 0.61187, 0.61184, 0.6119, 0.61169, 0.61168, 0.61162, 0.61181, 0.61184, 0.61184, 0.6118, 0.61176, 0.61191, 0.61187, 0.6121, 0.61187, 0.61193, 0.61195, 0.61176, 0.61194, 0.61171, 0.61198, 0.61171, 0.61171, 0.61198, 0.61172, 0.61202, 0.6116, 0.61173, 0.61199, 0.61169, 0.61171, 0.61171]
• MSE: 1.0161999999999925e-07
• RMSE:0.0003187789202566557
• NRMSE:0.3887547808008319

Adapter-tuning inference results:

• generated prices:[0.61163, 0.61162, 0.61191, 0.61195, 0.61209, 0.61231, 0.61224, 0.61207, 0.61187, 0.61184, 0.6119, 0.61169, 0.61168, 0.61162, 0.61181, 0.61184, 0.61184, 0.6118, 0.61176, 0.61173, 0.61168, 0.61165, 0.61178, 0.61173, 0.61164, 0.61174, 0.61163, 0.61174, 0.61163, 0.61174, 0.61162, 0.61162, 0.61167, 0.61168, 0.61165, 0.61167, 0.61168, 0.61162, 0.61167, 0.61174]
• MSE: 1.5644499999999023e-07
• RMSE:0.00039553128826932293
• NRMSE:0.4944141103367081

Chart visualization for comparison:

Conclusion

In this article, we discussed how to use the Adapter-tuning method to fine-tune the GPT-2 pre-trained model, and made a horizontal comparison of the fine-tuning methods we introduced, which allows us to intuitively choose a training method and model that are more suitable for our trading strategy.

We observed that while Adapter-tuning may require slightly longer training times and more VRAM than LoRA, it offers a different approach to capturing task-specific information. Choosing the best method depends on the specific project requirements and available resources. Full-parameter fine-tuning remains a strong baseline, while LoRA offers efficiency, and Adapter-tuning provides modularity and potential benefits for multi-task scenarios.

In the following articles, we will no longer continue to try different fine-tuning methods. We will try to use our fine-tuned model to formulate trading strategies and integrate them into EA. After these are completed, we will back test and evaluate the EA. If you are still interested in fine-tuning the model and want to get better results, you can try to follow my ideas and complete it step by step according to the example code. Believe me, this is not a difficult process.

See you in the next article!

Appendix：

Files	Description
adapter_tuning.py	Code for Adapter-tuning
test.py	Code for  compare the efficiency and performance of different fine-tuning methods
llm_data.csv	Raw data file
train.txt	Training data file