
Multiple Regressionsanalyse. Anlegen und Prüfen von Strategien aus einer Hand
Einleitung
Ein Bekannter von mir hat als Teilnehmer an einem Seminar über den Devisenhandel die Hausaufgabe bekommen, ein Handelssystem zu entwickeln. Nachdem er sich eine Woche damit herumgeschlagen hatte, sagte er, diese Aufgabe sei vermutlich schwieriger als das Schreiben einer Doktorarbeit. Damals schlug ich ihm vor, es doch einmal mit der multiplen Regressionsanalyse zu versuchen. Im Ergebnis hat er aus dem Nichts an einem Abend ein Handelssystem erstellt, das die Prüfung durch den Seminarleiter mit Erfolg bestanden hat.
Der Erfolg der Anwendung der multiplen Regressionsanalyse bestand darin, dass sich mit ihrer Hilfe schnell die Beziehungen zwischen den Indikatoren und dem Kurs ermitteln ließen. Die vorgefundenen Beziehungen erlauben die recht zuverlässige Vorhersage des Kurswertes anhand der Indikatorwerte. Moderne Statistikprogramme beinhalten die Möglichkeit, auf der Suche nach diesen Beziehungen tausende von Werten gleichzeitig „durchzusieben“, quasi als würde man in gewerbsmäßigem Stil „Gold waschen“.
Im Ergebnis erhalten wir, nachdem wir die multiple Regressionsanalyse mit den Indikatordaten „gefüttert“ haben, eine einsatzbereite Strategie bzw. einen „Strategiegenerator“, wenn wir diese Daten modifizieren.
In diesem Artikel wird das Vorgehen bei der Erstellung einer Handelsstrategie mittels multipler Regressionsanalyse dargestellt.
1. Man nehme...
Im Verlauf der erwähnten abendlichen Arbeit entstand ein Expert-System, dessen Herzstück aus einer einzigen Gleichung bestand:
Reg=22.7+205.2(buf_DeMarker[1]-buf_DeMarker[2])-14619.5*buf_BearsPower[1]+22468.8*buf_BullsPower[1]-139.3*buf_DeMarker[1]-41686*(buf_AC[1]-buf_AC[2]),
wobei Reg >0 bedeutet, dass wir „kaufen“, während wir bei Reg < 0 „verkaufen“.
Die Gleichung war das Ergebnis einer mit einer Datenauswahl aus gebräuchlichen Indikatoren gefüllten multiplen Regressionsanalyse. Auf der Grundlage der Gleichung wurde das Expert-System angelegt. Das für die Entscheidung über den Abschluss von Geschäften zuständige Stück Code enthielt tatsächlich nicht mehr als 15 Zeilen. Das Expert-System einschließlich seines vollständigen Programmcodes befindet sich im Anhang (R_check).
//--- checking the price change range double price=(mrate[2].close-mrate[1].close)/_Point; //--- if the range is big, do not take trades and close the current positions if(price>250 || price<-250) { ClosePosition(); return; } //--- regression equation double Reg=22.7+205.2*(buf_DeMarker[1]-buf_DeMarker[2]) -14619.5*buf_BearsPower[1]+22468.8*buf_BullsPower[1] -139.3*buf_DeMarker[1] -41686*(buf_AC[1]-buf_AC[2]); //--- checking for open positions if(myposition.Select(_Symbol)==true) //--- open positions found { if(myposition.PositionType()==POSITION_TYPE_BUY) { Buy_opened=true; // long position (Buy) } if(myposition.PositionType()==POSITION_TYPE_SELL) { Sell_opened=true; //--- short position (Sell) } } //--- if an open position follows the trend as predicted by the equation, abstain from doing anything. if(Reg>0 && Buy_opened==true) return; if(Reg<=0 && Sell_opened==true) return; //--- if an open position is against the trend as predicted, close the position. if(Reg<=0 && Buy_opened==true) ClosePosition(); if(Reg>0 && Sell_opened==true) ClosePosition(); //--- opening a position in the direction predicted by the equation. //--- using level 20 to filter the signal. if(Reg>20) BuyOrder(1); if(Reg<-20) SellOrder(1);
Die Datenstichprobe für die Regressionsanalyse stammt aus dem Kursverlauf für EURUSD H1 über das Zweimonatsintervall vom 1. Juli bis zum 31. August 2011.
In der Abbildung 1 sehen wir das Ergebnis der Arbeit des Expert-Systems (E-S) an dem Datenintervall, für das es angelegt wurde. Interessanterweise ist anhand der Musterdaten, anders als es in Prüfprogrammen häufig der Fall ist, kein übermäßiger Gewinn zu beobachten. Das liegt vermutlich daran, dass es nicht zu einer Überoptimierung gekommen ist.
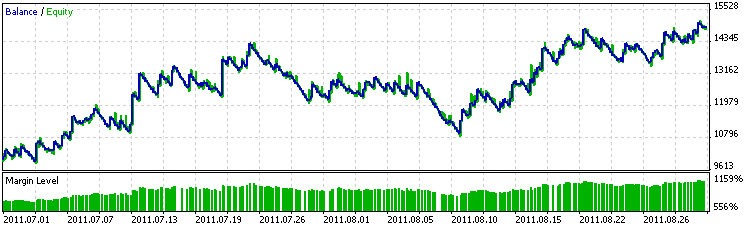
Abb. 1. Arbeitsdiagramm des E-S für den Beobachtungszeitraum
In der Abb. 2 werden die anhand der Verarbeitung der Prüfdaten (vom 1. September bis zum 1. November 2011) ermittelten Arbeitsergebnisse des E-S vorgestellt. Es hat sich gezeigt, dass eine aus den Daten für zwei Monate gewonnenen Stichprobe ausreicht, um das E-S für zwei weitere Monate in der Gewinnzone zu halten. Dabei war der Gewinn des E-S in dem Prüfzeitraum genauso hoch wie in dem Musterzeitraum.
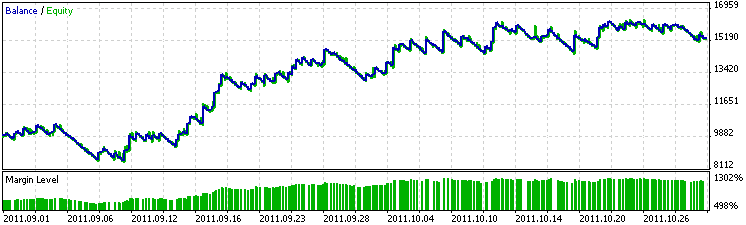
Abb. 2. Arbeitsdiagramm des E-S für den Prüfzeitraum
Somit wurde auf der Grundlage der multiplen Regressionsanalyse ein vergleichsweise schlichtes Expert-System angelegt, dass über die Musterdaten hinaus gewinnbringend geblieben ist. Folglich kann die Regressionsanalyse bei der Erstellung automatischer Handelssysteme erfolgreich eingesetzt werden.
Dabei sollten die Möglichkeiten der Regressionsanalyse gleichwohl nicht überschätzt werden. Wir werden uns ausführlicher mit ihren Vor- und Nachteilen befassen.
2. Multiple Regressionsanalyse (MRA)
Der wesentliche Zweck der multiplen Regression besteht in der Analyse der Beziehung zwischen mehreren unabhängigen und einer abhängigen Variablen. In unserem Fall ist das die Analyse der Beziehung zwischen den Indikatorwerten einer- und dem Kursverlauf andererseits.
In ihre einfachsten Form könnte diese Gleichung aussehen wie folgt:
Kursänderung = a * RSI + b * MACD + с
Die Aufstellung einer Regressionsgleichung ist nur bei Vorliegen einer Korrelation zwischen unabhängigen und einer abhängigen Variablen möglich. Da die Werte von Indikatoren in aller Regel miteinander verbunden sind, kann sich der von den Indikatoren geleistete Beitrag zur Vorhersage erheblich ändern, wenn der Analyse ein Indikator hinzugefügt oder aus dieser entfernt wird. Beachten Sie bitte, dass es sich bei einer Regressionsgleichung um eine reine Veranschaulichung der zahlenmäßigen Abhängigkeit handelt und nicht um eine Darstellung der ursächlichen Beziehungen. Die Koeffizienten (a, b) weisen den Beitrag jeder unabhängigen Variablen zu der Beziehung zu der abhängigen aus.
Eine Regressionsgleichung drückt die ideale Abhängigkeit der Variablen aus. Im Devisenhandel ist dies jedoch unmöglich, da Vorhersagen immer von der Realität abweichen. Den Unterschied zwischen dem Vorhersagewert und seinem realen Gegenstück bezeichnet man als Rest oder Residuum. Die Residuenanalyse ermöglicht die Ermittlung unter anderem des Vorliegens einer nicht linearen Abhängigkeit zwischen einem Indikator und dem Kurs. In unserem Fall gehen wir davon aus, dass zwischen den Indikatoren und dem Kurs lediglich eine lineare Abhängigkeit besteht. Glücklicherweise ist die Regressionsanalyse nicht anfällig für geringfügige Linearitätsabweichungen.
Andererseits kann sie nur zur Analyse quantitativer Parameter genutzt werden. Qualitative Parameter ohne Übergangswerte sind für diese Analyse nicht geeignet.
Da die Regressionsanalyse jede beliebige Anzahl von Variablen „zermahlen“ kann, entsteht die Versuchung, so viele von ihnen wie nur möglich einzubeziehen. Wenn die Anzahl der unabhängigen Variablen aber die der Beobachtungen ihrer jeweiligen gegenseitigen Beziehungen zu der abhängigen Variablen übersteigt, ist es sehr wahrscheinlich, dass wir eine Gleichung mit guten Vorhersagen erhalten, die allerdings auf zufälligen Schwankungen beruht.
Die Anzahl der Beobachtungen muss 10 bis 20 Mal so groß sein wie die Anzahl der unabhängigen Variablen.
In unserem Fall muss die Anzahl der Indikatoren in unserer Datenstichprobe 10 bis 20 Mal so groß sein wie die Anzahl der Abschlüsse in unserer Auswahl. Dann gilt die so gewonnene Gleichung als zuverlässig. Die Stichprobe, auf deren Grundlage das Expert-System in Abschnitt 1 entwickelt wurde, umfasste 33 Parameter und 836 Beobachtungen. Folglich war die Anzahl der Parameter 25 Mal so hoch wie die der Beobachtungen. Diese Vorgabe ist eine allgemeine Regel in der Statistik. Sie gilt auch für das Optimierungsprogramm des Strategieprüfprogramms der MetaTrader 5-Instanz auf dem Ausgabegerät (Terminal).
Dabei ist in dem Optimierungsprogramm eigentlich jeder Indikatorwert ein gesonderter Parameter. Anders ausgedrückt, wenn wir für einen Indikator 10 Werte prüfen, haben wir es mit 10 unabhängigen Parametern zu tun, was wir stets bedenken müssen, um einer Überoptimierung vorzubeugen. Möglicherweise sollte das Protokoll des Optimierungsprogramms eine weitere Variable ausweisen: die durchschnittliche Anzahl an Abschlüssen / die Anzahl der Werte aller optimierten Parameter. Bei einem Indikatorwert unter zehn, ist die Wahrscheinlichkeit einer Überoptimierung hoch.
Ebenfalls zu beachten sind die „Ausreißer“. Seltene, jedoch einschlägige Ereignisse (in unserem Fall Kursspitzen) können der Gleichung irrtümliche Abhängigkeiten hinzufügen. Zum Beispiel könnte es nach Bekanntwerden einer unerwarteten Neuigkeit auf dem Markt zu einer nur wenige Stunden dauernden heftigen Bewegung gekommen sein. In diesem Fall hätten die Werte der technischen Indikatoren keine große Bedeutung für die Vorhersage, wogegen sie für die Regressionsanalyse überaus wichtig sind, da es zu einer starken Kursänderung gekommen ist. Deshalb empfiehlt es sich, die Datenauswahl zu filtern oder auf mögliche Ausreißer zu prüfen.
3. Anlegen einer eigenen Strategie
Wir sind beim wesentlichen Teil angekommen. Hier untersuchen wir, wie sich aus unseren eigenen Daten eine Regressionsgleichung erstellen lässt. Die Umsetzung der Regressionsanalyse (RA) ähnelt der bereits in einem füheren Beitrag vorgestellten Diskriminanzanalyse. Die RA beinhaltet Folgendes:
- Die Aufbereitung der Daten für die Analyse;
- die Auswahl der besten Variablen aus den aufbereiteten Daten;
- die Ermittlung einer Regressionsgleichung.
Die multiple Regressionsanalyse ist Bestandteil zahlreicher anspruchsvoller Programme für die statistische Datenanalyse. Die verbreitetsten sind Statistica (von StatSoft) und SPSS (von IBM). Wir widmen uns im Weiteren der Anwendung der Regressionsanalyse (RA) anhand von Statistica 8.0.
3.1. Aufbereitung der Daten für die Analyse
Unsere Aufgabe besteht in der Erstellung einer Regressionsgleichung, in der anhand der Indikatorwerte für den aktuellen Balken die Kursentwicklung für den nächsten Balken vorhergesagt werden kann.
Zur Erfassung der Daten verwenden wir dasselbe Expert-System wie zur Aufbereitung der Daten für die Diskriminanzanalyse. Wir erweitern seinen Funktionsumfang, indem wir es um die Speicherung von Indikatorwerten aus anderen Zeiträumen ergänzen. Ein erweitertes Parameterarsenal kommt zum Einsatz, um die Strategie zwar auf der Grundlage derselben Indikatoren allerdings für unterschiedliche Zeiträume zu optimieren.
Die Datei, um die Daten in Statistica laden zu können, muss das Format CSV sowie folgenden Aufbau aufweisen Die Variablen sind spaltenweise angeordnet. das heißt: jede Spalte bezieht sich stets nur auf einen einzigen Indikator. Die Zeilen müssen die anschließenden Messungen (Fälle) enthalten, d. h. die Indikatorwerte für bestimmte Balken. Anders gesagt, in der waagerechten Kopfzeile der Tabelle stehen die Indikatoren, während die nachfolgenden Balken in senkrechter Richtung aufgeführt werden.
Die Analyse bezieht sich auf die Indikatoren:
- Accelerator Oscillator;
- Bears Power;
- Bulls Power;
- Awesome Oscillator;
- Commodity Channel Index;
- DeMarker;
- Fractal Adaptive Moving Average;
- MACD;
- Relative Strength Index;
- Money Flow Index;
- Stochastic;
- Williams Percent Range.
Jede Datenzeile unserer Datei enthält:
- Kursänderungen zwischen „Open“ und „Close“ im jeweiligen Balken;
- die Werte der Indikatoren, die im vorhergehenden Balken verzeichnet wurden.
Somit werden wir eine Gleichung suchen, die das zukünftige Verhalten des Kurses auf der Grundlage der bekannten Indikatorwerte beschreibt.
Neben dem absoluten Indikatorwert speichern wir seinen Abstand zu dem ihm vorhergehenden Wert, um die Änderungsrichtung der Indikatoren zu berücksichtigen. Diese Variablen haben in unserem Beispiel Bezeichnungen mit dem Präfix „d“. Für Indikatoren mit Signallinie speichern wir den Abstand zwischen der Haupt- und der Signallinie sowie deren Dynamik. Die Bezeichnungen für die von Indikatoren mit abweichenden Zeiträumen gesammelten Daten enden mit „_p“.
Zur Veranschaulichung der Optimierung wurde lediglich ein Zeitraum hinzugefügt, der doppelt so lang ist wie der übliche Zeitraum des Indikators. Darüber hinaus speichern wir die Zeit des Auftretens des neuen Balkens sowie den entsprechenden Stundenwert. Wir speichern die Differenz zwischen „Open“ und „Close“ für den Balken, an dem wir die Indikatoren berechnen. Das geschieht zur Ausfilterung der Ausreißer. Infolgedessen analysieren wir 33 Parameter, um eine multiple Regressionsgleichung anzulegen. Die beschriebene Datenerfassung wird in dem im Anhang zu diesem Beitrag beigefügten Expert-System R_collection umgesetzt.
Nach dem Aufrufen des Expert-Systems wird in dem Ordner terminal_data_directory/MQL5/Files die Datei MasterData.CSV angelegt. Beim Start des Expert-Systems in dem Prüfprogramm wird es in dem Dateiverzeichnis des Ausgabegerätes terminal_data_directory/tester/Agent-127.0.0.1-3000/MQL5/Files abgelegt. Die resultierende Datei kann bereits in Statistica verwendet werden.
Ein Beispiel für eine solche Datei befindet sich im Anhang in der Datei MasterDataR.CSV. Die Daten wurden mithilfe des Strategieprüfprogramms für die Zeit vom 3. Januar 2011 bis zum 11. November 2011 für das Kürzel EURUSD H1 gesammelt. In der Analyse wurden nur die Daten von August bis September verwendet. Die übrigen Daten wurden zu Übungszwecken in der Datei gespeichert.
Um die Datei in Statistica zu laden, gehen wir wie folgt vor:
- Öffnen Sie in Statistica zunächst „Datei“ (File), dann „Öffnen“ (Open) und wählen Sie „Datendateien“ (Data files), um Ihre .CSV-Datei zu öffnen.
- In dem Fenster „Text File Import Type“ lassen Sie „Delimited“ stehen und klicken Sie auf „OK“.
- In dem aufklappenden Fenster aktivieren Sie die unterstrichenen Punkte.
- In dem Feld „Decimal separator character“ muss unbedingt „Punkt“ angegeben werden unabhängig davon, ob er dort bereits vorhanden ist oder nicht.
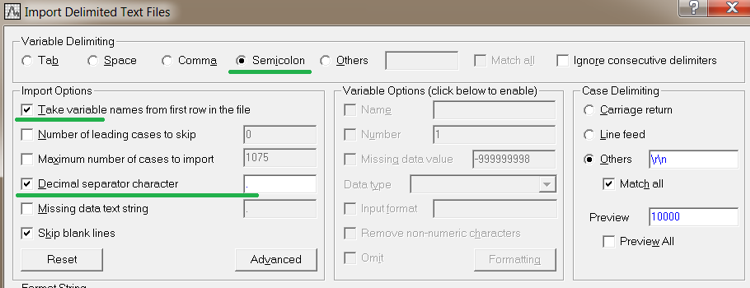
Abbildung 3. Import der Datei nach Statistica
Nach Anklicken von „OK“ erscheint eine Tabelle mit unseren für die Ausführung der multiplen Regressionsanalyse (MRA) aufbereiteten Daten. Ein Beispiel für die Datei zur Verwendung in Statistica liegt in der Datei MasterDataR.STA bei.
3.2. Automatische Auswahl der Indikatoren
Starten Sie die Regressionsanalyse (Statistik -> Multiple Regression).
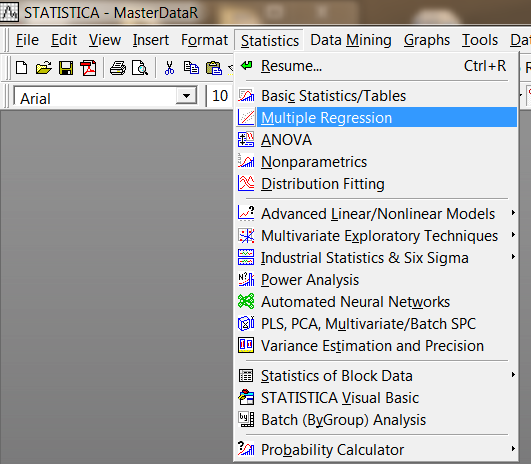
Abb. 4. Ausführen der Regressionsanalyse (RA)
Gehen Sie in dem sich öffnenden Fenster auf die Registerkarte „Erweitert“ (Advanced) und haken Sie die markierten Punkte an. Betätigen Sie die Schaltfläche „Variablen“ (Variables).
Wählen Sie im ersten Feld die abhängige Variable aus und im zweiten alle unabhängigen Variablen, auf deren Grundlage die Gleichung angelegt wird. Geben Sie in unserem Fall im ersten Feld die Variable „Kurs“ (Price) an und im zweiten die Variablen von „Kurs2“ (Price2) bis dWPR.
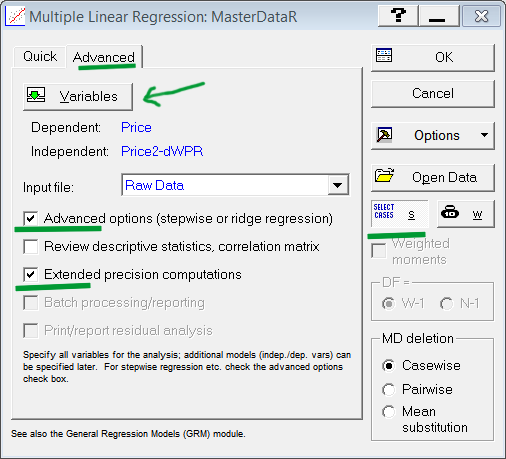
Abb. 5. Vorbereitung der Parameterauswahl
Betätigen Sie die Schaltfläche „Fälle auswählen“ (Select Cases) (Abb. 5).
Es öffnet sich ein Fenster für die Auswahl der in der Analyse zu verwendenden Fälle (Datenzeilen). Haken Sie die Felder an, wie in Abb. 6 dargestellt.
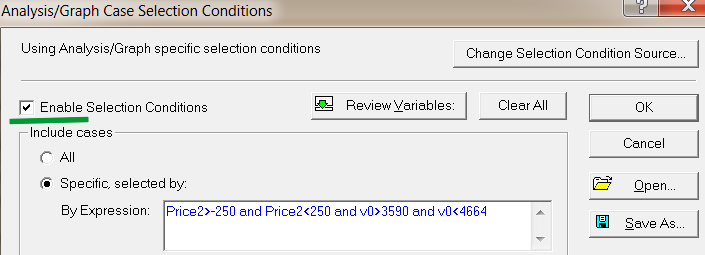
Abb. 6. Auswahl der Fälle
Wir geben nur Daten aus den Monaten Juli und August zur Analyse an. Das sind die Fälle von 3.590 bis 4.664. Die Fallnummern werden mithilfe der Variablen V0 festgelegt. Zur Minderung der Auswirkungen der Ausreißer und Kursspitzen fügen wir eine Datenfilterung hinsichtlich des Kurses hinzu.
Wir beziehen in die Analyse nur die Indikatorwerte ein, bei denen die Differenz zwischen „Open“ und „Close“ in dem letzten Balken nicht mehr als 250 Punkte betragen hat. Nachdem wir hier die Regeln für die Auswahl der Fälle für die Analyse festgelegt haben, erfolgt die Entnahme der Datenstichprobe zur Aufstellung der Regressionsgleichung. Betätigen Sie anschließend die Schaltfläche „OK“ hier und in dem Fenster für die Vorbereitung der Parameterauswahl (Abb. 5).
Es öffnet sich ein Fenster zur Auswahl des Verfahrens zur automatischen Datenentnahme. Wählen Sie das Verfahren „Schrittweise Vorwärts“ (Forward Stepwise) (Abb. 7).
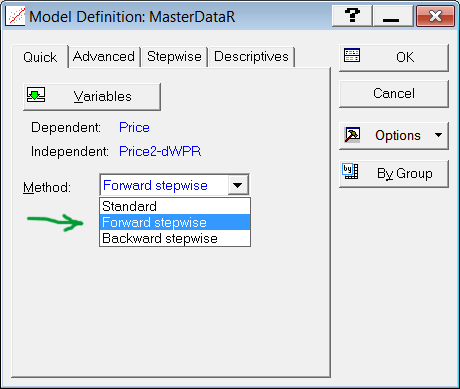
Abbildung 7. Auswahl der Methode
Klicken Sie auf „OK“. Es öffnet sich ein Fenster mit der Meldung, dass die Regressionsanalyse (RA) erfolgreich ausgeführt wurde.
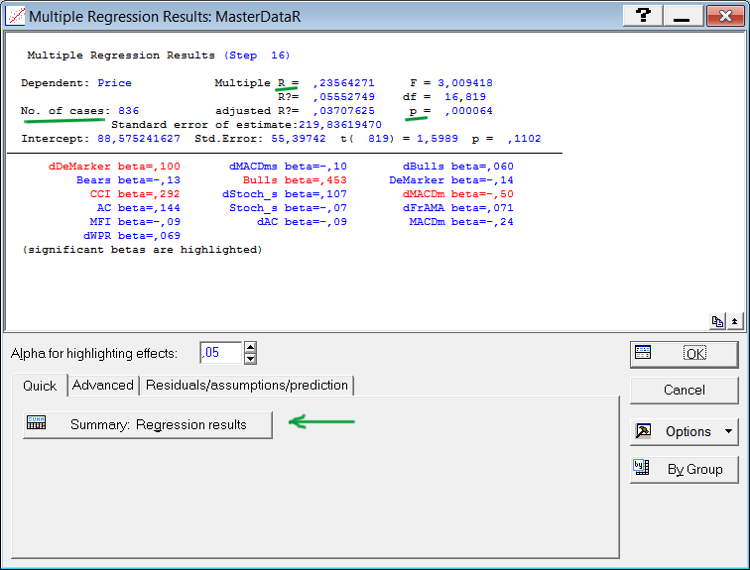
Abb. 8. Das Fenster mit den Ergebnissen der RA
Die automatische Parameterauswahl konzentriert sich auf diejenigen von ihnen, die den größten Beitrag zu der multiplen Korrelation zwischen den Indikatoren (den unabhängigen Variablen) und der abhängigen Variablen leisten. In unserem Fall wird eine Auswahl der Indikatoren gewählt, durch die der Kurs am stärksten bestimmt wird. Die automatische Auswahl bringt ihrem Wesen nach die Strategie hervor. In die aufgestellte Gleichung gehen nur die Indikatoren ein, die das Kursverhalten zuverlässig und am besten abbilden.
In dem Fenster mit den Ergebnissen (Abb. 8) sind im oberen Teil die statistischen Eigenschaften der resultierenden Gleichung enthalten, während unten die in die Gleichung aufgenommenen Parameter ausgewiesen werden. Beachten Sie bitte die unterstrichenen Eigenschaften. Multiple R ist der Wert der multiplen Korrelation zwischen dem Kurs und den in die Gleichung eingehenden Indikatoren. „p“ ist das Niveau der statistischen Zuverlässigkeit dieser Korrelation.
Als zuverlässig gilt ein Niveau von weniger als 0,05. Die Anzahl der für die Analyse verwendeten Fälle wird als „No. of cases“ bezeichnet. In der Aufstellung der Indikatoren sind diejenigen rot gekennzeichnet, deren Beitrag statistisch zuverlässig ist. Im Idealfall sollten alle Indikatoren rot markiert sein.
Die in Statistica verwendeten Regeln zur Einbeziehung von Parameter in die Analyse sind nicht immer optimal. Es könnte zum Beispiel eine große Zahl nicht zuverlässiger Parameter in die Regressionsanalyse gelangen. Deshalb sollten wir einen kreativen Ansatz wählen und dem Programm bei der Auswahl der Parameter behilflich sein.
Wenn in der Aufstellung unzuverlässige Parameter vorliegen, betätigen Sie die Schaltfläche „Zusammenfassung: Regressionsergebnisse“ (Summary: Regression results).
Es öffnet sich ein Fenster mit den Daten zu jedem Indikator (Abb. 9).
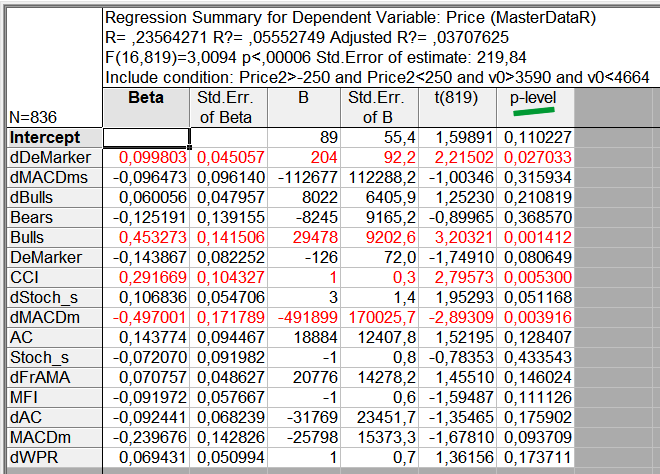
Abb. 9. Berechnung der in die RA einbezogenen Parameter
Sehen Sie nach, bei welchem unzuverlässigen Parameter das höchste „p“-Niveau (p-level) vorliegt, und merken Sie sich seinen Namen. Gehen Sie zurück zu dem Schritt der Einbeziehung der Parameter in die Analyse (Abb. 7) und entfernen Sie den betreffenden Parameter aus der Aufstellung der für die Analyse ausgewählten Parameter.
Um wieder zurückzukehren, betätigen Sie in dem Fenster mit den Analyseergebnissen die Schaltfläche „Abbrechen“ (Cancel) und wiederholen Sie die Analyse. Versuchen Sie, auf diese Weise alle unzuverlässigen Parameter zu entfernen. Orientieren Sie sich dabei an dem ermittelten Wert für die multiple Korrelation (Multiple R), der nicht weit unter dem ursprünglichen liegen dürfte. Die unzuverlässigen Parameter können einzeln aus der Analyse ausgeschlossen werden, aber auch alle auf einmal.
Im Endeffekt verbleiben in der Tabelle nur die zuverlässigen Parameter (Abb. 10). Dabei ist der Korrelationswert wahrscheinlich aufgrund zufälliger Übereinstimmungen um etwa 20% gesunken. Bekanntermaßen liegen in einer unendlich langen Zahlenreihe unendlich viele zufällige Übereinstimmungen vor.
Da wir große Datenstichproben verarbeiten, haben wir es auch hier mit zufälligen Übereinstimmungen und Beziehungen zu tun. Deshalb ist es erforderlich, in den eigenen Strategien nur Parameter zu verwenden, die statistisch zuverlässig sind.
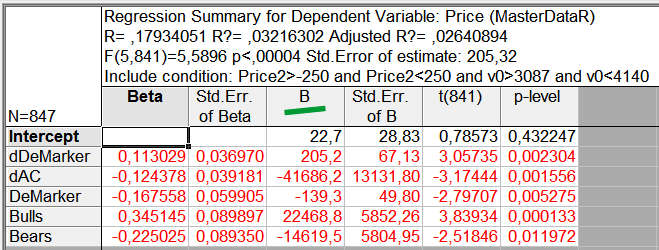
Abb. 10. In die Gleichung wurden nur zuverlässige Parameter einbezogen
Wenn es nach der Auswahl der Parameter nicht gelingt, eine Gruppe aus einigen, zuverlässig mit dem Kurs korrelierenden Indikatoren anzulegen, so enthält der Kurs vermutlich nur wenige Informationen über zurückliegende Ereignisse. In solchen Fällen sollte man auf der Grundlage technischer Analysen äußerst vorsichtig handeln oder es ganz sein lassen.
In unserem Beispiel wurden von 33 Parametern lediglich fünf als für die Entwicklung einer Strategie auf der Grundlage einer Regressionsgleichung geeignet erachtet. Diese Fähigkeit der Regressionsanalyse ist bei der Auswahl der Indikatoren für eine eigene Strategie von großem Nutzen.
3.3. Die Regressionsgleichung und ihre Analyse
Somit haben wir die Regressionsanalyse ausgeführt und eine Aufstellung der „richtigen“ Indikatoren erhalten. Jetzt „übersetzen“ wir das in eine Regressionsgleichung (RG). Deren Koeffizienten für jeden der Indikatoren werden in der Spalte B der Ergebnisse der RA (Abb. 10) ausgewiesen. In eben dieser Tabelle erscheint der Parameter „Intercept“ als eigenständiges Glied der Gleichung, in die er als unabhängiger Koeffizient eingeht.
Wir legen auf der Grundlage dieser Tabelle (Abb. 10) folgende Gleichung an, wozu wir uns der Koeffizienten aus der spalte B bedienen.
Kurs (Price) = 22.7 + 205.2*dDemarker - 41686.2*dAC - 139.3*DeMarker + 22468.8*Bulls - 14619.5*Bears
Diese Gleichung wurde bereits in Abschnitt 1 als MQL5-Code vorgestellt. Ebendort wurden auch die von dem Prüfprogramm ausgegebenen Ergebnisse der Arbeit des auf der Grundlage dieser Gleichung angelegten Expert-Systems ausgewiesen. Wie wir sehen, hat sich die RA als würdiger „Strategiegenerator“ erwiesen. Sie hat eine konkrete Strategie empfohlen und für diese aus dem bestehenden Angebot die passenden Indikatoren ausgewählt.
Um die Stabilität unserer Gleichung noch eingehender zu untersuchen, muss sie auf Folgendes überprüft werden:
- Ausreißer;
- die Normalität der Verteilung der Residuen; sowie
- die Nichtlinearität des Einflusses der einzelnen in ihr enthaltenen Parameter.
Diese Prüfungen können mithilfe einer Residuenanalyse ausgeführt werden. Um zu dieser Analyse zu gelangen, muss die Schaltfläche „OK“ im Ergebnisfenster (Abb. 8) betätigt werden. Bei der Ausführung dieser Überprüfungen an der ermittelten Gleichung zeigt sich, dass sich die Gleichung als stabil gegenüber einer geringen Zahl an Ausreißern und einer geringfügigen Abweichung von der Normalverteilung der Daten sowie gegenüber einer gewissen Nichtlinearität bei den Parametern ist.
Ist die Nichtlinearität einer Beziehung erheblich, kann eine Transformation gefunden werden, um den betreffenden Parameter an die lineare Form anzunähern. Zu diesem Zweck bietet Statistica die Analyseart stationäre nichtlineare Regression. Sie kann im Menü wie folgt aufgerufen werden: Statistik (Statistics) -> erweiterte lineare / nichtlineare Modelle (Advanced Linear/Nonlinear Models) -> Stationäre nichtlineare Regression (Fixed Nonlinear Regression). Alles in allem zeugen die durchgeführten Überprüfungen von der guten Stabilität der multiplen Regressionsanalyse gegenüber einer maßvollen Anzahl von Störungen innerhalb der analysierten Daten.
4. Die Regressionsanalyse als Strategieoptimierer
Da die Regressionsanalyse (RA) in der Lage ist, unzählige Parameter zu überprüfen, kann sie zur Optimierung einer Strategie genutzt werden. Wenn beispielsweise 50 Zeiträume für einen Indikator zu überprüfen sind, können sie als 50 Einzelwerte gespeichert und alle auf einmal an die RA weitergegeben werden. In einer Statistica-Tabelle können 65.536 Parameter untergebracht werden. Wenn für jeden Indikator 50 Zeiträume überprüft werden müssen, können fast 1.300 Indikatorwerte an die RA weitergegeben werden. Das übersteigt die Möglichkeiten des in MetaTrader 5 enthaltenen Prüfprogramms.
Wir werden eine solche Optimierung an den Daten unseres Beispiels vornehmen. Wie in Abschnitt 4.1 bereits gesagt wurden zur Veranschaulichung der Optimierung zu den Daten die Werte von Indikatoren mit einem doppelt so langen Zeitraum wie dem üblichen hinzugefügt. In den Dateien weisen diese Indikatoren in ihren Namen die Endung „_p“ auf. Einschließlich der Indikatoren mit den üblichen Zeiträumen enthält unsere Stichprobe jetzt 60 Parameter. Nachdem wir an ihnen alle in Abschnitt 3.2 dargestellten Manipulationen vorgenommen haben, erhalten wir folgende Tabelle (Abb. 11).
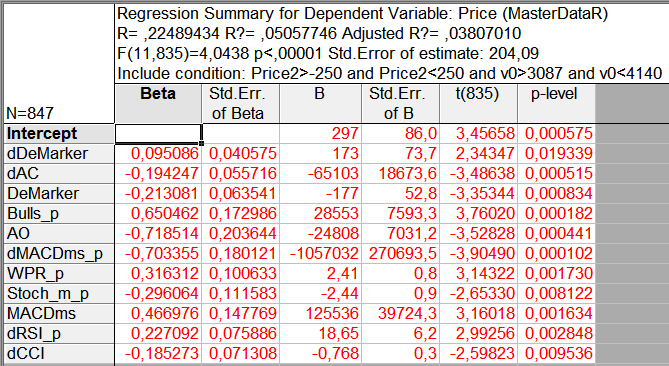
Abb. 11. Analyseergebnisse der Indikatoren mit unterschiedlichen Zeiträumen
In die RG sind 11 Parameter eingegangen: sechs von Indikatoren mit dem üblichen Zeitraum und fünf von solchen mit verlängertem Zeitraum. Die Korrelation der Parameter mit dem Kurs ist um ein Viertel größer geworden. In die Gleichung sind Werte des Indikators MACD indicator für beide Zeitraumvarianten eingegangen.
Da bei der RA die Werte ein und desselben Indikators für zwei unterschiedliche Zeiträume unterschiedliche Parameter darstellen, können in der Gleichung die Werte von Indikatoren mit unterschiedlichen Zeiträumen kombiniert werden. Infolge der Analyse kann sich z. B. zeigen, dass der Wert RSI(7) mit einem Kursanstieg verbunden ist, RSI(14) dagegen mit einem Rückgang. Das übliche Prüfprogramm leistet keine vergleichbare Analyse.
Die auf der Grundlage der erweiterten Analyse aufgestellte RG hat folgendes Aussehen (Abb. 11):
Kurs (Price) = 297 + 173*dDemarker - 65.103*dAC - 177*DeMarker + 28.553*Bulls_p - 24.808*AO - 1.057.032*dMACDms_p + 2,41*WPR_p - 2,44*Stoch_m_p + 125.536*MACDms + 18,65*dRSI_p - 0,768*dCCI
Wir sehen nach, welche Ergebnisse diese Gleichung in unserem Expert-System zeitigt. In der Abbildung 12 wird das Ergebnis des Probelaufs des Expert-Systems anhand der bei der RA verwendeten Daten vom 1. Juli bis zum 1. September 2011 abgebildet. Das Diagramm wurde fließender, und das Expert-System hat einen höheren Gewinn erzielt.
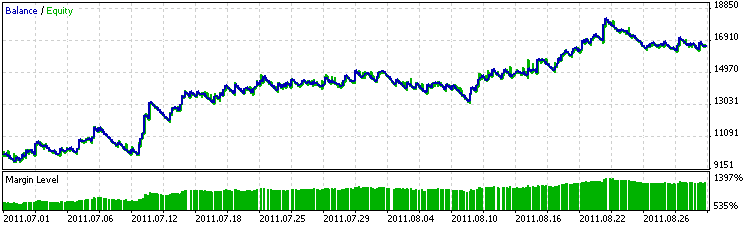
Abb. 12. Arbeitsdiagramm des Expert-Systems für den Musterzeitraum
Überprüfen wir das Expert-System jetzt an dem Prüfzeitraum vom 1. September bis zum 1. November 2011. Das Gewinndiagramm ist schlechter ausgefallen als das bei dem nur auf Indikatoren mit den üblichen Zeiträumen beruhenden Expert-System. Möglicherweise muss die ermittelte Gleichung auf die Normalität und Nichtlinearität ihrer inneren Parameter überprüft werden.
Da die Nichtlinearität bei den Indikatoren mit einem üblichen Zeitraum festgestellt werden konnte, könnte sie für den verlängerten Zeitraum von ausschlaggebender Bedeutung sein. In diesem Fall kann die Arbeit der Gleichung durch die Annäherung der Parameter an die lineare Form verbessert werden. Wie dem auch sei, das Expert-System ist während des Prüfzeitraums „nicht zusammengeschmolzen“, es hat lediglich keinen Gewinn erzielt. Somit erscheint die ermittelte Strategie als verhältnismäßig stabil.
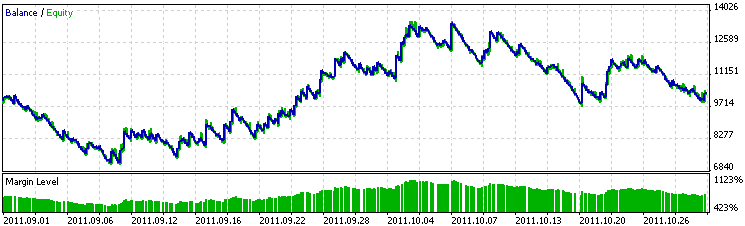
Abb. 13. Arbeitsdiagramm des Expert-Systems für den Prüfzeitraum
Es sei darauf hingewiesen, dass in MQL5 nicht mehr als 64 Parameter je Dateizeile ausgegeben werden können. Für eine groß angelegte Analyse von Indikatoren anhand unterschiedlicher Zeiträume müssen die Datentabellen zusammengeführt werden, das kann in Statistica oder MS Excel erfolgen.
Fazit
Die in diesem Beitrag vorgestellte kleine Untersuchung hat gezeigt, dass die Regressionsanalyse eine Möglichkeit bietet, aus einer Fülle von Indikatoren diejenigen auszuwählen, die für die Vorhersage der Kursentwicklung am aussagekräftigsten sind. Zudem wurde nachgewiesen, dass die RA zur Ermittlung der für die jeweils gegebene Stichprobe optimalen Indikatorzeiträume genutzt werden kann.
Dabei ist zu bedenken, dass Regressionsgleichungen leicht in die Programmiersprache MQL5 zu übersetzen sind und ihre Verwendung keine nennenswerten Programmierkenntnisse erfordert. Somit kann die multiple Regressionsanalyse zur Entwicklung einer Handelsstrategie genutzt werden. Dabei dient die Regressionsgleichung als Grundlage der Strategie.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/349
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Tipps für unerfahrene Auftraggeber
Tipps für unerfahrene Auftraggeber
 Die Box-Cox-Transformation
Die Box-Cox-Transformation
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
sehr ähnlich wie bei neuronalen Netzen
SZY: und selbst wenn es sich nicht um NS handelt, wird das Ergebnis eines solchen Tools der Arbeit von NS ähnlich sein - in der Geschichte der positiven Ergebnisse
sehr ähnlich zu neuronalen Netzen
SZY: Und selbst wenn es sich nicht um NS handelt, wird das Ergebnis eines solchen Werkzeugs der Arbeit von NS ähnlich sein - was die Geschichte der positiven Ergebnisse angeht.
Ja, genau, deshalb sind solche Methoden nicht ausreichend. (aber notwendig!)
;-)
Integer:.
Was sind die Faktoren? Alle Indikatoren mit allen möglichen Parametersätzen aus allen möglichen Symbolen?
Wir brauchen nicht alle, wir brauchen nur die vielversprechenden. Und deshalb ist der entscheidende Faktor die Fähigkeit, diese "vielversprechenden" zu finden.
Und die Aufgabe der Methode ist es, Hoffnungen zu zerstören, d.h. "falsches Versprechen" zu erkennen.
Was streng genommen auch wertvoll ist.
// "Töte die Hoffnung rechtzeitig!" (ts) me
Sehr geehrter Herr,
ich weiß nicht, wie man dieses oder die anderen Elemente, über die Sie geschrieben haben, verwendet.Ich habe versucht, den diskriminierenden EA zu schreiben, aber ich kann den EA nicht dazu bringen, mir zu erlauben, den Assistenten zu laden, ohne die Indikatoren über den Assistenten zu laden. Auf diese Weise sieht der Abschnitt "int OnInit()" anders aus als der in Ihrem Artikel.Muss ich alle Informationen aus diesem Abschnitt löschen, damit meine Abschnitte so aussehen wie Ihre? Wo befindet sich das Statistica-Programm auf MQL 5? Wie öffne ich es? Vielleicht wäre es besser, wenn ich Sie fragen würde, ob Sie mir bei dem, was ich zu tun versuche, helfen können oder ob Sie jemanden kennen, der das kann?Ich werde die Idee mit anderen teilen, möchte aber nicht, dass sie veröffentlicht oder vermarktet wird. Derzeit funktioniert der Plan zu 85%, könnte aber besser sein. Sobald er optimiert ist, wäre der Handel durch einen benutzerdefinierten Indikator einfacher, aber auch hier weiß ich nicht, wie ich einen solchen schreiben soll.Wissen Sie etwas über die Programmiersprache der Thinkorswim-Plattform von TD Ameritrade? Damit das funktioniert, brauchen wir nämlich Zugang zu den Indikatoren, die den Währungen zugrunde liegen, wie z.B. DX, 6e, 6a, 6j und andere Wirtschaftsindizes. Verfügt TOS über das Programm Statistica? Bitte kontaktieren Sie mich per E-Mail dennie3166@yahoo.com
Ich danke Ihnen vielmals,
Dennie.
Lieber Artem,
Liebe Trader,
Ich bin wirklich beeindruckt von diesem Artikel, aber leider funktionieren die angehängten Dateien "r_check.mq5" und "r_collection.mq5" nicht. Eigentlich erscheinen sie nicht einmal in meinem MT5.
Weiß jemand, was der Grund dafür sein könnte. Ich wäre Ihnen sehr dankbar!
Vielen Dank im Voraus!
Mit freundlichen Grüßen,
Nikolay Hristov