Sieht cool aus :)
Aber was es ist, und wie man es benutzt, muss ich noch herausfinden :)
Sieht cool aus :)
Aber was es ist, und wie man es benutzt, müssen wir noch herausfinden :)
kann als erste verborgene Schicht verwendet werden - zur Dimensionalitätsreduktion oder zum Clustering selbst, kann in probabilistischen Netzen verwendet werden, und viele andere Optionen.
Vielen Dank für das Material!
Ich werde versuchen, es in aller Ruhe zu lernen :)
Vielen Dank für den neuen Artikel über eine interessante Vernetzungsmethode. Wenn Sie die Literatur durchgehen, gibt es Dutzende, wenn nicht Hunderte von ihnen. Aber das Problem für die Händler liegt nicht im Mangel an Werkzeugen, sondern in deren richtiger Anwendung. Der Artikel wäre noch interessanter, wenn er ein Beispiel für die Anwendung dieser Methode in einem Expert Advisor enthalten würde.

Vielen Dank für den neuen Artikel über eine interessante Vernetzungsmethode. Wenn Sie die Literatur durchgehen, gibt es Dutzende, wenn nicht Hunderte von ihnen. Aber das Problem für die Händler liegt nicht im Mangel an Werkzeugen, sondern in deren richtiger Anwendung. Der Artikel wäre noch interessanter, wenn er ein Beispiel für die Anwendung dieser Methode in einem Expert Advisor enthalten würde.
1. Der Artikel ist gut. Er wird auf zugängliche Weise präsentiert, der Code ist nicht kompliziert.
2. Zu den Nachteilen des Artikels gehört die Tatsache, dass überhaupt nichts über die Eingangsdaten des Netzes gesagt wird. Man hätte ein paar Worte darüber schreiben können, was eingegeben wird - Vektor der Kurse für den Zeitraum/Indikator-Daten, Vektor der Kursabweichungen, normalisierte Kurse oder etwas anderes. Für die praktische Anwendung des Algorithmus ist die Frage der Eingabedaten und ihrer Aufbereitung von zentraler Bedeutung. Ich empfehle, für solche Algorithmen einen Vektor der relativen Preisänderungen zu verwenden: x[i]=Preis[i+1]-Preis[i].
Außerdem kann der Eingangsvektor zuvor normalisiert werden (x_normal[i]=x[i]/M), wobei die maximale Abweichung des Preises für den betrachteten Zeitraum als M verwendet werden kann (hier und im Folgenden verzichte ich der Kürze halber auf Variablendeklarationen):
M=x[ArrayMaximum(x)]-x[ArrayMinimum(x)];
In diesem Fall liegen alle Eingangsvektoren in einem Einheitshyperwürfel mit der Seite [-0,5,0,5], was die Qualität des Clustering deutlich erhöht. Sie können auch die normale Standardabweichung oder andere Mittelungsvariablen für die relativen Abweichungen der Kurse über den Zeitraum als M verwenden.
3. In dem Papier wird vorgeschlagen, das Quadrat der Norm der Differenz als Abstand zwischen dem Vektor der Neuronengewichte und dem Eingangsvektor zu verwenden:
for(i=0, sum=0; i<m; i++, sum+=Pow(x[i]-w[i],2));
Meiner Meinung nach ist diese Abstandsfunktion bei dieser Clusteraufgabe nicht effektiv. Effektiver ist die Funktion, die das Skalarprodukt oder das normalisierte Skalarprodukt berechnet, d.h. den Kosinus des Winkels zwischen dem Vektor der Gewichte und dem Eingangsvektor:
for(i=0, norma_x=0, norma_w=0; i<m; i++, norma_x+=x[i]*x[i], norma_w+=w[i]*w[i]); norma_x=sqrt(norma_x); norma_w=sqrt(norma_w); for(i=0, sum=0; i<m; i++, sum+=x[i]*w[i]); if(norma_x*norma_w!=0) sum=sum/(norma_x*norma_w);
In jedem Cluster werden dann Vektoren gruppiert, die sich durch die Richtung der Schwingungen ähneln, nicht aber durch die Größe dieser Schwingungen, was die Dimensionalität des zu lösenden Problems erheblich reduziert und die Eigenschaften der Gewichtsverteilungen des trainierten neuronalen Netzes erhöht.
4.Es ist richtig festgestellt worden, daß es notwendig ist, ein Abbruchkriterium für das Training des Netzes zu definieren. Das Abbruchkriterium sollte die erforderliche Anzahl von Clustern des trainierten Netzes bestimmen. Und sie (die Anzahl) hängt ihrerseits von dem allgemeinen Problem ab, das gelöst werden soll. Wenn die Aufgabe darin besteht, eine Zeitreihe für 1-2 Stichproben im Voraus zu prognostizieren, und zu diesem Zweck beispielsweise ein mehrschichtiges Perseptron verwendet wird, dann sollte sich die Anzahl der Cluster nicht wesentlich von der Anzahl der Neuronen der Eingangsschicht des Perseptrons unterscheiden.
Im Allgemeinen übersteigt die Anzahl der Balken in der Geschichte nicht 5.300.000 auf dem detailliertesten Minutenchart (10 Jahre*365 Tage*24 Stunden*60 Minuten). Auf dem Stundenchart sind es 87.000 Balken. Das heißt, die Erstellung eines Klassifizierers mit einer Anzahl von mehr als 10000-20000 Clustern ist wegen des "Übertrainings"-Effekts nicht gerechtfertigt, wenn jeder Kursvektor einen eigenen Cluster hat.
Ich entschuldige mich für mögliche Fehler.
1. Danke, ich habe mein Bestes für Sie getan:)
2. Ja, ich stimme zu. Aber noch die Eingänge - das ist ein eigenes großes Problem, über das man allein Dutzende von Artikeln schreiben kann.
3. und hier bin ich völlig anderer Meinung. Im Falle von normalisierten Eingaben ist der Vergleich von Skalarprodukten äquivalent zum Vergleich von euklidischen Normen - erweitern Sie die Formeln.
4. Da die maximale Anzahl von Clustern bereits einer der Parameter des Algorithmus ist.
max_nodes
Ich würde z.B. wie folgt vorgehen: Messen Sie den Fehler des Gewinners in den letzten N Schritten und bewerten Sie seine Dynamik auf irgendeine Weise (z.B. messen Sie die Steigung der Regressionslinie). Wenn der Fehler immer noch abnimmt und die Trainingsdaten bereits erschöpft sind, dann ist es eine Überlegung wert, sie zu glätten, um das Rauschen zu unterdrücken oder das Defizit an Beispielen irgendwie zu beseitigen.
3. ich verstehe nicht, wo die Gleichwertigkeit der Formeln liegt. Die Formel für den Kosinus des Winkels zwischen den Vektoren(x,w)/(|x||w|) ist "nicht sehr" ähnlich zu |x-w|^2. Die Normalisierung der Eingaben ändert nichts an den grundlegenden Unterschieden zwischen diesen Maßen:
Äquivalenz ist, dass das Maximum des Abstands immer dem Minimum des Skalarprodukts entspricht und umgekehrt. Bei normierten Vektoren ist die Beziehung eindeutig und monoton, so dass es keine Rolle spielt, ob man das Quadrat des Abstands oder den Winkel berechnet.
Hallo Alex,
Vielen Dank für die klare Erklärung zu diesem Thema.
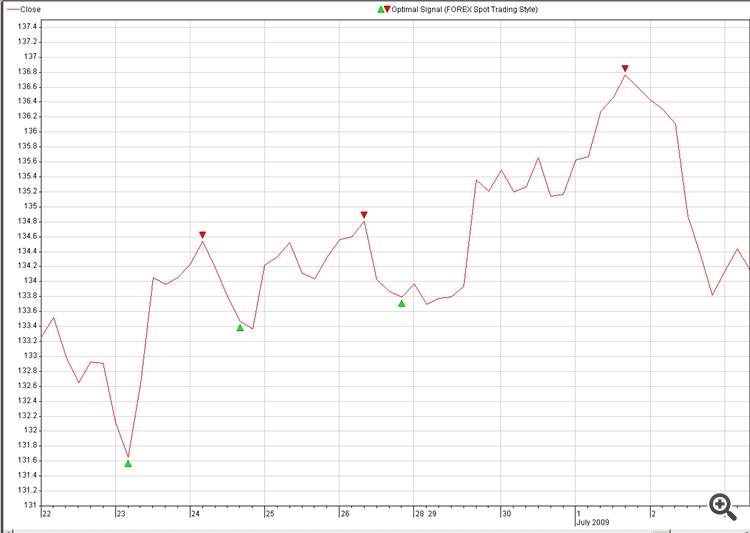
Wäre es möglich, einen praktischen Code für die Rekonstruktion des zukünftigen Preises zu teilen, zum Beispiel aus optimalen Signalen.
Die Idee ist:
1. Input (Quelle): mehrere Währungen (18)
2. Ziel: Optimales Signal der Währung, die wir vorhersagen möchten (Bild: 2. Optimale_Signale)
3. Finden Sie eine neuro-connections zwischen Quelle und Ziel und explodieren sie im Handel.
Eine weitere Frage zur NN-Rekonstruktion:
Ist es möglich, anstelle von Zufallsstichproben unsere Stichproben zu verwenden, wie auf Bild 2:
Unser Gehirn kann das Bild in weniger als einer Sekunde rekonstruieren, mal sehen, wie viel Zeit es für NN braucht, um dasselbe zu tun, nur ein Scherz, es ist keine Herausforderung.

Zufallsgenerierte Muster sind nicht sehr interessant zu sehen, da es keine Bedeutung dahinter gibt, aber wenn wir selbst Punkte mit einer Bedeutung dahinter zeichnen könnten, würde es viel mehr Spaß machen :-0)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Growing Neural Gas: Umsetzung in MQL5 :
In diesem Artikel wird ein Beispiel für die Entwicklung eines MQL5-Programms zur Umsetzung des als Growing Neural Gas (GNG) bezeichneten adaptiven Clustering-Algorithmus vorgestellt. Dieser Beitrag richtet sich an Anwender, die die Dokumentation zu dieser Programmiersprache gelesen haben und über gewisse Erfahrungen und Grundkenntnisse im Bereich Neuroinformatik verfügen.
Autor: Alexey Subbotin