Beispiel für CNA (Causality Network Analysis), SMOC (Stochastic Model Optimal Control) und Nash Game Theory mit Deep Learning

Einführung

Wir werden durch den Prozess des Hinzufügens von Deep Learning zu drei fortgeschrittenen Trading Experts Advisors gehen, diese drei Experten sind fortgeschrittene EAs, die als Artikel veröffentlicht wurden. 

Diese drei Artikel wurden hier veröffentlicht: www.mql5.com

1. Anwendung der Nash'schen Spieltheorie mit HMM-Filterung im Handel
2. Beispiel einer Kausalitätsnetzwerkanalyse (CNA) und eines Vektor-Autoregressionsmodells zur Vorhersage von Marktereignissen
3. Beispiel für stochastische Optimierung und optimale Kontrolle

Wenn Sie diese Artikel noch nicht gelesen haben, werde ich kurz erklären, worum es sich dabei handelt, aber ich empfehle dringend, die Artikel zu lesen.

Die Spieltheorie von Nash

Das Nash-Gleichgewicht gilt als eine der grundlegenden Komponenten der Spieltheorie. 

Das Nash-Gleichgewicht ist ein Konzept in der Spieltheorie, bei dem davon ausgegangen wird, dass jeder Spieler die Gleichgewichtsstrategien der anderen Spieler kennt und kein Spieler etwas zu gewinnen hat, wenn er nur seine eigene Strategie ändert.

In einem Nash-Gleichgewicht ist die Strategie eines jeden Spielers optimal, wenn die Strategien aller anderen Spieler berücksichtigt werden. Ein Spiel kann mehrere Nash-Gleichgewichte haben oder keines.

Analyse des Kausalitätsnetzes

Die Kausalitätsnetzwerkanalyse (Causality Network Analysis, CNA) ist eine Methode zum Verständnis und zur Modellierung komplexer kausaler Beziehungen zwischen Variablen in einem System. Bei der Anwendung auf die Finanzmärkte kann sie helfen zu erkennen, wie sich verschiedene Marktereignisse und Faktoren gegenseitig beeinflussen, was zu genaueren Vorhersagen führen kann.

Der Bot verwendet die schnelle Kausalitätsschlussfolgerung.

Die schnelle Kausalitätsschlussfolgerung (Fast Casual Inference) ist ein Konzept, das schnelle statistische Schlussfolgerungen mit Kausalanalysen kombiniert. Sie zielt darauf ab, schnell kausale Schlussfolgerungen aus Daten zu ziehen und dabei ein Gleichgewicht zwischen Geschwindigkeit und kausalem Verständnis herzustellen. Dieser Ansatz eignet sich für Szenarien, die rasche, datengestützte Entscheidungen erfordern und gleichzeitig Einblicke in Ursache-Wirkungs-Beziehungen benötigen. Zu den möglichen Anwendungen gehören Marktanalysen in Echtzeit, schnelle Entscheidungsfindung in Unternehmen und schnelle epidemiologische Studien. Bei dieser Methode wird eine gewisse Analysetiefe zugunsten der Geschwindigkeit aufgegeben, sodass sie sich für zeitkritische Umgebungen eignet, in denen das Verständnis von Kausalzusammenhängen entscheidend ist.

Stochastische Optimierung

Stochastische Modellierung und Kontrolloptimierung sind mathematische Techniken, die bei der Lösung von Problemen unter ungewissen Bedingungen helfen. Sie finden Anwendung im Finanzwesen, im Ingenieurwesen, in der künstlichen Intelligenz und in vielen anderen Bereichen.

Die stochastische Modellierung wird verwendet, um Systeme mit Zufallselementen zu beschreiben, wie z. B. Kursbewegungen an der Börse oder eine Warteschlange in einem Restaurant. Sie basiert auf Zufallsvariablen, Wahrscheinlichkeitsverteilungen und stochastischen Prozessen. Methoden wie Monte Carlo und Markov-Ketten können diese Prozesse modellieren und ihr Verhalten vorhersagen.

Die Verwaltungsoptimierung hilft Ihnen, die besten Lösungen für die Systemverwaltung zu finden. Sie wird eingesetzt, um verschiedene Prozesse zu automatisieren und zu verbessern, vom Autofahren bis zum Betrieb von Chemieanlagen. Zu den grundlegenden Methoden gehören lineare quadratische Regler, modellprädiktive Steuerung und Verstärkungslernen.

Deep Learning

Beim Deep Learning, tiefem Lernen, für den Handel werden künstliche neuronale Netze zur Analyse und Vorhersage von Finanzmarkttrends eingesetzt. Hier ist ein kurzer Überblick:

1. Analyse der Daten: Deep-Learning-Modelle verarbeiten riesige Mengen von Finanzdaten, darunter Kursverläufe, Handelsvolumina, Wirtschaftsindikatoren und sogar die Stimmung in den Nachrichten.
2. Mustererkennung: Diese Modelle können komplexe Muster und Beziehungen in Marktdaten erkennen, die für menschliche Händler oder herkömmliche Analysemethoden möglicherweise nicht erkennbar sind.
3. Vorhersage: Auf der Grundlage der ermittelten Muster versuchen Deep-Learning-Modelle, zukünftige Marktbewegungen, Preistrends oder optimale Handelsstrategien vorherzusagen.
4. Automatisierter Handel: Einige Systeme nutzen Deep Learning, um autonome Handelsentscheidungen zu treffen und auf der Grundlage der Vorhersagen des Modells Geschäfte zu tätigen.
5. Risikomanagement: Mithilfe von Deep Learning lassen sich Handelsrisiken durch die gleichzeitige Analyse mehrerer Risikofaktoren besser bewerten und verwalten.
6. Anpassungsfähigkeit: Diese Modelle können kontinuierlich lernen und sich an veränderte Marktbedingungen anpassen, wodurch sich ihre Leistung mit der Zeit verbessern kann.
7. Hochfrequenzhandel: Deep Learning kann besonders in Hochfrequenzhandelsszenarien nützlich sein, in denen Entscheidungen in Sekundenbruchteilen entscheidend sind.

Deep Learning im Handel bietet zwar leistungsstarke Funktionen, aber es ist wichtig zu wissen, dass die Märkte komplex und unvorhersehbar sind. Diese Modelle sind nicht unfehlbar und erfordern nach wie vor eine sorgfältige Überwachung und ein Risikomanagement.

Warum sollten wir einen EA mit Deep Learning haben?

Wir werden ein Deep Learning-Modell mit Python erstellen, ein ONNX-Modell erstellen und dieses Modell zu jedem der EAs hinzufügen und die Ergebnisse mit und ohne Deep Learning vergleichen.

ONNX-Modelle werden verwendet, weil sie leicht in Python erstellt werden können und eine Brücke zwischen verschiedenen Ökosystemen bilden, was Flexibilität und Effizienz bei der Modellentwicklung und -bereitstellung fördert. Python ist ein schneller Weg, um ONNX-Modelle oder Backtesting schnell zu einer Strategie zu machen. Für diesen Artikel werden wir Python 3.11.9 verwenden.

Wir werden Deep Learning mit diesem EA verwenden, weil die bisherigen Ergebnisse aus den Artikeln besser sein könnten. Wir werden Bedingungen für den EA hinzufügen, um Trades auszuführen oder nicht, wenn die Deep Learning-Modelle das auch sagen.

Das Python-Skript

Wir werden dieses .py-Skript verwenden. Dieses Skript erstellt ein DL-Modell in ONNX und verfügt auch über Metriken, um zu sehen, ob das Modell korrekt erstellt wurde. DL hat Probleme, wenn es nicht korrekt erstellt wurde, da es unter- oder überangepasst sein kann, was zu falschen Vorhersagen führt.

#python 3.11.9, tensorflow==2.12.0, keras==2.12.0,  tf2onnx==1.16.0
# python libraries
import MetaTrader5 as mt5
import tensorflow as tf
import numpy as np
import pandas as pd
import tf2onnx
#import tensorflow as tf
#import tf2onnx
import keras

print(f"TensorFlow version: {tf.__version__}")
print(f"Keras version: {keras.__version__}")
print(f"tf2onnx version: {tf2onnx.__version__}")


# input parameters

inp_history_size = 120

sample_size = inp_history_size*3*20
symbol = "EURUSD"
optional = "D1_2024"
inp_model_name = str(symbol)+"_"+str(optional)+".onnx" 

if not mt5.initialize():
    print("initialize() failed, error code =",mt5.last_error())
    quit()

# we will save generated onnx-file near the our script to use as resource
from sys import argv
data_path=argv[0]
last_index=data_path.rfind("\\")+1
data_path=data_path[0:last_index]
print("data path to save onnx model",data_path)

# and save to MQL5\Files folder to use as file
terminal_info=mt5.terminal_info()
file_path=terminal_info.data_path+"\\MQL5\\Files\\"
print("file path to save onnx model",file_path)

# set start and end dates for history data
from datetime import timedelta, datetime
#end_date = datetime.now()
end_date = datetime(2024, 1, 1, 0)
start_date = end_date - timedelta(days=inp_history_size*20)

# print start and end dates
print("data start date =",start_date)
print("data end date =",end_date)

# get rates
eurusd_rates = mt5.copy_rates_from(symbol, mt5.TIMEFRAME_D1, end_date, sample_size)

# create dataframe
df = pd.DataFrame(eurusd_rates)

# get close prices only
data = df.filter(['close']).values

# scale data
from sklearn.preprocessing import MinMaxScaler
scaler=MinMaxScaler(feature_range=(0,1))
scaled_data = scaler.fit_transform(data)

# training size is 80% of the data
training_size = int(len(scaled_data)*0.80) 
print("Training_size:",training_size)
train_data_initial = scaled_data[0:training_size,:]
test_data_initial = scaled_data[training_size:,:1]

# split a univariate sequence into samples
def split_sequence(sequence, n_steps):
    X, y = list(), list()
    for i in range(len(sequence)):
       # find the end of this pattern
       end_ix = i + n_steps
       # check if we are beyond the sequence
       if end_ix > len(sequence)-1:
          break
       # gather input and output parts of the pattern
       seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
       X.append(seq_x)
       y.append(seq_y)
    return np.array(X), np.array(y)

# split into samples
time_step = inp_history_size
x_train, y_train = split_sequence(train_data_initial, time_step)
x_test, y_test = split_sequence(test_data_initial, time_step)

# reshape input to be [samples, time steps, features] which is required for LSTM
x_train =x_train.reshape(x_train.shape[0],x_train.shape[1],1)
x_test = x_test.reshape(x_test.shape[0],x_test.shape[1],1)



# define model
from keras.models import Sequential
from keras.layers import Dense, Activation, Conv1D, MaxPooling1D, Dropout, Flatten, LSTM
from keras.metrics import RootMeanSquaredError as rmse
from tensorflow.keras import callbacks
model = Sequential()
model.add(Conv1D(filters=256, kernel_size=2, strides=1, padding='same', activation='relu', input_shape=(inp_history_size,1)))
model.add(MaxPooling1D(pool_size=2))
model.add(LSTM(100, return_sequences = True))
model.add(Dropout(0.3))
model.add(LSTM(100, return_sequences = False))
model.add(Dropout(0.3))
model.add(Dense(units=1, activation = 'sigmoid'))
model.compile(optimizer='adam', loss= 'mse' , metrics = [rmse()])

# Set up early stopping
early_stopping = callbacks.EarlyStopping(
    monitor='val_loss',
    patience=20,
    restore_best_weights=True,
)

# model training for 300 epochs
history = model.fit(x_train, y_train, epochs = 300 , validation_data = (x_test,y_test), batch_size=32, callbacks=[early_stopping], verbose=2)

# evaluate training data
train_loss, train_rmse = model.evaluate(x_train,y_train, batch_size = 32)
print(f"train_loss={train_loss:.3f}")
print(f"train_rmse={train_rmse:.3f}")

# evaluate testing data
test_loss, test_rmse = model.evaluate(x_test,y_test, batch_size = 32)
print(f"test_loss={test_loss:.3f}")
print(f"test_rmse={test_rmse:.3f}")

# Define a function that represents your model
@tf.function(input_signature=[tf.TensorSpec([None, inp_history_size, 1], tf.float32)])
def model_function(x):
    return model(x)

output_path = data_path+inp_model_name
# Convert the model to ONNX
onnx_model, _ = tf2onnx.convert.from_function(
    model_function, 
    input_signature=[tf.TensorSpec([None, inp_history_size, 1], tf.float32)],
    opset=13,
    output_path=output_path
)

print(f"Saved ONNX model to {output_path}")


# save model to ONNX
output_path = data_path+inp_model_name
onnx_model = tf2onnx.convert.from_keras(model, output_path=output_path)
print(f"saved model to {output_path}")

output_path = file_path+inp_model_name
onnx_model = tf2onnx.convert.from_keras(model, output_path=output_path)
print(f"saved model to {output_path}")

#prediction using testing data
test_predict = model.predict(x_test)
print(test_predict)
print("longitud total de la prediccion: ", len(test_predict))
print("longitud total del sample: ", sample_size)

plot_y_test = np.array(y_test).reshape(-1, 1)  # Selecciona solo el último elemento de cada muestra de prueba
plot_y_train = y_train.reshape(-1,1)
train_predict = model.predict(x_train)
#print(plot_y_test)

#calculate metrics
from sklearn import metrics
from sklearn.metrics import r2_score
#transform data to real values
value1=scaler.inverse_transform(plot_y_test)
#print(value1)
# Escala las predicciones inversas al transformarlas a la escala original
value2 = scaler.inverse_transform(test_predict.reshape(-1, 1))
#print(value2)
#calc score
score = np.sqrt(metrics.mean_squared_error(value1,value2))

print("RMSE         : {}".format(score))
print("MSE          :", metrics.mean_squared_error(value1,value2))
print("R2 score     :",metrics.r2_score(value1,value2))


#sumarize model
model.summary()

#Print error
value11=pd.DataFrame(value1)
value22=pd.DataFrame(value2)
#print(value11)
#print(value22)



value111=value11.iloc[:,:]
value222=value22.iloc[:,:]

print("longitud salida (tandas de 1 hora): ",len(value111) )
print("en horas son " + str((len(value111))*60*24)+ " minutos")
print("en horas son " + str(((len(value111)))*60*24/60)+ " horas")
print("en horas son " + str(((len(value111)))*60*24/60/24)+ " dias")


# Calculate error
error = value111 - value222

import matplotlib.pyplot as plt
# Plot error
plt.figure(figsize=(7, 6))
plt.scatter(range(len(error)), error, color='blue', label='Error')
plt.axhline(y=0, color='red', linestyle='--', linewidth=1)  # Línea horizontal en y=0
plt.title('Error de Predicción ' + str(symbol))
plt.xlabel('Índice de la muestra')
plt.ylabel('Error')
plt.legend()
plt.grid(True)
plt.savefig(str(symbol)+str(optional)+'.png') 

rmse_ = format(score)
mse_ = metrics.mean_squared_error(value1,value2)
r2_ = metrics.r2_score(value1,value2)

resultados= [rmse_,mse_,r2_]

# Abre un archivo en modo escritura
with open(str(symbol)+str(optional)+"results.txt", "w") as archivo:
    # Escribe cada resultado en una línea separada
    for resultado in resultados:
        archivo.write(str(resultado) + "\n")

# finish
mt5.shutdown()

#show iteration-rmse graph for training and validation
plt.figure(figsize = (7,10))
plt.plot(history.history['root_mean_squared_error'],label='Training RMSE',color='b')
plt.plot(history.history['val_root_mean_squared_error'],label='Validation-RMSE',color='g')
plt.xlabel("Iteration")
plt.ylabel("RMSE")
plt.title("RMSE" + str(symbol))
plt.legend()
plt.savefig(str(symbol)+str(optional)+'1.png') 

#show iteration-loss graph for training and validation
plt.figure(figsize = (7,10))
plt.plot(history.history['loss'],label='Training Loss',color='b')
plt.plot(history.history['val_loss'],label='Validation-loss',color='g')
plt.xlabel("Iteration")
plt.ylabel("Loss")
plt.title("LOSS" + str(symbol))
plt.legend()
plt.savefig(str(symbol)+str(optional)+'2.png') 

#show actual vs predicted (training) graph
plt.figure(figsize=(7,10))
plt.plot(scaler.inverse_transform(plot_y_train),color = 'b', label = 'Original')
plt.plot(scaler.inverse_transform(train_predict),color='red', label = 'Predicted')
plt.title("Prediction Graph Using Training Data" + str(symbol))
plt.xlabel("Hours")
plt.ylabel("Price")
plt.legend()
plt.savefig(str(symbol)+str(optional)+'3.png') 

#show actual vs predicted (testing) graph
plt.figure(figsize=(7,10))
plt.plot(scaler.inverse_transform(plot_y_test),color = 'b',  label = 'Original')
plt.plot(scaler.inverse_transform(test_predict),color='g', label = 'Predicted')
plt.title("Prediction Graph Using Testing Data" + str(symbol))
plt.xlabel("Hours")
plt.ylabel("Price")
plt.legend()
plt.savefig(str(symbol)+str(optional)+'4.png') 

Die Ausgabe dieses .py-Skripts sieht ähnlich aus wie diese:

177/177 - 51s - loss: 2.4565e-04 - root_mean_squared_error: 0.0157 - val_loss: 4.8860e-05 - val_root_mean_squared_error: 0.0070 - 51s/epoch - 291ms/step
177/177 [==============================] - 15s 82ms/step - loss: 1.0720e-04 - root_mean_squared_error: 0.0104
train_loss=0.000
train_rmse=0.010
42/42 [==============================] - 3s 74ms/step - loss: 4.4485e-05 - root_mean_squared_error: 0.0067
test_loss=0.000
test_rmse=0.007
Saved ONNX model to c:\XXXXXXXXXXXXXXX\EURUSD_D1_2024.onnx
saved model to c:\XXXXXXXXXXXXXXXX\EURUSD_D1_2024.onnx
saved model to C:\XXXXXXXXXX\MQL5\Files\EURUSD_D1_2024.onnx
42/42 [==============================] - 5s 80ms/step
[[0.40353602]
 [0.39568084]
 [0.39963558]
 ...
 [0.35914657]
 [0.3671721 ]
 [0.3618655 ]]
longitud total de la prediccion:  1320
longitud total del sample:  7200
177/177 [==============================] - 13s 72ms/step
RMSE         : 0.005155711558172936
MSE          : 2.6581361671078003e-05
R2 score     : 0.9915315181564703
Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #
=================================================================
 conv1d (Conv1D)             (None, 120, 256)          768

 max_pooling1d (MaxPooling1D  (None, 60, 256)          0
 )

 lstm (LSTM)                 (None, 60, 100)           142800

 dropout (Dropout)           (None, 60, 100)           0

 lstm_1 (LSTM)               (None, 100)               80400

 dropout_1 (Dropout)         (None, 100)               0

 dense (Dense)               (None, 1)                 101

=================================================================
Total params: 224,069
Trainable params: 224,069
Non-trainable params: 0
________________________________________________________________

Dieses Modell könnte überangepasst sein, da die Ergebnisse im Grenzbereich zwischen einer guten Vorhersage und einer Überanpassung liegen könnten:

RMSE         : 0.005155711558172936
MSE          : 2.6581361671078003e-05
R2 score     : 0.9915315181564703

Die wichtigsten Metriken sind diese drei, R2, gibt einen Prozentsatz der getesteten Ergebnisse von guten Vorhersagen, RMSE und MSE sind die Fehler, wenn Sie mehr darüber wissen wollen, können Sie es googeln.

Da wir dies für dasselbe Symbol (EURUSD) tun werden, müssen wir nur ein DL-Modell erstellen, das wir für das Jahr 2024 testen werden.

Wir haben den Zeitrahmen von 1 Tag gewählt, um den Rechenaufwand unseres Computers in Grenzen zu halten.

Das py-Skript zeigt auch einige gespeicherte Diagramme an (eine weitere Möglichkeit zu sehen, ob Modelle über- oder unterangepasst sind).

Die Diagramme sollten wie folgt aussehen:

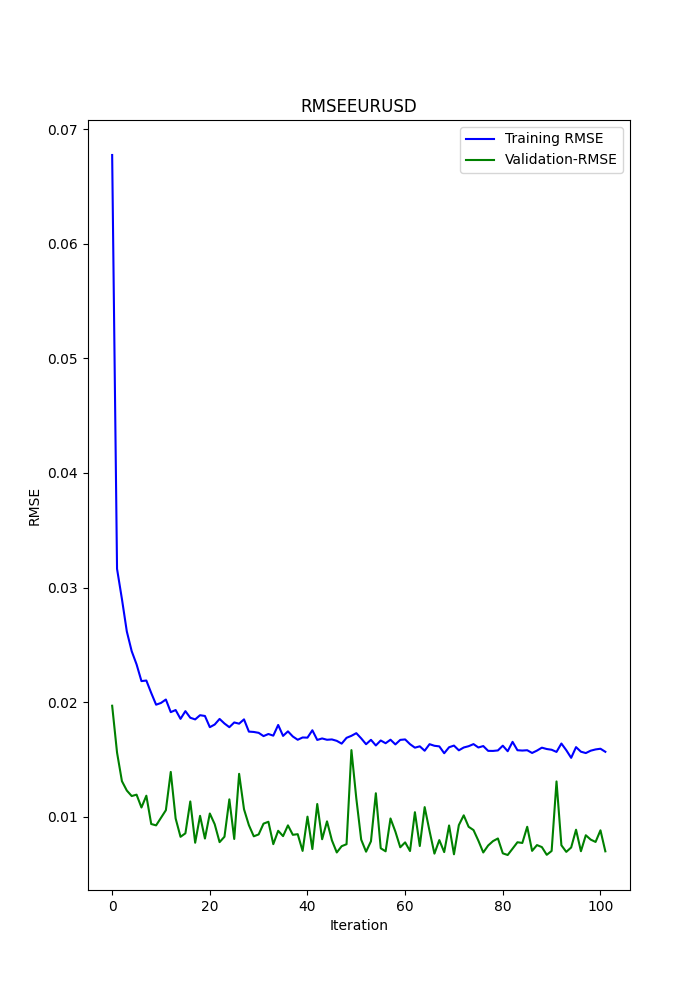
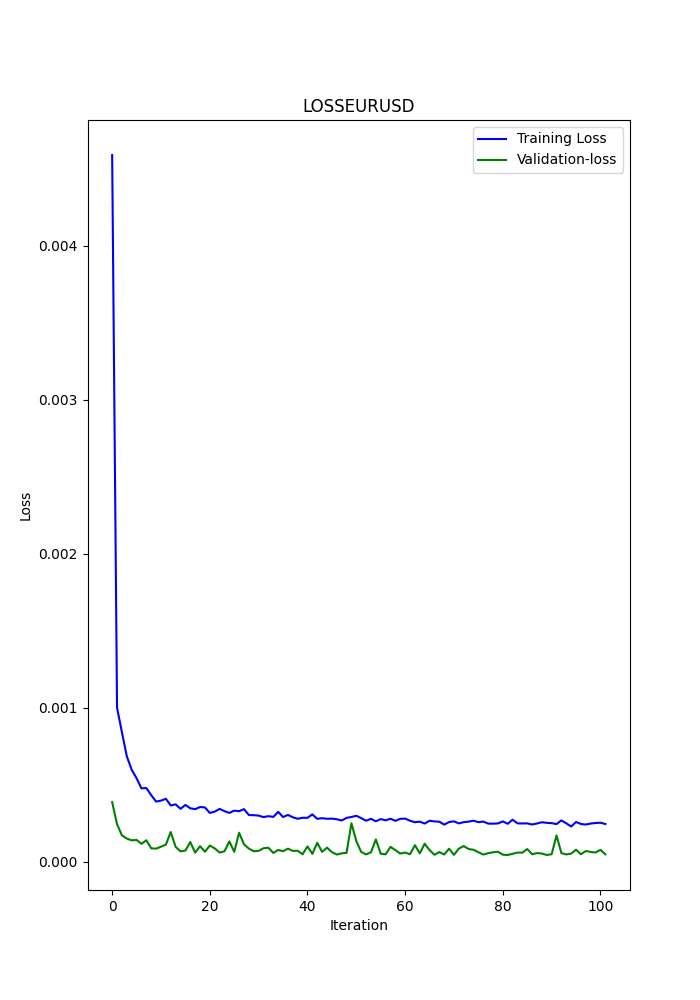
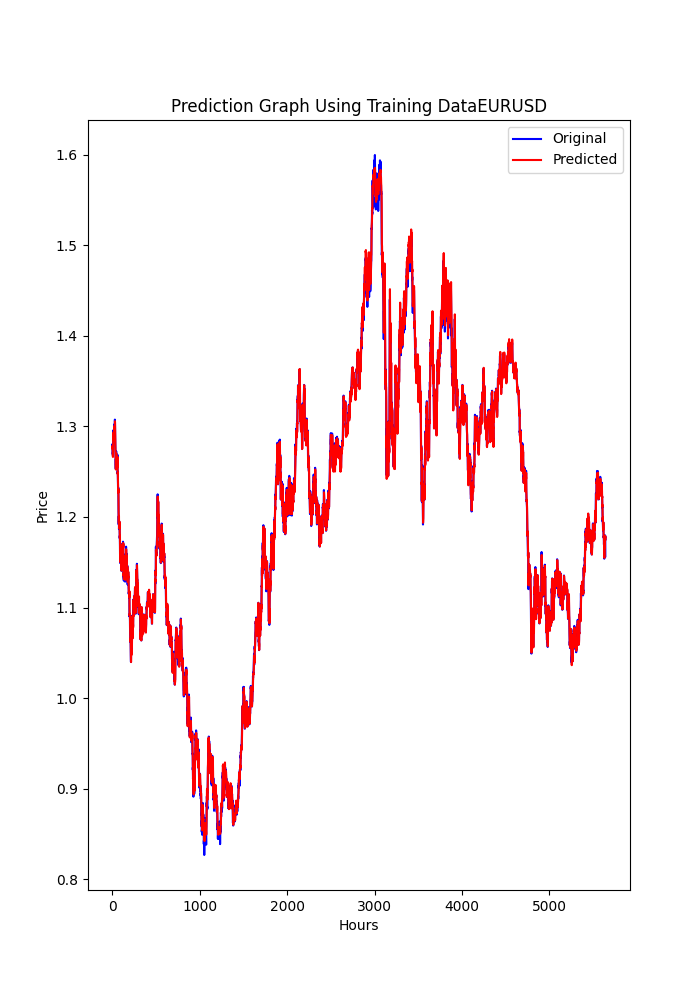
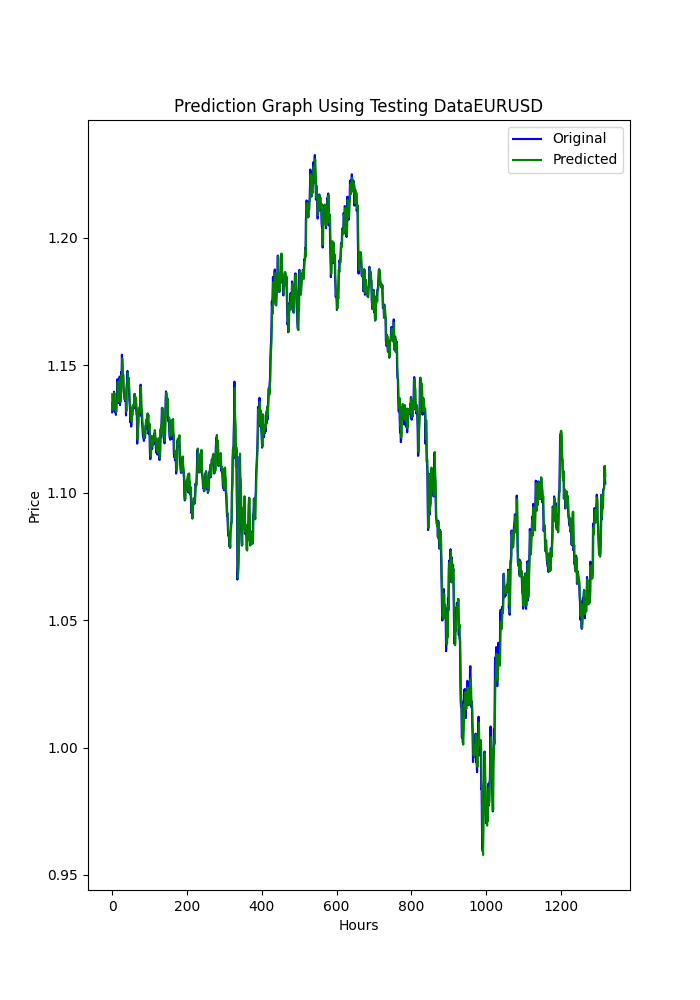
Das Skript speichert auch eine .txt-Datei, in der die Metriken in der gleichen Reihenfolge gespeichert werden, wie sie im Terminal erscheinen.

Um dieses Skript zu verwenden, müssen Sie zunächst Python 3.11.9 installieren und die Bibliotheken mit pip install installieren:

tensorflow==2.12.0, keras==2.12.0,  tf2onnx==1.16.0, MetaTrader5, pandas, numpy, scikit-learn, tf2onnx, keras

Ich empfehle dringend die Verwendung von Visual Studio Code, das Sie im Microsoft Store herunterladen können.

Möglicherweise werden Sie aufgefordert, Folgendes zu installieren

Microsoft Visual C++ 2015 - 2022 Redistributable

Ich habe das .py-Skript angehängt, öffnen Sie es einfach in VSC und führen Sie es aus.

Wenn Sie etwas ändern wollen (ein anderes Symbol, einen anderen Zeitrahmen, aus dem Sie die Daten beziehen wollen), ändern Sie nur diese Zeilen:

symbol = "EURUSD"
optional = "D1_2024"

Das Symbol ist offensichtlich, ich empfehle, optional den verwendeten Zeitraum und das letzte Datum der Daten zu ändern.

eurusd_rates = mt5.copy_rates_from(symbol, mt5.TIMEFRAME_D1, end_date, sample_size)

In dieser Zeile können Sie den Zeitrahmen ändern, z. B. H1 (1-Stunden-Zeitrahmen).

Jetzt, da wir das Deep Learning ONNX-Modell haben, können wir es zu den EAs hinzufügen, die wir bereits aus den anderen Artikeln kennen.

Ich füge das DL ONNX-Modell (2024) bei.

Was werden wir den EAs hinzufügen?

Die Änderungen für CNA

Dies ist ein grundlegender Prozess, den ich sehr langsam durchgehen werde.

1. Am Anfang, wo die Eingabeparameter stehen, müssen wir diese Zeilen hinzufügen:

#include <Trade\Trade.mqh>

#resource "/Files/EURUSD_D1.onnx" as uchar ExtModel[]

#define SAMPLE_SIZE 120

long     ExtHandle=INVALID_HANDLE;
int      ExtPredictedClass=-1;
datetime ExtNextBar=0;
datetime ExtNextDay=0;
float    ExtMin=0.0;
float    ExtMax=0.0;
CTrade   ExtTrade;
int dlsignal=-1;

//--- price movement prediction
#define PRICE_UP   0
#define PRICE_SAME 1
#define PRICE_DOWN 2

Denken Sie daran, diese Zeile mit dem von Ihnen erstellten ONNX-Modell zu ändern (die py-Skripte speichern in MQL5/Files/ ... das Modell).

#resource "/Files/EURUSD_D1_2024.onnx" as uchar ExtModel[]

In der OnInit() müssen Sie dies hinzufügen:

//--- create a model from static buffer
   ExtHandle=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT);
   if(ExtHandle==INVALID_HANDLE)
     {
      Print("OnnxCreateFromBuffer error ",GetLastError());
      return(INIT_FAILED);
     }

//--- since not all sizes defined in the input tensor we must set them explicitly
//--- first index - batch size, second index - series size, third index - number of series (only Close)
   const long input_shape[] = {1,SAMPLE_SIZE,1};
   if(!OnnxSetInputShape(ExtHandle,ONNX_DEFAULT,input_shape))
     {
      Print("OnnxSetInputShape error ",GetLastError());
      return(INIT_FAILED);
     }

//--- since not all sizes defined in the output tensor we must set them explicitly
//--- first index - batch size, must match the batch size of the input tensor
//--- second index - number of predicted prices (we only predict Close)
   const long output_shape[] = {1,1};
   if(!OnnxSetOutputShape(ExtHandle,0,output_shape))
     {
      Print("OnnxSetOutputShape error ",GetLastError());
      return(INIT_FAILED);
     }

Wo? Irgendwo ... es spielt keine Rolle (kurz vor der Funktionsrückgabe).

Der Funktion OnDeinit müssen wir auch dies hinzufügen:

if(ExtHandle!=INVALID_HANDLE)
     {
      OnnxRelease(ExtHandle);
      ExtHandle=INVALID_HANDLE;
     }

Wo? Irgendwo, damit wird das ONNX-Modell freigeschaltet.

Der Funktion OnTick müssen wir dies hinzufügen:

void OnTick()
  {
  //--- check new day
   if(TimeCurrent()>=ExtNextDay)
     {
      GetMinMax();
      //--- set next day time
      ExtNextDay=TimeCurrent();
      ExtNextDay-=ExtNextDay%PeriodSeconds(PERIOD_D1);
      ExtNextDay+=PeriodSeconds(PERIOD_D1);
     }

//--- check new bar
   if(TimeCurrent()<ExtNextBar)
      return;
//--- set next bar time
   ExtNextBar=TimeCurrent();
   ExtNextBar-=ExtNextBar%PeriodSeconds();
   ExtNextBar+=PeriodSeconds();
//--- check min and max
   float close=(float)iClose(_Symbol,_Period,0);
   if(ExtMin>close)
      ExtMin=close;
   if(ExtMax<close)
      ExtMax=close;
      
   PredictPrice();

Wo? Zu Beginn! Dies ist wichtig, weil das Ergebnis der Funktion PredictPrice() zur Logik der Auftragsausführung hinzugefügt werden muss.

In OnTick() müssen wir auch die Funktion ändern, die die Aufträge ausführt, in diesem Fall (CNA_DL). Wir ändern die ursprüngliche Zeile von:

int signal = GenerateSignal(symbol, prediction);

zu dieser Zeile:

int signal = GenerateSignal(symbol, prediction, ExtPredictedClass);

ExtPredictedClass ist das Ergebnis der Funktion PredictedPrice(), die wir zuvor hinzugefügt haben.

Jetzt müssen wir auch die Logik von GenerateSignal() ändern, damit sie die ExtPredictedClass verwendet:

Wir müssen den Header dieser Funktion ändern:

int GenerateSignal(string symbol, double prediction, int dlsgnl)

und wir fügen die neue Variable in die Logik ein, um Aufträge zu tätigen, in diesem Fall hier:

von diesem:

   bool buy_condition =  prediction >  0.00001 && rsi < 30 && trend_strong  && volatility_ok && fastMA > slowMA;
   bool sell_condition = prediction < -0.00001 && rsi > 70 && trend_strong && volatility_ok && fastMA < slowMA;

zu:

   bool buy_condition =  prediction >  0.00001 && rsi < 30 && trend_strong  && volatility_ok && fastMA > slowMA && dlsgnl==PRICE_UP;
   bool sell_condition = prediction < -0.00001 && rsi > 70 && trend_strong && volatility_ok && fastMA < slowMA && dlsgnl==PRICE_DOWN;

Der letzte Teil, den wir ändern müssen, ist dieser.

Wo müssen wir diese Funktionen in das Skript einfügen? Irgendwo, zum Beispiel am Ende.

//+------------------------------------------------------------------+
void PredictPrice(void)
  {
   static vectorf output_data(1);            // vector to get result
   static vectorf x_norm(SAMPLE_SIZE);       // vector for prices normalize

//--- check for normalization possibility
   if(ExtMin>=ExtMax)
     {
      Print("ExtMin>=ExtMax");
      ExtPredictedClass=-1;
      return;
     }
//--- request last bars
   if(!x_norm.CopyRates(_Symbol,_Period,COPY_RATES_CLOSE,1,SAMPLE_SIZE))
     {
      Print("CopyRates ",x_norm.Size());
      ExtPredictedClass=-1;
      return;
     }
   float last_close=x_norm[SAMPLE_SIZE-1];
//--- normalize prices
   x_norm-=ExtMin;
   x_norm/=(ExtMax-ExtMin);
//--- run the inference
   if(!OnnxRun(ExtHandle,ONNX_NO_CONVERSION,x_norm,output_data))
     {
      Print("OnnxRun");
      ExtPredictedClass=-1;
      return;
     }
//--- denormalize the price from the output value
   float predicted=output_data[0]*(ExtMax-ExtMin)+ExtMin;
//--- classify predicted price movement
   float delta=last_close-predicted;
   if(fabs(delta)<=0.00001)
      ExtPredictedClass=PRICE_SAME;
   else
     {
      if(delta<0)
         ExtPredictedClass=PRICE_UP;
      else
         ExtPredictedClass=PRICE_DOWN;
     }
  }
  
  
  
  void GetMinMax(void)
  {
   vectorf close;
   close.CopyRates(_Symbol,PERIOD_D1,COPY_RATES_CLOSE,0,SAMPLE_SIZE);
   ExtMin=close.Min();
   ExtMax=close.Max();
  }

Diese beiden Funktionen sind der Schlüssel für Vorhersagen, eine macht die Vorhersagen, und die andere ermittelt die Minimal- und Maximalwerte.

Änderungen im SMOC

Alles bleibt gleich, und die Änderungen sind die gleichen wie vorher, mit Ausnahme dieser Änderungen:

In den Eingabeparametern initialisieren wir weder dlsignal noch fügen wir CTrade hinzu:

#resource "/Files/EURUSD_D1.onnx" as uchar ExtModel[]

#define SAMPLE_SIZE 120

long     ExtHandle=INVALID_HANDLE;
int      ExtPredictedClass=-1;
datetime ExtNextBar=0;
datetime ExtNextDay=0;
float    ExtMin=0.0;
float    ExtMax=0.0;

//--- price movement prediction
#define PRICE_UP   0
#define PRICE_SAME 1
#define PRICE_DOWN 2

In OnTick() werden wir dies machen:

void OnTick()
  {
//--- check new day
   if(TimeCurrent()>=ExtNextDay)
     {
      GetMinMax();
      //--- set next day time
      ExtNextDay=TimeCurrent();
      ExtNextDay-=ExtNextDay%PeriodSeconds(PERIOD_D1);
      ExtNextDay+=PeriodSeconds(PERIOD_D1);
     }

//--- check new bar
   if(TimeCurrent()<ExtNextBar)
      return;
//--- set next bar time
   ExtNextBar=TimeCurrent();
   ExtNextBar-=ExtNextBar%PeriodSeconds();
   ExtNextBar+=PeriodSeconds();
//--- check min and max
   float close=(float)iClose(_Symbol,_Period,0);
   if(ExtMin>close)
      ExtMin=close;
   if(ExtMax<close)
      ExtMax=close;

   PredictPrice();

   static datetime lastBarTime = 0;
   datetime currentBarTime = iTime(Symbol(), PERIOD_CURRENT, 0);

// Only process on new bar
   if(currentBarTime == lastBarTime)
      return;

   lastBarTime = currentBarTime;

   double currentPrice = SymbolInfoDouble(Symbol(), SYMBOL_LAST);
   int decision = OptimalControl(currentPrice);

   string logMessage = StringFormat("New bar: Time=%s, Price=%f, Decision=%d",
                                    TimeToString(currentBarTime), currentPrice, decision);
   LogMessage(logMessage);

// Manage open order if exists
   if(orderTicket != 0)
     {
      ManageOpenOrder(decision, ExtPredictedClass);
     }

   if(orderTicket == 0 && decision != 0 && IsTrendFavorable(decision) && IsLongTermTrendFavorable(decision) && (ExtPredictedClass==PRICE_DOWN || ExtPredictedClass==PRICE_UP))
     {
      ExecuteTrade(decision, ExtPredictedClass);
     }
  }

In ManageOpenOrder() werden wir diese Änderung vornehmen:

void ManageOpenOrder(int decision, int dlsignal)
  {
   int barsOpen = iBars(Symbol(), PERIOD_CURRENT) - iBarShift(Symbol(), PERIOD_CURRENT, orderOpenTime);
   LogMessage(StringFormat("Bars open: %d for order ticket: %d", barsOpen, orderTicket));

   if(barsOpen >= maxBarsOpen ||
      (PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY && decision == -1 && dlsignal == PRICE_DOWN) ||
      (PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL && decision == 1 && dlsignal == PRICE_UP))
     {
      CloseOrder(orderTicket);
      orderTicket = 0;
      orderOpenTime = 0;
     }
   else
     {
      UpdateSLTP(orderTicket, decision);
     }
  }

In ExecuteTrade()

void ExecuteTrade(int decision, int dlsignal)
  {
   MqlTradeRequest request = {};
   MqlTradeResult result = {};
   double price;
   int decision1;
   
   

   if(decision == 1 && dlsignal == PRICE_UP)
     {
      price = SymbolInfoDouble(Symbol(), SYMBOL_ASK);
      request.type = ORDER_TYPE_BUY;
      decision1 = 1;
     }
   else
      if(decision == -1 && dlsignal == PRICE_DOWN)
        {
         price = SymbolInfoDouble(Symbol(), SYMBOL_BID);
         request.type = ORDER_TYPE_SELL;
        decision1 = -1;
        }
   double sl = CalculateDynamicSL(price, decision1);
   double tp = CalculateDynamicTP(price, decision1);



   double adjustedLotSize = AdjustLotSizeForDrawdown();
   request.volume = adjustedLotSize;

   request.action = TRADE_ACTION_DEAL;
   request.symbol = Symbol();
//request.volume = lotSize;
//request.type = (decision == 1 && dlsignal == PRICE_UP) ? ORDER_TYPE_BUY : ORDER_TYPE_SELL;
   request.price = price;
   request.sl = sl;
   request.tp = tp;
   request.deviation = 10;
   request.magic = 123456; // Magic number to identify orders from this EA
   request.comment = (decision == 1) ? "Buy Order" : "Sell Order";

   if(OrderSend(request, result))
     {
      Print((decision1 == 1 ? "Buy" : "Sell"), " Order Executed Successfully. Ticket: ", result.order);
      orderOpenTime = iTime(Symbol(), PERIOD_CURRENT, 0);
      orderTicket = result.order;
     }
   else
     {
      Print("Error executing Order: ", GetLastError());
     }
  }

Und nun die Änderungen am Nash Equity Script.

Änderungen in Nash Equity

Alle Änderungen sind die gleichen, mit Ausnahme der Funktion OnTick(), die wie diese aussehen wird:

void OnTick()
  {
//--- check new day
   if(TimeCurrent()>=ExtNextDay)
     {
      GetMinMax();
      //--- set next day time
      ExtNextDay=TimeCurrent();
      ExtNextDay-=ExtNextDay%PeriodSeconds(PERIOD_D1);
      ExtNextDay+=PeriodSeconds(PERIOD_D1);
     }

//--- check new bar
   if(TimeCurrent()<ExtNextBar)
      return;
//--- set next bar time
   ExtNextBar=TimeCurrent();
   ExtNextBar-=ExtNextBar%PeriodSeconds();
   ExtNextBar+=PeriodSeconds();
//--- check min and max
   float close=(float)iClose(_Symbol,_Period,0);
   if(ExtMin>close)
      ExtMin=close;
   if(ExtMax<close)
      ExtMax=close;

   PredictPrice();

   if(!IsNewBar())
      return; // Solo procesar en nueva barra

   MarketRegime hmmRegime = NOT_PRESENT;
   MarketRegime logLikelihoodRegime = NOT_PRESENT;
   DetectMarketRegime(hmmRegime, logLikelihoodRegime);

// Calcular señales para cada estrategia
   CalculateStrategySignals(_Symbol, TimeCurrent(), hmmRegime, logLikelihoodRegime);

// Verificar si la estrategia de Nash Equilibrium ha generado una señal
   if(strategies[3].enabled && strategies[3].signal != 0)
     {
      if(strategies[3].signal > 0 && ExtPredictedClass==PRICE_UP)
        {
         OpenBuyOrder(strategies[3].name);
        }
      else
         if(strategies[3].signal < 0 && ExtPredictedClass==PRICE_DOWN)
           {
            OpenSellOrder(strategies[3].name);
           }
     }

// Actualizar stops de seguimiento si es necesario
   if(UseTrailingStop)
     {
      UpdateTrailingStops();
     }
  }

Ergebnisse
CNA_DL

Einstellungen

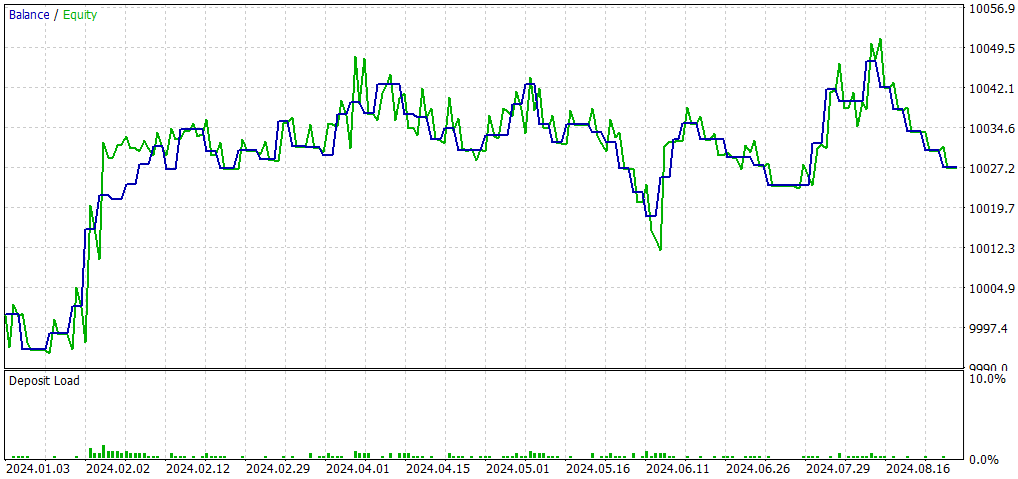
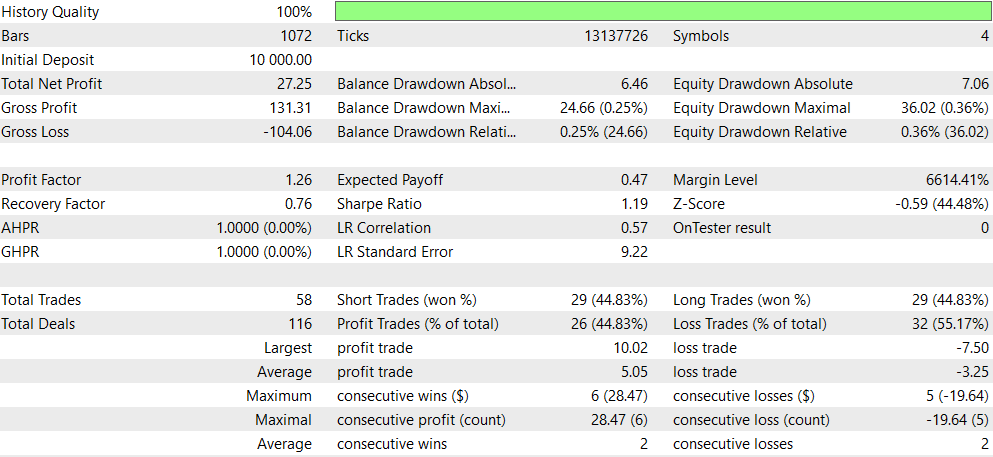
Verglichen mit der ursprünglichen EA (CNA_Final_v4):

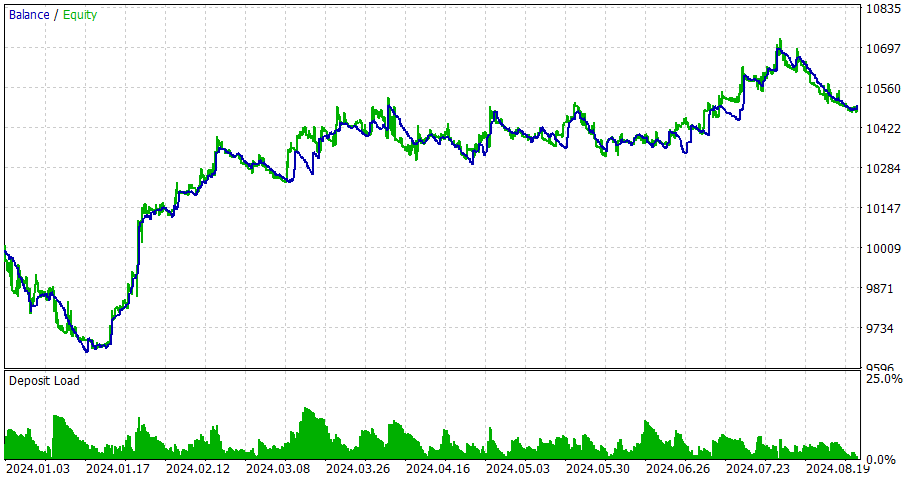
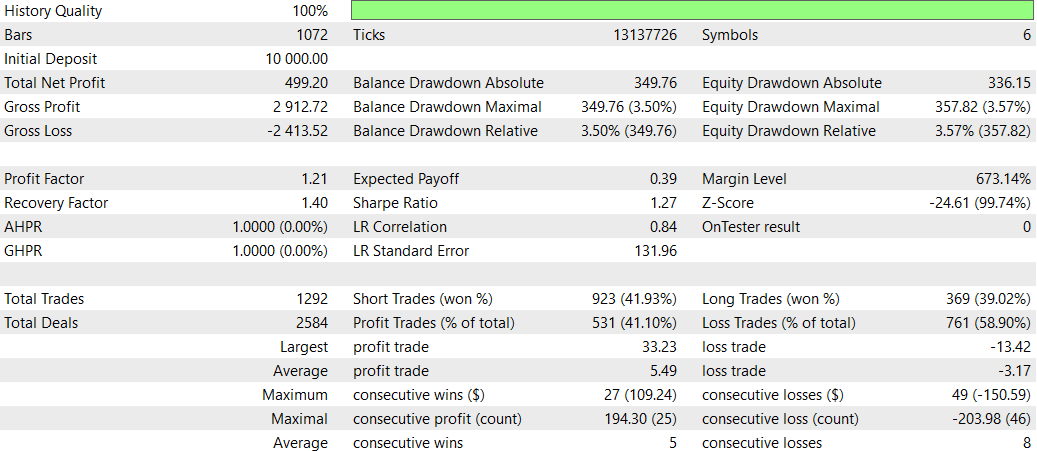
Vergleich von CNA mit und ohne Deep Learning

1. Rentabilität: Der EA ohne Deep Learning ist deutlich profitabler, geht aber auch ein höheres Risiko mit höheren Drawdown ein.
2. Risiko: Der EA mit Deep Learning hat einen geringeren Drawdown und scheint konservativer vorzugehen.
3. Handelsfrequenz: Der EA ohne Deep Learning handelt viel häufiger (1292 gegenüber 58 Trades).
4. Gewinnrate: Der EA mit Deep Learning hat eine etwas bessere Gewinnrate, aber beide liegen unter 50 %.
5. Strategisches Bias: Der EA ohne Deep Learning zeigt eine starke Präferenz für Verkaufspositionen, während der EA mit Deep Learning ausgewogen ist.
6. Konsistenz: Der EA mit Deep Learning scheint bei einer kleineren Anzahl von aufeinanderfolgenden Gewinnen/Verlusten konsistenter zu sein.

Zusammenfassend lässt sich sagen, dass der EA ohne Deep Learning profitabler, aber auch risikoreicher ist, während der EA mit Deep Learning konservativer ist und geringere Erträge, aber auch ein geringeres Risiko aufweist. Die Wahl zwischen ihnen hängt von der Risikotoleranz und den Anlagezielen des Händlers ab. Der Deep-Learning-EA könnte für einen stabileren, konservativen Handel bevorzugt werden, während der EA ohne Deep Learning für potenziell höhere Erträge auf Kosten eines höheren Risikos gewählt werden könnte.

SMOC_DL

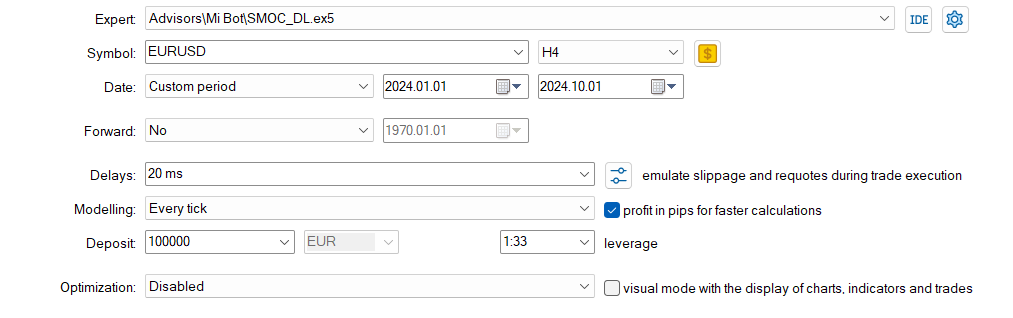
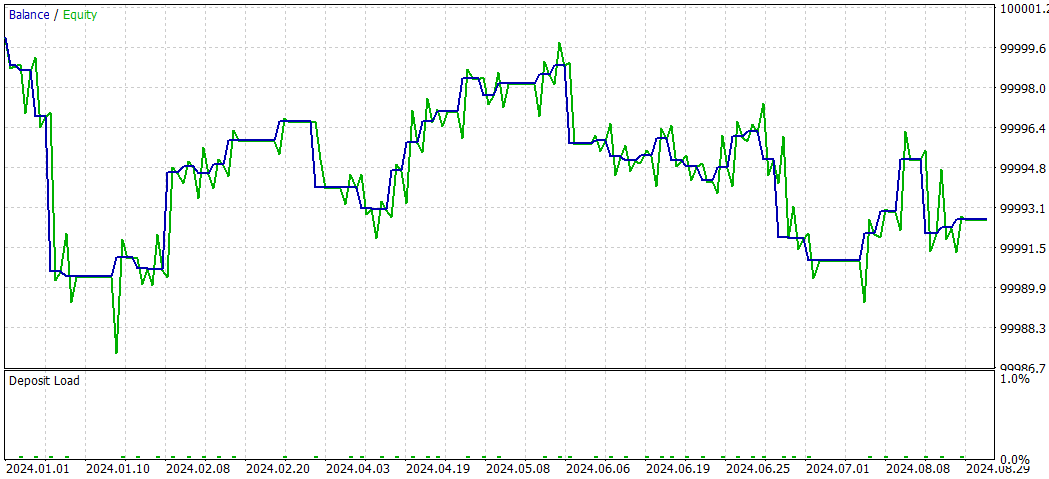
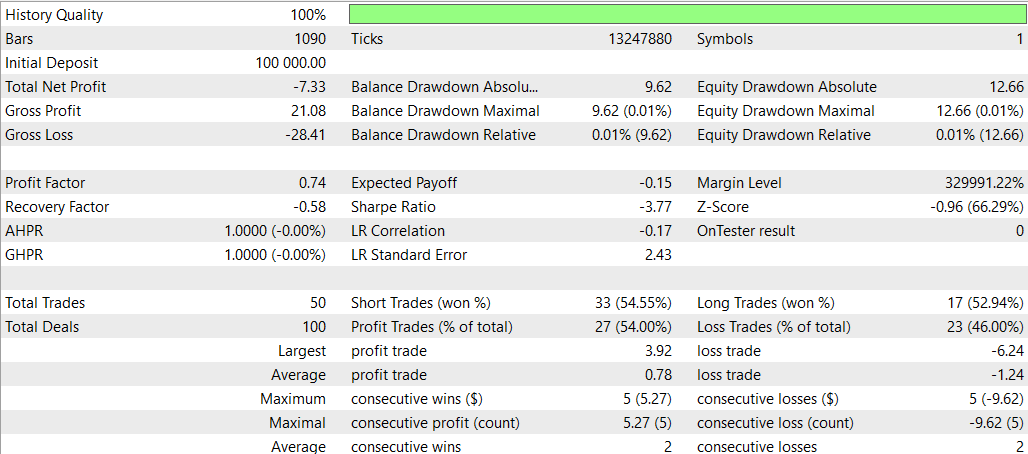
Und jetzt SMOC ohne Deep Learning

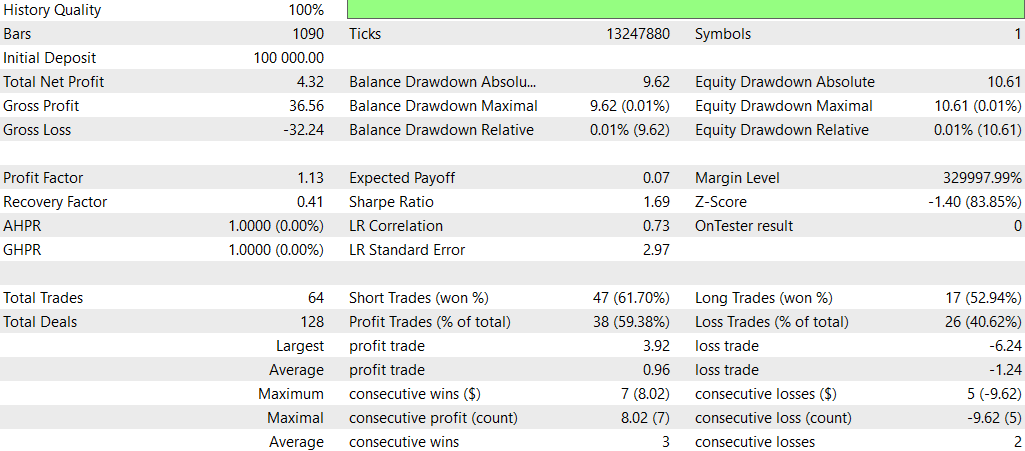
Vergleich SMOC_DL vs. SMOC:

1. Rentabilität: Strategie 2 ist rentabel (4,32), während Strategie 1 unrentabel ist (-7,33).
2. Risikobereinigte Renditen: Strategie 2 weist eine positive Sharpe Ratio (1,69) auf, was auf eine bessere risikobereinigte Rendite im Vergleich zur negativen Sharpe Ratio von Strategie 1 (-3,77) hinweist.
3. Gewinnrate: Strategie 2 hat eine höhere Gewinnquote (59,38 %) als Strategie 1 (54 %).
4. Anzahl der Handelsgeschäfte: Strategie 2 führt mehr Handelsgeschäfte aus (64) als Strategie 1 (50), was möglicherweise auf mehr erkannte Chancen hinweist.
5. Profit Factor: Bei Strategie 2 liegt der Gewinnfaktor über 1 (1,13), während er bei Strategie 1 unter 1 liegt (0,74), was darauf hindeutet, dass Strategie 2 im Verhältnis zu den Verlusten effektiver Gewinne erzielt.
6. Drawdown: Beide Strategien haben ähnlich niedrige Drawdowns (0,01 % des Kontos), was auf ein gutes Risikomanagement hindeutet.
7. Vertrieb im Handel: Bei beiden Strategien werden Verkaufspositionen bevorzugt, aber bei Strategie 2 ist die Verteilung zwischen Kauf- und Verkaufspositionen ausgewogener.

Insgesamt scheint Strategie 2 in den meisten Aspekten überlegen zu sein, einschließlich Rentabilität, risikobereinigte Renditen, Gewinnrate und Gewinnfaktor. Es werden auch mehr Handelsgeschäfte getätigt, was auf eine bessere Erkennung von Gelegenheiten hinweisen könnte. Beide Strategien zeichnen sich durch ein gutes Risikomanagement mit geringen Drawdowns aus. Auf der Grundlage dieser Daten wäre die Strategie 2 die bevorzugte Wahl zwischen den beiden. Ein geeigneter Ansatz für die Verwendung von DL wäre es, andere Zeitrahmen auszuprobieren.

NASH_DL

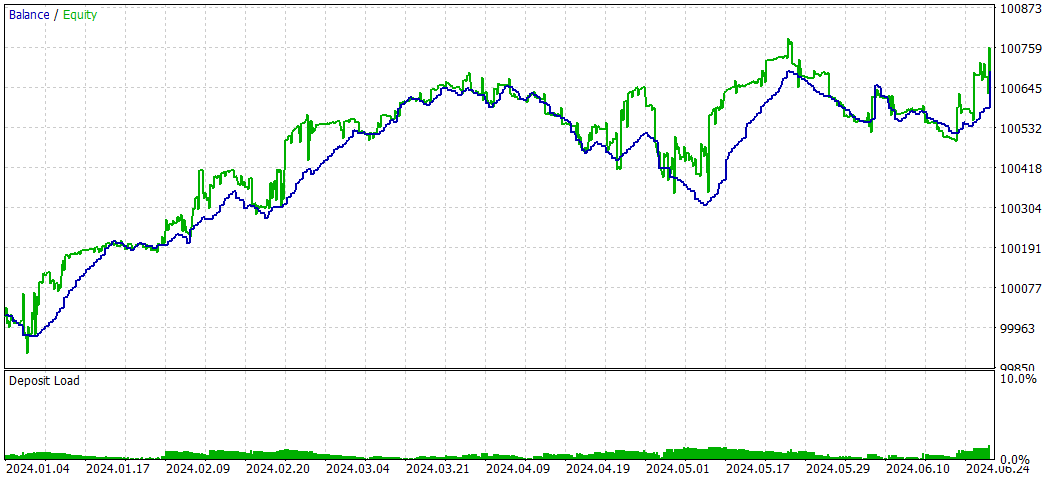
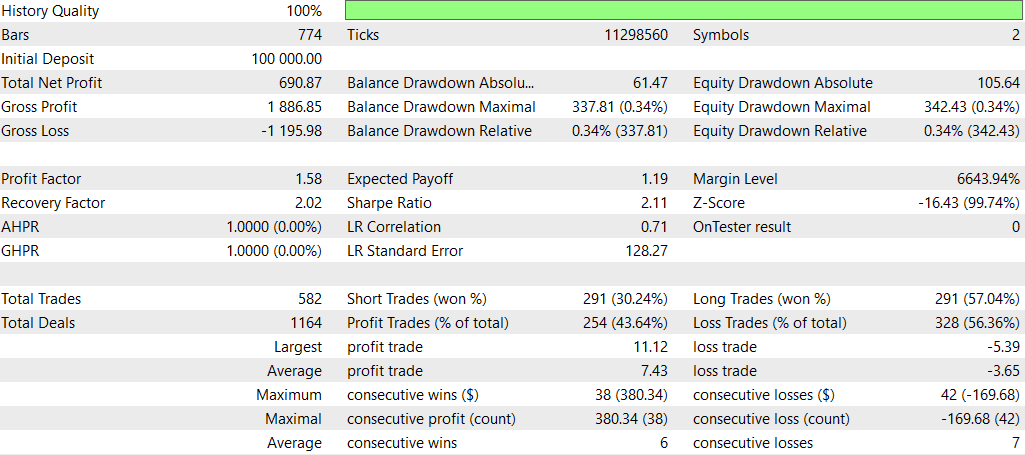
Und jetzt ohne Deep Learning:

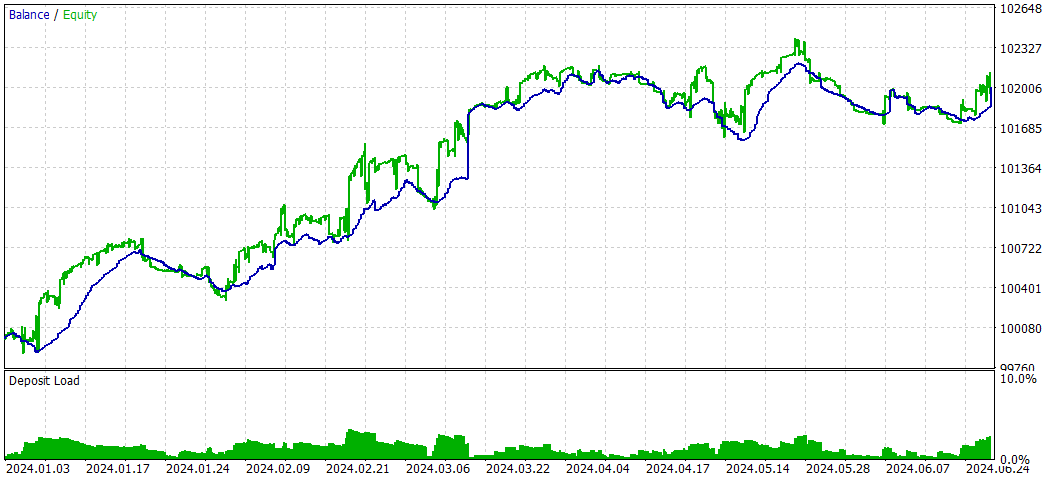
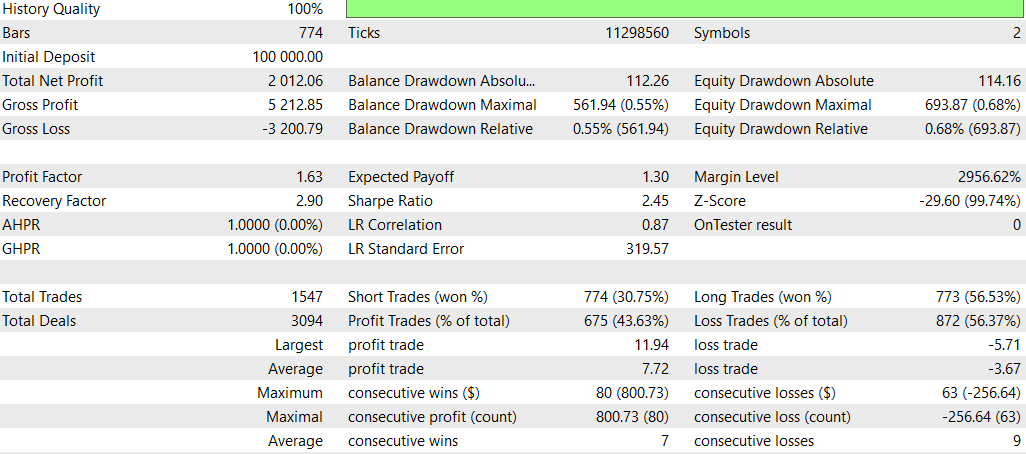
Insgesamt scheint die Strategie ohne DL bei der Gesamtrentabilität und den risikobereinigten Renditen besser abgeschnitten zu haben, obwohl sie eine höhere maximale Inanspruchnahme aufweist. Es wurde aktiver gehandelt und schien mit Kaufpositionen effektiver zu sein. Die DL-Strategie war konservativer, mit geringerem Drawdown, aber auch geringeren Gesamtrenditen.

Es ist jedoch wichtig zu beachten, dass dieser Vergleich auf einem einzigen Testzeitraum basiert. Um aussagekräftigere Schlussfolgerungen zu ziehen, sollten Sie diese Strategien über mehrere Zeiträume und Marktbedingungen hinweg testen.

Schlussfolgerung

Diese Studie untersuchte die Integration von Deep Learning (DL)-Modellen in drei fortgeschrittene Trading Expert Advisors (EAs): Causality Network Analysis (CNA), Stochastic Optimization and Optimal Control (SMOC) und Nash's Spieltheorie. Dabei wurden ONNX-Modelle mit Python erstellt und in bestehende MQL5-Skripte integriert.

Die Ergebnisse dieser Integration waren bei den verschiedenen Strategien unterschiedlich:

1. Bei der CNA-Strategie zeigte die DL-Version einen konservativeren Handel mit geringeren Erträgen, aber auch geringerem Risiko im Vergleich zur Nicht-DL-Version. Er war zwar weniger profitabel, zeigte aber eine bessere Konsistenz und ein ausgewogeneres Konzept für den Handel.
2. Im Fall von SMOC übertraf die DL-Version ihr nicht-DL-Pendant deutlich. Es zeigte eine bessere Rentabilität, höhere Gewinnquoten und bessere risikobereinigte Renditen, was darauf hindeutet, dass das DL-Modell den Entscheidungsprozess der Strategie effektiv verbessert.
3. Bei Nashs spieltheoretischem Ansatz schnitt die Nicht-DL-Variante insgesamt besser ab, mit einer höheren Gesamtrentabilität und risikobereinigten Renditen, obwohl sie eine höhere maximale Inanspruchnahme aufweist. Die DL-Version handelte konservativer, erzielte aber eine geringere Gesamtrendite.

Diese Ergebnisse verdeutlichen das Potenzial der Integration von Deep Learning in Handelsstrategien, unterstreichen aber auch die Bedeutung einer sorgfältigen Implementierung und Prüfung. Die Wirksamkeit der DL-Integration hängt von der zugrunde liegenden Strategie und den Marktbedingungen ab.

Es ist von entscheidender Bedeutung, dass diese Ergebnisse auf bestimmten Testzeiträumen und Marktbedingungen beruhen. Um aussagekräftigere Schlussfolgerungen zu ziehen, wären weitere Tests über verschiedene Zeiträume und Marktszenarien erforderlich.

Zusammenfassend lässt sich sagen, dass Deep Learning zwar Handelsstrategien verbessern kann, seine Integration jedoch mit Vorsicht und gründlichen Tests angegangen werden sollte. Die gemischten Ergebnisse für die verschiedenen Strategien deuten darauf hin, dass die Wirksamkeit von DL im Handel nicht universell ist und stark von der spezifischen Strategie und dem Marktkontext abhängt. Zukünftige Forschungsarbeiten könnten die Optimierung dieser DL-Modelle für verschiedene Zeitrahmen und Marktbedingungen untersuchen, um ihre Leistung in verschiedenen Handelsszenarien zu verbessern.