卡尔曼滤波器在外汇均值回归策略中的应用

概述

卡尔曼滤波器是一种递归算法，在算法交易中用于通过滤除价格走势中的噪声来估计金融时间序列的真实状态。它能够根据新的市场数据动态更新预测，这使得它在均值回归等自适应策略中极具价值。本文首先介绍卡尔曼滤波器，涵盖其计算方法和实现方式。接下来，我们以外汇领域一个经典的均值回归策略为例，应用该滤波器。最后，我们通过将卡尔曼滤波器与移动平均线（MA）在外汇不同货币对上进行比较，开展各种统计分析。

卡尔曼滤波器

卡尔曼滤波器由鲁道夫·E·卡尔曼（Rudolf E. Kalman）于1960年提出，是一种用于跟踪和预测动态系统的最优递归估计器。该滤波器最初是为航空航天和控制系统开发的，目前已广泛应用于金融、机器人技术和信号处理等领域。卡尔曼滤波器分两步运行：预测步骤，用于估计系统的下一个状态；更新步骤，用于根据新观测值完善估计，同时最小化噪声。 

在算法交易领域，人们可以简单地将卡尔曼滤波器视为交易者常用的常规状态滤波器，类似于移动平均线或线性回归模型。卡尔曼滤波器能够动态适应新数据、减少噪声，并能实时高效地更新估计值，因此在检测市场状态转变方面非常有效。然而，它假设系统具有线性动态特性，需要仔细调整参数，在检测突变时可能存在滞后性，并且与移动平均线等更简单的滤波器相比，计算更为复杂。

卡尔曼滤波器在算法交易中的一些常见用途：

• 均值回归交易：将当前价格与估计价格进行比较，作为入场筛选条件。
• 配对交易：动态估计相关资产之间的价差，并根据不断变化的市场条件调整对冲比例。
• 趋势跟踪：过滤短期噪声，更准确地检测长期价格趋势。
• 波动率估计：为风险管理和仓位调整提供市场波动率的自适应估计。

卡尔曼滤波器值的计算公式如下：

为了以一种简单的方式理解这个复杂的公式，让我们来看一个图形示例。

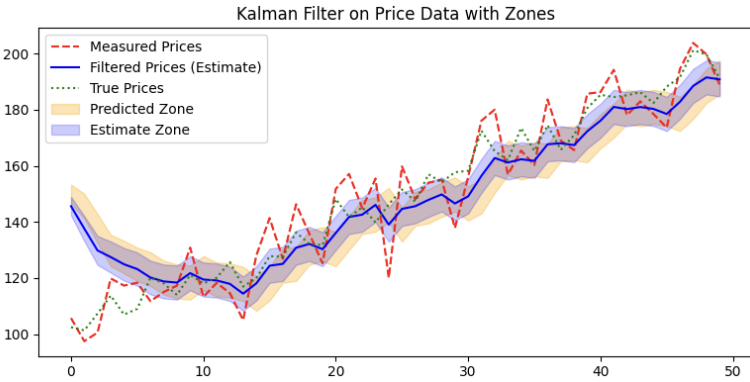
卡尔曼滤波器通过基于含噪声的测量值和预测值来更新对真实价格的估计。这一过程通常分三步进行：

1. 预测：滤波器首先对价格（预测价格）及其不确定性（预测协方差）做出初始猜测。这由橙色的预测区域表示——滤波器考虑到先前的估计和过程噪声，预期真实价格所在的区间。

2. 更新：当有新的价格数据（测量价格）可用时，卡尔曼滤波器会将其与预测价格进行比较。然后，会计算一个称为卡尔曼增益（紫色线）的值，以决定给予新测量值与预测值多大的权重。如果测量值噪声很大，滤波器会更信任其预测值。 

3. 估计：滤波器通过纳入新的测量值来更新预测价格。更新后的价格（由蓝色的估计区域表示）与预测值相比，不确定性有所降低。随着滤波器完善其估计，这一区域会缩小。 

这里，预测不确定性由测量值与预测值之间的协方差定义。协方差越大，估计越不自信；协方差越小，滤波器对其估计越有把握。如果测量值可靠，卡尔曼增益就高，滤波器会更信任新数据（不确定性缩小）。如果测量值噪声大，增益就低，滤波器会更依赖先前的预测。

噪声大小由方差定义，即测量方差和过程方差。与协方差不同，噪声不会自行调整，而是从一开始就根据您希望卡尔曼滤波器的平滑度来确定。

以下是一些方差如何影响曲线平滑度的示例：

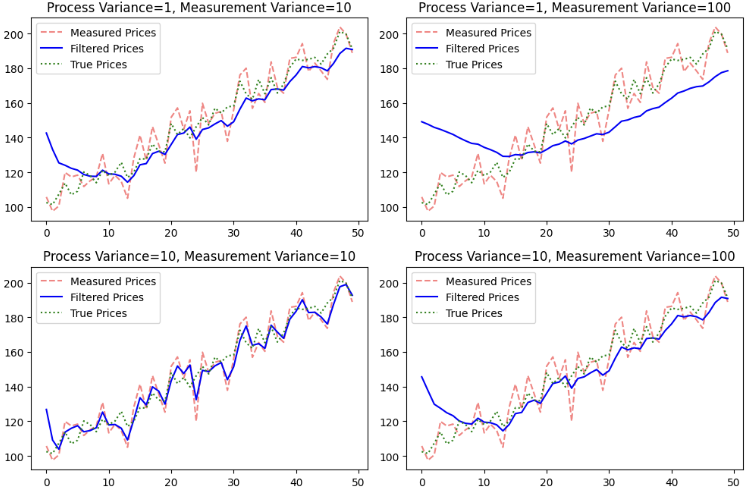
一般来说，过程方差（Q）表示模型预期真实状态随时间变化的程度，而测量方差（R）则反映了对观测数据的置信程度。较高的Q会使滤波器对突然变化更敏感，但会增加波动性。较高的R则通过更信任的过去估计值来平滑预测，但代价是调整会有延迟。低Q和适中的R能得出稳定的预测，而高Q和低R则会使滤波器反应更灵敏，但噪声也更大。

策略编码

均值回归策略通常遵循以下方法：在超卖时买入、超买时卖出、价格回归均值时平仓。该策略基于这样的假设：价格数据总体上保持稳定，不会倾向于达到极端水平。当价格处于一个极端时，预期它最终会回到均衡点。这一理论对于像外汇这样的半平稳数据尤其适用，多年来，均值回归策略在外汇市场上一直有利可图。

我们将使用100周期、偏差为2.0的布林带量化我们的策略。详细计划如下：

• 当上一收盘价低于下轨时买入。
• 当上一收盘价高于上轨时卖出。
• 只要价格穿过中轨，就平仓。
• 同一时间只持有一个仓位，以避免过度交易。
• 将止损差距设定为价格的1%，以规避均值回归策略中常见的肥尾风险（极端风险）。

我们计划在15分钟时间框架内交易外汇对，这一常见时间框架既能提供足够的交易机会，又能确保交易质量尚可。

我们总是先定义必要的函数，这样后续编写交易逻辑代码时会更加容易。在此情况下，我们只需编写买入和卖出函数，具体如下：

#include <Trade/Trade.mqh>
CTrade trade;
//+------------------------------------------------------------------+
//| Buy Function                                                     |
//+------------------------------------------------------------------+
void executeBuy(string symbol) {
       double ask = SymbolInfoDouble(symbol, SYMBOL_ASK);
       double lots=0.01;
       double sl = ask*(1-0.01);
       trade.Buy(lots,symbol,ask,sl);
}

//+------------------------------------------------------------------+
//| Sell Function                                                    |
//+------------------------------------------------------------------+
void executeSell(string symbol) {      
       double bid = SymbolInfoDouble(symbol, SYMBOL_BID);
       double lots=0.01;
       double sl = bid*(1+0.01);
       trade.Sell(lots,symbol,bid,sl);     
}

随后，我们在此处初始化全局变量和初始值。这会为智能交易系统（EA）初始化一个唯一标识号（magic数字），同时初始化我们后续将使用的布林带指标句柄。

input int Magic = 0;
input int bbPeriod = 100;
input double d = 2.0;

int barsTotal = 0;
int handleMa;

//+------------------------------------------------------------------+
//| Initialization                                                   |
//+------------------------------------------------------------------+
int OnInit()
{   handleBb = iBands(_Symbol,PERIOD_CURRENT,bbPeriod,0,d,PRICE_CLOSE);  
    trade.SetExpertMagicNumber(Magic);
    return INIT_SUCCEEDED;
}

最后，在OnTick()函数中，我们利用这一点来确保交易逻辑是按每根K线（而非每次价格变动）来处理的：

int bars = iBars(_Symbol,PERIOD_CURRENT);
  
if (barsTotal!= bars){
   barsTotal = bars;

我们通过创建缓冲区数组（该数组可从指标句柄中复制数据以存储当前值），来获取布林带的当前数值。

double bbLower[], bbUpper[], bbMiddle[];
CopyBuffer(handleBb,UPPER_BAND,1,1,bbUpper);
CopyBuffer(handleBb,LOWER_BAND,1,1,bbLower);
CopyBuffer(handleBb,0,1,1,bbMiddle);

此段代码会遍历交易账户中当前所有已开立的仓位，以检查这些仓位是否是由本特定EA开立的。如果本EA已开立了一个仓位，我们将NotInPosition变量设置为false。对于所有已回归至中轨的已开立仓位，我们将其平仓。

bool NotInPosition = true;
for(int i = 0; i<PositionsTotal(); i++){
    ulong pos = PositionGetTicket(i);
    string symboll = PositionGetSymbol(i);
    if(PositionGetInteger(POSITION_MAGIC) == Magic&&symboll== _Symbol){
       NotInPosition = false;
       if((PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY&&price>bbMiddle[0])
       ||(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL&&price<bbMiddle[0]))trade.PositionClose(pos);  
  }
}  

最终的交易逻辑将按如下方式执行：

if(price<bbLower[0]&&NotInPosition) executeBuy(_Symbol);
if(price>bbUpper[0]&&NotInPosition) executeSell(_Symbol);

编译该EA，然后前往策略测试图形工具，查看EA是否按预期运行。

在图形工具中，一次典型交易应如下所示：

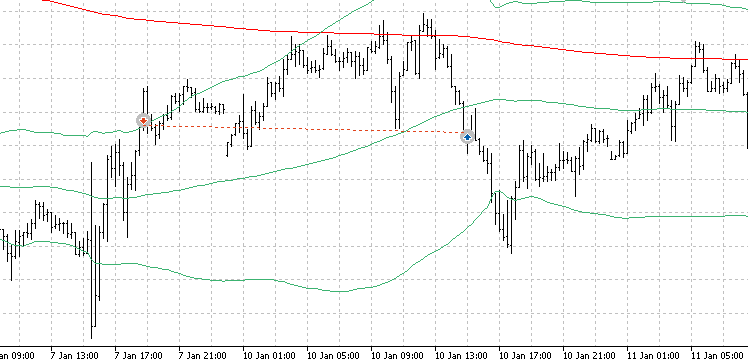
随后，我们返回MetaEditor，编写状态过滤器的代码。

首先，对于500周期指数移动平均线（500-EMA），我们希望均值回归策略在入场时能顺应趋势，以此作为附加的确认信号。我们在原始EA的代码中添加以下代码行：

int handleMa;
handleMa = iMA(_Symbol,PERIOD_CURRENT,maPeriod,0,MODE_EMA,PRICE_CLOSE);
 
double ma[];
CopyBuffer(handleMa,0,1,1,ma);
    
if(price<bbLower[0]&&price>ma[0]&&NotInPosition) executeBuy(_Symbol);
if(price>bbUpper[0]&&price<ma[0]&&NotInPosition) executeSell(_Symbol);

 之后，我们编写用于获取卡尔曼滤波器值的函数：

//+------------------------------------------------------------------+
//| Kalman Filter Function                                           |
//+------------------------------------------------------------------+
double KalmanFilter(double price,double measurement_variance,double process_variance)
{
    // Prediction step (state does not change)
    double predicted_state = prev_state;
    double predicted_covariance = prev_covariance + process_variance;

    // Kalman gain calculation
    double kalman_gain = predicted_covariance / (predicted_covariance + measurement_variance);

    // Update step (incorporate new price observation)
    double updated_state = predicted_state + kalman_gain * (price - predicted_state);
    double updated_covariance = (1 - kalman_gain) * predicted_covariance;

    // Store updated values for next iteration
    prev_state = updated_state;
    prev_covariance = updated_covariance;

    return updated_state;
}

该函数遵循如下图所示的递归流程：

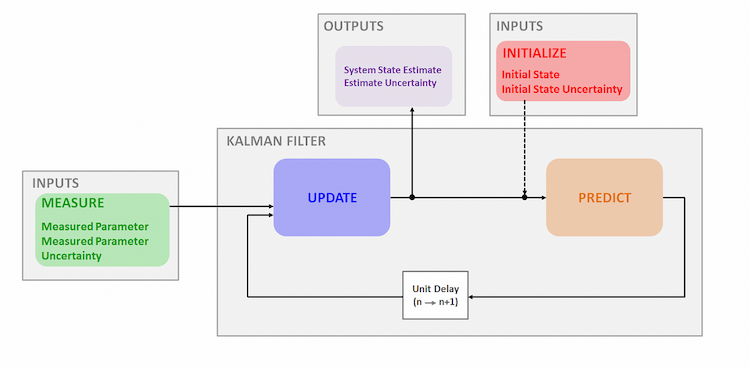
要在EA中实现卡尔曼状态过滤器，我们在OnTick()函数中添加以下代码：

double kalman = KalmanFilter(price,mv,pv);
if(price<bbLower[0]&&price>kalman&&NotInPosition) executeBuy(_Symbol);
if(price>bbUpper[0]&&price<kalman&&NotInPosition) executeSell(_Symbol);

卡尔曼滤波器通过持续更新对真实价格的估计值来工作，它能平滑掉价格中的噪声，并随时间推移适应价格变动。本质上讲，其充当了价格预测器的角色。当价格跌破布林带下轨时，这表明市场处于超卖状态，且预计价格将回归均值。这里，我们利用卡尔曼滤波器作为反转信号的确认依据。在超卖的情况下，如果价格高于卡尔曼估计值，则表明价格已经显现出潜在的上涨迹象。在卖出的情况下，则恰恰相反。

然而，尽管移动平均线也是一种常见的市场状态过滤器，但其目的与卡尔曼滤波器略有不同。移动平均线作为趋势指标，价格相对于移动平均线的位置表明了当前趋势的方向。

完整代码如下：

#include <Trade/Trade.mqh>
CTrade trade;

input double mv = 10;
input double pv = 1.0;
input int Magic = 0;
input int bbPeriod = 100;
input double d = 2.0;
input int maPeriod = 500;

double prev_state;       // Previous estimated price
double prev_covariance = 1;  // Previous covariance (uncertainty)
int barsTotal = 0;
int handleMa;
int handleBb;

//+------------------------------------------------------------------+
//| Initialization                                                   |
//+------------------------------------------------------------------+
int OnInit()
{   handleMa = iMA(_Symbol,PERIOD_CURRENT,maPeriod,0,MODE_EMA,PRICE_CLOSE);
    handleBb = iBands(_Symbol,PERIOD_CURRENT,bbPeriod,0,d,PRICE_CLOSE);
    prev_state = iClose(_Symbol,PERIOD_CURRENT,1);  
    trade.SetExpertMagicNumber(Magic);
    return INIT_SUCCEEDED;
}

//+------------------------------------------------------------------+
//| Deinitializer function                                           |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
  }

//+------------------------------------------------------------------+
//| OnTick Function                                                  |
//+------------------------------------------------------------------+
void OnTick()
{
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  
  if (barsTotal!= bars){
     barsTotal = bars;
     bool NotInPosition = true;
     double price = iClose(_Symbol,PERIOD_CURRENT,1); 
     double bbLower[], bbUpper[], bbMiddle[];
     double ma[];
     double kalman = KalmanFilter(price,mv,pv);
     
     CopyBuffer(handleMa,0,1,1,ma);
     CopyBuffer(handleBb,UPPER_BAND,1,1,bbUpper);
     CopyBuffer(handleBb,LOWER_BAND,1,1,bbLower);
     CopyBuffer(handleBb,0,1,1,bbMiddle);
     
     for(int i = 0; i<PositionsTotal(); i++){
         ulong pos = PositionGetTicket(i);
         string symboll = PositionGetSymbol(i);
         if(PositionGetInteger(POSITION_MAGIC) == Magic&&symboll== _Symbol){
            NotInPosition = false;
            if((PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY&&price>bbMiddle[0])
            ||(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL&&price<bbMiddle[0]))trade.PositionClose(pos);  
      }
    }  
    
     if(price<bbLower[0]&&price>kalman&&NotInPosition) executeBuy(_Symbol);
     if(price>bbUpper[0]&&price<kalman&&NotInPosition) executeSell(_Symbol);
    }
}

//+------------------------------------------------------------------+
//| Kalman Filter Function                                           |
//+------------------------------------------------------------------+
double KalmanFilter(double price,double measurement_variance,double process_variance)
{
    // Prediction step (state does not change)
    double predicted_state = prev_state;
    double predicted_covariance = prev_covariance + process_variance;

    // Kalman gain calculation
    double kalman_gain = predicted_covariance / (predicted_covariance + measurement_variance);

    // Update step (incorporate new price observation)
    double updated_state = predicted_state + kalman_gain * (price - predicted_state);
    double updated_covariance = (1 - kalman_gain) * predicted_covariance;

    // Store updated values for next iteration
    prev_state = updated_state;
    prev_covariance = updated_covariance;

    return updated_state;
}

//+------------------------------------------------------------------+
//| Buy Function                                                     |
//+------------------------------------------------------------------+
void executeBuy(string symbol) {
       double ask = SymbolInfoDouble(symbol, SYMBOL_ASK);
       double lots=0.01;
       double sl = ask*(1-0.01);
       trade.Buy(lots,symbol,ask,sl);
}

//+------------------------------------------------------------------+
//| Sell Function                                                    |
//+------------------------------------------------------------------+
void executeSell(string symbol) {      
       double bid = SymbolInfoDouble(symbol, SYMBOL_BID);
       double lots=0.01;
       double sl = bid*(1+0.01);
       trade.Sell(lots,symbol,bid,sl);     
} 

要更改状态过滤器，只需调整最终的买入/卖出标准即可。

统计分析

编译EA，然后进入MetaTrader 5交易终端，在左上角点击“视图”->“交易品种”->“外汇”，并为所有主要货币对和次要货币对选择“显示交易品种”。这样一来，这些货币对就会被添加到您的市场观察列表中，以便后续进行市场扫描。

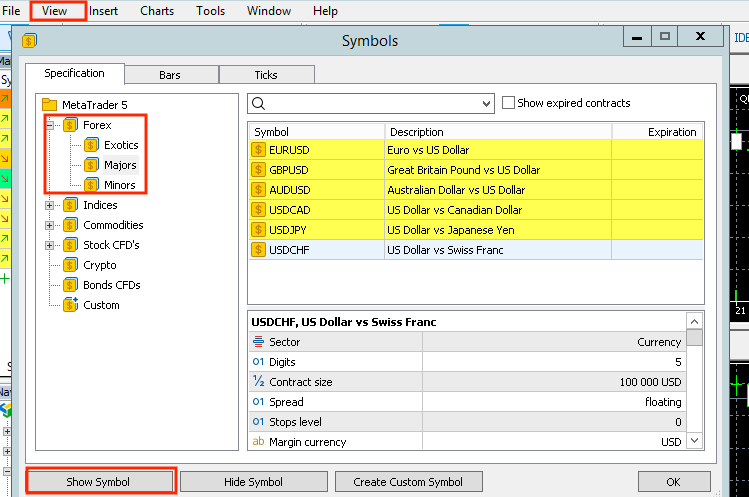
随后，我们在策略测试器的“市场扫描器”（Market Scanner）模块中，使用过去3年的历史数据对策略进行回测。这将有助于我们判断状态过滤器是否能提升可能交易的大多数外汇货币对的盈利能力。

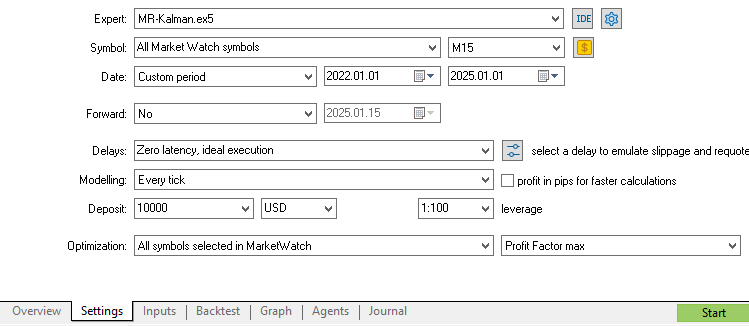
当然，经过筛选的交易数量取决于所用指标的参数设置。在本研究中，我们采用常用的参数值进行筛选，以确保交易数量相近：卡尔曼滤波器采用500周期指数移动平均线、测量方差设为10、过程方差设为1。建议读者们根据实际效果微调参数以获得最优结果。

我们首先测试不使用任何状态过滤器的基准结果，以此作为参照。预期结果显示，采用市场状态过滤器的EA平均表现应优于大多数基准结果。

表现最优的外汇货币对测试结果如下：

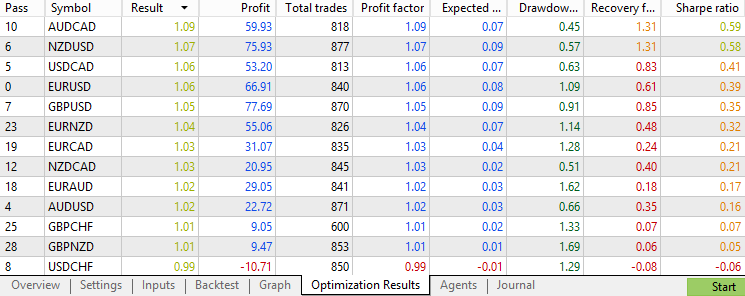
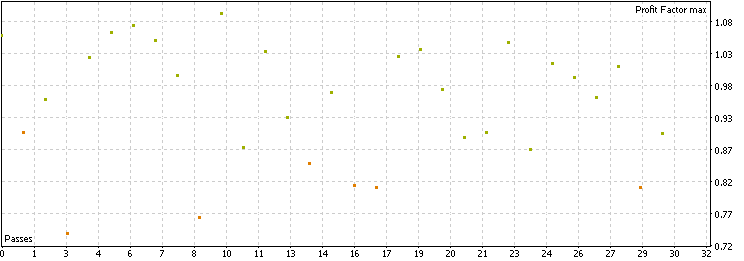
我们发现，过去3年中，该策略在每个货币对上平均执行了800多笔交易，样本量充足，结论具有普遍性。收益因子（profit factor）分布大多集中在0.8至1.1之间，表现尚可，但没有任何货币对的收益因子超过1.1，或夏普比率（Sharpe ratio）超过1。总体而言，原始策略在近年多个外汇货币对上均有效，但盈利能力并不突出。在后续与添加过滤器后的表现对比中，请牢记这一基准结果。

接下来，我们对加入移动平均线过滤器后的策略进行回测。结果如下：

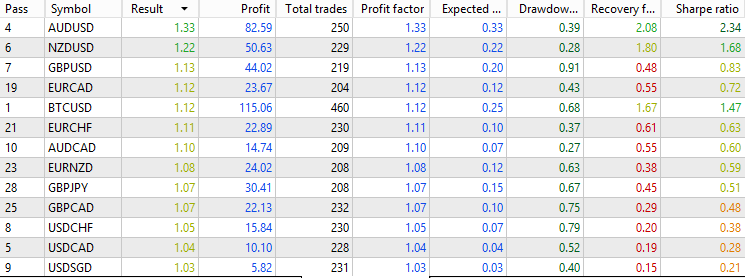
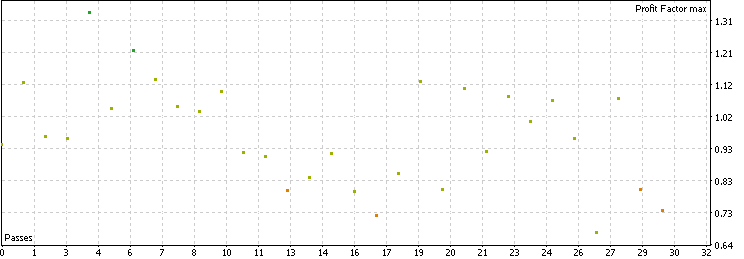
由此可见，使用移动平均线过滤器后，约70%的原始交易被过滤掉，每个货币对仅保留约250笔交易。此外，过滤后的交易质量平均高于基准水平。大多数外汇货币对的收益因子在0.9至1.2之间，其中表现最优的货币对收益因子达1.33，夏普比率为2.34。这表明，将移动平均线作为过滤器显著提升了这一经典均值回归策略的盈利能力。

现在，我们直面核心问题，看看采用卡尔曼滤波器时策略的表现如何。

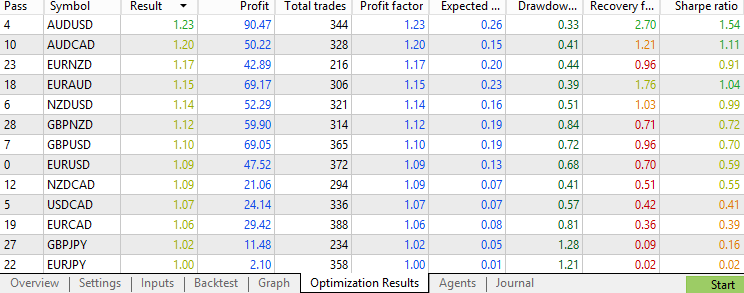
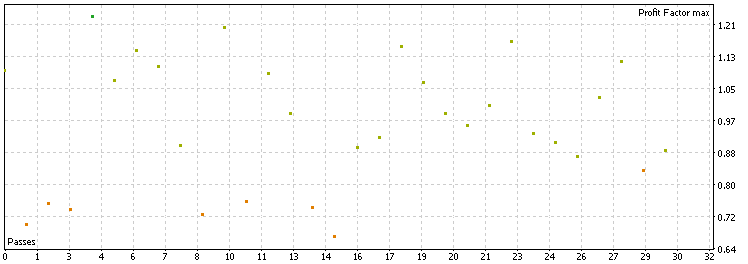
卡尔曼滤波器过滤掉了约60%的原始交易，每个货币对最终保留约350笔交易。从分布来看，大多数收益因子集中在0.85至1.2之间，与移动平均线过滤器的表现相近，且均优于基准水平。进一步分析收益因子超过1.0和1.2的外汇货币对数量后，可以得出结论：对于本策略而言，移动平均线滤波器和卡尔曼滤波器在提升平均交易质量方面的效果相当。在此场景下，卡尔曼滤波器并未表现出优于移动平均线的性能，这说明更复杂的模型未必能带来更好的结果。

我们曾提到，卡尔曼滤波器与移动平均线在过滤逻辑上存在差异。然而，就过滤低质量交易的效果而言，两者表现相似。为探究它们是否过滤了相同的交易，我们将分析两者过滤结果的差异，以判断卡尔曼滤波器的作用是否仅等同于指数移动平均线（EMA）。

作为参考，我们选择澳元兑美元（AUDUSD）货币对进行分析，因为该货币对在上述两种条件下均表现最优。

基准回测结果：

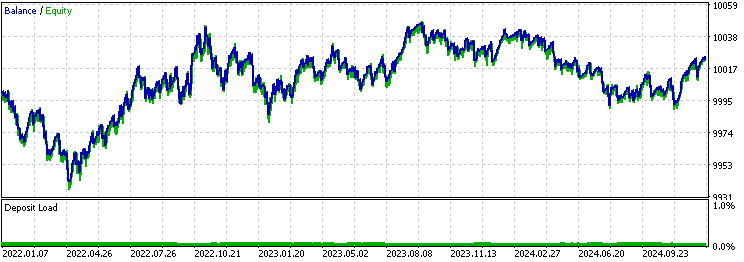
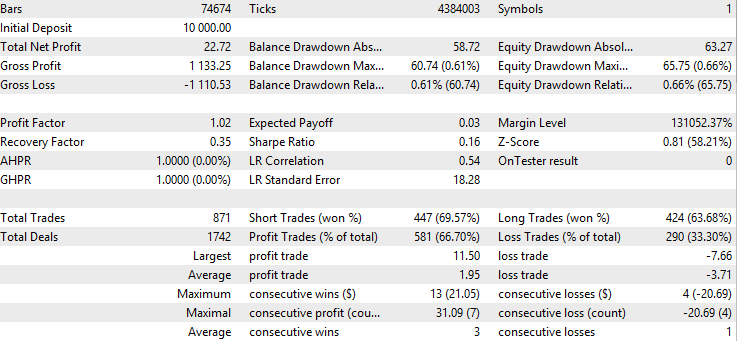
指数移动平均线过滤器的回测结果：

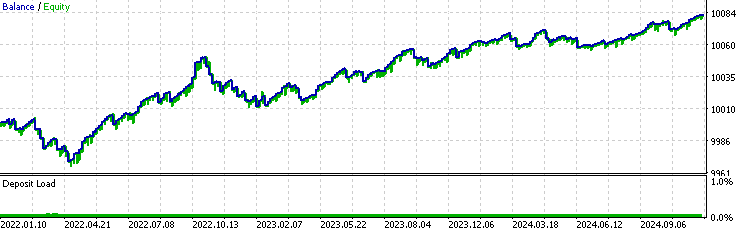
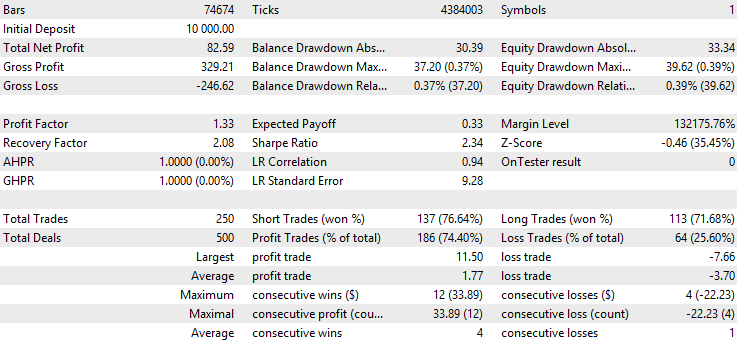
卡尔曼滤波器结果：

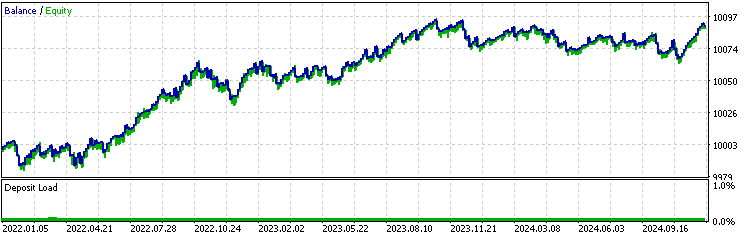
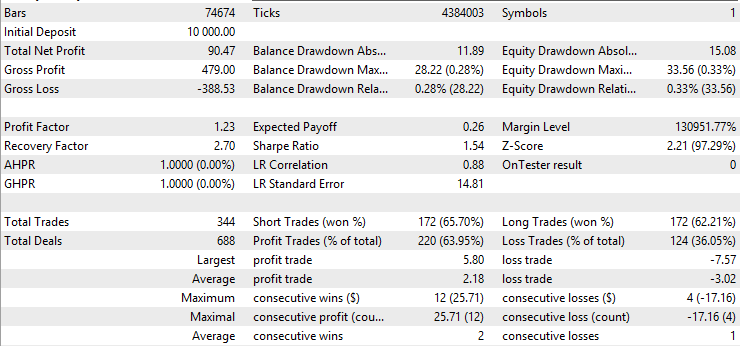
我们首先注意到的是，移动平均线版本的策略胜率显著高于基准版本和卡尔曼版本，但其平均盈利低于其他两者，且平均亏损高于其他两者。这就表明，移动平均线版本筛选的交易与卡尔曼版本存在本质差异。为进一步分析，我们可通过右键点击回测结果页面，导出回测的Excel报告：

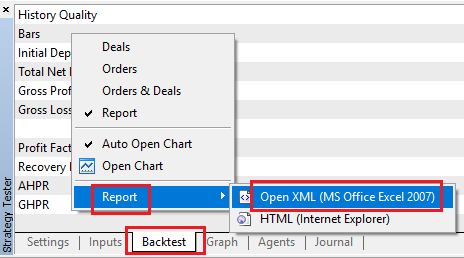
对于每份报告，我们注意到"Deals"（交易明细）标识的行号：

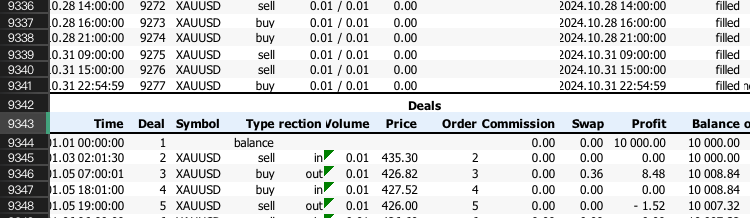
接下来，我们切换至Python或Jupyter Notebook环境。将以下代码复制粘贴到脚本中，并将skiprow参数值修改为每个Excel报告中"Deals"所在行的行号，即可完成数据读取。

import pandas as pd
import matplotlib.pyplot as plt
from matplotlib_venn import venn3
df1 = pd.read_excel("baseline.xlsx", skiprows=1805)
df2 = pd.read_excel("ma.xlsx", skiprows =563 )
df3 = pd.read_excel("kalman.xlsx",skiprows = 751)
df1 = df1[['Time']][1:-1]
df1 = df1[df1.index % 2 == 0]  # Filter for rows with odd indices
df2 = df2[['Time']][1:-1]
df2 = df2[df2.index % 2 == 0]
df3 = df3[['Time']][1:-1]
df3 = df3[df3.index % 2 == 0]

# Convert "Time" columns to datetime
df1['Time'] = pd.to_datetime(df1['Time'])
df2['Time'] = pd.to_datetime(df2['Time'])
df3['Time'] = pd.to_datetime(df3['Time'])

# Find intersections
set1 = set(df1['Time'])
set2 = set(df2['Time'])
set3 = set(df3['Time'])

# Create the Venn diagram
venn_labels = {
    '100': len(set1 - set2 - set3),  # Only in df1
    '010': len(set2 - set1 - set3),  # Only in df2
    '001': len(set3 - set1 - set2),  # Only in df3
    '110': len(set1 & set2 - set3),  # In df1 and df2
    '011': len(set2 & set3 - set1),  # In df2 and df3
    '101': len(set1 & set3 - set2),  # In df1 and df3
    '111': len(set1 & set2 & set3)   # In all three
}

# Plot the Venn diagram
plt.figure(figsize=(8, 8))
venn3(subsets=venn_labels, set_labels=('Baseline', 'EMA', 'Kalman'))
plt.title("Venn Diagram of Time Overlap")
plt.show()

这段代码的核心逻辑是：通过跳过指定行并选取偶数行索引，将三个版本的平仓时间点分别存储到三个独立的数据结构中。随后，将每个数据结构转换为集合，通过比较时间点的重叠情况生成韦恩图（Venn Diagram）。图中会用不同颜色区分各区域，直观展示不同版本策略的交易重叠数量。请注意，即使基准版本也可能缺少部分EMA和卡尔曼版本的交易，因为策略被设置为单线程运行（每次仅执行一个版本），导致某些交易机会被其他版本独占。

输出韦恩图示例：

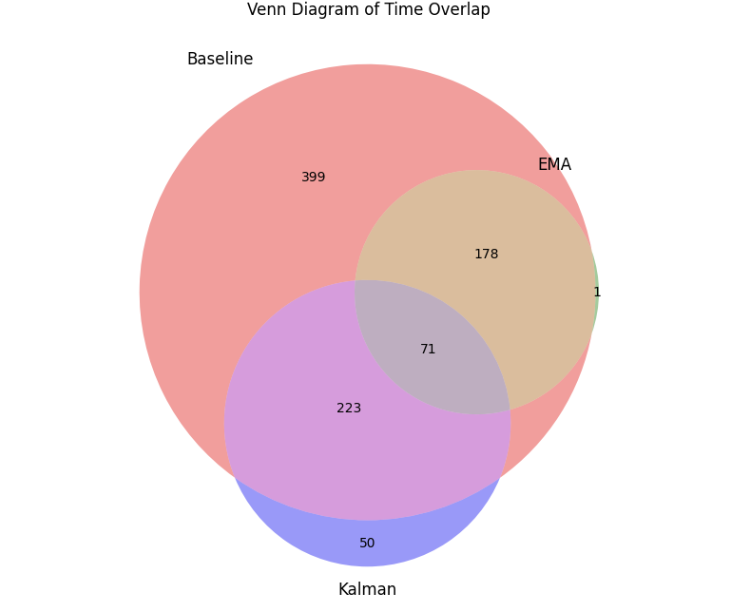
通过观察卡尔曼滤波器与移动平均线策略的重叠区域后发现，尽管两个版本各自执行了数百笔交易，但仅有71笔交易完全重合。这表明，尽管两者从原始策略中过滤掉的交易数量相近，但其过滤逻辑和效果存在显著的差异。这一发现进一步凸显了研究并应用卡尔曼滤波器的重要性——它提供了一种与常见趋势过滤器截然不同的独特筛选机制。

结论

本文介绍了一种用于算法交易的高级递归算法——卡尔曼滤波器。我们首先解析了其核心机制与实现方式，并通过图表和公式进行详细说明。随后，完整展示了基于外汇均值回归策略的开发流程，以及如何在MQL5编程环境中实现卡尔曼滤波器。最终，通过市场扫描、回测分析及重叠交易对比等多维度统计检验，系统评估了其相较于移动平均线与基准策略的过滤效能。

在实际交易中，卡尔曼滤波器已被顶尖量化机构广泛应用，但在零售交易领域仍属小众技术。本文旨在为MQL5开发者社区提供理论分析与实战指南，通过构建可复用的评估框架，帮助交易者科学地验证卡尔曼滤波器的过滤能力，从而更有效地将其融入策略开发体系。我们鼓励读者基于本文框架展开自主实验，将这一工具纳入自己的交易库。

文件表

文件名	文件使用
Kalman visualizations.ipynb	本文中图形的Python代码如下：
MR-Kalman.mq5	EA代码