Python中的虚假回归（伪回归）

简介

在深入机器学习算法交易领域之前，确认模型输入与我们想要预测的变量之间是否存在有意义的关系至关重要。本文阐述了在单位根测试中对模型残差的应用，以验证我们的数据集中是否存在这种关系的实用性。

遗憾的是，使用没有真正关系的数据集构建模型是有可能的。这些模型可能会产生令人印象深刻的低误差指标，从而营造出一种虚假的控制感和过于乐观的前景。 这些有缺陷的模型通常被称为“虚假回归”。

本文将首先培养对虚假回归的直观理解。之后，我们将生成合成时间序列数据来模拟虚假回归，并观察其特征效应。接着，我们将深入探讨识别虚假回归的方法，并依靠我们的见解来验证一个在Python中构建的机器学习模型。最后，如果我们的模型得到验证，将其导出为ONNX格式，并在MQL5中实现一个交易策略。

引言：虚假回归现象时有发生

19世纪中叶，伊格纳兹·塞梅尔维斯（Ignaz Semmelweis）是维也纳的一名执业医生。他对自己所在医院的统计数据深感沮丧。

图1：Ignaz Semmelweis

问题是，在该医院分娩的健康女性中，有五分之一死于分娩期间感染的发热疾病。伊格纳兹决定找出原因。当时的大多数医生都将此事归咎于他们相信由于携带邪灵的“坏空气”导致了这些问题的出现。尽管这在今天听起来可能很可笑，但在当时却是被广泛接受的观点。但这个观点并不能让伊格纳兹满意。随着时间的推移，有一天，伊格纳兹观察到，在医院一侧停尸房进行尸检的医生和医学生，在未洗手的情况下就直接跑到医院的另一侧去接生。在说服当地医院的医护人员实行手部卫生后，孕产妇死亡率从20%降至1%。

遗憾的是，伊格纳兹的发现并未引起人们的注意。他试图与其他医生和医疗机构分享自己的发现，但这些努力反而使他更加疏远了当时医学界及其坚信的“坏空气”理论。伊格纳兹·塞梅尔维斯在46岁时，在一家精神病院去世，成为了一名社会弃儿。我们能从那些忽视塞梅尔维斯明智建议的医生身上学到什么？为什么他们如此难以发现自己的错误？

问题在于，有可能使用毫无关系的数据构建模型，而且这样的模型可能会偶然产生较低的误差指标，并错误地证明不存在的关系。这样的模型被称为虚假回归。

虚假回归是指错误地证明了一个不存在的关系的模型。请注意，医生们可能会告诉自己，“今天空气中的邪灵太多了，所以明天会有更多的母亲去世。”正如他们所预测的，第二天确实有更多女性去世，但医生们的判断却是基于错误的原因。在构建机器学习模型时，我们的模型也可能会因为错误的原因而得出正确的结果。

如果你明确知道输入和输出数据之间存在关系，那么你就没有必要担心。然而，如果你不确定呢？或者如果你从未检验过，只是假设一定存在某种关系？

最有名的解决方案是对模型的残差进行专项测试。这些测试被称为单位根测试。我们不会在这篇讨论中定义单位根，那将是另一个独立的讨论话题。然而，为了实现我们的目标，只需要知道，如果我们能在残差中找到单位根，那么此回归就是虚假回归。

在讨论我们今天考虑的单位根解决方案时，存在一个物质性的限制，即尽管单位根存在，我们可能无法发现它们，这被称为第一类错误。另外，我们也可能错误地发现不存在的单位根，这被称为第二类错误。

为了检查我们的残差是否具有单位根，我们可以使用多种测试方法，如增广迪基-富勒检验（Augmented Dickey Fuller Test）和菲利普斯-佩伦-施密特-申检验（Kwiatkowski-Phillips-Schmidt-Shin Test）。每种测试方法都有其优点和缺点，并在不同条件下可能失效。为了观察虚假回归在实际中的应用，我们将生成自己的时间序列数据。我们将创建两个没有相互关系的时间序列数据集，并观察当我们使用这两个独立的数据集训练模型时会发生什么。

模拟虚假回归

虚假回归可能由多种原因引起，但最常见的原因是建模了两个独立且非平稳的时间序列。让我们来详细解释一下这个技术定义。时间序列简单来说就是随机变量的均匀记录观测值。当我们说一个时间序列平稳时，意味着它的统计属性（如均值、方差和自相关结构）随时间保持相对稳定。相反，如果一个时间序列的统计属性随时间波动，那么它就是非平稳的。

在我们的讨论中，我们将通过模拟自己的数据来采取一种实践的方法，以便在每个步骤中理解真实情况。这种方法使我们能够直接观察到效果。我们首先导入必要的文件包：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller , kpss
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

接下来，我们将为两个数据集定义统计属性，一个模拟输入数据，另一个模拟输出数据。这两个数据集都将包含随机和正态分布的数字。

size = 1000
mu , sigma = 0 , 1
mu_y , sigma_y = 2 , 4

以下代码生成了两个时间序列，x_non_stationary 和 y_non_stationary，它们代表随机游走。随机性是通过正态分布引入的，而累积和确保了序列中的每个值都依赖于前面的值，从而产生了动态且非平稳的行为。

x_non_stationary 和 y_non_stationary 数据集都是通过 numpy.random.normal 函数随机生成的。因此，这两个数据集之间没有任何关系。

steps = np.random.normal(mu,sigma,size)
steps_y = np.random.normal(mu_y,sigma_y,size)
x_non_stationary =  pd.DataFrame(100 + np.cumsum(steps),index= np.arange(0,1000))
x_non_stationary_lagged = x_non_stationary.shift(1)
x_non_stationary_lagged.dropna(axis=0,inplace=True)
y_non_stationary =   pd.DataFrame(100 + np.cumsum(steps_y),index= np.arange(0,1000))

让我们看看我们的两个随机数据集。

plt.plot(x_non_stationary)

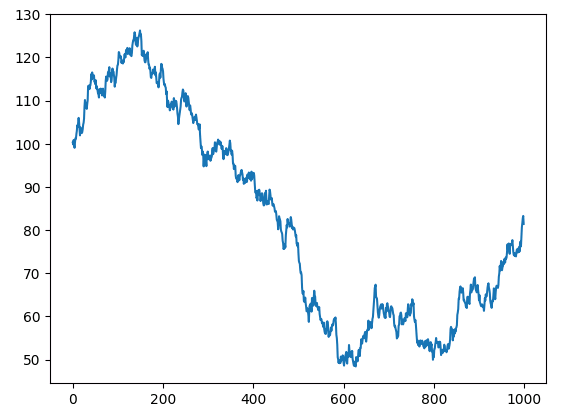
图2：随机游走x

让我们绘制非平稳时间序列y。

plt.plot(y_non_stationary)

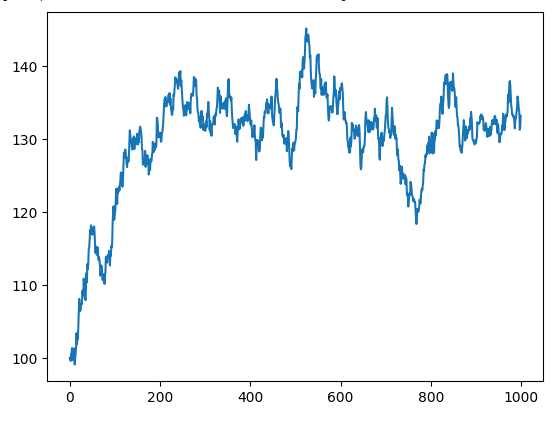
图3：随机游走y。

现在让我们观察两个独立的非平稳时间序列的回归结果。

ols = sm.OLS(y_non_stationary,x_non_stationary)
lm = ols.fit()
print(lm.summary())

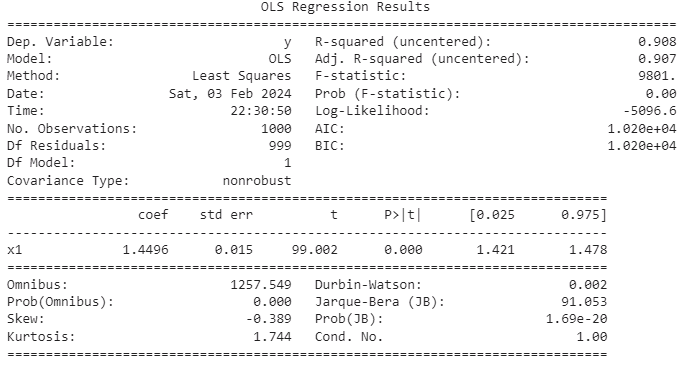
图4：回归两个独立非平稳变量的汇总结果

在许多时间序列中，存在一个被称为随机趋势的随机成分。即使两个时间序列是独立的，它们的随机趋势也可能表现出短暂的、局部的相关性。遗憾的是，这些瞬间的相关性有时会误导我们的模型，错误地得出两个独立时间序列之间存在关系的结论。由这种情况引起的虚假回归通常会产生较高的R方（决定系数）指标。很重要的一点需要记住，R方衡量的是因变量方差中受自变量方差影响的比例。因此，如果两个变量具有相关的随机趋势，R方指标的可靠性可能会被削弱。虚假回归问题在时间序列数据的背景下尤为重要，需要慎重考虑。

我们的模型具有一个调整后的R方指标，该指标接近1，这意味着模型认为拟合几乎完美。模型断言，响应变量中约90%的变异可以由预测变量的变异来解释。然而，这个演示作为提醒我们虚假回归相关陷阱的关键例子。我们了解输入和输出之间没有关系，它们都是随机的，没有共同之处。

此处问题依然存在，因为P值看起来不合理，而且我们的置信区间中明显不包含0。虽然这通常有可能被认定具有极好的拟合度，但仍需谨慎对待。在这种情况下，模型错误地引导了一个实际上并不存在的强烈关系。我们自己创建了输入和输出数据，因此我们知道它们之间没有关系。

预测变量的滞后

当我们发现一个预测变量的滞后版本时，就出现了虚假回归的明显迹象。在这种情况下，原本重要的系数会突然变得无关紧要，这很容易被我们观察到。这种现象是一个关键指标，它使我们避免得出错误的结论，并强调了理解和处理时间序列分析中的虚假回归的重要性。

我们将重复上述相同的程序，但这次我们还会包括输入数据的滞后版本。

ols = sm.OLS(y_non_stationary.iloc[0:998,0],x_matrix.loc[0:998,['current_x','lagged_x']])
lm = ols.fit()
print(lm.summary())

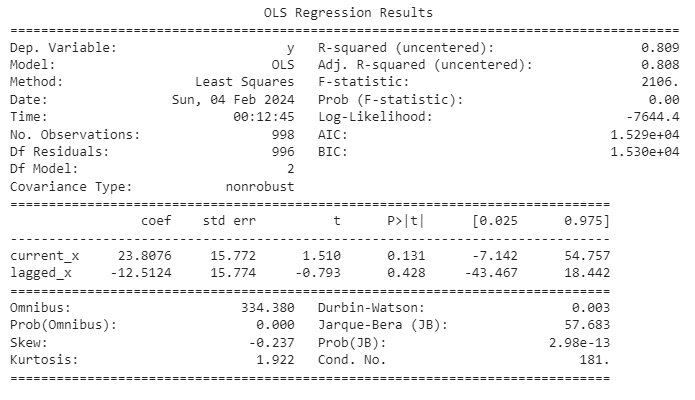
图5：关于虚假回归的统计摘要

再增加一层出于谨慎的考量，我们注意到R平方值超过了Durbin-Watson值。这一观察结果可以被视为另一个警示信号，指向可能存在的虚假回归问题。Durbin-Watson统计量在回归分析中用于检测回归模型残差中是否存在自相关。自相关出现在时间序列或回归模型的残差之间相互关联时。在时间序列数据的背景下，由于观测值依赖于先前的观测值，Durbin-Watson检验变得尤为重要。其结果为我们提供了关于自相关是否存在的宝贵见解，从而进一步指导我们评估模型的性能。

Durbin-Watson统计量

•     范围：Durbin-Watson统计量的值在0到4之间。
•     解释说明：接近2的值表明没有明显的自相关性。显著低于2的值表明存在正自相关（残差正相关）。显著高于2的值表明存在负自相关（残差负相关）。

虽然高R平方值和低Durbin-Watson值可能会让人怀疑存在虚假回归，但值得注意的是，仅凭这些指标并不能确凿地认定虚假回归的存在。在时间序列分析的领域中，额外的诊断测试和领域知识储备成为全面评估不可或缺的组成部分。 

单位根检验

识别虚假回归最可靠的方法在于对残差的分析。如果我们的模型残差缺乏平稳性，这表明该回归确实是虚假回归。然而，判断一个时间序列是否平稳并非易事。在我们的案例中，已知回归是虚假回归，因此残差是非平稳的，这时增广迪基-富勒检验（Augmented Dickey-Fuller Test）可能无法推翻原假设。换句话说，即使回归是虚假回归，它也可能无法证明数据不是平稳的，这说明了识别虚假回归所涉及的精细性和挑战性。这凸显了采用细致入微的方法的重要性，即结合统计检验和领域知识来有效应对时间序列分析的复杂性。

我们现在将使用sklearn在我们的训练集上拟合一个模型。

lm = LinearRegression()
lm.fit(x[train_start:train_end],y[train_start:train_end])

然后我们将计算残差。

residuals = y[test_start:test_end] - lm.predict(x[test_start:test_end])

让我们绘制残差。

residuals.plot()

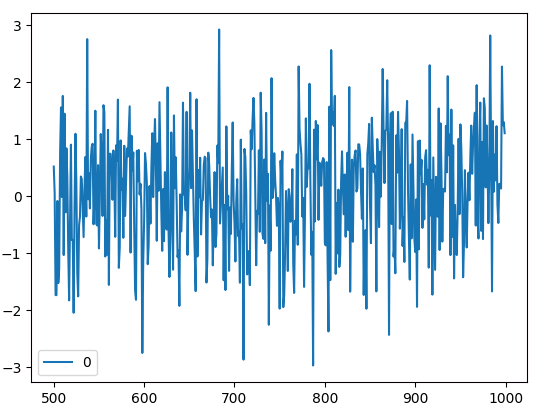
图6：使用Scikit-Learn构建的回归模型的残差

现在，我们将对残差进行增广迪基-富勒（ADF）检验，以确定其平稳性。

增广迪基-富勒检验

增广迪基-富勒 (ADF)检验是一种关键的统计工具，旨在评估时间序列的平稳性或识别表明非平稳性的单位根。在时间序列分析中，平稳性起着至关重要的作用，它意味着均值和方差等统计属性随时间保持不变。时间序列中存在单位根，表明非平稳性，我们可以合理的认为时间序列中的观测值可能具有非随机性。因此，ADF检验为仔细检查数据集的时间行为提供了一种稳健的方法，有助于深入了解其固有特性和对后续分析的潜在影响。

1. 零假设：ADF检验的零假设是时间序列具有单位根，表明非平稳性。
2. 备择假设：ADF检验的备择假设是时间序列不具有单位根，是平稳的。
3. 决策规则：ADF检验的决策规则涉及将检验统计量与临界值进行比较。如果检验统计量小于临界值，则拒绝零假设（存在单位根），表明平稳性。相反，如果检验统计量大于临界值，则没有足够证据拒绝零假设，表明非平稳性。

当我们对模型生成的残差进行增广迪基-富勒 (ADF) 检验时，所得结果将是判断残差是否具有平稳性或非平稳特性的关键决定因素。ADF检验在验证回归结果的过程中具有重要意义，在确保分析框架的可靠性方面发挥着关键作用。通过阐明残差的平稳性特性，该检验极大地增强了时间序列分析说明的稳健性。

对残差进行ADF

(-12.753804093890963, 8.423533501802878e-24, 2, 497, {'1%': -3.4435761493506294, '5%': -2.867372960189225, '10%': -2.5698767442886696}, 1366.9343966932422)

我们的主要关注点在于本实验得出的p值，特别是所提供列表中的第二个值，即8.423533501802878e-24。值得注意的是，这个p值接近于零，并且远远超过了任何合理的临界值。在增广迪基-富勒 (ADF) 测试的背景下，如果ADF统计量小于临界值，那么拒绝原假设就变得至关重要，这表明存在平稳性。

必须承认的是，ADF测试就像任何其他统计测试一样，都有其固有的局限性和假设条件。有多种因素可能导致ADF测试无法接受原假设，从而错误地拒绝单位根的存在，即使基础数据是非平稳的。理解这些细微差别对于全面解释测试结果至关重要。

1. 小样本量：ADF测试的性能可能会受到小样本量的影响。在这种情况下，测试可能缺乏足够的效力来检测非平稳性。
2. 滞后阶数不当：在ADF测试中，滞后阶数的选择至关重要。如果滞后阶数指定不正确，可能会导致结果不准确。使用过少或过多的滞后项可能会影响测试捕捉数据底层结构的能力。
3. 存在确定性趋势：如果数据中包含未在测试模型中考虑的确定性趋势（例如：线性趋势、二次趋势），ADF测试可能会无法拒绝原假设。在这种情况下，可能需要进行预处理步骤，如去趋势。
4. 差分不足：如果在ADF测试中使用的差分阶数不足以使数据平稳，测试可能会无法拒绝原假设。

Kwiatkowski-Phillips-Schmidt-Shin（KPSS）测试

Kwiatkowski-Phillips-Schmidt-Shin（KPSS）测试是评估时间序列数据平稳性的ADF测试的可行替代方案。尽管这两种测试在时间序列分析中都很常见，但它们在原假设和备择假设以及底层模型上存在差异。选择ADF测试还是KPSS测试取决于所检查时间序列的具体特征和主要的研究方向。同时使用这两种测试通常能提供更全面的平稳性分析，为研究人员提供对时间序列动态的深入理解。

1. 原假设：KPSS测试的原假设是时间序列是趋势平稳的。趋势平稳意味着序列存在一个单位根，表明存在确定性趋势。
2. 备择假设：KPSS测试的备择假设是时间序列不是趋势平稳的，表明它是差分平稳的或围绕随机趋势平稳的。
3. 决策规则：KPSS测试的决策规则涉及将测试统计量与在选定显著性水平（例如1%、5%或10%）下的临界值进行比较。如果测试统计量大于临界值，则拒绝原假设，表明时间序列不是趋势平稳的。相反，如果测试统计量小于临界值，则不能拒绝原假设，意味着趋势平稳。

在KPSS测试的情况下，通常采用的阈值是0.05的显著性水平。如果KPSS统计量低于此阈值，则表明数据中存在非平稳性。在我们的分析中，KPSS统计量的值为0.016，这证实了它偏离了临界阈值，并表明数据集倾向于非平稳性。这一结果进一步强调了考虑多种诊断工具（如ADF和KPSS测试）的重要性，以确保对时间序列特征的全面和准确评估。

对残差进行KPSS检验

(0.6709994557854182, 0.016181867655871072, 1, {'10%': 0.347, '5%': 0.463, '2.5%': 0.574, '1%': 0.739})

KPSS检验在某些情况下可能会错误地拒绝原假设（H0），从而导致第一类错误。当检验错误地得出时间序列不是趋势平稳的结论，而实际上它是趋势平稳的时，就会发生第一类错误。

以下是KPSS检验可能错误地拒绝原假设的一些情况：

1. 季节性模式：KPSS检验对趋势和季节性都很敏感。如果时间序列表现出强烈的季节性模式，检验可能会将其解释为非平稳趋势。在这种情况下，差分可能是解决季节性问题的必要手段。
2. 结构突变：如果时间序列中存在结构突变，如基础数据生成过程中的突然和显著变化，KPSS检验可能会将这些变化检测为非平稳趋势。结构突变可能导致拒绝原假设。
3. 异常值：数据中的异常值会影响KPSS检验的性能。异常值可能被视为趋势偏离，从而导致拒绝趋势平稳性。在解释KPSS检验结果时，对异常值的稳健性是一个重要考虑因素。
4. 非线性趋势：KPSS检验假设趋势是线性的。如果时间序列中的基础趋势是非线性的，检验可能会产生误导性结果。非线性趋势可能无法被检验充分捕捉，从而导致错误地拒绝平稳性。

谨慎解释KPSS检验结果，并考虑正在分析的时间序列的具体特征至关重要。此外，将KPSS检验与其他平稳性检验（如增广迪基-富勒（ADF）检验）相结合，可以对时间序列的平稳性属性进行更全面的评估。

综合以上

有了以上的基础，我们现在有机会将注意力从合成的数据转移，转而分析直接从MetaTrader 5终端获取的真实市场数据。为了促进这一转变，我们提议开发一个MetaQuotes语言5（MQL5）脚本。该脚本将专门设计用于从我们的交易终端检索数据，将其格式化并导出为CSV格式。

开始编写脚本时，第一步是声明全局变量，其中第一组用于存储技术指标的句柄。这些变量将在整个脚本执行过程中高效地管理和访问相关指标方面发挥关键作用，有助于MetaQuotes语言5（MQL5）程序的整体连贯性和组织性。

//---Our handlers for our indicators
int ma_handle;
int rsi_handle;
int cci_handle;
int ao_handle;

随后，我们需要精心设计数据结构，以便容纳和组织来自技术指标的数据。这些数据结构将在整个脚本执行过程中被使用。 

//---Data structures to store the readings from our indicators
double ma_reading[];
double rsi_reading[];
double cci_reading[];
double ao_reading[];

紧接着，我们为文件创建一个名称。

//---File name
string file_name = "Market Data.csv";

现在我们定义要获取多少数据。

//---Amount of data requested
int size = 3000;

开始开发我们的OnStart事件处理程序时，第一次调用时涉及我们指定技术指标的初始化。

//---Setup our technical indicators
ma_handle = iMA(_Symbol,PERIOD_CURRENT,20,0,MODE_EMA,PRICE_CLOSE);
rsi_handle = iRSI(_Symbol,PERIOD_CURRENT,60,PRICE_CLOSE);
cci_handle = iCCI(_Symbol,PERIOD_CURRENT,10,PRICE_CLOSE);
ao_handle = iAO(_Symbol,PERIOD_CURRENT);

继续执行脚本，接下来的任务是将指标句柄中的值转移到相应的数据结构中。这一关键过程包括将指标输出精确映射到预先建立的数据结构中。

//---Set the values as series
CopyBuffer(ma_handle,0,0,size,ma_reading);
ArraySetAsSeries(ma_reading,true);
CopyBuffer(rsi_handle,0,0,size,rsi_reading);
ArraySetAsSeries(rsi_reading,true);
CopyBuffer(cci_handle,0,0,size,cci_reading);
ArraySetAsSeries(cci_reading,true);
CopyBuffer(ao_handle,0,0,size,ao_reading);
ArraySetAsSeries(ao_reading,true);

当我们准备启动文件写入操作时，一个关键的前置步骤是在脚本中建立一个文件句柄。

//---Write to file
int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

随后，我们的脚本进入了一个关键阶段，即系统地遍历数据集，精心组织将数据写入指定CSV文件的过程。这一迭代过程包括对每个数据点的详细检查和提取，需遵循与已创建参数顺序相一致的原则。

for(int i=-1;i<=size;i++){
      if(i == -1){
            FileWrite(file_handle,"Open","High","Low","Close","MA 20","RSI 60","CCI 10","AO");
      }
      
        else{
                FileWrite(file_handle,iOpen(_Symbol,PERIOD_CURRENT,i),
                                        iHigh(_Symbol,PERIOD_CURRENT,i),
                                        iLow(_Symbol,PERIOD_CURRENT,i),
                                        iClose(_Symbol,PERIOD_CURRENT,i),
                                        ma_reading[i],
                                        rsi_reading[i],
                                        cci_reading[i],
                                        ao_reading[i]);
      } 
}

完成脚本设置后，请在您选择的交易品种上执行该脚本。随后，脚本将生成一个CSV文件，其格式如下例所示，从而提供所选交易品种相关数据的全面且结构化的表示。

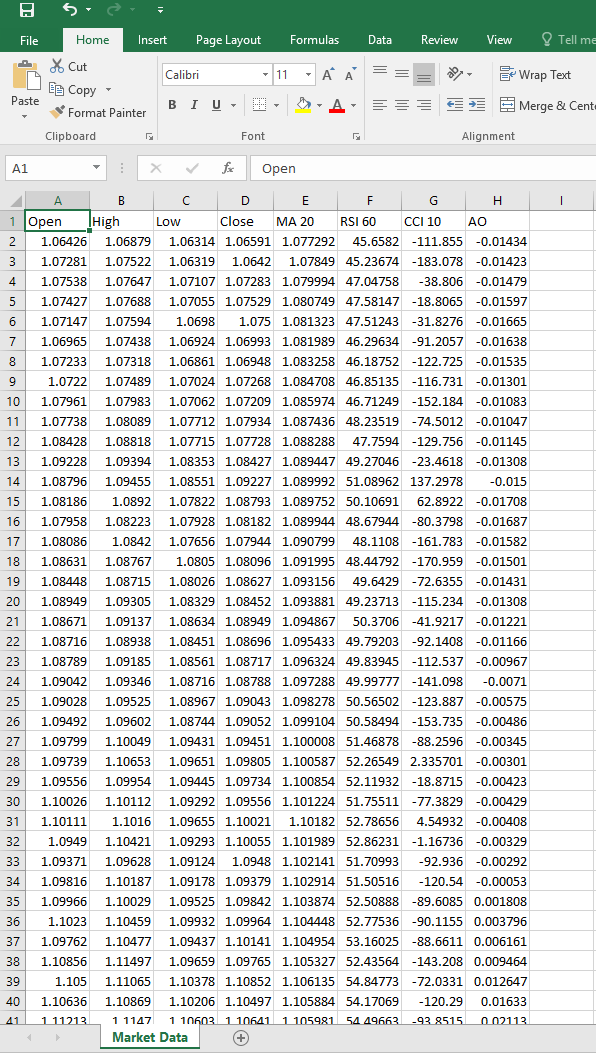
图7：我们的市场数据CSV文件

现在，我们的重点转向分析真实的市场数据，目标是构建一个回归模型，用于预测接下来15分钟内的预期价格变化。我们分析工作的核心标准是验证回归模型的真实性。一旦验证了模型的真实性，我们打算将验证后的模型导出为ONNX格式，随后利用它开发一个EA。

开始这一阶段，我们的第一步是加载必要的依赖项。在这些依赖项中，一个值得注意的添加项是“Arch”包，它以其全面的统计分析工具套件而闻名。整合“Arch”为我们提供了一系列在分析工作中极为宝贵的资源，加深了我们对市场数据分析的深度和复杂性。

import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from arch.unitroot import PhillipsPerron , ADF , KPSS
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import DoubleTensorType

然后我们读取由MQL5脚本创建的csv文件。

csv = pd.read_csv("/enter/your/path/here")

接着，我们确定目标，我们的目标是收盘价的增长。

csv["Target"] = csv["Close"] / csv["Close"].shift(-15)
csv.dropna(axis=0,inplace=True)

我们可以检查我们的数据集。

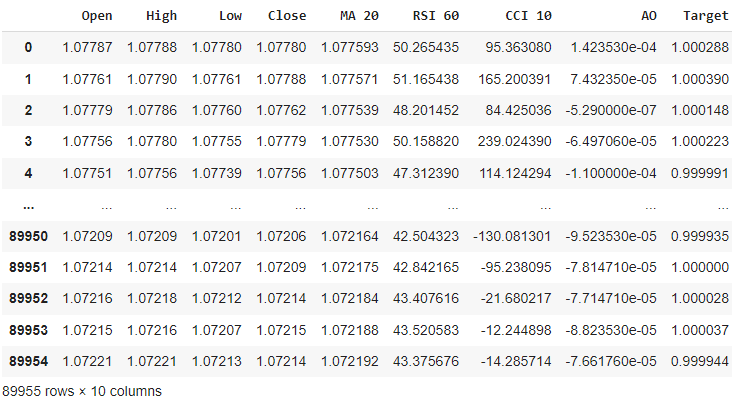
图8：使用Pandas读取我们的市场数据CSV文件

从那里开始，我们将准备数据的训练集和测试集

train = np.arange(0,20000)
test = np.arange(20020,89984)

现在我们将使用statsmodels进行多元线性回归拟合。

ols = sm.OLS(csv.loc[:,"Target"],csv.loc[:,["Open","High","Low","Close","MA 20","RSI 60","CCI 10","AO"]])
lm = ols.fit()
print(lm.summary())

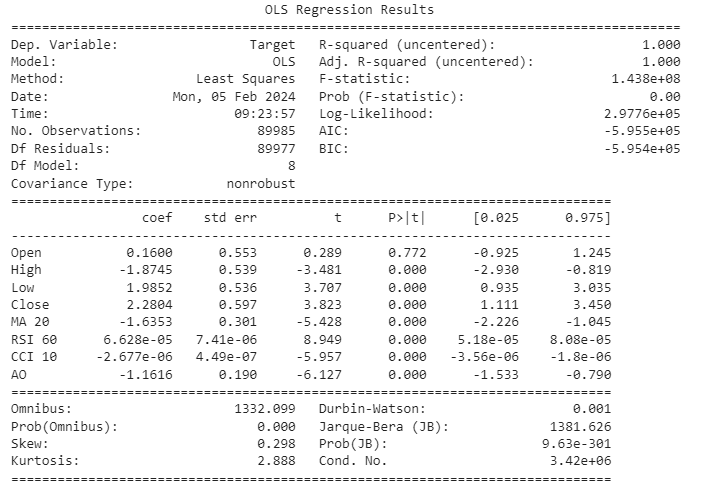
图9：使用所有变量预测价格增长的回归结果

让我们共同深入解读我们的模型结果。与开盘价特征相关的系数的置信区间包含0，这意味着其统计显著性不足。因此，我们决定从模型中排除这一特征，这是基于其贡献可能微不足道的考虑。进一步审查发现，相对强弱指数（RSI）和商品通道指数（CCI）的系数都接近0，它们各自的置信区间也接近这个值。鉴于此，我们谨慎地选择剔除这些特征，认为它们对信息量的边际贡献可能有限。

尽管我们的模型具有较高的R方值，代表着大部分方差来自模型中的特征，但同时考察的杜宾-沃森（DW）统计量却显示了一个较低的值。这促使我们采取谨慎的态度，因为低DW统计量表明可能存在残差相关性，这可能会损害我们模型的有效性。因此，我们主张对残差进行细致分析，特别是关注其平稳性。这一额外的审查层，对于确保模型在捕捉数据中的潜在模式的稳健性和可靠性至关重要。

让我们创建一个数据结构来存储我们认为可能重要的特征。

predictors = ["High","Low","Close","MA 20","AO"]

让我们记录下残差数据。

residuals = csv.loc[test[0]:test[-1],"Target"] - lm.predict(csv.loc[test[0]:test[-1],predictors])

让我们继续生成残差图，这是模型评估过程中的一个关键步骤。 

plt.plot(residuals)

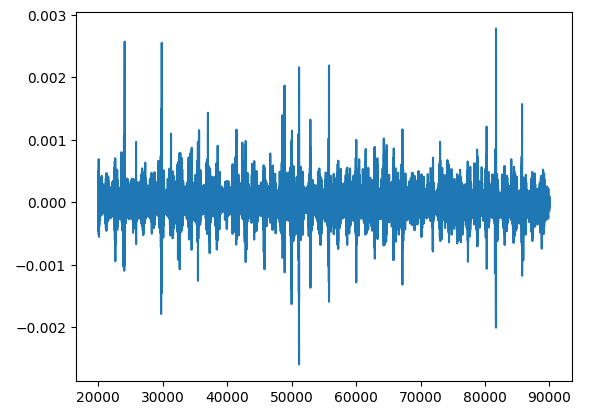
图10：绘制市场数据预测残差图

分析残差是了解模型拟合数据好坏的关键步骤。残差可以揭示模型是否存在系统误差或是否一直在犯同样的错误。这很重要，因为它有助于我们检查模型是否遵循某些基本规则，比如预测是否具有一致性变化，以及是否不依赖于先前的错误。

在查看残差时，我们需要留意的一件事是所谓的“单位根”。这基本上意味着残差随时间变化显示出一种不会消失的模式。这就像我们的误差中存在一种持续的趋势。在残差中发现单位根是一件大事，因为它会打乱我们对模型所做的一些基本假设，比如每个预测都是相互独立的。

处理单位根很重要，因为如果我们不这样做，它会破坏我们对模型好坏的估计，并使我们更难相信从模型中得出的结论。

因此，当我们深入研究残差时，我们不仅仅是在走形式。我们正在确保我们的模型经得起审查，并解决任何问题，如单位根，以使我们的预测更加可靠。

这样考虑可能会有所帮助：想象一下分类一只猫的任务，这似乎是一项简单的工作。在理想情况下，如果我们对猫的理解代表了一个不变的真理，那么每个分类都将是完美的，如果我们绘制出这样一个理想模型的误差，我们将得到一条平稳且直的线，表示为y=常数。这条线象征着真理的恒定性，即猫在任何时间点都是猫，如果我们在任何时间点称它为猫，我们的误差就是0。

然而，如果分类器的性能下降，引入错误分类，导致残差偏离这种完美平稳状态。这种偏离对应于分类器与真理的偏离，并表现为残差的波动。非平稳性出现在将狗误标为猫或反之的情况，这反映了分类器对猫的定义特征把握的不确定性。

为了更深入地了解统计严谨性，请考虑残差中的单位根与时间序列分析中的非平稳性之间的联系。残差中存在单位根，类似于分类器缺乏知识，表明非平稳性，导致残差波动性增加。知识缺乏越严重，波动越明显，就像将狗误分类为猫或反之。

理解这些概念很重要，因为它有助于我们微调模型以做出更好的预测。因此，即使乍一看情况不错，也值得再次检查以确保我们的残差表现正常。请记住，没有适用于所有情况的统一测试，因此最好使用多种方法并观察残差中的整体趋势。

Phillip-Perron检测

菲利普斯-佩伦检验（Phillips-Perron Test）是一种用于计量经济学和时间序列分析的统计检验，用于评估时间序列数据集中是否存在单位根。单位根意味着时间序列变量具有随机趋势，因此是非平稳的。平稳性是许多统计分析中的关键假设，非平稳时间序列数据可能导致虚假回归结果。

菲利普斯-佩伦检验是迪基-福勒检验的一种变体，由彼得·C.B.菲利普斯（Peter C.B. Phillips）和皮埃尔·佩伦（Pierre Perron）于1988年提出。与迪基-福勒检验一样，菲利普斯-佩伦检验旨在通过检查时间序列变量随时间的变化行为来检测单位根的存在。

菲利普斯-佩伦检验的基本思想是对差分后的时间序列变量进行回归，以其滞后值为自变量。然后使用检验统计量来评估滞后变量的系数是否显著不同于0。如果系数显著不同于0，则表明有证据表明不存在单位根，并暗示时间序列是平稳的。

菲利普斯-佩伦检验的一个显著特点是它允许数据中存在某种形式的序列相关性和异方差性，而原始的迪基-福勒检验没有考虑这些因素。这使得菲利普斯-佩伦检验对现实世界中时间序列数据中可能存在的某些假设违反情况具有鲁棒性。

1. 零假设：菲利普斯-佩伦检验的零假设是时间序列变量包含单位根，意味着它是非平稳的。
2. 备择假设：备择假设是时间序列变量不包含单位根，表明它是平稳的。
3. 决策规则：如果计算出的检验统计量小于临界值，则拒绝存在单位根的零假设，表明有证据表明时间序列是平稳的。如果计算出的检验统计量大于临界值，则无法拒绝零假设，表明没有足够的证据得出时间序列是平稳的结论。

我们将使用arch库来执行菲利普斯-佩伦检验。

pp = PhillipsPerron(residuals)

我们可以获得总结性结果。Phillips-Perron 检验的总结性统计量

原假设：该过程包含一个单位根。
备择假设：该过程是弱平稳的。

让我们一起来解读这些结果。检验统计量为-73.916。这个值表示估计系数与假设值1（表示存在单位根）之间的标准差数量。在这种情况下，一个非常大的负检验统计量表明存在反对单位根存在的强烈证据，支持时间序列的平稳性。

与检验统计量相关的p值为0.000。p值是衡量反对原假设的证据大小的指标。p值为0.000意味着在假设原假设为真的情况下，观察到的检验统计量出现的可能性极低。从实际意义上讲，这个极小的p值提供了反对单位根存在的强烈证据。

鉴于p值非常低（0.000），你通常会在传统的显著性水平（例如0.05）下拒绝原假设。证据表明，由于p值低于所选的显著性水平，时间序列很可能是平稳的。综上所述，根据提供的结果，你有强有力的证据来拒绝单位根的原假设，这表明时间序列很可能是平稳的。然而，我们不能仅凭测试来做出决策，我们还希望观察不同测试中的集中趋势指标。

增广迪基-富勒检验

我们将使用arch库来执行增广迪基-富勒检验。

adf = ADF(residuals)

我们能获得总结性的统计量。增广迪基-富勒（ADF）检验的总结性统计量

零假设：该过程包含一个单位根。
备择假设：该过程是弱平稳的。

现在我们来解读这一结果。检验统计量为-31.300 。ADF检验统计与菲利普斯-佩伦（Phillips-Perron）检验一样，用于评估时间序列中是否存在单位根。在此情况下，非常大的负值表明有强有力的证据反对单位根存在的原假设，支持时间序列是平稳的这一观点。

相关的p值为0.000。与菲利普斯-佩伦检验类似，p值为0.000意味着在假设原假设（即存在单位根）为真的情况下，观察到的检验统计量出现的可能性极低。非常小的p值提供了反对原假设的强有力证据。

鉴于p值很低（0.000），你通常会在传统的显著性水平下拒绝原假设。增广迪基-富勒检验的证据支持时间序列很可能是平稳的这一结论。

Phillips-Perron检验和增广迪基-富勒检验都提供了强有力的证据来反对单位根的存在，表明时间序列很可能是平稳的。这两种检验结果相似是预料之中的，因为它们都是为评估时间序列数据的平稳性而设计的。选择使用哪种检验通常取决于数据的具体特征和检验的假设条件。在你的情况下，两种检验都表明时间序列是平稳的。

接下来，我们将模型导出为开放神经网络交换（ONNX）格式。

ONNX，即开放神经网络交换，是一种开放且可互操作的格式，用于表示机器学习模型。该格式由开源协作社区开发，能够在各种框架和工具之间无缝交换模型，促进了机器学习生态系统中的互操作性。它提供了一种标准化的方式来表示和传输训练好的模型，使得开发者能够更容易地在不同平台上部署模型，并将其集成到各种应用中。ONNX支持广泛的机器学习模型和框架，提高了模型开发和部署工作流程的灵活性和效率。

此代码段定义了一个名为'double_input'的变量的初始类型，该变量将在生成ONNX文件时使用。指定的类型为'DoubleTensorType'，表示输入数据应为双精度。输入张量的形状由DataFrame（假定名为'csv'）中用于预测的特征列数决定（使用'csv.loc[:, predictors].shape[1]'获取）。形状中的'None'表示第一维的大小（可能表示实例或样本的数量）在此阶段未固定。

initial_type_double = [('double_input', DoubleTensorType([None, csv.loc[:,predictors].shape[1]]))]

此代码段使用'convert_sklearn'函数将训练好的线性回归模型（'lm'）转换为ONNX表示。之前代码段中定义的'initial_type_double'变量指定了输入数据的预期类型为双精度。此外，'target_opset'参数设置为12，表示所需的ONNX运算符集版本。生成的'onnx_model_double'将是提供的线性回归模型的ONNX表示，适用于部署和与其他支持ONNX格式的框架互操作。

onnx_model_double = convert_sklearn(lm, initial_types=initial_type_double, target_opset=12)

此代码段指定了保存线性回归模型的ONNX表示的文件名（"EURUSD_ONNX"）。使用前面提到的'convert_sklearn'函数转换得到的ONNX模型将以此文件名存储，便于将来使用或部署时轻松识别和访问。

onnx_model_filename = "EURUSD_ONNX"

此代码段将之前定义的文件名（"EURUSD_ONNX"）与后缀"_Double.onnx"组合，创建一个新的文件名（"EURUSD_ONNX_Double.onnx"）。随后，使用'onnx.save_model'函数将ONNX模型（'onnx_model_double'）保存到具有所构建文件名的文件中。此过程确保表示双精度线性回归模型的ONNX模型被存储，并可以使用指定的文件名轻松引用。

onnx_filename=onnx_model_filename+"_Double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

在MetaQuotes Language 5（MQL5）中，利用集成的多功能MetaEditor为我们的ONNX文件构建EA。

在MetaQuotes Language 5（MQL5）中为ONNX文件开发EA涉及利用集成且多功能的MetaEditor的功能。EA是一个用MQL5编写的脚本，它能够在MetaTrader 5平台上实现自动化交易。在此文中，EA将与ONNX文件接口连接，促进机器学习模型与交易策略的无缝集成，从而基于预测分析增强决策过程。MetaEditor提供了一个全面的环境用于编写、测试和优化EA，确保在MetaTrader 5框架内高效部署和执行。

我们首先在MQL5中包含Trade库，这是MetaTrader 5（MT5）中用于处理交易操作的标准库。Trade库提供了预定义的函数和结构，便于执行各种交易活动，如开仓和平仓、管理订单以及处理与交易相关的事件。在EA中包含此库，能够简化和高效地实现MQL5代码中的交易逻辑和操作。

//Our trade class helps us open trades
#include <Trade\Trade.mqh>
CTrade Trade;

这段MQL5代码片段涉及到一个EA的应用，并且整合了一个ONNX模型用于预测分析。代码中使用了#resource指令，将名为“EURUSD_ONNX_Double.onnx”的ONNX模型文件嵌入到EA的资源中，作为一个名为ONNXModel的字节数组。这样做可以方便地在EA内部访问和使用这个机器学习模型。

变量ONNXHandle被初始化为INVALID_HANDLE，表明它将用于存储与ONNX模型相关联的句柄或标识符，这个句柄将在EA执行过程中加载模型时被赋予。

另外，PredictedMove被初始化为-1，这意味着基于ONNX模型的预测移动或结果尚未确定。这个变量很可能在EA通过ONNX模型处理相关数据后被更新为预测值。预测逻辑和后续处理的具体细节将取决于EA代码的后续部分。

//Loading our ONNX model
#resource "ONNX\\EURUSD_ONNX_Double.onnx" as uchar EURUSD_ONNX_MODEL[]
long     ONNXHandle=INVALID_HANDLE;

在这段MQL5的EA代码中，声明了两组变量：一组用于移动平均线（ma_handle 和 ma_reading[]），另一组用于Awesome振荡器（ao_handle 和 ao_reading[]）。

变量 ma_handle 作为移动平均线指标的引用或标识符，允许智能交易系统与这个特定的技术分析工具进行交互并检索相关信息。数组 ma_reading[] 用于存储移动平均线的计算值，这样EA就可以访问并分析这些历史值以做出决策。

类似地，变量 ao_handle 被期望代表神奇振荡器指标的标识符，而数组 ao_reading[] 则被指定用于存储相应的计算值。 

//Handles for our technical indicators and dynamic arrays to store their readings
int ma_handle;
double ma_reading[];
int ao_handle;
double ao_reading[];

//Inputs
int input sl_width = 150; //How wide should the stoploss be?
int input  positions = 1; //How many positions should the we open?
int input lot_multiple = 1; //How many times greater than minimum lot should each position be?

//Symbol variables
double min_volume;
double bid,ask;

//We'll use this time stamp to keep track of the number of candles passing
static datetime time_stamp;

//Our model's forecast will be stored here
vector model_forecast(1);

OnInit 函数

OnInit() 函数是 MQL5 中EA的关键部分，它作为初始化函数，在将 EA 附加到 MetaTrader 5 的图表上时会自动执行。在这个函数中，通常会执行与 EA 设置和准备相关的各种任务。我们将要检查的其余代码嵌套在我们的 OnInit() 处理程序中。

在 EA 的 OnInit() 函数中的这个条件语句检查交易品种是否为 "EURUSD"，并且图表的时间框架是否设置为 M1（一分钟）。如果条件不满足，EA 会使用 Print() 函数在控制台打印一条消息，指出模型必须专门在一分钟时间框架上使用 "EURUSD" 货币对进行操作。随后，如果未满足指定条件，则使用 return(INIT_FAILED) 语句来终止 EA 的初始化过程，表明初始化失败。

int OnInit(){
    //Validating trading conditions
   if(_Symbol!="EURUSD" || _Period!=PERIOD_M1)
     {
      Print("Model must work with EURUSD on the M1 timeframe");
      return(INIT_FAILED);
     }

在MQL5中EA代码段中，以下部分负责从静态缓冲区创建一个ONNX模型。为了实现这一目的，使用了OnnxCreateFromBuffer函数，该函数接收存储在ONNXModel缓冲区中的ONNX模型数据，并使用默认设置来创建模型。

执行后，ONNXHandle变量被赋予与创建的ONNX模型相关联的句柄或标识符。随后，一个条件语句检查ONNXHandle是否为一个有效的句柄（不等于INVALID_HANDLE）。如果句柄无效，EA通过Print()函数向控制台打印一条错误信息，提供关于所遇错误的详细信息（通过GetLastError()获取），然后通过返回INIT_FAILED来提示初始化失败。

确实，这段代码对于EA初始化至关重要，因为它负责确保成功地在缓存区创建一个功能性的ONNX模型。此过程中如果发生任何问题都能及时得到反馈。

ONNXHandle=OnnxCreateFromBuffer(ONNXModel,ONNX_DEFAULT);

if(ONNXHandle==INVALID_HANDLE)
{
   Print("OnnxCreateFromBuffer error ",GetLastError());
   return(INIT_FAILED);
}

该行代码声明了一个名为input_shape的常量数组，该数组包含两个元素。这个数组被标记为长整型（long），用于存储整数。数组元素代表机器学习模型或算法输入数据的结构。在这种特定情况下，input_shape数组被初始化为值{1, 5}，表明输入数据预计是一行五列的格式。

//Defining the model's input shape
const long input_shape[] = {1,5};

在MQL5中的EA中，这段代码块表示使用OnnxSetInputShape函数检查ONNX模型设置输入格式是否合规。输入格式由input_shape数组指定，该数组表示输入数据的预期维度。

使用if语句评估OnnxSetInputShape函数条件的否定情况（如果设置失败则返回true）是否成立。如果条件成立，则EA使用Print()函数向控制台打印一条错误消息，该消息通过GetLastError()函数获得的错误信息来传达遇到的详细问题。随后，函数返回INIT_FAILED，表示初始化失败。

if(!OnnxSetInputShape(ONNXHandle,ONNX_DEFAULT,input_shape)) 
{
    Print("OnnxSetInputShape error ",GetLastError());
    return(INIT_FAILED); 
}

这段代码声明了一个名为output_shape的常量数组，该数组包含两个元素。与之前声明的input_shape类似，这个数组的类型是long，用于存储整数。在这个例子中，output_shape被赋值为{1, 1}，这表明机器学习模型输出的数据预期格式是一个具有单个元素的一维数组。

指定输出格式对于正确处理和解释机器学习模型生成的结果至关重要。 

//Defining the model's output shape
const long output_shape[] = {1,1};

在MQL5的EA中，这段代码块通过OnnxSetOutputShape函数检查为ONNX模型设置输出数据格式是否成功。输出格式由output_shape数组指定，该数组表示输出数据的预期维度。

if语句判断OnnxSetOutputShape函数条件的否定（如果设置不成功则返回true）是否成立。如果条件成立，则EA使用Print()函数向控制台打印一条错误消息，该消息通过GetLastError()函数获得的错误信息来传达遇到的详细问题。随后，函数返回INIT_FAILED，表示初始化失败。

与设置输入数据的格式类似，配置模型输出数据的格式同EA下游数据处理要求的格式保持一致至关重要。 

if(!OnnxSetOutputShape(ONNXHandle,0,output_shape))
{
    Print("OnnxSetOutputShape error ",GetLastError());
    return(INIT_FAILED);
}

在EA的OnInit()函数的这部分代码中，初始化两个技术指标。

1. ma_handle被赋予了一个基于指定品种（_Symbol）的一分钟图表（PERIOD_M1）上按收盘价（PRICE_CLOSE）计算的，周期为20的指数移动平均（EMA）的句柄或标识符。
2. ao_handle 被赋予了同一个品种的一分钟图表上计算的Awesome振荡器（AO）指标的句柄。
3. min_volume是经纪商允许的最小合约规模。

//Setting up our technical indicators
ma_handle = iMA(_Symbol,PERIOD_M1,20,0,MODE_EMA,PRICE_CLOSE);
ao_handle = iAO(_Symbol,PERIOD_M1);
min_volume = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
return(INIT_SUCCEEDED);
}

OnDeinit函数

在MQL5的EA中，OnDeinit 函数负责处理EA的去初始化过程。当EA被移除或交易终端被关闭时，该函数会自动执行。

在这个函数内部，一个条件语句会检查 ONNXHandle 变量是否持有一个有效的句柄（即不等于 INVALID_HANDLE）。如果条件为真，这意味着在EA的生命周期内，ONNX模型已经被初始化。在这种情况下，会调用 OnnxRelease 函数来释放与ONNX模型相关联的资源，随后将 ONNXHandle 设置为 INVALID_HANDLE。

这个去初始化例程确保了资源的正确释放，防止内存泄漏，并有助于提升EA全生命周期内的整体效率和资源利用率。这反映了一种负责任的编码习惯，即在EA执行期间管理和释放所获取的资源，从而增强了交易系统的健壮性和可靠性。

void OnDeinit(const int reason)
  {
      //OnDeinit we should freeup resources we don't require
      //We'll begin by releasing the ONNX models then removing the Expert Advisor
      if(ONNXHandle!=INVALID_HANDLE)
     {
      OnnxRelease(ONNXHandle);
      ONNXHandle=INVALID_HANDLE;
     }
   //Lastly remove the Expert Advisor
   ExpertRemove();
  }

OnTick 函数

在MQL5de EA中，OnTick 函数是至关重要的一环，它代表了每当接收到新的行情数据时执行的代码。在这个函数中：

使用 CopyBuffer 函数从移动平均（MA）和Awesome振荡器（AO）指标中获取历史数据。最近10个值被复制到数组（ma_reading 和 ao_reading）中，并使用 ArraySetAsSeries 函数将数组组织成类似序列的形式。

使用 iTime 函数获取指定品种（_Symbol）的一分钟图表（PERIOD_M1）上的当前时间戳（current_time）。

一个条件语句会检查当前时间戳是否与存储的时间戳（time_stamp）不同。如果存在差异，表明收到了新的行情数据，此时会调用 ModelForecast 函数。

这种代码结构使得EA能够在每个行情数据到来时捕获和组织最近的指标值，从而通过 ModelForecast 函数定期评估机器学习模型的预测。因此，OnTick 函数为基于最新市场状况和模型预测进行实时决策奠定了基础，有助于EA实现动态和自适应的特性。

void OnTick()
{
   //Update the arrays storing the technical indicator values to their current values
   //Then set the arrays as series so that the current reading is at the top and the oldest reading is last
   CopyBuffer(ma_handle,0,0,10,ma_reading);
   ArraySetAsSeries(ma_reading,true);
   CopyBuffer(ao_handle,0,0,10,ao_reading);
   ArraySetAsSeries(ao_reading,true);
   ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK);
   bid = SymbolInfoDouble(_Symbol,SYMBOL_BID);
//Update time marker
   datetime current_time = iTime(_Symbol,PERIOD_M1,0);
   //Periodically make forecasts if we have no open positions
   if(time_stamp != current_time){
      //No open positions
      if(PositionsTotal() == 0){
               ModelForecast();
      }  
      //We have open positions to manage
      else if(PositionsTotal() > 0){
               ManageTrade();
      }
   }
  }

模型推理

在MQL5 EA中，ModelForecast 函数旨在执行机器学习模型，以根据当前市场条件进行预测。以下是代码的详细说明：

在函数内部声明了两个向量：

1. model_forecast：用于存储机器学习模型的输出，即其预测或预报结果。
2. model_input：包含模型所需的输入特征。这些特征包括当前K线的高价、低价和收盘价，移动平均值（ma_reading[0]），以及Awesome振荡器的值（ao_reading[0]）。

调用 OnnxRun 函数使用ONNX模型（ONNXHandle）进行推理。ONNX_NO_CONVERSION 标志表示在推理过程中不进行数据类型转换。提供输入特征（model_input），并将推理结果存储在 model_forecast 向量中。

一个条件语句会检查推理过程是否成功。如果不成功，则使用 Print() 函数将错误信息打印到控制台，并通过 GetLastError() 函数获取并传达遇到的错误的详细信息。

如果推理成功，则将存储在 model_forecast 向量中的预测结果打印到控制台。

此函数封装了根据当前市场条件获取模型预测的基本步骤，从而在专家顾问中促进了动态和自适应的交易策略。通过包含错误处理机制，增强了系统的健壮性，为推理过程中可能出现的问题提供了注释。一旦完成，该函数将调用 NextMove() 函数。

//This function provides these utilities:
//          1) Inferencing using our ONNX model 
//          2) Calling the next function responsible for intepreting model forecasts and other subroutines
void ModelForecast(void){
      //These are the inputs for our ONNX model:
      //          1)High 
      //          2)Low
      //          3)Close
      //          4)20 PERIOD MA MODE: EMA  APPLIED_PRICE:PRICE CLOSE 
      //          5)Awesome Oscilator
      vector model_input{iHigh(_Symbol,PERIOD_M1,0),iLow(_Symbol,PERIOD_M1,0),iClose(_Symbol,PERIOD_M1,0),ma_reading[0],ao_reading[0]};
      //Inferencing with our model
      if(!OnnxRun(ONNXHandle,ONNX_NO_CONVERSION,model_input,model_forecast)){
            Print("Error performing inference: ",GetLastError());
      }
      //Pring model forecast to the terminal
      else{
               Print(model_forecast);
                NextMove();
      }
}

模型解析

为了解析我们的模型，需要完成两项工作：

1. 获取并解析模型输出：该函数使用 InterpretForecast 函数来解析预测模型的输出。InterpretForecast 函数被调用两次，第一次传入参数 1，第二次传入参数 -1。这些调用的目的是检查模型输出是否指示了特定方向：1 表示正面预测，-1 表示负面预测。
2. 根据解析结果采取行动：根据对模型输出的解析，该函数采取特定行动。如果模型预测正面结果（1），则调用 CheckOrder 函数并传入参数 1，然后返回。如果模型预测负面结果（-1），则调用 CheckOrder 函数并传入参数 -1。

综上所述，NextMove 函数旨在处理预测模型的输出，根据特定值（1 或 -1）对其进行解析，并通过使用解析后的值调用 CheckOrder 函数来采取相应行动。

//This function provides these utilities:
//          1) Getting the model output intepreted
//          2) Acting on the intepretations
void NextMove(){
      if(InterpretForecast(1)){
            CheckOrder(1);
            return;
      }     
      else if(InterpretForecast(-1)){
            CheckOrder(-1);
      }
}

InterpretForecast 函数的目的是根据指定的方向来解析预测模型的输出。该函数接受一个名为 direction 的参数，该参数可以是 1 或 -1。解析的结果取决于模型预测的值是否大于 1 或小于 1。

以下是代码的详细解析：

如果 direction 等于 1，函数会检查数组 model_forecast 的第一个元素（model_forecast[0]）是否大于 1。如果是，函数返回 true，表示模型预测的增长高于当前价格。

如果 direction 等于 -1，函数会检查数组 model_forecast 的第一个元素（model_forecast[0]）是否小于 1。如果是，函数返回 true，表示模型预测的增长低于当前价格。

如果 direction 既不是 1 也不是 -1，函数返回 false。这作为一个默认情况，表示指定的方向未被识别，函数无法提供有意义的解析。

综上所述，InterpretForecast 函数根据指定的方向检查模型的预测值，如果满足条件则返回 true，否则返回 false。

//This function provides these utilities:
//          1) Check whether the model forecasted a reading greater than or less than 1.
bool InterpretForecast(int direction){
      //1 means check if the model is forecasting growth greater than the current price
      if(direction == 1){
            return(model_forecast[0] > 1);
      }
      //-1 means check if the model is forecasting growth less than the current price
      if(direction == -1){
            return(model_forecast[0] < 1);
      }
      //Otherwise return false.
      return false;
}

订单执行

以下代码定义了 CheckOrder 函数。该函数负责根据指定的订单方向来执行交易。

验证开仓情况：初始的条件语句（PositionsTotal() == 0）作为一个先决条件检查，确保只有在投资组合中没有未平仓头寸时才开设新的头寸。

执行买入：如果 order_direction 参数等于 1（表示买入），该函数将使用一个 for 循环来迭代执行所需数量的头寸（positions）。在循环中，会调用 Trade.PositionOpen 函数来初始化买入头寸。该函数会接收相关参数，如交易品种（_Symbol）、订单类型（ORDER_TYPE_BUY）、交易量（min_volume * lot_multiple）和执行价格（ask）。

执行卖出订单：相反，如果 order_direction 参数等于 -1（表示卖出订单），并且当前没有未平仓的头寸（重新评估 PositionsTotal() == 0），该函数将通过类似的迭代过程来开设卖出头寸。再次使用 Trade.PositionOpen 函数，但参数会针对卖出头寸进行调整。

综上所述，CheckOrder 函数在确保没有现有头寸的情况下，根据指定的订单方向按规则执行交易。该代码将交易逻辑封装在算法交易策略中。

//This function is responsible for opening positions
void CheckOrder(int order_direction){
      //Only open new positions if we have no open positions
     if(PositionsTotal() == 0){
            //Buy
            if(order_direction == 1){
                  //Iterate over the desired number of positions
                  for(int i = 0; i < positions; i++){
                           Trade.PositionOpen(_Symbol,ORDER_TYPE_BUY,min_volume * lot_multiple,ask,0,0,"Volatitlity Doctor AI");
                  }
            }
            //Sell
            else if(order_direction == -1 && PositionsTotal() == 0){
                  //Iterate over the desired number of positions
                  for(int i = 0; i < positions; i++){
                        Trade.PositionOpen(_Symbol,ORDER_TYPE_SELL,min_volume  * lot_multiple ,bid,0,0,"Volatitlity Doctor AI");
            }
         }
   }
}

交易管理

ManageTrade 函数作为核心的交易管理模块，负责将调整止损（Stop Loss）和止盈（Take Profit）水平的任务委托给 CheckStop 函数。

CheckStop 函数会遍历所有已开仓的头寸，提取相关信息，如交易品种、订单编号、头寸类型、当前的止损水平和头寸的开仓价格。它确保头寸的交易品种与当前正在交易的品种（_Symbol）相匹配。对于每个有效的头寸，代码会根据预定参数（如买入价和卖出价、止损宽度 sl_width 以及点值 _Point）来计算新的止损和止盈水平。

然后，该函数会区分买入和卖出操作。对于执行买入操作，它基于卖出价来计算新的止损和止盈水平，并且仅在新的水平更有利时才进行调整。类似地，对于卖出操作，计算基于买入价，并且仅在新的水平更有利时才进行调整。

使用 NormalizeDouble 函数可以确保计算出的价格符合指定的数字位数（_Digits）。如果确实有必要，则使用 Trade.PositionModify 函数来修改现有订单，更新其止损和止盈水平。

//This function handles our trade management
void ManageTrade(){
   CheckStop();
}

//This funciton will update our S/L & T/P 
void CheckStop(){
      //First we iterate over the total number of open positions                      
      for(int i = PositionsTotal() -1; i >= 0; i--){
            //Then we fetch the name of the symbol of the open position
            string symbol = PositionGetSymbol(i);
            //Before going any furhter we need to ensure that the symbol of the position matches the symbol we're trading
                  if(_Symbol == symbol){
                           //Now we get information about the position
                           ulong ticket = PositionGetInteger(POSITION_TICKET); //Position Ticket
                           double position_price = PositionGetDouble(POSITION_PRICE_OPEN); //Position Open Price
                           long type = PositionGetInteger(POSITION_TYPE); //Position Type
                           double current_stop_loss = PositionGetDouble(POSITION_SL); //Current Stop loss value
                           //If the position is a buy
                           if(type == POSITION_TYPE_BUY){
                                  //The new stop loss value is just the ask price minus the stop we calculated above
                                  double new_stop_loss = NormalizeDouble(ask - ((sl_width * _Point) / 2) ,_Digits);
                                  //The new take profit is just the ask price plus the stop we calculated above
                                  double new_take_profit = NormalizeDouble(ask + (sl_width * _Point),_Digits);
                                  //If our current stop loss is less than our calculated stop loss 
                                  //Or if our current stop loss is 0 then we will modify the stop loss and take profit
                                 if((current_stop_loss < new_stop_loss) || (current_stop_loss == 0)){
                                       Trade.PositionModify(ticket,new_stop_loss,new_take_profit);
                                 }  
                           }
                            //If the position is a sell
                           else if(type == POSITION_TYPE_SELL){
                                  //The new stop loss value is just the ask price minus the stop we calculated above
                                  double new_stop_loss = NormalizeDouble(bid + ((sl_width * _Point)/2),_Digits);
                                  //The new take profit is just the ask price plus the stop we calculated above
                                  double new_take_profit = NormalizeDouble(bid - (sl_width * _Point),_Digits);
                                 //If our current stop loss is greater than our calculated stop loss 
                                 //Or if our current stop loss is 0 then we will modify the stop loss and take profit 
                                 if((current_stop_loss > new_stop_loss) || (current_stop_loss == 0)){
                                       Trade.PositionModify(ticket,new_stop_loss,new_take_profit);
                                 }
                           }  
                  }  
            }
}

我们的EA将在其菜单中包含这些参数。

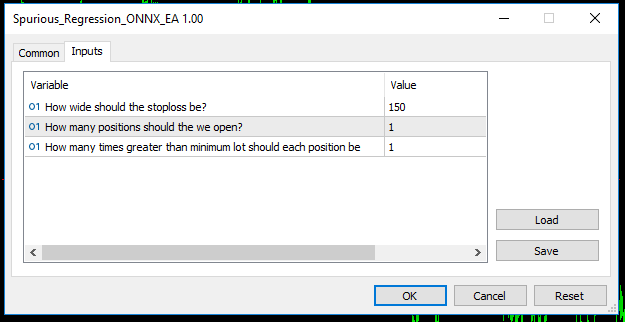
图11：我们的EA

并且应该自动为每个开仓订单设置止损和止盈水平。

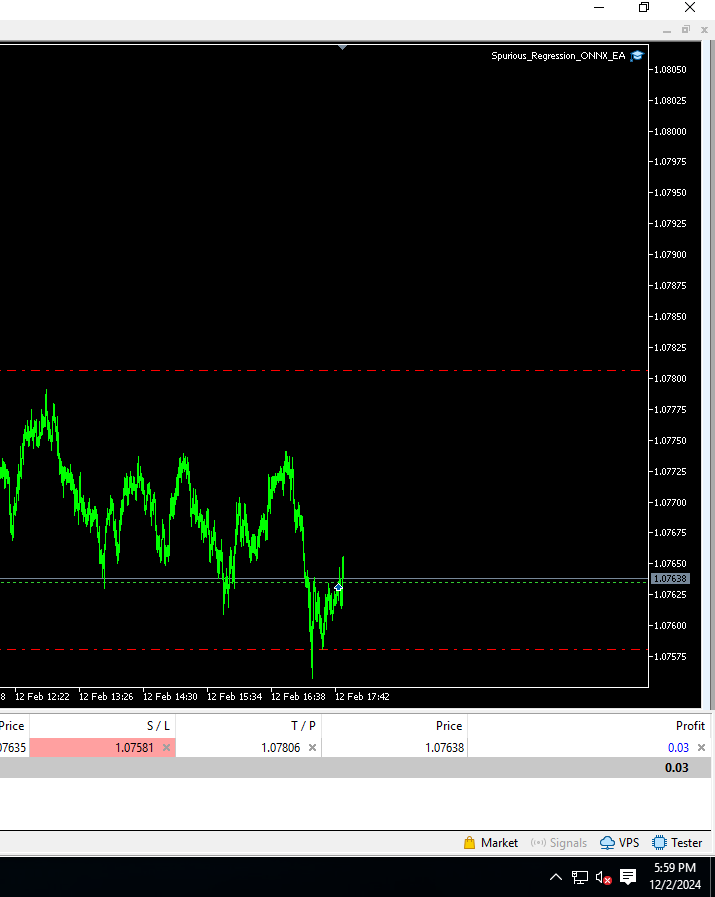
图12：我们运行中的EA

结论

总之，在时间序列数据的建模中，伪回归性对其构成了重大挑战，经常导致误导性和不可靠的结果。研究人员和从业者在解释回归结果时必须谨慎，尤其是在处理非平稳时间序列数据时。为了降低伪回归的风险，采用适当的统计技术至关重要，如单位根检验、协整分析和使用平稳变量。此外，采用先进的时间序列方法，如误差修正模型，可以增强回归分析的稳健性，并有助于得出更准确和有意义的解释。最终，研究人员在面对潜在的伪相关性时，要想得出可靠和有效的回归结果，就必须对基础数据的性质有细致的了解，并严格应用统计方法。