MetaTrader 5 / 积分
English Русский Español Deutsch 日本語 Português
preview
MQL5 中的范畴论 (第 2 部分)

MQL5 中的范畴论 (第 2 部分)

MetaTrader 5 — 积分 | 12 六月 2023, 10:41
737 0
Stephen Njuki
Stephen Njuki

概述

这是上一篇关于 MQL5 中范畴论讲义的延续。 回顾一下，我们所介绍的范畴论是作为数学的一个分支，它对组织和分类信息特别有用。 在此背景下，我们讨论了范畴论的一些基本概念，以及如何将其应用于金融时间序列数据的分析。 具体来说，我们研究了元素、域和态射。 元素是范畴论体系中信息的基本单位，它们通常被认为是一个集合的成员，且在这些系列中被视作一个域。 一个域可以通过称为态射的过程与其它域建立关系。 在这篇文章中，我们将首先通过查看恒等公理、关联公理、交换图，来详述类别的构成。 在进行的过程中，贯穿全文，我们将实验示例，并高亮显示非类别的示例。 最后，我们将介绍本体日志。

在我们深入研究范畴的公理定义之前，先看看一些“在行动中”类别的日常示例可能会有所帮助。 我们已经定义了域及其包含的元素。 故此，如果一开始我们把一个类别作为相关域的集合，那么以下内容可以作为说明性示例。

    • 交通方式的类别，其域代表不同的交通方式（例如汽车、飞机和火车、等）。 每个域的元素将代表各自种类的运输工具。 例如，在汽车类别中，我们可以有共享车、汽车租赁、私家车、出租车；而在飞机类别中，我们可以拥有私人飞机、商业飞机、租赁飞机；对于列车类别，我们能包含有轨电车、子弹头列车、蒸汽机车、等。 然后，它们之间的态射可用于定义完整的旅行行程。 例如，如果您乘坐 lyft （译者按：共享车连锁品牌）前往机场，乘坐商务航班，然后从该机场乘坐子弹头列车前往目的地，那么这些选择中的每一个都可以轻松映射到此类别中。  
    • 一顿饭的类别，其域代表每道菜的菜单。 若我们说要准备 5 道菜，即：开胃菜、汤、主菜、甜点和奶酪。 在这种情况下，每个域的元素将是菜单上相应那道菜的食物项目。 例如，开胃菜可以在其域（菜单）中包含选择：蜜饯胡萝卜配蜂蜜、小茴香和辣椒粉；或塞满罗马佩克立诺、大蒜和面包屑的蘑菇；或烧西兰花配西司椒和腌洋葱；同样明智的汤可以有：托斯卡纳白豆和烤大蒜汤；或南瓜鼠尾草浓汤；或冷瓜和罗勒汤。 这些菜单项中的每一个都代表其域中的一个元素。 与其类似，它们之间的态射将用于定义餐厅顾客选择的完整餐点。 例如，如果客户有蜜饯胡萝卜，然后是南瓜，以及所有其它菜品，那么上述每个选项都可以轻松地映射到该类别中。
    • 另一个类别示例可以是每周娱乐的类型。此处，我们的域可以是体育直播、电视流媒体和公园参观。 每个域的元素可以是：体育直播域的 NFL，或 MLB，或 NBA；电视流媒体域的 Netflix，或 HBO，或 AMC；参观公园域的迪斯尼，或动物园，或天然公园。 如此观众可随意从每个域中选择参加的体育比赛，观看的电视节目，和参观的公园。 选择的说明（态射）跨越了这些域，很容易就能映射此信息。

    如此，所有这些，显然还有更多的东西可以被范畴论记录下来。 但其终点是什么？有句话说“低能的工人总责怪他的工具”，我觉得这就是问题的关键。 因为用不用实际上是由用户决定的。 在我看来，范畴论批判性地运用了量化等价性。 这是我们在介绍基本概念之后将在后续文章中讨论的主题。 从表面来说，这就是为什么看起来可能毫不相关的分属两个不同主题的独立类别显现的原因，但在更深入的调查中发现它们是雷同或镜像对立的。 这些见解在决策中至关重要，因为在做出决策时您缺乏足够的信息。 但若是您有相关的类别，则可以弥合信息鸿沟。 


    识别

    同构是范畴论中同态的关键性质，因为它确保目标范畴域的结构在映射下得以保留。 它还保证保留源类别中域的代数运算。 例如，我们考虑一个服装类别，其中的域是衬衫和裤子，态射是将衬衫大小映射到裤子大小的函数。 此类别中的同态将保留衬衫尺寸与裤子相应尺寸的配对的功能。 而此类别中的同构将是一个函数，它不仅保留了尺寸的代数配对，而且还在衬衫和裤子的尺寸之间建立了一对一的对应关系。 这意味着对于任何尺寸的衬衫，只有一个对应的裤子尺寸，反之亦然。 举例来说，考虑将衬衫尺寸（例如“小”、“中”、“大”）映射到裤子尺寸（例如 “26”、“28”、“30”、“32”）的函数。 该函数是一个同态，因为它保留并定义了大小的配对（例如，“小”可以与 “26” 配对）。 但这不是同构，因为它没有在衬衫和裤子的尺寸之间建立一对一的对应关系，因为“小”也可以与 “28” 或 “26” 一起穿。 这里没有可逆性。


    non_iso


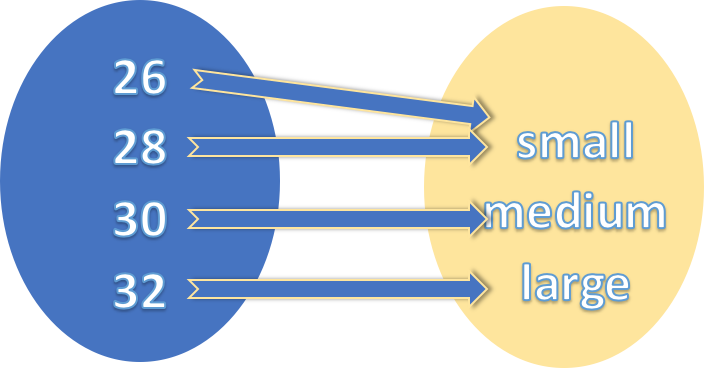
    另一方面，考虑将衬衫的尺寸（例如“小”、“中”、“大”）映射到裤子尺寸（例如 “28”、“30”、“32”）的函数。 这个函数不仅是同态，而且是同构，因为它也允许可逆性。


    iso


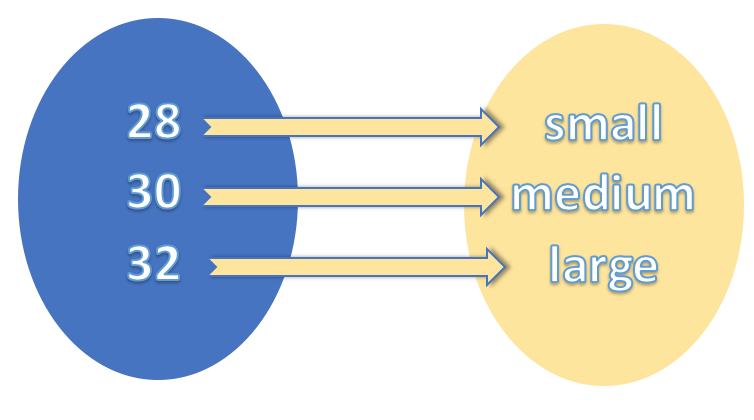
    在服装类别的示例中，域是衬衫和裤子，态射是将衬衫尺寸映射到裤子尺寸的函数，单个态射不能同构，因为所有单个态射本质上都是可逆的，并且存在“同构”。 同构的性质应对的是从一个域到一个协同域的一组态射（又名同态集），且仅当这个群的所有这些态射都可以逆转，同时保持同态的代数配对性质，它才能认为是存在。 这就是为什么在确认同构之前，列举域中的所有态射很重要的原因。 在不考虑所有可能态射的情况下，也许会出现两个对象是同构的，而实际上它们并非同构。 同构的前兆是域的基数。 对于两个域，此值必须相同。 如果域含有不匹配的基数，则它们之间的同态无法逆转，因为从一个域中，您将有多个元素映射到同一辅助元素。 因此，我们需要域之间的一组态射来定义同构。 典型情况是我们需要两个态射，一个从衬衫到裤子，另一个从裤子到衬衫，并在衬衫和裤子的尺寸之间建立一对一的对应关系。 这些态射应该是彼此逆反的，这意味着如果一个态射将“小”号的衬衫转换到 “28” 码的裤子上，另一个态射应该将 “28” 码的裤子逆转成“小”码的衬衫。 当我们复合这两个态射时，它应该为我们提供我们始建域的等同态射。

    范畴论中的这一公理要求推断出需要自映射态射。 然而，对于它们是否与界定一个类别有关，仍然存在争议。 

    接下来，我们来以 MQL5 解述同构。 我已经重写了第一篇文章中共享的大部分脚本，现在还包括模板。 从元素类到范畴类的所有类，都包含运用模板数据类型，从而实现了灵活性。 不过，我还“列举”了范畴类中可用的类型。 它们是：'datetime','string','double' 和 int。 “int” 类型是默认的，如果是诸如 “color” 之类的数据类型，就用到它。 所有代码都附在文末。 此处是我们新的同态类。

    //+------------------------------------------------------------------+
//| HOMO-MORPHISM CLASS                                              |
//+------------------------------------------------------------------+
template <typename TD,typename TC>
class CHomomorphism                 : public CObject
   {
      protected:
      
      int                           morphisms;
      
      public:
      
      CDomain<TD>                   domain;
      CDomain<TC>                   codomain;
      
      CMorphism<TD,TC>              morphism[];
      
      int                           Morphisms() { return(morphisms); }
      bool                          Morphisms(int Value) { if(Value>=0 && Value<INT_MAX) { morphisms=Value; ArrayResize(morphism,morphisms); return(true); } return(false); }
      
      bool                          Get(int MorphismIndex,CMorphism<TD,TC> &Morphism) { if(MorphismIndex>=0 && MorphismIndex<Morphisms()) { Morphism=morphism[MorphismIndex]; Morphism.domain=domain; Morphism.codomain=codomain; return(true); } return(false); }
      
                                    template <typename TDD,typename TDC>
      bool                          Set(int ValueIndex,CMorphism<TDD,TDC> &Value)
                                    {
                                       if
                                       (
                                       (string(typename(TD))!=string(typename(TDD)))
                                       ||
                                       (string(typename(TC))!=string(typename(TDC)))
                                       ||
                                       )
                                       {
                                          return(false);
                                       }
                                       // 
                                       if(ValueIndex>=0 && ValueIndex<Morphisms())
                                       {
                                          Value.domain=domain;
                                          Value.codomain=codomain;
                                       
                                          if(Index(Value)==-1)
                                          {
                                             morphism[ValueIndex]=Value;
                                             
                                             return(true);
                                          } 
                                       }
                                       
                                       return(false); 
                                    };
      
      
                                    template <typename TDD,typename TDC>
      int                           Index(CMorphism<TDD,TDC> &Value)
                                    {
                                       int _index=-1;
                                       //
                                       if
                                       (
                                       (string(typename(TD))!=string(typename(TDD)))
                                       ||
                                       (string(typename(TC))!=string(typename(TDC)))
                                       ||
                                       )
                                       {
                                          return(_index);
                                       }
                                       // 
                                       for(int m=0; m<morphisms; m++)
                                       {
                                          if(MorphismMatch(Value,morphism[m]))
                                          {
                                             _index=m; break;
                                          }
                                       }
                                       
                                       return(_index);
                                    }
      
                                    CHomomorphism(void){  Morphisms(0); };
                                    ~CHomomorphism(void){};
   };

    为了测试同构，我们取上一篇文章中所用的相同域，并将通过 “IsIsomorphic” 函数运行它们。 该函数返回一个布尔值，其中 true 表示成功，而 false 表示失败。 

    //+------------------------------------------------------------------+
//| Get Isomorphisms function                                        |
//+------------------------------------------------------------------+
template <typename TD,typename TC>
bool IsIsomorphic(CDomain<TD> &A,CDomain<TC> &B,CHomomorphism<TD,TC> &Output[])
   {
      if(A.Cardinality()!=B.Cardinality())
      {
         return(false);
      }
      
      int _cardinal=A.Cardinality();
      
      uint _factorial=MathFactorial(_cardinal);
      
      ArrayResize(Output,_factorial);
      
      for(uint f=0;f<_factorial;f++)
      {
         ArrayResize(Output[f].morphism,_cardinal);
         //
         for(int c=0;c<_cardinal;c++)
         {
            Output[f].morphism[c].domain=A;
            Output[f].morphism[c].codomain=B;
         }
      }
      
      int _index=0;
      CDomain<TC> _output[];ArrayResize(_output,_factorial);
      GetIsomorphisms(B, 0, _cardinal-1, _cardinal, _index, _output);
      
      for(uint f=0;f<_factorial;f++)
      {
         for(int c=0;c<_cardinal;c++)
         {
            CElement<TC> _ec;
            if(_output[f].Get(c,_ec))
            {
               for(int cc=0;cc<_cardinal;cc++)
               {
                  CElement<TC> _ecc;
                  if(B.Get(cc,_ecc))
                  {
                     if(ElementMatch(_ec,_ecc))
                     {
                        if(Output[f].morphism[c].Codomain(cc))
                        {
                           break;
                        }
                     }
                  }
               }
            }
            
            if(Output[f].morphism[c].Domain(c))
            {
            }
         }
      }
         
      return(true);
   }

    输出同态需要在现场指定，在我们的示例中，我们使用变量 “_h_i”。 这个输出值是同态类的数组，将包括两个输入域之间所有可能的同构同态的枚举。

          //IDENTITY
      CHomomorphism<int,int> _h_i[];
      //is evens isomorphic to odds?
      if(IsIsomorphic(_evens,_odds,_h_i))
      {
         printf(__FUNCSIG__+" evens can be isomorphic to odds by up to: "+IntegerToString(ArraySize(_h_i))+" homomorphisms. These could be... ");
         for(int s=0; s<ArraySize(_h_i); s++)
         {
            printf(__FUNCSIG__);
            
            string _print="";
            for(int ss=0; ss<ArraySize(_h_i[s].morphism); ss++)
            {
               _print+=PrintMorphism(_h_i[s].morphism[ss],0);
            }
            
            printf(_print+" at: "+IntegerToString(s));
         }
      }

    如果我们运行此代码，我们的日志应如下所示。

    2023.01.26 10:42:56.909 ct_2 (EURGBP.ln,H1)     void OnStart() evens can be isomorphic to odds by up to: 6 homomorphisms. These could be...
2023.01.26 10:42:56.909 ct_2 (EURGBP.ln,H1)     void OnStart()
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (0)|----->(1)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (2)|----->(3)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (4)|----->(5)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)      at: 0
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     void OnStart()
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (0)|----->(1)

2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (2)|----->(5)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (4)|----->(3)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)      at: 1
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     void OnStart()
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (0)|----->(3)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (2)|----->(1)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (4)|----->(5)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)      at: 2
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     void OnStart()
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (0)|----->(3)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (2)|----->(5)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (4)|----->(1)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)      at: 3
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     void OnStart()
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (0)|----->(5)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (2)|----->(3)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (4)|----->(1)
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)      at: 4
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     void OnStart()
2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1)     (0)|----->(5)
2023.01.26 10:42:56.911 ct_2 (EURGBP.ln,H1)     (2)|----->(1)
2023.01.26 10:42:56.911 ct_2 (EURGBP.ln,H1)     (4)|----->(3)
2023.01.26 10:42:56.911 ct_2 (EURGBP.ln,H1)      at: 5

    若这是一个偶数域，其打印是：

    2023.01.26 10:42:56.899 ct_2 (EURGBP.ln,H1)     void OnStart() evens are... {(0),(2),(4)}

    若这是一个奇数域，其打印是：

    2023.01.26 10:42:56.899 ct_2 (EURGBP.ln,H1)     void OnStart() odds are... {(1),(3),(5)}


    关联

    在范畴论中，关联公理是类别必须满足的基本性质之一。 使用服装类别的示例，其中域是特定的服装项目，诸如衬衫、裤子和鞋子，态射则是根据适用性与服装配对的函数。 关联公理，也称为“结合性定律”，表示态射组合是关联的。 这意味着在合成多个态射时，它们的应用顺序不会影响最终结果。

    例如，考虑态射“搭配穿”跨越所有 3 个服装域（衬衫、裤子和鞋子）。 若说我们有一个态射 f: T 恤 -> 纽扣衬衫，g: 纽扣衬衫 -> 牛仔裤，和 h: 牛仔裤 -> 运动鞋。 使用关联公理，我们可以将这些态射的组合定义为 h o (g o f) = (h o g) o f。 这意味着态射的顺序无关紧要，我们可以按任何我们想要的方式将它们分组在一起。这令类别的定义更简单，因为它允许我们避免计算多个态射的括号。 取而代之，我们可以将态射分组在一起，无论它们的顺序如何，最终结果将是相同的。

    我们看看在 MQL5 中它如何动作。 我们需要重新组合我在上一篇文章中共享的范畴类。

    //+------------------------------------------------------------------+
//| CATEGORY CLASS                                                   |
//+------------------------------------------------------------------+
class CCategory
   {
      protected:
      
      int                           domains_datetime;
      int                           domains_string;
      int                           domains_double;
      int                           domains_int;
      
      int                           ontologies;
      
      CDomain<datetime>             domain_datetime[];
      CDomain<string>               domain_string[];
      CDomain<double>               domain_double[];
      CDomain<int>                  domain_int[];
      
      COntology                     ontology[];
      
      public:
      
      int                           Domain(string T)
                                    { 
                                       if(T=="datetime"){ return(domains_datetime); }
                                       else if(T=="string"){ return(domains_string); }
                                       else if(T=="double"){ return(domains_double); }
                                       
                                       return(domains_int);
                                    };
      
      bool                          Domain(string T,int Value)
                                    { 
                                       if(Value>=0 && Value<INT_MAX)
                                       { 
                                          if(T=="datetime")
                                          { 
                                             if(ArrayResize(domain_datetime,Value)>=Value)
                                             {
                                                domains_datetime=Value;  
                                                return(true); 
                                             } 
                                          }
                                          else if(T=="string")
                                          { 
                                             if(ArrayResize(domain_string,Value)>=Value)
                                             {
                                                domains_string=Value;  
                                                return(true); 
                                             } 
                                          }
                                          else if(T=="double")
                                          { 
                                             if(ArrayResize(domain_double,Value)>=Value)
                                             {
                                                domains_double=Value;  
                                                return(true); 
                                             } 
                                          }
                                          else //if(T=="int")
                                          { 
                                             if(ArrayResize(domain_int,Value)>=Value)
                                             {
                                                domains_int=Value;  
                                                return(true);
                                             }  
                                          }
                                       } 
                                       
                                       return(false); 
                                    };
                                    
                                    
      int                           Ontology(){ return(ontologies); };
      bool                          Ontology(int Value){ if(Value>=0 && Value<INT_MAX){ ontologies=Value; ArrayResize(ontology,ontologies); return(true); } return(false); };
      
      
                                    template <typename T>
      bool                          Set(int ValueIndex,CDomain<T> &Value)
                                    {
                                       if(Index(Value)==-1 && ValueIndex>=0)
                                       {
                                          if
                                          (
                                          ValueIndex<Domain(string(typename(T)))
                                          ||
                                          (ValueIndex>=Domain(string(typename(T))) && Domain(string(typename(T)),ValueIndex+1))
                                          )
                                          {
                                             if(string(typename(T))=="datetime")
                                             {
                                                domain_datetime[ValueIndex]=Value;
                                                return(true);
                                             }
                                             else if(string(typename(T))=="string")
                                             {
                                                domain_string[ValueIndex]=Value;
                                                
                                                return(true);
                                             }
                                             else if(string(typename(T))=="double")
                                             {
                                                domain_double[ValueIndex]=Value;
                                                return(true);
                                             }
                                             else //if(string(typename(T))=="int")
                                             {
                                                domain_int[ValueIndex]=Value;
                                                return(true);
                                             }
                                          }
                                       }
                                       //
                                       return(false);
                                    };
                                    
                                    template <typename T>
      bool                          Get(int DomainIndex,CDomain<T> &D)
                                    {
                                       if(DomainIndex>=0 && DomainIndex<Domain(string(typename(T))))
                                       {
                                          if(string(typename(T))=="datetime")
                                          {
                                             D=domain_datetime[DomainIndex];
                                             
                                             return(true);
                                          }
                                          else if(string(typename(T))=="string")
                                          {
                                             D=domain_string[DomainIndex];
                                             
                                             return(true);
                                          }
                                          else if(string(typename(T))=="double")
                                          {
                                             D=domain_double[DomainIndex];
                                             
                                             return(true);
                                          }
                                          else //if(string(typename(T))=="int")
                                          {
                                             D=domain_int[DomainIndex];
                                             
                                             return(true);
                                          }
                                       }
                                       
                                       return(false);
                                    };
                                    
      bool                          Set(int ValueIndex,COntology &Value)
                                    {
                                       if
                                       (
                                       ValueIndex>=0 && ValueIndex<Ontology()
                                       )
                                       {
                                          ontology[ValueIndex]=Value;
                                          return(true);
                                       }
                                       else if(ValueIndex>=Ontology())
                                       {
                                          if(Ontology(Ontology()+1))
                                          {
                                             ontology[Ontology()-1]=Value;
                                             return(true);
                                          }
                                       }
                                       //
                                       return(false);
                                    };
                                    
      bool                          Get(int OntologyIndex,COntology &O)
                                    {
                                       if(OntologyIndex>=0 && OntologyIndex<Ontology())
                                       {
                                          O=ontology[OntologyIndex];
                                          
                                          return(true);
                                       }
                                       
                                       return(false);
                                    };
      
      
                                    template <typename T>
      int                           Index(CDomain<T> &Value)
                                    {
                                       int _index=-1;
                                       //
                                       for(int d=0; d<Domain(string(typename(T))); d++)
                                       {
                                          if(string(typename(T))=="string")
                                          {
                                             if(DomainMatch(Value,domain_string[d]))
                                             {
                                                _index=d; break;
                                             }
                                          }
                                          else if(string(typename(T))=="datetime")
                                          {
                                             if(DomainMatch(Value,domain_int[d]))
                                             {
                                                _index=d; break;
                                             }
                                          }
                                          else if(string(typename(T))=="double")
                                          {
                                             if(DomainMatch(Value,domain_double[d]))
                                             {
                                                _index=d; break;
                                             }
                                          }
                                          else if(string(typename(T))=="int")
                                          {
                                             if(DomainMatch(Value,domain_int[d]))
                                             {
                                                _index=d; break;
                                             }
                                          }
                                       }
                                       
                                       return(_index);
                                    }
      
      
      int                           Index(COntology &Value)
                                    {
                                       int _index=-1;
                                       //
                                       for(int o=0; o<Ontology(); o++)
                                       {
                                          if(!OntologyMatch(Value,ontology[o]))
                                          {
                                             _index=o; break;
                                          }
                                       }
                                       
                                       return(_index);
                                    }
      
                                    CCategory()
                                    { 
                                       domains_datetime=0; 
                                       domains_string=0; 
                                       domains_double=0; 
                                       domains_int=0; 
                                       
                                       ontologies=0; 
                                    };
                                    ~CCategory()
                                    { 
                                    };
   };

    请注意 “enumerated” 数据类型是允许的。 在以后的文章中，我将尝试将它们作为一个对象集成到单个数组之中，从而令它更整洁。 除了上一篇文章中用自然数填充域的函数之外，还添加了 “FillDomain” 函数。

    //+------------------------------------------------------------------+
//| Fill Domain(Set) with one-cardinal elements from input E array.  |
//+------------------------------------------------------------------+
template <typename TD,typename TE>
void FillDomain(CDomain<TD> &D,CElement<TE> &E[])
   {
      if(string(typename(TD))!=string(typename(TE)))
      {
         return;
      }
      
      int _cardinal=ArraySize(E);
      //
      if(_cardinal<0||INT_MAX<=_cardinal)
      {
         return;
      }
      
      //Set its cardinal to input array size
      if(D.Cardinality(_cardinal))
      {
         for(int c=0;c<_cardinal;c++)
         {
            D.Set(c,E[c],true);
         }
      }
   }

    故此，为了检查关联，我们将创建一个类别 “_ca”。 然后我们声明 3 个简单的字符串类型集合，每个都填充一种服装类型。 我们将这些集合（数组）复制到新的元素数组（'_et'、'_ep'、'_es'），然后将这些元素中的每一个添加到它自己的域（'_dt'、'_dp'、'_ds'）。 完成此操作后，我们将类别的域数设置为 3，然后继续按索引用新创建并填充了服装类型元素的域来设置。

          //ASSOCIATION
      CCategory _ca;
      
      string _tops[__EA]={"T-shirt","button-up","polo","sweatshirt","tank top"};          //domain 0
      string _pants[__EA]={"jeans","slacks","khakis","sweatpants","shorts"};              //domain 1

      string _shoes[__EA]={"sneakers","dress shoes","loafers","running shoes","sandals"}; //domain 2
      
      CElement<string> _et[];ArrayResize(_et,__EA);
      CElement<string> _ep[];ArrayResize(_ep,__EA);
      CElement<string> _es[];ArrayResize(_es,__EA);
      
      for(int e=0;e<__EA;e++)
      { 
         _et[e].Cardinality(1); _et[e].Set(0,_tops[e]);
         _ep[e].Cardinality(1); _ep[e].Set(0,_pants[e]);
         _es[e].Cardinality(1); _es[e].Set(0,_shoes[e]); 
      }
      
      CDomain<string> _dt,_dp,_ds;
      FillDomain(_dt,_et);FillDomain(_dp,_ep);FillDomain(_ds,_es);
      
      //
      if(_ca.Domain("string",__DA))//resize domains array to 3
      {
         if(_ca.Set(0,_dt) && _ca.Set(1,_dp) && _ca.Set(2,_ds))//assign each filled domain above to a spot (index) within the category
         {
            if(_ca.Domain("string")==__DA)//check domains count 
            {
               for(int e=0;e<__EA;e++)
               {
                  COntology _o_01_2;
                  CMorphism<string,string> _m1_01_2,_m2_01_2;
                  SetCategory(_ca,0,1,e,e,_o_01_2," is worn with ",_m1_01_2);
                  SetCategory(_ca,1,2,e,e,_o_01_2," is worn with ",_m2_01_2,ONTOLOGY_POST);printf(__FUNCSIG__+" (0 & 1) followed by 2 Log is: "+_o_01_2.ontology);
                  
                  COntology _o_0_12;
                  CMorphism<string,string> _m1_0_12,_m2_0_12;
                  SetCategory(_ca,1,2,e,e,_o_0_12," is worn with ",_m1_0_12);
                  SetCategory(_ca,0,2,e,e,_o_0_12," is worn with ",_m2_0_12,ONTOLOGY_PRE);printf(__FUNCSIG__+" 0 following (1 & 2) Log is: "+_o_0_12.ontology);
               }
            }
         }
      }

    为了检查关联性，我们将在本体日志中输出态射的结果。 为此，我们将创建一个 “COntology” 类。 以下面的同名枚举和结构对此进行勾勒。

    //+------------------------------------------------------------------+
//| ONTOLOGY ENUM                                                    |
//+------------------------------------------------------------------+
enum EOntology
  {
      ONTOLOGY_PRE=-1,
      ONTOLOGY_NEW=0,
      ONTOLOGY_POST=1
  };
//+------------------------------------------------------------------+
//| ONTOLOGY STRUCT                                                  |
//+------------------------------------------------------------------+
struct SOntology
  {
      int                           in;
      int                           out;
      
                                    SOntology()
                                    {
                                       in=-1;
                                       out=-1;
                                    };
                                    ~SOntology(){};
  };
//+------------------------------------------------------------------+
//| ONTOLOGY CLASS                                                   |
//+------------------------------------------------------------------+
class COntology
  {
      protected:
      
      int                           facts;
      
      SOntology                     types[];
      SOntology                     universe[];
      
      public:
      
      string                        ontology;
      
      int                           Facts() { return(facts); }
      bool                          Facts(int Value) { if(Value>=0 && Value<INT_MAX) { facts=Value; ArrayResize(types,facts); ArrayResize(universe,facts); return(true); } return(false); }
      
      bool                          GetType(int TypeIndex,int &TypeIn,int &TypeOut) { if(TypeIndex>=0 && TypeIndex<Facts()) { TypeIn=types[TypeIndex].in; TypeOut=types[TypeIndex].out; return(true); } return(false); }
      bool                          SetType(int ValueIndex,int ValueIn,int ValueOut) 
                                    { 
                                       if(ValueIndex>=0 && ValueIndex<Facts()) 
                                       { 
                                          types[ValueIndex].in=ValueIn; types[ValueIndex].out=ValueOut; 
                                          return(true); 
                                       } 
                                       else if(ValueIndex>=0 && ValueIndex>=Facts() && ValueIndex<INT_MAX-1) 
                                       { 
                                          if(Facts(ValueIndex+1))
                                          {
                                             types[ValueIndex].in=ValueIn; types[ValueIndex].out=ValueOut; 
                                             return(true); 
                                          }
                                       } 
                                       
                                       return(false); 
                                    }
      
      bool                          GetUniverse(int UniverseIndex,int &UniverseIn,int &UniverseOut) { if(UniverseIndex>=0 && UniverseIndex<Facts()) { UniverseIn=universe[UniverseIndex].in; UniverseOut=universe[UniverseIndex].out; return(true); } return(false); }
      bool                          SetUniverse(int ValueIndex,int ValueIn,int ValueOut) 
                                    { 
                                       if(ValueIndex>=0 && ValueIndex<Facts()) 
                                       { 
                                          universe[ValueIndex].in=ValueIn; universe[ValueIndex].out=ValueOut; 
                                          return(true); 
                                       } 
                                       else if(ValueIndex>=0 && ValueIndex>=Facts() && ValueIndex<INT_MAX-1) 
                                       { 
                                          if(Facts(ValueIndex+1))
                                          {
                                             universe[ValueIndex].in=ValueIn; universe[ValueIndex].out=ValueOut; 
                                             return(true); 
                                          }
                                       } 
                                       
                                       return(false); 
                                    }
      
      string                        old_hash;
      string                        new_hash;
      
                                    COntology()
                                    {
                                       ontology="";
                                       
                                       facts=0;
                                       
                                       ArrayResize(types,facts);
                                       ArrayResize(universe,facts);
                                       
                                       old_hash="";
                                       new_hash="";
                                    };
                                    ~COntology(){};
  };

    从本体输出来看，运行脚本应该为我们提供以下日志。

    2023.01.26 10:42:56.911 ct_2 (EURGBP.ln,H1)     void OnStart() (0 & 1) followed by 2 Log is: T-shirt is worn with jeans is worn with sneakers
2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1)     void OnStart() 0 following (1 & 2) Log is: T-shirt is worn with jeans is worn with sneakers
2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1)     void OnStart() (0 & 1) followed by 2 Log is: button-up is worn with slacks is worn with dress shoes
2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1)     void OnStart() 0 following (1 & 2) Log is: button-up is worn with slacks is worn with dress shoes
2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1)     void OnStart() (0 & 1) followed by 2 Log is: polo is worn with khakis is worn with loafers
2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1)     void OnStart() 0 following (1 & 2) Log is: polo is worn with khakis is worn with loafers
2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1)     void OnStart() (0 & 1) followed by 2 Log is: sweatshirt is worn with sweatpants is worn with running shoes
2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1)     void OnStart() 0 following (1 & 2) Log is: sweatshirt is worn with sweatpants is worn with running shoes
2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1)     void OnStart() (0 & 1) followed by 2 Log is: tank top is worn with shorts is worn with sandals
2023.01.26 10:42:56.913 ct_2 (EURGBP.ln,H1)     void OnStart() 0 following (1 & 2) Log is: tank top is worn with shorts is worn with sandals


     

    总之，关联公理允许按照态射的组合轻松定义类别的关联，从而消除了在定义多个态射时计算括号的需要。 这令理解类别中对象之间的关系变得更加简单，在这种情况下，所有三个域中的服装项目；衬衫、裤子和鞋子。 


    交换图例

    交换图例是表示类别中两个态射之间关系的图示。 它由一组域、态射及其组合构成，以特定方式排列，从而表明态射交换，这意味着它们的组成顺序无关紧要。这也意味着对于一个类别中的任何三个域 A、B 和 C，以及它们的态射 f：A -> B，g：B -> C 和 h：A -> C；这些态射的组成必须满足：

    f o g = h

    使用外汇价格换算的一个例子可能是套利；EURUSD、EURJPY 和 USDJPY 的价格之间的关系。 在此示例中，域可以是货币本身（欧元、美元、日元），而态射可以表示根据汇率将一种货币兑换为另一种货币的过程。 举例，设 f：EUR -> USD 表示以 EURUSD 汇率将欧元兑换为美元的过程的态射；设 g：美元 -> 日元 代表以 USDJPY 汇率将美元兑换为日元的过程的态射；并设 h：EUR -> JPY 表示将欧元兑换为日元的态射。 以下换算规则是以上组合：f o g = h，这将转换为：

    以 EURUSD 汇率将欧元兑换为美元，然后按 USDJPY 汇率将该美元兑换为日元 = 按 EURJPY 汇率将欧元兑换为日元。

    我们用 MQL5 来描述这一点。 我们将声明一个类别 “_cc”，并用 3 个域填充它，每个域使用 2 种货币。 这些域可以被认为是资产配置中的投资组合。 与关联公理一样，我们将填充类别值，并用本体日志检查，如下所示。

          //COMMUTATION
      CCategory _cc;
      
      string _a[__EC]={"EUR","GBP"};       //domain 0
      string _b[__EC]={"USD","CAD"};       //domain 1
      string _c[__EC]={"CHF","JPY"};       //domain 2
      
      CElement<string> _e_a[];ArrayResize(_e_a,__EC);
      CElement<string> _e_b[];ArrayResize(_e_b,__EC);
      CElement<string> _e_c[];ArrayResize(_e_c,__EC);
      
      for(int e=0;e<__EC;e++)
      { 
         _e_a[e].Cardinality(1); _e_a[e].Set(0,_a[e]);
         _e_b[e].Cardinality(1); _e_b[e].Set(0,_b[e]);
         _e_c[e].Cardinality(1); _e_c[e].Set(0,_c[e]); 
      }
      
      CDomain<string> _d_a,_d_b,_d_c;
      FillDomain(_d_a,_e_a);FillDomain(_d_b,_e_b);FillDomain(_d_c,_e_c);
      
      //
      if(_cc.Domain("string",__DC))//resize domains array to 3
      {
         if(_cc.Set(0,_d_a) && _cc.Set(1,_d_b) && _cc.Set(2,_d_c))//assign each filled domain above to a spot (index) within the category
         {
            if(_cc.Domain("string")==__DC)//check domains count 
            {
               for(int e=0;e<__EC;e++)
               {
                  COntology _o_ab_bc;
                  string _ab=_a[e]+_b[e],_bc=_b[e]+_c[e];
                  double _ab_bid=SymbolInfoDouble(_ab,SYMBOL_BID),_bc_bid=SymbolInfoDouble(_bc,SYMBOL_BID);
                  string _aspect_ab=" is exchanged at: "+DoubleToString(_ab_bid,(int)SymbolInfoInteger(_ab,SYMBOL_DIGITS))+", for: ";
                  string _aspect_bc=" is exchanged at: "+DoubleToString(_bc_bid,(int)SymbolInfoInteger(_bc,SYMBOL_DIGITS))+", for: ";
                  CMorphism<string,string> _m_ab,_m_bc;
                  SetCategory(_cc,0,1,e,e,_o_ab_bc,_aspect_ab,_m_ab);
                  SetCategory(_cc,1,2,e,e,_o_ab_bc,_aspect_bc,_m_bc,ONTOLOGY_POST);printf(__FUNCSIG__+" a to b then b to c logs: "+_o_ab_bc.ontology);
                  
                  COntology _o_ac;
                  string _ac=_a[e]+_c[e];
                  string _aspect_ac=" is exchanged at: "+DoubleToString(SymbolInfoDouble(_ac,SYMBOL_BID),(int)SymbolInfoInteger(_ac,SYMBOL_DIGITS))+", for: ";
                  CMorphism<string,string> _m_ac;
                  SetCategory(_cc,0,2,e,e,_o_ac,_aspect_ac,_m_ac);printf(__FUNCSIG__+" a to c logs: "+_o_ac.ontology+" vs product of bid rate for ab and bc of: "+DoubleToString(_ab_bid*_bc_bid,(int)SymbolInfoInteger(_ac,SYMBOL_DIGITS)));//ontology
               }
            }
         }
      }

    我们通过比较来自交换态射 “_m_ac” 的速率，与从态射 “_m_ab” 和 “_m_bc” 得到的两个速率的乘积来检查兑换。 这里存在差异，但这些差异主要是由于经纪商提供的历史数据的质量和清算点差（仅附加在出价上）。 运行此脚本后，日志应该为我们提供这些内容。

    2023.01.26 17:27:19.093 ct_2 (EURGBP.ln,H1)     void OnStart() a to b then b to c logs: EUR is exchanged at: 1.08966, for: USD is exchanged at: 0.91723, for: CHF
2023.01.26 17:27:19.093 ct_2 (EURGBP.ln,H1)     void OnStart() a to c logs: EUR is exchanged at: 0.99945, for: CHF vs product of bid rate for ab and bc of: 0.99947
2023.01.26 17:27:19.093 ct_2 (EURGBP.ln,H1)     void OnStart() a to b then b to c logs: GBP is exchanged at: 1.65097, for: CAD is exchanged at: 97.663, for: JPY
2023.01.26 17:27:19.093 ct_2 (EURGBP.ln,H1)     void OnStart() a to c logs: GBP is exchanged at: 161.250, for: JPY vs product of bid rate for ab and bc of: 161.239



    本体日志

    本体是对一个类别的主观总结。 它们是范畴论中的重要工具，因为它们提供了一种通过给定类别中的态射来解释域的结构和关系的途径。 若说区别，它们是一种数学结构（或数据模型，相当于数据库逻辑流图），描述域的类型及其在域中的态射。 本体有几种类型，包括：
    • 分类本体描述一组对象及其子类，并根据 “is-a” 关系定义它们之间的关系。
    • 分层本体描述一组对象及其属性，并根据 “part-of” 关系定义它们之间的关系。
    • 关系本体描述一组对象及其关系，并根据任意二元关系定义它们之间的关系。

    对于外汇交易系统，关系本体可能是最合适的。 这将允许对各种类型的交易策略，以及它们之间的关系进行建模，例如在某些市场条件下哪些策略最有效。 此外，关系本体可以很容易地扩展，譬如包括历史数据等附加信息，这对于开发交易系统很有用。

    在范畴论的跨域应用时，关系本体论的作用，可由金融市场中的各种示例来证明。 以下是五个示例：

    1. 货币对：外汇市场由货币对组成，货币对是相互交易的两种货币的集合。 这些货币之间的关系可利用关系本体进行建模，其中货币对被视为域，汇率被视为连接它们的态射。 上面已经配合交换图分享了一个示例。
    2. 时间序列数据：外汇价格通常表示为时间序列数据，可利用关系本体进行建模，其中时间序列数据被视为一个域，价格随时间变化被视为态射。
    3. 技术指标：技术指标，如移动平均线、或相对强弱指数，可用于分析外汇价格。 这些指标可利用关系本体进行建模，其中指标被视为域，指标值被视为态射。
    4. 交易策略：交易者经常采用各种交易策略，例如趋势跟踪、或基于动量的策略。 这些策略可利用关系本体进行建模，其中交易策略被视为一个域，基于该策略执行的交易被视为态射。
    5. 订单簿：订单簿是外汇市场上所有买卖订单的记录。 这可利用关系本体进行建模（如果由经纪商提供），其中订单簿被视为一个域，而下达的订单被视为态射。

    总体而言，当在交易中跨域使用时，关系本体在范畴论中很有用，因为它们允许以清晰和结构化的方式对复杂系统和关系进行建模和分析。本体论使用“类型”和“方面”来体现类别的主观视角。 可以将类型视为特定类别中的一组域。 它可以是简单的，也可以是复合的。 简单时，它只包含一个域。 当复合时，它将多个域聚集在一起。 方面之于类型，就像态射之于类别内的域一样。基于外汇（Forex）市场中货币对的关系本体可以建模如下：

    类型:

    1. 货币对：货币对是本体中的主要类型，代表相互交易的两种货币。 例如，货币对 “EUR/USD” 代表欧元和美元之间的汇率。
    2. 汇率：汇率是一种货币可以兑换成另一种货币的比率。 它表示货币对组成对象之间的态射。 例如，EUR/USD 货币对的汇率可能是 1.20，这意味着 1 欧元可以兑换 1.20 美元。
    3. 时间：时间是一种表示应用汇率的时间的类型。 它将汇率态射与时间序列数据连接起来。

    方面：

    1. 历史汇率：历史汇率是在不同时间点记录的汇率。 它们分析外汇市场的趋势和形态。
    2. 波动性：波动率是衡量汇率随时间变化程度的指标。 它评估与特定货币对相关的风险。
    3. 相关性：相关性是衡量两个货币对之间关系的指标。 它识别外汇市场中的多样化或对冲机会。

    总体而言，这种关系本体允许清晰和结构化地表示外汇市场中货币对、汇率、时间和其它方面之间的关系。 它可分析市场的动态，并做出明智的决策。格罗滕迪克（Grothendieck）宇宙用于定义类型宇宙的概念，这是范畴论本体论中的关键，类型宇宙是给定类别内的一组类型。 它允许对类型进行排序，并解决“集合的集合”问题。

    若要查看本体的实际应用，我们看一下金融行业的一个例子。 不同的实体，如美国证券交易委员会（SEC）和对冲基金，可能会采用本体以不同的方式对同一类别中的财务数据进行组织和分类。 这可能导致在每个实体里所用的本体其类型和方面的数据表现不同。从 SEC 的角度来看，本体可用于组织与证券和交易活动相关的数据，重点关注合规性和监管问题。 这可能包括“证券”、“交易活动”、“内幕交易”和“违反证券法”、等类型。本体还可能包括与合规性和执行相关的方面，例如“调查”和“处罚”。从对冲基金的角度来看，同一类别的本体可用于组织与投资策略、投资组合管理和绩效指标相关的数据。 这可能包括“投资策略”、“投资组合管理”、“绩效指标”和“风险管理”、等类型。本体还可能包括与基金运营和管理相关的方面，例如“管理资产”和“基金经理”。正如我们所看到的，虽然两个实体可能都在使用本体来组织财务数据，但其本体中表示的类型和方面是不同的，反映了 SEC 与对冲基金的不同目标、层面和关注点。 故此，SEC 的本体将侧重于证券交易中的合规性、法规和违规行为，而对冲基金的本体将专注于投资、风险管理和投资组合管理。

     

    继续进一步描绘在外汇中的类型，简单类型和复合类型是指可代表市场不同方面的数据类型。简单类型是可以用单个值表示的基本数据类型。 例如，在外汇中，两种货币之间的汇率可以被视作一种简单类型，由单个值表示，例如 1.20（意味着 1 个单位的基准货币可以兑换 1.20 单位的报价货币）。 另一方面，复合类型是由多个值、或其它数据类型复合的数据类型。 例如，烛条图就可被视为复合类型，因为它由多个值组成，例如给定时间段的开盘价、收盘价、最高价和最低价。 就方面的而言，简单方面是连接两种简单类型的方面，例如，两种货币之间的汇率可以被认为是一个简单的方面。 复利方面是连接两种复利类型、或一种复利类型和简单类型，例如，交易策略就可被视为复利方面，因为它将策略与基于它执行的交易联系起来。总体而言，简单类型和方面是可用于表示本体中基本信息的基本构建片段，而复合类型和方面是由多个值或其它数据类型组成的更复杂的数据类型，可用于表示正在建模的系统的各个更复杂的方面。

    本体日志是一种通过为感兴趣的域提供逻辑结构来组织和表示知识的方式。 它们有助于定义特定域、子域、任务、实例或流程中的概念、属性和关系。本体日志是存在于特定域中的一组概念、属性和关系的形式表示。 它用于定义该领域内知识的结构，并提供知识的一致性和逻辑表示。 这令机器和人类更容易理解和使用域中的信息。 本体日志可用于各种领域，例如人工智能、自然语言处理、知识表示和信息科学。 它们通常与其它类型的本体（如上层本体和域本体）结合使用，从而提供域的全面视图。 本体日志通常以机器可读的格式表示，例如 OWL（Web Ontology Language）或 RDF（资源描述框架），这令它们易于被机器处理和使用。 它们也是人类可读的，这令人们更容易理解和使用本体日志中表示的信息。

    在范畴论的背景下，本体日志通过为感兴趣的域提供逻辑结构来组织和表示知识。 它们有助于定义特定域、子域、任务、实例或流程中的概念、属性和关系。范畴论是数学的一个分支，它处理数学系统的结构，它为模拟对象和态射之间的关系提供了一个框架。 本体日志在范畴论的背景下使用时，提供了一种以结构化和逻辑方式组织和表示领域内知识的方法。

    范畴论中常用的本体日志有几种类型，诸如：

    1. 上层本体：上层本体是一种常用本体，它提供域的高级视图，并定义适用于多个子域的一般概念和关系。 这是跨不同本体提供统一结构的通用方式。
    2. 域本体：域本体是一种特定的本体，专注于更大域中的特定子域。 它定义了特定于该子域的概念和关系。
    3. 任务本体：任务本体是一种特定的本体，专注于域中的特定任务或问题。 它定义了特定于该任务或问题的概念和关系。
    4. 实例本体：实例本体是一种特定的本体，专注于特定概念或类的实例。 它定义特定于这些实例的属性和关系。
    5. 流程本体：流程本体是一种特定的本体，侧重于域内发生的流程或操作。 它定义了特定于这些流程或操作的概念和关系。

    这些类型的本体日志用于构建域的知识和关系，并促进对信息的理解、表示和操作。 它们有助于为域内的知识提供一致性和逻辑性的表述，并且可以与关系本体结合使用，从而提供域的全面视图。

    流程本体日志是一种特定类型的本体日志，侧重于域中发生的流程或操作。 它定义了特定于这些流程或操作的概念和关系。 因此，可以在流程本体日志中使用的方面类型将取决于特定域，以及正在建模的流程或操作。 此处是可以在流程本体日志中使用的少量方面示例：

    1. 输入和输出：过程的输入和输出方面可用于定义启动过程所需的资源、材料或信息，以及过程生成的最终产品、服务或信息。
    2. 步骤或阶段：该过程可以分解为较小的步骤或阶段，每个步骤都可以定义为一个概念，代表该步骤的操作和目标。 还可以对步骤之间的关系进行建模。
    3. 扮演者：扮演者是参与流程的实体或代理，例如人员、机器或组织。 可以定义在流程中扮演者与角色之间的关系。
    4. 约束：约束是流程必须遵守的规则、法规或限制。 此方面可用于定义成功完成流程必须满足的条件和要求。
    5. 指标：指标是用于评估过程性能（如效率、质量或成本）的度量或指标。 该方面可用于定义评估过程的测量值和指标，以及如何计算它们。
    6. 时域方面：时域方面是指过程的时间，例如过程的开始和结束时间、持续时间和频率。 此方面可用于对过程的时间方面进行建模。

    总体而言，过程本体日志可用于以结构化和逻辑的方式对过程的各个方面进行建模，包括输入和输出、步骤或阶段、扮演者、约束、度量和时域方面，以及它们之间的关系，这可以促进对信息的理解、表示和操作。外汇市场类别中过程本体的一个例子可能是执行交易的过程。 流程本体将定义特定于执行交易过程的概念和关系。 此处是如何对此过程本体的各个方面进行建模的示例：

    1. 输入和输出：该过程的输入包括交易策略、要交易的货币对和交易账户余额。 该过程的输出是执行的交易。
    2. 步骤或阶段：该过程可以分解为较小的步骤或阶段，例如选择货币对，设置交易参数，下订单和监控交易。
    3. 扮演者：参与该过程的扮演者包括交易者、交易平台和市场。 交易者是启动流程的主要扮演者，交易平台是用于执行交易的工具，市场是交易发生的环境。
    4. 约束：限制包括保证金、杠杆和风险管理方面的法规。 必须遵守这些约束才能成功完成交易。
    5. 指标：用于评估流程绩效的指标包括交易的损益、风险回报率和成功交易的百分比。
    6. 时域方面：时域方面是指过程的时间，例如交易的开始和结束时间，交易的持续时间和交易的频率。

    这个过程本体日志可用于以结构化和逻辑的方式对外汇市场执行交易过程的各个方面进行建模。 它可用于促进与执行交易过程相关的信息的理解、表示和操作，并且可以与其它类型的本体结合使用，从而提供金融市场的全面视图。


    结束语

    总之，范畴论为复杂系统（如金融市场）的建模和分析提供了一个强大的框架。 在 MQL5 中实现范畴论可以通过提供域和态射之间关系的结构化和逻辑表示，来帮助交易者更好地理解市场，并安全航行。 本文强调了范畴论中范畴公理定义的重要性，以及它们如何为域和态射之间的关系建模提供基础。 本文还讨论了本体日志的概念，以及如何使用它们为感兴趣的主题（在本例中为金融市场）提供逻辑结构。 总体而言，在 MQL5 中实现范畴论，对于希望更深入地了解市场，并做出更明智交易决策的交易者来说是一个有价值的工具。 它提供了一种结构化和合乎逻辑的方式来分析市场，可以帮助交易者识别也许难以发现的形态和机会。

    本文由MetaQuotes Ltd译自英文
    原文地址： https://www.mql5.com/en/articles/11958

    附加的文件 |
    下载ZIP
    ct_2.mq5 (62.16 KB)
    注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

    该作者的其他文章

    前往讨论
    在 MetaTrader 5 中测试和优化二元期权策略 在 MetaTrader 5 中测试和优化二元期权策略
    在本文中，我将在 MetaTrader 5 中检查并优化二元期权策略。
    MQL5 酷宝书 — 宏观经济事件数据库 MQL5 酷宝书 — 宏观经济事件数据库
    本文讨论了基于 SQLite 引擎处理数据库的可能性。 形成的 CDatabase 类就是为了方便和有效地运用 OOP 原则。 随后它会参与宏观经济事件数据库的创建和管理。 本文提供了使用 CDatabase 类的多种方法的示例。
    创建综合性猫头鹰交易策略 创建综合性猫头鹰交易策略
    我的交易策略基于经典的基本面，以及在所有类型的市场中广泛采用的指标的改进。 这是一个现成的工具，允许您追随提议的新型盈利交易策略。
    在 Linux 上利用 C++ 多线程支持开发 MetaTrader 5 概念验证 DLL 在 Linux 上利用 C++ 多线程支持开发 MetaTrader 5 概念验证 DLL
    我们将开始探索如何仅基于 Linux 系统开发 MetaTrader 5 平台的步骤和工作流程，其中最终产品能在 Windows 和 Linux 系统上无缝运行。 我们将了解 Wine 和 Mingw；两者都是制作跨平台开发任务的基本工具。 特别是 Mingw 的线程实现（POSIX 和 Win32），我们在选择追随哪一个时需要仔细考虑。 然后，我们构建一个能在 MQL5 代码中所用的概念验证 DLL，最后比较两种线程实现的性能。 这一切都是为了您的基金能进一步扩张自己。 阅读本文后，您应该可以轻松地在 Linux 上构建 MT 相关工具。