Нейросети в трейдинге: Возмущённые модели пространства состояний для анализа рыночной динамики

Введение

Финансовый рынок традиционно любят описывать через графики, индикаторы и статистические зависимости. Это удобный язык, он привычен. Он пережил десятки рыночных циклов и до сих пор исправно служит практикующим трейдерам. Однако за внешней простотой ценового ряда скрывается куда более сложная картина. Рынок живёт не в барах и не в таймфреймах, он существует в непрерывном потоке состояний, где каждое изменение цены — это следствие множества микрособытий, решений, реакций и задержек. И чем выше частота торговли, тем заметнее становится разрыв между тем как рынок устроен на самом деле, и тем, как мы привыкли его моделировать.

Классические методы анализа временных рядов опираются на предположение относительной стационарности: пусть параметры меняются медленно, пусть распределения устойчивы хотя бы на выбранном участке истории. Эти допущения работают ровно до тех пор, пока рынок ведёт себя вежливо. Но стоит ускорить масштаб, перейти к минутам, секундам или тикам — и аккуратная картина рассыпается: цена начинает двигаться рывками, волатильность перестаёт быть фоном и выходит на первый план. Шум становится не помехой, а частью сигнала. Именно здесь большинство традиционных моделей теряет устойчивость, а многие нейросетевые решения — интерпретируемость и контроль.

Современные нейросети в трейдинге часто идут по пути усложнения — глубже, шире, больше параметров, больше данных. Такой подход способен давать впечатляющие результаты на истории, но он же несёт в себе системный риск. Модель начинает учить не рынок, а его прошлые артефакты. Она хорошо запоминает, но плохо обобщает. В условиях реального потока котировок это проявляется быстро и беспощадно. Переобучение, деградация, резкое падение качества — знакомая картина для любого, кто пытался перенести красивую нейросеть из тестера в живую торговлю.

На этом фоне всё больший интерес вызывают модели, которые изначально строятся вокруг динамики состояний. Не вокруг прогнозирования следующей цены как числа, а вокруг эволюции скрытого рыночного состояния. Такой подход хорошо известен в классической теории управления и фильтрации. Калмановские фильтры, модели пространства-состояний, рекуррентные системы — всё это инструменты, проверенные временем. Они дисциплинируют модель, заставляют её помнить прошлое, не теряя связи с настоящим, и, что особенно важно для трейдинга, позволяют мыслить рынок как систему, а не как набор разрозненных наблюдений.

Однако и у классических моделей пространства состояний есть предел. Их линейность, столь ценная для устойчивости и интерпретации, становится узким местом, когда рынок входит в нелинейные режимы. Резкие всплески ликвидности, асинхронные реакции участников, каскадные движения, где маленькое событие запускает цепочку последствий, — в таких условиях жёстко зафиксированная динамика состояния перестаёт отражать реальность. Модель становится слишком гладкой для живого рынка.

Именно здесь возникает идея возмущённых моделей пространства состояний. Вместо того чтобы полностью отказываться от структурной дисциплины State-Space подхода, мы аккуратно нарушаем его симметрию. Добавляем управляемые возмущения в динамику скрытого состояния, не как шум, который нужно отфильтровать, а как информативный сигнал. По сути, мы признаём очевидный факт: рынок не развивается по идеально гладкой траектории, его состояние постоянно смещается под воздействием событий, которые невозможно заранее полностью описать, но можно научиться корректно учитывать.

Для практикующего трейдера это означает смену угла зрения. Мы перестаём спрашивать модель: Куда пойдёт цена? И начинаем задавать более зрелый вопрос: В каком состоянии находится рынок сейчас, и как это состояние эволюционирует? Такой подход лучше согласуется с реальной торговой практикой. Мы не угадываем будущее, а оцениваем текущую конфигурацию сил: напряжение, инерцию, потенциал движения. Всё то, что опытный трейдер интуитивно чувствует, глядя на ленту или стакан, но что трудно формализовать классическими индикаторами.

Возмущённые модели пространства состояний позволяют встроить эту интуицию в математически строгую и вычислительно устойчивую форму. Они сохраняют память о прошлом, умеют работать с длинными последовательностями, не требуют агрессивного увеличения параметров и при этом способны реагировать на локальные рыночные импульсы без разрушения общей структуры модели. Это особенно важно в условиях высокочастотного шума, где избыточная гибкость модели становится врагом, а не союзником.

Отдельного внимания заслуживает вычислительная сторона вопроса. Финансовый рынок не прощает медлительности. Модель, которая красиво работает офлайн, но не масштабируется в реальном времени, практической ценности не имеет. Подходы, основанные на пространстве состояний, обладают важным преимуществом — линейной или квазилинейной сложностью по времени. Это делает их естественными кандидатами для потоковой обработки данных, где решения принимаются последовательно, без пересчёта всей истории.

Одно из подобных решений было предложено в работе "Perturbed State Space Feature Encoders for Optical Flow with Event Cameras". Формально она относится к области компьютерного зрения и решает задачу прогнозирования оптического потока на основе событийных камер. На первый взгляд — далекая от трейдинга тема, но если отбросить терминологию и посмотреть на саму идею, сходство становится почти очевидным. Авторы работают не с кадрами как таковыми, а с потоком событий, каждое из которых фиксирует изменение состояния системы. Не само изображение важно, а динамика переходов, не статическая картинка, а процесс.

Именно этот сдвиг мышления делает предложенный подход особенно интересным для финансовых рынков. В их интерпретации сцена — это динамическая среда, оптический поток — результат накопленного движения, а события — локальные возмущения, которые нарушают текущую траекторию состояния. Рынок устроен удивительно похоже. Цена — это не объект наблюдения, а след. Реальное содержание скрыто в последовательности микроизменений: сделках, изменениях в стакане, всплесках активности, затишьях. Каждое такое событие слегка сдвигает рыночное состояние, иногда почти незаметно, иногда — с эффектом домино.

Ключевой момент работы заключается в том, что авторы не пытаются подавить эти возмущения или усреднить их до удобного сигнала. Напротив, они встраивают их прямо в динамику пространства состояний. Состояние системы эволюционирует не по жёстко заданному правилу. А с учётом локальных нарушений, которые несут информацию о происходящих изменениях. Это не шум, от которого нужно избавиться, это язык, на котором система говорит о себе.

Важно и то, как именно это реализовано. Подход авторов не разрушает дисциплину State-Space моделей. Напротив, он сохраняет их сильные стороны — устойчивость, последовательность, контролируемую динамику и аккуратно расширяет их за счёт параметризованных возмущений. В результате модель остаётся вычислительно лёгкой и предсказуемой в поведении, но при этом перестаёт быть слепой к локальным импульсам. Для трейдинга это принципиально. Нам нужна модель, которая не паникует от каждого тика, но и не пропускает момент, когда рынок действительно меняется.

Рынок меняется. Это очевидно. Возмущённые модели пространства состояний — это попытка примирить строгость классических методов с реальной, неровной природой финансовых рынков. Без обещаний чудес, без излишнего пафоса, но с уважением к сложности системы, с которой практикующий трейдер имеет дело каждый торговый день.

Архитектура фреймворка

Переходя к описанию архитектуры фреймворка, важно сразу зафиксировать главный принцип, на котором она построена. Авторы фреймворка не пытаются реконструировать все и сразу. Задача модели куда более прагматична и потому эффективна: последовательно кодировать текущее состояние и отслеживать, как оно эволюционирует под воздействием поступающих событий. Архитектура выстроена вокруг этой идеи и потому выглядит сдержанно, почти консервативно, но именно в этом и заключается её сила.

Предложенный авторами фреймворка подход опирается на последние достижения в области много­кадровой оценки оптического потока для изображений, которые они адаптируют под событийное зрение. Ключевыми элементами служат модуль TRi-frame Optical Flow, работающий сразу с тремя последовательными представлениями, и его развитие — модуль Motion Propagation, связывающий несколько таких блоков уже на горизонте из пяти временных шагов. Эти механизмы показали, что расширение временного контекста даёт качественно более устойчивое представление движения по сравнению с анализом изолированных пар кадров.

Большинство традиционных решений в событийном зрении ограничиваются обработкой двух соседних представлений, делая ставку на высокое временное разрешение данных. Такой подход действительно позволяет реагировать быстро, но он часто упускает важную информацию о развитии движения во времени. События не существуют в вакууме, их ценность раскрывается именно в последовательности — когда становится видно, как локальные изменения складываются в целостную динамику. В своей работе авторы фреймворка сознательно расширяют временное окно до пяти последовательных событийных представлений. Это позволяет извлекать более богатую информацию о движении и, как следствие, повышать точность оценок оптического потока.

Пространственное кодирование в предложенной архитектуре построено вокруг P-SSE. Этот модуль обеспечивает глобальное эффективное поле восприятия при линейной вычислительной сложности, что принципиально важно для работы с плотными потоками событий. За счёт механизма возмущений P-SSE стабилизирует матрицу динамики состояний и делает её более выразительной. Модель получает возможность уверенно захватывать сложные пространственно-временные зависимости, не жертвуя устойчивостью и производительностью. В рамках всей методологии P-SSE играет ключевую роль, так как именно он связывает локальные наблюдения с глобальной структурой движения.

Поток событий, зафиксированных событийной камерой между двумя моментами времени, рассматривается как последовательность событий. Каждое событие несёт минимально необходимую информацию: пространственное положение, момент возникновения и знак изменения яркости. В практическом смысле это не кадры и не привычные изображения, а непрерывный поток микрособытий, отражающих локальные изменения сцены.

Для дальнейшего анализа вводится последовательность соседних временных точек. Именно на этом локальном временном горизонте модель оценивает динамику движения. Вместо того чтобы работать с разрозненными событиями напрямую, авторы фреймворка предлагают сначала агрегировать их в компактные, подобные изображениям представления. Каждое такое представление аккумулирует события, произошедшие между двумя соседними временными метками, и кодирует их в виде многоканальных признаков, распределённых по пиксельной сетке. Это важный компромисс между точностью и вычислительной эффективностью: сохраняется ключевая информация о динамике, не перегружая модель избыточной детализацией. В результате, на выходе формируется последовательность многоканальных тензоров, каждый из которых отражает локальное состояние событийного потока на своём временном интервале.

Дальнейшая обработка строится по иерархическому рекуррентному принципу. Вместо линейного прохода по всей последовательности, модель работает с перекрывающимися триплетами событийных представлений. Сначала анализируются группы из трёх соседних состояний, сдвинутые во времени с шагом в один интервал. Такой подход позволяет локально оценить движение, опираясь не на отдельную пару состояний, а на более устойчивый фрагмент динамики. Это снижает чувствительность к шуму и делает оценку более согласованной во времени.

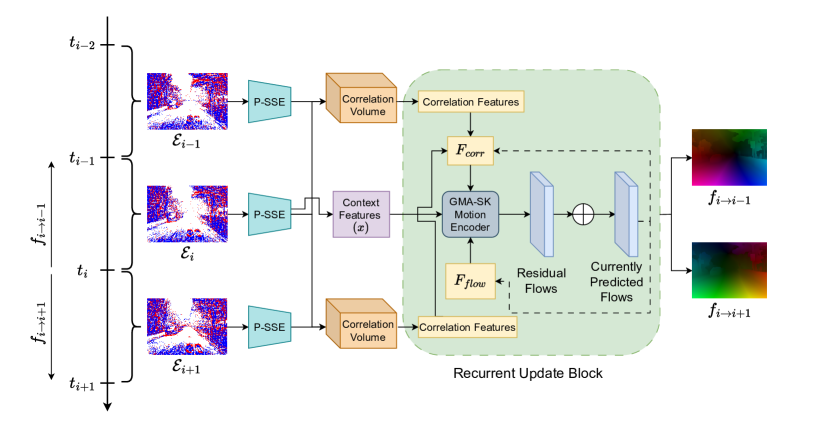
Каждый такой триплет обрабатывается модулем E-TROF, который формирует первичную оценку оптического потока с учётом контекста сразу нескольких временных шагов. Далее эти локальные оценки не остаются изолированными. Они связываются между собой через модуль E-MOP, отвечающий за распространение движения во времени. Этот этап позволяет согласовать локальные оценки и выстроить целостную картину динамики на расширенном временном горизонте.

Модуль E-TROF работает с триплетом последовательных событийных представлений и формирует двунаправленную оценку движения, центрированную в текущем моменте времени. Иначе говоря, модель одновременно оценивает, как состояние системы развивается вперёд и назад относительно текущей точки. Такой симметричный взгляд на динамику принципиально повышает устойчивость оценок и снижает зависимость от случайных локальных искажений.

Процесс начинается с этапа кодирования признаков. Каждое событийное представление преобразуется в компактное латентное описание с помощью модели P-SSE. На этом шаге данные проецируются в пространство признаков с пониженным пространственным разрешением. Это сознательный выбор. Он позволяет существенно снизить вычислительные затраты, не теряя при этом структурной информации о движении. В контексте финансовых рынков это легко интерпретируется как переход от сырых тиков к более устойчивому представлению рыночного состояния, где шум уже частично отфильтрован, но динамика сохранена.

На следующем этапе формируются корреляционные объёмы для прямого и обратного направлений. Они отражают степень сходства между соответствующими элементами соседних представлений и служат основой для восстановления движения. Один объём кодирует связь текущего состояния с будущим, другой — с прошлым. Такое разделение позволяет модели явно учитывать асимметрию динамики и не смешивать причины и следствия. Дополнительно из центрального представления извлекаются контекстные признаки с использованием того же самого энкодера. Это обеспечивает согласованность пространства признаков и исключает перекосы, возникающие при использовании разных кодирующих схем.

Далее осуществляется ключевой для всей архитектуры этап — объединение прямых и обратных корреляционных признаков. Этот процесс построен итеративно и по духу близок к RAFT. Но здесь он применяется сразу к обоим направлениям движения. Инициализация выполняется максимально нейтрально: начальные смещения принимаются равными нулю. Затем на каждой итерации модель уточняет оценки, опираясь на текущие значения потоков и соответствующие им выборки из корреляционных объёмов. Корреляционные и потоковые признаки проходят через обучаемые кодировщики и объединяются в единое представление, отражающее согласованную двунаправленную динамику.

Важно, что на этом этапе модель не просто улучшает поток. Она постепенно выстраивает внутреннее понимание движения как согласованного процесса. В терминах рынка это похоже на последовательную калибровку оценки текущего режима: сначала грубую, затем всё более точную, с учётом того, откуда рынок пришёл и куда он, с наибольшей вероятностью, движется.

В целом логика E-TROF выглядит строго и последовательно. Здесь нет резких эвристик или случайных решений. Архитектура шаг за шагом формирует представление динамики, опираясь на симметрию, рекуррентность и контролируемое накопление информации. Именно такая организация делает модель особенно привлекательной для переноса идей в финансовый контекст. Здесь ключевую роль играет не разовый прогноз, а устойчивое отслеживание эволюции состояния рынка во времени.

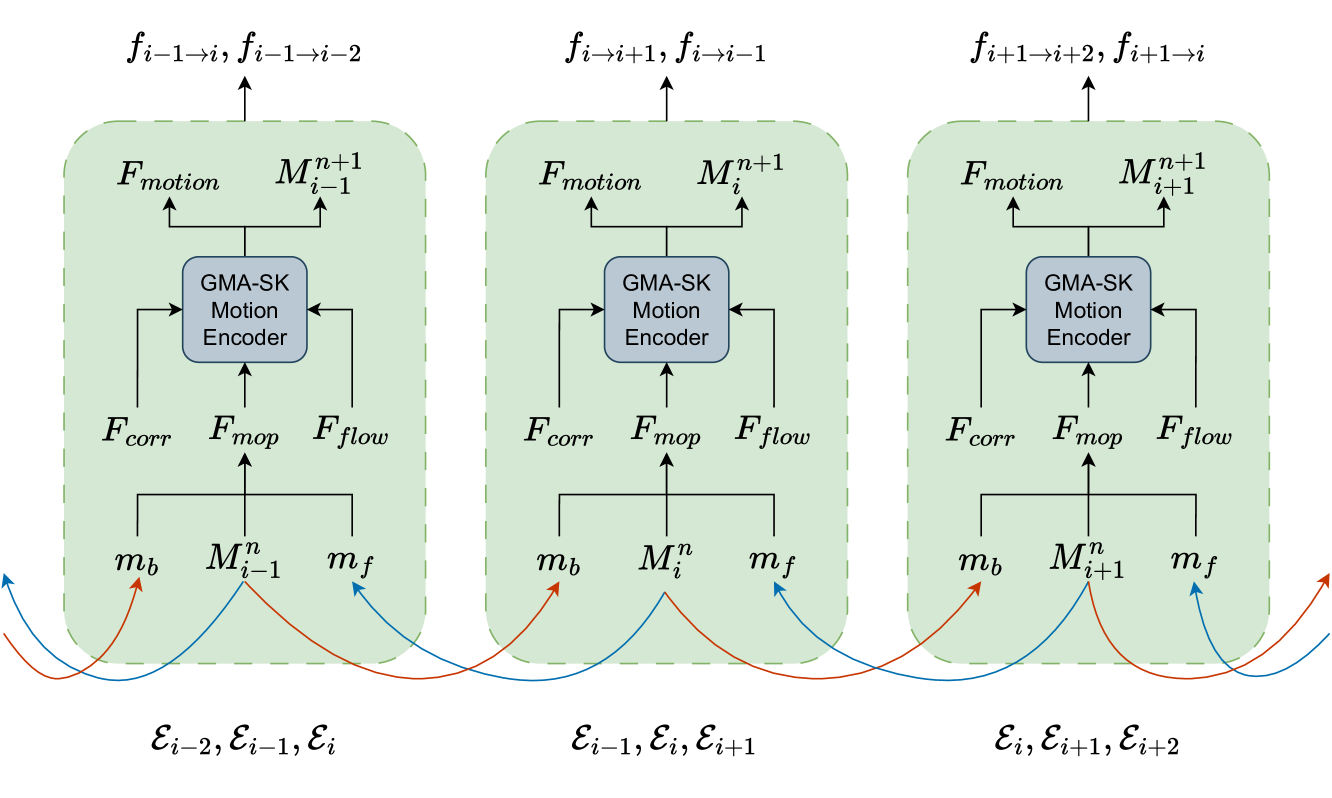
Модуль E-MOP отвечает за распространение информации о движении между соседними триплетами событийных представлений. Его задача — связать локальные оценки, полученные в каждом E-TROF сегменте, и превратить их в согласованную картину динамики на расширенном временном горизонте. За счёт этого двунаправленные оценки движения перестают быть изолированными и начинают уточняться совместно, опираясь на контекст соседних временных фрагментов.

В основе работы E-MOP лежит представление состояния движения. Для каждого триплета формируется вектор признаков, описывающий текущую динамику, который на первом шаге инициализируется нейтральным значением и затем последовательно уточняется. Важно, что это состояние не является фиксированным, оно живёт и развивается вместе с моделью, аккумулируя информацию по мере итераций. Такой механизм хорошо согласуется с идеей рынка как системы, состояние которой формируется не мгновенно, а через постепенное накопление сигналов.

Для обмена информацией между соседними триплетами извлекается двунаправленная временная информация о движении. Это достигается путём переноса признаков состояния движения из предыдущего и следующего сегментов во временной центр текущего триплета. Перенос выполняется с учётом уже предсказанных потоков движения. Проще говоря, модель пересматривает соседние состояния, приводя их в координатную систему текущего момента. Такой шаг позволяет корректно сопоставить динамику разных временных отрезков и избежать искажений, связанных с временным сдвигом.

После этого текущее состояние движения объединяется с перенесёнными признаками из прошлого и будущего. Полученное объединённое представление становится основой для дальнейшего уточнения. На практике это означает, что каждый триплет начинает учитывать не только собственные наблюдения, но и то, как рынок вёл себя чуть раньше и как он начал вести себя чуть позже. В финансовом контексте это особенно ценно: локальный импульс редко бывает изолированным, он почти всегда вписан в более широкую динамику.

Сформированные таким образом признаки движения сначала используются для вычисления обновлённых признаков движения, а затем — для итеративного уточнения двунаправленных оценок движения. Этот процесс повторяется несколько раз, и на каждом шаге состояние движения становится всё более информативным. Непрерывное обновление позволяет модели постепенно углублять временный контекст, не увеличивая длину входной последовательности и не усложняя архитектуру.

В результате E-MOP выполняет роль связующего механизма между локальными оценками, превращая набор отдельных триплетов в единую временную структуру. Модель начинает видеть движение как непрерывный процесс. В терминах финансовых рынков это эквивалентно переходу от анализа отдельных участков графика к целостному восприятию рыночного режима, где прошлое и будущее мягко корректируют интерпретацию текущего состояния.

Предложенный авторами фреймворка энкодер P-SSE построен на базе моделей пространства состояний и решает сразу две принципиальные задачи: обеспечивает глобальное эффективное поле восприятия и при этом сохраняет линейную вычислительную сложность. Это редкое сочетание, особенно ценное для задач, где приходится работать с длинными последовательностями и плотными потоками данных. В основе энкодера лежит линейная динамическая система, которая переводит входной сигнал в выходной отклик через скрытое состояние. Именно это скрытое состояние аккумулирует информацию о прошлом и задаёт инерцию дальнейшей эволюции.

В непрерывной форме система описывается стандартным уравнением пространства состояний: состояние изменяется под действием собственной динамики и входного сигнала, а выход формируется как проекция текущего состояния с возможным прямым вкладом входа. Матрица динамики отвечает за то, как система помнит прошлое, матрицы проекции — за то, как это прошлое проявляется во внешних признаках. Наличие прямого пропуска входа играет роль стабилизирующего механизма и позволяет модели гибко реагировать на текущие изменения, не разрушая накопленную динамику.

Поскольку реальные данные имеют дискретную природу, непрерывная система приводится к дискретному виду. Для этого используется стандартная схема дискретизации с удержанием нулевого порядка. В результате динамика состояния переходит в рекуррентную форму, где новое состояние вычисляется как линейная комбинация предыдущего состояния и текущего входа. Такой переход не меняет сути модели, но делает её естественно совместимой с цифровыми потоками данных. Важно, что здесь используется аппроксимация первого порядка, которая хорошо зарекомендовала себя в практических реализациях и обеспечивает устойчивость обучения.

Существенное отличие от классических моделей пространства состояний заключается в том, что параметры системы не являются фиксированными. Матрицы, отвечающие за взаимодействие входа и состояния, а также шаг дискретизации, динамически формируются на основе входных данных. Иначе говоря, сама система адаптируется к текущему сигналу. В финансовом контексте это выглядит особенно уместно: рынок не живёт по одному и тому же уравнению в разные периоды, и способность модели мягко подстраивать свою динамику под входной поток становится ключевым преимуществом.

Изначально такие модели предназначены для одномерных последовательностей. Однако в рассматриваемой архитектуре этот подход расширяется на двумерные карты признаков. Для этого используется последовательное сканирование по строкам или столбцам. На каждом шаге карта признаков преобразуется в длинную последовательность, к которой применяется State-Space преобразование. Затем результат возвращается в исходную двумерную форму. Повторение таких блоков в сочетании с позиционными представлениями позволяет модели захватывать глобальный контекст по всей двумерной структуре, несмотря на то что базовая операция остаётся одномерной. Это аккуратный и вычислительно дисциплинированный способ получить глобальное восприятие без тяжёлых механизмов внимания.

Архитектура P-SSE выстроена модульно и повторяет логику трансформеров, но вместо Self-Attention здесь используются блоки пространства состояний. Последовательное применение таких блоков формирует итоговое представление признаков, которое далее используется для извлечения корреляционных и контекстных характеристик. По сути, энкодер превращает локальные наблюдения в согласованное описание глобальной динамики, сохраняя при этом строгий контроль над вычислительной сложностью.

Отдельного внимания заслуживает вопрос устойчивости обучения. Для стабилизации динамики сначала обучается матрица возмущений для матрицы состояния на большом эталонном датасете. Затем в процессе основной тренировки применяется техника сначала возмутить, затем диагонализировать. Этот приём позволяет избежать деградации динамики состояния и сохранить контролируемое поведение модели на длинных последовательностях. В отличие от ранних работ, где подобные методы проверялись лишь на синтетических задачах, здесь они применяются в полноценной прикладной модели.

Обучение проводится под прямым контролем ошибки между прогнозными и эталонными двунаправленными потоками. Используется L1-критерий, хорошо зарекомендовавший себя в задачах динамического прогнозирования. В более широком смысле это подчёркивает философию всей архитектуры: не усложнять цель обучения, а сосредоточиться на устойчивом и воспроизводимом качестве динамики.

Если перенести эту логику в плоскость финансовых рынков, P-SSE выглядит как зрелая попытка формализовать то, что опытный трейдер делает интуитивно. Модель не реагирует на каждый отдельный импульс, но и не игнорирует их. Она накапливает состояние, позволяет ему эволюционировать и аккуратно корректирует динамику под воздействием новых событий. Это дисциплинированный механизм отслеживания рыночного состояния, способный работать долго, стабильно и без излишнего шума.

В совокупности эти решения — расширенный временной контекст, рекуррентное уточнение и возмущённые модели пространства состояний — существенно повышают устойчивость и качество динамики состояний. Модель начинает лучше чувствовать структуру движения, извлекая сложные пространственно-временные зависимости из потока событий. И делает это с устойчивым выигрышем как в точности, так и в вычислительной эффективности.

Реализация средствами MQL5

После того как мы подробно разобрали теоретические аспекты предложенных подходов, настало время перейти к практической части работы и посмотреть, как эти идеи можно применить в контексте финансовых рынков. Главная ценность подхода авторов заключается в использовании модели пространства состояний с возмущением — именно с неё мы начинаем нашу адаптацию.

Идея проста, но мощна. Вместо того чтобы рассматривать рынок как статическую последовательность цен или объёмов, вводим скрытое состояние, которое аккумулирует всю предыдущую информацию и при этом подвержено локальным возмущениям, отражающим неожиданные события. Каждое такое возмущение несёт сигнал о том, что в динамике рынка происходит что-то значимое — будь то резкий всплеск объёма, смена тренда или аномальная активность участников. В отличие от классических моделей, которые либо игнорируют такие локальные события, либо реагируют на них слишком поздно, возмущённая модель пространства состояний позволяет корректно встроить их в эволюцию состояния, сохранив устойчивость и последовательность анализа.

Для нашей работы это означает, что мы потенциально можем построить модель, способную отслеживать рыночное состояние в реальном времени, фиксируя микроизменения и одновременно удерживая глобальный контекст. Это фундаментальная база, на которой далее строятся все остальные компоненты. Именно с этого шага начинается превращение чисто теоретической идеи в практический инструмент для анализа финансовой динамики.

В рамках предложенного авторами фреймворка модуля P-SSE для реализации возмущений используется отдельная обучаемая матрица. Эта матрица предназначена для аккуратного корректирования основной динамики системы. Она не заменяет её, а лишь добавляет локальные сдвиги, позволяя модели гибко реагировать на неожиданные изменения входного потока. Важно, что элементы матрицы возмущений строго ограничены и не превышают 10 % от основной матрицы динамики состояния. Это обеспечивает, что возмущение достаточно маленькое, чтобы не нарушить устойчивость динамики, но при этом заметно влияет на локальные модификации состояния.

Однако при динамическом обучении матрицы постоянно меняют свои значения, и строгое соблюдение 10 % от текущей амплитуды становится технически проблематичным. Нормализация решает эту задачу: сначала приводим обе матрицы к единой шкале,  чтобы их значения лежали в фиксированном диапазоне.

Далее при добавлении возмущения достаточно умножить матрицу на понижающий коэффициент, который задаёт относительную силу возмущения. Это даёт точный контроль над масштабом корректировки вне зависимости от абсолютных значений элементов матрицы состояния. Такой приём одновременно упрощает обучение, стабилизирует динамику и сохраняет возможность вносить локальные корректировки, которые действительно чувствуются моделью, не разрушая его глобальную структуру.

Для эффективной реализации этого процесса на GPU мы создадим небольшой кернел на OpenCL, который применяет возмущение ко всей матрице одновременно. На практике это работает следующим образом: каждому элементу исходной матрицы сопоставляется уникальный поток вычислений, идентифицируемый его индексами строки и столбца.

__kernel void PerturbedMatrix(__global const float* inputs,
                              __global const float* perturb,
                              __global float*       output,
                              const float perturb_mult)
  {
   const size_t id = get_global_id(0);
   const size_t var = get_global_id(1);
   const size_t total = get_global_size(0);
   const size_t variables = get_global_size(1);
//---
   int shift = RCtoFlat(var, id, variables, total, 0);
   output[shift] = IsNaNOrInf(inputs[shift] + perturb[shift] * perturb_mult, 0.0f);
  }

Эти двумерные индексы преобразуются в линейный индекс массива, чтобы обеспечить корректный доступ к элементам в памяти устройства. Затем к значению исходного элемента прибавляется соответствующий элемент матрицы возмущений, умноженный на заранее заданный коэффициент, определяющий масштаб воздействия.

После сложения выполняется проверка на недопустимые значения — NaN или Inf — и, при необходимости, такие элементы заменяются на безопасное значение. В результате каждый элемент исходной матрицы получает управляемое возмущение, а итоговая матрица формируется целиком и одновременно для всех элементов.

Таким образом, кернел обеспечивает не только параллельное применение возмущений, но и контроль их амплитуды и устойчивость вычислений. В контексте финансовых рынков это похоже на одновременное добавление малых корректировок ко всем компонентам модели состояния, учитывая микроизменения рынка, без нарушения глобальной картины динамики. Такой подход позволяет модели гибко реагировать на новые сигналы, сохраняя согласованность и стабильность прогнозов.

Здесь важно подчеркнуть, что матрицы состояния и возмущений являются обучаемыми параметрами. Это означает, что в процессе обучения на них необходимо корректно распределять градиенты ошибки, учитывая вклад каждого элемента в итоговый результат. Без этого шаг обновления параметров мог бы быть неэффективным или нестабильным, особенно учитывая добавленное возмущение.

Для решения этой задачи мы вводим дополнительный кернел на OpenCL, который вычисляет градиенты отдельно для каждой матрицы.

__kernel void PerturbedMatrixGrad(__global float*       inputs_gr,
                                  __global float*       perturb_gr,
                                  __global const float* output_gr,
                                  const float perturb_mult)
  {
   const size_t id = get_global_id(0);
   const size_t var = get_global_id(1);
   const size_t total = get_global_size(0);
   const size_t variables = get_global_size(1);
//---
   int shift = RCtoFlat(var, id, variables, total, 0);
   float grad = IsNaNOrInf(output_gr[shift], 0.0f);
   inputs_gr[shift] = grad;
   perturb_gr[shift] = IsNaNOrInf(perturb_mult * grad, 0.0f);
  }

Логика работы кернела строится на том, что каждому элементу возмущённой матрицы соответствует поток вычислений. Сначала двумерные индексы строки и столбца преобразуются в линейный индекс, чтобы корректно обращаться к одномерным буферам памяти. Далее из буфера градиентов на уровне результатов извлекается текущий сигнал ошибки. Этот сигнал затем распределяется по двум обучаемым матрицам. Градиент в полном объеме передается элементу матрицы состояния, а для матрицы возмущений градиент масштабируется коэффициентом возмущения.

Таким образом, каждый элемент получает корректный сигнал для обновления в процессе обратного распространения, при этом сохраняется управление силой влияния возмущения через масштабный коэффициент. Проверка на недопустимые значения гарантирует, что градиенты остаются численно стабильными и не вызовут разрыва обучения.

В совокупности с предыдущим кернелом PerturbedMatrix это создаёт полный цикл: сначала добавляем контролируемое возмущение ко всей матрице состояния, затем во время обратного прохода аккуратно распределяем градиенты между основной и возмущающей матрицами. В контексте финансовых рынков это эквивалентно тому, что модель одновременно корректирует глобальное состояние и учитывает локальные сигналы, обучаясь при этом с контролируемой чувствительностью к изменениям микро-динамики.

Но это только фундамент нашей работы. В следующей статье мы продолжим погружение, переходя к тонкостям практической реализации предложенных подходов и демонстрируя, как теоретические идеи превращаются в рабочие инструменты для анализа рыночной динамики.

Заключение

Предложенные в работе "Perturbed State Space Feature Encoders for Optical Flow with Event Cameras" решения предлагают принципиально новый подход к анализу динамики финансовых рынков. Использование моделей пространства состояний с возмущениями позволяет одновременно аккумулировать глобальную информацию о состоянии системы и учитывать локальные микроизменения. Это обеспечивает высокую точность и устойчивость прогнозов. Архитектура P-SSE обеспечивает эффективное глобальное поле восприятия при линейной вычислительной сложности, а интеграция рекуррентных блоков и механизмов двунаправленной корреляции позволяет модели последовательно уточнять оценки динамики, опираясь на контекст соседних временных отрезков.

В совокупности эти решения делают фреймворк мощным инструментом для построения адаптивных моделей, способных анализировать сложную и высокочастотную рыночную динамику.

Ссылки

• Perturbed State Space Feature Encoders for Optical Flow with Event Cameras
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы