Alım-satımda kaos teorisi (Bölüm 2): İncelemeye devam

Önceki makale özeti

İlk makalede kaos teorisinin temel kavramlarını ve bunların finansal piyasaların analizine uygulanmasını ele aldık. Çekiciler, fraktallar ve kelebek etkisi gibi temel kavramlara baktık ve bunların piyasa dinamiklerinde kendilerini nasıl gösterdiklerini tartıştık. Finans bağlamında kaotik sistemlerin özelliklerine ve volatilite kavramına özel dikkat gösterdik.

Ayrıca klasik kaos teorisi ile Bill Williams'ın yaklaşımını karşılaştırarak bu konseptlerin alım-satımdaki bilimsel ve pratik uygulamaları arasındaki farkları daha iyi anlamamızı sağladık. Finansal zaman serisini analiz etmek için bir araç olarak Lyapunov üssü makalede merkezi bir yer aldı. Hem teorik anlamını hem de MQL5 dilinde hesaplanmasının pratik bir uygulamasını ele aldık.

Makalenin son bölümünü, Lyapunov üssü kullanılarak trendin tersine dönmesi ve devam etmesinin istatistiksel analizine ayırdık. Örnek olarak H1 zaman diliminde EURUSD paritesini kullanarak, bu analizin pratikte nasıl uygulanabileceğini gösterdik ve elde edilen sonuçların yorumlanmasını tartıştık.

Makale, kaos teorisini finansal piyasalar bağlamında anlamanın temelini atmış ve bunu alım-satımda uygulamak için pratik araçlar sunmuştur. İkinci makalede, daha karmaşık yönlere ve bunların pratik uygulamalarına odaklanarak bu konudaki anlayışımızı derinleştirmeye devam edeceğiz.

İlk olarak piyasa kaosunun bir ölçüsü olarak fraktal boyuttan bahsedeceğiz.

Piyasa kaosunun bir ölçüsü olarak fraktal boyut

Fraktal boyut, kaos teorisinde ve finansal piyasalar da dahil olmak üzere karmaşık sistemlerin analizinde önemli bir rol oynayan bir kavramdır. Bir nesnenin veya sürecin karmaşıklığının ve kendine benzerliğinin nicel bir ölçüsünü sağlar, bu da onu piyasa hareketlerindeki rastgelelik derecesini değerlendirmek için özellikle yararlı kılar.

Finansal piyasalar bağlamında fraktal boyut, fiyat grafiklerinin "pürüzlülüğünü" ölçmek için kullanılabilir. Daha yüksek bir fraktal boyut daha karmaşık, kaotik bir fiyat yapısına işaret ederken, daha düşük bir boyut daha yumuşak, öngörülebilir bir hareketi ifade edebilir.

Fraktal boyutu hesaplamak için çeşitli yöntemler vardır. En popüler olanlardan biri kutu sayma yöntemidir. Bu yöntem, grafiği farklı büyüklüklerde hücrelerden oluşan bir ızgara ile kaplamayı ve grafiği farklı ölçeklerde kaplamak için gereken hücre sayısını saymayı içerir.

Yöntemi kullanarak fraktal boyut D'yi hesaplamak için denklem aşağıdaki gibidir:

D = -lim(ε→0) [log N(ε) / log(ε)]

Burada N(ε), nesneyi kaplamak için gereken ε büyüklüğündeki hücre sayısıdır.

Fraktal boyutun finansal piyasa analizine uygulanması, yatırımcılara ve analistlere piyasa hareketlerinin doğası hakkında ek bilgiler sağlayabilir. Örneğin:

• Piyasa modlarının belirlenmesi: Fraktal boyuttaki değişiklikler trendler, yatay hareketler veya kaotik dönemler gibi farklı piyasa durumları arasındaki geçişleri gösterebilir.
• Volatilite değerlendirmesi: Yüksek fraktal boyut genellikle volatilitenin arttığı dönemlere karşılık gelir.
• Tahmin: Fraktal boyutta zaman içinde meydana gelen değişikliklerin analiz edilmesi, gelecekteki piyasa hareketlerinin tahmin edilmesine yardımcı olabilir.
• Alım-satım stratejilerini optimize etme: Piyasanın fraktal yapısını anlamak, alım-satım algoritmalarının geliştirilmesine ve optimize edilmesine yardımcı olabilir.

Şimdi MQL5 dilinde fraktal boyutun hesaplanmasının pratik uygulamasına bakalım. MQL5'te fiyat grafiğinin fraktal boyutunu gerçek zamanlı olarak hesaplayacak bir gösterge geliştireceğiz.

Gösterge, fraktal boyutu hesaplamak için kutu sayma yöntemini kullanır.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Fractal Dimension"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpBoxSizesCount = 5;    // Number of box sizes
input int    InpMinBoxSize    = 2;    // Minimum box size
input int    InpMaxBoxSize    = 100;  // Maximum box size
input int    InpDataLength    = 1000; // Data length for calculation

double FractalDimensionBuffer[];

int OnInit()
{
   SetIndexBuffer(0, FractalDimensionBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Fractal Dimension");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      FractalDimensionBuffer[i] = CalculateFractalDimension(close, i);
   }
   
   return(rates_total);
}

double CalculateFractalDimension(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double x[]; 
   double y[];
   ArrayResize(x, InpBoxSizesCount);
   ArrayResize(y, InpBoxSizesCount);
   
   for(int i = 0; i < InpBoxSizesCount; i++)
   {
      int boxSize = (int)MathRound(MathPow(10, MathLog10(InpMinBoxSize) + (MathLog10(InpMaxBoxSize) - MathLog10(InpMinBoxSize)) * i / (InpBoxSizesCount - 1)));
      x[i] = MathLog(1.0 / boxSize);
      y[i] = MathLog(CountBoxes(price, index, boxSize));
   }
   
   double a, b;
   CalculateLinearRegression(x, y, InpBoxSizesCount, a, b);
   
   return a; // The slope of the regression line is the estimate of the fractal dimension
}

int CountBoxes(const double &price[], int index, int boxSize)
{
   double min = price[index - InpDataLength];
   double max = min;
   
   for(int i = index - InpDataLength + 1; i <= index; i++)
   {
      if(price[i] < min) min = price[i];
      if(price[i] > max) max = price[i];
   }
   
   return (int)MathCeil((max - min) / (boxSize * _Point));
}

void CalculateLinearRegression(const double &x[], const double &y[], int count, double &a, double &b)
{
   double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;
   
   for(int i = 0; i < count; i++)
   {
      sumX += x[i];
      sumY += y[i];
      sumXY += x[i] * y[i];
      sumX2 += x[i] * x[i];
   }
   
   a = (count * sumXY - sumX * sumY) / (count * sumX2 - sumX * sumX);
   b = (sumY - a * sumX) / count;
}

Gösterge, kutu sayma yöntemini kullanarak bir fiyat grafiğinin fraktal boyutunu hesaplar. Fraktal boyut, bir grafiğin "pürüzlülüğünün" veya karmaşıklığının bir ölçüsüdür ve piyasadaki kaos derecesini değerlendirmek için kullanılabilir.

Girdiler:

• InpBoxSizesCount - hesaplama için farklı "kutu" büyüklüklerinin sayısı
• InpMinBoxSize - minimum "kutu" büyüklüğü
• InpMaxBoxSize - maksimum "kutu" büyüklüğü
• InpDataLength - hesaplama için kullanılan mum sayısı

Gösterge çalışma algoritması:

1. Grafikteki her nokta için gösterge, son InpDataLength mumlarının verilerini kullanarak fraktal boyutu hesaplar.
2. Kutu sayma yöntemi, InpMinBoxSize ile InpMaxBoxSize arasında farklı "kutu" büyüklükleriyle uygulanır.
3. Grafiği kaplamak için gereken "kutu" sayısı her "kutu" büyüklüğü için hesaplanır.
4. "Kutu" sayısının logaritmasının "kutu" büyüklüğünün logaritmasına bağımlılık grafiği oluşturulur.
5. Lineer regresyon yöntemi ile bu grafiğin eğimi bulunur ve bu eğim fraktal boyutun ölçümüdür.

Fraktal boyuttaki değişiklikler piyasa modunda bir değişikliğe işaret edebilir.

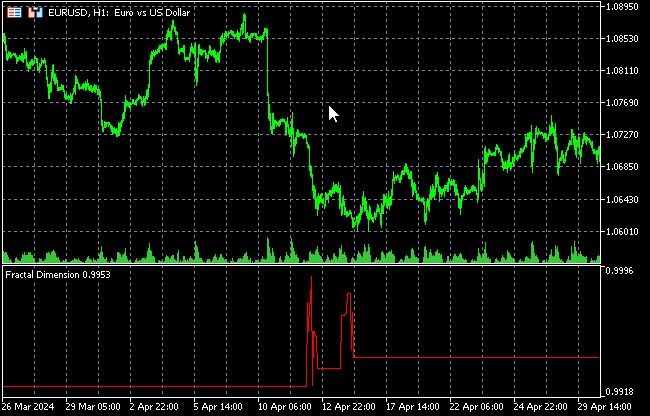
Fiyat hareketlerindeki gizli kalıpları ortaya çıkarmak için tekrarlama analizi

Tekrarlama analizi, finansal piyasaların dinamiklerini incelemek için etkili bir şekilde uygulanabilen güçlü bir doğrusal olmayan zaman serisi analizi yöntemidir. Bu yaklaşım, finansal piyasalar da dahil olmak üzere karmaşık dinamik sistemlerdeki tekrarlayan kalıpları görselleştirmeye ve nicel olarak değerlendirmeye olanak tanır.

Tekrarlama analizinin ana aracı tekrarlama grafiğidir. Bu diyagram, bir sistemin zaman içinde tekrar eden durumlarının görsel bir temsilidir. Bir tekrarlama diyagramında, i ve j zamanlarındaki durumlar belirli bir anlamda benzer ise bir nokta (i, j) renklendirilir.

Bir finansal zaman serisinin tekrarlama diyagramını oluşturmak için aşağıdaki adımları izleriz:

1. Faz uzayı yeniden yapılandırması: Gecikme yöntemini kullanarak, tek boyutlu fiyat zaman serisini çok boyutlu bir faz uzayına dönüştürüyoruz.
2. Benzerlik eşiğinin belirlenmesi: İki durumu benzer olarak kabul edeceğimiz bir kriter seçiyoruz.
3. Tekrarlama matrisinin oluşturulması: Her bir zaman noktası çifti için, karşılık gelen durumların benzer olup olmadığını belirliyoruz.
4. Görselleştirme: Tekrarlama matrisini, benzer durumların noktalarla belirtildiği iki boyutlu bir görüntü olarak gösteriyoruz.

Tekrarlama diyagramları, bir sistemdeki farklı dinamik türlerini tanımlamamıza olanak tanır:

• Homojen bölgeler durağan dönemleri gösterir.
• Çapraz çizgiler deterministik dinamikleri gösterir.
• Dikey ve yatay yapılar laminer koşullara işaret edebilir.
• Bir yapının olmaması rastgele bir sürecin karakteristik özelliğidir.

Bir tekrarlama diyagramındaki yapıları ölçmek için, tekrarlama yüzdesi, çapraz çizgilerin entropisi, maksimum çapraz çizgi uzunluğu vb. gibi çeşitli tekrarlama ölçütleri kullanılır.

Finansal zaman serisine tekrarlama analizi uygulamak şu konularda yardımcı olabilir:

1. Farklı piyasa modlarını belirleme (trend, yatay, kaotik durum)
2. Mod değişikliğini algılama
3. Piyasanın farklı dönemlerdeki öngörülebilirliğini değerlendirme
4. Gizli döngüsel kalıpları ortaya çıkarma

Alım-satımda tekrarlama analizinin pratik uygulaması için, bir tekrarlama diyagramı oluşturacak ve gerçek zamanlı olarak tekrarlama ölçütlerini hesaplayacak MQL5 dilinde bir gösterge geliştirebiliriz. Böyle bir gösterge, özellikle diğer teknik analiz yöntemleriyle birleştirildiğinde, alım-satım kararları vermek için ek bir araç olarak hizmet edebilir.

Bir sonraki bölümde, böyle bir göstergenin belirli bir uygulamasına bakacağız ve değerlerini bir alım-satım stratejisi bağlamında nasıl yorumlayacağımızı tartışacağız.

MQL5'te tekrarlama analizi göstergesi

Gösterge, finansal piyasaların dinamiklerini incelemek için tekrarlama analizi yöntemini uygular. Üç temel tekrarlama ölçütünü hesaplar: tekrarlama oranı, determinizm ve laminarite.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 3
#property indicator_plots   3
#property indicator_label1  "Recurrence Rate"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Determinism"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_label3  "Laminarity"
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrGreen

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 1;     // Time delay
input int    InpThreshold          = 10;    // Threshold (in points)
input int    InpWindowSize         = 200;   // Window size

double RecurrenceRateBuffer[];
double DeterminismBuffer[];
double LaminarityBuffer[];

int minRequiredBars;

int OnInit()
{
   SetIndexBuffer(0, RecurrenceRateBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, DeterminismBuffer, INDICATOR_DATA);
   SetIndexBuffer(2, LaminarityBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Recurrence Analysis");
   
   minRequiredBars = InpWindowSize + (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   if(rates_total < minRequiredBars) return(0);
   
   int start = (prev_calculated > 0) ? MathMax(prev_calculated - 1, minRequiredBars - 1) : minRequiredBars - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      CalculateRecurrenceMeasures(close, rates_total, i, RecurrenceRateBuffer[i], DeterminismBuffer[i], LaminarityBuffer[i]);
   }
   
   return(rates_total);
}

void CalculateRecurrenceMeasures(const double &price[], int price_total, int index, double &recurrenceRate, double &determinism, double &laminarity)
{
   if(index < minRequiredBars - 1 || index >= price_total)
   {
      recurrenceRate = 0;
      determinism = 0;
      laminarity = 0;
      return;
   }

   int windowStart = index - InpWindowSize + 1;
   int matrixSize = InpWindowSize - (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   int recurrenceCount = 0;
   int diagonalLines = 0;
   int verticalLines = 0;
   
   for(int i = 0; i < matrixSize; i++)
   {
      for(int j = 0; j < matrixSize; j++)
      {
         bool isRecurrent = IsRecurrent(price, price_total, windowStart + i, windowStart + j);
         if(isRecurrent)
         {
            recurrenceCount++;
            
            // Check for diagonal lines
            if(i > 0 && j > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j - 1))
               diagonalLines++;
            
            // Check for vertical lines
            if(i > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j))
               verticalLines++;
         }
      }
   }
   
   recurrenceRate = (double)recurrenceCount / (matrixSize * matrixSize);
   determinism = (recurrenceCount > 0) ? (double)diagonalLines / recurrenceCount : 0;
   laminarity = (recurrenceCount > 0) ? (double)verticalLines / recurrenceCount : 0;
}

bool IsRecurrent(const double &price[], int price_total, int i, int j)
{
   if(i < 0 || j < 0 || i >= price_total || j >= price_total) return false;

   double distance = 0;
   for(int d = 0; d < InpEmbeddingDimension; d++)
   {
      int offset = d * InpTimeDelay;
      if(i + offset >= price_total || j + offset >= price_total) return false;
      double diff = price[i + offset] - price[j + offset];
      distance += diff * diff;
   }
   distance = MathSqrt(distance);
   
   return (distance <= InpThreshold * _Point);
}

Göstergenin ana özellikleri:

Gösterge, fiyat grafiğinin altında ayrı bir pencerede görüntülenir ve verileri depolamak ve görüntülemek için üç arabellek kullanır. Gösterge üç ölçüt hesaplar: Genel tekrarlama düzeyini gösteren “tekrarlama oranı” (mavi çizgi), sistemin öngörülebilirliğinin bir ölçüsü olan “determinizm” (kırmızı çizgi) ve sistemin belirli bir durumda kalma eğilimini değerlendiren “laminarite” (yeşil çizgi).

Gösterge girdileri şunlardır: Faz uzayı yeniden yapılandırması için gömme boyutunu tanımlayan InpEmbeddingDimension (varsayılan olarak 3), yeniden yapılandırma sırasındaki zaman gecikmesi için InpTimeDelay (varsayılan olarak 1), nokta cinsinden durum benzerliği eşiği için InpThreshold (varsayılan olarak 10) ve analiz penceresinin büyüklüğünü ayarlamak için InpWindowSize (varsayılan olarak 200).

Göstergenin çalışma algoritması, fiyatların tek boyutlu bir zaman serisinden faz uzayının yeniden yapılandırılması için gecikme yöntemine dayanmaktadır. Analiz penceresindeki her nokta için, diğer noktalara göre "tekrarı" hesaplanır. Ardından, elde edilen tekrarlama yapısına dayalı olarak üç ölçüt hesaplanır: Toplam nokta sayısı içinde tekrarlama noktalarının payını belirten “tekrarlama oranı”, çapraz çizgiler oluşturan tekrarlama noktalarının payını belirten “determinizm” ve dikey çizgiler oluşturan tekrarlama noktalarının payını belirten “laminarite”.

Takens'in gömme (embedding) teoreminin volatilite tahmininde uygulanması

Takens'in gömme teoremi, finansal veriler de dahil olmak üzere zaman serisi analizi için önemli etkileri olan dinamik sistemler teorisinde temel bir sonuçtur. Bu teorem, dinamik bir sistemin zaman gecikmesi yöntemi kullanılarak sadece bir değişkenin gözlemlerinden yeniden oluşturulabileceğini belirtir.

Finansal piyasalar bağlamında Takens teoremi, fiyatların veya getirilerin tek boyutlu bir zaman serisinden çok boyutlu bir faz uzayını yeniden oluşturmamıza olanak tanır. Bu, özellikle finansal piyasaların önemli bir özelliği olan volatiliteyi analiz ederken kullanışlıdır.

Takens teoreminin volatiliteyi tahmin etmek için uygulanmasındaki temel adımlar şunlardır:

1. Faz uzayı yeniden yapılandırması:
   • Gömme boyutunun (m) seçilmesi
   • Zaman gecikmesinin (τ) seçilmesi
   • Orijinal zaman serisinden m boyutlu vektörler oluşturma
2. Yeniden yapılandırılan uzayın analizi:
   • Her nokta için en yakın komşuları bulma
   • Yerel nokta yoğunluğunun hesaplanması
3. Volatilite tahmini:
   • Gelecekteki volatiliteyi tahmin etmek için yerel yoğunluk bilgisini kullanma

Bu adımları daha ayrıntılı olarak inceleyelim.

Faz uzayı yeniden yapılandırması:

Kapanış fiyatlarından oluşan bir zaman serimiz olsun {p(t)}. Aşağıdaki gibi m boyutlu vektörler oluşturuyoruz:

x(t) = [p(t), p(t + τ), p(t + 2τ), ..., p(t + (m-1)τ)]

Burada m gömme boyutu ve τ zaman gecikmesidir.

Doğru m ve τ değerlerinin seçilmesi başarılı bir yeniden yapılandırma için kritik öneme sahiptir. Tipik olarak, τ karşılıklı bilgi veya otokorelasyon fonksiyonu yöntemleri kullanılarak seçilir, m ise yanlış en yakın komşu yöntemi kullanılarak seçilir.

Yeniden yapılandırılan uzayın analizi:

Faz uzayını yeniden yapılandırdıktan sonra, sistem çekicisinin yapısını analiz edebiliriz. Volatilite tahmini için, faz uzayındaki noktaların yerel yoğunluğu hakkında bilgi özellikle önemlidir.

Her x(t) noktası için k adet en yakın komşusunu buluruz (genellikle k 5 ila 20 aralığında seçilir) ve bu komşulara olan ortalama uzaklığı hesaplarız. Bu mesafe, yerel yoğunluğun ve dolayısıyla yerel volatilitenin bir ölçüsü olarak hizmet eder.

Volatilite tahmini

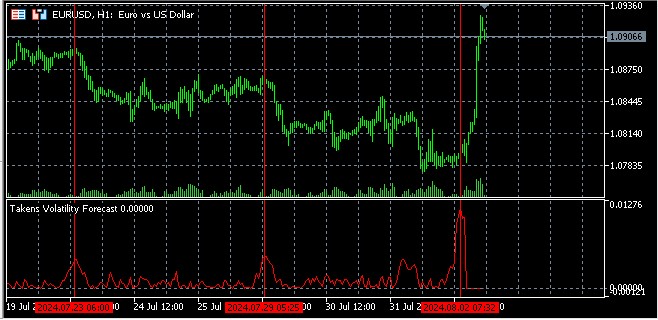
Yeniden yapılandırılan faz uzayını kullanarak volatiliteyi tahmin etmenin arkasındaki temel fikir, bu uzayda birbirine yakın olan noktaların yakın gelecekte benzer davranışlar sergilemesinin muhtemel olduğudur.

t+h zaman noktasında volatiliteyi tahmin etmek için şunları yaparız:

• Yeniden yapılandırılan uzayda mevcut x(t) noktası için k adet en yakın komşuyu buluruz.
• Bu komşular için volatiliteyi h adım ilerisi için hesaplarız.
• Bu volatilitelerin ortalamasını bir tahmin olarak kullanırız.

Matematiksel olarak bu aşağıdaki gibi ifade edilebilir:

σ̂(t+h) = (1/k) Σ σ(ti+h), burada ti, x(t)'nin k adet en yakın komşusunun indeksleridir.

Bu yaklaşımın avantajları:

• Doğrusal olmayan piyasa dinamiklerini dikkate alır.
• Getirilerin dağılımı hakkında varsayımlar gerektirmez.
• Volatilitedeki karmaşık kalıpları tespit edebiliriz.

Dezavantajları:

• Parametrelerin seçimine duyarlıdır (m, τ, k).
• Büyük miktarda veri için hesaplama açısından maliyetli olabilir.

Uygulama

Bu volatilite tahmin yöntemini uygulayacak bir MQL5 göstergesi oluşturalım:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Predicted Volatility"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double PredictedVolatilityBuffer[];

int OnInit()
{
   SetIndexBuffer(0, PredictedVolatilityBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Takens Volatility Forecast");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedVolatilityBuffer[i] = PredictVolatility(close, i);
      }
   }
   
   return(rates_total);
}

double PredictVolatility(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }
   
   double distances[];
   ArrayResize(distances, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double sum = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         sum += diff * diff;
      }
      distances[i] = sqrt(sum);
   }
   
   int sortedIndices[];
   ArrayCopy(sortedIndices, distances);
   ArraySort(sortedIndices);
   
   double sumVolatility = 0;
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - sortedIndices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double futureReturn = (price[neighborIndex + InpForecastHorizon] - price[neighborIndex]) / price[neighborIndex];
      sumVolatility += MathAbs(futureReturn);
   }
   
   return sumVolatility / InpNeighbors;
}

Zaman gecikmesi ve gömme boyutunu belirleme yöntemleri

Takens teoremini kullanarak faz uzayını yeniden yapılandırırken, iki anahtar parametrenin doğru seçilmesi kritik önem taşır: zaman gecikmesi (τ) ve gömme boyutu (m). Bu parametrelerin yanlış seçimi, yanlış yeniden yapılandırmaya ve sonuç olarak hatalı sonuçlara yol açabilir. Bu parametreleri belirlemek için iki ana yöntemi ele alalım.

Zaman gecikmesini belirlemek için otokorelasyon fonksiyonu (AutoCorrelation Function, ACF) yöntemi

Yöntem, otokorelasyon fonksiyonunun ilk olarak sıfırı geçtiği veya belirli bir düşük değere, örneğin başlangıç değerinin 1/e'sine ulaştığı bir τ zaman gecikmesi seçme fikrine dayanmaktadır. Bu, zaman serisinin birbirini izleyen değerlerinin birbirinden yeterince bağımsız hale geldiği bir gecikme seçilmesine olanak tanır.

ACF yönteminin MQL5'te uygulanması aşağıdaki gibi görünebilir:

int FindOptimalLagACF(const double &price[], int maxLag, double threshold = 0.1)
{
   int size = ArraySize(price);
   if(size <= maxLag) return 1;
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += price[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(price[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (price[i] - mean) * (price[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

Burada ilk olarak zaman serisinin ortalamasını ve varyansını hesaplıyoruz. Ardından, 1'den maxLag'e kadar her gecikme için otokorelasyon fonksiyonunun değerini hesaplıyoruz. ACF değeri belirli bir eşiğe (varsayılan olarak 0.1) eşit veya daha az olduğunda, bu gecikmeyi optimum zaman gecikmesi olarak geri döndürüyoruz.

ACF yönteminin artıları ve eksileri vardır. Bir yandan uygulaması kolay ve sezgiseldir. Öte yandan, verilerdeki doğrusal olmayan bağımlılıkları dikkate almaz, bu da genellikle doğrusal olmayan davranış sergileyen finansal zaman serilerini analiz ederken önemli bir dezavantaj olabilir.

Zaman gecikmesini belirlemek için karşılıklı bilgi (Mutual Information, MI) yöntemi

Bu yöntem bilgi teorisine dayanmaktadır ve verilerdeki doğrusal olmayan bağımlılıkları dikkate alabilmektedir. Buradaki fikir, karşılıklı bilgi fonksiyonunun ilk yerel minimumuna karşılık gelen bir τ gecikmesi seçmektir.

Karşılıklı bilgi yönteminin MQL5'te uygulanması aşağıdaki gibi görünebilir:

double CalculateMutualInformation(const double &price[], int lag, int bins = 20)
{
   int size = ArraySize(price);
   if(size <= lag) return 0;
   
   double minPrice = price[ArrayMinimum(price)];
   double maxPrice = price[ArrayMaximum(price)];
   double binSize = (maxPrice - minPrice) / bins;
   
   int histogram[];
   ArrayResize(histogram, bins * bins);
   ArrayInitialize(histogram, 0);
   
   int totalPoints = 0;
   
   for(int i = 0; i < size - lag; i++)
   {
      int bin1 = (int)((price[i] - minPrice) / binSize);
      int bin2 = (int)((price[i + lag] - minPrice) / binSize);
      if(bin1 >= 0 && bin1 < bins && bin2 >= 0 && bin2 < bins)
      {
         histogram[bin1 * bins + bin2]++;
         totalPoints++;
      }
   }
   
   double mutualInfo = 0;
   for(int i = 0; i < bins; i++)
   {
      for(int j = 0; j < bins; j++)
      {
         if(histogram[i * bins + j] > 0)
         {
            double pxy = (double)histogram[i * bins + j] / totalPoints;
            double px = 0, py = 0;
            for(int k = 0; k < bins; k++)
            {
               px += (double)histogram[i * bins + k] / totalPoints;
               py += (double)histogram[k * bins + j] / totalPoints;
            }
            mutualInfo += pxy * MathLog(pxy / (px * py));
         }
      }
   }
   
   return mutualInfo;
}

int FindOptimalLagMI(const double &price[], int maxLag)
{
   double minMI = DBL_MAX;
   int optimalLag = 1;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double mi = CalculateMutualInformation(price, lag);
      if(mi < minMI)
      {
         minMI = mi;
         optimalLag = lag;
      }
      else if(mi > minMI)
      {
         break;
      }
   }
   
   return optimalLag;
}

Burada ilk olarak orijinal seri ile belirli bir gecikme için kaydırılmış versiyonu arasındaki karşılıklı bilgiyi hesaplayan CalculateMutualInformation fonksiyonunu tanımlıyoruz. Ardından, FindOptimalLagMI fonksiyonunda, farklı gecikme değerleri üzerinde yineleme yaparak karşılıklı bilginin ilk yerel minimumunu arıyoruz.

Karşılıklı bilgi yöntemi, verilerdeki doğrusal olmayan bağımlılıkları hesaba katabildiği için ACF yöntemine göre bir avantaja sahiptir. Bu da onu genellikle karmaşık, doğrusal olmayan davranışlar sergileyen finansal zaman serilerini analiz etmek için daha uygun hale getirir. Ancak bu yöntemin uygulanması daha karmaşıktır ve daha fazla hesaplama gerektirir.

ACF ve MI yöntemleri arasındaki seçim, belirli göreve ve analiz edilen verilerin özelliklerine bağlıdır. Bazı durumlarda, her iki yöntemi de kullanmak ve sonuçları karşılaştırmak faydalı olabilir. Özellikle finansal zaman serileri için optimum zaman gecikmesinin zaman içinde değişebileceğini hatırlamak da önemlidir, bu nedenle bu parametrenin periyodik olarak yeniden hesaplanması tavsiye edilebilir.

Optimum gömme boyutunu belirlemek için yanlış en yakın komşular algoritması

Optimum zaman gecikmesi belirlendikten sonra, faz uzayı yeniden yapılandırmasındaki bir sonraki önemli adım uygun bir gömme boyutunun seçilmesidir. Bu amaçla kullanılan en popüler yöntemlerden biri yanlış en yakın komşular (False Nearest Neighbors, FNN) algoritmasıdır.

FNN algoritmasının fikri, faz uzayındaki çekicinin geometrik yapısının doğru bir şekilde yeniden üretileceği bir minimum gömme boyutu bulmaktır. Algoritma, doğru bir şekilde yeniden yapılandırılan bir faz uzayında, daha yüksek boyutlu bir uzaya geçerken yakın noktaların yakın kalması gerektiği varsayımına dayanmaktadır.

Şimdi FNN algoritmasının MQL5 dilinde uygulanmasına bakalım:

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

int FindOptimalEmbeddingDimension(const double &price[], int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = ArraySize(price);
   int minRequiredSize = (maxDim - 1) * delay + 1;
   if(size < minRequiredSize) return 1;
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = price[i - k * delay] - price[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(price, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

IsFalseNeighbor fonksiyonu iki noktanın yanlış komşular olup olmadığını belirler. Mevcut boyuttaki ve bir birim daha yüksek boyuttaki noktalar arasındaki mesafeyi hesaplar. Mesafedeki göreceli değişim belirli bir eşiği aşarsa, noktalar yanlış komşular olarak kabul edilir.

FindOptimalEmbeddingDimension ana fonksiyonu 1'den maxDim'e kadar olan boyutlar arasında yineleme yapar. Her boyut için, zaman serisinin tüm noktalarını gözden geçiriyoruz. Her nokta için mevcut boyuttaki en yakın komşuyu buluyoruz. Daha sonra IsFalseNeighbor fonksiyonunu kullanarak bulunan komşunun yanlış olup olmadığını kontrol ediyoruz. Toplam komşu sayısını ve yanlış komşu sayısını sayıyoruz. Ardından, yanlış komşuların oranını hesaplıyoruz. Yanlış komşuların oranı belirtilen tolerans eşiğinden azsa, mevcut boyutu optimum olarak kabul ediyoruz ve geri döndürüyoruz.

Algoritmanın birkaç önemli parametresi vardır. delay - önceden ACF veya MI yöntemi tarafından belirlenen zaman gecikmesi. maxDim - dikkate alınacak maksimum gömme boyutu. threshold - yanlış komşuları tespit etme eşiği. tolerance - yanlış komşuların oranı için tolerans eşiği. Bu parametrelerin seçimi sonucu önemli ölçüde etkileyebilir, bu nedenle farklı değerlerle denemeler yapmak ve analiz edilen verilerin özelliklerini dikkate almak önemlidir.

FNN algoritmasının bir dizi avantajı vardır. Faz uzayındaki verilerin geometrik yapısını dikkate alır. Yöntem, verilerdeki gürültüye karşı oldukça dayanıklıdır. Çalışılan sistemin doğası hakkında herhangi bir ön varsayım gerektirmez.

MQL5'te kaos teorisine dayalı tahmin yönteminin uygulanması

Faz uzayını yeniden yapılandırmak için optimum parametreleri belirledikten sonra, kaos teorisine dayalı tahmin yöntemini uygulamaya başlayabiliriz. Bu yöntem, faz uzayındaki yakın durumların yakın gelecekte benzer bir evrim geçireceği fikrine dayanmaktadır.

Yöntemin temel fikri şu şekildedir: sistemin geçmişte mevcut duruma en yakın olan durumlarını buluruz. Gelecekteki davranışlarına dayanarak, mevcut durum için bir tahmin yaparız. Bu yaklaşım analog veya en yakın komşu yöntemi olarak bilinir.

Bu yöntemin MetaTrader 5 için bir gösterge olarak uygulanmasına bakalım. Gösterge aşağıdaki adımları gerçekleştirecektir:

1. Zaman gecikmesi yöntemi kullanılarak faz uzayı yeniden yapılandırması.
2. Sistemin mevcut durumu için k adet en yakın komşunun bulunması.
3. Bulunan komşuların davranışlarına dayanarak gelecekteki değerin tahmin edilmesi.

İşte bu yöntemi uygulayan göstergenin kodu:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_plots   2
#property indicator_label1  "Actual"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Predicted"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double ActualBuffer[];
double PredictedBuffer[];

int OnInit()
{
   SetIndexBuffer(0, ActualBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PredictedBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, _Digits);
   IndicatorSetString(INDICATOR_SHORTNAME, "Chaos Theory Predictor");
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      ActualBuffer[i] = close[i];
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedBuffer[i] = PredictPrice(close, i);
      }
   }
   
   return(rates_total);
}

double PredictPrice(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;

   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }

   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);

   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }

   // Custom sort function for sorting distances and indices together
   SortDistancesWithIndices(distances, indices, dataSize);

   double prediction = 0;
   double weightSum = 0;

   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - indices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double weight = 1.0 / (distances[i] + 0.0001);  // Avoid division by zero
      prediction += weight * price[neighborIndex + InpForecastHorizon];
      weightSum += weight;
   }

   return prediction / weightSum;
}

void SortDistancesWithIndices(double &distances[], int &indices[], int size)
{
   for(int i = 0; i < size - 1; i++)
   {
      for(int j = i + 1; j < size; j++)
      {
         if(distances[i] > distances[j])
         {
            double tempDist = distances[i];
            distances[i] = distances[j];
            distances[j] = tempDist;

            int tempIndex = indices[i];
            indices[i] = indices[j];
            indices[j] = tempIndex;
         }
      }
   }
}

Gösterge faz uzayını yeniden yapılandırır, mevcut durum için en yakın komşuları bulur ve tahminler yapmak için gelecekteki değerlerini kullanır. Hem mevcut hem de tahmin edilen değerleri bir grafik üzerinde göstererek tahminin kalitesini görsel olarak değerlendirmemizi sağlar.

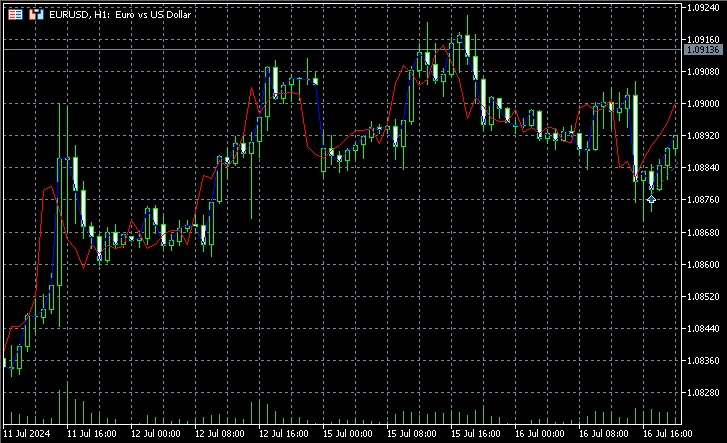
Uygulamanın önemli yönleri arasında tahmin için ağırlıklı ortalama kullanımı yer almaktadır; burada her bir komşunun ağırlığı mevcut duruma olan uzaklığıyla ters orantılıdır. Bu, daha yakın komşuların daha doğru bir tahmin vermesinin muhtemel olduğunu dikkate almamızı sağlar. Ekran görüntülerine bakılırsa, gösterge fiyat hareketinin yönünü birkaç çubuk önceden tahmin ediyor.

Konsept Uzman Danışman oluşturma

En ilginç kısma geldik. Aşağıda kaos teorisine dayalı tam otomatik çalışma için kod bulunmaktadır:

#property copyright "Copyright 2024, Author"
#property link      "https://www.example.com"
#property version   "1.00"
#property strict

#include <Arrays\ArrayObj.mqh>
#include <Trade\Trade.mqh>
CTrade Trade;
input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period
input double InpLotSize            = 0.1;   // Lot size

ulong g_ticket = 0;
datetime g_last_bar_time = 0;
double optimalTimeDelay;
double optimalEmbeddingDimension;
int OnInit()
{
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
}

void OnTick()
{  
   OptimizeParameters();
   
   if(g_last_bar_time == iTime(_Symbol, PERIOD_CURRENT, 0)) return;
   g_last_bar_time = iTime(_Symbol, PERIOD_CURRENT, 0);
   
   double prediction = PredictPrice(iClose(_Symbol, PERIOD_CURRENT, 0), 0);
   Comment(prediction);
   
   if(prediction > iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close selling
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close SELL position: ", GetLastError());
         }
      }
      
      // Open buy
      double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
      ulong ticket = Trade.Buy(InpLotSize, _Symbol, ask, 0, 0, "ChaosBuy");
      if(ticket == 0)
         Print("Failed to open BUY position: ", GetLastError());
   }
   else if(prediction < iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close buying
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close BUY position: ", GetLastError());
         }
      }
      
      // Open sell
      double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
      ulong ticket = Trade.Sell(InpLotSize, _Symbol, bid, 0, 0, "ChaosSell");
      if(ticket == 0)
         Print("Failed to open SELL position: ", GetLastError());
   }
}

double PredictPrice(double price, int index)
{
   int vectorSize = optimalEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      currentVector[i] = iClose(_Symbol, PERIOD_CURRENT, index + i * optimalTimeDelay);
   }
   
   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         double diff = currentVector[j] - iClose(_Symbol, PERIOD_CURRENT, index + i + j * optimalTimeDelay);
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }
   
   // Use SortDoubleArray to sort by 'distances' array values
   SortDoubleArray(distances, indices);
   
   double prediction = 0;
   double weightSum = 0;
   
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index + indices[i];
      double weight = 1.0 / (distances[i] + 0.0001);
      prediction += weight * iClose(_Symbol, PERIOD_CURRENT, neighborIndex + InpForecastHorizon);
      weightSum += weight;
   }
   
   return prediction / weightSum;
}

void SortDoubleArray(double &distances[], int &indices[])
{
    int size = ArraySize(distances);
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = i + 1; j < size; j++)
        {
            if(distances[i] > distances[j])
            {
                // Swap distances
                double tempDist = distances[i];
                distances[i] = distances[j];
                distances[j] = tempDist;
                
                // Swap corresponding indices
                int tempIndex = indices[i];
                indices[i] = indices[j];
                indices[j] = tempIndex;
            }
        }
    }
}

int FindOptimalLagACF(int maxLag, double threshold = 0.1)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += series[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(series[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (series[i] - mean) * (series[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

int FindOptimalEmbeddingDimension(int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = series[i - k * delay] - series[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(series, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

void OptimizeParameters()
{
   double optimalTimeDelay = FindOptimalLagACF(50);
   double optimalEmbeddingDimension = FindOptimalEmbeddingDimension(optimalTimeDelay, 10);
   Print("Optimal Time Delay: ", optimalTimeDelay);
   Print("Optimal Embedding Dimension: ", optimalEmbeddingDimension);
}

Bu kod, finansal piyasalarda fiyatları tahmin etmek için kaos teorisi kavramlarını kullanan bir MetaTrader 5 Uzman Danışmanıdır. Uzman Danışman, yeniden yapılandırılan faz uzayında en yakın komşu yöntemine dayalı tahmin yöntemini uygular.

Uzman Danışman aşağıdaki girdilere sahiptir:

• InpEmbeddingDimension - faz uzayı yeniden yapılandırması için gömme boyutu (varsayılan olarak 3)
• InpTimeDelay - yeniden yapılandırma için zaman gecikmesi (varsayılan olarak 5)
• InpNeighbors - tahmin için en yakın komşu sayısı (varsayılan olarak 10)
• InpForecastHorizon - tahmin ufku (varsayılan olarak 10)
• InpLookback - analiz için geriye bakma dönemi (varsayılan olarak 1000)
• InpLotSize - işlem için lot büyüklüğü (varsayılan olarak 0.1)

Uzman Danışman şu şekilde çalışır:

1. Her yeni çubukta, sırasıyla otokorelasyon fonksiyonu (ACF) yöntemini ve yanlış en yakın komşular (FNN) algoritmasını kullanarak optimalTimeDelay ve optimalEmbeddingDimension parametrelerini optimize eder.
2. Daha sonra en yakın komşular yöntemini kullanarak sistemin mevcut durumuna göre bir fiyat tahmini yapar.
3. Fiyat tahmini mevcut fiyattan yüksekse, Uzman Danışman tüm açık satış pozisyonlarını kapatır ve yeni bir alış pozisyonu açar. Fiyat tahmini mevcut fiyattan düşükse, Uzman Danışman tüm açık alış pozisyonlarını kapatır ve yeni bir satış pozisyonu açar.

Uzman Danışman, aşağıdakileri yapan PredictPrice fonksiyonunu kullanır:

• Optimum gömme boyutunu ve zaman gecikmesini kullanarak faz uzayını yeniden yapılandırır.
• Sistemin mevcut durumu ile geriye bakma dönemindeki tüm durumlar arasındaki mesafeleri bulur.
• Durumları artan mesafeye göre sıralar.
• InpNeighbors adet en yakın komşu için gelecekteki fiyatların ağırlıklı ortalamasını hesaplar; burada her komşunun ağırlığı mevcut duruma olan uzaklığıyla ters orantılıdır.
• Fiyat tahmini olarak ağırlıklı ortalama geri döndürür.

Uzman Danışman ayrıca sırasıyla optimumTimeDelay ve optimumEmbeddingDimension parametrelerini optimize etmek için kullanılan FindOptimalLagACF ve FindOptimalEmbeddingDimension fonksiyonlarını da içerir.

Genel olarak Uzman Danışman, kaos teorisi kavramlarını kullanarak finansal piyasalarda fiyatların tahmin edilmesine yönelik yenilikçi bir yaklaşım sunmaktadır. Yatırımcıların daha bilinçli kararlar vermesine yardımcı olabilir ve potansiyel olarak yatırım getirilerini artırabilir.

Otomatik optimizasyon ile test etme

Uzman Danışmanımızın çalışmasını birkaç sembol üzerinde değerlendirelim. İlk döviz paritesi, EURUSD, 01.01.2016 tarihinden itibaren:

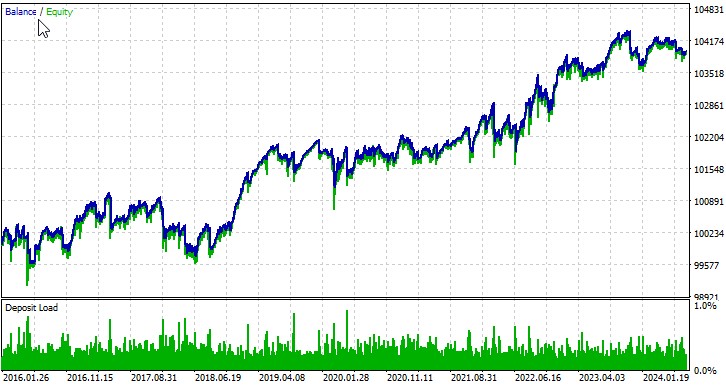
İkinci parite, AUDUSD:

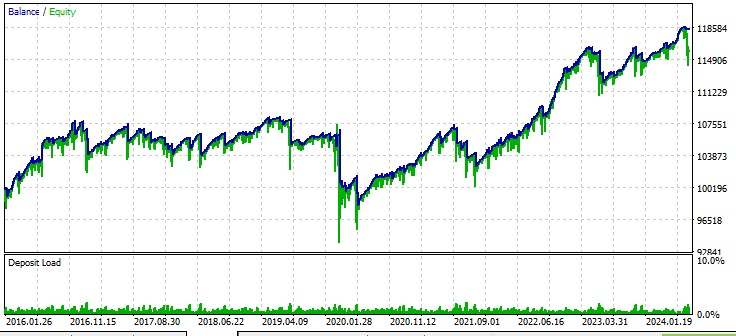
Üçüncü parite, GBPUSD:

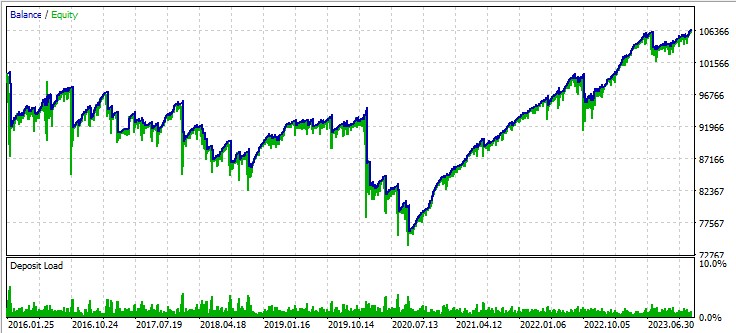
Sonraki adımlar

Kaos teorisine dayalı Uzman Danışmanımızın daha da geliştirilmesi için derinlemesine test ve optimizasyon yapılması gerekecektir. Farklı piyasa koşullarındaki etkinliğini daha iyi anlamak için farklı zaman dilimlerinde ve finansal enstrümanlarda geniş ölçekli testlere ihtiyaç vardır. Makine öğrenimi yöntemlerinin kullanılması, Uzman Danışman parametrelerinin optimize edilmesine yardımcı olarak değişen piyasa gerçeklerine uyarlanabilirliğini artırabilir.

Risk yönetim sisteminin iyileştirilmesine özellikle dikkat edilmelidir. Mevcut piyasa volatilitesini ve kaotik volatilite tahminlerini dikkate alan dinamik pozisyon boyutlandırma yönetiminin uygulanması, strateji direncini önemli ölçüde artırabilir.

Sonuç

Bu makalede, kaos teorisinin finansal piyasaların analizi ve tahminine uygulanmasını inceledik. Faz uzayı yeniden yapılandırması, optimum gömme boyutunun ve zaman gecikmesinin belirlenmesi ve en yakın komşu tahmin yöntemi gibi temel kavramları inceledik.

Geliştirdiğimiz Uzman Danışman, kaos teorisini algoritmik alım-satımda kullanma potansiyelini göstermektedir. Çeşitli döviz pariteleri üzerindeki test sonuçları, stratejinin farklı enstrümanlar üzerinde değişen derecelerde başarıya sahip olsa da kar üretebildiğini göstermektedir.

Bununla birlikte, kaos teorisinin finansa uygulanmasının bir dizi zorluğu beraberinde getirdiğini belirtmek önemlidir. Finansal piyasalar, birçoğunun bir modelde dikkate alınması zor, hatta imkansız olan birçok faktörden etkilenen son derece karmaşık sistemlerdir. Dahası, kaotik sistemlerin doğası uzun vadeli tahminleri temelde imkansız kılar - bu ciddi araştırmacıların ana varsayımlarından biridir.

Sonuç olarak, kaos teorisi piyasa tahmini için Kutsal Kase olmasa da, finansal analiz ve algoritmik alım-satım alanlarında daha fazla araştırma ve geliştirme için umut verici bir alanı temsil etmektedir. Kaos teorisi yöntemlerini makine öğrenimi ve büyük veri analizi gibi diğer yaklaşımlarla birleştirmenin yeni olanaklar sunabileceği açıktır.