Exemplo de Otimização Estocástica e Controle Ótimo

Introdução à Modelagem Estocástica e Otimização de Controle

Modelagem estocástica e otimização de controle são métodos matemáticos que ajudam a resolver problemas sob incerteza. Eles são usados em finanças, engenharia, inteligência artificial e muitas outras áreas.

A modelagem estocástica é usada para descrever sistemas com elementos aleatórios, como movimentos de preços no mercado de ações ou uma fila em um restaurante. Ela se baseia em variáveis aleatórias, distribuições de probabilidade e processos estocásticos. Métodos como Monte Carlo e cadeias de Markov podem modelar esses processos e prever seu comportamento.

A otimização de controle ajuda a encontrar melhores soluções para controlar sistemas. Ela é usada para automatizar e melhorar o funcionamento de vários processos, desde a direção de veículos até a operação de plantas químicas. Os métodos básicos incluem o controlador quadrático linear, controle preditivo baseado em modelo e aprendizado por reforço. A otimização de controle estocástico combina ambas as abordagens e é aplicada a problemas onde decisões precisam ser tomadas mesmo sem informações completas sobre o futuro, por exemplo, em investimentos ou gestão de cadeias de suprimento.

Esses métodos permitem modelar sistemas incertos e tomar decisões informadas em ambientes complexos, tornando-se ferramentas importantes no mundo moderno.

EA

O consultor SMOC (Smart Money Optimal Control) usa uma combinação de indicadores técnicos, modelos matemáticos e métodos de gerenciamento de risco para tomar decisões de negociação no mercado Forex como um exemplo simples demonstrando suas capacidades.

Principais características:

1. Modelo de Gestão Preditiva: o EA usa um algoritmo de controle ótimo para prever movimentos futuros de preços e tomar decisões de negociação.
2. Parâmetros adaptativos: o sistema ajusta o horizonte de previsão e o tamanho do lote dependendo da volatilidade do mercado e do rebaixamento da conta.
3. Múltiplos indicadores técnicos: Inclui médias móveis simples (SMA), SAR parabólico, índice de força relativa (RSI) e amplitude verdadeira média (ATR) para análise de tendência e volatilidade.
4. Stop Loss e Take Profit dinâmicos: o EA calcula e atualiza os níveis de SL e TP com base na volatilidade do mercado.
5. Gerenciamento de risco: Inclui funções para ajustar o tamanho da posição com base no saldo da conta e no rebaixamento.

Possíveis áreas de aplicação:

• Estratégias de negociação de médio e longo prazo
• Mercados com tendências acentuadas
• Portfólios que exigem gerenciamento de risco complexo

Prós:

1. Abordagem adaptativa: o sistema se adapta às mudanças nas condições de mercado, potencialmente aumentando sua resiliência.
2. Análise complexa: ao combinar múltiplos indicadores e modelos matemáticos, visa refletir diversos aspectos do comportamento do mercado.
3. Contabilização de risco: o advisor inclui proteção contra rebaixamentos e determinação dinâmica do tamanho da posição.
4. Registro detalhado: Um arquivo de log é mantido para análise de desempenho e depuração.

Contras:

1. Complexidade: Algoritmos complexos podem tornar o sistema difícil de entender e otimizar.
2. Exigente computacionalmente: Os cálculos de controle ótimo podem ser pesados, limitando seu uso em sistemas menos potentes.
3. Possível overfitting: Com muitos parâmetros e indicadores, há risco de ajuste excessivo aos dados históricos.
4. Pressuposto de mercado: A eficácia da estratégia se baseia no pressuposto de que o comportamento passado dos preços pode prever os movimentos futuros, o que nem sempre é verdade nos mercados financeiros.

Principais características do advisor SMOC

Controle Preditivo Baseado em Modelo (MPC): o EA usa um algoritmo de controle ótimo para prever os movimentos futuros de preços e tomar decisões de negociação. Isso é implementado na função OptimalControl().

//+------------------------------------------------------------------+
//| Function for optimal control using Model Predictive Control      |
//+------------------------------------------------------------------+
int OptimalControl( double currentPrice)
  {
   int predictionHorizon = CalculateAdaptiveHorizon();
   double mu = EstimateDrift();
   double sigma = EstimateVolatility();
   double baseThreshold = 0.001 ;
   double decisionThreshold = baseThreshold * ( 1 + ( 1 - successRate));
   double dt = 1.0 / 1440.0 ;

   double bestExpectedReturn = - DBL_MAX ;
   int bestDecision = 0 ;
   double bestU1 = 0 , bestU2 = 0 ;

// Optimize the search space
   double u1Start = 0.01 , u1End = 0.99 , u1Step = 0.01 ;
   double u2Start = 0.01 , u2End = 0.99 , u2Step = 0.01 ;

// Calculate historical average price
   int lookbackPeriod = 20 ; // You can adjust this
   double historicalPrices[];
   ArraySetAsSeries (historicalPrices, true );
   CopyClose ( Symbol (), PERIOD_CURRENT , 0 , lookbackPeriod, historicalPrices);
   double avgHistoricalPrice = ArraySum(historicalPrices) / lookbackPeriod;

   for ( double u1 = u1Start; u1 <= u1End; u1 += u1Step)
     {
       for ( double u2 = u2Start; u2 <= u2End; u2 += u2Step)
        {
         double expectedReturn = CalculateExpectedReturn(currentPrice, mu, sigma, dt, predictionHorizon, u1, u2);

         // Compare with historical average
         if (currentPrice > avgHistoricalPrice)
           {
            expectedReturn *= - 1 ; // Invert expected return to favor selling when price is high
           }

         if (expectedReturn > bestExpectedReturn)
           {
            bestExpectedReturn = expectedReturn;
            bestU1 = u1;
            bestU2 = u2;
           }
        }
     }

   LogMessage( StringFormat ( "OptimalControl - Best u1: %f, Best u2: %f, Best Expected Return: %f, Decision Threshold %f" ,
                           bestU1, bestU2, bestExpectedReturn, decisionThreshold));

   if (bestExpectedReturn > decisionThreshold)
       return 1 ; // Buy
   if (bestExpectedReturn < decisionThreshold)
       return - 1 ; // Sell
   return 0 ; // Hold
  }

Utiliza o Controle Preditivo Baseado em Modelo (MPC) para tomar decisões ótimas de negociação. A função OptimalControl é o núcleo deste algoritmo, projetada para determinar se deve comprar, vender ou manter, com base nas condições atuais de mercado e nas previsões.

A função OptimalControl recebe o preço atual como entrada e retorna um número inteiro representando a decisão de negociação:

• 1 para compra
• -1 para venda
• 0 para manter

Componentes-chave

1. Horizonte de Previsão Adaptativo: A função calcula um horizonte de previsão adaptativo, permitindo ao algoritmo ajustar o intervalo de previsão de acordo com as condições de mercado.
2. Avaliação de Parâmetros de Mercado: Avalia parâmetros-chave do mercado:
   • Deriva (μ): Retorno esperado de um ativo
   • Volatilidade (σ): taxa de variação no preço de um ativo.
3. Limiar de Decisão: O limiar dinâmico é calculado com base no limiar base e na taxa de sucesso do algoritmo. Isso adapta a sensibilidade do algoritmo às mudanças do mercado.
4. Processo de Otimização: A função utiliza busca em grade (grid search) para otimizar dois parâmetros de controle (u1 e u2) em um espaço de busca definido.
5. Comparação de Preços Históricos: O preço atual é comparado com a média histórica para ajustar a estratégia dependendo se o preço atual está relativamente alto ou baixo.
6. Cálculo do Retorno Esperado: Para cada combinação de parâmetros de controle, o retorno esperado é calculado usando uma função separada (não mostrada neste trecho de código).
7. Tomada de Decisão: Com base no melhor retorno esperado e no limiar de decisão, é tomada a decisão de comprar, vender ou manter o ativo.

Revisão detalhada

1. A função começa inicializando variáveis e calculando os parâmetros necessários.
2. Em seguida, entra em um loop aninhado para encontrar os parâmetros ótimos de controle (u1 e u2).
3. Para cada combinação de u1 e u2, o retorno esperado é calculado.
4. Se o preço atual estiver acima da média histórica, ele inverte o retorno esperado. Isso cria uma tendência a vender quando os preços estão altos e comprar quando estão baixos.
5. Ela rastreia o melhor retorno esperado e os parâmetros correspondentes.
6. Após a otimização, os melhores parâmetros e a rentabilidade esperada são registrados.
7. Por fim, o retorno esperado é comparado ao valor limiar para tomar a decisão de negociação.

Ideias principais

• O algoritmo se adapta às condições de mercado usando um horizonte adaptativo e um limiar dinâmico.
• Envolve tanto otimização de curto prazo (usando a abordagem MPC) quanto compreensão de longo prazo de tendências (com base em preços históricos).
• O uso de busca em grade para otimização permite uma exploração completa do espaço de parâmetros, potencialmente levando a decisões mais robustas.

Possíveis melhorias

1. A busca em grade pode ser substituída por um algoritmo de otimização mais eficiente para melhorar o desempenho.
2. A comparação de preços históricos pode ser mais complexa, incluindo múltiplos períodos de tempo.
3. Recursos de gerenciamento de risco podem ser adicionados para equilibrar otimização de retorno com minimização de risco.

 /+------------------------------------------------------------------+
//| Calculate expected return for given parameters                   |
//+------------------------------------------------------------------+
double CalculateExpectedReturn( double currentPrice, double mu, double sigma, double dt, int horizon, double u1, double u2)
  {
   double tempPrice = currentPrice;
   double totalReturn = 0 ;

   for ( int i = 0 ; i < horizon; i++)
     {
       double Z = MathSqrt (- 2.0 * MathLog (u1)) * MathCos ( 2.0 * M_PI * u2);
       double nextPrice = tempPrice * MathExp ((mu - 0.5 * sigma * sigma) * dt + sigma * MathSqrt (dt) * Z);
      totalReturn += nextPrice - tempPrice;
      tempPrice = nextPrice;
     }

   return totalReturn / horizon;
  }

É um componente crítico em modelos financeiros e sistemas de negociação algorítmica. Esta função estima o retorno esperado de um ativo ao longo de um horizonte de tempo especificado usando um processo estocástico conhecido como movimento browniano geométrico (GBM).

 double CalculateExpectedReturn( double currentPrice, double mu, double sigma, double dt, int horizon, double u1, double u2)

Parâmetros

1. currentPrice : Preço atual do ativo
2. mu : Parâmetro de deriva (retorno esperado)
3. sigma: parâmetro de volatilidade
4. dt: Passo de tempo (normalmente 1/número de etapas por ano)
5. Horizon: O número de passos de tempo a serem simulados.
6. u1, u2: Números aleatórios usados para gerar variáveis aleatórias normalmente distribuídas.

Visão geral das funções

Esta função modela o caminho de preço de um ativo usando o modelo de movimento browniano geométrico, que é amplamente utilizado em matemática financeira para modelar preços de ações. Em seguida, ela calcula o retorno médio ao longo do caminho modelado.

Explicação detalhada

1. Inicialização:
   • tempPrice é inicializado com o preço atual.
   • totalReturn é definido como 0 para acumular os retornos.
2. Loop de simulação: A função entra em um loop que percorre o número de vezes definido pelo horizonte. Em cada iteração: Gera uma variável aleatória normal:

 double Z = MathSqrt (- 2.0 * MathLog (u1)) * MathCos ( 2.0 * M_PI * u2);

Esta linha implementa a transformação de Box-Muller para gerar uma variável aleatória normal padrão. Este é um componente-chave na modelagem de um passeio aleatório nos preços dos ativos.

Calcular o próximo preço:

 double nextPrice = tempPrice * MathExp ((mu - 0.5 * sigma * sigma) * dt + sigma * MathSqrt (dt) * Z);

Esta linha implementa a fórmula do movimento browniano geométrico:

• (mu - 0.5 * sigma * sigma) * dt é o componente de deriva
• sigma * MathSqrt(dt) * Z é o componente de choque aleatório

Retorno acumulado:

totalReturn += nextPrice - tempPrice;

A função calcula e acumula o retorno a cada etapa.

Atualização do preço:

tempPrice = nextPrice;

O preço atual é atualizado para a próxima iteração.

Calcular o retorno médio:

 return totalReturn / horizon;

A função retorna o retorno médio ao longo do horizonte simulado.

Importância na modelagem financeira

1. Avaliação de risco: Ao simular múltiplos caminhos de preço, este recurso ajuda a avaliar os riscos potenciais associados a um ativo.
2. Precificação de opções: Esse tipo de modelagem é fundamental em modelos de precificação de opções, especialmente nos métodos de Monte Carlo.
3. Otimização de portfólio: Retornos esperados são insumos essenciais em algoritmos de otimização de portfólio.
4. Estratégias de negociação: Estratégias de negociação algorítmica geralmente usam retornos esperados para tomar decisões de compra/venda.

Limitações e considerações

1. Pressupostos do modelo: O modelo GBM assume que os retornos são normalmente distribuídos e independentes, o que pode não ser sempre verdadeiro nos mercados reais.
2. Estimativa de parâmetros: A precisão da função depende amplamente da estimativa correta de mu e sigma.
3. Simulação única: Esta função executa uma única simulação. Na prática, geralmente são executadas múltiplas simulações para obter uma estimativa mais confiável.
4. Horizonte de tempo: A escolha do horizonte e do dt pode afetar significativamente os resultados e deve ser feita com cuidado de acordo com o caso de uso específico.

Esta função é um bloco fundamental em finanças quantitativas, fornecendo uma maneira de estimar retornos futuros com base nos parâmetros atuais de mercado. Sua implementação em algoritmos de negociação permite a tomada de decisões orientadas por dados em ambientes financeiros complexos.

Parâmetros adaptativos: o sistema ajusta seu horizonte de previsão e tamanho do lote com base na volatilidade do mercado e no rebaixamento da conta. Isso é alcançado usando funções como CalculateAdaptiveHorizon() e AdjustLotSizeForDrawdown().

//+------------------------------------------------------------------+
//| Calculate adaptive horizon                                       |
//+------------------------------------------------------------------+
int CalculateAdaptiveHorizon()
  {
   double currentVolatility = EstimateVolatility();
   int baseHorizon = 5 ;
   return MathMax (baseHorizon, MathMin ( 20 , ( int )(baseHorizon * ( 1 + currentVolatility))));
  }

 // Función para ajustar el tamaño del lote basado en drawdown
double AdjustLotSizeForDrawdown()
  {
   static int consecutiveLosses = 0 ;
   static double maxBalance = 0 ;

   double currentBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double currentEquity = AccountInfoDouble ( ACCOUNT_EQUITY );

   if (currentBalance > maxBalance)
      maxBalance = currentBalance;

   double drawdown = (maxBalance - currentEquity) / maxBalance;

   double baseLotSize = CalculateDynamicLotSize();

   if (drawdown > 0.1 ) // 10% drawdown
     {
       return baseLotSize * 0.5 ; // Reducir el tamaño del lote a la mitad
     }
   else
       if (consecutiveLosses > 3 )
        {
         return baseLotSize * 0.75 ; // Reducir el tamaño del lote en un 25%
        }

   return baseLotSize;
  }

Este é um componente importante no gerenciamento de risco de negociação. Este recurso ajusta o tamanho do lote de negociação com base no rebaixamento atual da conta e no número de perdas consecutivas.

Visão geral das funções

A função AdjustLotSizeForDrawdown foi projetada para ajustar dinamicamente o tamanho do lote de negociação para gerenciar riscos em condições de mercado voláteis. Ela leva em consideração dois fatores principais:

1. Rebaixamento atual da conta de negociação
2. Número de derrotas consecutivas

Componentes-chave

1. Variáveis estáticas:
   • consecutiveLosses: rastreia o número de negociações perdedoras consecutivas
   • maxBalance: mantém o saldo máximo atingido na conta
2. Informações da conta:
   • currentBalance: Saldo atual da conta de negociação
   • currentEquity: Patrimônio atual da conta de negociação
3. Cálculo de drawdown: O rebaixamento é calculado como uma porcentagem de queda do saldo máximo até o patrimônio atual.
4. Tamanho de lote base: A função chama CalculateDynamicLotSize() (não mostrado neste trecho) para determinar o tamanho de lote base.
5. Ajuste do tamanho do lote: A função ajusta o tamanho do lote com base em duas condições:
• Se o rebaixamento exceder 10%
• Se houver mais de 3 derrotas consecutivas

Explicação detalhada

Atualização do saldo máximo:

 if (currentBalance > maxBalance)
   maxBalance = currentBalance;

Isso permite acompanhar o saldo máximo atingido, o que é crucial para calcular o drawdown.

Cálculo do drawdown:

 double drawdown = (maxBalance - currentEquity) / maxBalance;

Isso calcula o drawdown atual como uma porcentagem do saldo máximo.

Obtenção do tamanho de lote base:

 double baseLotSize = CalculateDynamicLotSize();

Isso chama uma função separada para calcular o tamanho de lote inicial.

Ajuste para alto drawdown:

 if (drawdown > 0.1 ) // 10% drawdown
  {
   return baseLotSize * 0.5 ; // Reduce lot size by half
  }

Se o drawdown exceder 10%, a função reduz o tamanho do lote pela metade para reduzir o risco.

Ajuste para derrotas consecutivas:

 else if (consecutiveLosses > 3 )
  {
   return baseLotSize * 0.75 ; // Reduce lot size by 25%
  }

Se houver mais de 3 derrotas consecutivas, a função reduz o tamanho do lote em 25%.

Retorno padrão: Se nenhuma das condições for atendida, a função retorna o tamanho de lote base sem ajuste.

Importância no gerenciamento de risco:

1. Proteção contra drawdown: Ao reduzir os tamanhos de lote durante grandes drawdowns, este recurso ajuda a proteger a conta contra perdas adicionais em condições adversas de mercado.
2. Gerenciamento de sequências de perdas: Ajustar para derrotas consecutivas ajuda a mitigar os efeitos psicológicos e financeiros de uma sequência de perdas.
3. Ajuste dinâmico de risco: Este recurso permite gerenciar dinamicamente seus riscos ajustando-se às condições atuais do mercado e aos resultados de negociação.

Considerações e possíveis melhorias

1. Ajuste gradual: O recurso pode ser modificado para implementar um ajuste mais gradual dos tamanhos de lote com base em diferentes níveis de drawdown.
2. Mecanismo de recuperação: Um mecanismo adicional pode ser adicionado para aumentar gradualmente os tamanhos de lote à medida que a conta se recupera de um drawdown.
3. Tamanho máximo do lote: A introdução de um limite máximo para o tamanho do lote pode fornecer uma camada adicional de gerenciamento de risco.
4. Rastreamento de vitórias: O recurso pode ser expandido para rastrear vitórias consecutivas e, potencialmente, aumentar os tamanhos de lote durante períodos favoráveis.

Este recurso é um aspecto vital do gerenciamento de risco em sistemas de negociação, ajudando a preservar o capital em condições de mercado difíceis e a mitigar os efeitos de sequências de perdas.

Vários indicadores técnicos: o advisor inclui vários indicadores técnicos para análise:

• Médias Móveis Simples (SMA)
• Parabolic SAR
• Índice de Força Relativa (RSI)
• Average True Range (ATR)

 // Initialize indicator handles
   smaHandle = iMA ( Symbol (), PERIOD_CURRENT , 50 , 0 , MODE_SMA , PRICE_CLOSE );
   psarHandle = iSAR ( Symbol (), PERIOD_CURRENT , 0.02 , 0.2 );
   rsiHandle = iRSI ( Symbol (), PERIOD_CURRENT , 14 , PRICE_CLOSE );
   atrHandle = iATR ( Symbol (), PERIOD_CURRENT , 14 );

Stop Loss e Take Profit dinâmicos: O EA calcula e atualiza os níveis de SL e TP com base na volatilidade do mercado usando as funções CalculateDynamicSL() e CalculateDynamicTP().

 double CalculateDynamicSL( double price, int decision)
  {
   double atrValue[];
   if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
     {
      LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
       return 0.0 ;
     }
   double volatility = atrValue[ 0 ];
   double dynamicSL = (decision == 1 ) ? price - (volatility * multi * 1.2 ) : price + (volatility * multi * 0.8 );

   return NormalizeDouble (dynamicSL, _Digits );
  }


double CalculateDynamicTP( double price, int decision)
  {
   double atrValue[];
   if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
     {
      LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
       return 0.0 ;
     }
   double volatility = atrValue[ 0 ];
   double dynamicTP = (decision == 1 ) ? price + (volatility * multi * 1.8 ) : price - (volatility * multi * 2.2 );

   return NormalizeDouble (dynamicTP, _Digits );
  }

Este recurso calcula níveis dinâmicos de stop loss (SL) e take profit (TP) com base na volatilidade atual do mercado, melhorando o gerenciamento de risco e potencialmente melhorando os resultados de negociação.

Revisão de recursos

Ambas as funções usam o indicador Average True Range (ATR) para medir a volatilidade do mercado e ajustar os níveis de SL e TP de acordo. Elas levam em consideração se a negociação é uma compra (1) ou venda (-1).

 double CalculateDynamicSL( double price, int decision)

Esta função calcula um nível dinâmico de Stop Loss com base no preço atual, direção da negociação e volatilidade do mercado.

 double CalculateDynamicTP( double price, int decision)

Esta função calcula um nível dinâmico de take profit com base no preço atual, direção da negociação e volatilidade do mercado.

Componentes-chave

1. Indicador ATR: Ambas as funções usam o indicador ATR para medir a volatilidade do mercado.
2. Preço: O preço atual do ativo no mercado.
3. Decisão: Um número inteiro (1 para compra, presumivelmente -1 para venda) que indica a direção da negociação.
4. Multiplicador: A variável global multi é usada para ajustar o impacto da volatilidade.

Explicação detalhada

Função CalculateDynamicSL

Get ATR value :

 double atrValue[];
if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
{
   LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
   return 0.0 ;
}
double volatility = atrValue[ 0 ];

Este código recupera o valor mais recente do ATR, que reflete a volatilidade do mercado.

Calculate dynamic SL :

 double dynamicSL = (decision == 1 ) ? price - (volatility * multi * 1.2 ) : price + (volatility * multi * 0.8 );

Para uma negociação de compra (decision== 1), ele define o SL abaixo do preço atual.

Para uma negociação de venda, o SL é definido acima do preço atual.

A distância é calculada como um múltiplo do ATR, ajustado usando a variável multi e um fator (1,2 para compras, 0,8 para vendas — fiz isso para mostrar a diferença no artigo).

Normalizar e retornar:

 return NormalizeDouble (dynamicSL, _Digits );

O valor do SL é normalizado para o número adequado de casas decimais para o instrumento em negociação.

Função CalculateDynamicTP

Obter valor do ATR: Esta parte é idêntica à função de SL.

Calcular TP dinâmico:

 double dynamicTP = (decision == 1 ) ? price + (volatility * multi * 1.8 ) : price - (volatility * multi * 2.2 );

Para uma transação de compra, o TP é definido acima do preço atual.

Para uma negociação de venda, o TP é definido abaixo do preço atual.

A distância é calculada como um múltiplo do ATR ajustado pela variável multi e por um fator (1,8 para compras, 2,2 para vendas — fiz isso para mostrar a diferença, você pode usar o que precisar).

Normalizar e retornar: semelhante à função de SL.

Importância na negociação

1. Gerenciamento de risco baseado em volatilidade: Usando o ATR, esses recursos adaptam os níveis de SL e TP às condições atuais de mercado, proporcionando um gerenciamento de risco mais adequado.
2. Relação risco/retorno assimétrica: Os níveis de TP são definidos mais distantes do preço de entrada do que os níveis de SL, potencialmente criando uma relação risco/retorno favorável.
3. Ajuste dinâmico: À medida que a volatilidade do mercado muda, esses recursos ajustam automaticamente os níveis de SL e TP para novas negociações.

Considerações e possíveis melhorias

1. Tratamento de erros: Ambas as funções têm tratamento básico de erros para recuperar o ATR, mas isso pode ser estendido.
2. Configuração: Os multiplicadores (1,2; 0,8; 1,8; 2,2) podem ser convertidos em parâmetros para facilitar a configuração.
3. Configuração: Os multiplicadores (1,2; 0,8; 1,8; 2,2) podem ser convertidos em parâmetros para facilitar a configuração.
4. Distância máxima: Da mesma forma, pode ser definida uma distância máxima para limitar o risco em condições altamente instáveis.

Esses recursos representam uma abordagem para definir níveis de SL e TP que se adaptam às condições de mercado para potencialmente melhorar os resultados de negociação e, ao mesmo tempo, gerenciar o risco de forma eficaz.

Gerenciamento de risco: Inclui funções para ajustar o tamanho da posição com base no saldo da conta e no drawdown, implementadas em AdjustLotSizeForDrawdown() e CalculateDynamicLotSize().

 // Function to adjust the lot size based on drawdown
double AdjustLotSizeForDrawdown()
{
   // Static variables to keep track of consecutive losses and maximum balance
   static int consecutiveLosses = 0 ;
   static double maxBalance = 0 ;

   // Get current account balance and equity
   double currentBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double currentEquity = AccountInfoDouble ( ACCOUNT_EQUITY );

   // Update the maximum balance if current balance is higher
   if (currentBalance > maxBalance)
      maxBalance = currentBalance;

   // Calculate the current drawdown as a percentage
   double drawdown = (maxBalance - currentEquity) / maxBalance;

   // Calculate the base lot size using a separate function
   double baseLotSize = CalculateDynamicLotSize();

   // If drawdown is greater than 10%, reduce lot size by half
   if (drawdown > 0.1 ) // 10% drawdown
   {
       return baseLotSize * 0.5 ; // Reduce lot size by half
   }
   else if (consecutiveLosses > 3 )
   {
       return baseLotSize * 0.75 ; // Reduce lot size by 25% after 3 consecutive losses
   }

   // Return the base lot size if no adjustments are needed
   return baseLotSize;
}

Esta função AdjustLotSizeForDrawdown() foi projetada para ajustar dinamicamente o tamanho do lote de negociação com base no drawdown da conta e no desempenho recente. Aqui está uma visão geral de suas funções principais:

1. Usa variáveis estáticas para rastrear derrotas consecutivas e o saldo máximo alcançado.
2. Calcula o drawdown atual comparando o saldo máximo com o patrimônio atual.
3. A função implementa duas estratégias de gerenciamento de risco:
   • Se o drawdown exceder 10%, o tamanho do lote é reduzido pela metade.
   • Se houver mais de 3 derrotas consecutivas, o tamanho do lote é reduzido em 25%.
4. O tamanho base do lote é calculado usando outra função chamada CalculateDynamicLotSize(), que não está mostrada neste trecho.
5. Se nenhuma das condições de risco for atendida, a função retorna o tamanho do lote base sem ajuste.

Essa abordagem ajuda a proteger sua conta de negociação durante períodos de desempenho ruim ou alta volatilidade, reduzindo o impacto. É uma maneira simples, mas eficaz, de implementar o dimensionamento adaptativo de posição em negociação algorítmica.

 // Function to dynamically calculate the lot size
double CalculateDynamicLotSize()
{
   // Get current account balance and equity
   double accountBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double equity = AccountInfoDouble ( ACCOUNT_EQUITY );
   double riskPercentage = 0.01 ; // 1% risk per trade

   // Use the lower value between balance and equity to be conservative
   double baseAmount = MathMin (accountBalance, equity);

   // Calculate the value of a pip for the current symbol
   double tickSize = SymbolInfoDouble ( _Symbol , SYMBOL_TRADE_TICK_SIZE );
   double tickValue = SymbolInfoDouble ( _Symbol , SYMBOL_TRADE_TICK_VALUE );
   double pipValue = (tickValue / tickSize) * 10 ; // Assuming a pip is 10 ticks

   // Calculate lot size based on desired risk
   double riskAmount = baseAmount * riskPercentage;
   double stopLossPips = 50 ; // Adjust according to your strategy

   double lotSize1 = NormalizeDouble (riskAmount / (stopLossPips * pipValue), 2 );

   // Ensure the lotSize is within the allowed limits
   double minLot = SymbolInfoDouble ( _Symbol , SYMBOL_VOLUME_MIN );
   double maxLot = SymbolInfoDouble ( _Symbol , SYMBOL_VOLUME_MAX );
   double lotSize2 = MathMax (minLot, MathMin (maxLot, lotSize1));

   return lotSize2;
}

Esta função CalculateDynamicLotSize() foi projetada para calcular o tamanho apropriado do lote de negociação com base no saldo da conta, na tolerância ao risco e nas condições atuais de mercado. Aqui está uma visão geral de suas funções principais:

1. Ela extrai o saldo e o patrimônio atuais da conta, usando o menor dos dois valores para uma abordagem mais conservadora.
2. A função usa uma porcentagem fixa de risco por negociação, neste caso definida como 1%.
3. Ela calcula o valor do pip para o símbolo de negociação atual, assumindo que um pip equivale a 10 tique-taques.
4. O tamanho do lote é então calculado com base em:
   • Valor de risco (1% do valor base)
   • Stop loss predefinido em pips (neste exemplo, definido como 50 pips)
   • Valor calculado do item
5. A função garante que o tamanho calculado do lote esteja dentro do tamanho mínimo e máximo permitido para o símbolo de negociação.
6. O tamanho final do lote é retornado, normalizado para duas casas decimais.

Essa abordagem dinâmica de tamanho de lote ajuda a manter um nível consistente de risco nas negociações, independentemente do tamanho da conta ou das condições de mercado. É um componente importante de uma estratégia de gerenciamento de risco e funciona em conjunto com a função AdjustLotSizeForDrawdown() que discutimos anteriormente.

A combinação dessas duas funções fornece um sistema robusto de gerenciamento de risco que:

1. Ajusta os tamanhos de posição com base no desempenho da conta e no drawdown
2. Mantém uma porcentagem constante de risco por negociação
3. Adapta-se aos saldos de conta e condições de mercado em mudança

Essa abordagem pode ajudar os traders a manter disciplina e proteger seu capital em condições de mercado tanto favoráveis quanto desafiadoras.

Recursos importantes:

1. OptimalControl(double currentPrice): Esta é a função central de tomada de decisão do EA. Ela usa Controle Preditivo Baseado em Modelo para determinar se deve comprar, vender ou manter. Calcula o retorno esperado no horizonte de previsão e compara com o limiar de decisão.
2. CalculateExpectedReturn(...): Esta função calcula o retorno esperado para um determinado conjunto de parâmetros usados na função OptimalControl.
3. ManageOpenOrder(int decision): Gerencia ordens abertas existentes, decidindo se as fecha com base no número de barras abertas ou se a decisão atual conflita com uma posição aberta.
4. ExecuteTrade(int decision): Executa uma nova negociação com base na decisão do OptimalControl, configurando os níveis apropriados de stop-loss e take-profit.
5. UpdateSLTP(ulong ticket, int decision): Atualiza os níveis de stop loss e take profit de uma posição existente com base nas condições atuais de mercado.
6. EstimateDrift() e EstimateVolatility(): Estas funções estimam a deriva de preço e a volatilidade usadas nos cálculos de controle ótimo.
7. IsTrendFavorable(int decision) e IsLongTermTrendFavorable(int decision): Estas funções verificam se a tendência atual de mercado está alinhada com a decisão de negociação, usando médias móveis e RSI.
8. AdjustLotSizeForDrawdown() e CalculateDynamicLotSize(): Estas funções ajustam o volume de negociação com base no drawdown atual e no saldo da conta, implementando gerenciamento de risco dinâmico.
9. LogMessage(string message): Registra eventos e decisões importantes em um arquivo para análise posterior e depuração.

Resultados

Período de 1 dia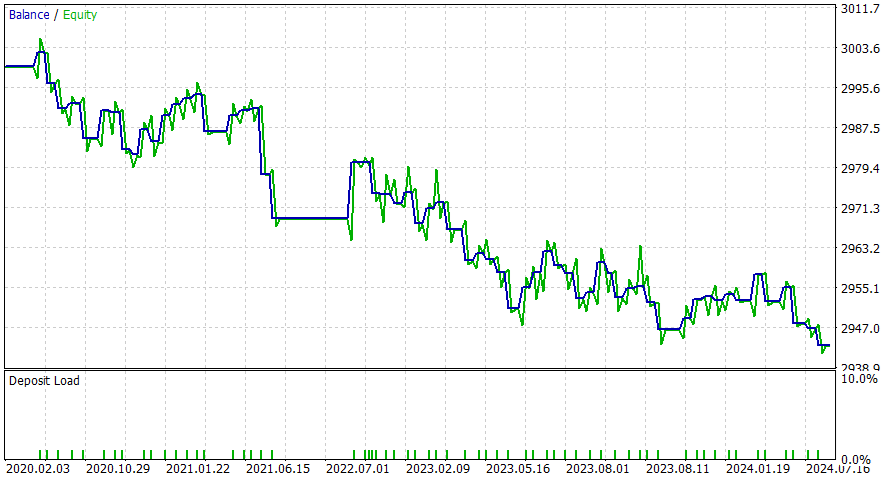

Período de 1 hora

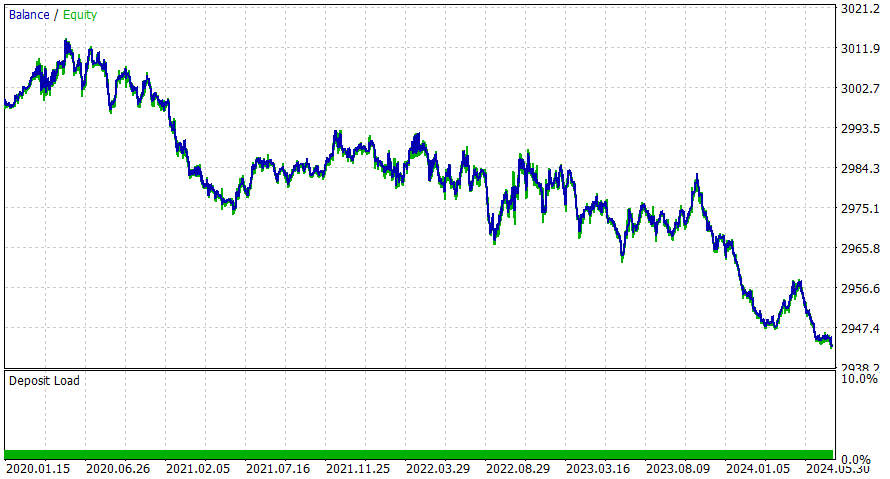
Período de 4 horas

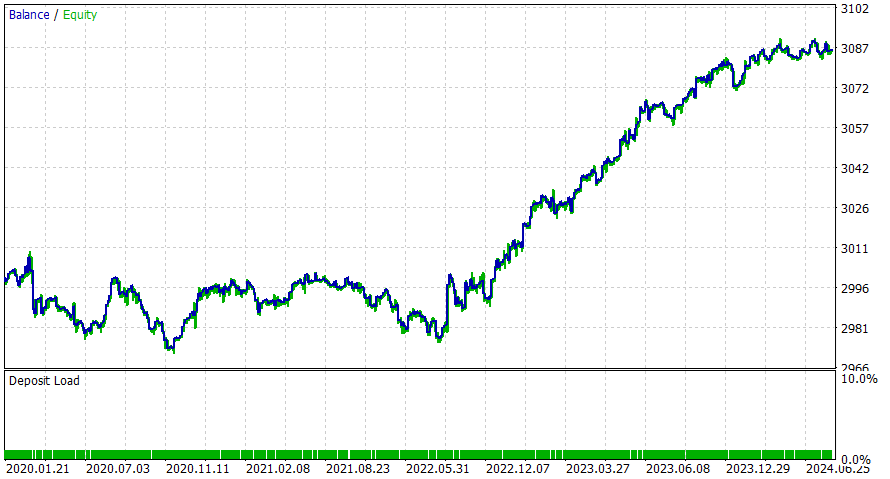
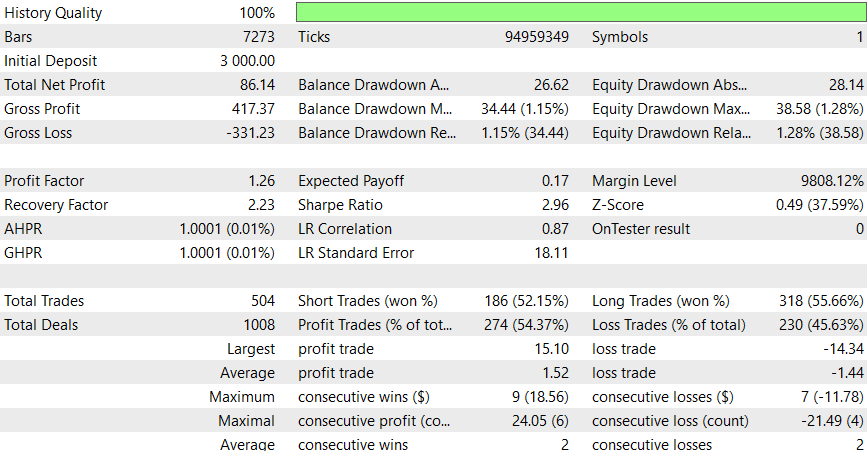
Período de 6 horas

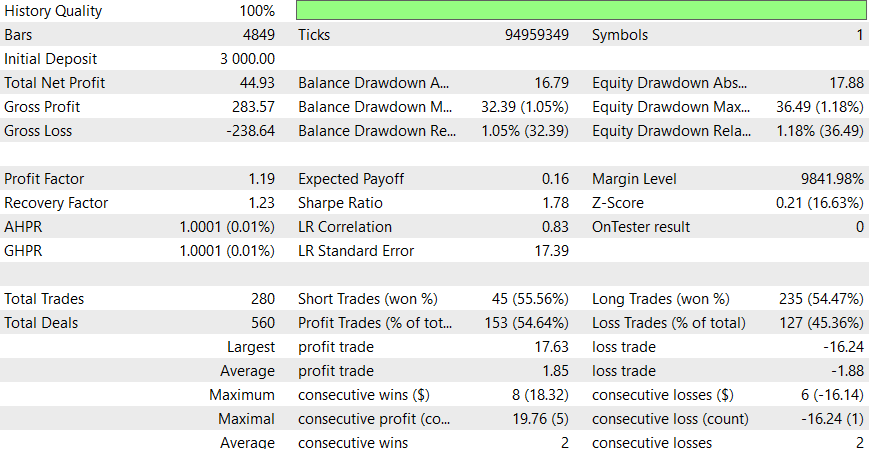
Este EA parece funcionar melhor durante o período intradiário, mas tenho certeza de que você pode obter resultados melhores adicionando SL ou aplicando as possíveis melhorias sugeridas.

Conclusão

O Expert Advisor SMOC é uma versão simplificada de uma abordagem sofisticada de negociação automatizada com modelagem estocástica e otimização de controle. Combinando vários métodos de análise, incluindo médias móveis, RSI, ATR e algoritmos de controle ótimo personalizados, ele visa tomar decisões de negociação informadas. A natureza adaptativa do sistema, com recursos como dimensionamento dinâmico de lote e ajuste de risco baseado em drawdown, demonstra foco na sustentabilidade de longo prazo. No entanto, como em qualquer sistema de negociação, backtests e testes prospectivos rigorosos serão fundamentais para avaliar seu desempenho e confiabilidade no mundo real.

Despedida: Este é apenas um exemplo simples de um advisor avançado.