Alım-satımda kaos teorisi (Bölüm 1): Giriş, finansal piyasalarda uygulama ve Lyapunov üssü

Kaos teorisine giriş ve finansal piyasalarla ilişkisi

Kaos teorisi nedir ve finansal piyasalara nasıl uygulanabilir? Bu konuyu makale içerisinde ele alacağız.

Kaos teorisinin ne olduğu ve Bill Williams tarafından ortaya atılan piyasada kaos kavramının geleneksel, bilimsel temelli teoriden nasıl farklılaştığı sorularına yanıt verecek bir dizi makale yazacağım. Teori piyasayı nasıl tanımlıyor? Alım-satımın hangi alanlarında ve nasıl uygulanabilir? 

Hem teorik temeli analiz edeceğiz hem de yatırımcılara alım-satımda yardımcı olabilecek bir dizi araç oluşturacağız.

Kaos teorisinin temel kavramları: Çekiciler, fraktallar ve kelebek etkisi

Kaos teorisi, finansal piyasalar gibi karmaşık sistemleri daha iyi anlamamıza yardımcı olan ilginç bir matematik ve fizik alanıdır. Şimdi bu teorinin üç ana kavramına bakalım:

1. Çekiciler: Bunlar sistemin durumları için mıknatıs gibidir - sistem zaman içinde bunlara doğru çekilir. Finansal piyasalarda, bunlar piyasanın tekrar tekrar geri döndüğü belirli fiyatlar veya yinelenen kalıplar olabilir. Kaotik sistemlerde bulunabilen garip çekiciler özellikle ilginçtir. Karmaşık görünürler ve piyasanın rastgele davranışındaki gizli düzeni ortaya çıkarabilirler.

2. Fraktallar: Bunlar, herhangi bir büyütme seviyesinde aynı görünen geometrik şekillerdir. Finansal piyasalarda fraktallar fiyat grafiklerinde görülebilir - aynı formasyon hem kısa hem de uzun zaman dilimlerinde görülebilir. Bu, aynı analiz yöntemlerinin farklı zaman aralıklarında uygulanmasına olanak tanıyarak fiyat değişikliklerinin analiz edilmesine ve risklerin değerlendirilmesine yardımcı olur.

3. Kelebek etkisi: Bu etki, başlangıçtaki en küçük değişikliklerin bile büyük ve beklenmedik sonuçlara yol açabileceğini ifade eder. Finans dünyasında bu, verilerdeki veya modeldeki küçük değişikliklerin tahminleri önemli ölçüde değiştirebileceği anlamına gelir. Bu durum, finansal piyasalarda uzun vadeli tahmin yapmayı zorlaştırmakta ve modellerimizi sürekli olarak güncellemenin ve yeni koşullara uyarlamanın önemini vurgulamaktadır.

Bu kavramları anlamak, analistlerin ve yatırımcıların piyasalara yeni bir gözle bakmalarına, gizli kalıpları ve işlemler için olası giriş veya çıkış noktalarını keşfetmelerine yardımcı olur. Kaos teorisi, analiz ve tahmin için geleneksel modellerin ötesine geçen yeni yollar açar.

Finansal piyasalar bağlamında kaotik sistemler

Finansal piyasalar, analiz ve tahmin için önemli olan kaotik sistem özelliklerine sahiptir.

• Doğrusal olmama: Küçük değişiklikler orantısız dalgalanmalara neden olur.
• Başlangıç koşullarına duyarlılık: Küçük olaylar büyük hareketlere yol açabilir.
• Öz organizasyon: Dış kontrol olmaksızın trendlerin ve kalıpların oluşması.
• Fraktal yapı: Fiyat grafikleri fraktal özellikler gösterir.
• Sınırlı öngörülebilirlik: Tahmin doğruluğu artan ufukla birlikte azalır.
• Garip çekiciler: Belirli seviyeler veya durumlar etrafında dalgalanmalar.
• Durumlar arası geçişler: İstikrardan volatiliteye ani geçişler.

Bunu anlamak, sofistike analiz yöntemleri, risk yönetimi ve alım-satım algoritmaları geliştirmeye yardımcı olur.

Alım-satımda volatilite

Volatilite, kaos teorisi ile ilişkili olarak alım-satım ve finans alanında önemli bir kavramdır. Bir varlığın fiyatının belirli bir süre içinde ne kadar değiştiğini ölçer. Alım-satımda volatilite, riskin değerlendirilmesine, opsiyonların fiyatlandırılmasına ve alım-satım stratejilerinin geliştirilmesine yardımcı olur.

Finansal piyasalar genellikle kaotik sistemler gibi davranır. Kelebek etkisine benzer şekilde küçük değişikliklere beklenmedik tepkiler verebilir. Piyasalar ayrıca kendi kendilerini organize edebilir, dışarıdan müdahale olmadan trendler ve kalıplar oluşturabilir ve fiyat grafikleri farklı zaman dilimlerinde fraktal özellikler olarak adlandırılan benzerlikler gösterir.

Kaos teorisi, gizli kalıpları bulmaya ve öngörülebilirliği değerlendirmeye yardımcı olan faz uzayı yeniden yapılandırması ve Lyapunov üssü gibi volatilite analizi için benzersiz araçlar sunar. Bu kaotik modeller, özellikle piyasa rejimlerinin belirlenmesinde ve volatilitede ani değişikliklerin öngörülmesinde GARCH modelleri gibi geleneksel yöntemleri tamamlayabilir.

Volatilitenin kaotik doğasının anlaşılması, piyasa dinamiklerinin daha doğru analizi ve tahmini için yeni fırsatlar yaratmakta, bu da verimli alım-satım stratejilerinin ve risk yönetimi yöntemlerinin geliştirilmesine olanak sağlamaktadır.

Geleneksel kaos teorisi ve Bill Williams'ın yaklaşımı

Geleneksel kaos teorisi ile Bill Williams'ın "kaos" konsepti birbirinden çok farklıdır. İlki, katı matematiksel ilkelere dayanır ve sistemleri analiz etmek için sofistike araçlar kullanır. İkincisi ise sezgisel bir yaklaşım ve matematiksel kaos teorisiyle doğrudan bağlantısı olmayan Alligator ve Fractals gibi teknik göstergeler kullanır.

Geleneksel kaos teorisi, doğrusal olmayan dinamikler alanındaki katı matematiksel ilkelere ve bilimsel araştırmalara dayanmaktadır. Katı matematiksel yöntemler kullanır ve kaosun belirleyici ancak öngörülemez davranış sergilediğini düşünür. Williams "kaos" terimini daha gevşek bir şekilde, piyasaların genel öngörülemezliğine atıfta bulunarak kullanmaktadır. Yöntemleri, piyasaların kaotik doğasının derin analizinden ziyade alım-satımda pratik uygulamaya yöneliktir.

Williams kaos teorisinden bazı terimleri uyarlamış olsa da, yaklaşımı daha çok teknik analize ve piyasa hareketlerinin kişisel yorumuna dayanmaktadır. Bu durum, "kaos" teriminin bu bağlamda kullanılmasını yanıltıcı bulan kaos teorisyenlerinin eleştirilerine neden olmuştur.

Piyasa analizinde kaos teorisi

Kaos teorisi, finansal piyasaların karmaşıklığını ve öngörülemezliğini kabul ederek piyasa dinamiklerinin analizine yeni bir bakış açısı sunmaktadır. Geleneksel yöntemlerin aksine kaos teorisi, piyasa süreçlerinin doğrusal olmayışını ve karmaşıklığını dikkate alır.

Bu yaklaşım, küçük olayların neden büyük piyasa hareketlerine yol açabildiğini ve uzun vadeli tahminlerin neden genellikle yanlış olduğunu açıklamaya yardımcı olur. Kaos teorisi, piyasa çöküşleri ve balonlar gibi olguları analiz etmemize olanak tanıyarak daha doğru ve uyarlanabilir piyasa analizi için yeni araçlar sağlar.

Lyapunov üssü ve finansal zaman serisi analizindeki uygulamaları

Lyapunov üssü, bir sistemin başlangıç koşullarına ne kadar duyarlı olduğunu anlamamıza yardımcı olan kaos teorisinden bir araçtır. Finansal piyasalarda bu önemlidir çünkü piyasa koşullarındaki küçük değişikliklerle fiyatların ne kadar değişeceğini tahmin etmeyi sağlar.

Lyapunov üssünün pozitif olması, sistemin kaotik davrandığı anlamına gelir: küçük değişiklikler gelecekte büyük dalgalanmalara yol açabilir. Eğer üs negatifse, sistem daha istikrarlıdır ve fiyatlar daha az değişecektir.

Bu üssü kullanarak piyasanın ne zaman daha volatil ve öngörülebilir hale geleceğini belirleyebilirsiniz. Yüksek değerler, keskin fiyat değişikliklerine işaret edebilir; dolayısıyla riski değerlendirmek ve alım-satım stratejilerini ayarlamak açısından faydalıdır.

Finansal verilerde Lyapunov üssünü hesaplamak için bir faz uzayı oluşturmak ve bu uzaydaki birbirine yakın noktaların nasıl ayrıştığını analiz etmek gerekir. Bu süreç, boyut ve zaman gecikmesi gibi doğru parametrelerin seçilmesini gerektirir.

Lyapunov üssünü kullanmanın önemli bir yönü, tahminlerin ne kadar süreyle doğru olacağını değerlendirmektir. Üssün değeri ne kadar yüksek olursa, tahminlerin güvenilir kaldığı süre de o kadar kısa olur. Bu özellikle kısa vadeli alım-satım ve risk yönetimi için kullanışlıdır.

Şimdi Lyapunov üssünü MQL5'te uygulamaya başlayabiliriz.

Lyapunov üssünün MQL5 kullanılarak uygulanması

Bu gösterge, finansal zaman serisi analizi için Lyapunov üssünün hesaplanmasını uygular. Piyasadaki kaosun derecesini ve fiyat hareketlerinin potansiyel öngörülebilirliğini değerlendirmeyi sağlar.

Girdiler:

input int    InpTimeLag = 1;       // Time lag
input int    InpEmbedDim = 2;      // Embedding dimension
input int    InpDataLength = 1000; // Data length for calculation

• InpTimeLag - faz uzayı yeniden yapılandırması için zaman gecikmesi.
• InpEmbedDim - faz uzayı yeniden yapılandırması için gömme boyutu (embedding dimension).
• InpDataLength - göstergeyi hesaplamak için kullanılan mum sayısı.

Bir global değişken vardır:

double LyapunovBuffer[];

Başlatma:

int OnInit()
{
   SetIndexBuffer(0, LyapunovBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Lyapunov Exponent");
   return(INIT_SUCCEEDED);
}

OnInit() fonksiyonunda, gösterge arabelleğini yapılandırır, ekran hassasiyetini 5 ondalık basamağa ayarlar ve gösterge için kısa bir ad belirleriz.

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      LyapunovBuffer[i] = CalculateLyapunovExponent(close, i);
   }
   
   return(rates_total);
}

OnCalculate() fonksiyonu her tikte çağrılır ve InpDataLength değerinden başlayarak her mum için Lyapunov üssünün hesaplanmasını gerçekleştirir.

Lyapunov üssü hesaplaması:

double CalculateLyapunovExponent(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double sum = 0;
   int count = 0;
   
   for(int i = 0; i < InpDataLength - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      int nearestNeighbor = FindNearestNeighbor(price, index - InpDataLength + i, index);
      if(nearestNeighbor != -1)
      {
         double initialDistance = MathAbs(price[index - InpDataLength + i] - price[nearestNeighbor]);
         double finalDistance = MathAbs(price[index - InpDataLength + i + InpTimeLag] - price[nearestNeighbor + InpTimeLag]);
         
         if(initialDistance > 0 && finalDistance > 0)
         {
            sum += MathLog(finalDistance / initialDistance);
            count++;
         }
      }
   }
   
   if(count > 0)
      return sum / (count * InpTimeLag);
   else
      return 0;
}

CalculateLyapunovExponent() fonksiyonu, yerel Lyapunov üssünü hesaplamak için algoritma uygular. Yeniden yapılandırılan faz uzayında yörüngelerin sapmasını hesaplamak için en yakın komşu yöntemini kullanır.

En yakın komşuyu arama:

int FindNearestNeighbor(const double &price[], int startIndex, int endIndex)
{
   double minDistance = DBL_MAX;
   int nearestIndex = -1;
   
   for(int i = startIndex; i < endIndex - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      if(MathAbs(i - startIndex) > InpTimeLag)
      {
         double distance = 0;
         for(int j = 0; j < InpEmbedDim; j++)
         {
            distance += MathPow(price[startIndex + j * InpTimeLag] - price[i + j * InpTimeLag], 2);
         }
         distance = MathSqrt(distance);
         
         if(distance < minDistance)
         {
            minDistance = distance;
            nearestIndex = i;
         }
      }
   }
   
   return nearestIndex;
}

FindNearestNeighbor() fonksiyonu, Öklid mesafesini kullanarak yeniden yapılandırılan faz uzayında en yakın noktayı bulur.

Sonuçların yorumlanması

• Göstergenin pozitif değerleri kaotik piyasa davranışının varlığını göstermektedir.
• Negatif değerler daha istikrarlı ve potansiyel olarak öngörülebilir fiyat dinamiklerine işaret etmektedir.
• Göstergenin mutlak değeri ne kadar yüksekse, ilgili karakteristik (kaotik veya kararlı) o kadar belirgindir.

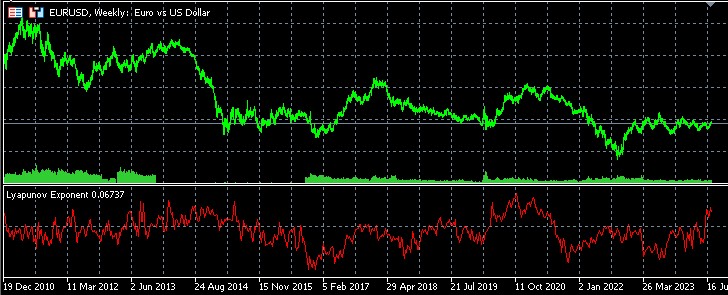
Lyapunov üssü kullanılarak trend terse dönüşlerinin ve devamlılıklarının istatistiksel analizi

Lyapunov üssü ile finansal piyasaların dinamikleri arasındaki ilişkinin derinlemesine incelenmesi için MQL5 dilinde özel bir komut dosyası geliştirdim. Bu araç, Lyapunov üs değerleri bağlamında trend terse dönüşlerinin ve devamlılıklarının ayrıntılı istatistiksel analizine olanak tanıyarak yatırımcılara ve analistlere piyasa davranışı hakkında değerli bilgiler sağlar.

Komut dosyası, belirli sayıda çubuğu analiz ederek seçilen finansal enstrümanın geçmiş verileriyle çalışır. Her bir çubuk için yerel Lyapunov üssü, faz uzayı yeniden yapılandırması ve en yakın komşu arama yöntemi kullanılarak hesaplanır. Bu yaklaşım, zamanın her bir noktasında sistemdeki kaos derecesini değerlendirmemizi sağlar.

Eş zamanlı olarak, komut dosyası fiyat dinamiklerini analiz eder, terse dönüşleri ve trend devamlılıklarını belirler. Terse dönüş, mevcut kapanış fiyatının bir öncekinden daha yüksek olduğu ve bir sonrakinin mevcut olandan daha düşük olduğu (veya tam tersi) durum olarak tanımlanır. Diğer tüm durumlar trend devamlılığı olarak değerlendirilir.

Komut dosyasının önemli bir özelliği, trendin tersine dönme ve devam etme anlarını Lyapunov üssünün değerleriyle karşılaştırabilmesidir. Bu, piyasanın kaotik davranışı ile fiyat dinamikleri arasındaki istatistiksel kalıpları belirlememize olanak tanır. Komut dosyası, Lyapunov üssünün pozitif ve negatif değerleriyle meydana gelen trend terse dönüşlerinin ve devamlılıklarının sayısını hesaplar.

Analizin tamamlanmasının ardından komut dosyası, Lyapunov üssünün pozitif ve negatif değerleri için trendin tersine dönme ve devam etme mutlak değerleri ve yüzdeleri de dahil olmak üzere ayrıntılı istatistikler görüntüler. Bu bilgiler, yatırımcıların trendin tersine dönmesinin piyasadaki volatilitenin arttığı dönemlere ne sıklıkla denk geldiğini ve aksine trendin devam etmesinin daha istikrarlı dönemlere ne sıklıkla denk geldiğini değerlendirmelerine olanak tanır.

İstatistiksel analiz sonuçlarının yorumlanması

Lyapunov üssü kullanılarak trend terse dönüşlerinin ve devamlılıklarının istatistiksel analizinden elde edilen sonuçlar, saatlik zaman diliminde EURUSD piyasasının dinamikleri hakkında ilginç veriler sunuyor.

Öncelikle, Lyapunov üssünün pozitif ve negatif değerleri arasındaki olay dağılımının neredeyse eşit olması dikkat çekicidir. Pozitif ve negatif Lyapunov üslerine sahip durumların yaklaşık yarısında hem terse dönüşler hem de trend devamlılıkları gözlemlenmektedir. Bu, H1'deki EURUSD piyasasının göreceli istikrar ve kaos dönemleri arasında bir denge gösterdiğine işaret edebilir.

Tipik olarak daha kaotik, öngörülemez davranışla ilişkilendirilen pozitif Lyapunov üs değerleri, tüm durumların yarısından biraz fazlasında gözlemlenmiştir (terse dönüşler için %50.61 ve devamlılıklar için %51.09). Bu, piyasada volatilitenin veya belirsizliğin arttığı dönemlerin hafif bir baskınlığını işaret edebilir.

Genellikle sistemin daha düzenli, daha az kaotik davranışının bir işareti olarak yorumlanan Lyapunov üssünün negatif değerleri, terse dönüşlerin %49.39'unda ve trend devamlılıklarının %48.91'inde gözlemlenmiştir. Bu dönemler, belirli kalıpları takip eden daha öngörülebilir fiyat hareketleri ile karakterize edilebilir.

İlginç bir şekilde, trendin tersine dönme ve devam etme yüzdesi hem pozitif hem de negatif Lyapunov değerleri için neredeyse aynıdır. Her iki durumda da fark %0.5'ten azdır. Bu, Lyapunov üssünün kendisinin bir trendin tersine dönmesini veya devam etmesini öngörmek için belirleyici bir faktör olmadığını işaret edebilir.

Olayların pozitif ve negatif Lyapunov değerleri arasındaki bu eşit dağılımı, istikrar ve kaos dönemlerinin yaklaşık olarak eşit sıklıkta değiştiği EURUSD piyasasının karmaşık yapısını yansıtabilir. 

Sonuç

Kaos teorisi, finansal piyasaların analizinde yenilikçi bir yaklaşım sunarak piyasaların karmaşık ve doğrusal olmayan doğasının daha iyi anlaşılmasını sağlar. Bu makalede, kaos teorisinin temel kavramlarını (çekiciler, fraktallar ve kelebek etkisi) ve bunların finansal zaman serisine uygulanmasını inceledik. Piyasa dinamiklerindeki kaos derecesini değerlendirmek için bir araç olarak Lyapunov üssüne özellikle dikkat gösterdik.