Cuadrícula y martingale: ¿qué son y cómo usarlos?

Introducción

En este artículo, queremos mostrar con la ayuda de las matemáticas y la programación cuáles son realmente estas estrategias y si realmente son tan rentables como muchos piensan. En el artículo habrá una parte matemática y otra práctica. En la parte matemática, escribiremos fórmulas que pueden utilizarse para calcular la esperanza matemática de estas estrategias y otros parámetros importantes que, a nuestro juicio, muchos no consideran. En la parte práctica, escribiremos la cuadrícula y el martingale más simples, y compararemos con la realidad lo que dicen nuestras fórmulas. El artículo resultará especialmente útil a los principiantes, porque, por lo general, al principio los tráders se encuentran precisamente con estas estrategias y empiezan a creer en ellas, lo cual termina conllevando para ellos una decepción y una completa pérdida de tiempo, como ocurrió en su día con el autor. Si no estuviéramos familiarizados con las matemáticas, aún podríamos haber creído en estas estrategias. Pero, aún así, estas estrategias todavía tienen un fundamento, si las examinamos correctamente. Vamos a intentar demostrarlo aquí.

¿Qué tienen estas dos estrategias en común?

Para entender por qué estas dos estrategias son tan populares, deberemos comprender lo que quiere cualquier tráder principiente que llega a Fórex. Entre los principiantes siempre existe un porcentaje bastante grande de matemáticos y soñadores que piensan en un enriquecimiento rápido y fácil gracias a su intelecto. Ambas estrategias implementan la apariencia de un comercio de ganancias seguras en forma de gráficos que suben todo el tiempo en el simulador de estrategias. En muchas partes de la historia de cotizaciones, incluso sin filtros, podremos probarlas de forma que parecerá que este es el Grial. En cualquier esfera y en cualquier negocio hay momentos en los que personas más expertas podrían engañarlo y enriquecerse a su costa. Lo mismo pasa aquí. Pero hay muchos de estos engaños en Fórex, y estas 2 estrategias son la prueba más visual y popular de ello. Al utilizar por primera vez estas estrategias, verá que funcionan en todas las parejas de divisas con increíbles factores de beneficio y esperanzas matemáticas, e incluso pueden arreglárselas con cualquier spread, por lo que parece que este algoritmo está fuera del mercado. Esto se debe a que se basan en matemáticas puras, sin ninguna lógica. Sí, incluso al autor, un desarrollador experimentado, le gustaría encontrar algoritmos a los que no les importa dónde va el precio y siempre ganan. Los matemáticos, en general, son gente extraña, solo hay que darles una excusa: ellos se inventarán lo que sea, y también lo probarán con fórmulas, y luego, ¡ups!, nos daremos de bruces con un error. En general, estas dos estrategias explotan la ilusión del punto de equilibrio para convencernos de que las usemos. Ambas estrategias funcionan con cualquier pareja de divisas y en cualquier periodo, o más bien crean la ilusión de funcionar y lo convencen a uno de su simplicidad y eficiencia. Una vez hemos comprendido todo en estas estrategias, tarde o temprano uno se da cuenta de que no sabe nada. Pero esto es necesario, porque solo así comenzaremos a pensar racionalmente y a entender la verdadera naturaleza del mercado y qué estrategias realmente necesitamos usar.

La cuadrícula y sus fórmulas básicas

La cuadrícula de órdenes se inventó con el objetivo de obtener beneficios en cualquier mercado, independientemente de si es bajista o alcista. Según los creadores de la cuadrícula: si hay un movimiento pronunciado, la cuadrícula, con la ayuda de un sistema inteligente de apertura de órdenes, debe abrir las órdenes de tal forma que, de una u otra manera, la suma de estas órdenes en algún momento acumule suficientes beneficios para cerrarlas todas a la vez. Ilustraremos lo dicho en la siguiente imagen:

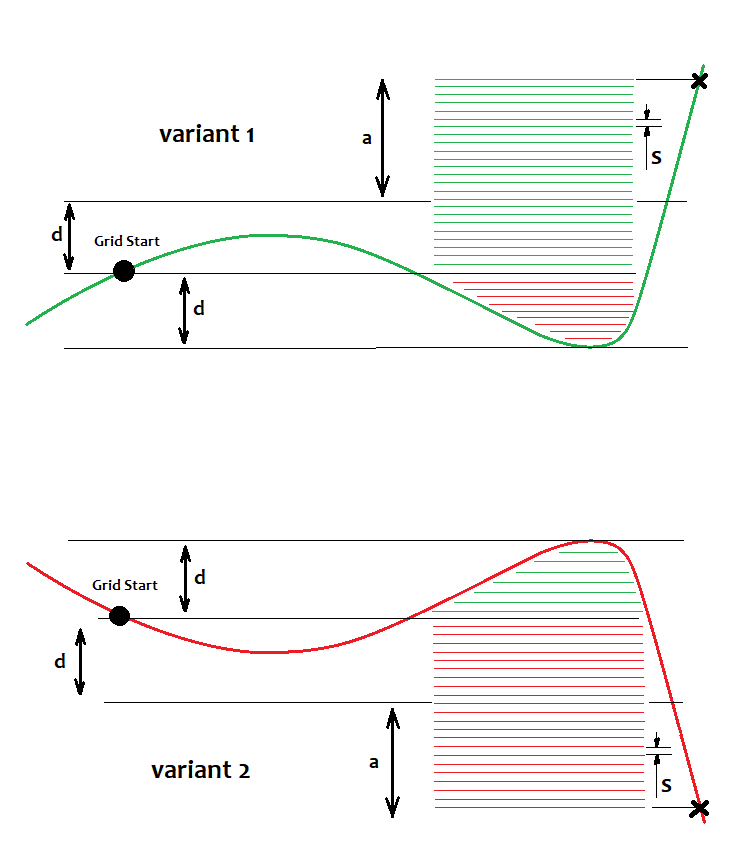
Aquí tenemos 2 variantes para un mercado alcista y un mercado alcista, respectivamente. Independientemente de la variante que obtengamos, según la idea de los autores, todavía tenemos que sacar beneficios. Quienes utilizan la cuadrícula siempre dicen que usan órdenes pendientes que se ejecutan al mejor precio. Esto es cierto; si bien a nuestro parecer, las órdenes de mercado no resultan peores, aunque solo sea porque podemos controlar los spreads y los deslizamientos en el momento de la entrada y, en este caso, podremos esperar un poco con la misma. No obstante, en el marco de esta estrategia, las órdenes limitadas son mejores. Tenemos un punto de partida en relación al cual se colocan las órdenes, todo lo que se encuentre por encima, será para la compra con un salto de "s"; todo lo se encuentre por debajo, será para la venta, respectivamente. Si el precio les da alcance, se convertirá en precio de mercado. En la figura, hemos dibujado órdenes abiertas según una situación de precios específica. Podemos no dibujar los límites, ya que estarán en los mismos niveles, solo que subirán y bajarán indefinidamente. Sin embargo, solo las órdenes reales abiertas resultan importantes para nosotros, porque sus beneficios o pérdidas se suman a los beneficios o pérdidas totales, respectivamente. Para asegurar el beneficio, es necesario que haya más de algunas órdenes que de otras en "K" veces, es decir, debemos hacer posible que K=a/d, donde K>=K0. K0 es un cierto coeficiente, cuyo alcance permite al beneficio total de todas las órdenes en la cuadrícula superar el umbral cero. También podemos simplemente calcular el beneficio actual de una posición u órdenes, en el caso de MetaTrader 4. O bien tendremos una situación en la que el precio se mueve inmediatamente en una dirección y fijamos el beneficio cuando el precio ha pasado "n" puntos hacia arriba o hacia abajo. Estrictamente hablando, este coeficiente se puede calcular, pero normalmente se selecciona sin problemas de forma manual. Podemos calcularlo así:

• Nl=d/s - 1
• NP=(a+d)/s -1
• Pr=Suma(1,NP)(s*i)=(s+s*NP)*Np/2
• Ls=Suma(1,Nl)(s*j+ s*NP)=(s+s*Nl)*Nl/2+s*NP^2

Sumando las pérdidas o los beneficios de todas las órdenes, podemos ver que estas cantidades suponen progresiones aritméticas; existe una fórmula que describe la suma de una progresión aritmética (utilizando su primer y último término), y esta se aplica aquí.

Partiendo de la condición Pr-Ls=0, y resolviendo esta ecuación, podemos encontrar "a", y luego calcular K0=a/d. Además, utilizando estas fórmulas, podremos también llegar al factor de beneficio y la esperanza matemática de los ciclos comerciales en los que hay posiciones abiertas tanto de compra como de venta.

• Prf=Pr/Ls 
• M=(Pr-Ls)/(Np+Nl)

Estas fórmulas calculan el factor de beneficio y la esperanza matemática de un ciclo comercial específico, no el gráfico entero. Siempre que nuestro gráfico finalice en el punto final del ciclo, nuestro factor de beneficio será positivo. Entendemos por ciclo una cuadrícula individual. Construimos una cuadrícula, la procesamos, cerramos las posiciones y construimos una nueva cuadrícula, y así sucesivamente; podemos seguir hasta el infinito con un depósito infinito. Así es como se verá en la curva de balance:

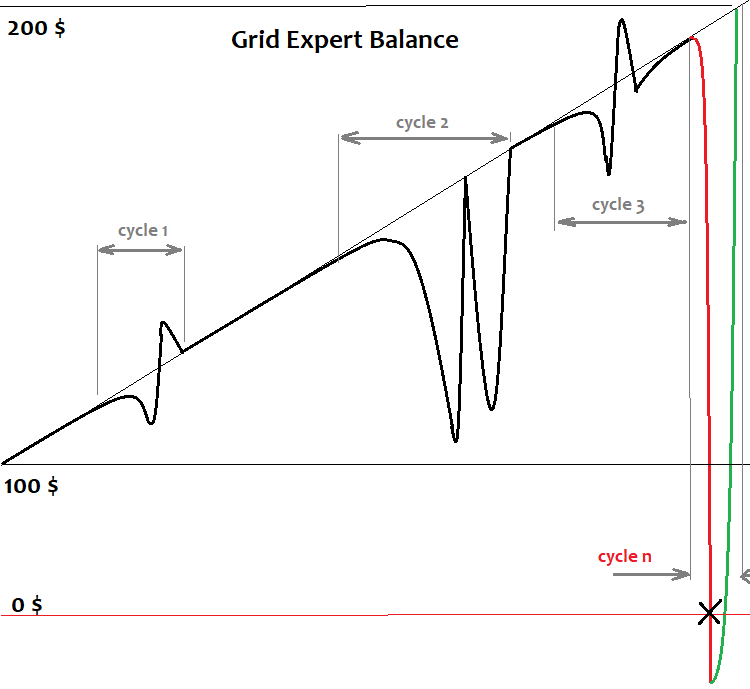
Aquí tenemos una representación simplificada del gráfico de balance de un robot de cuadrícula cuando se ejecuta a través de la historia. Siempre existe un cierto número de ciclos que soporta nuestro depósito, lo cual permite que el gráfico ascienda, pero siempre llega un ciclo para el que el depósito ya no es suficiente, y todo nuestro beneficio visible termina por volver al bróker. Desde el punto de vista matemático, esto se considera un ciclo incompleto; un ciclo incompleto nunca es rentable y sus pérdidas se superpondrán a todos los beneficios obtenidos en ciclos que funcionaron hasta el final. En este caso, es posible que el ciclo no haya terminado aún porque no hay suficientes órdenes para continuar la cuadrícula. El caso es que cualquier bróker tiene un límite en el número de órdenes abiertas simultáneamente en el terminal o para una pareja concreta, lo cual nos obliga a considerar estas características. No se puede construir una cuadrícula indefinidamente. E incluso asumiendo que puediéramos hacer esto por arte de magia, seguiríamos viendo el guión que hemos descrito arriba. Al final del artículo, explicaremos matemáticamente por qué sucede esto, de una forma simple y rápida, para que todos entiendan todo y no queden preguntas sin responder.

El martingale y sus fórmulas básicas

Al igual que la cuadrícula, el martingale se diseñó para ganar independientemente de la dirección del mercado, el tipo de posición y la dirección en la que comerciemos. Se basa en la misma ilusión de beneficio eterno. Si abrimos una orden y es rentable, simplemente la cerramos y seguimos comerciando. En cuanto tengamos una orden con pérdidas, aumentamos el lote "n" veces en la siguiente orden en relación con la posición perdedora; si nuestra orden es rentable, simplemente la cerramos y restablecemos el lote a su valor inicial. Si la orden vuelve a tener pérdidas, repetimos el proceso, solo que ahora incrementamos el lote "n" veces en relación a la suma de los lotes de todas las posiciones con pérdidas en este ciclo, y así sucesivamente hasta obtener un transacción rentable. La última transacción del ciclo siempre es rentable y su beneficio siempre supera las pérdidas de las transacciones no rentables, por lo que nuestro gráfico vuelve a empezar a constar de ciclos; siempre que el gráfico termine con el último ciclo, obtendremos una esperanza matemática positiva y un factor de beneficio. No importa tanto cómo y dónde abramos estas órdenes. Lo deseable es que estas órdenes tengan beneficios y pérdidas fijas, o simplemente que cierren usando stops fijos. Este es el aspecto del gráfico de balance del robot:

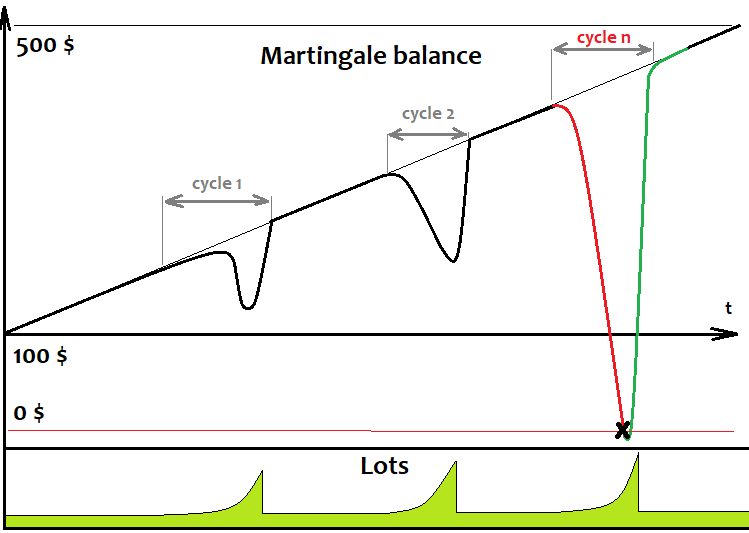
Como podemos ver, es muy similar al gráfico de balance de la cuadrícula, ya que el martingale funciona en ciclos, al igual que la cuadrícula. Solo que siempre abre una orden a la vez, y hasta que se cierra, no tiene derecho a abrir otra. Al igual que sucede con la cuadrícula, llega un momento en que el depósito no alcanza para dar por finalizado el ciclo; entonces se produce el cierre de emergencia de las órdenes y, por consiguiente, se pierde el depósito. Para garantizar ciclos rentables, el beneficio de la última transacción debe cubrir las pérdidas de las operaciones anteriores:

• Nl
• Np=1
• Pr=L[Nl+Np]*TP[Nl+Np]*TickSize
• Ls=Suma(1,Nl)(L[i]*SL[i])*TickSize

Aquí el beneficio no se calcula en puntos, sino en las unidades de la divisa de su cuenta, porque se realizan manipulaciones con el lote y es inconveniente contar en puntos. Los lotes de una orden concreta se calculan usando la recursividad:

• L[1]=StartLot
• for(2,Nl) L[i]=(K*Suma(1,i-1)(L[j]*SL[j]))/TP[i]

Donde "K" es el factor de beneficio del ciclo. Aquí, obviamente, no se consideran los spreads y las comisiones, ni tampoco los swaps, por supuesto, pero no creemos que eso sea importante. Si surge la necesidad, las fórmulas se pueden modificar sin problemas, aunque no le vemos sentido a esto. Intentaremos crear las fórmulas por analogía con la cuadrícula. SL y TP suponen las pérdida resultantes o el beneficio deseado de la orden. Podemos obtener esta definición solucionando la ecuación simple: K=(L[i]* TP[i])/Suma(1,i-1)(L[j]*SL[j]).

Creamos y ponemos a prueba una cuadrícula sencilla

Para poner a prueba las suposiciones anteriores, vamos a escribir juntos una cuadrícula y un martingale simples en el lenguaje mql5. Luego los probaremos y veremos el resultado. Empecemos por la cuadrícula. Primero, añadimos a nuestro modelo algunas clases necesarias para trabajar con posiciones:

#include <Trade\PositionInfo.mqh>
#include <Trade\Trade.mqh>
CPositionInfo  m_position=CPositionInfo();// trade position object
CTrade         m_trade=CTrade();          // trading object

Estas 2 bibliotecas siempre se encuentran en MetaTrader 5 por defecto, por lo que nadie tendrá problemas con la compilación. 

A continuación, describimos todos los parámetros de entrada necesarios:

///grid variables
input int MaxChannelSizePoints=500;//Max Of a+d
input int MinMoveToClose=100;//Mininum Move
input int GridStepPoints=20;//Grid Step In Points
input int BarsI=999;//Bars To Start Calculate
input double KClose=3.5;//Asymmetry
///

////////minimum trading implementation
input int SlippageMaxOpen=15; //Slippage For Open In Points
input double Lot=0.01;//Lot
input int MagicC=679034;//Magic
/////////

El primer bloque implementa los parámetros de la cuadrícula, mientras que el segundo implementa de forma mínima la posibilidad de comerciar con un lote fijo.

Al iniciar el asesor experto, debemos comprobar y restaurar los parámetros de la cuadrícula de la sesión anterior, en caso de que el funcionamiento finalizara de forma incorrecta. Esto no es imprescindible, pero resulta mejor pensar en estos aspectos con antelación:

void DimensionAllMQL5Values()//////////////////////////////
   {
   ArrayResize(Time,BarsI,0);
   ArrayResize(High,BarsI,0);
   ArrayResize(Low,BarsI,0);
   }

void CalcAllMQL5Values()///////////////////////////////////
   {
   ArraySetAsSeries(High,false);                        
   ArraySetAsSeries(Low,false);                              
   ArraySetAsSeries(Time,false);                                                            
   CopyHigh(_Symbol,_Period,0,BarsI,High);
   CopyLow(_Symbol,_Period,0,BarsI,Low);
   CopyTime(_Symbol,_Period,0,BarsI,Time);
   ArraySetAsSeries(High,true);                        
   ArraySetAsSeries(Low,true);
   ArraySetAsSeries(Time,true);
   }

Necesitamos este código para implementar las matrices predefinidas para realizar el análisis inicial. Así, luego no necesitaremos estas matrices, las usaremos solo para el cálculo inicial.

La restauración se realizará de la forma siguiente:

void RestoreGrid()//recover the grid if the robot is restarted
   {
   DimensionAllMQL5Values();
   CalcAllMQL5Values(); 
   bool ord=PositionSelect(Symbol());
   if ( ord && int(PositionGetInteger(POSITION_MAGIC)) == MagicC )
      {
      GridStartTime=datetime(PositionGetInteger(POSITION_TIME));
      GridStartPrice=double(PositionGetDouble(POSITION_PRICE_OPEN));
      GridUpPrice=GridStartPrice;
      GridDownPrice=GridStartPrice;      
      
      for(int i=0;i<BarsI;i++)
         {
         if ( High[i] > GridUpPrice ) GridUpPrice=High[i];
         if ( Low[i] < GridDownPrice ) GridDownPrice=Low[i];
         if ( Time[i] < GridStartTime ) break;         
         }
      bCanUpdate=true;
      bTryedAlready=false;         
      }
   }

Para monitorear el estado actual de la cuadrícula, necesitamos variables auxiliares que muestren los precios superior e inferior durante la existencia de la cuadrícula, así como el precio inicial de la misma y el momento en que se colocó.

datetime GridStartTime;//grid construction time
double GridStartPrice;//grid starting price
double GridUpPrice;//upper price within the corridor
double GridDownPrice;//lower price within the corridor

Y 2 booleanas más para monitorear o actualizar las variables de la cuadrícula durante el movimiento del precio, y también para implementar los intentos adicionales de cierre de la cuadrícula si falla el primer intento.

bool bCanUpdate;//whether it is possible to update the grid
bool bTryedAlready;//whether there was an attempt to close a position

Este será el aspecto de la creación y la actualización de los parámetros de la cuadrícula durante su desarrollo:

void CreateNewGrid()//create a new grid
   {
   SymbolInfoTick(Symbol(),LastTick);  
   GridStartTime=TimeCurrent();
   GridStartPrice=LastTick.bid;
   GridUpPrice=GridStartPrice;
   GridDownPrice=GridStartPrice;
    
   double SummUp=LastTick.ask+double(GridStepPoints)*_Point;
   double SummDown=LastTick.bid-double(GridStepPoints)*_Point;
   
   while ( SummUp <= LastTick.ask+double(MaxChannelSizePoints)*_Point )
      {
      m_trade.BuyStop(Lot,SummUp,Symbol());
      SummUp+=double(GridStepPoints)*_Point;
      }
     
   while ( SummDown >= LastTick.bid-double(MaxChannelSizePoints)*_Point )
      {
      m_trade.SellStop(Lot,SummDown,Symbol());
      SummDown-=double(GridStepPoints)*_Point;
      }
   }

void UpdateGrid()//update the grid parameters
   {
   SymbolInfoTick(Symbol(),LastTick);
   if ( LastTick.bid > GridUpPrice ) GridUpPrice=LastTick.bid;
   if ( LastTick.bid < GridDownPrice ) GridDownPrice=LastTick.bid;
   }

Estas son las funciones encargadas de cerrar las posiciones y eliminar las órdenes limitadas restantes; también podemos ver una función de predicado que detecta la condición para cerrar la cuadrícula:

void ClosePosition()//close a position by a symbol
   {
   bool ord;
   ord=PositionSelect(Symbol());
   if ( ord && int(PositionGetInteger(POSITION_MAGIC)) == MagicC  )
      {
      if(m_position.SelectByIndex(0)) m_trade.PositionClose(m_position.Ticket());          
      }
   }

void CleanLimitOrders()//clear limit orders
   {
   int orders=OrdersTotal();
   for(int i=0;i<orders;i++)
      {
      ulong ticket=OrderGetTicket(i);
      if(ticket!=0)
         {
         m_trade.OrderDelete(ticket);
         }
      }
   }

bool bCanClose()//closure condition
   {
   if ( GridStartPrice == GridUpPrice && (GridStartPrice-GridDownPrice)/_Point >= MinMoveToClose ) return true;
   if ( GridStartPrice == GridDownPrice && (GridUpPrice-GridStartPrice)/_Point >= MinMoveToClose ) return true;
   
   if ( GridStartPrice != GridUpPrice && GridStartPrice != GridDownPrice 
   && (GridStartPrice-GridDownPrice)/(GridUpPrice-GridStartPrice) >= KClose 
   && (GridStartPrice-GridDownPrice)/_Point >= MinMoveToClose ) return true;
   if ( GridStartPrice != GridDownPrice && GridStartPrice != GridUpPrice 
   && (GridUpPrice-GridStartPrice)/(GridStartPrice-GridDownPrice) >= KClose
   && (GridUpPrice-GridStartPrice)/_Point >= MinMoveToClose ) return true;
   
   /*
   if ( GridUpPrice >= GridStartPrice+MaxChannelSizePoints*_Point 
   //|| GridDownPrice <= GridStartPrice-MaxChannelSizePoints*_Point ) return true;
   */
   return false;
   }

Hemos comentado la última condición de la función de predicado, esta cierra la cuadrícula si el precio se sale de la misma; podrá usarla a voluntad, ya que no cambia la esencia. Queda por escribir la función comercial principal:

void Trade()//the main function where all actions are performed
   {
   bool ord=PositionSelect(Symbol());
   
   if ( bCanUpdate ) UpdateGrid();
   
   if ( ord && bCanClose() )//if there is a position and the closing condition is met
       {
       ClosePosition();
       CleanLimitOrders();
       bCanUpdate=false;
       bTryedAlready=true;
       }
   if ( bTryedAlready ) ClosePosition();
          
   if ( !bCanUpdate && !ord )
       {
       CleanLimitOrders();
       CreateNewGrid();
       bCanUpdate=true;
       bTryedAlready=false;
       }
   }

 Bueno, ahora vamos a definir qué llamaremos y dónde, y qué haremos al inicializar el asesor experto:

int OnInit()
  {
  m_trade.SetExpertMagicNumber(MagicC);//set the magic number for positions
  RestoreGrid();//restore the grid if present
   return(INIT_SUCCEEDED);
  }

void OnTick()
  {
  Trade();
  }

Con esto, podemos dar por completado el montaje de la cuadrícula. Ahora la probaremos para ver cómo se comporta y sacar las conclusiones correspondientes:

Como podemos ver, se han confirmado las suposiciones sobre el ciclo con pérdidas. Al principio, funciona bastante bien, y luego llega un momento en que la cuadrícula no es suficiente y se produce un ciclo de pérdidas, lo cual reduce todos los beneficios a un estado negativo. No veremos situaciones de este tipo en zonas donde haya un buen movimiento de tendencia, pero donde domine el flat, veremos una pérdida tras otra; podrá probarlo usted mismo y verá que, en general, obtendrá pérdidas, ya que todavía tenemos spread de una u otra forma.

Construyendo y probando el martingale más simple

Ahora que nos hemos ocupado de la cuadrícula, podemos pasar al martingale. Su código será mucho más sencillo. Para trabajar con posiciones, también utilizaremos las bibliotecas que usamos en la cuadrícula, no tiene sentido mostrar este código por segunda vez. Comencemos de inmediato con los parámetros de entrada:

input int SLE=100;//Stop Loss Points
input int TPE=300;//Take Profit Points
input int SlippageMaxOpen=15; //Slippage For Open In Points
input double Lot=0.01;//Start Lot
input int MagicC=679034;//Magic
input int HistoryDaysLoadI=10;//History Deals Window Days

Para mayor sencillez, hemos seleccionado un esquema en el que las posiciones se cierran estrictamente por stop loss o take profit; lo único que diremos sobre la última variable, es que resulta necesaria para no cargar todo la historia de órdenes cada vez, sino solo alguna ventana necesaria (solamente para la optimización). El resto de las variables resultará comprensible para todo el mundo.

Nuestro asesor tendrá solo 2 funciones:

double CalcLot()//calculate the lot
   {
   bool ord;
   double TotalLot=0;
   HistorySelect(TimeCurrent()-HistoryDaysLoadI*86400,TimeCurrent());
   for ( int i=HistoryDealsTotal()-1; i>=0; i-- )
      {
      ulong ticket=HistoryDealGetTicket(i);
      ord=HistoryDealSelect(ticket);
      if ( ord && HistoryDealGetString(ticket,DEAL_SYMBOL) == _Symbol 
      && HistoryDealGetInteger(ticket,DEAL_MAGIC) == MagicC 
      && HistoryDealGetInteger(ticket,DEAL_ENTRY) == DEAL_ENTRY_OUT )
         {
         if ( HistoryDealGetDouble(ticket,DEAL_PROFIT) < 0 )
            {
            TotalLot+=HistoryDealGetDouble(ticket,DEAL_VOLUME);
            }
         else
            {
            break;
            }
         }
      } 
   return TotalLot == 0 ? Lot: TotalLot;
   }


void Trade()//the main function where all actions are performed
   {
   bool ord=PositionSelect(Symbol());
   SymbolInfoTick(Symbol(),LastTick);
   if ( !ord )
      {
      if ( MathRand() > 32767.0/2.0 )
         {
         m_trade.Buy(CalcLot(),_Symbol,LastTick.ask,LastTick.bid-double(SLE)*_Point,LastTick.ask+double(TPE)*_Point);
         }
      else
         {
         m_trade.Sell(CalcLot(),_Symbol,LastTick.ask,LastTick.ask+double(SLE)*_Point,LastTick.bid-double(TPE)*_Point);
         }
      }
   }

La primera es necesaria para calcular el lote final con el que abriremos una posición tras mirar la historia de transacciones. Si la última transacción no ha sido rentable, el siguiente lote será igual a la suma de los lotes de las transacciones no rentables anteriores, hasta la primera rentable. Si la última transacción es rentable, restableceremos el lote a su valor original. En la función principal, solo tenemos que abrir órdenes aleatoriamente en diferentes direcciones con stops fijos; los volúmenes se calcularán según la primera función. Bueno, para que todo esto funcione correctamente, deberemos asignar su propio número mágico al experto en el inicializador y llamar a la función principal en el manejador OnTick, tal como se hizo en la cuadrícula.

Con esto, podemos dar por completado el montaje del martingale más sencillo. Ahora lo probaremos y veremos el resultado:

Esta situación resulta muy similar a la de la cuadrícula; podremos seleccionar los ciclos y ver cómo funcionan por un tiempo. Luego comenzará un ciclo con pérdidas en el que el margen ya no será suficiente para abrir la siguiente posición, e inevitablemente perderemos nuestro dinero. Al igual que la cuadrícula, a veces funcionará, pero al final volverá a tener pérdidas. Ahora que hemos revisado ambas estrategias y las hemos probado en la práctica, podemos ir un poco más allá y extraer conclusiones matemáticas que nos ofrezcan respuestas más importantes que la simple comprensión de estas estrategias.

Matemáticas generales de la cuadrícula y el martingale

¿Por qué son tan importantes en nuestra opinión las matemáticas generales de la cuadrícula y el martingale? Porque, habiendo entendido y absorbido su esencia matemática, podrá despedirse para siempre de una serie de ideas que nunca le traerán provecho (por mucho que quiera creer en ellas), o, al menos, comprenderá qué condiciones pueden posibilitar el funcionamiento de estas estrategias. Asimismo, comprenderá de una vez por todas por qué el martingale y la cuadrícula a secas son estrategias que garantizan las pérdidas, y por qué lo afirmamos con tanta confianza.

Imaginemos que cualquier estrategia consiste en un número infinito de estrategias más sencillas, y como resultado, cuando se abre cualquier orden, una de ellas se activa. Vamos a asumir que estas órdenes se cierran con pérdidas o beneficios fijos. Así, les asignamos las matrices correspondientes С[i] , Lot[i] , donde el tamaño de estas matrices es igual y tiende al infinito. También vamos a considerar que el lote que usa cada una de las estrategias es siempre diferente. También introduciremos la probabilidad de que se activen algunas de estas estrategias. PC[i], obviamente, estos eventos forman un grupo completo, así que la Suma(0,n)( PC[i] ) = 1. Todos los resultados de estos eventos forman nuevos espacios de eventos S i], T [i], que representan, respectivamente, la activación de acuerdo con las pérdidas y los beneficios. Estos eventos tienen sus propias probabilidades condicionales PS[i], PT[i] que, obviamente, también forman un grupo completo. A continuación, mostramos una representación gráfica de lo mencionado:

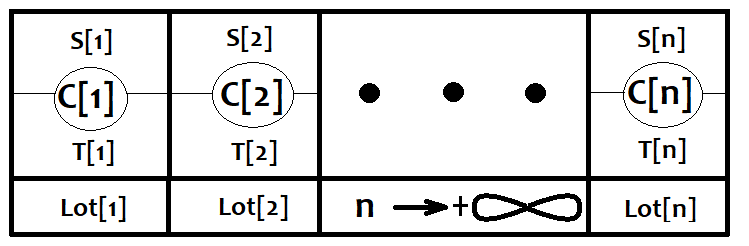
Ahora, vamos a considerar cualquier estrategia tomada por separado de esta lista y calcularemos su esperanza matemática.

• M[i]=(PT[i]*TP-PS[i]*SL)*Lot[i]*TickSize.

Cuando no conocemos la dirección del movimiento del precio en los puntos donde se abre la posición, tenemos derecho a decir que M[i]=0. Donde M[i] es el conjunto de esperanzas matemáticas de las estrategias específicas. En otras palabras, si no sabemos hacia dónde irá el precio, no importa cómo comerciemos, aun así, obtendremos "0" cuando el número de transacciones tienda al infinito.

Ahora, vamos a escribir la fórmula general para la esperanza matemática:

• M0=Suma(0,n)(PC[i]*M[i])

Sabemos que, cuando n tiende al infinito, todos M[i] tienden a cero, lo cual significa que todos los términos de nuestra suma con un número finito de tales estrategias tenderán a "0", pero con un número infinito de transacciones. Esto, a su vez, significa que la esperanza matemática total M0 sigue siendo igual a "0". Si pensamos un poco más, resulta que un conjunto infinito de esos conjuntos finitos de estrategias también será igual a cero, ya que sumar un número infinito de ceros dará como resultado "0". En el caso de la cuadrícula, el tamaño del lote será el mismo en todas partes, y en el caso del martingale será diferente en todas partes, pero estas diferencias no afectarán de ninguna forma a la esperanza matemática final. Podemos describir ambas estrategias con esta fórmula general y no molestarnos en luchar con la combinatoria, el cierre y apertura. Todo es muy claro y sencillo.

No obstante, como estas estrategias se pueden describir con esta fórmula, también podemos describir cualquier estrategia y, por consiguiente, hemos llegado a una conclusión indiscutible que muchos tráders seguro que no querrán aceptar, pero que les conviene. La conclusión es que todas las estrategias que usan la variación y la manipulación de los volúmenes de las transacciones, así como los sistemas "chamánicos" de apertura y cierre de órdenes (sin conocer la dirección aproximada del movimiento al abrir y cerrar transacciones, o al menos algunos parámetros auxiliares del mercado), son por definición insostenibles. Es decir, sin una previsión correcta, todos nuestros esfuerzos serán una pérdida de tiempo y dinero.

Cómo usar correctamente la cuadrícula y el martingale

Empecemos por la cuadrícula. Es mejor usar la cuadrícula cuando sabemos que el mercado está a punto de moverse en una dirección o cuando la probabilidad de un evento determinado aumenta mucho. No obstante, existe el riesgo de caer en un gap, y los gaps y las cuadrículas no se llevan nada bien. Esto se debe a que las órdenes se colocan con un determinado salto y puede ocurrir que el siguiente tick pase cerca de todas las órdenes y aparezca mucho más allá de la cuadrícula. Obviamente, esto sucederá muy rara vez, pero inevitablemente reducirá el rendimiento del sistema. Debemos establecer un tamaño para la cuadrícula igual o ligeramente inferior al movimiento predicho, además, no necesitamos saber la dirección del movimiento, sino solo su valor aproximado. Su gráfico de balance, si el algoritmo de detección de tendencias tiene éxito, se verá así:

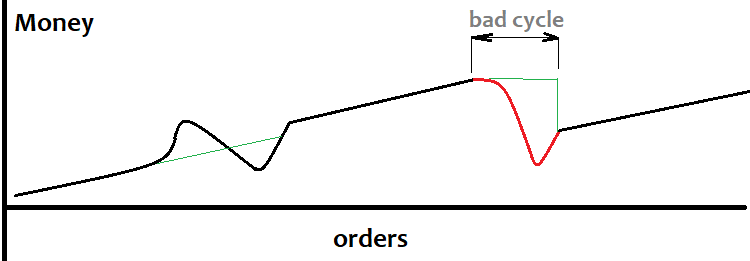
La tendencia no siempre se puede detectar con precisión de antemano, por consiguiente, los ciclos con pérdidas sucederán con bastante frecuencia; en la figura se marcan en rojo. Además, la reducción también será considerable. Quienes tengan métodos para detectar grandes movimientos podrán usar la cuadrícula con éxito, construyendo una según su señal. No nos hemos ocupado aún de resolver este problema; si alguien tiene buenos algoritmos para detectar estas cosas, nos agradaría mucho verlos.

A continuación, determinaremos cuándo se puede usar el martingale. Si tenemos alguna señal con una expectativa "0", pero sabemos que la secuencia de pérdidas es tal que la probabilidad de una transacción rentable estará próxima a uno para un número de pérdidas consecutivas, entonces esa señal podrá utilizarse para el martingale. Nuestro gráfico de balance tendrá este aspecto:

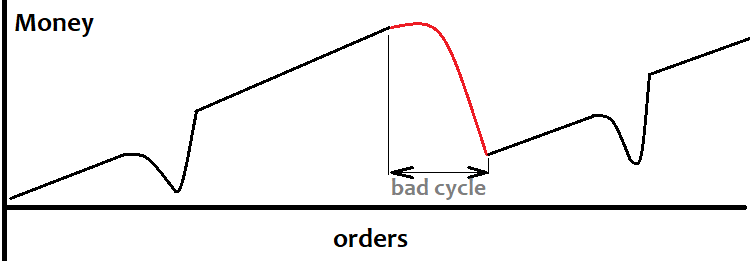
En nuestra opinión, resulta peligroso usar el martingale en cualquier caso, pues resulta casi imposible conseguir que se den las condiciones que hemos descrito. Con la cuadrícula, en cambio, todo parece más sencillo y, lo más importante, más claro.

Conclusión

En este artículo, hemos intentado explicar de forma clara y visual qué suponen estas dos estrategias, qué tienen en común y, lo más importante, qué tienen de bueno y malo. Hemos presentado un material lo más simple y comprensible posible para que lo entiendan incluso los principiantes. Este artículo es más bien para principiantes, pero las conclusiones extraídas resultan mucho más importantes que una simple valoración de las estrategias y los límites de su aplicación. Hemos obtenido conclusiones matemáticas generales que permitirán a los principiantes (y creemos que no solo a ellos) invertir su tiempo de la forma más productiva posible al desarrollar sus propios sistemas comerciales. El artículo en sí no aporta nada nuevo a la comprensión de la física del mercado, pero esperamos que templará un poco los ánimos de aquellos que todavía intentan explotar de forma irreflexiva estos principios, por su propio bien.