MetaTrader 5 / Trading systems
Русский 中文 Español Deutsch 日本語 Português
preview
Forecasting with ARIMA models in MQL5

Forecasting with ARIMA models in MQL5

MetaTrader 5 — Trading systems | 26 June 2023, 10:12
4 420 4
Francis Dube
Francis Dube

Introduction

The article Implementing an ARIMA training algorithm in MQL5, describes the CArima class for building ARIMA models. Although it is technically possible to use the class as it is to apply a model and make predictions, it is not intuitive. In this article we will address this shortcomming and extend the class to enable easier to use methods for applying models to make predictions. We will discuss some of the complications related to implementing predictions as well as some new features added to the class. To conclude we will  use the complete class to build a  model , use it to predict forex prices by applying it to an  expert advisor and indicator.


The series of inputs

It is well known that ARIMA models rely on temporal dependences in a dataset. Therefore to make one or more predictions we need to feed the model a series of input data. The specification of the model determines the minimum size of the input series. Knowning this, it becomes obvious that if the input series is inadequate it will not be possible to make any predictions or at the very least the predictions will not be reflective of the applied model. Different types of ARIMA models make varying demands on the size of the input series beyond just the order of the model.

Implementing predictions for pure autoregressive models is trivial as all that is required are inputs equal to the largest lag of the model. Mixed models that use moving average terms create problems when making forecasts. We have no actual error or innovation series yet. To overcome this we must first decide how the initial values of errors will be calculated.

This process involves first using any available model parameters to get the initial state of the model which excludes any of the moving average terms, as they are assumed to be 0 at this stage. Then the known series values are used to calculate initial error values by cycling through an number of redundant predictions.These initial predictions are redundant because they will have nothing to do with the final prediction(s) we are ultimately interested in. This obviously puts more demands on the number of inputs needed for prediction. The critical thing to appreciate here is how many redundant prediction cycles should be peformed in order to come up with suitable  error series values to make valid  predictions.

Still there is more to consider in terms of the number of model inputs. The CArima class has the ability to specify  models with non-contiguous lags. This puts even more demands on the number of required inputs. In this instance the largest lag of either types (AR/MA) will add to the input size requirements. Consider a model defined by the function                                                                                             

price(t) = constant_term + AR*price(t-4)

This function specifies a model with a single AR term at a lag of four. That means the current price is partially determined by the value 4 time slots prior. Even though we only require one such value we have to be cognisant of maintaining the temporal relations of the inputs. Therefore instead of just one input requirement we actually need four, in addition to other model requirements. The final determinant on the size of the inputs series depends on the whether any differencing is required.


Accounting for differencing

The demands of differencing add to the number of inputs required not because of anything related to the calculation of the predicted value(s), but due to the fact that differencing leads to a loss of information. When creating a differenced series, it will always be one less in length relative to the original series. This shorter series will ultimately be passed as input to the model. So in general, extra inputs are needed to compensate that correspond with the order of differencing specified by the model.

Besides the impact that  differencing has on the inputs size it also affects the final predictions made as they will be in the differenced domain. The predictions along with the supplied input series must be combined and integrated so as to return combined values to the original domain.


Predicting far into the future

Some times users may be interested in pedicting several time slots into the future based on a single set of inputs. Although doing so is not recommended, it is an avenue worth exploring and unpacking. When making predictions far into the future we have to appreciate certain truths. First, the further we go , we eventually have to use predictions from previous time slots as inputs for any autoregressive terms.  Once we cross beyond the known values of the sries , which are used as initial inputs, we no longer have the means to calculate error values. Since true future values are unknown. Therefore moving average terms for such time slots will and can only be assumed to be zero. Which leads to the predicted series degenerating into either a pure autoregressive process if specifed or a  process defined by the constant term only. Making multiple predictions far into the future should be done whilst being aware of the inherent limitations.

Additions to the CArima class

The first change made to the class relates to its parent CPowellsMethod. The Optimize() method now has access modifier protected  and cannot be accessed from outside the class. Naturally, this change extends to CArima as well. Due to this modification, the name of the include file containing the CPowellsMethod class is changed to just Powells.mqh.

//-----------------------------------------------------------------------------------
// Minimization of Functions.
// Unconstrained Powell’s Method.
// References:
// 1. Numerical Recipes in C. The Art of Scientific Computing.
//-----------------------------------------------------------------------------------
class PowellsMethod:public CObject
  {
protected:
   double            P[],Xi[];
   double            Pcom[],Xicom[],Xt[];
   double            Pt[],Ptt[],Xit[];
   int               N;
   double            Fret;
   int               Iter;
   int               ItMaxPowell;
   double            FtolPowell;
   int               ItMaxBrent;
   double            FtolBrent;
   int               MaxIterFlag;
   int               Optimize(double &p[],int n=0);
public:
   void              PowellsMethod(void);
   void              SetItMaxPowell(int n)           { ItMaxPowell=n; }
   void              SetFtolPowell(double er)        { FtolPowell=er; }
   void              SetItMaxBrent(int n)            { ItMaxBrent=n;  }
   void              SetFtolBrent(double er)         { FtolBrent=er;  }
   double            GetFret(void)                   { return(Fret);  }
   int               GetIter(void)                   { return(Iter);  }
private:
   void              powell(void);
   void              linmin(void);
   void              mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc);
   double            brent(double ax,double bx,double cx,double &xmin);
   double            f1dim(double x);
   virtual double    func(const double &p[]) { return(0); }
  };


A significant feature added to the class, is the ability to save and load mdoels. this allows one to train and save a model for later use or inclusion with any other Mql5 program. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::SaveModel(const string model_name)
  {
   uint model_order[]= {m_const,m_ar_order,m_diff_order,m_ma_order};

   CFileBin file;
   ResetLastError();
   if(!file.Open("models\\"+model_name+".model",FILE_WRITE|FILE_COMMON))
     {
      Print("Failed to save model.Error: ",GetLastError());
      return false;
     }

   m_modelname=(m_modelname=="")?model_name:m_modelname;

   long written=0;

   written = file.WriteIntegerArray(model_order);

   if(!written)
     {
      Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   if(m_ar_order)
     {
      written = file.WriteIntegerArray(m_arlags);

      if(!written)
        {
         Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
         return false;
        }
     }

   if(m_ma_order)
     {
      written = file.WriteIntegerArray(m_malags);

      if(!written)
        {
         Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
         return false;
        }
     }

   written = file.WriteDoubleArray(m_model);

   if(!written)
     {
      Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   written = file.WriteDouble(m_sse);

   if(!written)
     {
      Print("Failed write operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }


   file.Close();

   return true;

  }


The SaveModel method enables saving models, it requires a string input which will be the new name of the model.The method itself writes to a binary .model  file stored in  models directory of the common files folder ( Terminal\Common\Files\models ) . The saved file contains the model order as well as its parameters, if it has been trained, including the sum of square errors (sse) value. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::LoadModel(const string model_name)
  {
   int found=StringFind(model_name,".model");

   if(found>=0)
      m_modelname=StringSubstr(model_name,0,found);
   else
      m_modelname=model_name;

   if(StringFind(m_modelname,"\\")>=0)
      return false;

   string filename="models\\"+m_modelname+".model";

   if(!FileIsExist(filename,FILE_COMMON))
     {
      Print("Failed to find model, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   CFileBin file;
   ResetLastError();
   if(file.Open(filename,FILE_READ|FILE_COMMON)<0)
     {
      Print("Failed open operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   uint model_order[];


   file.Seek(0,SEEK_SET);

   if(!file.ReadIntegerArray(model_order,0,4))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   m_const=bool(model_order[0]);
   m_ar_order=model_order[1];
   m_diff_order=model_order[2];
   m_ma_order=model_order[3];

   file.Seek(sizeof(uint)*4,SEEK_SET);

   if(m_ar_order && !file.ReadIntegerArray(m_arlags,0,m_ar_order))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   if(!m_ar_order)
      ArrayFree(m_arlags);



   if(m_ar_order)
      file.Seek(sizeof(uint)*(4+m_ar_order),SEEK_SET);


   if(m_ma_order && !file.ReadIntegerArray(m_malags,0,m_ma_order))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   ArrayPrint(m_malags);

   if(!m_ma_order)
      ArrayFree(m_malags);


   if(m_ar_order || m_ma_order)
      file.Seek(sizeof(uint)*(4+m_ar_order+m_ma_order),SEEK_SET);



   if(!file.ReadDoubleArray(m_model,0,m_ma_order+m_ar_order+1))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   file.Seek(sizeof(uint)*(4+m_ar_order+m_ma_order) + sizeof(double)*ArraySize(m_model),SEEK_SET);

   if(!file.ReadDouble(m_sse))
     {
      Print("Failed read operation, ",__LINE__,".Error: ",GetLastError());
      return false;
     }

   if(m_model[1])
      m_istrained=true;
   else
      m_istrained=false;

   ZeroMemory(m_differenced);
   ZeroMemory(m_leads);
   ZeroMemory(m_innovation);

   m_insize=0;

   return true;
  }


The LoadModel method needs the model name  and it reads in all the attributes of a model previously saved. Both methods return either true or false and useful error messages are written to the terminal's journal. 

string            GetModelName(void)                      { return m_modelname;}

The GetModelName() method returns the name of a model, it will return an empty string if the model has never been saved otherwise it returns the name set when saving the model.

//+------------------------------------------------------------------+
//| calculate the bayesian information criterion                     |
//+------------------------------------------------------------------+
double CArima::BIC(void)
  {
   if(!m_istrained||!m_sse)
     {
      Print(m_modelname," Model not trained. Train the model first to calculate the BIC.");
      return 0;
     }

   if(!m_differenced.Size())
     {
      Print("To calculate the BIC, supply a training data set");
      return 0;
     }
   uint n = m_differenced.Size();
   uint k = m_ar_order+m_ma_order+m_diff_order+uint(m_const);

   return((n*MathLog(m_sse/n)) + (k*MathLog(n)));

  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CArima::AIC(void)
  {
   if(!m_istrained||!m_sse)
     {
      Print(m_modelname," Model not trained. Train the model first to calculate the AIC.");
      return 0;
     }

   if(!m_differenced.Size())
     {
      Print("To calculate the AIC, supply a training data set");
      return 0;
     }

   uint n = m_differenced.Size();
   uint k = m_ar_order+m_ma_order+m_diff_order+uint(m_const);

   return((2.0*k)+(double(n)*MathLog(m_sse/double(n))));
  }
//+------------------------------------------------------------------+


Also new are BIC and AIC methods. The BIC method returns the bayesian information criterion based on a model's sse value.The AIC method calculates the akiake information criterion and works similarly to the BIC function.The Bayesian Information Criterion (BIC) and Akaike Information Criterion (AIC) are statistical measures used for model selection. Both criteria aim to balance the goodness of fit of a model with its complexity, so that simpler models are preferred if they fit the data almost as well as more complex models.

The BIC and AIC differ in how they balance goodness of fit and complexity. The BIC puts more weight on model simplicity than the AIC, meaning it favors even simpler models over the AIC. On the other hand, the AIC is more likely to select more complex models than the BIC. In simple terms, the BIC and AIC allow us to compare different models and choose the one that best fits our data while taking into account the complexity of the model. By choosing a simpler model, we can avoid overfitting, which occurs when a model is too complex and fits the data too closely, making it less useful for predicting new observations.

They both return 0 on error and should be called right after a model has been trained whilst training data is still loaded. When a trained model is initialized, the data used to train will not be available so neither the BIC nor the AIC can be calculated.

uint              GetMinModelInputs(void)                 { return(m_diff_order + GetMaxArLag() + (GetMaxMaLag()*m_infactor));}

It is also now possible to query the minimum number of inputs required by a model. This is done with the GetMinModelInputs() method. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CArima::Summary(void)
  {

   string print = m_modelname+" Arima("+IntegerToString(m_ar_order)+","+IntegerToString(m_diff_order)+","+IntegerToString(m_ma_order)+")\n";
   print+= "SSE : "+string(m_sse);

   int k=0;
   if(m_const)
      print+="\nConstant: "+string(m_model[k++]);
   else
      k++;
   for(uint i=0; i<m_ar_order; i++)
      print+="\nAR coefficient at lag "+IntegerToString(m_arlags[i])+": "+string(m_model[k++]);
   for(uint j=0; j<m_ma_order; j++)
      print+="\nMA coefficient at lag "+IntegerToString(m_malags[j])+": "+string(m_model[k++]);

   Print(print);

   return;

  }


Lastly, calling the Summary() writes the model's attributes to the terminal, it no longer returns a string.

Implementing predictions

   bool              Predict(const uint num_pred,double &predictions[]);
   bool              Predict(const uint num_pred,double &in_raw[], double &predictions[]);
   bool              SaveModel(const string model_name);
   bool              LoadModel(const string model_name);
   double            BIC(void);
   double            AIC(void);

Applying a model to make predictions is implemented through two overloaded methods named Predict(). Both take as input two similar inputs:

  • num_pred - This integer value defines the number of predictions desired.
  • predictions - Is a double type array where the predicted values are output. 
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::Predict(const uint num_pred,double &predictions[])
  {
   if(!num_pred)
     {
      Print("Invalid number of predictions");
      return false;
     }

   if(!m_istrained || !m_insize)
     {
      ZeroMemory(predictions);
      if(m_istrained)
         Print("Model not trained");
      else
         Print("No input data available to make predictions");
      return false;
     }

   ArrayResize(m_differenced,ArraySize(m_differenced)+num_pred,num_pred);

   ArrayResize(m_innovation,ArraySize(m_differenced));

   evaluate(num_pred);

   if(m_diff_order)
     {
      double raw[];
      integrate(m_differenced,m_leads,raw);
      ArrayPrint(raw,_Digits,NULL,m_insize-5);
      ArrayCopy(predictions,raw,0,m_insize+m_diff_order);
      ArrayFree(raw);
     }
   else
      ArrayCopy(predictions,m_differenced,0,m_insize);

   return true;
  }

The Predict methods differ  in terms of the number of function parameters.The first method requiring two parameters is used to make predictions based on the training data used to derive the model's optimal coefficients. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CArima::Predict(const uint num_pred,double &in_raw[],double &predictions[])
  {
   if(!num_pred)
     {
      Print("Invalid number of predictions");
      return false;
     }

   if(!m_istrained)
     {
      ZeroMemory(predictions);
      Print("Model not trained");
      return false;
     }

   int numofinputs=0;

   if(m_ar_order)
      numofinputs+=(int)GetMaxArLag();
   if(m_ma_order)
      numofinputs+=int(GetMaxMaLag()*m_infactor);
   if(m_diff_order)
      numofinputs+=(int)m_diff_order;

   if(in_raw.Size()<(uint)numofinputs)
     {
      ZeroMemory(predictions);
      Print("Input dataset size inadequate. Size required: ",numofinputs);
      return false;
     }

   ZeroMemory(m_differenced);

   if(m_diff_order)
     {
      difference(m_diff_order,in_raw,m_differenced,m_leads);
      m_insize=m_differenced.Size();
     }
   else
     {
      m_insize=in_raw.Size();
      ArrayCopy(m_differenced,in_raw);
     }


   if(m_differenced.Size()!=(m_insize+num_pred))
      ArrayResize(m_differenced,m_insize+num_pred,num_pred);

   ArrayFill(m_differenced,m_insize,num_pred,0.0);

   if(m_innovation.Size()!=m_insize+num_pred)
      ArrayResize(m_innovation,ArraySize(m_differenced));

   ArrayInitialize(m_innovation,0.0);

   evaluate(num_pred);

   if(m_diff_order)
     {
      double raw[];
      integrate(m_differenced,m_leads,raw);
      ArrayCopy(predictions,raw,0,m_insize+m_diff_order);
      ArrayFree(raw);
     }
   else
      ArrayCopy(predictions,m_differenced,0,m_insize);

   return true;

  }


The second Predict method requires a third input parameter array which should contain the series of inputs to be used to calculate the predictions. Both methods return a boolean balue and also make use of the private evaluate function. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CArima::evaluate(const uint num_p)
  {

   double pred=0;
   uint start_shift=(m_ma_order)?((!m_innovation[m_insize-1])?m_insize-(GetMaxMaLag()*m_infactor):m_insize):m_insize;
   uint d_size=(uint)ArraySize(m_differenced);

   int p_shift;

   for(uint i=start_shift; i<d_size; i++)
     {
      p_shift=0;
      pred=0;
      if(i>=m_insize)
         m_innovation[i]=0.0;
      if(m_const)
         pred+=m_model[p_shift++];
      for(uint j=0; j<m_ar_order; j++)
         pred+=m_model[p_shift++]*m_differenced[i-m_arlags[j]];
      for(uint k=0; i>=GetMaxMaLag() && k<m_ma_order; k++)
         pred+=m_model[p_shift++]*m_innovation[i-m_malags[k]];
      if(i>=m_insize)
         m_differenced[i]=pred;
      if(i<m_insize)
         m_innovation[i]=pred-m_differenced[i];
     }

   return;
  }


The evaluate() method is similar to the func() method with some slight differences. It takes the desired number of predictions as its only argument  and sweeps across up to five arrays depending on the model specification. It calculates new predictions and adds new values to the error (innovation) series as needed. Once done the predicted values are extracted and copied to the destination array supplied to Predict() method. The Predict methods return true on success and false if any error is encountered.


Using the class

To demonstrate user of the modified CArima class, we will build a script that trains a few models and saves the best one by performing a brute force search. Then we will show how this saved model can be used in an indicator by using it to make one step ahead predictions. Lastly we will use the same model to create a simple expert advisor. 

//+------------------------------------------------------------------+
//|                                                 TrainARModel.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Arima.mqh>

enum ENUM_QUOTES
  {
   closeprices,//Close price
   medianprices//Mid price
  };

input uint MaximumSearchLag=5;
input bool DifferenceQuotes=true;
input datetime TrainingDataStartDate=D'2020.01.01 00:01';
input datetime TrainingDataStopDate=D'2021.01.01 23:59';
input string Sy="AUDUSD";//Set The Symbol
input ENUM_TIMEFRAMES SetTimeFrame=PERIOD_M1;
input ENUM_QUOTES quotestypes = closeprices;
input string SetModelName = "ModelName";

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   CArima *arima[];
   uint max_it=MaximumSearchLag;
   double sse[],quotes[],mid_prices[];


   if(!max_it)
      ++max_it;


   MqlRates prices[];

   int a_size=CopyRates(Sy,SetTimeFrame,TrainingDataStartDate,TrainingDataStopDate,prices);

   if(a_size<=0)
     {
      Print("downloaded size is ", a_size," error ",GetLastError());
      return;
     }

   ArrayResize(arima,max_it);
   ArrayResize(sse,max_it);
   ArrayResize(quotes,a_size);

   for(uint i=0; i<prices.Size(); i++)
     {

      switch(quotestypes)
        {
         case medianprices:
            quotes[i]=(prices[i].high+prices[i].low)/2;
            break;
         case closeprices:
            quotes[i]=prices[i].close;
            break;
        }
     }

   uint u=0;
   for(uint i=0; i<max_it; i++)
     {
      u=uint(DifferenceQuotes);
      arima[i]=new CArima(i+1,u,0,true);
      if(arima[i].Fit(quotes))
        {
         sse[i]=arima[i].GetSSE()*1.e14;
         Print("Fitting model ",i+1," completed successfully.");
        }
      else
        {
         sse[i]=DBL_MAX;
         Print("Fitting model ",i+1, " failed.");
        }


     }

   int index = ArrayMinimum(sse);
   Print("**** Saved model *****");
   arima[index].Summary();
//save the best model for later use.
   arima[index].SaveModel(SetModelName);

   for(int i=0; i<(int)arima.Size(); i++)
      if(CheckPointer(arima[i])==POINTER_DYNAMIC)
         delete arima[i];

  }
//+------------------------------------------------------------------+


The script facilitates a bruteforce search for an optimal pure autoregressive model that fits a sample of close prices. It should be emphasized that this is just a simple demonstration. Its possible to implement more complex models with variations in the number and types of (AR/MA) terms, not forgetting the ability to specify non contiguous lags for those terms. So the possibilities are vast. For now we limit ourselves to fitting a pure autoregressive model.


Model Training


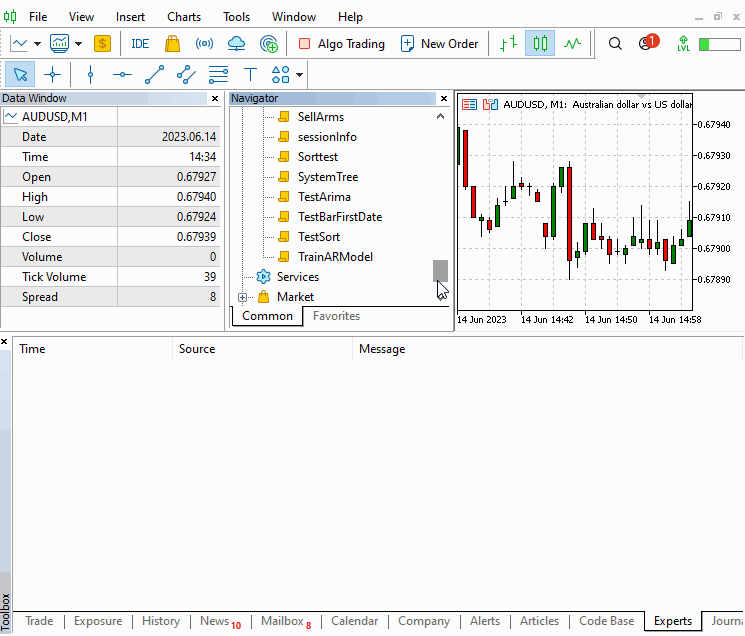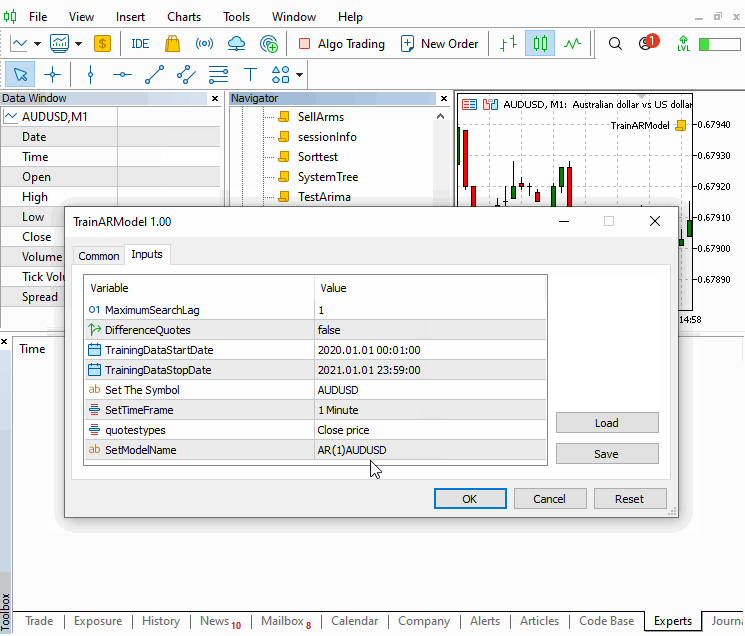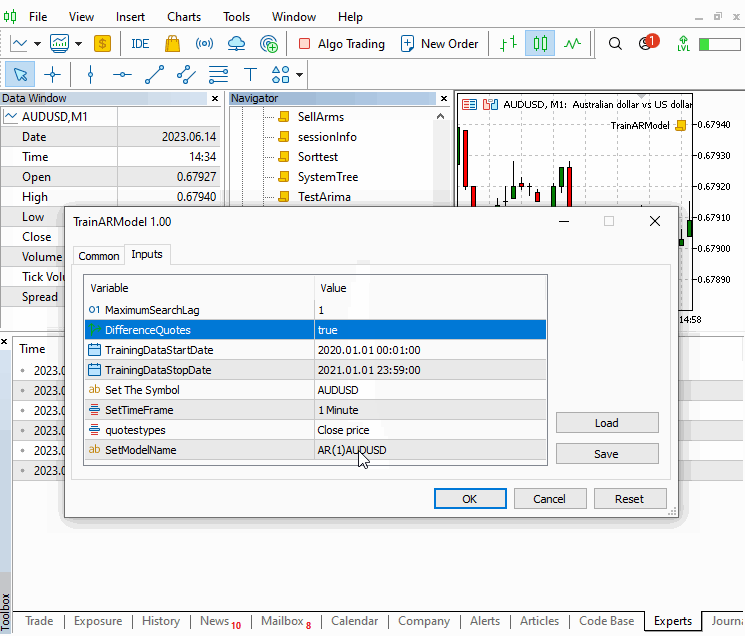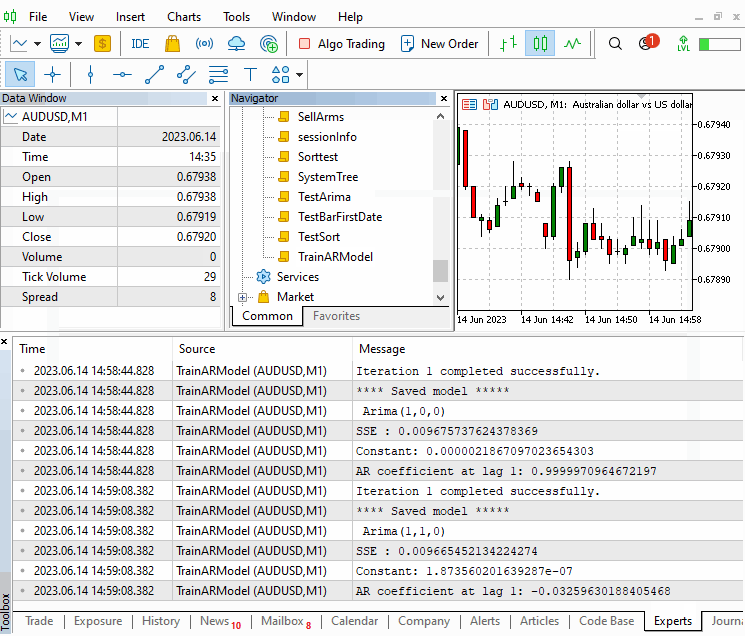
The script allows setting the maximum AR order to terminate searches, as well as the symbol, timeframe and date period of the price sample data. Its important to  use a sample prices that are representative of the conditions that are likely to be encountered when applying the model to make predictions.

Saved Model Parameters Displayed


The script determines the optimal model by selecting the one with the least sse value amongst the set of trained models.The selected model is then saved and its attributes printed to the terminal.

//+------------------------------------------------------------------+
//|                                         ArimaOneStepForecast.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property indicator_chart_window
#property indicator_buffers 1
#property indicator_plots   1
#include<Arima.mqh>
//--- plot PredictedPrice
#property indicator_label1  "PredictedPrice"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- input parameters
input string   ModelName = "Model name";

//--- indicator buffers
uint     NumberOfPredictions=1;
double         PredictedPriceBuffer[];
double         forecast[];
double         pricebuffer[];
uint         modelinputs;

CArima arima;
double mj[];

//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,PredictedPriceBuffer,INDICATOR_DATA);


   ArraySetAsSeries(PredictedPriceBuffer,true);

   if(!arima.LoadModel(ModelName))
      return(INIT_FAILED);
//---
   modelinputs=arima.GetMinModelInputs();

   ArrayResize(pricebuffer,modelinputs);

   ArrayResize(forecast,NumberOfPredictions);

   if(modelinputs<=0)
      return(INIT_FAILED);

   arima.Summary();

   arima.GetModelParameters(mj);

   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   ArraySetAsSeries(time,true);
   int limit = (prev_calculated<=0)?1000-(int)modelinputs-1:rates_total-prev_calculated+1;

   if(NewBar(time[0]))
     {
      for(int i = limit; i>=0; i--)
        {
         if(CopyClose(_Symbol,_Period,i+1,modelinputs,pricebuffer)==modelinputs)
            if(arima.Predict(NumberOfPredictions,pricebuffer,forecast))
               PredictedPriceBuffer[i]=forecast[NumberOfPredictions-1];
        }
     }

//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool NewBar(datetime c_time)
  {
   static datetime prev_time;

   if(c_time>prev_time)
     {
      prev_time=c_time;
      return true;
     }

   return false;
  }
//+------------------------------------------------------------------+


The indicator uses the the selectd model to make one step ahead predictions.

Indicator

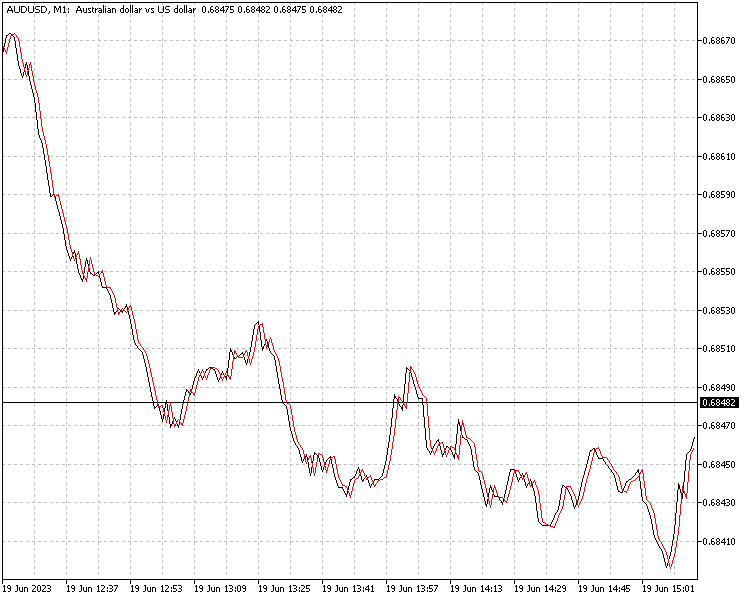
The specified model is loaded during indicator initialization. The Predict method is then used in the main indicator loop to make forward predictions based on the supplied close price inputs. 

//+------------------------------------------------------------------+
//|                                               ArForecasterEA.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <Trade\Trade.mqh>
#include <Trade\SymbolInfo.mqh>
#include <Trade\PositionInfo.mqh>
#include <Trade\AccountInfo.mqh>
#include <Arima.mqh>
//---
input string ModelName   ="model name"; // Saved Arima model name
input long   InpMagicNumber = 87383;
input double InpLots          =0.1; // Lots
input int    InpTakeProfit    =40;  // Take Profit (in pips)
input int    InpTrailingStop  =30;  // Trailing Stop Level (in pips)

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int    InpOpenThreshold =1; // Differential to trigger trade (in points)
int    InpStopLoss     = 0;//   Stoploss (in pips)

//---
//+------------------------------------------------------------------+
//| ARIMA Sample expert class                                         |
//+------------------------------------------------------------------+
class CArExpert
  {
protected:
   double            m_adjusted_point;             // point value adjusted for 3 or 5 points
   CTrade            m_trade;                      // trading object
   CSymbolInfo       m_symbol;                     // symbol info object
   CPositionInfo     m_position;                   // trade position object
   CAccountInfo      m_account;                    // account info wrapper
   CArima            *m_arima;                      // Arma object pointer
   uint              m_inputs;                     // Minimum number of inputs for Arma model
   //--- indicator buffers
   double            m_buffer[];                   // close prices buffer
   double            m_pbuffer[1];                 // predicted close prices go here


   //---
   double            m_open_level;


   double            m_traling_stop;
   double            m_take_profit;
   double            m_stop_loss;

public:
                     CArExpert(void);
                    ~CArExpert(void);
   bool              Init(void);
   void              Deinit(void);
   void              OnTick(void);

protected:
   bool              InitCheckParameters(const int digits_adjust);
   bool              InitModel(void);
   bool              CheckForOpen(void);
   bool              LongModified(void);
   bool              ShortModified(void);
   bool              LongOpened(void);
   bool              ShortOpened(void);
  };


The expert advisor again applies the saved model to implement a simple strategy. Based on the next bar prediction we buy if the forecast close is larger than the last known close. And sell if the forecast is less. 

Back test results

                                         

  This is just a simple demonstration it should not be used to trade on a live account.

The code for the complete CArima class and it dependencies are contained in the zip file attached at the end of the article, along with the script , indicator and EA described in the article.


Conclusion

Autoreggressive models can be easily trained using the MT5 terminal and applied in all sorts of programs. The hard part is model specification and selection. To overcome these challenges and build effective autoregressive models in forex analysis, traders should follow some best practices. These include:
  • Start with a clear research question: Before building an autoregressive model, traders should define a clear research question and hypothesis that they want to test. This helps ensure that the modeling process remains focused and relevant to the trader's goals.
  • Gather high-quality data: The accuracy of the model depends largely on the quality of the data used. Traders should use reliable sources of data and ensure that it is clean, complete, and relevant to their research question.
  • Test multiple models: Traders should test multiple models with different lag lengths and parameters to determine the most accurate and effective model for their data.
  • Validate the model: Once a model has been built, traders should validate its accuracy using statistical techniques.
  • Monitor and adjust the model: As market conditions change over time, the effectiveness of the model may also change. Traders should monitor the performance of their model over time and make adjustments as needed to ensure that it continues to provide accurate insights into future price movements.
By following these best practices, traders can build effective autoregressive models in forex analysis and gain valuable insights into future market trends. I hope the code will be useful to other users and maybe inspire them to extend the library further. Good luck.


File
Description
Mql5/include/Powells.mqh
 include file containing declaration and definition of CPowellsMethod class
Mql5/include/Arima.mqh
include file for the CArima class
Mql5/indicator/ArimaOneStepForecast.mql5
Indicator source code showing how to load and apply a model in an indicator
Mql5/scripts/TrainARModel.mql5
 script demonstrating how to train a model, and save it for later use
Mql5/experts/ArForecasterEA.mql5
 expert advisor showing use of  a saved model in an EA.


Attached files |
Download ZIP
Arima.mqh (22.87 KB)
Powells.mqh (17.57 KB)
ArForecasterEA.mq5 (14.83 KB)
ArimaOneStepForecast.mq5 (3.48 KB)
TrainARModel.mq5 (2.77 KB)
Mql5.zip (12.64 KB)
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

Other articles by this author

Last comments | Go to discussion (4)
CapeCoddah
CapeCoddah | 26 Jun 2023 at 13:34

Hello Francis!

An excellent article!  As I am converting an MQ4 EA that use several averages,  I am going to study your code to determine the best integration and will be back in touch later

CapeCoddah

arturmeier
arturmeier | 3 Aug 2023 at 02:35
Thank you for the article
Timo Kosiol
Timo Kosiol | 24 Aug 2023 at 09:29

Thanks for your very informative article. Can I predict more than one step ahead?

I guess just increasing "NumberOfPredictions" isn't enough, is it?

thomasochere666
thomasochere666 | 20 Oct 2023 at 13:41
I know you have created something really good here but the trainARmodel script does not work for me, what do you recommend i should do.
Creating an EA that works automatically (Part 15): Automation (VII) Creating an EA that works automatically (Part 15): Automation (VII)
To complete this series of articles on automation, we will continue discussing the topic of the previous article. We will see how everything will fit together, making the EA run like clockwork.
Matrices and vectors in MQL5: Activation functions Matrices and vectors in MQL5: Activation functions
Here we will describe only one of the aspects of machine learning - activation functions. In artificial neural networks, a neuron activation function calculates an output signal value based on the values of an input signal or a set of input signals. We will delve into the inner workings of the process.
Category Theory in MQL5 (Part 11): Graphs Category Theory in MQL5 (Part 11): Graphs
This article is a continuation in a series that look at Category Theory implementation in MQL5. In here we examine how Graph-Theory could be integrated with monoids and other data structures when developing a close-out strategy to a trading system.
Category Theory in MQL5 (Part 10): Monoid Groups Category Theory in MQL5 (Part 10): Monoid Groups
This article continues the series on category theory implementation in MQL5. Here we look at monoid-groups as a means normalising monoid sets making them more comparable across a wider span of monoid sets and data types..