Discrete wavelet transform

Der Indikator Diskrete Wavelet-Transformation ist eine erweiterte Implementierung der numerischen und funktionalen Analyse für MetaTrader 4, der diskreten Wavelet-Transformationsmethode (DWT). Das besondere Merkmal der DWT ist die Art und Weise, wie das Wavelet in Form eines diskreten Signals (Sample) dargestellt wird. Die DWT wird häufig zur Filterung und Vorverarbeitung von Daten, zur Analyse des Zustands und zur Erstellung von Prognosen für die Aktien- und Devisenmärkte, zur Erkennung von Mustern, zur Verarbeitung und Synthese verschiedener Signale, z. B. von Sprache und medizinischen Signalen, zur Lösung von Problemen der Bildkompression und -verarbeitung, beim Lernen neuronaler Netze und in vielen anderen Fällen verwendet.

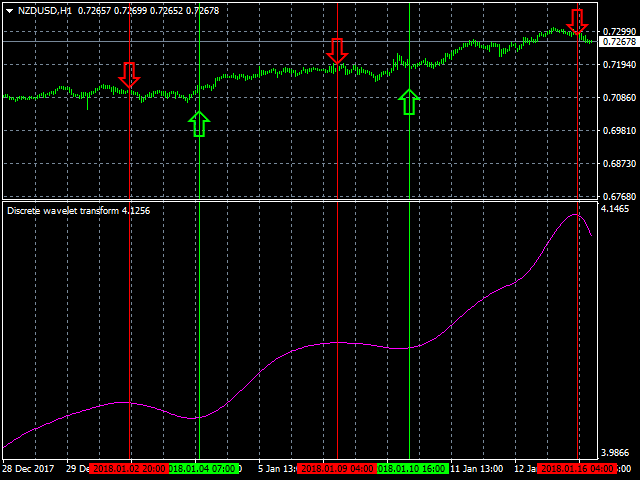
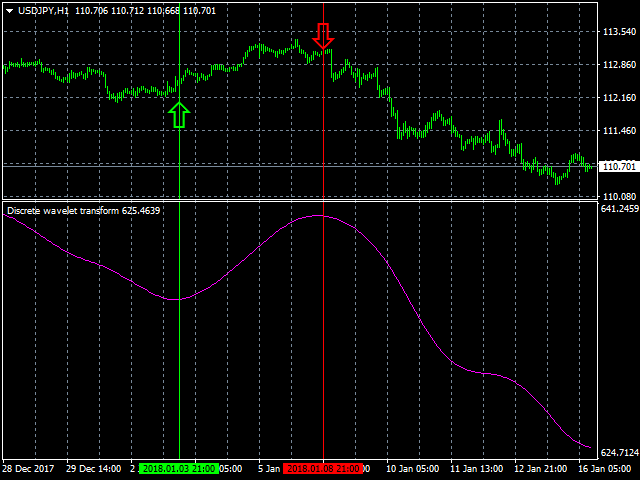
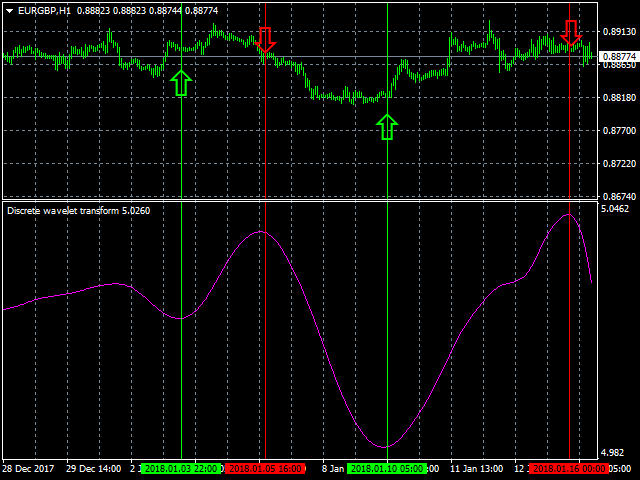
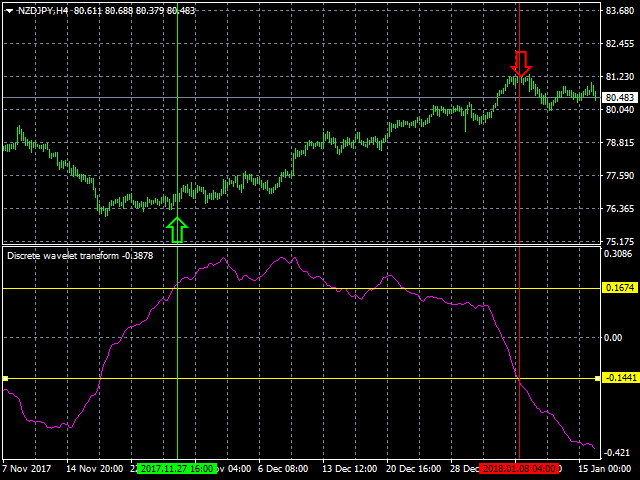
Der Indikator der diskreten Wavelet-Transformation ist ein Filter, der zum Auffinden optimaler Marktein- und -ausstiegspunkte unter Trendbedingungen verwendet wird. Er ermöglicht eine genauere Vorhersage und Analyse des aktuellen und sich abzeichnenden Trends.

• 1. Haar (haar)
• 2. Daubechies (db1, db2, db3, db4, db5, db6, db7, db8, db9, db10)
• 3. Coiflet (coif1, coif2, coif3, coif4, coif5)
• 4. Biorthogonal (bior11, bior13, bior15, bior22, bior24 и др)
• 5. Umgekehrt biorthogonal (rbior11, rbior13, rbior15, rbior22, bior24 и др)

sowie die Berechnungsoptionen und die endgültigen Filterdarstellungsvarianten

• 1. DWT ist die diskrete Wavelet-Transformation
• 2. MODWT ist die diskrete Wavelet-Transformation mit Überlappung
• 3. SWT ist die stationäre Wavelet-Transformation

Die Filter unterscheiden sich in ihren Grundfunktionen, den Wavelet-Transformationskoeffizienten und den Berechnungsmethoden (hauptsächlich iterativ). Jeder Filter hat seine eigenen Eigenschaften im Zeit- und Frequenzraum. Die Verwendung verschiedener Filter ermöglicht die Identifizierung bestimmter Eigenschaften des analysierten Signals.

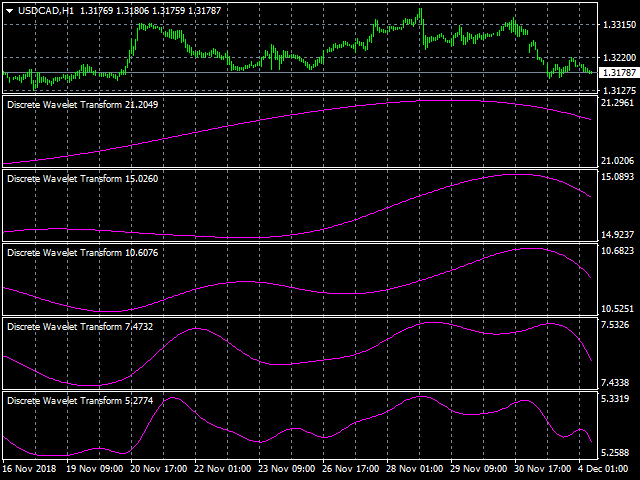
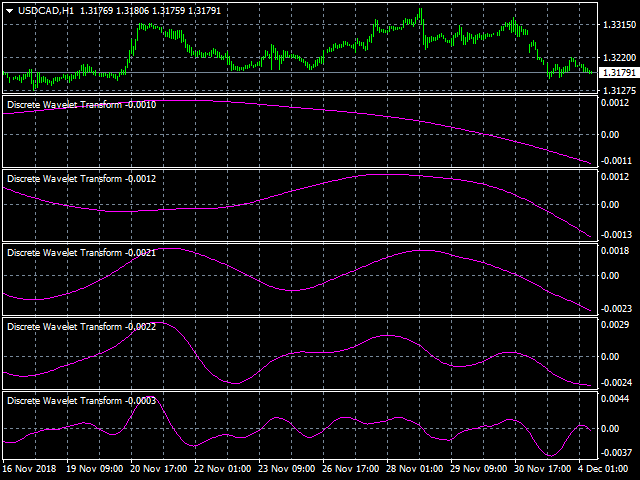
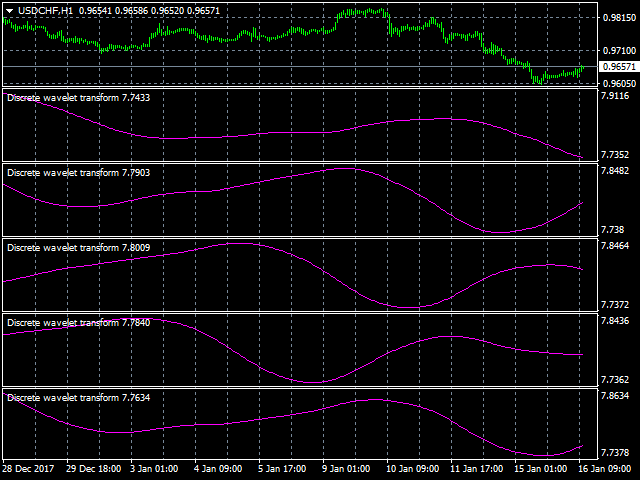
Die Anzahl der bei der Signalanalyse verwendeten Wavelets bestimmt den Grad der Zerlegung. Die Genauigkeit der Signaldarstellung nimmt auf höheren Zerlegungsebenen ab, aber die Möglichkeit der Filterung des Signals in höherer Qualität mit besserer Rauschunterdrückung und effizienter Kompression steigt.

Einstellbare Parameter

• type - Berechnungsart (0-DWT, 1-MODWT, 2-SWT);
• Filter - Filtertyp;
• Indikator - für die Transformation verwendeter Indikator (0-1);
• Länge - Länge des Indikators;
• J - das Niveau der Zerlegung.