
Clusteranalyse (Teil I): Die Steigung von Indikatorlinien
Zusammenfassung
Die Clusteranalyse ist eines der wichtigsten Elemente der künstlichen Intelligenz. Das Beobachtete, das in der Regel in Form von Tupeln von Zahlen oder Punkten vorliegt, wird in Clustern oder Haufen gruppiert. Das Ziel ist, durch die erfolgreiche Zuordnung eines beobachteten Punktes zu einem Cluster oder einer Kategorie, die bekannten Eigenschaften dieser Kategorie dem beobachteten neuen Punkt zuzuordnen und dann entsprechend zu handeln. Das Ziel hier ist zu sehen, ob und wie gut die Steigung eines Indikators uns sagt, ob der Markt flach ist oder einem Trend folgt.
Zahlen- und Namenskonvention
Der als Beispiel verwendete Indikator "HalfTrend" ist in der Tradition von MQL4 so aufgebaut, dass der Index (iB) der Balken oder Kerzen im Preis-Chart von seinem größten Wert (rates_total), dem Index des ältesten Balkens, bis hinunter zu Null, dem neuesten und dem aktuellen Balken, zählt. Beim ersten Aufruf der Funktion OnCalculate() nach dem Start des Indikators ist der Wert von prev_calculated gleich Null, da noch nichts berechnet wurde; bei späteren Aufrufen kann man damit erkennen, welche Balken bereits berechnet wurden und welche nicht.
Der Indikator verwendet eine zweifarbige Indikatorlinie, die durch zwei Datenpuffer up[] und down[] - jeweils mit einer eigenen Farbe - realisiert wird. Jeweils nur einer der beiden Puffer erhält einen gültigen Wert größer Null, der andere wird an gleicher Stelle (Pufferelement mit gleichem Index iB) mit Null belegt und damit nicht gezeichnet.
Um die Weiterverwendung dieser Clusteranalyse für andere Indikatoren oder Programme so einfach wie möglich zu gestalten, wurden so wenig Ergänzungen wie möglich im Indikator HalfTrend vorgenommen. Die hinzugefügten Zeilen sind im Code des Indikators durch folgende Kommentare 'eingeklammert':
//+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ .... //+------------------------------------------------------------------+
Die Funktionen und Daten der Clusteranalyse finden Sie vollständig in der Datei ClusterTrend.mqh, die sich im Anhang befindet. Grundlage der gesamten Berechnung ist die folgende Datenstruktur aller Cluster:
struct __IncrStdDev { double µ, // average σ, // stdandard deviation max,min, // max. and min. values S2; // auxiliary variable uint ID,n; // ID and no. of values };
µ ist der Mittelwert, σ ist die Standardabweichung - die Wurzel aus der Varianz, Sie gibt an, wie eng die Werte im Cluster um den Mittelwert schwanken, max und min sind jeweils der größte und der kleinste Wert im Cluster und S2 ist eine Hilfsvariable. n ist die Anzahl der Werte im Cluster und ID ist der Identifikator des Clusters.
Diese Datenstruktur ist in einem zweidimensionalen Array organisiert:
__cluster cluster[][14];
Da in MQL5 nur die erste Dimension von mehrdimensionalen Arrays dynamisch angepasst werden kann, wird ihr die Anzahl der zu untersuchenden Wertetypen zugewiesen. Sie kann also leicht geändert werden. Die zweite Dimension ist die Anzahl der Klassifizierungswerte, die in dem folgenden eindimensionalen Array festgelegt sind:
double CatCoeff[9] = {0.0,0.33,0.76,1.32,2.04,2.98,4.21,5.80,7.87};
Beide Zeilen stehen unmittelbar untereinander, weil die Anzahl der Koeffizienten in CatCoeff die feste Größe der zweiten Dimension von Cluster bedingt, sie muss um 5 größer sein. Der Grund wird weiter unten erläutert. Da sich beide Arrays gegenseitig bedingen, können sie leicht gemeinsam geändert werden.
Es wird nur die Differenz zwischen einem Indikatorwert und seinem vorherigen Wert untersucht: x[iB] - x[iB+1]. Diese Differenzen werden in Punkte (_Point) umgerechnet, um die Vergleichbarkeit verschiedener Handelsinstrumente wie EURUSD mit 5 Nachkommastellen und XAUUSD (Gold) mit nur zwei Nachkommastellen zu ermöglichen.
Die Herausforderung
Um zu handeln, ist es wichtig zu wissen, ob der Markt flach ist oder einen schwachen oder starken Trend hat. In einer Seitwärtsbewegung würde man von der Begrenzung eines Kanals um einen geeigneten Durchschnittsindikator zurück zum Indikator, zurück zur Mitte des Kanals handeln, während man in einem Trend in Richtung des Trends weg vom Durchschnittsindikator, weg von der Mitte des Kanals handeln muss, also genau umgekehrt. Ein nahezu perfekter Indikator, der von einem EA verwendet wird, müsste also diese beiden Zustände klar voneinander trennen. Ein EA braucht eine Zahl, in der sich das Marktgeschehen widerspiegelt, und er braucht Schwellenwerte, um in diesem Fall zu wissen, ob die Zahl des Indikators einen Trend oder eine Seitwärtsbewegung signalisiert. Visuell scheint es oft einfach zu sein, diesbezüglich eine Einschätzung vorzunehmen. Aber das visuelle Gefühl ist oft schwer in eine Formel bzw. eine Zahl zu konkretisieren. Die Clusteranalyse ist eine mathematische Methode, um Daten zu gruppieren bzw. sie Kategorien zuzuordnen. Sie hilft uns, diese beiden Zustände des Marktes zu trennen.Die Clusteranalyse definiert oder erreicht durch Optimierung:
- die Anzahl von Clustern
- die Zentren der Cluster
- die Zuordnung der Punkte zu nur einem der Cluster - wenn möglich (= keine überlappenden Cluster).
- dass alle oder möglichst viele (evtl. mit Ausnahme von Ausreißern) der Zahlentupel einem Cluster zugeordnet werden können,
- dass die Größe der Cluster so klein wie möglich ist,
- dass sie sich so wenig wie möglich überlappen (dann wäre nicht klar, ob ein Punkt zu einem oder seinem Nachbarcluster gehört),
- dass die Anzahl der Cluster so klein wie möglich ist.
Dies führt dazu, dass gerade bei vielen Punkten, Werten oder Elementen und vielen Clustern die Sache rechnerisch sehr aufwendig werden kann.
Die O-Notation (Landau-Symbole)
Die Darstellung des Berechnungsaufwandes erfolgt in Form der O-Notation. O(n) bedeutet hier zum Beispiel, dass die Berechnung nur einmal auf alle n Elemente zugreifen muss. Bekannte Beispiele für die Bedeutung dieser Größe sind die Werte für Sortieralgorithmen. Die schnellsten haben normalerweise O(nlog(n)), die langsamsten O(n²). Das war nicht nur früher ein wichtiges Kriterium für große Datenmengen und für die damals noch nicht so schnellen Computer. Heute sind die Computer um ein Vielfaches schneller, gleichzeitig sind aber auch die Datenmengen in einigen Bereichen (optische Analyse der Umgebung und Kategorisierung von Objekten) sehr stark gestiegen.
Der erste und bekannteste Algorithmus der Clusteranalyse ist k-means. Er ordnet n Beobachtungen oder Vektoren mit d Dimensionen k Clustern zu, indem er die (euklidischen) Abstände zu den Zentren der Cluster minimiert. Dies führt zu einem Rechenaufwand von O(n^(dk+1)). Wir haben nur eine Dimension d, die jeweilige Indikatordifferenz zum vorherigen Wert, aber die gesamte Kurshistorie z.B. eines Demokontos von MQ für GBPUSD D1 (Tageskerzen) umfasst 7265 Balken bzw. Kerzen von Kursen, das n in der Formel. Da wir am Anfang nicht wissen, wie viele Cluster sinnvoll sind oder wir brauchen, verwende ich k=9 Cluster oder Kategorien. Nach dieser Beziehung würde dies zu einem Aufwand von O(7265^(1*9+1)) oder O(4,1*10^38) führen. Viel zu viel für normale Handelscomputer. Mit dem hier vorgestellten Weg ist es möglich, das Clustering in 16 mSec zu erreichen, was 454.063 Werten pro Sekunde entspräche. Bei der Berechnung der Balken von GBPUSD m15 (Balken mit 15 Minuten) mit diesem Programm haben wir 556.388 Balken und wieder 9 Cluster und es das dauert dann 140 mSec oder 3.974.200 Werte pro Sekunde. Das zeigt, dass das Clustering sogar besser als O(n) ist, was mit der Art und Weise, wie das Terminal von MQ die Daten organisiert, begründet werden kann, denn schließlich fließt der Rechenaufwand zur Berechnung des Indikators auch in diesen Zeitraum ein.
Der Indikator
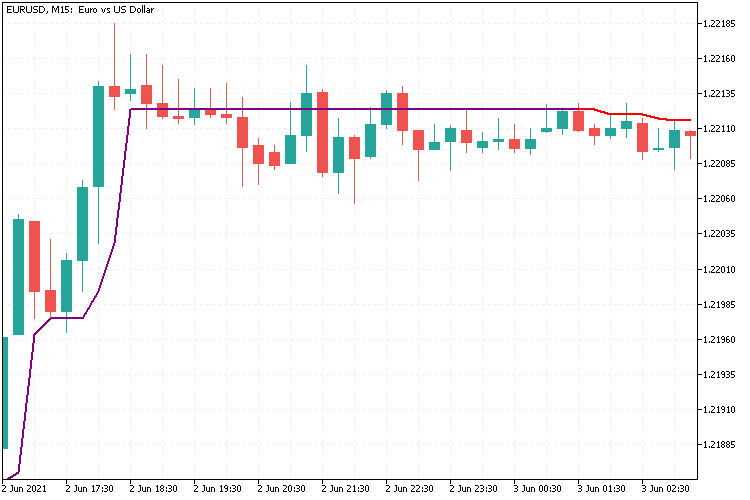
Als Indikator verwende ich den "HalfTrend" von MQ, der unten angehängt ist. Er zeigt längere Passagen, in denen er horizontal verläuft:
Meine Frage an diesen Indikator war nun, ob es eine klare Trennung, d.h. Schwelle gibt, die als Zeichen für die Seitwärtsbewegung und eine Schwelle, die einen Trend signalisiert, sei es nach oben oder unten, interpretiert werden kann. Natürlich sieht jeder sofort, dass wenn dieser Indikator genau waagerecht ist, der Markt flach ist. Aber bis zu welcher Höhe der Steigung sind die Veränderungen im Markt so gering, dass der Markt noch als flach zu betrachten ist und ab welcher Höhe muss man einen Trend annehmen. Man stelle sich vor, der EA sieht nur eine Zahl, in der sich das gesamte Chartbild konzentriert und nicht, wie im obigen Bild, das größere Bild. Dies soll durch die Clusteranalyse gelöst werden. Doch bevor wir uns der Clusteranalyse zuwenden, betrachten wir zunächst die Änderungen, die im Indikator vorgenommen wurden.
Änderungen im Indikator
Da der Indikator so wenig wie möglich verändert werden soll, wurde das Clustering in eine externe Datei ClusterTrend.mqh ausgelagert, die am Anfang des Indikators eingebunden wird:
Natürlich ist diese Datei angehängt. Aber das allein reicht nicht aus. Um den Leser seine eigenen Versuche so einfach wie möglich zu machen, wurde die Eingabevariable NumValues hinzugefügt:
input int NumValues = 1;
Der Wert 1 bedeutet, dass (nur) ein Wertetyp untersucht werden soll. Wenn Sie z. B. einen Indikator analysieren wollen, der zwei Durchschnitte berechnet und die Steigung beider und als Drittes den Abstand zwischen diesen beiden auszuwerten, muss der Wert von NumValues auf 3 gesetzt werden. Das Array, über das die Berechnung erfolgt, wird dann automatisch angepasst. Wird der Wert auf Null gesetzt, wird keine Clusteranalyse durchgeführt. Dieser zusätzliche Rechenaufwand kann also einfach über die Einstellungen abgeschaltet werden.
Weiterhin gibt es die globalen Variablen
string ShortName;
long StopWatch=0;
ShortName wird in OnInit() der Kurzname des Indikators zugewiesen:
ShortName = "HalfTrd "+(string)Amplitude;
IndicatorSetString(INDICATOR_SHORTNAME,ShortName);
der zur Identifikation beim Drucken der Ergebnisse verwendet wird.
StopWatch wird für die Zeitnahme verwendet und wird unmittelbar vor der Übergabe des ersten Wertes für die Clusteranalyse gesetzt und nach dem Ausdrucken der Ergebnisse ausgelesen:
if (StopWatch==0) StopWatch = GetTickCount64();
...
if (StopWatch!=0) StopWatch = GetTickCount64()-StopWatch;
Wie fast alle Indikatoren hat auch dieser eine große Schleife über alle verfügbaren Balken der Kurshistorie. Dieser Indikator berechnet seine Werte so, dass der Balken im Chart mit dem Index iB=0, die aktuellen, zuletzt erhaltenen Kurse enthält, während der größtmögliche Index den Anfang der Kurshistorie, die ältesten Balken, darstellt. Als Letztes vor dem Ende dieser Schleife, der schließenden Klammer, wird der zu analysierende Wert berechnet und zur Auswertung an die Clusterfunktion übergeben. Dort ist alles automatisiert. Es wird weiter unten erklärt.
Im Codeblock direkt vor dem Ende der Schleife wird als Erstes dafür gesorgt, dass die Clusteranalyse mit den historischen Kursen nur einmal für jeden Balken durchgeführt wird und nicht jedes Mal, wenn ein neuer Kurs eintrifft:
//+------------------------------------------------------------------+
//| added for cluster analysis |
//+------------------------------------------------------------------+
if ( (prev_calculated == 0 && iB > 0 ) // we don't use the actual bar
|| (prev_calculated > 9 && iB == 1)) // during operation we use the second to last bar: iB = 1
{
Dann prüfen wir, dass es der allererste Balken der Initialisierung ist, um die Stoppuhr zu setzen und um vorherige Ergebnisse zu löschen (falls vorhanden):
if (prev_calculated==0 && iB==limit) { // only at the very first pass/bar
StopWatch = GetTickCount64(); // start the stop whatch
if (ArraySize(Cluster) > 0) ArrayResize(Cluster,0); // in case everything is recalculated delete prev. results
}
Dann wird der Indikatorwert des Balkens mit dem Index iB und des vorherigen Balkens (iB+1) ermittelt. Da diese Indikatorlinie zweifarbig ist (siehe oben) und dies mit den beiden Puffern up[] und down[] realisiert wurde, wobei einer immer 0,0 ist und somit nicht gezeichnet wird, ist der Indikatorwert, derjenige der beiden Puffer, der größer als Null ist:
double actBar = fmax(up[iB], down[iB]), // get actual indi. value of bar[iB]
prvBar = fmax(up[iB+1], down[iB+1]); // get prev. indi. value
Um sicherzustellen, dass die Clusteranalyse mit Werten zu Beginn der Berechnung beeinflusst wird, obwohl der Indikator noch gar nicht berechnet wurde, gibt es diese Sicherheitsüberprüfung:
if ( (actBar+prvBar) < _Point ) continue; // skip initially or intermediately missing quotes
Jetzt können wir die absolute Differenz aus dem Indikatorwert und seinem vorherigen Wert übergeben.
enterVal(fabs(actBar-prvBar)/_Point, // abs. of slope of the indi. line
0, // index of the value type
1.0 - (double)iB/(double)rates_total, // learning rate: use either 1-iB/rates_total or iB/rates_total whatever runs from 0 .. 1
NumValues // used for initialization (no. of value types) and if < 1 no clustering
);
Warum verwenden wir im ersten Argument die absolute Differenz fabs(actBar-prvBar)? Wenn wir die reine Differenz übergeben würden, müssten wir die doppelte Anzahl von Clustern ermitteln, die für größer als Null und die für kleiner als Null. Dann würde es auch relevant werden, ob ein Kurs innerhalb der verfügbaren Kurshistorie insgesamt gestiegen oder gefallen ist, und das könnte die Ergebnisse verzerren. Letztlich kommt es (für mich) auf die Stärke einer Steigung an, nicht auf ihre Richtung. Auf dem Devisenmarkt kann man meiner Meinung nach davon ausgehen, dass das Auf und Ab der Preise in etwa gleich ist - vielleicht anders als auf dem Aktienmarkt.
Das zweite Argument, 0, ist der Index für den Typ des übergebenen Wertes (0=der erste, 1=der zweite,..). Bei z.B. zwei Indikatorlinien und deren Differenz müssten wir 0, 1 und 2 für den jeweiligen Wert setzen.
Das dritte Argument
1.0 - (double)iB/(double)rates_total, // learning rate: use either 1-iB/rates_total or iB/rates_total whatever runs from 0 .. 1
betrifft die Lernrate. Der Index iB läuft vom größten Wert bis zu 0. rates_total ist die Gesamtzahl aller Balken. Somit ist iB/rates_total das Verhältnis von dem, was noch nicht berechnet wurde und fällt von fast 1 (nichts berechnet) auf Null (alles berechnet) und somit steigt 1 minus diesem Wert von fast 0 (noch nichts gelernt) auf 1 (fertig). Die Bedeutung dieses Verhältnisses wird weiter unten erklärt.
Der letzte Parameter wird für die Initialisierung benötigt und gibt an, ob die Cluster berechnet werden sollen. Ist er größer Null, gibt er (siehe oben) die Anzahl der Wertetypen, z. B. Indikatorlinien, an und bestimmt damit die Größe der ersten Dimension des globalen Arrays Cluster[][] in der Datei ClusterTrend.mqh (siehe oben).
Unmittelbar nach dem Ende der großen Schleife über die gesamte Kurshistorie werden alle Ergebnisse pro Kategorie/Cluster zeilenweise im Experten-Log ausgegeben:
prtStdDev(_Symbol+" "+EnumToString(Period())+" "+ShortName, // printed at the beginning of each line
0, // the value type to be printed
NumValues); // if <=0 this value type is not printed
Hier ist das erste Argument zur Information und wird am Anfang jeder Zeile gedruckt, das zweite, 0, bezeichnet den berechneten Indikatortyp (0=der erste, 1=der zweite,..) und schließlich wie oben NumValues. Ist sie 0, wird dieser Indikatortyp nicht ausgegeben.
Insgesamt sieht der hinzugefügte Block wie folgt aus:
//+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ if ( (prev_calculated == 0 && iB > 0 ) // we don't use the actual bar || (prev_calculated > 9 && iB == 1)) // during operation we use the second to last bar: iB = 1 { if (prev_calculated==0 && iB==limit) { // only at the very first pass/bar StopWatch = GetTickCount64(); // start the stop whatch if (ArraySize(Cluster) > 0) ArrayResize(Cluster,0); // in case everything is recalculated delete prev. results } double actBar = fmax(up[iB], down[iB]), // get actual indi. value of bar[iB] prvBar = fmax(up[iB+1], down[iB+1]); // get prev. indi. value if ( (actBar+prvBar) < _Point ) continue; // skip initially or intermediately missing quotes enterVal(fabs(actBar-prvBar)/_Point, // abs. of slope of the indi. line 0, // index of the value type 1.0 - (double)iB/(double)rates_total, // learning rate: use either 1-iB/rates_total or iB/rates_total whatever runs from 0 .. 1 NumValues // used for initialization (no. of value types) and if < 1 no clustering ); } //+------------------------------------------------------------------+ } // end of big loop: for(iB = limit; iB >= 0; iB--) .. //+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ if (prev_calculated < 1) // print only once after initialization { prtStdDev(_Symbol+" "+EnumToString(Period())+" "+ShortName, // printed at the beginning of each line 0, // the value type to be printed NumValues); // if <=0 this value type is not printed if (StopWatch!=0) StopWatch = GetTickCount64()-StopWatch; Print ("Time needed for ",rates_total," bars on a PC with ",TerminalInfoInteger(TERMINAL_CPU_CORES), " cores and Ram: ",TerminalInfoInteger(TERMINAL_MEMORY_PHYSICAL),", Time: ", TimeToString(StopWatch/1000,TIME_SECONDS),":",StringFormat("%03i",StopWatch%1000) ); } //+------------------------------------------------------------------+
Dies sind alle Änderungen im Indikator.
Die Clusteranalyse in der Datei "ClusterTrend.mqh".
Die Datei befindet sich im gleichen Ordner wie der Indikator, muss also in der Form "ClusterTrend.mqh" eingebunden werden.
Am Anfang gibt es einige Vereinfachungen mit #define. #define crash(strng) provoziert künstlich eine Division durch 0, die der Compiler nicht erkennt, da es für ein Indikatorprogramm eigentlich (noch?) unmöglich ist, sich selbst zu beenden. Auch das gelingt zwar nicht ganz, aber wenigstens wird alert(), das auf eine falsche Dimensionsangabe aufmerksam macht, nur einmal aufgerufen. Korrigieren Sie das und kompilieren Sie den Indikator neu.
Die Struktur der für diese Analyse verwendeten Daten wurde bereits oben beschrieben.
Kommen wir nun zum Kern der Idee dieses Ansatzes.
Eigentlich werden Mittelwert, Varianz und auch die Clusteranalyse mit Daten berechnet, die insgesamt vorhanden sein müssen. Zuerst müssen die Daten gesammelt werden, und dann werden in einem zweiten Schritt diese Werte und die Clusterung durch eine oder mehrere Schleifen durchgeführt. Traditionell würde man den Durchschnitt in einer zweiten Schleife innerhalb der großen Schleife über alle Daten, um diese zu summieren, ermitteln. Dies wäre sehr zeitaufwändig. Ich habe aber eine Veröffentlichung von Tony Finch gefunden: "Incremental calculation of weighted mean and variance", in der er Mittelwert und Varianz inkrementell, also in einem Durchgang über alle Daten, berechnet, statt alle Daten zu summieren und dann die Summe durch die Anzahl der Werte zu teilen. Der neue (einfache) Mittelwert über alle bisherigen Werte einschließlich des neu übertragenen wird also nach Formel (4) [S.. 1] berechnet:
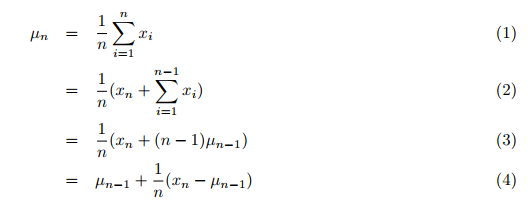
wobei:
- µn = der aktualisierte Mittelwert,
- µn-1 = der vorherige Mittelwert,
- n = die aktuelle Anzahl (einschl. des neuen) der Werte,
- xn = der neue, n-te Wert.
Auch die Varianz wird on-the-fly berechnet, anstatt in einer zweiten Schleife nach dem Mittelwert. Die inkrementelle Varianz berechnet nach (Formel 24,25; S. 3):
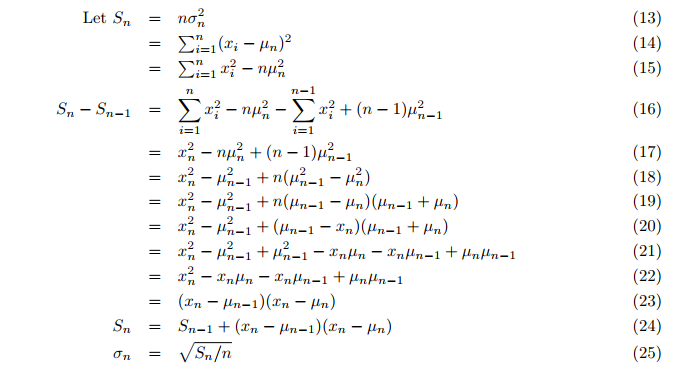
Wobei:
- Sn = aktualisierter Wert der Hilfsvariablen S,
- σ = die Varianz.
So können Mittelwert und Varianz der Grundgesamtheit in einem Durchgang berechnet werden, jeweils aktuell für den jüngsten, neuen Wert in der Funktion incrStdDeviation(..):
Auf dieser Basis kann ein so berechneter Mittelwert bereits nach einem ersten Teil der historischen Daten zur Klassifizierung verwendet werden. Sie fragen sich vielleicht, warum können wir nicht einfach einen gleitenden Durchschnitt verwenden, der mit einer geringen Datenmenge schnell und einfach brauchbare Ergebnisse erzielt? Ein gleitender Durchschnitt passt sich an. Aber für das Ziel einer Klassifizierung brauchen wir einen relativ konstanten Vergleichswert. Stellen Sie sich vor, dass der Wasserstand eines Flusses gemessen werden soll. Es ist klar, dass sich der Vergleichswert des normalen Wasserstandes nicht mit der aktuellen Höhe ändern darf. In Zeiten mit starken Trends würden z.B. auch die Differenzen des gleitenden Durchschnitts zunehmen und die Differenzen zu diesem Wert würden ungerechtfertigt kleiner werden. Und wenn der Markt flach wird, sinkt auch der Durchschnitt und das würde die Differenz zu diesem Basiswert real erhöhen. Wir brauchen also einen sehr stabilen Wert, eben einen Durchschnitt von so viel wie möglich.
Nun stellt sich die Frage nach dem Clustering. Traditionell würde man wieder alle Werte zur Bildung von Clustern verwenden. Nun, die schrittweise Berechnung des Mittelwertes gibt uns eine andere Möglichkeit: Wir verwenden die ältesten 50% der historischen Daten für den Mittelwert und die neuesten 50% für das Clustering (ohne die Mittelwertberechnung zu beenden). Dieser Prozentsatz (50%) wird hier als Lernrate bezeichnet, in dem Sinne, dass bis zu 50% nur der Mittelwert "gelernt" wird. Dessen Berechnung wird aber nach Erreichen der 50% nicht gestoppt, sondern sie ist nun so stabil, dass sie gute Ergebnisse liefert. Trotzdem bleibt die Zahl 50% meine willkürliche Entscheidung, deshalb habe ich zum Vergleich zwei weitere Mittelwerte gebildet: 25% und 75%, die nach Erreichen ihrer Lernrate mit der Mittelwertberechnung beginnen. Damit können wir sehen, wie und wie stark sich die Steigung verändert hat.
Mittelwert und Cluster erstellen
Fast alles wird von der Funktion enterVal() der Datei ClusterTrend.mqh organisiert:
//+------------------------------------------------------------------+ //| | //| enter a new value | //| | //+------------------------------------------------------------------+ // use; enterVal( fabs(indi[i]-indi[i-1]), 0, (double)iB/(double)rates_total ) void enterVal(const double val, const int iLne, const double learn, const int NoVal) { if (NoVal<=0) return; // nothing to do if true if( ArrayRange(Cluster,0)<NoVal || Cluster[iLne][0].n <= 0 ) // need to inicialize setStattID(NoVal); incrStdDeviation(val, Cluster[iLne][0]); // the calculation from the first to the last bar if(learn>0.25) incrStdDeviation(val, Cluster[iLne][1]); // how does µ varies after 25% of all bars if(learn>0.5) incrStdDeviation(val, Cluster[iLne][2]); // how does µ varies after 50% of all bars if(learn>0.75) incrStdDeviation(val, Cluster[iLne][3]); // how does µ varies after 75% of all bars if(learn<0.5) return; // I use 50% to learn and 50% to devellop the categories int i; if (Cluster[iLne][0].µ < _Point) return; // avoid division by zero double pc = val/(Cluster[iLne][0].µ); // '%'-value of the new value compared to the long term µ of Cluster[0].. for(i=0; i<ArraySize(CatCoeff); i++) { if(pc <= CatCoeff[i]) { incrStdDeviation(val, Cluster[iLne][i+4]); // find the right category return; } } i = ArraySize(CatCoeff); incrStdDeviation(val, Cluster[iLne][i+4]); // tooo big? it goes to the last category }
val ist der vom Indikator empfangene Wert, iLine ist der Index des Wertetyps, learn die Lernrate oder das Verhältnis von berechnet/Historie und schließlich NoVal um zu wissen, wie viele - wenn überhaupt - Wertetypen berechnet werden sollen.
Zunächst erfolgt eine Prüfung (NoVal<=0), ob eine Clusterung beabsichtigt ist oder nicht.
Gefolgt von der Prüfung (ArrayRange(Cluster,0) < NoVal), ob die erste Dimension des Arrays Cluster[][] die Größe der zu berechnenden Wertetypen hat. Wenn nicht, wird die Initialisierung durchgeführt, alle Werte werden auf Null gesetzt und die ID wird durch die Funktion setStattID(NoVal) (siehe unten) zugewiesen.
Ich möchte den Umfang des Codes gering halten, um es anderen leicht zu machen, ihn zu benutzen, und damit ich ihn nach einiger Zeit, in der ich nicht damit gearbeitet habe, wieder verstehe. Deshalb wird der Wert val über ein und dieselbe Funktion incrStdDeviation(val, Cluster[][]) der entsprechenden Datenstruktur zugewiesen und dort verarbeitet.
Die Funktion incrStdDeviation(val, Cluster[iLne][0]) berechnet den Mittelwert vom ersten bis zum letzten Wert. Wie bereits erwähnt, bezeichnet der erste Index [iLine] den Wertetyp und der zweite Index [0] die Datenstruktur des Wertetyps für die Berechnung. Wie oben erwähnt, benötigen wir 5 mehr als die Anzahl der Elemente im statischen Array CatCoeff[9]. Jetzt sehen wir warum:
- [0] .. [3] werden für die verschiedenen Mittelwerte [0]:100%, [1]:25%, [2]:50%, [3]:75% benötigt,
- [4] .. [12] werden für die 9 Kategorien von CatCoeff[9] benötigt: 0.0, .., 7.87
- [13] wird als letzte Kategorie für Werte benötigt, die größer sind als die größte Kategorie von CatCoeff[8] (hier 7,87).
Jetzt können wir verstehen, wofür wir einen stabilen Mittelwert benötigen. Um die Kategorie oder den Cluster zu finden, berechnen wir das Verhältnis von val/Cluster[iLne][0].µ. Dies ist der übergreifende Mittelwert des Wertetyps mit dem Index iLine. Die Koeffizienten des Arrays CatCoeff[] sind also Multiplikatoren des Gesamtmittelwertes, wenn wir die Gleichung umstellen:
pc = val/µ => pc*µ = val
Systematisch bedeutet das, dass wir nicht nur die Anzahl der Cluster vordefiniert haben (die meisten Clustering-Methoden erfordern dies), wir haben auch die Eigenschaften der Cluster vordefiniert und das ist eher ungewöhnlich, aber das ist der Grund, warum diese Clustering-Methode nur einen Durchgang benötigt, während die anderen Methoden mehrere Durchgänge über alle Daten benötigen, um die optimalen Eigenschaften der Cluster zu finden (siehe oben). Der allererste Koeffizient von (CatCoeff[0]) ist Null. Dies wird gewählt, weil der Indikator "HalfTrend" so ausgelegt ist, dass er für mehrere Balken horizontal verläuft und somit die Differenz der Indikatorwerte dann Null ist. Es ist also zu erwarten, dass diese Kategorie eine signifikante Größe erreichen wird. Alle anderen Zuordnungen werden vorgenommen, wenn:
pc <= CatCoeff[i] => val/µ <= CatCoeff[i] => val <= CatCoeff[i]*µ.
Da es durchaus Ausreißer gibt, die die vorgegebenen Kategorien in CatCoeff[] sprengen würden, gibt es eine zusätzliche Kategorie für solche Werte:
i = ArraySize(CatCoeff);
incrStdDeviation(val, Cluster[iLne][i+4]); // tooo big? it goes to the last category
Auswertung und Druckausgabe
Direkt nach dem Ende der großen Schleife des Indikators und nur, wenn es der erste Durchlauf (prev_calculated < 1) ist, werden die Ergebnisse durch prtStdDev() in das Journal gedruckt, dann wird die StopWatch angehalten und ebenfalls ausgedruckt (s.o.):
//+------------------------------------------------------------------+ //| added for cluster analysis | //+------------------------------------------------------------------+ if (prev_calculated < 1) { prtStdDev(_Symbol+" "+EnumToString(Period())+" "+ShortName, 0, NumValues); if (StopWatch!=0) StopWatch = GetTickCount64()-StopWatch; Print ("Time needed for ",rates_total," bars on a PC with ",TerminalInfoInteger(TERMINAL_CPU_CORES), " cores and ",TerminalInfoInteger(TERMINAL_MEMORY_PHYSICAL)," Ram: ",TimeToString(StopWatch/1000,TIME_SECONDS)); } //+------------------------------------------------------------------+
prtStdDev(..) druckt zunächst die Kopfzeile mit HeadLineIncrStat(pre) und dann für jeden Wertetyp (Index iLine) alle 14 Ergebnisse in je einer Zeile mit retIncrStat():
void prtStdDev(const string pre, int iLne, const int NoVal) { if (NoVal <= 0 ) return; // if true no printing if (Cluster[iLne][0].n==0 ) return; // no values entered for this 'line' HeadLineIncrStat(pre); // print the headline int i,tot = 0,sA=ArrayRange(Cluster,1), sC=ArraySize(CatCoeff); for(i=4; i<sA; i++) tot += (int)Cluster[iLne][i].n; // sum up the total volume of all but the first [0] category retIncrStat(Cluster[iLne][0].n, pre, "learn 100% all["+(string)sC+"]", Cluster[iLne][0], 1, Cluster[iLne][0].µ); // print the base the first category [0] retIncrStat(Cluster[iLne][1].n, pre, "learn 25% all["+(string)sC+"]", Cluster[iLne][1], 1, Cluster[iLne][0].µ); // print the base the first category [0] retIncrStat(Cluster[iLne][2].n, pre, "learn 50% all["+(string)sC+"]", Cluster[iLne][2], 1, Cluster[iLne][0].µ); // print the base the first category [0] retIncrStat(Cluster[iLne][3].n, pre, "learn 75% all["+(string)sC+"]", Cluster[iLne][3], 1, Cluster[iLne][0].µ); // print the base the first category [0] for(i=4; i<sA-1; i++) { retIncrStat(tot, pre,"Cluster["+(string)(i)+"] (<="+_d22(CatCoeff[i-4])+")", Cluster[iLne][i], 1, Cluster[iLne][0].µ); // print each category } retIncrStat(tot, pre,"Cluster["+(string)i+"] (> "+_d22(CatCoeff[sC-1])+")", Cluster[iLne][i], 1, Cluster[iLne][0].µ); // print the last category }
Hier: tot += (int)Cluster[iLne][i].n ist die Anzahl der Werte in den Kategorien 4-13, die addiert werden, um einen Vergleichswert (100%) für diese Kategorien zu haben. Und das ist, was ausgedruckt wird:
GBPUSD PERIOD_D1 HalfTrd 2 ID Cluster Num. (tot %) µ (mult*µ) σ (Range %) min - max GBPUSD PERIOD_D1 HalfTrd 2 100100 learn 100% all[9] 7266 (100.0%) 217.6 (1.00*µ) 1800.0 (1.21%) 0.0 - 148850.0 GBPUSD PERIOD_D1 HalfTrd 2 100025 learn 25% all[9] 5476 (100.0%) 212.8 (0.98*µ) 470.2 (4.06%) 0.0 - 11574.0 GBPUSD PERIOD_D1 HalfTrd 2 100050 learn 50% all[9] 3650 (100.0%) 213.4 (0.98*µ) 489.2 (4.23%) 0.0 - 11574.0 GBPUSD PERIOD_D1 HalfTrd 2 100075 learn 75% all[9] 1825 (100.0%) 182.0 (0.84*µ) 451.4 (3.90%) 0.0 - 11574.0 GBPUSD PERIOD_D1 HalfTrd 2 400000 Cluster[4] (<=0.00) 2410 ( 66.0%) 0.0 (0.00*µ) 0.0 0.0 - 0.0 GBPUSD PERIOD_D1 HalfTrd 2 500033 Cluster[5] (<=0.33) 112 ( 3.1%) 37.9 (0.17*µ) 20.7 (27.66%) 1.0 - 76.0 GBPUSD PERIOD_D1 HalfTrd 2 600076 Cluster[6] (<=0.76) 146 ( 4.0%) 124.9 (0.57*µ) 28.5 (26.40%) 75.0 - 183.0 GBPUSD PERIOD_D1 HalfTrd 2 700132 Cluster[7] (<=1.32) 171 ( 4.7%) 233.3 (1.07*µ) 38.4 (28.06%) 167.0 - 304.0 GBPUSD PERIOD_D1 HalfTrd 2 800204 Cluster[8] (<=2.04) 192 ( 5.3%) 378.4 (1.74*µ) 47.9 (25.23%) 292.0 - 482.0 GBPUSD PERIOD_D1 HalfTrd 2 900298 Cluster[9] (<=2.98) 189 ( 5.2%) 566.3 (2.60*µ) 67.9 (26.73%) 456.0 - 710.0 GBPUSD PERIOD_D1 HalfTrd 2 1000421 Cluster[10] (<=4.21) 196 ( 5.4%) 816.6 (3.75*µ) 78.9 (23.90%) 666.0 - 996.0 GBPUSD PERIOD_D1 HalfTrd 2 1100580 Cluster[11] (<=5.80) 114 ( 3.1%) 1134.9 (5.22*µ) 100.2 (24.38%) 940.0 - 1351.0 GBPUSD PERIOD_D1 HalfTrd 2 1200787 Cluster[12] (<=7.87) 67 ( 1.8%) 1512.1 (6.95*µ) 136.8 (26.56%) 1330.0 - 1845.0 GBPUSD PERIOD_D1 HalfTrd 2 1300999 Cluster[13] (> 7.87) 54 ( 1.5%) 2707.3 (12.44*µ) 1414.0 (14.47%) 1803.0 - 11574.0 Time needed for 7302 bars on a PC with 12 cores and Ram: 65482, Time: 00:00:00:016
Was sehen wir also? Gehen wir von Spalte zu Spalte. Die erste Spalte zeigt Ihnen das Symbol, den Zeitrahmen, den Namen des Indikators und seine "Amplitude", wie es ShortName zugewiesen wurde. Die zweite Spalte zeigt die ID der jeweiligen Datenstruktur an. Die 100nnn zeigen, dass es sich nur um eine Mittelwertberechnung handelt, wobei die letzten drei Ziffern die Lernrate von, 100, 25, 50 und 75 angeben. 400nnn .. 1300nnn sind die Kategorien, Cluster oder Haufen. Dabei geben die letzten drei Ziffern die Kategorie bzw. den Multiplikator für deren Mittelwert µ an, der ebenfalls in der dritten Spalte unter Cluster in Klammern angegeben ist. Das ist klar und selbsterklärend.
Jetzt wird es interessant. Spalte 4 zeigt die Anzahl der Werte in der jeweiligen Kategorie und in Klammern den Prozentsatz. Das Interessante hier ist, dass der Indikator die meiste Zeit horizontal ist (Kat.#4 2409 Balken oder Tage 66,0%), was darauf hindeutet, dass man mit Range-Trading in zwei Dritteln der Zeit Erfolg haben könnte. Aber es gibt mehr (lokale) Maxima in den Kategorien #8, #9 und #10, während Kategorie #5 überraschend wenige Werte erhielt (112, 3,1%). Und dies kann nun als Lücke zwischen zwei Schwellenwerten interpretiert werden und uns folgende ungefähre Werte liefern:
wenn fabs(Steigung) < 0,5*µ => dann ist der Markt in einer Seitwärtsbewegung, versuchen Sie einen Range Trading
wenn fabs(Steigung) > 1.0*µ => hat der Markt einen Trend, versuchen Sie, die Welle zu reiten
Die ersten 4 Zeilen mit den IDs 100nnn helfen uns abzuschätzen, wie stabil µ ist. Wie beschrieben, brauchen wir keinen Wert, der zu stark schwankt. Wir sehen, dass µ von 217,6 (Punkte pro Tag) bei 100100 auf 182,1 für 100075 fällt (nur die letzten 25% der Werte werden für dieses µ verwendet) oder um 16%. Ein bisschen, aber nicht zu viel, wie ich finde. Aber was sagt uns das? Die Volatilität des GBPUSD hat abgenommen. Der erste Wert in dieser Kategorie ist vom 28.05.2014 00:00:00. Möglicherweise könnte, sollte dies berücksichtigt werden.
Wenn ein Mittelwert berechnet wird, zeigt die Varianz σ wertvolle Informationen und das bringt uns zu Spalte 6 (σ (Range %)). Sie gibt an, wie nahe die einzelnen Werte am Mittelwert liegen. Bei normalverteilten Werten liegen 68 % aller Werte innerhalb der Varianz. Für die Varianz bedeutet dies, je kleiner, desto besser oder, anders ausgedrückt, je genauer (weniger unscharf) ist der Mittelwert. Hinter dem Wert in Klammern steht das Verhältnis σ/(max-min) aus den letzten beiden Spalten. Auch dies ist ein Maß für die Güte der Varianz und des Mittelwertes.
Schauen wir nun, ob sich die Ergebnisse von GBPUSD D1 auf kleineren Zeitfenstern wie M15-Kerzen wiederholen. Dazu muss man einfach den Zeitrahmen des Charts von D1 auf M15 umstellen:
GBPUSD PERIOD_M15 HalfTrd 2 ID Cluster Num. (tot %) µ (mult*µ) σ (Range %) min - max GBPUSD PERIOD_M15 HalfTrd 2 100100 learn 100% all[9] 556389 (100.0%) 18.0 (1.00*µ) 212.0 (0.14%) 0.0 - 152900.0 GBPUSD PERIOD_M15 HalfTrd 2 100025 learn 25% all[9] 417293 (100.0%) 18.2 (1.01*µ) 52.2 (1.76%) 0.0 - 2971.0 GBPUSD PERIOD_M15 HalfTrd 2 100050 learn 50% all[9] 278195 (100.0%) 15.9 (0.88*µ) 45.0 (1.51%) 0.0 - 2971.0 GBPUSD PERIOD_M15 HalfTrd 2 100075 learn 75% all[9] 139097 (100.0%) 15.7 (0.87*µ) 46.1 (1.55%) 0.0 - 2971.0 GBPUSD PERIOD_M15 HalfTrd 2 400000 Cluster[4] (<=0.00) 193164 ( 69.4%) 0.0 (0.00*µ) 0.0 0.0 - 0.0 GBPUSD PERIOD_M15 HalfTrd 2 500033 Cluster[5] (<=0.33) 10528 ( 3.8%) 3.3 (0.18*µ) 1.7 (33.57%) 1.0 - 6.0 GBPUSD PERIOD_M15 HalfTrd 2 600076 Cluster[6] (<=0.76) 12797 ( 4.6%) 10.3 (0.57*µ) 2.4 (26.24%) 6.0 - 15.0 GBPUSD PERIOD_M15 HalfTrd 2 700132 Cluster[7] (<=1.32) 12981 ( 4.7%) 19.6 (1.09*µ) 3.1 (25.90%) 14.0 - 26.0 GBPUSD PERIOD_M15 HalfTrd 2 800204 Cluster[8] (<=2.04) 12527 ( 4.5%) 31.6 (1.75*µ) 4.2 (24.69%) 24.0 - 41.0 GBPUSD PERIOD_M15 HalfTrd 2 900298 Cluster[9] (<=2.98) 11067 ( 4.0%) 47.3 (2.62*µ) 5.5 (23.91%) 37.0 - 60.0 GBPUSD PERIOD_M15 HalfTrd 2 1000421 Cluster[10] (<=4.21) 8931 ( 3.2%) 67.6 (3.75*µ) 7.3 (23.59%) 54.0 - 85.0 GBPUSD PERIOD_M15 HalfTrd 2 1100580 Cluster[11] (<=5.80) 6464 ( 2.3%) 94.4 (5.23*µ) 9.7 (23.65%) 77.0 - 118.0 GBPUSD PERIOD_M15 HalfTrd 2 1200787 Cluster[12] (<=7.87) 4390 ( 1.6%) 128.4 (7.12*µ) 12.6 (22.94%) 105.0 - 160.0 GBPUSD PERIOD_M15 HalfTrd 2 1300999 Cluster[13] (> 7.87) 5346 ( 1.9%) 241.8 (13.40*µ) 138.9 (4.91%) 143.0 - 2971.0 Time needed for 556391 bars on a PC with 12 cores and Ram: 65482, Time: 00:00:00:140
Natürlich ist die durchschnittliche Steigung jetzt viel kleiner. Sie fällt von 217,6 Punkten pro Tag auf 18,0 Punkte in 15 Minuten. Aber auch hier ist ein ähnliches Verhalten zu sehen:
wenn fabs(Steigung) < 0,5*µ => dann ist der Markt in einer Seitwärtsbewegung, versuchen Sie einen Range Trading
wenn fabs(Steigung) > 1.0*µ => hat der Markt einen Trend, versuchen Sie, die Welle zu reiten
Auch alles andere, was über die Interpretation des täglichen Zeitrahmens gesagt wurde, behält seine Gültigkeit.
Schlussfolgerung
Am Beispiel des Indikators "HalfTrend" konnte gezeigt werden, dass mit einer einfachen Kategorisierung bzw. Clusteranalyse, die ansonsten sehr rechenintensiv ist, sehr wertvolle Informationen über das Verhalten des Indikators gewonnen werden kann. Normalerweise werden Mittelwert und Varianz in separaten Schleifen berechnet, gefolgt von zusätzlichen Schleifen zur Clusterbildung. Hier sind wir in der Lage, all das in einer einzigen großen Schleife zu ermitteln, die auch den Indikator berechnet, wobei der erste Teil der Daten zum Lernen verwendet wird, der zweite Teil zur Anwendung des Gelernten. Und das alles in weniger als einer Sekunde und trotz der mehr als einer halben Million Daten. Damit ist es möglich, diese Informationen aktuell und on-the-fly zu ermitteln und anzuzeigen, was für den Handel sehr wertvoll ist.
Alles ist so konzipiert, dass Anwender die für eine solche Analyse notwendigen Codezeilen schnell und einfach in ihre eigenen Indikatoren einfügen können. Damit können sie nicht nur testen, ob, wie und wie gut ihr eigener Indikator die Frage nach Trend oder Flat beantwortet, sondern sie erhalten auch Anhaltspunkte für die Weiterentwicklung der eigenen Idee.
Was kommt als Nächstes?
Im nächsten Artikel werden wir diesen Ansatz auf Standardindikatoren anwenden. Daraus werden sich neue Betrachtungsweisen und erweiterte Interpretationen ergeben. Und natürlich sind dies auch Beispiele, wie Sie selber vorgehen können, wenn Sie dieses Toolkit selbst nutzen wollen.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/9527
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Tipps von einem professionellen Programmierer (Teil II): Speichern und Austauschen von Parametern zwischen einem Expert Advisor, Skripten und externen Programmen
Tipps von einem professionellen Programmierer (Teil II): Speichern und Austauschen von Parametern zwischen einem Expert Advisor, Skripten und externen Programmen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Hallo Carl, kann dieser Indikator in mt4 ausgeführt werden? Wenn ja, welche Änderungen müssen vorgenommen werden.
Vielen Dank!
Hallo Carl, kann dieser Indikator in mt4 ausgeführt werden? Wenn ja, welche Änderungen müssen vorgenommen werden.
Vielen Dank!
Nun, er muss geändert werden. Es gibt einige Artikel über den Unterschied zwischen mt4 und mt5 wie:
https://www.mql5.com/de/articles/81
https://www.mql5.com/de/articles/66
https://www.mql5.com/en/forum/179991 // MT4 => MT5 converter
https://www.mql5.com/de/code/16006 // mt4 orders to mt5
https://www.mql5.com/en/blogs/post/681230
https://www.mql5.com/de/users/iceron/publications => Wählen Sie seine CrossPlattform Artikel
Es ist nur andersherum.
vielen Dank für Ihre Idee!
Haben Sie schon von dem Produkt namens "Trend Pro" gehört?
Ich denke, der Indikator in Ihrem Artikel ist dem "Trend Pro" sehr ähnlich. Zumindest vom Aussehen her.
Ich denke, die Indikatoren in Ihrem Artikel sind "Trend Pro" sehr ähnlich.
Wenn nicht, kennen Sie den Unterschied zwischen ihnen.
Hallo Carl, danke für deine Idee!
Haben Sie schon von dem Produkt "Trend Pro" gehört?
Ich denke, der Indikator in Ihrem Artikel ist dem von "Trend Pro" sehr ähnlich. Zumindest vom Aussehen her.
Sind sie identisch?
Wenn nicht, kennen Sie den Unterschied zwischen ihnen?