Kategorientheorie in MQL5 (Teil 10): Monoide Gruppen
Einführung
Im vorigen Artikel haben wir unsere Betrachtung von Monoiden fortgesetzt, indem wir uns mit Monoid-Aktionen befasst haben, die wir als Mittel zur Umwandlung monoider Mengen durch Erweiterung ihrer möglichen Elemente gesehen haben. Bis jetzt haben wir die Konzepte von Domänen, Morphismen, Kategorieaxiomen, bis hin zu monomorphen und epimorphen Ausdrücken behandelt. Während einige argumentieren mögen, dass die Umsetzung von Konzepten der Kategorientheorie ein umfassenderes Studium aller/der meisten ihrer Konzepte erfordert, wird hier der Ansatz verfolgt, zu untersuchen, welche Ideen aus einer grundlegenden oder begrenzten Sicht des Themas von Nutzen sein können. Jeder dieser Artikel für sich genommen, auch wenn in einigen Fällen Konzepte aus früheren Artikeln übernommen wurden, erwies sich als wirksam bei der Erleichterung von Händlerentscheidungen und in einigen Fällen als potenziell geeignet, Handelssysteme zu definieren. In diesem Artikel werden wir Monoide - Gruppen betrachten, und diese werden wie die Monoid-Aktionen, die wir im vorherigen Artikel behandelt haben, als eine Neudefinition eines Monoids an einem Handelsentscheidungspunkt angesehen. Wir erinnern uns, dass monoide Aktionen als eine Erweiterung der monoiden Menge betrachtet wurden. Hier werden wir einen weiteren monoiden Parameter neu bewerten, nämlich das Identitätselement, wenn wir unsere Monoide noch einmal neu definieren. Der Umfang dieses Artikels umfasst nicht den Aufbau kompletter Handelssysteme, wie es in einigen früheren Artikeln der Fall war, in denen wir Instanzen der Expert Signal- und/oder Expert Trailing-Klasse mit dem Ziel kodiert haben, komplette Expert Advisors mit dem eingebauten MQL5-Assistenten zusammenzustellen. Vielmehr werden wir uns einzelne Funktionen ansehen, die Teil unserer kodierten Monoid-, Monoid-Action- und Monoid-Group-Klassen sind, und untersuchen, wie sie einem Händler an wichtigen Entscheidungspunkten nützlich sein können.
Einsicht in Monoide Gruppen
Zur Erinnerung: Monoide bestehen aus drei Dingen, nämlich einer Menge, einem Identitätselement, das zu dieser Menge gehört, und einer binären Operation, die zwei beliebige Elemente dieser Menge annimmt und immer ein Element zurückgibt, das Mitglied der Menge ist. Außerdem ist die Ausgabe immer das Identitätselement, wenn ein Mitglied der Menge mit dem Identitätselement in der Binäroperation gepaart ist. Monoid-Aktionen, die in unserem letzten Artikel behandelt wurden, sind eine Form von Funktionen, die durch eine Menge und eine binäre Operation definiert sind, die Mitglieder der Monoid-Menge mit der Menge dieser Funktion paaren und immer ein Element ausgeben, das ein Mitglied der Funktionsmenge ist. Wir sahen sie als Mittel zur Umwandlung eines Monoids, denn der Ausgang der binären Operation eines Monoids war geschlossen, da alle Ausgänge strikte Mitglieder der Monoidmenge waren.
Zu Beginn könnte es jedoch konstruktiv sein, zunächst darauf hinzuweisen, dass es keine Unterscheidung zwischen Gruppen und dem, was wir hier als Monoid-Gruppen bezeichnen, an sich gibt. Der einzige Unterschied, der durch die Vorsilbe „Monoid“ angedeutet wird, besteht darin, dass wir uns strikt auf Mengen (oder Domänen) beziehen, die zu einer Kategorie gehören. Eine monoide Gruppe ist daher nach der Definition von Gruppen ein Monoid mit der zusätzlichen Eigenschaft, dass jedes Element in der monoiden Menge ein anderes, inverses Element haben sollte. Wenn ein Element und sein Inverses in der binären Operation des Monoids gepaart werden, ist die Ausgabe immer das Identitätselement des Monoids.
Formal bestimmt die Invers-Eigenschaft eine Monoid-Gruppe:
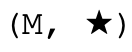
Abgesehen von regelmäßigen Monoiden, gilt für jedes
![]()
dass es auch ein inverses Element gibt
![]()
dergestalt, dass:
![]()
wobei e das Identitätselement des Monoids ist.
Die Anwendung durch Händler wird in ähnlicher Weise wie im vorherigen Artikel aufgefasst. Wir erinnern uns, dass wir Monoide (die Mengen) als einen Pool von Entscheidungsoptionen betrachten, aus denen ein Händler wählen kann, und in unserem letzten Artikel haben wir uns mit der Erweiterung dieses Pools durch Monoid-Aktionen beschäftigt. Wir haben untersucht, wie sich dies auf die Leistung eines Handelssystems auswirkt, wenn wir den Anwendungsbereich bestimmter Monoide auf der Grundlage einer Liste von Faktoren erweitern, die die relative Bedeutung der Entscheidungspunkte (Merkmale) des Handelssystems gewichten. Die Ergebnisse waren im Vergleich zu den Ergebnissen des vorherigen Artikels, der eingeschränkte (Standard-) Monoide betrachtete, schlechter als der Durchschnitt. Für Monoidgruppen werden wir, anstatt den Umfang unserer Monoidmengen zu erweitern, auf eingeschränkte Monoide zurückgreifen, die eine Wirkung hatten und in Gruppen umgewandelt wurden. Wir werden die Veränderung der Mengenzusammensetzung nach dieser monoiden Aktion untersuchen, aber die tatsächliche Implementierung eines Handelssystems wird in diesem Artikel nicht berücksichtigt. Der Leser ist aufgefordert, dies selbst zu erkunden.Implementierung von Monoidgruppen in MQL5
Um unsere MQL5-Umgebung für die Implementierung von Monoidgruppen einzurichten, starten wir die IDE und erstellen eine neue Skriptdatei mit Hilfe des Assistenten.
Auf der nächsten Registerkarte geben wir unserem Skript den Namen „ct_10“ und klicken auf Fertig stellen. Dieses Skript bezieht sich auf die Klassendatei „ct_10.mqh“, die eine Abwandlung der Klasse „ct_9.mqh“ ist, auf die wir uns im vorherigen Artikel bezogen haben. Der Vollständigkeit halber ist es vielleicht hilfreich, die Schritte zur Erstellung der Monoidklasse durchzugehen, die Teil von „ct_9.mqh“ war, auf die wir uns in den beiden vorangegangenen Artikeln bezogen haben. Dies wurde übergangen, sollte aber in Zukunft konstruktiv sein. Unsere Grundeinheit ist die Elementklasse, die in erster Linie ein Array von Objekten des Datentyps „T“ darstellt. Der Datentyp 'T' wird bei der Initialisierung des Elements festgelegt.
//+------------------------------------------------------------------+ //| ELEMENT CLASS | //+------------------------------------------------------------------+ template <typename T> class CElement : public CObject { protected: int cardinal; T element[]; public: bool Cardinality(int Value) { ... } int Cardinality() { return(cardinal); } ... CElement(void) { Cardinality(0); }; ~CElement(void) {}; };
Die Elementklasse wird ihrerseits von einer Menge (Domänenklasse) als Array aufgerufen.
//+------------------------------------------------------------------+ //| DOMAIN CLASS | //+------------------------------------------------------------------+ template <typename T> class CDomain : public CObject { protected: int cardinal; CElement<T> elements[]; public: bool Cardinality(int Value) { ... } int Cardinality() { return(cardinal); } ... CDomain(void) { Cardinality(0); }; ~CDomain(void) {}; };
Wir waren noch weiter gegangen und hatten nicht nur die Kategorie Klasse definiert, die feierlich monoide Gruppen von Gruppen abgrenzt, sondern auch Klassen für Morphismen, Homomorphismen und ein Kontinuum anderer Konzepte. Da diese und die Kategorieklasse an sich für die Konstruktion der Monoidklasse nicht entscheidend sind, werden wir sie in diesem Artikel nicht aufführen oder berücksichtigen. Ein Monoid besteht also aus drei Dingen, nämlich einer Menge, einem Identitätselement und einer binären Operation. Wenn wir damit beginnen, zu definieren, was eine binäre Operation ist, können wir dies erreichen, indem wir unsere Optionen in Form einer Enumeration auflisten. Wir haben in den letzten 2 Artikeln etwas verwendet, das dem hier ähnelt.
//+------------------------------------------------------------------+ //| Enumeration for Monoid Operations | //+------------------------------------------------------------------+ enum EOperations { OP_FURTHEST=5, OP_CLOSEST=4, OP_MOST=3, OP_LEAST=2, OP_MULTIPLY=1, OP_ADD=0 };
Wir werden dies für unseren Artikel nicht überarbeiten, aber es genügt zu sagen, dass es ein Mittel darstellt, mit dem man anpassen und definieren kann, was sie als binäre Operationen für ihre jeweiligen Monoidmengenelemente betrachten. Und hier gibt es interessante Möglichkeiten. Anstatt eine neue Klasse mit einer Mengeninstanz (Domäne) zu definieren, konstruieren wir unsere Klasse so, dass sie öffentlich von der Domänenklasse erbt. Das ist code-effizient und sagt auch intuitiv, dass ein Monoid einfach eine Domäne mit einer binären Operation und einem Identitätselement ist.
//+------------------------------------------------------------------+ //| Monoid Class | //+------------------------------------------------------------------+ template <typename T> class CMonoid : public CDomain<T> { protected: //double weights[]; int identity; EOperations operation; public: double weights[]; ... void Operation(EOperations Value) { operation=Value; } EOperations Operation() { return(operation); } ... CMonoid(){ identity=0; operation=OP_ADD; }; ~CMonoid(){}; };
Zu dieser Klasse fügen wir dann die beiden zusätzlichen Axiome einer binären Operation und eines Identitätselements hinzu. Unser Identitätselement ist jedoch keine weitere Instanz eines Elements, da dies eine Wiederholung wäre, da es sich bereits im Array der Elemente des Bereichs befindet. Stattdessen verweisen wir einfach auf einen Index dieses Arrays, der auf unser Identitätselement zeigt. Die monoide Klasse kann durch einen automatischen Zeiger in unserem Skript initialisiert werden, wie im folgenden Beispiel gezeigt.
Die im letzten Artikel behandelten monoiden Aktionen haben ihre Klasse von dieser monoiden Klasse geerbt.
Bei monoiden Gruppen gibt es jedoch semantisch keinen Unterschied im Klassencode zwischen einem Monoid und einer monoiden Gruppe. Die Voraussetzung der Inversion kann nur bei monoiden Gruppen geprüft werden. Für unsere Zwecke wird die Klasse der monoiden Gruppe also eine Prüffunktion „HasInversion“ (hat Inversion) enthalten, wie unten gezeigt:
//+------------------------------------------------------------------+ //| Monoid Group Class | //+------------------------------------------------------------------+ template <typename T> class CMonoidGroup : public CMonoid<T> { protected: public: bool HasInversion() { bool _has_inversion=true; for(int i=0;i<this.Cardinality();i++) { bool _has_inverse=false; for(int ii=0;ii<this.Cardinality();ii++) { if(Operate(i,ii)==Identity()){ _has_inverse=true; } } if(!_has_inverse){ _has_inversion=false; break; } } return(_has_inversion); } CMonoidGroup(){}; ~CMonoidGroup(){}; };
In den beiden vorangegangenen Artikeln konnten und konnten Elemente der Monoid- und Monoid-Aktionsklasse keine normalisierten Daten darstellen. Das bedeutet, dass sie vor der Verwendung in den binären Operationen in ein Format umgewandelt werden mussten, das einen fairen Vergleich ermöglichte. Dieses Format wird in diesem Artikel als Gewicht (weight) bezeichnet. In den früheren Artikeln wurden diese Gewichtswerte zur Laufzeit berechnet und verwendet. Hier werden wir die Monoid-Gruppen-Klasse Parameter einführen lassen, um die Werte dieser Gewichte innerhalb der Klasse zu setzen, zu speichern und zu erhalten. Alle Gewichte sind vom Datentyp Double.
CMonoidGroup<int> _vg; //valid inversion group CMonoidGroup<int> _ig; //invalid inversion group _vg.Weights(5); //set group size _ig.Weights(5); //set group size for(int i=0;i<5;i++) { CElement<int> _ve;_ve.Cardinality(1); _ve.Set(0,i-2); _vg.Set(i,_ve,true); //set element _vg.SetWeight(i,double(i-2)); //set weight CElement<int> _ie;_ie.Cardinality(1); _ie.Set(0,i); _ig.Set(i,_ie,true); //set element _ig.SetWeight(i,double(i)); //set weight } _vg.Operation(OP_ADD); //set monoid operation to add _vg.Identity(2); //set identity element index to 2 _ig.Operation(OP_ADD); //set monoid operation to add _ig.Identity(2); //set identity element index to 2 as above or any index printf(" it is: "+string(_vg.HasInversion())+", vg has inversion, given the weights. "); ArrayPrint(_vg.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT); printf(" it is: "+string(_ig.HasInversion())+", ig has inversion, given the weights. "); ArrayPrint(_ig.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT);
Um diesen Code in Aktion zu sehen, erstellen wir eine Instanz der monoiden Gruppe und führen Druckprüfungen mit unseren Klassenfunktionen durch, um zu sehen, welche Ausgabe wir erhalten. Unser Code, dessen vollständige Auflistung diesem Artikel beigefügt ist, bestätigt lediglich die Inversion innerhalb einer Menge. Jedes Element sollte ein inverses haben.
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: true, vg has inversion, given the weights.
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)-2, -1,0,1,2
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: false, ig has inversion, given the weights.
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1) 0,1,2,3,4
Für praktische Zwecke wurde der monoiden Gruppe „_vg“ eine Größe von 5 gegeben, aber ihre tatsächliche Größe ist unbegrenzt, da jede Paarung von Zahlen in der Binäroperation immer zu einer Zahl führen sollte, die ein Mitglied der Gruppenmenge ist, um allen Axiomen einer Gruppe zu entsprechen. Mit dem, was wir verwendet haben, ergibt die Paarung von zwei und eins die Zahl drei, die nicht in der Menge enthalten ist. Somit ist „_vg“ eine ungebundene Menge von ganzen Zahlen (Z).
Verwendung von Monoidgruppen im algorithmischen Handel
In den beiden vorangegangenen Artikeln haben wir, seit wir uns mit Monoiden beschäftigen, diese als Entscheidungspunkte betrachtet. Insbesondere wurden sie bei der Entscheidung über:
- Länge des zu berücksichtigenden Rückblickszeitraums;
- zu verwendender Zeitrahmen;
- zu verwendender angewandter Preis;
- zu verwendender Indikator;
- zu verwendende Handelsmethode (mit oder gegen den Trend).
Die Mengen dieser Monoide stellen die Optionen dar, mit denen ein Händler konfrontiert werden kann, wenn er eine Entscheidung trifft. Was in diesen Artikeln nicht eindeutig erwähnt wurde, obwohl es implementiert wurde, war die Gewichtung der einzelnen Elemente in den jeweiligen Mengen der Monoide. Bevor die monoiden Binäroperationen auf alle Mengenelemente angewendet werden können, um eine Auswahl zu treffen, müssen die Mengenelemente normalisiert werden. In einigen Fällen, wie z. B. bei den angewandten Preisen, war es nicht einfach, Vergleiche auf der Basis einzelner Preisbalken anzustellen, wie es in manchen Handelssituationen erforderlich ist. Wir mussten also einen Weg finden, um diese Mengenelemente so zu quantifizieren, dass sie sich an die sich im Laufe der Zeit ändernde Preisentwicklung oder an die gewählte Basismetrik anpassen. Diese „Quantifizierung“ der Mengenelemente bezeichnen wir in diesem Artikel als Gewichte.
Für die Anwendung müssen wir nach der Gewichtung unserer Elementwerte die Funktion „OperateModulo“ in der überarbeiteten Monoid-Aktionsklasse anwenden, um Gruppen zu verwenden, wie in den letzten Artikeln beschrieben. Die eigentliche Gruppenmenge, die in unserer Aktionsklasse enthalten ist, wird nicht aufgeführt, da es sich einfach um eine Liste von Ganzzahlen bis zu einer Größe handelt, die durch unsere Eingaben in das Skript definiert wird. Was protokolliert wird, ist eine relative Menge zu dieser Gruppe, da die Modulo-Aktion auf die ursprüngliche Menge zwangsläufig zu Wiederholungen führt.
Und so würde die Funktion „Operate“ dies implementieren, als eine Methode mit der monoiden Aktionsklasse.
int OperateModulo(int Index,int Modulo=1) { int _operate=-1; if(Index>=0 && Index<this.Cardinality()) { int _value=int(round(set.weights[Index])); _operate=_value%Modulo; } return(_operate); }
Sobald also unsere monoiden Mengen in eine kleinere „cirkuläre“ Menge umgewandelt sind, kann die binäre Operation für dieses kleinere Monoid bei der Paarung zweier beliebiger Elemente dasjenige ausgeben, das am weitesten vom Identitätselement entfernt ist, wobei in unserem Fall das Identitätselement immer der mittlere Index ist. Um die Größe der monoiden Gruppe festzulegen, muss die Größe eine ungerade Zahl sein.
Wenn zwei Elemente gleich weit von der Identität entfernt sind, wird das Identitätselement gewählt. Zusammenfassend lässt sich also sagen, dass wir mit unserer Monoid-Aktion die monoide Grundmenge zu eine Gruppe normalisieren. Wir würden dann unsere Entscheidung aus der Paarung der Elemente auf der Grundlage ihres Wertes in der monoiden Aktionsmenge mit der binären Operation der monoiden Aktion treffen.
Da wir für diesen Artikel keinen Expert Advisor kodieren und testen, werden wir zur Veranschaulichung der Ausgaben von Monoidgruppen bei jedem unserer fünf oben genannten Merkmale die Monoidmenge mit den Optionen, denen ein Händler gegenübersteht, die Gewichte, in die diese Mengenwerte umgewandelt werden, die Monoidaktionswerte auf diese Gewichte, die Monoidgruppenwerte ergeben, und die relative Menge dieser Monoidgruppe drucken. Beachten Sie, dass wir uns seit einem früheren Artikel wieder auf relative Mengen beziehen, denn um die Menge der Monoid-Aktion als Gruppe zu haben, werden wir Modulo als Eingabegröße verwenden, um alle Werte unserer Gewichte zu normalisieren und in eine Aktionsmenge einzupassen, die ebenfalls eine Gruppe sein wird. Bei der Normalisierung dieser Werte mit modulo sind Wiederholungen vorprogrammiert, weshalb die Aktionsmenge streng genommen keine Gruppe ist, sondern eine relative Menge zu einer Gruppe, deren Mitglieder einfach alle ganzen Zahlen von null bis zur Eingabeanzahl minus eins sind.
Unsere ausgedruckten Protokolle schließen mit den Elementen der Aktionsmenge ab, die sich wie oben erwähnt auf eine Gruppe bezieht. Es ist dann Sache des Lesers, die berechneten Werte in jedem Aktionsmonoid vom Zeitrahmenmonoid bis zum Entscheidungsmonoid zu übertragen, indem er eine Auswahl gemäß den oben dargelegten Axiomen von Gruppen trifft. Um es noch einmal zu wiederholen: Bei binären Operationen in einer Gruppe gilt, genau wie bei Monoiden, wenn eines der gepaarten Elemente die Identität ist, das nicht-identische Element die Ausgabe, und wenn die gepaarten Elemente invers zueinander sind, dann ist die Ausgabe das identische Element.
Außerdem kann es aufschlussreich sein, eine Auswahl zu treffen, die mit dem Zeitrahmen beginnt und dann auf den Zeitraum zurückblickt, den wir in den beiden vorangegangenen Artikeln betrachtet haben. Auf diese Weise erhalten wir unsere Gewichte für das Zeitrahmenmonoid.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void WeighTimeframes(CMonoidGroup<ENUM_TIMEFRAMES> &G) { for(int i=0;i<G.Cardinality();i++) { ResetLastError(); int _value=0; ArrayResize(__r,3);//ArrayInitialize(_buffer,0.0);//ArraySetAsSeries(_buffer,true); if(CopyRates(_Symbol,__TIMEFRAMES[i],0,3,__r)>=3) { _value=int(round(10000.0*fabs(__r[0].close-__r[1].close)/fmax(_Point,fabs(__r[0].close-__r[1].close)+fabs(__r[1].close-__r[2].close)))); } else{ printf(__FUNCSIG__+" Failed to copy: "+EnumToString(__TIMEFRAMES[i])+" close prices. err: "+IntegerToString(GetLastError())); } ResetLastError(); if(!G.SetWeight(i,_value)) { printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError())); } } }
Beachten Sie, dass alle Gewichtungen jetzt auf ein ganzzahliges Format normalisiert werden, da wir modulo bei der Umwandlung in eine Menge in Bezug auf eine Gruppe verwenden wollen, und zwar durch Monoidaktion. Da die Gewichtung für unsere Zeitrahmen ein positives Double war, das nie mehr als eins war, wird dies in eine ganze Zahl umgewandelt, die einen beliebigen Wert zwischen 0 und 10.000 haben kann. Auch unser Parameter für die Eingabegröße von Zeitrahmen, der standardmäßig 51 beträgt, wird der Wert sein, den wir verwenden, um den Rest, ein Mitglied der Gruppe, zu erhalten. Die restlichen Werte werden im Array für die Gewichte der Monoid-Aktionsklasse gespeichert.
Wenn wir also unser Skript an den Chart von USDJPT auf dem einminütigen Zeitrahmen anhängen, dann war dies die Ausgabe für das Zeitrahmen-Monoid am 15.06.2023.
2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)with an input size of: 21 timeframe weights, and their respective monoid action values (group normalised) are:
2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)7098, 8811, 1686, 1782, 1280, 5920, 1030, 5130
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1) {(0),(12),(6),(18),(20),(19),(1),(6)}
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)and action group values (relative set) are:
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20
Wir verwenden eine leicht geänderte Reihe von Zeitrahmen aus unseren früheren Artikeln. Auch hier ist es Ihnen überlassen, die Zeitspanne zu wählen, die für Ihr Studium am besten geeignet ist. Wenn wir Protokolle für Rückschau-Monoide erstellen, erhalten wir die folgenden Ausgaben:
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)with an input size of: 5 lookback weights, and their respective monoid action values (group normalised) are:
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)3149, 1116, 3575, 3779, 7164, 8442, 4228, 5756
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(4),(1),(0),(4),(4),(2),(3),(1)}
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are:
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 0,1,2,3,4
Die obigen Ausdrucke gehen davon aus, dass ein einstündiger Zeitrahmen im Zeitrahmen-Monoid ausgewählt wurde. Die Wiederholung der tatsächlichen endgültigen Auswahl bei jedem Monoid, die den Gruppenaxiomen folgt, ist in diesem Artikel oder dem beigefügten Code nicht vorgesehen. Es bleibt dem Leser überlassen, diesen ersten Schritt in monoiden Gruppen zu erforschen und in die Richtung zu gehen, die seiner Meinung nach am besten zu seiner Strategie passt. Für die angewandten Preisausdrucke ergäben sich die nachstehenden Protokolle, wenn wir davon ausgehen, dass ein Rückblickzeitraum von 8 Jahren gewählt wurde.
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)with an input size of: 21 appliedprice weights, and their respective monoid action values (group normalised) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)1469254, 1586223, 1414566, 2087897 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(10),(9),(6),(14)} 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20
Schlussfolgerung
Wir haben uns angeschaut, was Monoidgruppen sind, indem wir das Konzept der Symmetrie in ein typisches Monoid einführten, wobei wir das zusätzliche Axiom hinzufügten, dass alle Mitglieder einer Monoidgruppe ein Inverses haben müssen und auch binäre Operationen zwischen Spiegelelementen darauf beschränkt sind, immer das Identitätselement der Monoidgruppe auszugeben. Dies ist eine Fortsetzung unseres letzten Artikels, in dem wir monoide Aktionen betrachtet haben.
Wir haben angedeutet, wie Monoid-Gruppen können einfallsreich sein, um Händler in eingeschränkten Monoid-Sets wie wir in einem früheren Artikel hatte. In diesem Artikel gingen wir davon aus, dass monoide Mengen ein fester Pool der Wahlmöglichkeiten eines Händlers zu einem bestimmten Zeitpunkt sind. Dies unterscheidet sich von dem Weg der monoiden Aktionen, den wir im letzten Artikel eingeschlagen haben, wo wir die Auswirkungen der Erweiterung ausgewählter monoider Mengen auf die Handelsleistung untersucht haben.
Indem wir das Potenzial monoider Gruppen nur „andeuten“ und nicht, wie in den beiden vorangegangenen Artikeln, die Verwendung von Expertenratgebern zeigen, wird der Leser eingeladen, dieses Material weiter zu vertiefen, indem er an jedem Monoid Selektionen nach den Regeln der Gruppen durchführt, die wir erwähnt, aber nicht kodiert haben.
In unserem nächsten Artikel werden wir uns mit einem anderen Konzept der Kategorientheorie befassen.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/12800
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.