MQL5 中的范畴论 (第 10 部分):幺半群组
概述
在上一篇文章中,我们继续通过应对”幺半群-动作“来观察幺半群,我们见识到通过扩展其可能的元素来转换幺半群集的一种手段。 总体上,迄今为止,我们已经涵盖了以下概念:域、态射、范畴条例、及至单态回拉和表态外推。 虽然有些人可能会争辩说,范畴论概念的实现需要对其所有/大部分概念进行更广泛的研究,但此处采取的方式是从该主题的基本或有限视角出发,探索哪些思路可加以运用。 这些文章中的每一篇,尽管在某些情况下这些概念是从以前的文章中借鉴而来的,但在促进交易者决策方面展现出有效性,并在某些情况下,它们有定义交易系统的潜力。 至于本文,我们计划研究幺半群 - 组,就如同我们在上一篇文章中涵盖的幺半群动作,可作为在交易决策之处重新定义幺半群的视角。 回想一下幺半群动作成为幺半群集合扩展时的所见,于此我们将重新评估另一个幺半群参数,即衡点元素,我们要再一次重定义幺半群。 本文的纵深将不包括构建完整的交易系统,如同之前一些文章中的情况一样,我们曾编写的智能系统信号和/或智能系统尾随类的实例,目的都是利用内置的 MQL5 向导来装配完整的智能系统。 我们宁愿查看已编码幺半群、“幺半群-动作”、和:幺半群-组”类当中的单独函数,并检验它们在关键决策点如何对交易者起作用。
理解幺半群组
扼要回顾一下,幺半群 有三件事,即一个集合、一个属于该集合的衡点元素、和一个二元操作,该操作所取任意两个元素都来自该集合,且返回的元素始终为该集合成员。 此外,在二元操作中如果集合的任何成员已与衡点元素配对,则输出始终是该成员。 我们最近文章中涵盖的“幺半群-动作”是一种函数形式,由集合和二元操作定义,它将幺半群集合的成员与该函数的集合配对,其输出也始终是函数集合的成员。 我们将它们视为转换幺半群的一种手段,因为请记住,幺半群的二元运算输出是封闭的,因为所有输出都严格是幺半群集的成员。
开始之初,首先要指出的是,组本身和我们在这里所指的”幺半群-组“之间没有区别,这可能是建设性的。 唯一的区别是,正如前缀 “monoid” 所暗示的那样,我们所指的是严格属于一个类别的集合(或域)。 因此,根据组定义,幺半群组是含有附加属性的幺半群,即幺半群集中的每个元素都应该有另一个与其逆反的元素。 当元素及其逆元素在幺半群二元操作中配对时,输出始终是幺半群的衡点元素。
正式的 inverse 属性,用于设置”幺半群-组“
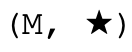
除了正规的幺半群,对于每个
![]()
还有一个逆反项
![]()
如此:
![]()
其中 e 是幺半群的衡点元素。
按照类似于我们在上一篇文章中的方式,考虑在交易者当中应用它。 回想一下,我们将幺半群(集合)视为交易者可从中选择的决策选项池,在上一篇文章中,我们看到过以”幺半群-动作“扩展该其大小。 我们实测了如果基于交易系统决策点(特征)相对重要性的权重因子列表来扩展特定幺半群的纵深,会对交易系统的性能产生什么影响。 与以前参考受限(默认)幺半群的文章中得到的结果相比,上述结果差于平均水准。 对于”幺半群-组“,比之扩展幺半群集的纵深,我们宁愿回转到含有动作的受限幺半群,并转换到组。 我们将回顾据此幺半群动作的集合组合变化,但在本文中不会研究交易系统的真正实现。 这是邀请读者去独立探索的东西。在 MQL5 中实现幺半群组
在设置 MQL5 环境以实现“幺半群-组”时,我们将启动 IDE,并自向导创建一个新的脚本文件。
然后,我们在下一个选项卡上为脚本命名 “ct_10”,并单击“完成”。 该脚本将引用类文件 'ct_10.mqh',它是我们在上一篇文章 'ct_9.mqh' 中所提类的修订版。 为了完整起见,走遍创建幺半群类的步骤也许会有所帮助,该类是我们在前两篇文章中提到的 'ct_9.mqh' 的一部分。 这些已经过润色,但它应该是建设性的。 回想一下,我们的基本构建单元是元素类,它主要构成数据类型为 “T” 的对象数组。 数据类型 “T” 是在初始化元素时进行设置的。
//+------------------------------------------------------------------+ //| ELEMENT CLASS | //+------------------------------------------------------------------+ template <typename T> class CElement : public CObject { protected: int cardinal; T element[]; public: bool Cardinality(int Value) { ... } int Cardinality() { return(cardinal); } ... CElement(void) { Cardinality(0); }; ~CElement(void) {}; };
元素类若为数组又被称集合(域类)。
//+------------------------------------------------------------------+ //| DOMAIN CLASS | //+------------------------------------------------------------------+ template <typename T> class CDomain : public CObject { protected: int cardinal; CElement<T> elements[]; public: bool Cardinality(int Value) { ... } int Cardinality() { return(cardinal); } ... CDomain(void) { Cardinality(0); }; ~CDomain(void) {}; };
我们已经走得更远了,不仅定义了范畴类,其在仪式上,定义的“幺半群组”与“群”不同,此外还定义了一些类,涵盖态射、单态、和其它概念的连续体。 因为这些和范畴类本身对于构造幺半群类无关紧要,因此本文不会列出、或研究它们。 那么,回想一下,幺半群是三件事,即集合、一个衡点元素、和一个二元运算。 如果我们从定义什么是二元操作开始,我们应当以列举我们的选项的形式来达成这一点。 在过去的 2 篇文章中,我们所用到的东西均与此类似。
//+------------------------------------------------------------------+ //| Enumeration for Monoid Operations | //+------------------------------------------------------------------+ enum EOperations { OP_FURTHEST=5, OP_CLOSEST=4, OP_MOST=3, OP_LEAST=2, OP_MULTIPLY=1, OP_ADD=0 };
我们不会在我们的文章中对此加以修改,但足以说明它确实设置了一种方法,令人可据其自行定义他们各自认知的幺半群集合元素的二元运算。 此处的可能性很有趣。 转至幺半群类,比之定义一个集合(域)实例的新类,我们在构造我们的类时宁愿自域类公开继承。 这是高效的代码,它也直观地说幺半群只是一个域,含有二元运算,以及附于它的衡点元素。
//+------------------------------------------------------------------+ //| Monoid Class | //+------------------------------------------------------------------+ template <typename T> class CMonoid : public CDomain<T> { protected: //double weights[]; int identity; EOperations operation; public: double weights[]; ... void Operation(EOperations Value) { operation=Value; } EOperations Operation() { return(operation); } ... CMonoid(){ identity=0; operation=OP_ADD; }; ~CMonoid(){}; };
在这个类中,我们添加了二元运算和衡点元素这两个额外条例。 我们的衡点元素并非另一个元素的实例,这会导致重复,因为其已身处域的元素数组之中。 我们宁可简单地引用指向衡点元素所处的数组索引。 幺半群类能够通过脚本中的指针自动初始化,如下例所示。
上一篇文章中涵盖的幺半群动作类继承自幺半群类。
但对于“幺半群组”,从语义上讲,幺半群和“幺半群组”之间在类代码里并无区别。 “幺半群组”只有检查逆转的需求。 故此,出于我们的目的,“幺半群组”类会具有 “HasInversion” 检查函数,如下所示。
//+------------------------------------------------------------------+ //| Monoid Group Class | //+------------------------------------------------------------------+ template <typename T> class CMonoidGroup : public CMonoid<T> { protected: public: bool HasInversion() { bool _has_inversion=true; for(int i=0;i<this.Cardinality();i++) { bool _has_inverse=false; for(int ii=0;ii<this.Cardinality();ii++) { if(Operate(i,ii)==Identity()){ _has_inverse=true; } } if(!_has_inverse){ _has_inversion=false; break; } } return(_has_inversion); } CMonoidGroup(){}; ~CMonoidGroup(){}; };
在前两篇文章中,幺半群和“幺半群-动作”类的元素能够且曾经构成无常规化数据。 这意味着在进行二元运算之前,必须将它们转换为能够等价比较的格式。 在本文中,这种形式称为加权。 在前面的文章中,这些权重值是在运行时进行计算并使用的。 在此,我们计划在“幺半群-组”类中引入参数来设置、存储、和获取这些权重值。 所有加权都将是双精度型数据。
CMonoidGroup<int> _vg; //valid inversion group CMonoidGroup<int> _ig; //invalid inversion group _vg.Weights(5); //set group size _ig.Weights(5); //set group size for(int i=0;i<5;i++) { CElement<int> _ve;_ve.Cardinality(1); _ve.Set(0,i-2); _vg.Set(i,_ve,true); //set element _vg.SetWeight(i,double(i-2)); //set weight CElement<int> _ie;_ie.Cardinality(1); _ie.Set(0,i); _ig.Set(i,_ie,true); //set element _ig.SetWeight(i,double(i)); //set weight } _vg.Operation(OP_ADD); //set monoid operation to add _vg.Identity(2); //set identity element index to 2 _ig.Operation(OP_ADD); //set monoid operation to add _ig.Identity(2); //set identity element index to 2 as above or any index printf(" it is: "+string(_vg.HasInversion())+", vg has inversion, given the weights. "); ArrayPrint(_vg.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT); printf(" it is: "+string(_ig.HasInversion())+", ig has inversion, given the weights. "); ArrayPrint(_ig.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT);
为了查看该段代码的实际效果,我们来创建一个“幺半群组”的实例,并运行类函数打印检查结果,看看我们得到什么输出。 在本文中附带了我们的代码完整清单,只是确认集合内的逆转。 每个元素都应该有一个相对于衡点元素的逆元素。
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: true, vg has inversion, given the weights.
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)-2, -1,0,1,2
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: false, ig has inversion, given the weights.
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1) 0,1,2,3,4
出于实际目的,幺半群组 “_vg” 给定的大小为 5,但其实际大小是无限的,由于要匹配一个组的所有条例,二元运算中任何配对的数字,其结果数字都应始终是组集成员。 而我们所用的配对,二和一将产生三,但其并未在集合中列出。 所以 “_vg” 是一组未绑定的整数 (Z)。
幺半群组在算法交易中的运用
在前两篇文章中,自从我们开始查验幺半群以来,我们一直将它们作为决策关键。 具体来说,它们已被用于决定:
- 要考虑的回顾分析周期长度;
- 所用时间帧;
- 采用的应用价格;
- 所用的指标;
- 以及运用的交易方法(无论顺势,亦或逆势)。
在据它们作为决策关键时,这些幺半群中的每一个集合均构成了交易者可能面临的选项。 尽管它已实现,但在这些文章中没有明确提到的是,幺半群各自集合中的每个元素均有权重。 为了进行选择,且在所有集合元素执行幺半群二元运算之前,需要对集合元素进行常规化。 在某些情况下,以应用价格举例,在价格柱线的基础上进行比较并不容易,而这却是某些交易状况所要求的。 因此,我们必须找到一种方式来量化这些集合元素,使之能适配价格动作,或任何选定的随时间变化的基本衡量度。 如此,集合元素的这种“量化”就是本文所称的加权。
现在,为了加以应用,针对元素值进行加权之后,我们需要调用据前一篇文章里幺半群动作类基础上修订的 “OperateModulo” 函数,以便分组。 实际组集未在动作类中列出,因为它只是一个整数型列表,其大小由脚本输入定义。 其所记录的是相对于该组的集合,因为初始集合上的取模动作必然会产生重复。
作为幺半群动作类的方法,这就是 'Operate' 函数如何实现这一点的。
int OperateModulo(int Index,int Modulo=1) { int _operate=-1; if(Index>=0 && Index<this.Cardinality()) { int _value=int(round(set.weights[Index])); _operate=_value%Modulo; } return(_operate); }
故此,一旦我们的幺半群集被转换为一个较小的“循环”集,那针对这个较小的幺半群,任何两个元素配对时的二元运算输出是离衡点元素最远的那个,在我们的例子中,衡点元素始终位于集合中间索引处。 设置“幺半群组”的大小要求该值为奇数。
如果两个元素离衡点元素等距,则选择衡点元素。 好了,在此扼要回顾一下我们的幺半群动作,它可有效地将基本幺半群集合归纳到一个组。 然后,我们在做出决定时,会基于二元操作的配对元素离它们于幺半群动作集中的位置。
由于我们并不准备在本文中编码和测试智能系统,为了阐明幺半群组的输出,对于之前曾提到的五个特征中的每一个,我们都会把交易者要面对的幺半群集的选项打印出来,这些集合值均已加权转换,这些加权后的幺半群动作值亦是幺半群组值, 以及相对于该幺半群组的集合。 注意,自早期的文章以来,我们再次引用了相对集,这是因为出于把幺半群动作集归并到一个组,我们将采用输入的大小取模,把我们所有的加全值常规化,并拟合到一个动作集之中,该动作集也将是一个组。 针对这些值取模进行常规化时,我们必然会遇到重复,这就是为什么动作集严格来说不是一个组,而是一个组的相对集,其成员简单地从整数零排列到输入的大小减一。
如上所述,据我们打印的日志能得出结论,动作集的元素是相对于组。 然后,由读者将每个幺半群动作中的已计算数值,从时间帧幺半群,按照以上勾勒的组项进行选择,并转运到决策幺半群。 只是为了重申在群集合中的二元操作,就像幺半群一样,如果任何元素与衡点元素配对,则输出的就是非衡点元素,另外如果配对的元素彼此相逆,那么输出将是衡点元素。
此外,从时间帧开始进行选择,然后回顾我们在前两篇文章中研究的周期进行对比,也许会更明晰。 话虽如此,这就是我们如何得到加权的时间帧幺半群。
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void WeighTimeframes(CMonoidGroup<ENUM_TIMEFRAMES> &G) { for(int i=0;i<G.Cardinality();i++) { ResetLastError(); int _value=0; ArrayResize(__r,3);//ArrayInitialize(_buffer,0.0);//ArraySetAsSeries(_buffer,true); if(CopyRates(_Symbol,__TIMEFRAMES[i],0,3,__r)>=3) { _value=int(round(10000.0*fabs(__r[0].close-__r[1].close)/fmax(_Point,fabs(__r[0].close-__r[1].close)+fabs(__r[1].close-__r[2].close)))); } else{ printf(__FUNCSIG__+" Failed to copy: "+EnumToString(__TIMEFRAMES[i])+" close prices. err: "+IntegerToString(GetLastError())); } ResetLastError(); if(!G.SetWeight(i,_value)) { printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError())); } } }
注意,所有加权项现在都将常规化为整数格式,因为我们希望使用取模来把幺半群动作转换为相对于组的集合。 故此,针对我们的时间帧,由于加权是个从不超过一的正双精度值,我们已将其转换为一个整数,其值可以是从 0 到 10,000 之间的任何值。 此外,我们有一个对应时间帧的输入大小参数,默认值为 51,其也是我们取余数的参数值,即组集的成员。 余数值存储在“幺半群动作”类的 weights 数组之中。
由此,如果我们将脚本附加到一分钟时间帧内的 USDJPT 图表上,于 2023 年 06 月 15 日某时,这是时间帧幺半群于此间的输出。
2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)with an input size of: 21 timeframe weights, and their respective monoid action values (group normalised) are:
2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)7098, 8811, 1686, 1782, 1280, 5920, 1030, 5130
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1) {(0),(12),(6),(18),(20),(19),(1),(6)}
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)and action group values (relative set) are:
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20
我们正在用的是来自过去文章,并略微修改后的一组时间帧。 再次,由您来选择最适合您正在研习内容的时间帧。 如果我们运行回溯幺半群,下面就是我们的打印日志。
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)with an input size of: 5 lookback weights, and their respective monoid action values (group normalised) are:
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)3149, 1116, 3575, 3779, 7164, 8442, 4228, 5756
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(4),(1),(0),(4),(4),(2),(3),(1)}
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are:
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 0,1,2,3,4
上面的打印假设在时间帧幺半群中选择了一小时时间帧。 至于在每个幺半群重复实际的最终选择,遍历群条例,在本文或随附的代码中均未实现。 这留给读者去探索,并在幺半群组处迈出第一步,朝着他们认为最适合自己策略的方向努力。 对于应用的价格打印,如果我们选择回溯周期 8,我们将得到下面的日志。
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)with an input size of: 21 appliedprice weights, and their respective monoid action values (group normalised) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)1469254, 1586223, 1414566, 2087897 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(10),(9),(6),(14)} 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20
结束语
我们通过在典型幺半群里引入对称性概念,看清了幺半群是什么,其中我们添加了额外条例,即幺半群的所有成员都需要有其逆元素,且镜像元素之间的二元运算被限制为始终输出幺半群组的衡点元素。 这是我们上一篇文章的后续文章,在上一篇文章中,我们研究了幺半群动作。
我们已经暗示了幺半群组如何像我们在上一篇文章中那样,在受约束的幺半群集中为交易者提供资源。 在那篇文章中,我们将幺半群集视为供交易者在给定阶段进行选择的固定池。 这与我们在上一篇文章中采取的幺半群动作不同,那时我们看到的是扩大选择幺半群对交易绩效的影响。
只“暗示”幺半群的潜力,而未像我们在前两篇文章中那样展示在智能系统里运用它们,邀请读者深入学习这些材料,按照我们提到的(但未编码)组规则实现从每个幺半群里选择。
在下一篇文章中,我们将讨论范畴论的另一个概念。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/12800
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。