Techniken des MQL5-Assistenten, die Sie kennen sollten (Teil 01): Regressionsanalyse
Der MQL5-Assistent ermöglicht die schnelle Erstellung und Bereitstellung eines Expert Advisors, indem die meisten untergeordneten Aspekte des Handels in der Bibliothek von MQL5 vorcodiert sind. Dies ermöglicht es Händlern, sich auf ihre individuellen Aspekte ihres Handels zu konzentrieren, wie z. B. spezielle Ein- und Ausstiegsbedingungen. In der Bibliothek enthalten sind einige Eingangs- und Ausgangssignalklassen wie Signale des Indikators „Accelerator Oscillator“ oder Signale des Indikators „Adaptive Moving Average“ und viele andere. Abgesehen davon, dass sie für die meisten Händler auf nachlaufenden Indikatoren basieren, sind sie möglicherweise nicht in erfolgreiche Strategien umwandelbar. Aus diesem Grund ist die Möglichkeit, Ihr eigenes nutzerdefiniertes Signal zu erstellen, unerlässlich. In diesem Artikel werden wir untersuchen, wie dies mit der Regressionsanalyse durchgeführt werden kann.
2. Erstellen der Klasse
2.1 Die Regressionsanalyse ist laut Wikipedia eine Reihe statistischer Prozesse zum Schätzen der Beziehungen zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen. Es kann für das Expertensignal eines Händlers nützlich sein, da Preisdaten eine Zeitreihe sind. Dies ermöglicht es daher, die Fähigkeit früherer Preise und Preisänderungen zu testen, zukünftige Preise und Preisänderungen zu beeinflussen. Die Regressionsanalyse kann durch folgende Gleichung dargestellt werden: 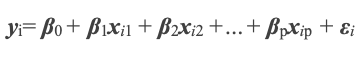
Wobei y die abhängige und daher vorherzusagende Variable von früheren x-Werten abhängt, jede mit ihren eigenen Koeffizienten β und einem Fehler ε. Wir können uns vorstellen, die x-Werte und der y-Wert seien frühere bzw. prognostizierte Preisniveaus. Neben der Arbeit mit Preisniveaus können auf ähnliche Weise auch Preisänderungen untersucht werden. Das unbekannte y ist abhängig von xs, βs und ε. Davon sind allerdings nur xs und β0 (der y-Achsenabschnitt) bekannt. Der y-Achsenabschnitt ist bekannt, weil es der Preis unmittelbar vor xi 1 ist. Wir müssen also die entsprechenden βs für jedes x finden und dann das ε. Weil jedes xi1 zum vorherigen Zeitpunkt der Zeitreihe ein yI war, können wir die β-Werte mithilfe von Simultangleichungen lösen. Wenn die nächste Preisänderung beispielsweise nur von zwei vorherigen Änderungen abhängt, könnte unsere aktuelle Gleichung lauten:
Und die vorherigen Gleichungen wären:
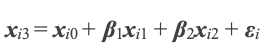
Da wir den Fehler ε separat schätzen, können wir mit den beiden Simultangleichungen die β-Werten lösen. Die Nummerierung der x-Werte in der Wikipedia-Formel ist nicht im MQL5-Serienformat, was bedeutet, dass das x mit der höchsten Nummer das neueste ist. Ich habe daher die x-Werte in den obigen 2 Gleichungen neu nummeriert, um zu zeigen, wie sie gleichzeitig sein können. Wieder beginnen wir mit den y-Achsenabschnitten xi1 und xi0 zur Darstellung von β0 in Gleichung 1. Das Lösen von Simultangleichungen wird aus Effizienzgründen besser mit Matrizen gehandhabt. Die Werkzeuge dafür befinden sich in der MQL5-Bibliothek.
2.2 Die MQL5-Bibliothek verfügt über eine umfangreiche Sammlung von Klassen für Statistiken und gängige Algorithmen, die es eindeutig überflüssig machen, sie von Grund auf neu zu codieren. Sein Code ist auch für die Öffentlichkeit zugänglich, was bedeutet, dass er unabhängig überprüft werden kann. Für unsere Zwecke verwenden wir die Funktion „RMatrixSolve“ unter der Klasse „CDenseSolver“ in der Datei „solvers.mqh“. Das Herzstück dieser Funktion ist die Verwendung der Matrix-LU-Zerlegung, um schnell und effizient β zu lösen. Im MetaQuotes-Archiv wurden Artikel dazu geschrieben und auch Wikipedia hat eine Erklärung .
Bevor wir uns mit der Lösung der β-Werte befassen, wäre es hilfreich, sich anzusehen, wie die Klasse „CExpertSignal“ strukturiert ist, da sie die Grundlage für unsere Klasse bildet. In fast allen Experten-Signalklassen, die im Assistenten zusammengestellt werden können, gibt es eine „LongCondition“-Funktion (kaufen) und eine „ShortCondition“-Funktion (verkaufen). Wie Sie erwarten würden, geben die beiden einen Wert zurück, der festlegt, ob Sie jeweils kaufen oder verkaufen sollten. Dieser Wert muss eine ganze Zahl im Bereich von 0 bis 100 sein, um ihn den Eingabeparametern „Signal_ThresholdOpen“ und „Signal_ThresholdClose“ des Assistenten zuzuordnen. Normalerweise möchten Sie beim Handel, dass Ihre Bedingungen zum Schließen einer Position weniger konservativ sind als Ihre Bedingungen zum Öffnen. Dies bedeutet, dass die Schwelle zum Öffnen höher ist als die Schwelle zum Schließen. Bei der Entwicklung unseres Signals werden wir daher Eingabeparameter zum Berechnen der Schwelle zum Schließen und getrennte, aber ähnliche Eingabeparameter für die Schwelle zum Öffnen haben. Die Auswahl der bei der Berechnung einer Bedingung zu verwendenden Eingaben wird davon bestimmt, ob wir offene Positionen haben oder nicht. Wenn wir offene Positionen haben, verwenden wir die Schließ-Parameter. Wenn keine Positionen vorhanden sind, verwenden wir Eröffnungs- Parameter. Der Code unserer Experten-Signalklassenschnittstelle, die diese beiden Parametersätze zeigt, ist unten.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class CSignalDUAL_RA : public CExpertSignal { protected: CiMA m_h_ma; // highs MA handle CiMA m_l_ma; // lows MA handle CiATR m_ATR; //--- adjusted parameters int m_size; double m_open_determination,m_close_determination; int m_open_collinearity,m_open_data,m_open_error; int m_close_collinearity,m_close_data,m_close_error; public: CSignalDUAL_RA(); ~CSignalDUAL_RA(); //--- methods of setting adjustable parameters //--- PARAMETER FOR SETTING THE NUMBER OF INDEPENDENT VARIABLES void Size(int value) { m_size=value; } //--- PARAMETERS FOR SETTING THE OPEN 'THRESHOLD' FOR THE EXPERTSIGNAL CLASS void OpenCollinearity(int value) { m_open_collinearity=value; } void OpenDetermination(double value) { m_open_determination=value; } void OpenError(int value) { m_open_error=value; } void OpenData(int value) { m_open_data=value; } //--- PARAMETERS FOR SETTING THE CLOSE 'THRESHOLD' FOR THE EXPERTSIGNAL CLASS void CloseCollinearity(int value) { m_close_collinearity=value; } void CloseDetermination(double value) { m_close_determination=value; } void CloseError(int value) { m_close_error=value; } void CloseData(int value) { m_close_data=value; } //--- method of verification of settings virtual bool ValidationSettings(void); //--- method of creating the indicator and timeseries virtual bool InitIndicators(CIndicators *indicators); //--- methods for detection of levels of entering the market virtual bool OpenLongParams(double &price,double &sl,double &tp,datetime &expiration); virtual bool OpenShortParams(double &price,double &sl,double &tp,datetime &expiration); //--- methods of checking if the market models are formed virtual int LongCondition(void); virtual int ShortCondition(void); protected: //--- method of initialization of the oscillator bool InitRA(CIndicators *indicators); //--- methods of getting data int CheckDetermination(int ind,bool close); double CheckCollinearity(int ind,bool close); // double GetY(int ind,bool close); double GetE(int ind,bool close); double Data(int ind,bool close); // };
Außerdem finden Sie hier eine Auflistung unserer Funktionen „LongCondition“ und „ShortCondition“.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int CSignalDUAL_RA::LongCondition(void) { int _check=CheckDetermination(0,PositionSelect(m_symbol.Name())); if(_check>0){ return(_check); } return(0); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int CSignalDUAL_RA::ShortCondition(void) { int _check=CheckDetermination(0,PositionSelect(m_symbol.Name())); if(_check<0){ return((int)fabs(_check)); } return(0); }
Um jedoch fortzufahren, verwenden wir zum Auflösen nach β-Werten die Funktion „GetY“. Dies ist unten aufgeführt.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalDUAL_RA::GetY(int ind,bool close) { double _y=0.0; CMatrixDouble _a;_a.Resize(m_size,m_size); double _b[];ArrayResize(_b,m_size);ArrayInitialize(_b,0.0); for(int r=0;r<m_size;r++) { _b[r]=Data(r,close); for(int c=0;c<m_size;c++) { _a[r].Set(c,Data(r+c+1, close)); } } int _info=0; CDenseSolver _S; CDenseSolverReport _r; double _x[];ArrayResize(_x,m_size);ArrayInitialize(_x,0.0); _S.RMatrixSolve(_a,m_size,_b,_info,_r,_x); for(int r=0;r<m_size;r++) { _y+=(Data(r,close)*_x[r]); } //--- return(_y); }
Die erwähnte „Daten“-Funktion wechselt zwischen Änderungen des Schlusskurses des gehandelten Symbols oder Änderungen des gleitenden Durchschnitts desselben Schlusskurses. Die verwendete Option wird entweder durch den Eingabeparameter „m_open_data“ oder den Eingabeparameter „m_close_data“ definiert, je nachdem, ob wir die Eröffnungsschwelle oder die Schließschwelle berechnen. Die Auflistung zur Auswahl von Daten ist in der Aufzählung unten dargestellt.
enum Edata { DATA_TREND=0, // changes in moving average close DATA_RANGE=1 // changes in close };
Und die 'Daten'-Funktion, die dies auswählt, ist unten aufgeführt.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalDUAL_RA::Data(int ind,bool close) { if(!close) { if(Edata(m_open_data)==DATA_TREND) { m_h_ma.Refresh(-1); return((m_l_ma.Main(StartIndex()+ind)-m_l_ma.Main(StartIndex()+ind+1))-(m_h_ma.Main(StartIndex()+ind)-m_h_ma.Main(StartIndex()+ind+1))); } else if(Edata(m_open_data)==DATA_RANGE) { return((Low(StartIndex()+ind)-Low(StartIndex()+ind+1))-(High(StartIndex()+ind)-High(StartIndex()+ind+1))); } } else if(close) { if(Edata(m_close_data)==DATA_TREND) { m_h_ma.Refresh(-1); return((m_l_ma.Main(StartIndex()+ind)-m_l_ma.Main(StartIndex()+ind+1))-(m_h_ma.Main(StartIndex()+ind)-m_h_ma.Main(StartIndex()+ind+1))); } else if(Edata(m_close_data)==DATA_RANGE) { return((Low(StartIndex()+ind)-Low(StartIndex()+ind+1))-(High(StartIndex()+ind)-High(StartIndex()+ind+1))); } } return(0.0); }
Sobald wir die β-Werte haben, können wir mit der Schätzung des Fehlers fortfahren.
2.3 Der Standardfehler nach Wikipedia kann mit der unten stehenden Formel geschätzt werden.
![]()
Mit s als Standardabweichung und n als Stichprobenumfang dient der Fehler als ernüchternde Erinnerung daran, dass nicht alle Prognosen, egal wie sorgfältig sie sind, immer zu 100 % genau sind. Wir sollten immer einkalkulieren und mit einem Fehler unsererseits rechnen. Die in der Formel angegebene Standardabweichung wird zwischen unseren vorhergesagten Werten und den tatsächlichen Werten gemessen. Zu Vergleichszwecken können wir uns auch einen rohen Fehler ansehen, beispielsweise die letzte Differenz zwischen unserer Prognose und der tatsächlichen. Diese beiden Optionen können aus der folgenden Aufzählung ausgewählt werden.
enum Eerror { ERROR_LAST=0, // use the last error ERROR_STANDARD=1 // use standard error }
Die Funktion 'GetE' gibt dann unsere Fehlerschätzung abhängig von den Eingabeparametern 'm_open_error' oder 'm_close_error' zurück, während die obige Formel verwendet wird. Dies ist unten aufgeführt.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalDUAL_RA::GetE(int ind,bool close) { if(!close) { if(Eerror(m_open_error)==ERROR_STANDARD) { double _se=0.0; for(int r=0;r<m_size;r++) { _se+=pow(Data(r,close)-GetY(r+1,close),2.0); } _se=sqrt(_se/(m_size-1)); _se=_se/sqrt(m_size); return(_se); } else if(Eerror(m_open_error)==ERROR_LAST){ return(Data(ind,close)-GetY(ind+1,close)); } } else if(close) { if(Eerror(m_close_error)==ERROR_STANDARD) { double _se=0.0; for(int r=0;r<m_size;r++){ _se+=pow(Data(r,close)-GetY(r+1,close),2.0); } _se=sqrt(_se/(m_size-1)); _se=_se/sqrt(m_size); return(_se); } else if(Eerror(m_close_error)==ERROR_LAST){ return(Data(ind,close)-GetY(ind+1,close)); } } //--- return(Data(ind,close)-GetY(ind+1,close)); }
Auch hier wird die Verwendung von „m_open_error“ oder „m_close_error“ davon bestimmt, ob wir offene Positionen haben oder nicht. Sobald wir unsere Fehlerschätzung haben, sollten wir in der Lage sein, eine grobe Vorhersage für y zu machen. Die Regressionsanalyse hat jedoch eine Reihe von Fallstricken. Eine davon ist die Fähigkeit der unabhängigen Variablen, zu ähnlich zu sein und daher den vorhergesagten Wert zu übertreiben. Dieses Phänomen wird als Kollinearität bezeichnet und es lohnt sich, darauf zu achten.
2.4 Die Kollinearität, die Wikipedia hier definiert, kann als das Auftreten hoher Interkorrelationen zwischen zwei oder mehr unabhängigen Variablen in einem multiplen Regressionsmodell vermutet werden, gemäß Investopedia. Es gibt per se keine Formel und wird durch den Varianzinflationsfaktor (VIF) erfasst. Dieser Faktor wird über alle unabhängigen Variablen gemessen (x), um ein Gefühl dafür zu bekommen, wie jede dieser Variablen bei der Vorhersage von y einzigartig ist. Sie wird durch die folgende Formel angegeben, wobei R die Regression jeder unabhängigen Variablen gegen die anderen ist.
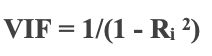
Für unsere Zwecke nehmen wir jedoch unter Berücksichtigung der Kollinearität die Umkehrung der Spearman-Korrelation zwischen zwei neueren Datensätzen unabhängiger Variablen und normalisieren sie. Die Länge unserer Datensätze wird durch den Eingabeparameter „m_size“ festgelegt, dessen Mindestlänge 3 beträgt. Durch Normalisierung subtrahieren wir es einfach von zwei und invertieren das Ergebnis. Dieses normalisierte Gewicht kann dann entweder mit der Fehlerschätzung oder dem vorhergesagten Wert oder beiden multipliziert werden oder unbenutzt bleiben. Diese Optionen sind in der folgenden Enumeration aufgeführt.
enum Echeck { CHECK_Y=0, // check for y only CHECK_E=1, // check for the error only CHECK_ALL=2, // check for both the y and the error CHECK_NONE=-1 // do not use collinearity checks };
Die Wahl des angewendeten Gewichts wird auch durch entweder den Eingabeparameter 'm_open_collinearity' oder 'm_close_collinearity' festgelegt. Wieder abhängig davon, ob Positionen offen sind. Die Auflistung „CheckCollinearity“ ist unten angegeben.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalDUAL_RA::CheckCollinearity(int ind,bool close) { double _check=0.0; double _c=0.0,_array_1[],_array_2[],_r=0.0; ArrayResize(_array_1,m_size);ArrayResize(_array_2,m_size); ArrayInitialize(_array_1,0.0);ArrayInitialize(_array_2,0.0); for(int s=0; s<m_size; s++) { _array_1[s]=Data(ind+s,close); _array_2[s]=Data(m_size+ind+s,close); } _c=1.0/(2.0+fmin(-1.0,MathCorrelationSpearman(_array_1,_array_2,_r))); double _i=Data(m_size+ind,close), //y intercept _y=GetY(ind,close), //product sum of x and its B coefficients _e=GetE(ind,close); //error if(!close) { if(Echeck(m_open_collinearity)==CHECK_Y){ _check=_i+(_c*_y)+_e; } else if(Echeck(m_open_collinearity)==CHECK_E){ _check=_i+_y+(_c*_e); } else if(Echeck(m_open_collinearity)==CHECK_ALL){ _check=_i+(_c*(_y+_e)); } else if(Echeck(m_open_collinearity)==CHECK_NONE){ _check=_i+(_y+_e); } } else if(close) { if(Echeck(m_close_collinearity)==CHECK_Y){ _check=_i+(_c*_y)+_e; } else if(Echeck(m_close_collinearity)==CHECK_E){ _check=_i+_y+(_c*_e); } else if(Echeck(m_close_collinearity)==CHECK_ALL){ _check=_i+(_c*(_y+_e)); } else if(Echeck(m_close_collinearity)==CHECK_NONE){ _check=_i+(_y+_e); } } //--- return(_check); }
Abgesehen von der Überprüfung auf Kollinearität gibt es Zeiten, in denen die Regressionsanalyse aufgrund exogener Marktänderungen nicht so prädiktiv ist, wie sie es sein könnte. Um dies zu verfolgen und die Fähigkeit der unabhängigen Variablen unseres Signals zu messen, unsere abhängige Variable (die Vorhersage) zu beeinflussen, verwenden wir das Bestimmtheitsmaß.
2.5 Das Bestimmtheitsmaß ist ein statistisches Maß, das untersucht, wie Unterschiede in einer Variablen durch den Unterschied in einer zweiten Variablen erklärt werden können, wenn das Ergebnis eines bestimmten Ereignisses gemäß Investopedia. Wikipedia bietet auch eine umfassendere Definition und unsere unten gezeigten Formeln sind übernommen worden von dort.
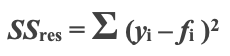
Die Formel für die Summe der Quadrate (wobei y der tatsächliche Wert und f der prognostizierte Wert ist),
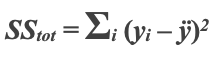
Die Formel für die Gesamtsumme (wobei y ein tatsächlicher Wert und ÿ der gleitende Durchschnitt dieser Werte ist),
Und schließlich das für den Koeffizienten selbst, der auch als R-Quadrat bezeichnet wird.
Dieser Koeffizient misst das Ausmaß, in dem unsere xs das y beeinflussen. Dies ist wichtig, da es, wie bereits erwähnt, Zeiten gibt, in denen die Regression abebbt, was bedeutet, dass es sicherer ist, sich von den Märkten fernzuhalten. Indem wir dies durch einen Filter überwachen, ist es wahrscheinlicher, dass wir handeln, wenn das System zuverlässig ist. Normalerweise soll dieser Koeffizient über 0 liegen, wobei 1 ideal ist. Der bei der Definition unseres Schwellenwerts verwendete Eingabeparameter ist „m_open_determination“ oder „m_close_determination“, wiederum abhängig von der Anzahl der offenen Positionen. Wenn das von der unten aufgeführten Funktion „CheckDetermination“ berechnete Bestimmtheitsmaß kleiner als dieser Parameter ist, geben die Kauf- und Verkaufsbedingungen Null zurück.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int CSignalDUAL_RA::CheckDetermination(int ind,bool close) { int _check=0; m_h_ma.Refresh(-1);m_l_ma.Refresh(-1); double _det=0.0,_ss_res=0.0,_ss_tot=0.0; for(int r=0;r<m_size;r++) { _ss_res+=pow(Data(r,close)-GetY(r+1,close),2.0); _ss_tot+=pow(Data(r,close)-((m_l_ma.Main(r)-m_l_ma.Main(r+1))-(m_h_ma.Main(r)-m_h_ma.Main(r+1))),2.0); } if(_ss_tot!=0.0) { _det=(1.0-(_ss_res/_ss_tot)); if(_det>=m_open_determination) { double _threshold=0.0; for(int r=0; r<m_size; r++){ _threshold=fmax(_threshold,fabs(Data(r,close))); } double _y=CheckCollinearity(ind,close); _check=int(round(100.0*_y/fmax(fabs(_y),fabs(_threshold)))); } } //--- return(_check); }
Sobald wir das Bestimmtheitsmaß überprüfen können, hätten wir ein funktionsfähiges Signal. Was als Nächstes folgt, wäre das Zusammenbauen dieses Signals im MQL5-Assistenten zu einem Expert Advisor.
3. Assemblieren mit dem MQL5 Wizard
3.1 Die nutzerdefinierte Auflistung von Hilfscodes kann zusammen mit dem Code aus dem MQL5-Assistenten beim Zusammenstellen eines Expert Advisors verwendet werden. Dies ist völlig optional und entspricht dem Stil des Händlers. Für die Zwecke dieses Artikels werden wir uns die nutzerdefinierte Eröffnung von Pending Orders ansehen, die auf dem vorherrschenden ATR des Symbols basiert, sowie ein System von nachlaufenden offenen Positionen, das auf demselben Indikator basiert. Wir verwenden keine Take-Profit-Ziele.
3.1.1 ATR-basierte Pending Orders können festgelegt werden, indem die Funktionen „OpenLongParams“ und „OpenShortParams“ überladen und in unserer Signalklasse wie unten gezeigt angepasst werden.
//+------------------------------------------------------------------+ //| Detecting the levels for buying | //+------------------------------------------------------------------+ bool CSignalDUAL_RA::OpenLongParams(double &price,double &sl,double &tp,datetime &expiration) { CExpertSignal *general=(m_general!=-1) ? m_filters.At(m_general) : NULL; //--- if(general==NULL) { m_ATR.Refresh(-1); //--- if a base price is not specified explicitly, take the current market price double base_price=(m_base_price==0.0) ? m_symbol.Ask() : m_base_price; //--- price overload that sets entry price to be based on ATR price =m_symbol.NormalizePrice(base_price-(m_price_level*(m_ATR.Main(0)/m_symbol.Point()))*PriceLevelUnit()); sl =0.0; tp =0.0; expiration+=m_expiration*PeriodSeconds(m_period); return(true); } //--- return(general.OpenLongParams(price,sl,tp,expiration)); } //+------------------------------------------------------------------+ //| Detecting the levels for selling | //+------------------------------------------------------------------+ bool CSignalDUAL_RA::OpenShortParams(double &price,double &sl,double &tp,datetime &expiration) { CExpertSignal *general=(m_general!=-1) ? m_filters.At(m_general) : NULL; //--- if(general==NULL) { m_ATR.Refresh(-1); //--- if a base price is not specified explicitly, take the current market price double base_price=(m_base_price==0.0) ? m_symbol.Bid() : m_base_price; //--- price overload that sets entry price to be based on ATR price =m_symbol.NormalizePrice(base_price+(m_price_level*(m_ATR.Main(0)/m_symbol.Point()))*PriceLevelUnit()); sl =0.0; tp =0.0; expiration+=m_expiration*PeriodSeconds(m_period); return(true); } //--- return(general.OpenShortParams(price,sl,tp,expiration)); }
Der vom MQL5-Assistenten generierte Expert Advisor hat einen Eingabeparameter 'Signal_PriceLevel'. Standardmäßig ist es Null, aber wenn ihm ein Wert zugewiesen wird, stellt es den Abstand in Preispunkten des gehandelten Symbols vom aktuellen Preis dar, zu dem eine Marktorder platziert wird. Wenn diese Eingabe negativ ist, werden Stop-Orders platziert. Wenn Aufträge mit positivem Limit platziert werden. Der Datentyp ist double. Für unsere Zwecke ist diese Eingabe ein Bruchteil oder ein Vielfaches der aktuellen Preispunkte im ATR.
3.1.2 Die ATR-Trailing-Klasse ist auch eine angepasste 'CExpertTrailing'-Klasse, die auch den ATR verwendet, um den Stop-Loss zu setzen und zu verschieben. Die Implementierung seiner Schlüsselfunktionen ist in der folgenden Auflistung aufgeführt.
//+------------------------------------------------------------------+ //| Checking trailing stop and/or profit for long position. | //+------------------------------------------------------------------+ bool CTrailingATR::CheckTrailingStopLong(CPositionInfo *position,double &sl,double &tp) { //--- check if(position==NULL) return(false); //--- m_ATR.Refresh(-1); double level =NormalizeDouble(m_symbol.Bid()-m_symbol.StopsLevel()*m_symbol.Point(),m_symbol.Digits()); //--- sl adjustment to be based on ATR double new_sl=NormalizeDouble(level-(m_atr_weight*(m_ATR.Main(0)/m_symbol.Point())),m_symbol.Digits()); double pos_sl=position.StopLoss(); double base =(pos_sl==0.0) ? position.PriceOpen() : pos_sl; //--- sl=EMPTY_VALUE; tp=EMPTY_VALUE; if(new_sl>base && new_sl<level) sl=new_sl; //--- return(sl!=EMPTY_VALUE); } //+------------------------------------------------------------------+ //| Checking trailing stop and/or profit for short position. | //+------------------------------------------------------------------+ bool CTrailingATR::CheckTrailingStopShort(CPositionInfo *position,double &sl,double &tp) { //--- check if(position==NULL) return(false); //--- m_ATR.Refresh(-1); double level =NormalizeDouble(m_symbol.Ask()+m_symbol.StopsLevel()*m_symbol.Point(),m_symbol.Digits()); //--- sl adjustment to be based on ATR double new_sl=NormalizeDouble(level+(m_atr_weight*(m_ATR.Main(0)/m_symbol.Point())),m_symbol.Digits()); double pos_sl=position.StopLoss(); double base =(pos_sl==0.0) ? position.PriceOpen() : pos_sl; //--- sl=EMPTY_VALUE; tp=EMPTY_VALUE; if(new_sl<base && new_sl>level) sl=new_sl; //--- return(sl!=EMPTY_VALUE); }
Auch hier wird 'm_atr_weight' ein optimierbarer Parameter sein, wie bei 'm_price_level', der festlegt, wie nah wir offenen Positionen folgen können.
3.2 Die Wizard-Erstellung wird dann auf unkomplizierte Weise durchgeführt, wobei die einzigen bemerkenswerten Schritte die Auswahl unseres Signals sind, wie unten gezeigt.

Und das Hinzufügen unserer nutzerdefinierten Trailing-Methode, die unten gezeigt wird.

4. Testen im Strategietester
4.1 Die Kompilierung folgt der Assemblierung im MQL5-Assistenten, um die Expert Advisor-Datei zu erstellen und auch zu bestätigen, dass es keine Fehler in unserem Code gibt.
4.2 Die Standardeingaben des Expert Advisors müsste auch auf der Registerkarte Strategietester-Eingaben festgelegt werden. Der Schlüssel hier ist sicherzustellen, dass 'Signal_TakeLevel' und 'Signal_StopLevel' auf Null gesetzt sind. Dies liegt daran, dass der Ausstieg für die Zwecke dieses Artikels wie erwähnt nur durch den nachlaufenden Stopp oder den Eingangsparameter „Signal_ThresholdClose“ definiert wird.
4.3 Die Optimierung sollte idealerweise mit den realen Ticks des Brokers durchgeführt werden, mit dem Sie handeln möchten. Für diesen Artikel werden wir EURUSD im 4-Stunden-Zeitrahmen über seinen V-förmigen Zeitraum vom 01.01.2018 bis 01.01.2021 optimieren. Zu Vergleichszwecken führen wir zwei Optimierungen durch, die erste verwendet nur Market Orders, während die zweite für Pending Orders offen ist. Ich verwende „offen für“ Pending-Orders, weil wir immer noch die Option in Betracht ziehen, nur Market-Orders zu verwenden, da „Signal_PriceLevel“ Null sein kann, da die Optimierung von einem negativen Wert zu einem positiven Wert erfolgt. Die Optimierung kann zuvor für die Option eingerichtet werden, die Pending Orders verwendet, wie unten gezeigt. Der einzige Unterschied zwischen dieser Option und der Option, die keine Pending Orders verwendet, besteht darin, dass später der Eingabeparameter „Signal_PriceLevel“ auf 0 belassen wird, was nicht Teil der optimierten Eingaben ist.
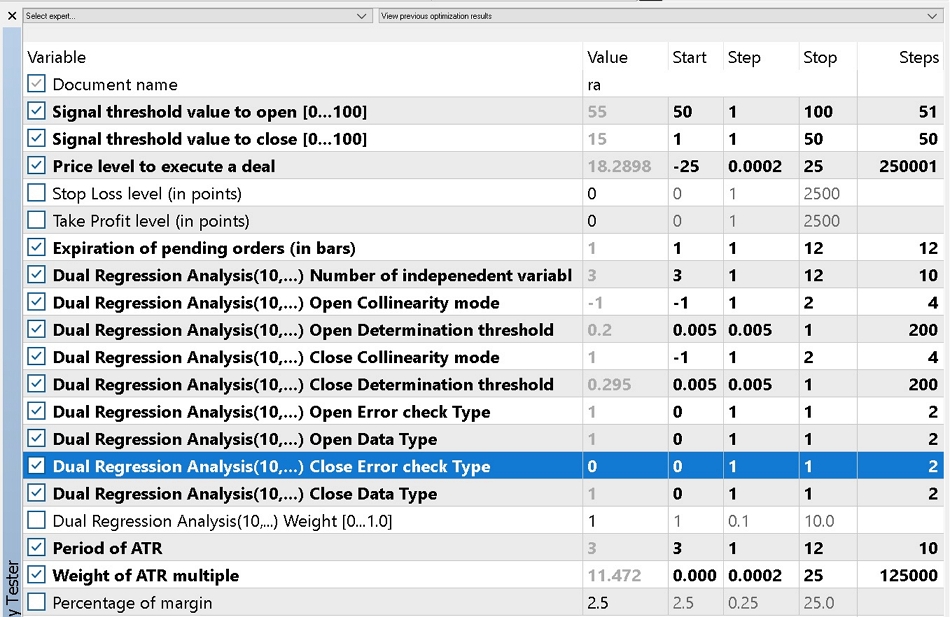
4.4 Die Ergebnisse unserer Optimierung sind unten dargestellt. Der erste ist der Bericht und die Eigenkapitalkurve der besten Ergebnisse aus dem Handel nur mit Marktaufträgen.
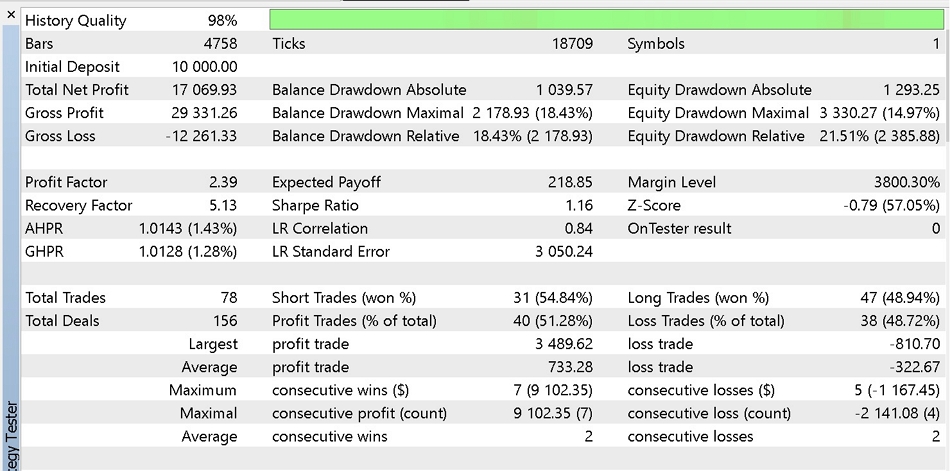
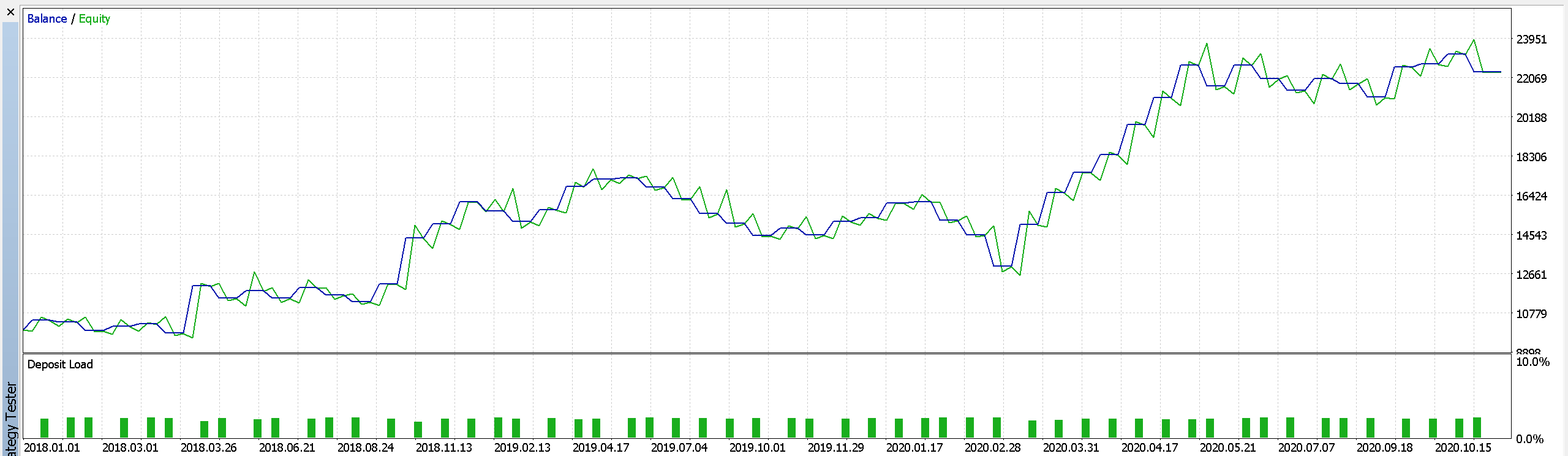
Bericht Teil 1.
Dann ein ähnlicher Bericht und eine Kurve aus der Verwendung von Pending Orders.
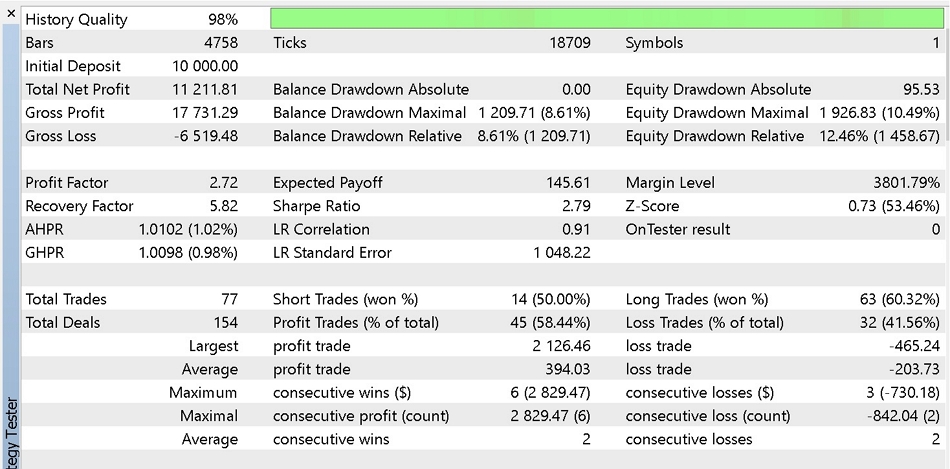
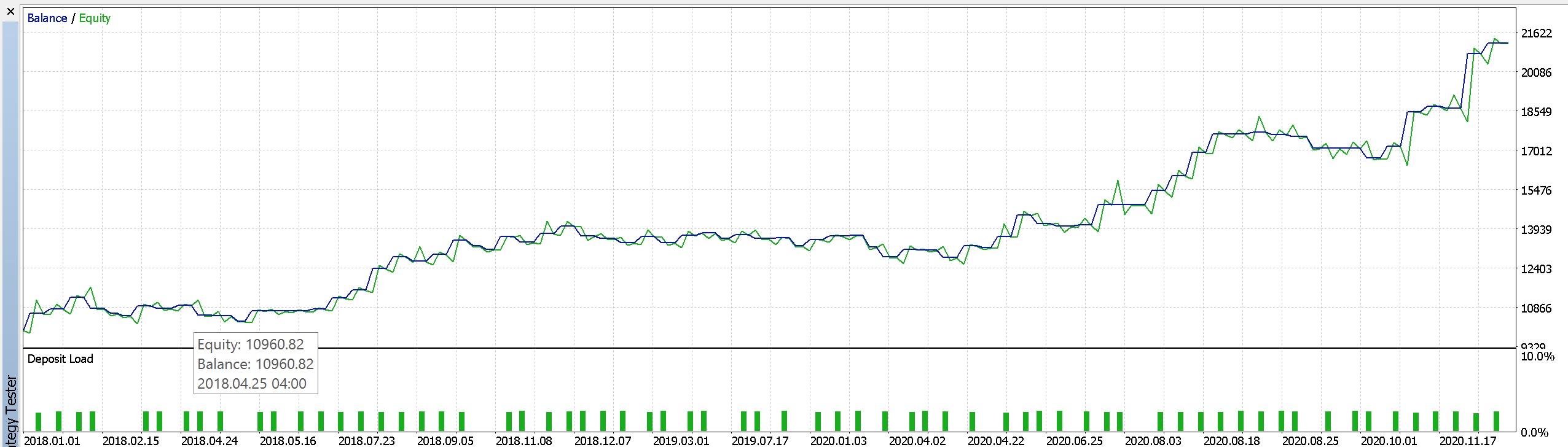
Bericht Teil 2.
Es scheint, dass unser Regressionsanalysesignal von der Verwendung von ausstehenden Aufträgen profitiert, da es weniger Drawdowns auf Kosten einiger Gewinne gibt. Es könnten auch andere Modifikationen vorgenommen werden, um dieses System zu verbessern, wie z. B. das Ändern der Trailing-Stop-Klasse oder des Money-Management-Typs. Für unsere Testzwecke haben wir einen festen Margenprozentsatz verwendet und unsere Kriterien auf „komplexes Kriterium“ gesetzt optimiert. Es ist jedoch wünschenswert, so umfassend wie möglich historische Tick-Daten zu testen und vor der Bereitstellung von Dingen, die den Rahmen dieses Artikels sprengen würden, genügend Vorwärtsgänge zu unternehmen.
5. Schlussfolgerung
5.1 Der MQL5-Assistent ist eindeutig ein einfallsreiches Werkzeug, das im Arsenal jedes Händlers sein sollte. Was wir hier betrachtet haben, ist, wie man einige statistische Konzepte der Regressionsanalyse wie Kollinearität und Bestimmtheitsmaß nehmen und sie als Grundlage für ein robustes Handelssystem verwenden kann. Die nächsten Schritte wären umfangreiche Tests historischer Tick-Daten und die Untersuchung, ob dieses Signal mit anderen einzigartigen Signalen basierend auf der Erfahrung eines Händlers oder auf integrierten Signalen in der MQL5-Bibliothek gepaart werden kann, um ein umfassenderes Handelssystem zu entwickeln. Wie es in dieser Artikelserie der Fall sein wird, soll dieser Artikel keinen Gral liefern, sondern eher einen Prozess, der angepasst werden kann, um besser zu der Herangehensweise eines Händlers an die Märkte zu passen. Danke fürs Lesen.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/11066
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 8): Ein konzeptioneller Sprung
Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 8): Ein konzeptioneller Sprung
 Lernen Sie, wie man ein Handelssystem mit Ichimoku entwirft
Lernen Sie, wie man ein Handelssystem mit Ichimoku entwirft
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
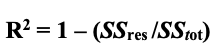
Hallo Stephen,
ein sehr guter Artikel. Ich habe einige Tests gemacht und es hat gute Ergebnisse geliefert. Sieht so aus, als hätten wir ein ermutigendes Handelssystem.
Ich würde gerne wissen, wie ich Eingaben mit nicht fixen Zeitrahmen zur Optimierung verwenden kann.
Ich habe versucht, diese Zeilen zu ändern, aber OnInit "gab Nicht-Null-Code 1" ohne Fehlermeldung zurück.
Können Sie mir helfen?
Hallo Stephen,
ein sehr guter Artikel. Ich habe einige Tests gemacht und es hat gute Ergebnisse geliefert. Sieht so aus, als hätten wir ein ermutigendes Handelssystem.
Ich würde gerne wissen, wie ich Eingaben mit nicht fixen Zeitrahmen zur Optimierung verwenden kann.
Ich habe versucht, diese Zeilen zu ändern, aber OnInit "zurückgegeben Nicht-Null-Code 1" mit keine Fehlermeldung.
Können Sie mir helfen?
Hallo Stephen,
ein sehr guter Artikel. Ich habe einige Tests gemacht und es hat gute Ergebnisse geliefert. Sieht so aus, als hätten wir ein ermutigendes Handelssystem.
Ich würde gerne wissen, wie ich Eingaben mit nicht fixen Zeitrahmen zur Optimierung verwenden kann.
Ich habe versucht, diese Zeilen zu ändern, aber OnInit "zurückgegeben Nicht-Null-Code 1" mit keine Fehlermeldung.
Können Sie mir helfen?
Hallo,
ich sehe das gerade. Entschuldigung. Das kann ein bisschen schwierig sein, weil die assistentengestützten Expert Advisors dazu neigen, den Zeitrahmen des Charts, an den sie angehängt sind, zu verwenden und sich daran zu halten. Und darauf wird an vielen verschiedenen Stellen verwiesen, nicht nur in der OnInit()-Funktion, die Sie offenbar zu ändern versuchen. Wenn also der von Ihnen eingegebene Zeitrahmen nicht mit dem Zeitrahmen übereinstimmt, der an anderen Stellen verwendet und erwartet wird (der Zeitrahmen des Diagramms), dann wird dies zwangsläufig zu Fehlern führen.
Im Großen und Ganzen ist es jedoch sinnvoll, Daten und Preispuffer in mehr als einem Zeitrahmen zu lesen, und ich denke, ich werde in naher Zukunft einen Artikel darüber schreiben, wie dies erreicht werden kann. Vielen Dank für Ihr Feedback.
Ich erhalte einen Fehler, wenn ich einen Experten kompiliere, der mit dem SignalDUAL_RA erstellt wurde. Er geht zurück auf die matrix.mqh
Die CMatrixDouble ist ein Funktionsaufruf der in MetaEditor eingebauten Klassen, matrix.mqh, also nehme ich an, dass der Fehler nicht dort liegt.
Können Sie mir helfen, dieses Problem zu lösen?
Kann irgendjemand helfen?
kompiliert er bei mir nicht mit dem zuvor erwähnten Problem (siehe Bildschirmfoto). Ich habe das Problem wie folgt gelöst
_a[r].Set(c,Data(r+c,close)); sollte_a.Set(r,c,Data(r+c,close)) sein;
mit der Verwendung von _a[r] bearbeiten wir die r-te Zeile nicht direkt, sondern übergeben sie als Referenz. Diese Korrektur hat funktioniert.