
什么是马丁格尔?使用马丁格尔是否合理?
什么是马丁格尔?
如果你在搜索引擎框内输入“马丁格尔”,将返回大量包含此系统描述的页面。有意思的是,除了其他内容,你将看到确保该系统工作的在线赌场网址,你需要的就是输入你的信用卡号码然后开始掘金。奇怪的是——难道赌场就这样简单把金钱拱手相让?如果马丁格尔真的如此管用,那为何赌场还没有全部破产呢?
那么,什么是马丁格尔?以下是在维基百科中找到的定义:
- 一场赌局以特定的最小赌注开始;
- 每次赌输后赌注应提高,让赢家可以补回所有损失外加小额利润;
- 如果赢下赌局,则赌博者返回至最小赌注。
马丁格尔用途是什么?
用以分析马丁格尔的最简单赌博是抛硬币。输赢的概率相等——如果硬币正面朝上则赢,反面朝上则输。这种赌博的马丁格尔系统运作方式是:
- 以一个小赌注开始赌博;
- 每次赌输后,赌注翻倍;
- 如果赢下赌局,则返回至最小赌注。
马丁格尔还可在轮盘赌中用于对红色或黑色下注。概率因有零的存在而低于 50/50,但依然非常接近。
应用到交易中时,可以使用该赌博的如下的形式。类似投掷硬币,我们在任何方位建仓(短仓或长仓),让止损和获利点和交易价格保持同等距离。当我们在随机方向建仓时,盈利和亏损的概率近似于 50/50。因此我将仅在本文中描述在投掷硬币时如果亏损则赌注翻倍会出现的经典问题。
数学部分
让我们使用马丁格尔系统就抛硬币赌博的亏损概率对可能盈利的依赖度进行一项数学计算。让我们引入以下交易品种:
- 设定 – 抛一组硬币,抛出赢钱的硬币即结束。即除最后一次抛掷,其它抛掷均输钱。首次抛掷时为最小赌注,随后每次抛出后,赌注均翻倍。
- Q – 初始保证金;
- q – ;起始赌注金额;
- k – 组合内可导致输光的最大抛掷(亏损)次数(假设经过 K 次抛掷后保证金为零。)
随着我们在每次输钱抛掷后赌注翻倍,我们可获得以下等式:
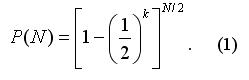
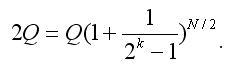
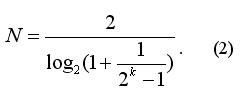
如果我们将 N 视为非整数(无法将资产结果 (2) 圆整),则 P(N)不依赖 K,且等于 1/2 (你可以将 (2) 插入 (1) 中并使用最简单的对数性质来进行简单验证)。即,使用马丁格尔并不能带来任何优势;我们一样可以将我们所有资本 Q 下注, 而赢钱概率也是同样的(1/2)。
数学部分总结
坦白说,在刚开始准备本文的计算部分时,我预期马丁格尔会提高亏损的概率。但这预期看起来是错误的,亏损的风险并未提高。尽管如此,本文还是非常生动地描述了使用马丁格尔的无意义性。
Expert Advisor
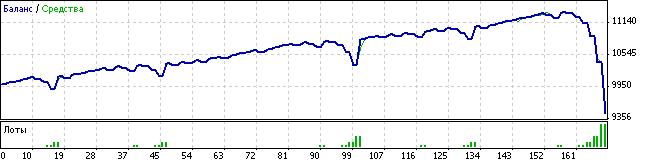
获得以上公式后,我首先做的就是编写一个小程序,仿效抛硬币的流程并组成依赖系数 K 的亏损概率(P)统计数据。经过检查,我发现程序结果(可称之为“试验”)与数学计算相吻合。当然,理想的变量应为编写和抛硬币规则相同的 Expert Advisor,并确保理论和试验数据保持一致。但这是不可能的,因为起始赌注的计算公式为:
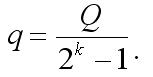
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/1481
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 MQL5 初学者: 图形对象的防破坏保护
MQL5 初学者: 图形对象的防破坏保护
 使用神经网络预测价格
使用神经网络预测价格
 对冲 Expert Advisor 编码基础
对冲 Expert Advisor 编码基础
