
What is Martingale and Is It Reasonable to Use It?
What Is Martingale?
If you write "martingale" in a search engine box, it will return a large
number of pages with the description of this system. It is interesting that among
others you will meet web-sites of online casinos, which assure that this system
works, all you need is entering your credit card number to start scooping up money.
What is strange - are the casinos ready to give their money such easily? If the
Martingale really works so good, then why have not all the casinos turned bankrupt
yet?
So, what is Martingale? Here is the definition from Wikipedia:
- A game starts with a certain minimal bet;
- After each each loss the bet should be increased so, that the win would recover all previous losses plus a small profit;
- In case of win a gambler returns to the minimal bet.
Where Is Martingale Used?
The simplest gamble for analyzing the Martingale is chuck-farthing. The chances
to win and to lose are equal - the gambler wins if a coin comes up heads and loses
if the coin comes up tails. The Martingale system for this game works in such a
way:
- Start the game with a small bet;
- After each loss double the bet;
- In case of win return to the minimal bet.
The Martingale can also be used in playing the roulette, betting on red or black.
The chances are less than 50/50, because there is also Zero, still very close to
it.
As applied to trading, the following variant of the game can be used. Analogous
to tossing a coin we open a position in any direction (short or long) with stop-loss
and take-profit equally distant from the trade price. As we open the position in
a random direction, the probability of profit and loss is analogous - 50/50. So
in this article I will describe only the classical problem of tossing a coin with
doubling the bet at a loss.
Mathematical Part
Let us conduct a mathematical calculation of the dependence of the loss probability on the possible profit at the game with a coin using the Martingale system. Let us introduce the following symbols:
- Set – a set of tosses, ending by a winning one. I.e. all tosses except the last one are losing. At the first toss the bet is minimal, at each next toss in the set the bet is doubled;
- Q – initial deposit;
- q – price of the starting bet;
- k – maximal number of tosses (losing) in the set, leading to bankruptcy (suppose after k toss the deposit is equal to zero).
As we double the bet after each losing toss, we can derive the following equation:
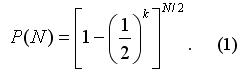
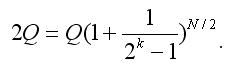
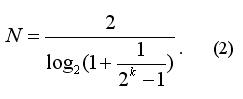
If we consider N a noninteger (do not round off the results of the equity (2) to a whole number), then P(N) does not depend on k and is equal to 1/2 (you can easily verify it, inserting (2) into (1) and using the simplest properties of logarithms). I.e. using the Martingale does not provide any advantages; we could as well bet all our capital Q and the winning probability would be the same (1/2).
Conclusions of the Mathematical Part
Frankly speaking, at the beginning of preparing calculations for this article I expected that the Martingale would increase the probability of loss. It appeared to be wrong and the risk of loss is not increased. Still this article very vividly describes the meaninglessness of using the Martingale.
Expert Advisor
After getting the above formulas, the first thing I did was writing a small program, emulating the process of playing chuck-farthing and composing the statistics of the losing probability (P) dependence on the coefficient k. After the check I found that the program results (it can be called "an experiment") coincide with mathematical calculations.Of course, the ideal variant would be writing an Expert Advisor, trading by the same rules as in chuck-farthing and making sure that theoretical and experimental data are identical. But it is impossible because the starting bet is calculated using the formula:
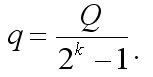
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/1481
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Mathematics in Trading: How to Estimate Trade Results
Mathematics in Trading: How to Estimate Trade Results
 Construction of Fractal Lines
Construction of Fractal Lines
 Breakpoints in Tester: It's Possible!
Breakpoints in Tester: It's Possible!
 MQL4 Language for Newbies. Technical Indicators and Built-In Functions
MQL4 Language for Newbies. Technical Indicators and Built-In Functions
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
How to implement profitable martingale:
1 - start with low base lots (0.1 or less)
2 - high win rate.. at least 70%
3 - low consecutive losses (minimize z-score)
4 - semi-martingale.. rather then strictly doubling the number of lots.. allow this factor to be varied based on market/performance.. in my experience, doubling is a very aggressive approach
5 - equity stoploss.. force martingale to reset to minimum lots if a given equity drawdown is observed.. you will take a large hit, but still be in the green & in the game
..I have such a system trading on a live account.. due to the limitations above it is not hugely profitable but has been running for over a year with a constant return on capital
2
its funny the articles that are written on martingale. It is true that without an edge, even 0.50% above 50/50, you would lose over time (over a continuous series of repititions). This was also proven in an article detailing the gambler's fallacy (see follow up also here) . The good news is that the financial markets can only go so far in any particular direction before a pullback. You can use this fact alone to your advantage (edge). I think the largest single direction trend a market ever made was EURUSD 2000 pips without a pullback of at least 38.2%, There was another move of 3600 pips, but there were significant retracements in-between. Even better news is that martingale is not required to become profitable in the markets. There is a spreadsheet where you can work out the numbers yourself and see.
It works if the net profit factor is above 1 and the win rate is higher than 50%, martingale is a double or nothing either doubles your money or doubles your losses, so if you have a 60% win rate with 1:1 RR ratio you can use it safely, if not then dont.
Whats funny about forex that you dont start from 50% win rate from the start because the market is changing not a fix probability set like a roulette or blackjack game.So if you start it like a betting system you will have like 40% win rate with 1:1 RR if you take trades random, maybe on the 9999999999999999999999th trade you hit 49.9% but thats still not enough.So it is better to filter out crappy trades first and then increase your win rate to be martingale compatible! And this is the advantage of investing vs gambling, you can filter out bad trades, on the roulette or blackjack you cant filter out bad hands or spins unless you cheat, but surely not the statistical way!!
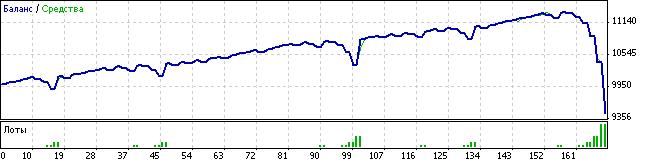
This is how my 60% win rate, real martingale system looks like, and how it should suppose to look like, on LEVEL 7 settings (2^7)
Here are my martingale type systems:
1) CLASSICAL MARTINGALE AFTER 567 TRADES (60% WR, 1:1 RR)
As you can see after 500 trades it barely hit LEVEL 7 and even if we would lost that we would lose only half of the profit and continue from there to grow it back!
Of course you need a big account for this like one that can support like 10 lot size trades to be only 1% account risk, but statistically its very improbable to blow your account since its only 1% risk versus huge potential gains...The martingale presented in this article is BS with like 40-45% win rate which is sadly not enough, not even 50% is, must be 51 or higher...
2) PROGRESSIVE DYNAMIC GROWTH MARTINGALE (60% WR, 1:1 RR)
3) PROGRESSIVE STATIC GROWTH MARTINGALE (60% WR, 1:1 RR)
4) ANTI MARTINGALE or INVERSE MARTINGALE (60% WR, 1:1 RR)
enjoy and good programming ;)