神经网络变得简单（第 84 部分）：可逆归一化（RevIN）
263
0
概述
在上一篇文章中，我们讨论了构象方法，其初衷是为天气预报而开发的。这是一个非常有趣的方法。在测试已训练模型时，我们得到了一个相当不错的结果。但我们所做的每件事情都正确吗？是否可能获得更好的结果？我们来看看学习过程。很容易看出，我们显然并未使用该模型来预测后续最有可能的时间序列数值，来实现其预期目的。把时间序列投喂模型输入数据，我们用预测结果降低模型的传播误差梯度来训练它。我们从评论者的结果开始。
if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder)) || !Encoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
然后是扮演者的结果。
if(!Actor.backProp(GetPointer(bActions), GetPointer(Encoder)) || !Encoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
当为了运营盈利能力而调整其政策时，数据再次取自扮演者。
Critic.TrainMode(false); if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder)) || !Actor.backPropGradient((CNet *)GetPointer(Encoder), -1, -1, false) || !Encoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
当然，这并无错误。它在训练各种模型实践中广泛运用。然而，在这种情况下，在训练初始环境状态的编码器模型时，我们关注的不是预测后续状态，而是识别允许我们优化后续模型操作的单独特征。
当然，我们的主要任务是找到扮演者的最优政策。如此这般，初看，令编码器适配扮演者的目标并无错误。但在这种情况下，编码器解决的问题略有不同。在实践中，它变成后续模型的模块。它的架构也许并非解决所需任务的最优选择。
进而，当用 3 个不同任务的误差梯度训练编码器时，我们也许会遇到单独任务的梯度方向不同的问题。在这种情况下，模型将寻找最能满足所有任务集的 “中庸之道”。这样的解决方案或许远非最优。
我认为这很明显，使用模型的结构化逻辑也应当在学习过程中实现。在这样的范式中，我们需要训练编码器来预测环境的后续状态。构象方式已正式运用在编码器之中。然后，我们训练扮演者的政策，同时考虑所预测的环境状态。
理论如此，非常清晰。然而，在实际实现中，我们在描述环境状态各个特征的分布时面临着巨大的差距。在模型输入处接收描述环境状态的“原始”数据后，我们将其归一化，将其带至一种可比较的形式。但我们如何在模型输出处得到不同的数值呢？
当训练各种自动编码器模型时，我们就遇到了类似的问题。在这些情况下，我们找到了一种解决方案，即采用归一化后的原始数据作为目标。不过，在这种情况下，我们需要不同于输入数据的，描述环境后续状态的数据。论文《可逆实例归一化抵消精确时间序列预测中的分布移位》中提出了解决此问题的方法之一。
论文作者提议一种简单而有效的归一化和逆归一化方法：可逆实例归一化（RevIN）。该算法首先归一化输入序列，然后在模型的输出序列进行逆归一化，以便解决时间序列预测当中的分布移位相关问题。RevIN 是对称结构，按归一化层中输入数据的伸缩和移位相等量值，在逆归一化层中缩放和移位输出，从而将原始分布信息返回到模型输出。
RevIN 是一个灵活的、可训练的层，能够应用于所有任意选择的层，有效地抑制一层中的非稳态信息（实例的平均值和方差），并在近乎对称位置另一层将其恢复，例如输入和输出层。
1. RevIN 算法
为了领略 RevIN 算法，我们来研究离散时间内，时间序列的多元预测问题，针对一组输入数据 X = {xi}i=[1..N]，和相应的目标 Y = {yi}i=[1..N]，其中 N 表示序列中的元素数量。
设 K、Tx 和 Ty 分别表示变量的数量、输入序列的长度、和模型预测的长度。给定输入序列 Xi∈ RK*Tx，我们的意向是解决时间序列预测问题，即预测后续值 Yi∈ RK*Ty。在 RevIN 中，输入序列 Tx 的长度、和预测长度 Ty 也许会有所不同，因为观测值沿时间维度进行了归一化和逆归一化。所提议方法 RevIN，由对称结构的归一化和逆归一化层组成。首先，我们用其均值和标准差归一化输入 Xi，作为即时归一化，这已被广泛接受。每个输入实例 Xi 的均值和标准差计算如下：
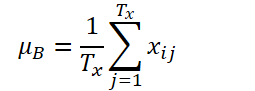
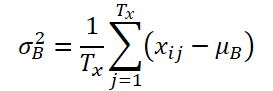
归一化序列可以具有更一致的均值和标准差，其中非稳态信息会减少。结果就是，归一化层允许模型准确预测序列内的局部动态，同时接收以均值和偏差形式的一致分布输入。
该模型接收转换后的数据作为输入，并预测未来值。不过，与原始分布相比，输入数据的统计数据不同，并且仅通过观察归一化输入，很难捕捉到输入数据的原始分布。因此，为了令这项任务更容易应对模型，我们通过在对称位置（输出层）逆转归一化，把已从输入数据中删除的非稳态特征显式返回到模型输出。逆非归一化步骤能够把模型输出返回到原始时间序列值。相应地，我们通过应用逆归一化操作对模型输出进行逆归一化：
归一化步骤中用到的相同统计数据，也用于缩放和移位。现在 ŷi 是模型的最终预测。
简单地加到网络中差不多对称的位置，RevIN 就可以有效降低分布偏差，在时间序列数据中作为可训练的归一化层，通常可适用于任意深度的神经网络。事实上，所提议方法是一个灵活的、可学习的层，能够应用于所有任意选择的层，甚至多个层。该方法的作者将其添加到各种模型的中间层，以此来确认其作为柔性层的有效性。无论如何，RevIN 在应用于编码器-解码器结构的差不多对称层时最有效。在典型的时间序列预测模型中，编码器和解码器之间的界限往往不明确。因此，该方法的作者将 RevIN 应用到模型的输入和输出层，因为它们可以被视为编码器-解码器结构，即基于输入数据生成后续数值。
RevIN 方法的原始可视化表述如下。
2. 利用 MQL5 实现
我们已研究过该方法的理论层面。现在我们可以转到利用 MQL5 实际实现所提议的方式。
从上面讲述的方法的理论中，您可以看到，由该方法的作者提议的初始数据归一化完全重复了我们之前实现的 CNeuronBatchNormOCL 批量归一化层的算法。因此，我们能用现有的类来归一化数据。但为了逆归一化数据，我们需要创建一个新的神经层 CNeuronRevINDenormOCL。
2.1创建新的逆归一化层
显然，数据逆归一化过程将使用数据归一化所用的对象。这就是为什么新的 CNeuronRevINDenormOCL 层是从 CNeuronBatchNormOCL 归一化层派生而来的。
class CNeuronRevINDenormOCL : public CNeuronBatchNormOCL { protected: int iBatchNormLayer; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; } public: CNeuronRevINDenormOCL(void) : iBatchNormLayer(-1) {}; ~CNeuronRevINDenormOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, int NormLayer, CNeuronBatchNormOCL *normLayer); virtual int GetNormLayer(void) { return iBatchNormLayer; } //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronRevInDenormOCL; } virtual CLayerDescription* GetLayerInfo(void); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) { return true; } };
根据 RevIN 方法算法，我们应该复用归一化阶段训练的参数来进行逆归一化。此处逻辑是，在归一化阶段，我们研究输入数据的分布。之后，我们将输入数据转换为可比较的形式，消除“间隙”。然后，模型搭配归一化数据操作。在模型的输出中，我们对数据进行逆归一化，返回输入数据的分布参数。因此，我们期待模型输出包含基于输入数据“自然”分布的预测数据。
显然，在逆归一化步骤中，模型参数不会更新。因此，在类结构中，我们以“空存根”覆盖更新模型参数的方法。无论如何，我们将不得不实现前馈验算算法，和误差梯度分布。但首事先行。
在这个类中，我们没有声明任何其它内部对象。因此，类构造函数和析构函数保持为空。不过，我们在模型中创建一个变量来存储归一化层标识符：iBatchNormLayer。于此，我们还创建了一个公开方法来获取该变量的值：GetNormLayer(void)。
我们新类的对象在 CNeuronRevINDenormOCL::Init 方法中初始化。在参数中，为了成功初始化内部对象和变量，该方法接收所需的所有信息。此处应提到的是，与之前研究的类似神经层方法存在非常显着的差异。在方法的参数中，除了常量之外，我们还将传递一个指向 CNeuronBatchNormOCL 批量归一化层对象的指针。
bool CNeuronRevINDenormOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, int NormLayer, CNeuronBatchNormOCL *normLayer) { if(NormLayer > 0) { if(!normLayer) return false; if(normLayer.Type() != defNeuronBatchNormOCL) return false; if(BatchOptions == normLayer.BatchOptions) BatchOptions = NULL; if(!CNeuronBatchNormOCL::Init(numOutputs, myIndex, open_cl, numNeurons, normLayer.iBatchSize, normLayer.Optimization())) return false; if(!!BatchOptions) delete BatchOptions; BatchOptions = normLayer.BatchOptions; }
另一个根本区别在于方法的主体。此处，我们根据接收到的批量归一化层标识符创建分支算法。如果它大于 0，那么我们检查接收到的指向批量归一化层的指针。我们还检查所接收对象的类型。之后，我们调用父类的相同方法。只有在成功通过所有指定的控制点后，我们才会替换优化参数缓冲区。
请注意，我们不会复制数据。取而代之，我们完全更改了指向缓冲区对象的指针。因此，在模型训练过程中，我们将始终依据相关的归一化参数操作。
该算法的第二个分支设计用于在加载以前保存的模型的过程中，初始化空的类对象。此处我们仅调用参数最少的父类相同方法
else if(!CNeuronBatchNormOCL::Init(numOutputs, myIndex, open_cl, numNeurons, 0, ADAM)) return false;
接下来，无论选择哪种路径，我们都会保存获取的批量归一化层标识符，并结束该方法。
iBatchNormLayer = NormLayer; //--- return true; }
2.2组织前馈验算
我们开始前馈验算算法的实现，先在 OpenCL 程序端创建 RevInFeedForward 内核。类似于批量归一化层算法的实现，我们将在一维任务空间中启动这个内核。
在内核参数中，我们将传递指向 3 个数据缓冲区的指针：源数据、归一化参数、和结果。我们还将传递 2 个常量：带有归一化批量参数的缓冲区大小、和参数优化类型。
__kernel void RevInFeedForward(__global float *inputs, __global float *options, __global float *output, int options_size, int optimization) { int n = get_global_id(0);
我提醒您，归一化参数缓冲区的大小取决于所选的参数优化算法。该缓冲区具有以下结构。
在内核主体中，我们识别任务空间中的线程。我们还判定所分析数据在缓冲区的偏移量。在源数据和结果缓冲区中，偏移量等于线程标识符。优化参数缓冲区的偏移量是根据给定的缓冲区结构，和指定的参数优化方法判定的。
int shift = (n * optimization == 0 ? 7 : 9) % options_size;
此外，于此我们必须考虑到，所分析环境状态的数量可能与我们预测的深度不同。在这种情况下，我们应该保持环境和预测环境状态的结构。换言之，在预测后续状态时，要完全保留一个环境状态描述的分析参数数量和顺序。因此，为了判定归一化参数缓冲区中的偏移量，我们将基于所分析线程，和缓冲区结构，用计算出的偏移量除以归一参数缓冲区大小之后取余数。
下一步是将全局缓冲区中的数据提取到局部变量之中。
float mean = options[shift]; float variance = options[shift + 1]; float k = options[shift + 3];
计算预测参数的逆归一化数值。
float res = 0; if(k != 0) res = sqrt(variance) * (inputs[n] - options[shift + 4]) / k + mean; if(isnan(res)) res = 0;
操作的结果将写入结果缓冲区的相应元素。
output[n] = res; }
在 OpenCL 程序端实现数据逆归一化算法之后，我们需要从主程序实现调用所创建内核。为此，我们需要覆盖 CNeuronRevINDenormOCL::feedForward 方法。
bool CNeuronRevINDenormOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!OpenCL || !NeuronOCL) return false; //--- PrevLayer = NeuronOCL; //--- if(!BatchOptions) iBatchSize = 0; if(iBatchSize <= 1) { activation = (ENUM_ACTIVATION)NeuronOCL.Activation(); return true; }
如同父类的相同方法，该方法将在参数中接收指向前一层对象的指针，其中包含输入数据。
在方法的主体中，我们检查接收到的指针，并将其保存在相应的变量之中。
然后我们检查归一化批量大小。如果它不超过 “1”，则我们认为这是逆归一化，并原封不动地传递来自上一层的数据。当然，我们不会复制所有数据。我们只复制激活函数标识符。当访问结果或梯度缓冲区时，我们返回指向上一层缓冲区的指针。该功能已在父类中实现。
接下来，我们实现将内核直接放入执行队列的算法。此处我们首先定义任务空间。
uint global_work_offset[1] = {0}; uint global_work_size[1] = {Neurons()};
之后，我们将必要的参数传递给内核。
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_RevInFeedForward, def_k_revffinputs, NeuronOCL.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_RevInFeedForward, def_k_revffoptions, BatchOptions.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_RevInFeedForward, def_k_revffoutput, Output.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgument(def_k_RevInFeedForward, def_k_revffoptions_size, (int)BatchOptions.Total())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgument(def_k_RevInFeedForward, def_k_revffoptimization, (int)optimization)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
将内核发送到执行队列。
if(!OpenCL.Execute(def_k_RevInFeedForward, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
不要忘记在每个步骤控制操作。
2.3误差梯度传播算法
实现前馈验算后，我们需要实现反向传播算法。如上所述，该层不包含任何可学习的参数。它采用在归一化阶段的训练参数。因此，所有参数更新方法都替换为“存根”。
不过，该层参与反向传播算法，误差梯度经由它传播到前一神经层。如前，我们首先在 OpenCL 程序端创建 RevInHiddenGradient 内核。这一次，内核参数的数量增加了。我们传递 4 个数据缓冲区指针：前一层的结果和误差梯度的缓冲区、优化参数、和当前层结果层的误差梯度。我们还传递 3 个常量：归一化参数缓冲区的大小、参数优化类型、和上一层的激活函数。
__kernel void RevInHiddenGraddient(__global float *inputs, __global float *inputs_gr, __global float *options, __global float *output_gr, int options_size, int optimization, int activation) { int n = get_global_id(0); int shift = (n * optimization == 0 ? 7 : 9) % options_size;
在内核主体中，我们首先识别线程，并判定数据缓冲区中的偏移。判定缓冲区偏移的算法在上面与前馈内核相关的部分中进行了讲述。
接下来，我们将全局数据缓冲区中的数据加载到局部变量之中。
float variance = options[shift + 1]; float inp = inputs[n]; float k = options[shift + 3];
然后我们通过逆归一化函数的导数来调整误差梯度。这里需要注意的是，在逆归一化阶段，所有归一化参数都是常数，而函数的导数则明显简化。
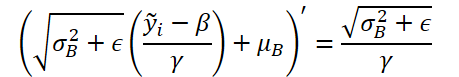
我们在代码中实现所述函数。
float res = 0; if(k != 0) res = sqrt(variance) * output_gr[n] / k; if(isnan(res)) res = 0;
之后，我们由前一个神经层的激活函数的导数来调整误差梯度。
switch(activation) { case 0: res = clamp(res + inp, -1.0f, 1.0f) - inp; res = res * (1 - pow(inp == 1 || inp == -1 ? 0.99999999f : inp, 2)); break; case 1: res= clamp(res + inp, 0.0f, 1.0f) - inp; res = res * (inp == 0 || inp == 1 ? 0.00000001f : (inp * (1 - inp))); break; case 2: if(inp < 0) res *= 0.01f; break; default: break; }
将操作结果保存在前一个神经层的误差梯度缓冲区的相应元素之中。
//---
inputs_gr[n] = res;
}
下一步是在主程序端实现调用内核。该功能在 CNeuronRevINDenormOCL::calcInputGradients 方法中实现。将内核放入执行队列的算法与上面讲述的前馈方法的算法相同。因此，我们现在不再赘述。
还有，我们不会研究该类的辅助方法。它们的算法非常简单，因此您可以据附件自行研究。此外，附件还包含新类和以前创建方法的所有完整代码。如此这般，您可以研究本文中用到的所有程序。
2.4在更高级别的类中现场编辑
说几句有关更高级别类中进行特定编辑的方法，其是由我们的新 CNeuronRevINDenormOCL 类的特性导致的。这涉及该类对象的初始化和加载。
在描述初始化 CNeuronRevINDenormOCL 类对象的方法时，我们提到了将指针传递给数据归一化层对象的特殊性。注意，在描述模型架构时，我们没有指向该对象的指针，原因很简单 — 该对象尚未创建。我们只能指示层的序号，而这是我们从所描述模型架构中得知的。
不过，我们清晰地知道归一化层位于逆归一化层之前。甚至，它们之间可以有任意数量的神经层。这意味着，在创建逆归一化层对象时，必须已在模型中创建归一化层。我们可以访问它，但只能在模型内部访问。因为对单个神经层的访问对外部程序是封闭的。
因此，在 CNet::Create 方法中，我们创建一个单独的模块来初始化 CNeuronRevINDenormOCL 逆归一化层对象。
case defNeuronRevInDenormOCL: if(desc.layers>=layers.Total()) { delete temp; return false; }
于此，我们首先检查在模型中是否已创建配有指定标识符的层。
然后我们检查指定层的类型。它应该是一个批量归一化层。
if(((CLayer *)layers.At(desc.layers)).At(0).Type()!=defNeuronBatchNormOCL) { delete temp; return false; }
仅在成功通过特定控制之后，我们才会创建一个新对象。
revin = new CNeuronRevINDenormOCL(); if(!revin) { delete temp; return false; }
初始化它。
if(!revin.Init(outputs, 0, opencl, desc.count, desc.layers, ((CLayer *)layers.At(desc.layers)).At(0))) { delete temp; delete revin; return false; }
将其添加到对象数组之中。
if(!temp.Add(revin)) { delete temp; delete revin; return false; } break;
此外，在加载之前已训练模型时也存在细微差别。如您所知，在我们的新类初始化方法中，我们根据归一化层的标识符创建了一个分支算法。这样做是为了能够加载预先训练的模型。要点是，在加载对象之前，我们需要创建一个“空白”的它。该功能在 CLayer::CreateElement 方法中执行。难处在于，在加载数据之前，我们尚不知道归一化层的标识符。这就是为什么我们指定 “-1” 作为标识符，指定 “NULL” 作为对象指针。
case defNeuronRevInDenormOCL: if(CheckPointer(OpenCL) == POINTER_INVALID) return false; revin = new CNeuronRevINDenormOCL(); if(CheckPointer(revin) == POINTER_INVALID) result = false; if(revin.Init(iOutputs, index, OpenCL, 1, -1, NULL)) { m_data[index] = revin; return true; } delete revin; break;
然后，在加载期间，所有数据都被加载到我们类的内部对象和变量之中。但此处也存在细微差别。在数据加载期间，我们会在预训练模型后保存归一化参数。但我们不需要这个。为了进一步训练和操作模型，我们需要在归一化层和逆归一化层之间同步参数。否则，输入数据的分布和预测之间就会出现落差。因此，我们转到 CNet::Load 方法，在加载下一个神经层后，我们检查其类型。
bool CNet::Load(const int file_handle) { ........ ........ //--- read array length num = FileReadInteger(file_handle, INT_VALUE); //--- read array if(num != 0) { for(i = 0; i < num; i++) { //--- create new element CLayer *Layer = new CLayer(0, file_handle, opencl); if(!Layer.Load(file_handle)) break; if(Layer.At(0).Type() == defNeuronRevInDenormOCL) { CNeuronRevINDenormOCL *revin = Layer.At(0); int l = revin.GetNormLayer(); if(!layers.At(l)) { delete Layer; break; }
如果检测到 CNeuronRevINDenormOCL 逆归一化层，我们请求一个指向归一化层的指针，并检查是否加载了这样的层。
我们还检查该层的类型。
CNeuronBaseOCL *neuron = ((CLayer *)layers.At(l)).At(0); if(neuron.Type() != defNeuronBatchNormOCL) { delete Layer; break; }
成功通过指定的控制之后，我们传递指向相应归一化层的指针来初始化层对象。
if(!revin.Init(revin.getConnections(), 0, opencl, revin.Neurons(), l, neuron)) { delete Layer; break; } } if(!layers.Add(Layer)) break; } } FileClose(file_handle); //--- result return (layers.Total() == num); }
然后我们遵循之前创建的算法。
您可以在附件中找到所有类、及其方法的完整代码，以及准备本文时用到的所有程序。
2.5进行训练的模型架构
我们已经利用 MQL5 实现了由 RevIN 方法作者提议的方式。现在是时候将它们包含在我们的模型架构之中了。如早前所讨论的，我们将在编码器模型中使用逆归一化，从而实现训练它、并预测环境后续状态的能力。我们将在 NForecast 常量中定义环境的预测状态数量（在我们的例子中，后续蜡烛）。
#define NForecast 6 //Number of forecast
由于我们计划分开训练扮演者和评论者的编码器，故我们还会将编码器架构的描述移动到单独的方法 CreateEncoderDescriptions 之中。在该方法的参数中，我们仅传递一个指向动态数组的指针，以便保存所创建模型架构。此处应注意的是，我们实现的 CNeuronRevINDenormOCL 类不允许将解码器作为单独的模型分配。
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
在方法的主体中，我们检查收到的指针，并在必要时创建动态数组对象的新实例。
如前，我们向模型投喂描述环境状态的“原始”输入数据。
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
接收到的数据在批量归一化层中进行初级处理。我们需要保存层的序号。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
归一化输入数据之后，我们创建数据嵌入，并将其添加到内部堆栈当中。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; { int temp[] = {4, 1, 1, 1, 2}; ArrayCopy(descr.windows, temp); } prev_count = descr.count = GPTBars; int prev_wout = descr.window_out = EmbeddingSize / 2; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = prev_count * 5; descr.step = descr.window = prev_wout; prev_wout = descr.window_out = EmbeddingSize; if(!encoder.Add(descr)) { delete descr; return false; }
然后我们添加数据的位置编码。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPEOCL; descr.count = prev_count; descr.window = prev_wout * 5; if(!encoder.Add(descr)) { delete descr; return false; }
我们将准备好的数据馈送到 5 层 CNeuronConformer 模块之中。
//--- layer 5-10 for(int i = 0; i < 5; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConformerOCL; descr.count = prev_count; descr.window = prev_wout; descr.step = 4; descr.window_out = EmbeddingSize; descr.layers = 5; if(!encoder.Add(descr)) { delete descr; return false; } }
为了测试该方法，我们使用具有相应数量元素的全连接层作为解码器。不过，为了提高预测品质，建议使用架构更复杂的解码器。
//--- layer 11 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NForecast*BarDescr; descr.activation = TANH; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
我们正在搭配归一化数据操作，并假设其偏差接近 1，其均值接近 0。因此，我们使用双曲正切（tanh）作为解码器输出的激活函数。如您所知，其值范围是从 “-1” 到 “1”。
最后，我们对预测值进行逆归一化。
//--- layer 12 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; prev_count = descr.count = prev_count; descr.activation = None; descr.optimization = ADAM; descr.layers=1; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
为了完全依据描述模型架构工作，我们来研究扮演者和评论者的构造。CreateDescriptions 方法中描述了指定模型的架构。它与上一篇文章中讲述的非常相似，但有细微差别。
在参数中，该方法接收指向 2 个动态数组的指针。
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; }
在方法的主体中，我们检查收到的指针，并在必要时创建新的对象实例。
我们向扮演者提供一个描述账户状态和持仓的张量。
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = AccountDescr; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
生成该表述的嵌入。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
然后来到交叉关注度模块，它根据环境的预测状态分析账户的当前状态。
//--- layer 2-4 for(int i = 0; i < 3; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCrossAttenOCL; { int temp[] = {1, NForecast}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, BarDescr}; ArrayCopy(descr.windows, temp); } descr.window_out = 16; descr.step = 4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } }
在扮演者模型的末尾，有一个含有随机政策的决策制定模块。
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
评论者模型的构造方式与此类似。仅替代了描述帐户状态，评论者依据环境预测状态的上下文分析扮演者的动作。
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
//--- layer 2-4 for(int i = 0; i < 3; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCrossAttenOCL; { int temp[] = {1, NForecast}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, BarDescr}; ArrayCopy(descr.windows, temp); } descr.window_out = 16; descr.step = 4; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } }
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
在评论者的输出中，我们得到了该个体动行的清晰、非随机的评估。
2.6模型训练程序
在描述了已训练模型的架构之后，我们转到创建程序来训练它们。为了训练编码器，我们将创建一个智能交易系统：“...\Experts\RevIN\StudyEncoder.mq5”。EA 架构遵循前几篇文章中的架构。如此这般，我们已经在本系列内多次讨论过它。因此，我们仅关注模型训练方法 Train。
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9); //--- vector<float> result, target; bool Stop = false; //--- uint ticks = GetTickCount();
在方法的主体中，如常，我们根据它们的盈利能力生成一个选择轨迹的概率向量。对于未来环境状态预测，所有验算都是相同的。因为编码器不分析账户状态和持仓。不过，如果存在基于不同历史间隔的验算的经验回放缓冲区，我们不会删除该功能。
然后我们准备局部变量，并组织一个模型训练循环系统。
for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++) { int tr = SampleTrajectory(probability); int batch = GPTBars + 48; int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast - batch)); if(state <= 0) { iter--; continue; } Encoder.Clear(); int end = MathMin(state + batch, Buffer[tr].Total - NForecast);
在外部循环的主体中，我们从来自经验回放缓冲区中的轨迹进行采样，及其学习开始状态。然后，我们判定训练批量的最终状态，并清除内部模型堆栈。之后，我们针对选定的历史数据段运行嵌套学习循环。
for(int i = state; i < end && !IsStopped() && !Stop; i++) { bState.AssignArray(Buffer[tr].States[i].state); //--- State Encoder if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
此处，我们首先从训练集中加载所需的状态。我们将其移动到数据缓冲区。然后我们通过调用模型的相应方法来执行编码器的前馈验算。
在下一步中，我们准备目标数据。为此，我们组织了另一个嵌套循环，从训练样本中获取所需数量的后续状态，并将它们添加到数据缓冲区之中。
//--- Collect target data bState.Clear(); for(int fst = 1; fst <= NForecast; fst++) { if(!bState.AddArray(Buffer[tr].States[i + fst].state)) break; }
收集目标值后，我们可以运行编码器反向传播验算，从而把预测值和目标值之间的误差最小化。
if(!Encoder.backProp(GetPointer(bState), (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
然后，我们将训练进度通知用户，并转到下一次训练迭代。
if(GetTickCount() - ticks > 500) { double percent = (double(i - state) / ((end - state)) + iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, Encoder.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
所有训练迭代成功完成之后，我们清除注释字段。
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError()); ExpertRemove(); //--- }
我们将有关已达成训练结果的信息输出到日志中，并初始化 EA 终止。
训练模型来预测环境的未来状态非常实用。不过，我们的目标是训练扮演者政策。在下一步中，我们创建扮演者和评论者训练 EA “...\Experts\RevIN\Study.mq5”。智能系统是基于相同的架构构造的，故此我们只涉及特定的更改。
首先，在 EA 初始化期间，如果没有预先训练的编码器，我们会生成程序初始化不正确的错误。
int OnInit() { //--- ........ ........ //--- load models float temp; if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true)) { PrintFormat("Error of load Encoder: %d", GetLastError()); return INIT_FAILED; } ........ ........ //--- return(INIT_SUCCEEDED); }
其次，该模型中的编码器未经过训练，因此不应保存。
void OnDeinit(const int reason) { //--- if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE)) { Actor.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true); Critic.Save(FileName + "Crt.nnw", 0, 0, 0, TimeCurrent(), true); } delete Result; delete OpenCL; }
此外，在使用编码器作为扮演者和评论者的输入数据源时，还有一件事。在本文的开头，我们讨论过使用归一化数据来训练和操作模型的重要性。编码器输出处的逆归一化层，另一方面，把我们的预测返回到原始数据分布，令它们不可比。
不过，我们很久以前就实现了访问模型隐藏层的功能，以便提取数据。故此，我们将使用此功能从编码器的倒数第二层获取归一化预测数据。我们将用该数据作为扮演者和评论者的初始数据。我们在 LatentLayer 常量中指定指向所需层的指针。
#define LatentLayer 11
调用评论者的前馈如下所示：
if(!Critic.feedForward((CBufferFloat*)GetPointer(bActions), 1, false, GetPointer(Encoder),LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
或
if(!Critic.feedForward((CNet *)GetPointer(Actor), -1, (CNet*)GetPointer(Encoder),LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
相应地，我们编写调用扮演者前馈
if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, GetPointer(Encoder),LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
在调用我们模型的反向传播方法时，不要忘记指定层标识符。
if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder),LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
if(!Actor.backProp(GetPointer(bActions), GetPointer(Encoder),LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Critic.TrainMode(false); if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder),LatentLayer) || !Actor.backPropGradient((CNet *)GetPointer(Encoder), LatentLayer, -1, true)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
我对环境交互 EA 进行了类似的有针对性的更改。您可自行据附件中的代码检查它们。附件包含所有程序的完整代码。
3. 测试
所有必要的程序创建之后，我们终于可以训练和测试模型了。这将令我们能够评估所提议解决方案的有效性。
我们采用 EURUSD、H1 的历史数据来训练和测试模型。
时间不会停滞不前。随着时间的推移，我们的历史数据库不断增长。故此，在准备本文时，我决定扩展训练数据集的历史间隔，从而包括 2023 全年。2024 年 1 月的数据将用来测试经过训练的模型。
为了创建主要训练数据集，我用到了 Real-ORL 框架。您可在此链接中找到其详细说明。我从 20 个真实信号中下载了交易数据。然后，我在完全优化模式下运行 EA “...\Experts\RevIN\ResearchRealORL.mq5”。
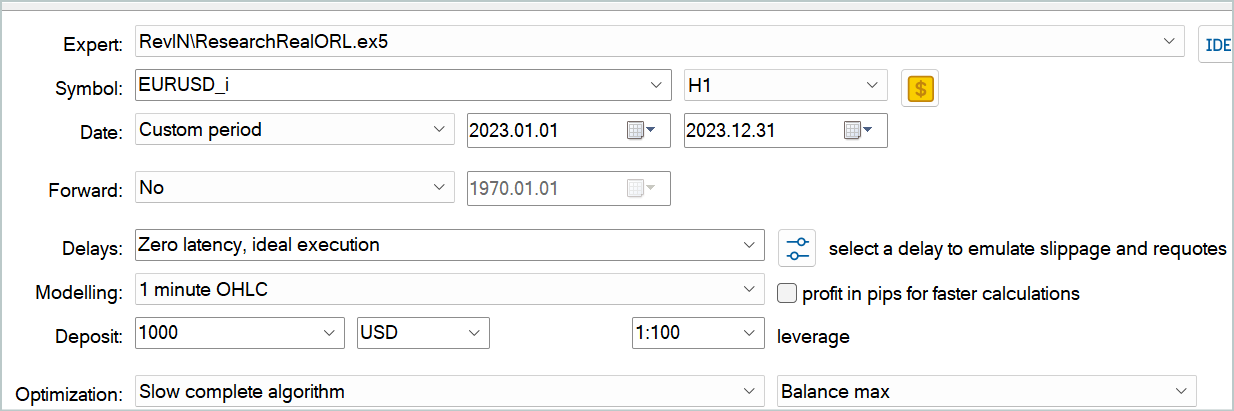
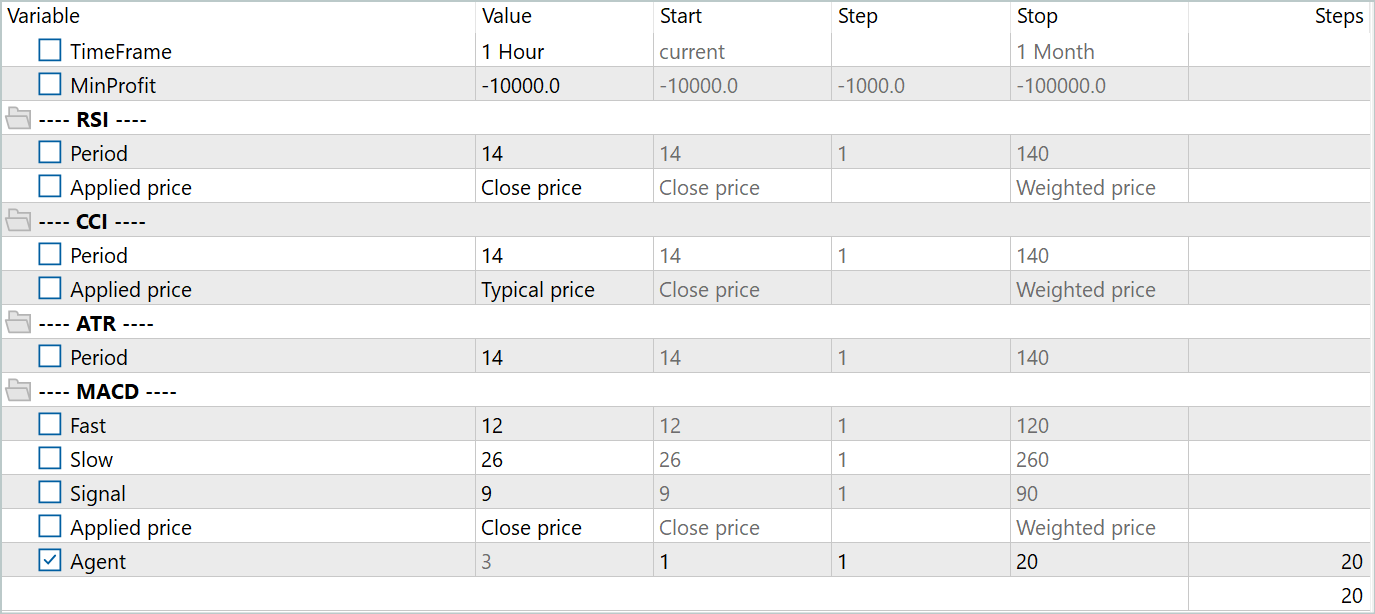
结果就是，我得到了 20 条轨迹。它们并非全都是有利可图的。
在该步骤中，我们首先开始训练编码器。编码器训练完成后，我们将执行扮演者和评论者的初步训练。这主要是因为 20 条轨迹太少，无法获得扮演者的最优政策。
在下一步中，我们将扩展我们的训练数据集。为此，在慢速完全优化模式下，我们运行 EA “...\Experts\RevIN\Research.mq5”。它在训练期间依据真实历史数据测试当前的扮演者政策，并将验算添加到我们的训练数据集之中。
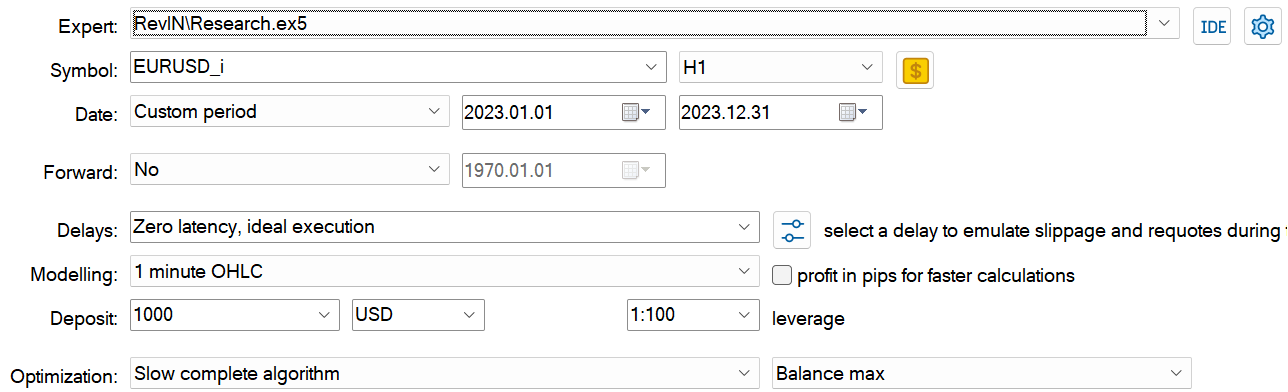
在该阶段，您不应该期望任何出色的结果。负面结果也是结果。这也为进一步的模型训练实验提供了很好的经验。进而，此类迭代有助于了解扮演者当前政策的行动区域中的环境。
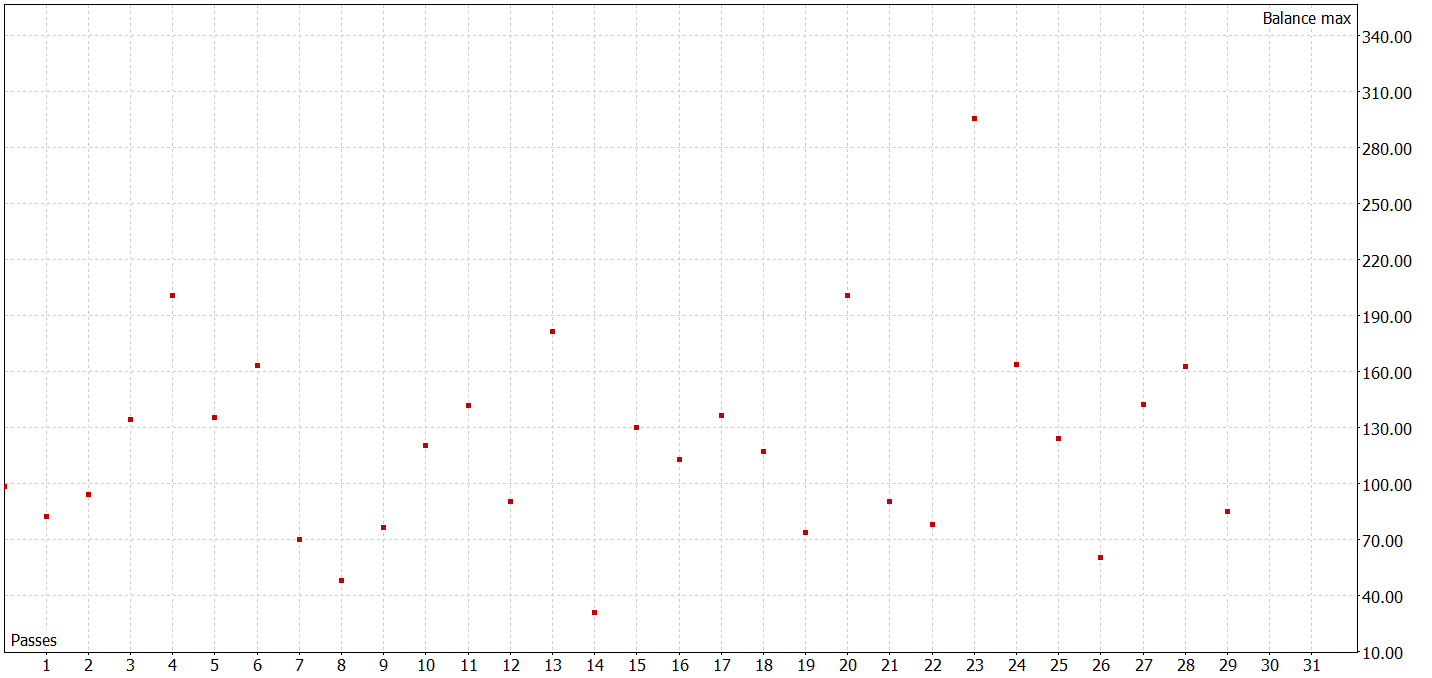
经过若干次扮演者政策训练迭代，并将额外数据收集到训练数据集当中，我设法训练了一个能够在训练和测试数据集上都产生利润的模型。
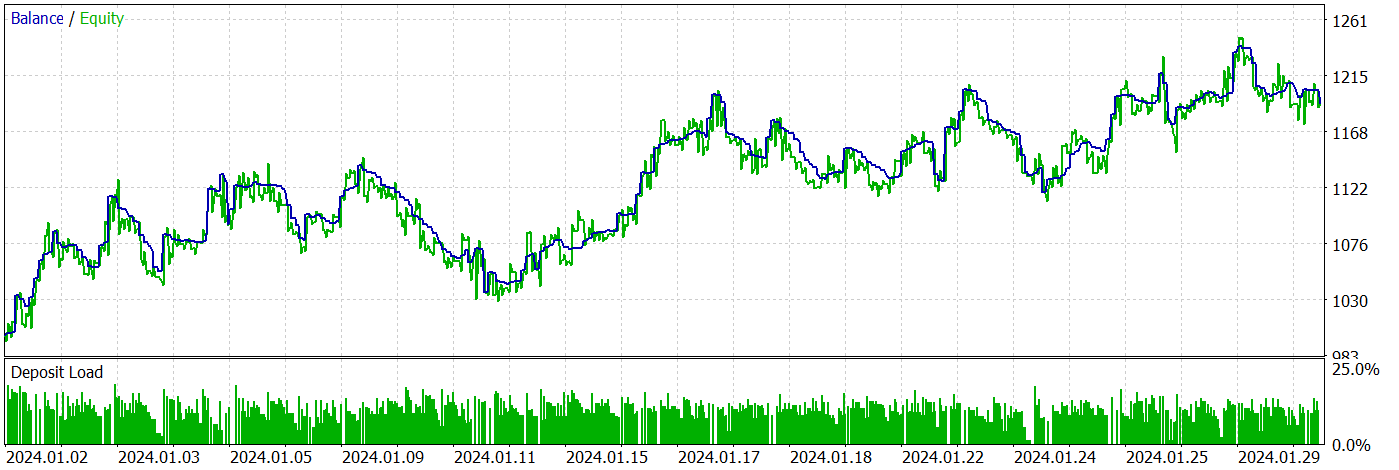
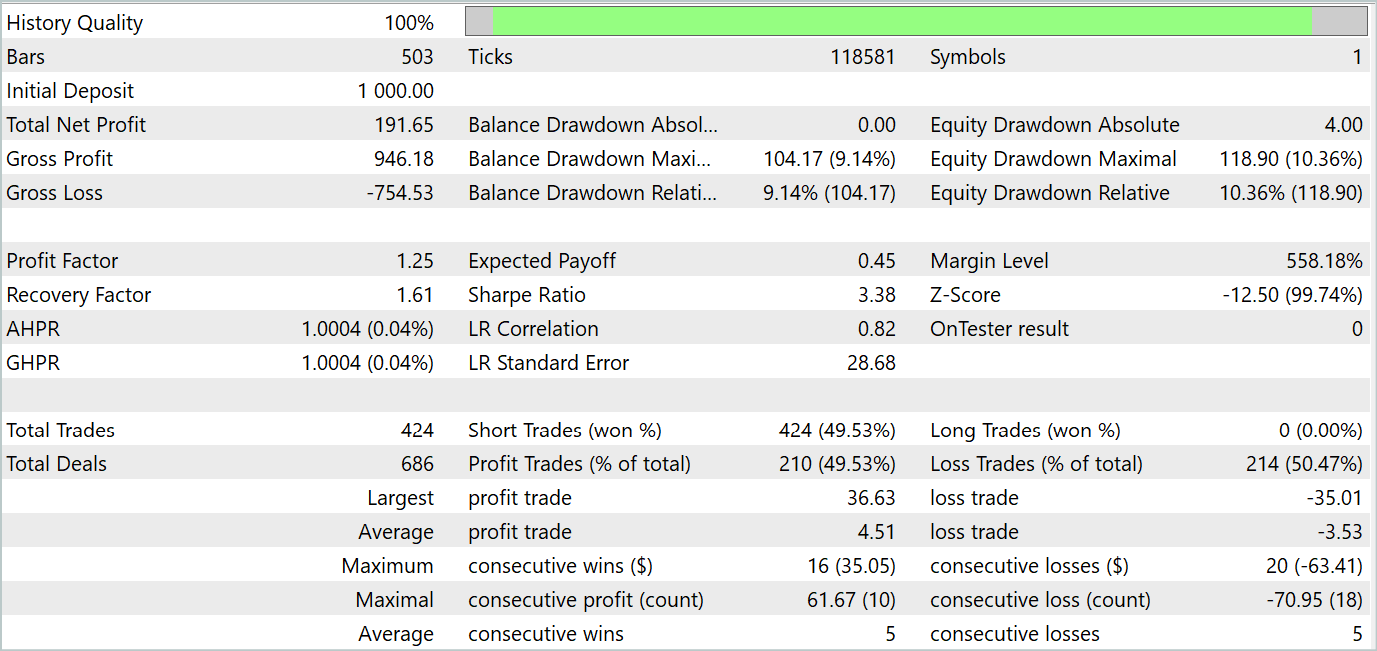
在测试期间，EA 进行了 424 笔交易，其中 210 笔以盈利结束。这是 49.53%。然而，由于最大和平均盈利的交易超过无盈利交易，因此测试区间最终获利。最大余额和净值回撤显示出接近的结果（分别为 9.14% 和 10.36%）。测试期间的盈利因子为 1.25。锋锐比率达到 3.38。
结束语
在本文中，我们领略了 RevIN 方法，它代表了归一化和逆归一化技术发展的重要一步。它与时间序列预测背景下的深度学习模型尤其相关。它允许我们保存和检索有关时间序列的统计信息，这对于准确预测至关重要。RevIN 展现出数据动态随时间变化的稳健性。这令其成为与时间序列中分布偏移问题打交道的有效工具。
RevIN 的重要优势之一是其灵活性，和对各种深度学习模型的适用性。它可以轻松实现到各种神经网络架构中，甚至可以应用于多层，提供稳定的预测品质。
在本文的实践部分，我们利用 MQL5 实现了所提议方法。我们依据真实历史数据训练模型，并采用未包含在训练数据集中的新数据对其进行测试。
测试结果显示，已训练模型具有普适训练数据的能力，并可在历史训练集上、以及超出部分上产生盈利。
不过，应当记住，本文中讲述的所有程序都具有演示性质，仅用于测试所提议的方式。
参考
文中所用程序
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | Research.mq5 | EA | 样本收集 EA |
| 2 | ResearchRealORL.mq5 | EA | 运用 Real-ORL 方法收集示例的 EA |
| 3 | Study.mq5 | EA | 模型训练 EA |
| 4 | StudyEncoder.mq5 | EA | 编码训练 EA |
| 5 | Test.mq5 | EA | 模型测试 EA |
| 6 | Trajectory.mqh | 类库 | 系统状态定义结构 |
| 7 | NeuroNet.mqh | 类库 | 创建神经网络的类库 |
| 8 | NeuroNet.cl | 代码库 | OpenCL 程序代码库 |
本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/14673
您应当知道的 MQL5 向导技术（第 15 部分）：协同牛顿多项式的支持向量机
神经网络变得简单（第 83 部分）：“构象”时空连续关注度转换器算法
