MQL5 中的范畴论 (第 14 部分)：线性序函子

概述

塞缪尔·艾伦伯格（Samuel Eilenberg）和桑德斯·麦克莱恩（Saunders Mac Lane）于 1950 年代引入的范畴论可看作一种研究系统的手段，强调每个阶段的转变，而非阶段本身。它已被用于广阔衔接的应用领域，包括使用 Haskell 等语言进行函数式编程；通过研究自然语言的结构和组成性来学习语言学；通过提供理解不同拓扑结构和不变性的统一方法，到代数拓扑学；不一而足。

在系列中，范畴理论到目前为止已经局部化了，从某种意义上说，它关注的是子范畴级别的信息和结构；在我们的案例中，主要是集合（对象）。我们已研究过它们的关系和属性，都在一个范畴内。

本文和少量类似文章的目的，继续迈进，缩小一个范畴，并开始研究不同范畴之间的关系。形式上，这些被称为函子（Functors）。由此，我们将研究各种范畴及它们的可能关系。在交易者的数据集内，有若干值得研究的范畴候选者。然而，为了强调范畴论的超然品质，我们将跳出框框，在本文中，我们将研究加利福尼亚海岸收集的海潮数据与纳斯达克指数波动性的桥连关系。海潮当中有什么能预示该指数的波动性吗？我们希望在文章结束时能在某种程度上回答这个问题。

本文和随后的一些类似文章本身不会引入新概念，而是将回顾已经涵盖的内容，并希望以不同的方式应用它，这也许意味着更广阔尺度。

海潮和纳斯达克指数

海潮数据由美国国家海洋和大气管理局（NOAA）通过其网站发布并向公众提供，可在此处查看。该数据每天四次记录基准面的海潮高度。全年每天无间断记录每次潮汐时间和高度的全部数据。下面是一个预览：

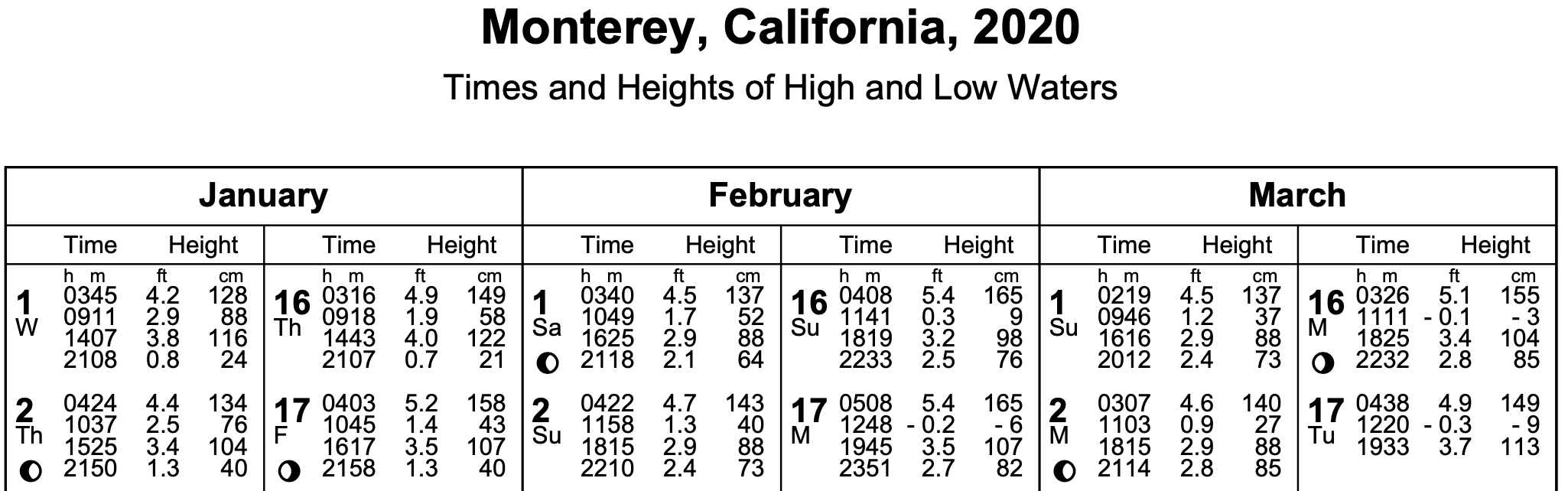
所有海洋被划分为 4 个区域，每个区域内的潮汐值都来自许多观测站。例如，从南美洲智利一直到阿拉斯加的北美和南美西海岸，有 33 个观测站。对于我们的分析，我们将选择 2020 年从加利福尼亚州蒙特雷观测站收集的数据。

纳斯达克是一个成熟的证券交易所，但我们在此主要取其指数，该指数由相当多的科技公司组成，例如 MSFT、AAPL、GOOG 和 AMZN，这些公司总部都位于加利福尼亚州。该指数可以从大多数券商那里交易，如此其价格馈送将告知我们的范畴，因而我们看看这些彻底改变了行业并体现了加州创新精神的公司的市值是否与来自其海岸收集的海潮数据有任何方式的联系。

利用范畴论函子映射数据

到目前为止，我们还未在该系列中明确讨论函子，不过在文章中我们研究了幺半群、幺半群组、图论和秩序；这意味着我们正在与函子打交道，因为这些概念中的每一个都可以被认为是一个范畴，它们的关系通常构成了它们所在文章的基础。因此，例如，幺半群之间的态射是事实上的函子。

形式上，函子是范畴之间的映射，它保留了由对象定义的结构和关系，及其它们在每个范畴内的态射。如果 C 和 D 是范畴，则从 C 到 D 的函子 F

即它由两件事组成：对于 C 中的每个对象 c，D 中都有一个关联的对象 F(c)，对于 C 中的每两个对象 b、c，其态射为 f

存在相关的态射 F(f)

如果我们有态射，在 D 中函子也有保持组合意义的附加公理

和

在 C 中，则 F 在 C 中保留组合物，如此

且 C 中的恒等态射为 D 中的每个映射对象保留，这样如果

则

将不同范畴联系起来的重点源于发现。每个系统若是被归类到一个范畴，默认情况下通常不仅无法转换到另一个范畴，而且还要在更广泛的背景下为每个范畴建立“相对地位”和大概的重要性。该实例就是为什么函子可将拥有自己的加权组合态射的可交易证券的范畴映射到另一种交易策略范畴的原因。对于交易者而言，函子的益处可能取决于主观，但如果函子映射涵盖了时间滞后，那我们就能根据我们的投资组合所用证券构建策略，或者接下来根据我们的当前策略应持有哪些证券。

回顾线性序或总序，除了满足传递性和反身性公理外，还满足反对称性和可比性需求。这通常意味着线性序中的所有数据都应该是数字，或者如果是文本，则应该是离散的，这样二元运算 “<=” 仍然可以应用，而不会产生歧义，或产生未定义的结果。如果我们将一天作为单个数据点，NOAA 网站上呈现的海潮数据就是多维的。每个高度有 4 个日期戳项、4 个高度的浮点值、以及当天的日期戳项。如果我们采用线性序来比较每个数据点的时间戳值，那么海潮数据就变成了一个简单的时间序列，每个点有 2 项数据，日期作为日期戳，潮汐高度作为浮点数据。

将这种线性序表示为一个范畴意味着任何两个连续数据点之间的二元运算变成一个态射，如果我们自每天捕获这些潮汐值以来，按天数将这些数据分组，每个数据点都变成一个对象，其中包含 4 项数据、记录高度的 4 个时间戳、和 4 个高度值。然而，我们确实需要对这些数据进行更多的常规化，因为并非所有观测日都有 4 个数据点。有些仅有 3 个。鉴于我们的范畴都拥有简单的同构关系，因此我们在每个域（天）中的元素数量上保持一致非常重要。

纳斯达克指数的波动率范畴将效仿海潮，因为我们基于时间序列链接价格数据点作为态射。

比较性分析与见解

如果将我们的潮汐范畴映射到纳斯达克指数范畴，我们这样做的时候不得不带有时间滞后，以便从中获得任何预测收益。但首先我们需要构造一个海潮范畴类的实例，其表述如下所示：

protected:

      ...
      
      CCategory _category_ocean,_category_nasdaq;
      
      CDomain<string> _domain_ocean,_domain_nasdaq;
      
      CHomomorphism<string,string> _hmorph_ocean,_hmorph_nasdaq; 

鉴于我们对使用这个函子进行预测很感兴趣，我们的范畴会是动态的，因为它将在每根新柱线上重新定义，但从它到 NASDAQ 范畴的函子将是恒定的。由于我们的滞后时间只有一天，故可从 csv 文件中读取海潮数据，来定义上述与所记录海洋幅度相联的三个态射，如下所示：

void CTrailingCT::SetOcean(int Index)
   {
      ...
      
      if(_handle!=INVALID_HANDLE)
      {
         ...
         
         while(!FileIsLineEnding(_handle))
         {
            ...
            
            if(_date>_data_time)
            {
               _category_ocean.SetDomain(_category_ocean.Domains(),_domain_ocean);
               
               break;
            }
            else if(__DATETIME.day_of_week!=6 && __DATETIME.day_of_week!=0 && datetime(int(_data_time)-int(_date))<=PeriodSeconds(PERIOD_D1))//_date<=_data_time && datetime(int(_data_time)-(1*PeriodSeconds(PERIOD_D1)))<=_date)
            {
               _element_value.Let();_element_value.Cardinality(1);_element_value.Set(0,DoubleToString(_value));
               _domain_ocean.Cardinality(_elements);_domain_ocean.Set(_elements-1,_element_value);
               
               _elements++;
            }
         }
         
         FileClose(_handle);
      }
      else
      {
         printf(__FUNCSIG__+" failed to load file. Err: "+IntegerToString(GetLastError()));
      }
   } 

类似地，我们将通过以下清单构造纳斯达克波动率集合：

void CTrailingCT::SetNasdaq(int Index)
   {
      m_high.Refresh(-1);
      m_low.Refresh(-1);
      
      _value=0.0;
      
      _value=(m_high.GetData(Index+StartIndex()+m_high.MaxIndex(Index,_category_ocean.Homomorphisms()))-m_low.GetData(Index+StartIndex()+m_low.MinIndex(Index,_category_ocean.Homomorphisms())))/m_symbol.Point();
      
      _element_value.Let();_element_value.Cardinality(1);_element_value.Set(0,DoubleToString(_value));
      _domain_nasdaq.Cardinality(1);_domain_nasdaq.Set(0,_element_value);
      
      _category_nasdaq.SetDomain(_category_nasdaq.Domains(),_domain_nasdaq);
   } 

其态射也以一种并无太大区别的样式拼装。现在，已在定义中注明的函子不仅映射了两个范畴中的对象，而且还映射了态射。这有几分一个检查另一个的意味。如果我们从函子的对象映射部分开始，即海潮数据到纳斯达克，它的初始化方式如下：

double CTrailingCT::GetOutput()
   {
      ...
      
      ...
      
      _domain.Init(3+1,3);
      
      for(int r=0;r<4;r++)
      {
         CDomain<string> _d;_d.Let();
         _category_ocean.GetDomain(_category_ocean.Domains()-r-1,_d);
         
         for(int c=0;c<_d.Cardinality();c++)
         {
            CElement<string> _e; _d.Get(c,_e);
            
            string _s; _e.Get(0,_s);
            
            _domain[r][c]=StringToDouble(_s);
         }
      }
      
      _codomain.Init(3);
      
      for(int r=0;r<3;r++)
      {
         CDomain<string> _d;
         _category_nasdaq.GetDomain(_category_nasdaq.Domains()-r-1,_d);
         
         CElement<string> _e; _d.Get(0,_e);
         
         string _s; _e.Get(0,_s);
            
         _codomain[r]=StringToDouble(_s);
      }
      
      _inputs.Init(3);_inputs.Fill(m_consant_morph);
      
      M(_domain,_codomain,_inputs,_output,1);
      
      return(_output);
   } 

同样脉络，我们的态射函子构造将采用以下形式：

double CTrailingCT::GetOutput()
   {
      ...
      
      ...
      
      _domain.Init(3+1,3);
      
      for(int r=0;r<4;r++)
      {
         ...
         
         if(_category_ocean.Domains()-r-1-1>=0){ _category_ocean.GetDomain(_category_ocean.Domains()-r-1-1,_d_old); }
         
         for(int c=0;c<_d_new.Cardinality();c++)
         {
            ...
            
            CElement<string> _e_old; _d_old.Get(c,_e_old);
            
            string _s_old; _e_old.Get(0,_s_old);
            
            _domain[r][c]=StringToDouble(_s_new)-StringToDouble(_s_old);
         }
      }
      
      _codomain.Init(3);
      
      for(int r=0;r<3;r++)
      {
         ...
         
         if(_category_nasdaq.Domains()-r-1-1>=0){ _category_nasdaq.GetDomain(_category_nasdaq.Domains()-r-1-1,_d_old); }
         
         ...
         
         CElement<string> _e_old; _d_old.Get(0,_e_old);
         
         string _s_old; _e_old.Get(0,_s_old);
            
         _codomain[r]=StringToDouble(_s_new)-StringToDouble(_s_old);
      }
      
      _inputs.Init(3);_inputs.Fill(m_consant_morph);
      
      M(_domain,_codomain,_inputs,_output,1);
      
      return(_output);
   } 

这里的大部分工作是令海潮数据可由 MQL5 访问。为此，从公用数据文件夹中的 csv 文件里按制表格式访问数据，它类似于我们在海潮范畴中的元素。数据格式包括一个日期戳字段，用来与我们的交易服务器同步时间，从而选择正确的数值。MQL5 IDE 有其它可以访问这些辅助数据的替代方法，其一就是通过数据库，因为从 IDE 进行原生连接设计是可以的。那么，如果您在本地计算机上有一个数据库，或与一个数据库的云连接，就可以探索这一点。出于我们的目的，因我希望读者能够轻松复制此处发布的测试结果，故此正在使用的 csv 文件位于公用文件夹。

我们的函子映射的两件事交织在多个范畴，这意味着为了避免重复，我们将简单地取一个链接检查或验证另一个。由于一开始我们不知道这些设置中哪一个最适合我们的交易系统，我们将测试两者。

因此，在第一个设置中，我们将让跨对象的函子确认或验证协域（纳斯达克集）中对象之间的态射。这可以用示意图表述如下：

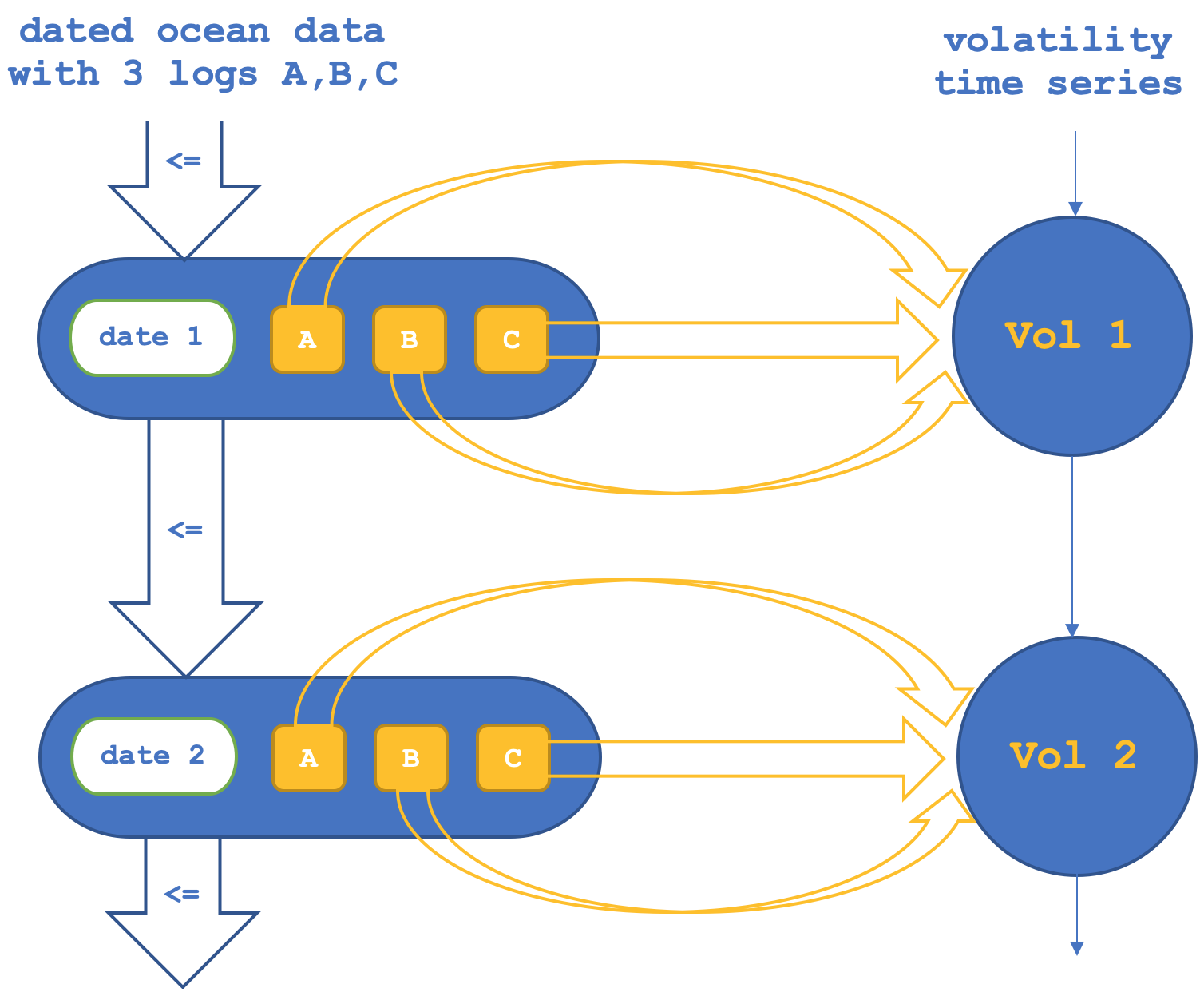
如果我们运行测试，尝试仅基于对象函子预测纳斯达克波动率，我们会得到如下报告（此段代码附件为 “TraillingCT_14_1a”）：

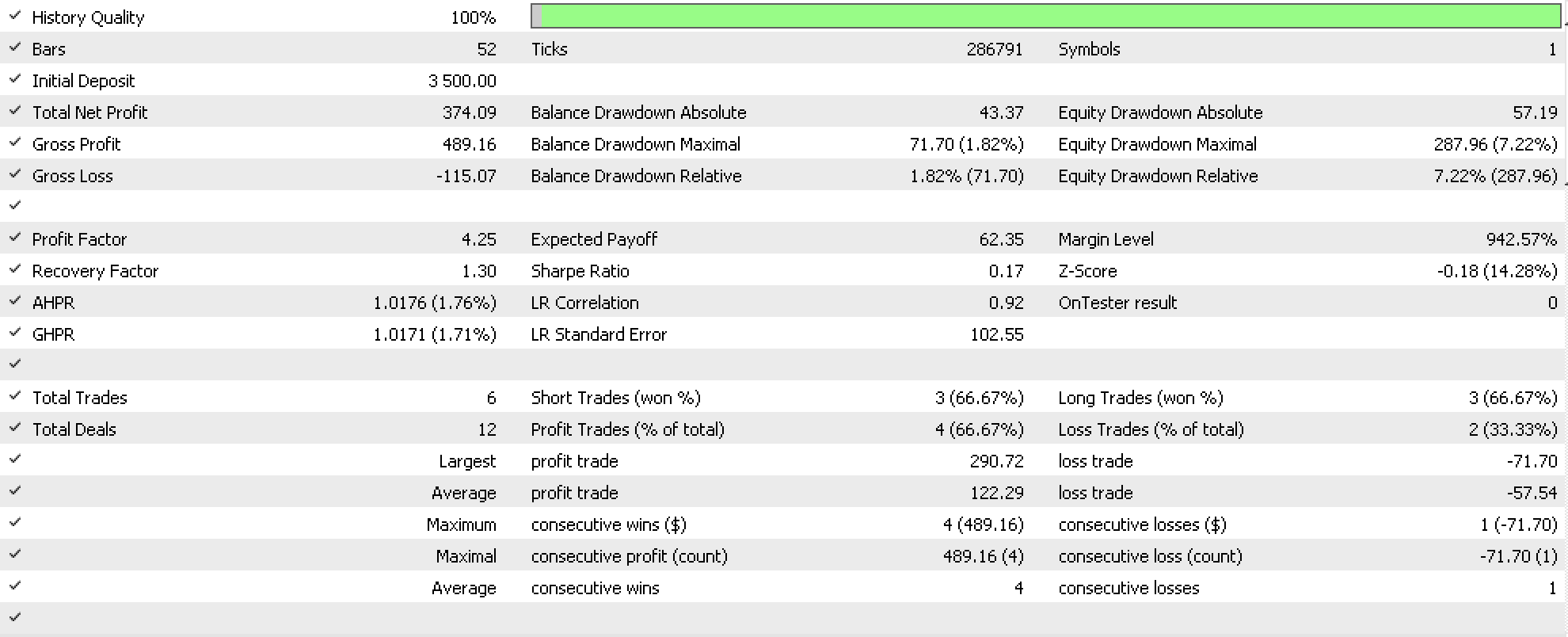
若如前所述，我们也尝试逆反方法，即我们专注于态射中的函子，然后确认对象，这可以表述如下：

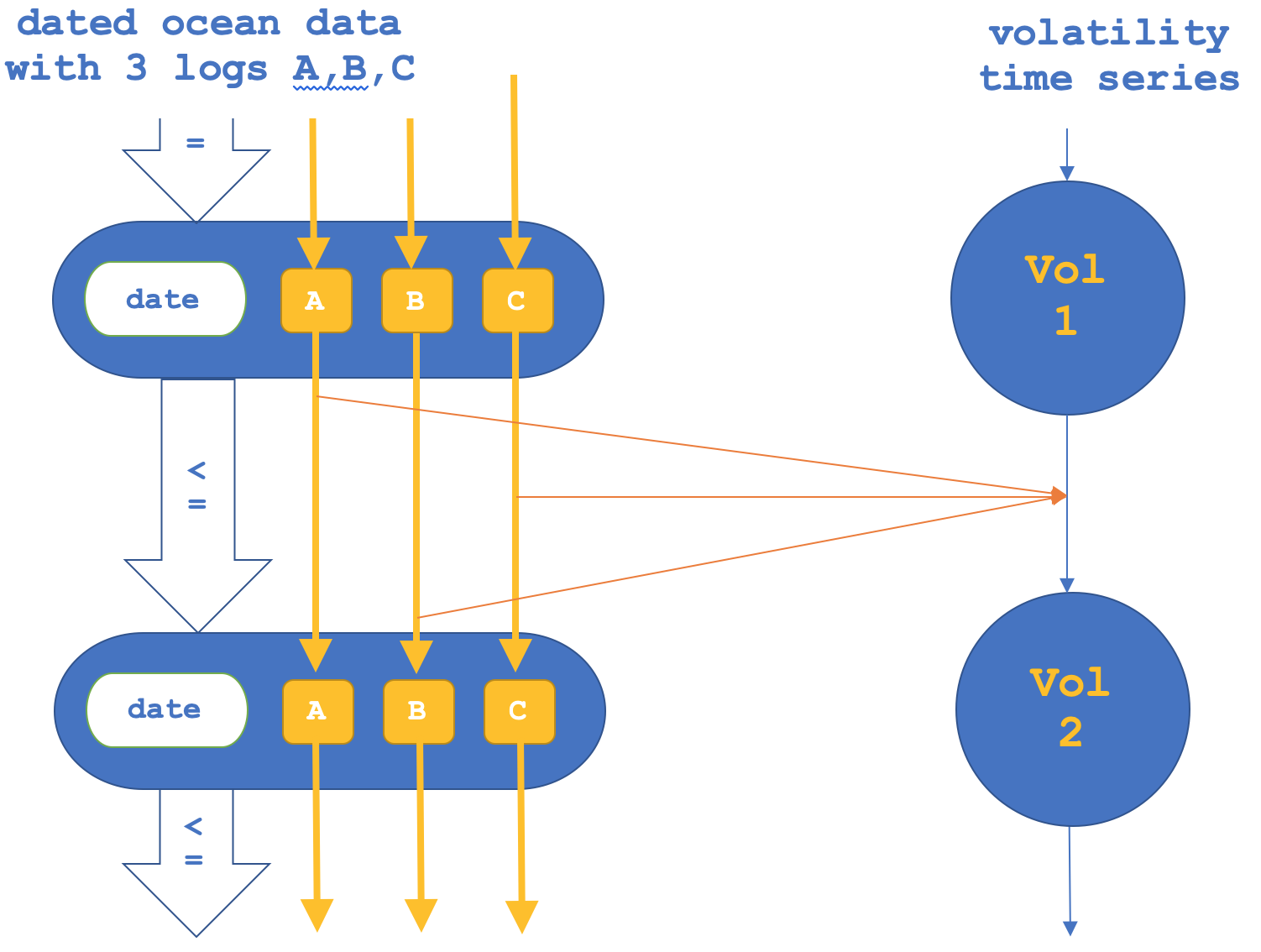
仅针对态射函子的测试报告如下所示：

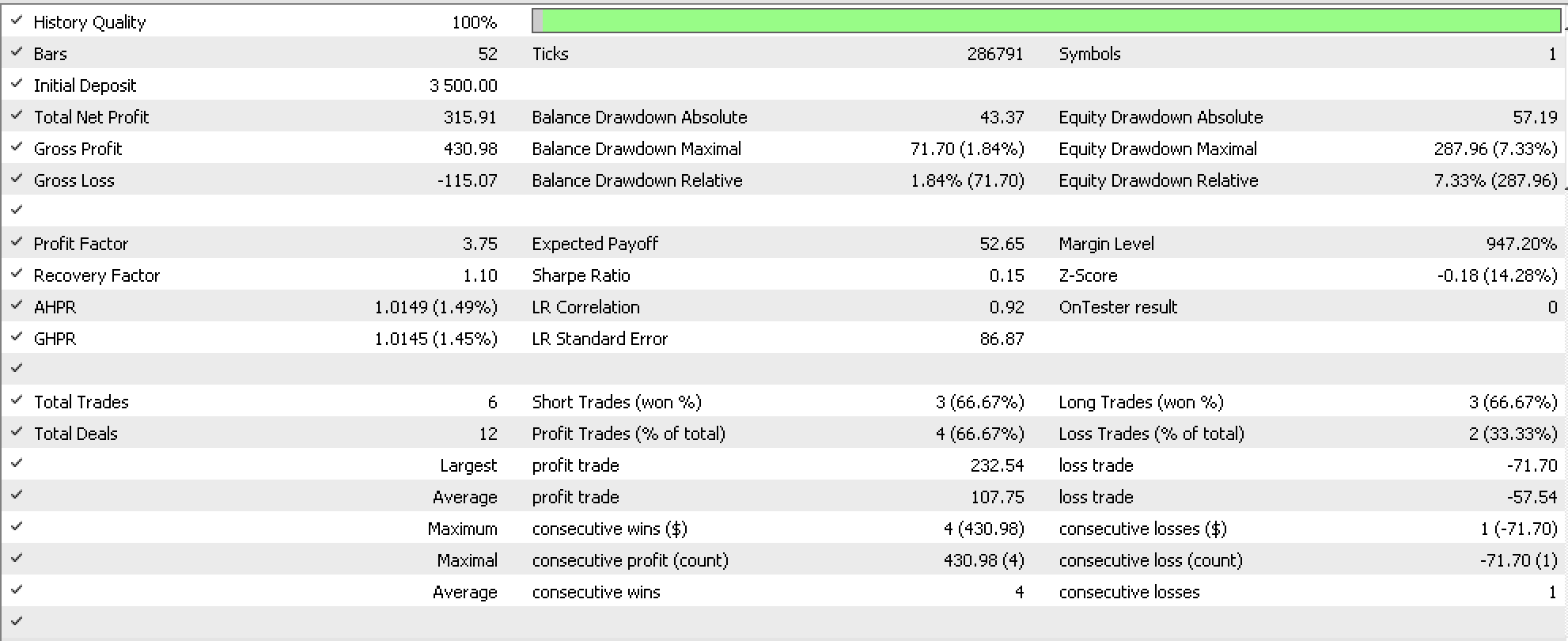
我们从上面的两个测试选项来看，即使从 2020 年 1 月 1 日至 2020 年 3 月 15 日非常短的测试窗口内，映射对象比之映射态射，在日线时间帧内也产生了不同的结果。对于交易者来说，两者中哪一个对于任何形式的预测更有用，而不仅只针对波动性，这需要对被测试的交易系统的特定方面进行长时间的测试，无论是入场信号、资金管理、亦或尾随停止，就如同这种情况下。

这次测试选择的区间虽然很短暂，但实际上对纳斯达克来说意义重大，因为当该指数达到历史高点时，在新冠疫情爆发期间，纳斯达克指数急剧下跌。由此，虽然这个测试确实表明可能与海潮数据相关，但它肯定不意味着有任何因果关系。

与这些系列中的案例一样，使用的输入信号非常基本，在这种情况下，它是内置的令人敬畏的振荡器，且采用相应信号文件的默认设置。持仓规模也如常一样是固定保证金。我们在日线时间帧内测试了纳斯达克指数，因为我们的域范畴数据是在每天的三个时间间隔收集的。故此，在将其格式化为范畴等效线性序时，每一天都构成一个域（对象），其拥有 3 个元素，它们是如前所述的每天三个数据点。

自此处最大的收获应该是，可以检查和测试不同、且看似不相关的数据集，从中寻找有用的滞后关系，并可助力交易决策。在我们上面的测试中，滞后是单日，您的可能会更长。我们在此处可以选择可能的替代数据集，海洋潮汐，这是一份很长的列表。但也许，分享一些可以替代上面所用的海潮数据的样本集合可能会有所帮助，这些数据集也将为我们的市场和外源系统的相互联系提供更多见解。

替代数据集可以包括商品价格；技术新闻，其中关于新技术趋势的文章数量，例如人工智能与娱乐等替代新闻文章的数量，可以滞后跟踪可能的关系；通过基于词典的方法量化的社交媒体情绪数据，也可以检查与纳斯达克（或任何交易证券）波动性的关系，特别是如果它与科技股有关。这些示例再次偏向于深奥的一面，以帮助人们建立优势、但更接近主项的数据集，如其它证券的价格、或其指标值。

结束语

回顾一下，我们已经探讨了如何通过函子将线性序格式范畴中的数据链接到证券价格。在这种情况下，我们的域数据是一个不太可能的数据集，从加利福尼亚海岸获取的海潮高程，并与纳斯达克的波动性链接，且通过函子滞后一天。这种链接可以采用两种格式，从对象到对象、或态射到态射。从我们的测试来看，由于测试窗口较短暂，这两种格式都具有相同的入场信号和持仓规模调整方法，因此产生了显著不同的结果。

范畴论函子很有价值，有助于映射不同类型的数据。我们在本文里采用了一个相当难于梳理和组成的数据集，但读者可以查看更适口的来源，尽管它们不一定能为他带来优势，但出于测试目的，它们也是富有洞察力的。

从交易者的视角来看，未来将线性序链接到集合的可能性和扩展性可以采取多种方向。这些可能包括：跨学科应用，即能够源于股票市场趋势，经函子转移到其它感兴趣的领域，如上所述的替代数据集；预测建模，其中函子跨越精心设置的时间滞后，正如本文所测试的那样，甚至可以应用于金融市场之外的天气预报等领域；数据集成和知识图谱，这里提出的概念可以提高人工智能等领域的代表性；机器学习和迁移学习，其中与金融数据相关的函子线性序可以进一步开发，例如，如果可以测试、甚至在不同领域中应用在两个范畴之间获得的函子权重，从而有可能改善机器学习模型及其效率。

还存在许多其它可能性。这些方法并不详尽，但这些包括统计分析和数据融合、偶然推理和相关性研究、定量金融与算法融资、数据驱动的决策、等等。如果他/她是交易者，应用程序的选择将取决于一个人的视野或交易方式。

我们鼓励读者根据他们的专业和市场方式探索这个领域，因为这里探讨的概念仅微微触及表面。这个学科的领域具有很大的潜力，从某种意义上说，它总是邀请您更深入地研究跨学科数据分析的未知边缘领域。

关于测试附加源的注意事项：

将文件 'TrailingCT_14_1a.mqh' 和 'TrailingCT_14_1b.mqh' 放在文件夹 'MQL5\include\Expert\Trailing\' 中，而 'ct_14_1s.mqh' 可以放在 include 文件夹中。

您可能需要按照本指南了解如何利用向导拼装智能系统，因为您需要将它们拼装为智能系统的一部分。如文章中所述，我使用 Awesome Oscillator 作为入场信号，以及固定保证金作为资金管理，这两者都是 MQL5 标准库的一部分。如常，本文的目标不是向您展示圣杯，而是可以自行打造策略的思路。所附的 MQL5 文件是由向导拼装的，您可以编译它们，或自行拼装。