MQL5'te İstatistiksel Olasılık Dağılımları

MetaTrader 5 — Örnekler | 16 Aralık 2021, 15:42

Tüm olasılık teorisi, istenmeyenlik felsefesine dayanır.
(Leonid Sukhorukov)

Tanıtım

Aktivite doğası gereği, bir tüccar çok sık olasılık ve rastgelelik gibi kategorilerle uğraşmak zorundadır. Rastgelelik antipot bir "düzenlilik" kavramıdır. Genel felsefi yasalar sayesinde, bir kural olarak rastgeleliğin düzenliliğe dönüşmesi dikkat çekicidir. Bu noktada zıt durumu incelemeyeceğiz. Temel olarak, rastgelelik-düzenlilik korelasyonu önemli bir ilişkidir, çünkü piyasa bağlamında alınırsa, bir satıcı tarafından alınan kar miktarını doğrudan etkiler.

Bu yazıda, gelecekte bazı piyasa düzenliliklerini bulmamıza yardımcı olacak temel teorik araçları ortaya çıkaracağım.

1. Dağılımlar, Öz, Türler

Bu nedenle, bazı rastgele değişkenleri tanımlamak için tek boyutlu bir istatistiksel olasılık dağılımına ihtiyacımız olacak. Belirli bir yasa ile rastgele değişkenlerin bir örneğini tanımlayacaktır, yani herhangi bir dağılım yasasının uygulanması bir dizi rastgele değişken gerektirecektir.

Neden [teorik] dağılımları analiz etmelisiniz? Değişken öznitelik değerlerine bağlı olarak frekans değişim desenlerini tanımlamayı kolaylaştırırlar. Ayrıca, gerekli dağılımın bazı istatistiksel parametrelerini alabilirsiniz.

Olasılık dağılımlarının türlerine gelince, rastgele değişken kümesinin türüne bağlı olarak dağılım ailesini sürekli ve ayrık olarak bölmek profesyonel literatürde gelenekseldir. Bununla birlikte, örneğin, x=x0, satırına göre f(x) dağılım eğrisinin simetrisi , konum parametresi, mod sayısı, rastgele değişken aralığı ve diğerleri gibi ölçütlere göre başka sınıflandırmalar da vardır.

Dağılım yasasını tanımlamanın birkaç yolu vardır. Aralarındaki en popüler olanları belirtmeliyiz:

2. Teorik Olasılık Dağılımları

Şimdi, MQL5 bağlamında istatistiksel dağılımları tanımlayan sınıflar oluşturmaya çalışalım. Ayrıca, profesyonel literatürün MQL5 kodlamasına başarıyla uygulanabilen C++ ile yazılmış birçok kod örneği sağladığını da eklemek isterim. Bu yüzden tekerleği yeniden icat etmedim ve bazı durumlarda C++ kodunu en iyi uygulamaları kullandım.

Karşılaştığım en büyük zorluk, MQL5'te birden fazla miras desteğinin olmamasıydı. Bu yüzden karmaşık sınıf hiyerarşilerini kullanamadım. Tarifler http://www.nr.com/ adlı kitap: Bilimsel Bilgi İşlem Sanatı [2] benim için işlevlerin çoğunu ödünç aldığım en uygun C++ kodu kaynağı haline geldi. Çoğu zaman MQL5'in ihtiyaçlarına göre rafine edildiler.

2.1.1 Normal Dağılım

Geleneksel olarak, dağılımıhttp://en.wikipedia.org/wiki/Normal_distributionile başlıyoruz.

Gauss dağılımı olarak da adlandırılan normal dağılım, olasılık yoğunluğu fonksiyonu tarafından verilen bir olasılık dağılımıdır:

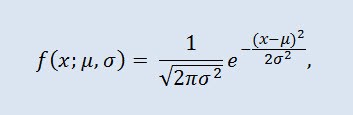
burada parametre μ — rastgele bir değişkenin ortalamasıdır (beklentisi) ve dağılım yoğunluğu eğrisinin maksimum koordinatını gösterir ve σ² varyanstır.

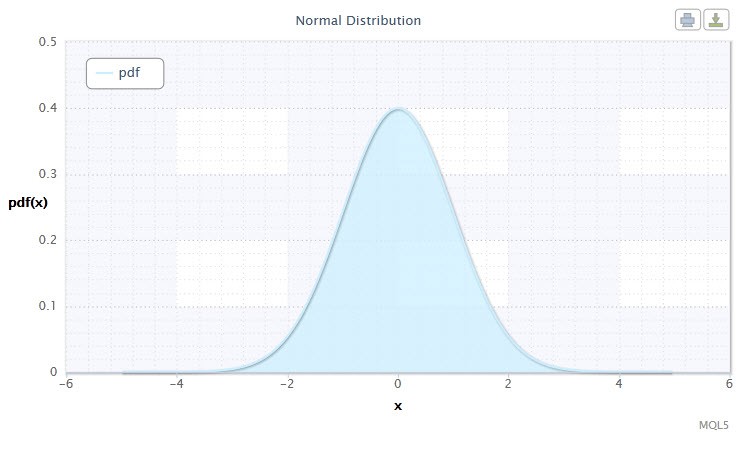
Şekil 1. Normal dağılım yoğunluğu Nor(0,1)

Bunun notasyonu aşağıdaki biçime sahiptir: X ~ Nor(μ, σ²), burada:

X, normal dağılımdan seçilen rastgele bir değişkendir Nor;
μ ortalama parametredir (-∞ ≤ μ ≤ +∞);
σ varyans parametresidir (0<σ).

Rastgele X değişkeninin geçerli aralığı: -∞ ≤ X ≤ +∞.

Bu makalede kullanılan formüller diğer kaynaklarda sağlananlardan farklı olabilir. Böyle bir fark bazen matematiksel olarak çok önemli değildir. Bazı durumlarda parametre haline getirirken görülen farklılıklara göre koşulludur.

Normal dağılım, hiçbiri geçerli bir güce sahip olmayan çok sayıda rastgele neden arasındaki etkileşimin bir sonucu olarak ortaya çıkan düzenliliği yansıttığı için istatistiklerde önemli bir rol oynar. Ve normal dağılım finansal piyasalarda nadir bir örnek olmasına rağmen, anormalliklerinin kapsamını ve doğasını belirlemek için ampirik dağılımlarla karşılaştırmak önemlidir.

Şimdi CNormaldist sınıfını normal dağılımı için aşağıdaki gibi tanımlayalım:

//+------------------------------------------------------------------+
//|                Normal Distribution class definition              |
//+------------------------------------------------------------------+
class CNormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //mean parameter (μ)
   sig;                 //variance parameter (σ)
   //+------------------------------------------------------------------+
   //| CNormaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CNormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Normal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return(0.398942280401432678/sig)*exp(-0.5*pow((x-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5*erfc(-0.707106781186547524*(x-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)                |
   //| quantile function                                                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Normal Distribution!");
      return -1.41421356237309505*sig*inverfc(2.*p)+mu;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };

//+------------------------------------------------------------------+

Fark ettiğiniz gibi, CNormaldist sınıfı, hata işlev sınıfını tanımlayan СErf temel sınıfından türemiştir. Bazı CNormaldist sınıf yöntemlerinin hesaplanmasında gerekli olacaktır. СErf sınıfı ve yardımcı işlev erfcc aşağıyukarı şöyle görünür:

//+------------------------------------------------------------------+
//|                Error Function class definition                   |
//+------------------------------------------------------------------+
class CErf
  {
public:
   int               ncof;    // coefficient array size
   double            cof[28]; // Chebyshev coefficient array
   //+------------------------------------------------------------------+
   //| CErf class constructor                                           |
   //+------------------------------------------------------------------+
   void CErf()
     {
      int Ncof=28;
      double Cof[28]=//Chebyshev coefficients
        {
         -1.3026537197817094,6.4196979235649026e-1,
         1.9476473204185836e-2,-9.561514786808631e-3,-9.46595344482036e-4,
         3.66839497852761e-4,4.2523324806907e-5,-2.0278578112534e-5,
         -1.624290004647e-6,1.303655835580e-6,1.5626441722e-8,-8.5238095915e-8,
         6.529054439e-9,5.059343495e-9,-9.91364156e-10,-2.27365122e-10,
         9.6467911e-11, 2.394038e-12,-6.886027e-12,8.94487e-13, 3.13092e-13,
         -1.12708e-13,3.81e-16,7.106e-15,-1.523e-15,-9.4e-17,1.21e-16,-2.8e-17
        };
      setCErf(Ncof,Cof);
     };
   //+------------------------------------------------------------------+
   //| Set-method for ncof                                              |
   //+------------------------------------------------------------------+
   void setCErf(int Ncof,double &Cof[])
     {
      ncof=Ncof;
      ArrayCopy(cof,Cof);
     };
   //+------------------------------------------------------------------+
   //| CErf class destructor                                            |
   //+------------------------------------------------------------------+
   void ~CErf(){};
   //+------------------------------------------------------------------+
   //| Error function                                                   |
   //+------------------------------------------------------------------+
   double erf(double x)
     {
      if(x>=0.0) return 1.0-erfccheb(x);
      else return erfccheb(-x)-1.0;
     }
   //+------------------------------------------------------------------+
   //| Complementary error function                                     |
   //+------------------------------------------------------------------+
   double erfc(double x)
     {
      if(x>=0.0) return erfccheb(x);
      else return 2.0-erfccheb(-x);
     }
   //+------------------------------------------------------------------+
   //| Chebyshev approximations for the error function                  |
   //+------------------------------------------------------------------+
   double erfccheb(double z)
     {
      int j;
      double t,ty,tmp,d=0.0,dd=0.0;
      if(z<0.) Alert("erfccheb requires nonnegative argument!");
      t=2.0/(2.0+z);
      ty=4.0*t-2.0;
      for(j=ncof-1;j>0;j--)
        {
         tmp=d;
         d=ty*d-dd+cof[j];
         dd=tmp;
        }
      return t*exp(-z*z+0.5*(cof[0]+ty*d)-dd);
     }
   //+------------------------------------------------------------------+
   //| Inverse complementary error function                             |
   //+------------------------------------------------------------------+
   double inverfc(double p)
     {
      double x,err,t,pp;
      if(p >= 2.0) return -100.0;
      if(p <= 0.0) return 100.0;
      pp=(p<1.0)? p : 2.0-p;
      t = sqrt(-2.*log(pp/2.0));
      x = -0.70711*((2.30753+t*0.27061)/(1.0+t*(0.99229+t*0.04481)) - t);
      for(int j=0;j<2;j++)
        {
         err=erfc(x)-pp;
         x+=err/(M_2_SQRTPI*exp(-pow(x,2))-x*err);
        }
      return(p<1.0? x : -x);
     }
   //+------------------------------------------------------------------+
   //| Inverse error function                                           |
   //+------------------------------------------------------------------+
   double inverf(double p)
     {return inverfc(1.0-p);}
  };
//+------------------------------------------------------------------+
double erfcc(const double x)
/* 
 complementary error function erfc(x) with
 a relative error of 1.2 * 10^(-7)               
*/
  {
   double t,z=fabs(x),ans;
   t=2./(2.0+z);
   ans=t*exp(-z*z-1.26551223+t*(1.00002368+t*(0.37409196+t*(0.09678418+
             t*(-0.18628806+t*(0.27886807+t*(-1.13520398+t*(1.48851587+
             t*(-0.82215223+t*0.17087277)))))))));
   return(x>=0.0 ? ans : 2.0-ans);
  }
//+------------------------------------------------------------------+

2.1.2 Günlük-Normal Dağılım

Şimdi log normal dağılımına bir göz atalım.

Olasılık teorisinde log-normal dağılım, kesinlikle sürekli dağılımlardan oluşan iki parametreli bir ailedir. Rasgele bir değişken günlük normalde dağıtılırsa, logaritmasının normal bir dağılım vardır.

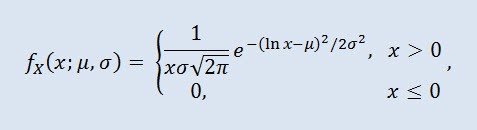
burada μ konum parametresi (0<μ), σ ölçek parametresi (0<σ) ise.

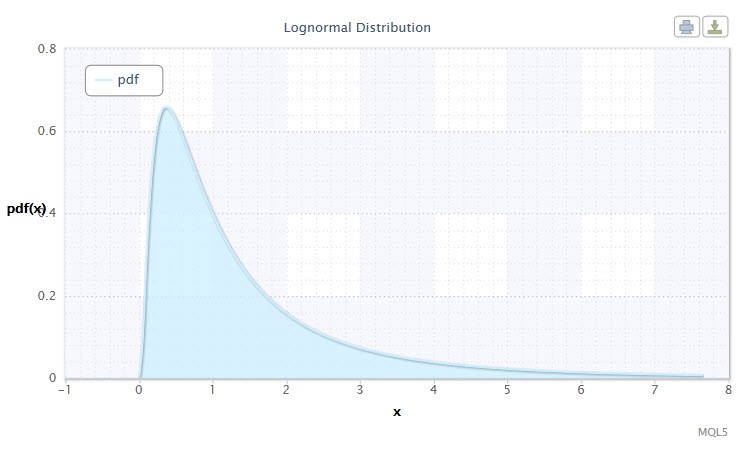
Şekil 2. Log-normal dağılım yoğunluğu Logn(0,1)

Bunun notasyonu aşağıdaki biçime sahiptir: X ~ Logn(μ, σ²), burada:

X, log-normal dağılım Logn'den seçilen rastgele bir değişkendir;
konum parametresi (0<μ) μ);
σ ölçek parametresidir (0<σ).

Rastgele değişken X'in geçerli aralığı: 0 ≤ X ≤ +∞.

Şimdi CLognormaldist sınıfını oluşturalım (log normal dağılımını açıklamaktadır). Aşağıdaki gibi görünecektir:

//+------------------------------------------------------------------+
//|                Lognormal Distribution class definition           |
//+------------------------------------------------------------------+
class CLognormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CLognormaldist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CLognormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Lognormal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return(0.398942280401432678/(sig*x))*exp(-0.5*pow((log(x)-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return 0.5*erfc(-0.707106781186547524*(log(x)-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)(quantile)      |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Lognormal Distribution!");
      return exp(-1.41421356237309505*sig*inverfc(2.*p)+mu);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Görüldüğü gibi, günlük-normal dağılımı normal dağılımdan çok farklı değildir. Fark, x parametresinin log(x) parametresiyle değiştirilmesidir.

2.1.3 Cauchy Dağılımı

Olasılık teorisinde cauchy dağılımı (fizikte Lorentz dağılımı veya Breit-Wigner dağılımı olarak da adlandırılır) kesinlikle sürekli dağılımların bir sınıfıdır. Cauchy dağıtılmış rasgele değişken, beklentisi ve varyansı olmayan bir değişkenin yaygın bir örneğidir. Yoğunluk aşağıdaki formu alır:

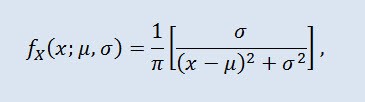
burada μ konum parametresi (-∞ ≤ μ ≤ +∞) ve σ ölçek parametresidir (0<σ).

Cauchy dağılımının notasyonu aşağıdaki biçime sahiptir: X ~ Cau(μ, σ), burada:

X, Cauchy dağılımı Cau'dan seçilen rastgele bir değişkendir;
μ konum parametresidir (-∞ ≤ μ ≤ +∞);
σ ölçek parametresidir (0<σ).

Rastgele X değişkeninin geçerli aralığı: -∞ ≤ X ≤ +∞.

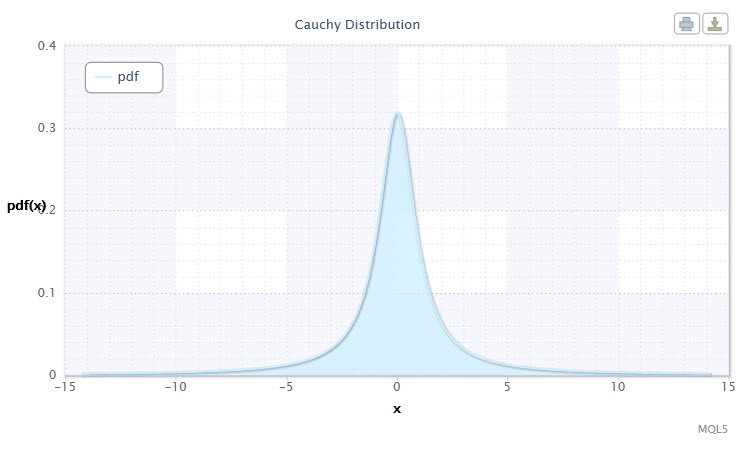
Şekil 3. Cauchy dağılım yoğunluğu Cau(0,1)

CCauchydist sınıfınınyardımıylaoluşturulan MQL5 formatında aşağıdaki gibi görünür:

//+------------------------------------------------------------------+
//|                Cauchy Distribution class definition              |
//+------------------------------------------------------------------+
class CCauchydist //
  {
public:
   double            mu,//location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CCauchydist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CCauchydist() 
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Cauchy Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return 0.318309886183790671/(sig*(1.+pow((x-mu)/sig,2)));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5+0.318309886183790671*atan2(x-mu,sig); //todo      
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Cauchy Distribution!");
      return mu+sig*tan(M_PI*(p-0.5));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Radyanlardaark teğetinin ana değerini döndürenatan2() işlevinin kullanıldığı burada belirtilmelidir:

double atan2(double y,double x)
/*
 Returns the principal value of the arc tangent of y/x,
 expressed in radians. To compute the value, the function 
 uses the sign of both arguments to determine the quadrant.
 y - double value representing an y-coordinate.
 x - double value representing an x-coordinate. 
*/
  {
   double a;
   if(fabs(x)>fabs(y))
      a=atan(y/x);
   else
     {
      a=atan(x/y); // pi/4 <= a <= pi/4
      if(a<0.)
         a=-1.*M_PI_2-a; //a is negative, so we're adding
      else
         a=M_PI_2-a;
     }
   if(x<0.)
     {
      if(y<0.)
         a=a-M_PI;
      else
         a=a+M_PI;
     }
   return a;
  }

2.1.4HiperbolikSekant Dağılımı

Hiperbolik sekant dağılımı finansal rütbe analizi ile ilgilenenlerin ilgisini çekecektir.

Olasılık kuramı ve istatistiklerinde hiperbolik sekant dağılımı, olasılık yoğunluk fonksiyonu ve karakteristik fonksiyonu hiperbolik sekant fonksiyonu ile orantılı olan sürekli bir olasılık dağılımıdır. Yoğunluk formül tarafından verilir:

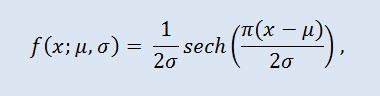
burada μ konum parametresi (-∞ ≤ μ ≤ +∞) ve σ ölçek parametresidir (0<σ).

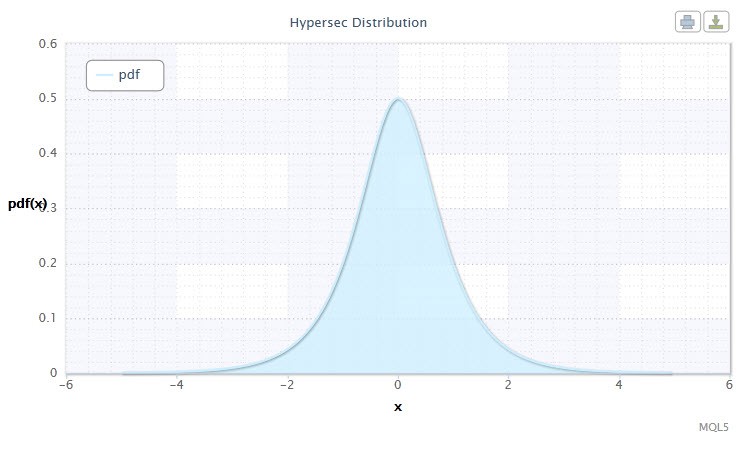
Şekil 4. Hiperbolik sekant dağılım yoğunluğu HS(0,1)

Bunun notasyonu aşağıdaki biçime sahiptir: X ~ HS(μ, σ), burada:

X rastgele bir değişkendir;
μ konum parametresidir (-∞ ≤ μ ≤ +∞);
σ ölçek parametresidir (0<σ).

Rastgele X değişkeninin geçerli aralığı: -∞ ≤ X ≤ +∞.

CHypersecdist sınıfını kullanarak aşağıdaki gibi tanımlayalım:

//+------------------------------------------------------------------+
//|        Hyperbolic Secant Distribution class definition           |
//+------------------------------------------------------------------+
class CHypersecdist //
  {
public:
   double            mu,// location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CHypersecdist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CHypersecdist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Hyperbolic Secant Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return sech((M_PI*(x-mu))/(2*sig))/2*sig;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 2/M_PI*atan(exp((M_PI*(x-mu)/(2*sig))));
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Hyperbolic Secant Distribution!");
      return(mu+(2.0*sig/M_PI*log(tan(M_PI/2.0*p))));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Bu dağılımın adını, olasılık yoğunluk fonksiyonu hiperbolik sekant işleviyle orantılı olan hiperbolik sekant işlevinden aldığını görmek zor değildir.

Hiperbolik sekant fonksiyonu sechaşağıdaki gibidir:

//+------------------------------------------------------------------+
//|              Hyperbolic Secant Function                          |
//+------------------------------------------------------------------+
double sech(double x)
// Hyperbolic Secant Function
  {
   return 2/(pow(M_E,x)+pow(M_E,-x));
  }

2.1.5Öğrenci t-Dağılımı

Öğrencinin t dağılımı istatistiklerde önemli bir dağılımdır.

Olasılık teorisinde, Öğrencinin t dağılımı genellikle tamamen sürekli dağılımlardan oluşan tek parametreli bir ailedir. Bununla birlikte, dağılım yoğunluğu işlevi tarafından verilen üç parametreli bir dağılım olarak da kabul edilebilir:

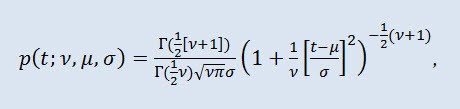
Burada Г Euler'in Gama işlevidir, ν şekil parametresidir (ν>0), μ konum parametresidir (-∞ ≤ μ ≤ +∞), σ ölçek parametresidir (0<σ).

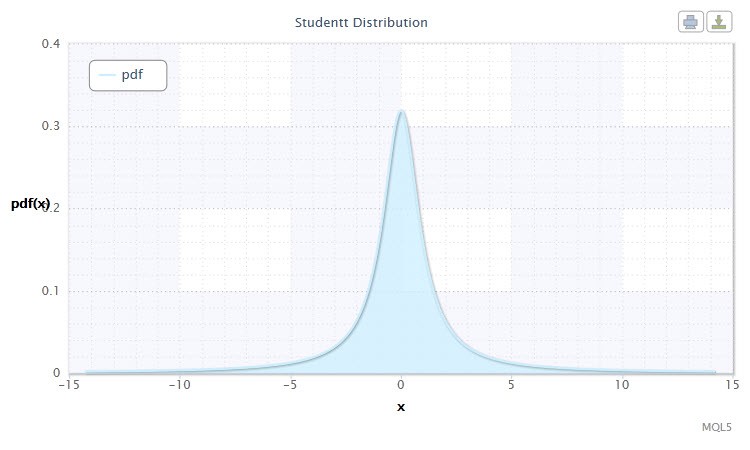
Şekil 5. Öğrencinin t-dağılımyoğunluğu Stt(1,0,1)

Bunun notasyonu şu biçime sahiptir: t ~ Stt (ν,μ,σ), burada:

t, Öğrencinin t dağılımı Stt’sinden seçilen rastgele bir değişkendir;
ν şekil parametresidir (ν>0)
μ konum parametresidir (-∞ ≤ μ ≤ +∞);
σ ölçek parametresidir (0<σ).

Rastgele X değişkeninin geçerli aralığı: -∞ ≤ X ≤ +∞.

Genellikle, özellikle hipotez testinde standart bir t dağılımı μ=0 ve σ=1 ile kullanılır. Böylece, parametre ν ile tek parametreli bir dağılıma dönüşür.

Bu dağılım genellikle beklenti değeri hipotezlerini, regresyon ilişki katsayılarını, homojenlik hipotezlerini vb. test ederken, güven aralıkları aracılığıyla beklenti, öngörülen değerler ve diğer özelliklerin tahmin edilmesinde kullanılır.

Dağılımı CStudenttdist sınıfı aracılığıyla tanımlayalım:

//+------------------------------------------------------------------+
//|                Student's t-distribution class definition         |
//+------------------------------------------------------------------+
class CStudenttdist : CBeta // CBeta class inheritance
  {
public:
   int               nu;     // shape parameter (ν)
   double            mu,     // location parameter (μ)
   sig,                     // scale parameter (σ)
   np,                      // 1/2*(ν+1)
   fac;                     // Г(1/2*(ν+1))-Г(1/2*ν)
   //+------------------------------------------------------------------+
   //| CStudenttdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CStudenttdist()
     {
      int Nu=1;double Mu=0.0,Sig=1.0; //default parameters ν, μ and σ
      setCStudenttdist(Nu,Mu,Sig);
     }
   void setCStudenttdist(int Nu,double Mu,double Sig)
     {
      nu=Nu;
      mu=Mu;
      sig=Sig;
      if(sig<=0. || nu<=0.) Alert("bad sig,nu in Student-t Distribution!");
      np=0.5*(nu+1.);
      fac=gammln(np)-gammln(0.5*nu);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-np*log(1.+pow((x-mu)/sig,2.)/nu)+fac)/(sqrt(M_PI*nu)*sig);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double t)
     {
      double p=0.5*betai(0.5*nu,0.5,nu/(nu+pow((t-mu)/sig,2)));
      if(t>=mu) return 1.-p;
      else return p;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Student-t Distribution!");
      double x=invbetai(2.*fmin(p,1.-p),0.5*nu,0.5);
      x=sig*sqrt(nu*(1.-x)/x);
      return(p>=0.5? mu+x : mu-x);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
   //+------------------------------------------------------------------+
   //| Two-tailed cumulative distribution function (aa) A(t|ν)          |
   //+------------------------------------------------------------------+
   double aa(double t)
     {
      if(t < 0.) Alert("bad t in Student-t Distribution!");
      return 1.-betai(0.5*nu,0.5,nu/(nu+pow(t,2.)));
     }
   //+------------------------------------------------------------------+
   //| Inverse two-tailed cumulative distribution function (invaa)      |
   //| p=A(t|ν)                                                         |
   //+------------------------------------------------------------------+
   double invaa(double p)
     {
      if(!(p>=0. && p<1.)) Alert("bad p in Student-t Distribution!");
      double x=invbetai(1.-p,0.5*nu,0.5);
      return sqrt(nu*(1.-x)/x);
     }
  };
//+------------------------------------------------------------------+

CStudenttdist sınıf listesi, CBeta'nın tamamlanmamış beta işleviniaçıklayanbir temel sınıf olduğunu gösterir.

CBeta sınıfı aşağıdaki gibigörünür:

//+------------------------------------------------------------------+
//|            Incomplete Beta Function class definition             |
//+------------------------------------------------------------------+
class CBeta : public CGauleg18
  {
private:
   int               Switch;                     //when to use the quadrature method
   double            Eps,Fpmin;
public:
   //+------------------------------------------------------------------+
   //| CBeta class constructor                                          |
   //+------------------------------------------------------------------+
   void CBeta()
     {
      int swi=3000;
      setCBeta(swi,EPS,FPMIN);
     };
   //+------------------------------------------------------------------+
   //| CBeta class set-method                                           |
   //+------------------------------------------------------------------+
   void setCBeta(int swi,double eps,double fpmin)
     {
      Switch=swi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            betai(const double a,const double b,const double x); //incomplete beta function Ix(a,b)
   double            betacf(const double a,const double b,const double x);//continued fraction for incomplete beta function
   double            betaiapprox(double a,double b,double x); //Incomplete beta by quadrature
   double            invbetai(double p,double a,double b);    //Inverse of incomplete beta function
  };

Bu sınıf ayrıca CGauleg18 temel sınıfına sahiptir ve bu sınıf, Gauss-Legendre dörtgeni gibi sayısal entegrasyon yöntemi için katsayılar sağlar.

2.1.6 Lojistik Dağılım

Çalışmamızda lojistik dağılımın bir sonrakini göz önünde bulundurmayı öneriyorum.

Olasılık kuramı ve istatistikte lojistik dağılım sürekli bir olasılık dağılımıdır. Kümülatif dağılım fonksiyonu lojistik fonksiyonudur. Şekil olarak normal dağılımı andırır, ancak daha ağır taraflara sahiptir. Dağılım yoğunluğu:

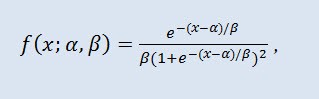
Burada α konum parametresi (-∞ ≤ α ≤ +∞), β ölçek parametresi (0<β).

Şekil 6. Lojistik dağılım yoğunluğu Logi(0,1)

Bunun notasyonu aşağıdaki biçime sahiptir: X ~ Logi (α,β), durumunda:

X rastgele bir değişkendir;
konum parametresi (-∞ ≤ α ≤ +∞) α);
β ölçek parametresidir (0<β).

Rastgele X değişkeninin geçerli aralığı: -∞ ≤ X ≤ +∞.

CLogisticdist sınıfı, yukarıda açıklanan dağılımın uygulanmasıdır:

//+------------------------------------------------------------------+
//|                Logistic Distribution class definition            |
//+------------------------------------------------------------------+
class CLogisticdist
  {
public:
   double            alph,//location parameter (α)
   bet;                   //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLogisticdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CLogisticdist() 
     {
      alph=0.0;bet=1.0; //default parameters μ and σ
      if(bet<=0.) Alert("bad bet in Logistic Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-(x-alph)/bet)/(bet*pow(1.+exp(-(x-alph)/bet),2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double et=exp(-1.*fabs(1.81379936423421785*(x-alph)/bet));
      if(x>=alph) return 1./(1.+et);
      else return et/(1.+et);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Logistic Distribution!");
      return alph+0.551328895421792049*bet*log(p/(1.-p));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.7 Üstel Dağılım

Rastgele bir değişkenin üstel dağılımına da bir göz atalım.

Rastgele birdeğişken X, yoğunluğu aşağıdakiler tarafından verilmişse, φ parametresi φ > 0, olan üstel dağılımdır:

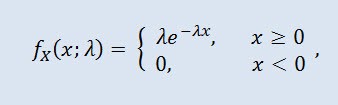
burada λ ölçek parametresi (λ>0).

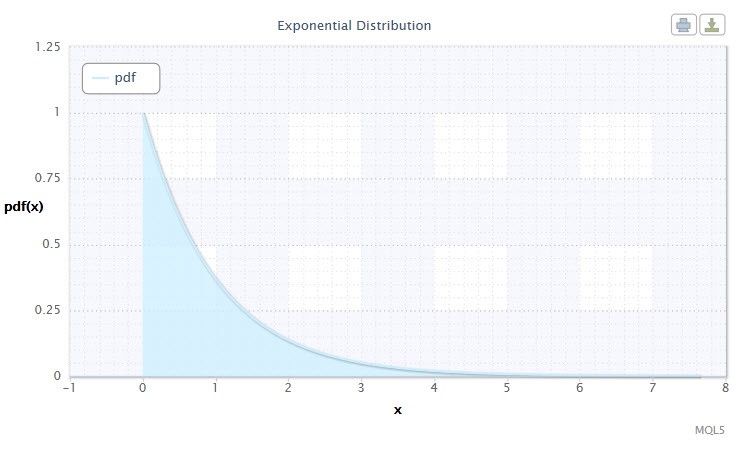
Şekil 7. Üstel dağılımyoğunluğu Exp(1)

Bunun notasyonu aşağıdaki biçime sahiptir: X ~ Exp(λ), burada:

X rastgele bir değişkendir;
λ, ölçek parametresidir (λ>0).

Rastgele değişken X'in geçerli aralığı: 0 ≤ X ≤ +∞.

Bu dağılım, belirli zamanlarda meydana gelen bir dizi olayı tek tek tanımlaması açısından dikkat çekicidir. Böylece, bu dağılımı kullanarak bir tüccar bir dizi kayıp anlaşmasını ve diğerlerini analiz edebilir.

MQL5 kodunda, dağılım CExpondist sınıfı aracılığıyla açıklanmıştır:

//+------------------------------------------------------------------+
//|                Exponential Distribution class definition         |
//+------------------------------------------------------------------+
class CExpondist
  {
public:
   double            lambda;   //scale parameter (λ)
   //+------------------------------------------------------------------+
   //| CExpondist class constructor                                     |
   //+------------------------------------------------------------------+
   void  CExpondist()
     {
      lambda=1.0;              //default parameter λ
      if(lambda<=0.) Alert("bad lambda in Exponential Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Exponential Distribution!");
      return lambda*exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x < 0.) Alert("bad x in Exponential Distribution!");
      return 1.-exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Exponential Distribution!");
      return -log(1.-p)/lambda;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.8 Gama Dağılımı

gama dağılımını rastgele değişken sürekli dağılımının bir sonraki türü olarak seçtim.

Olasılık teorisinde gama dağılımı, kesinlikle sürekli olasılık dağılımlarından oluşan iki parametreli bir ailedir. Parametre α bir tam sayıysa, bu tür gama dağılımı Erlang dağılımı olarak da adlandırılır. Yoğunluk aşağıdaki formu alır:

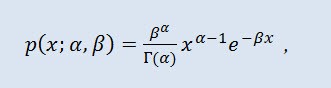
burada Г Euler'in Gama işlevidir, α şekil parametresidir (0<α), β ölçek parametresidir (0<β).

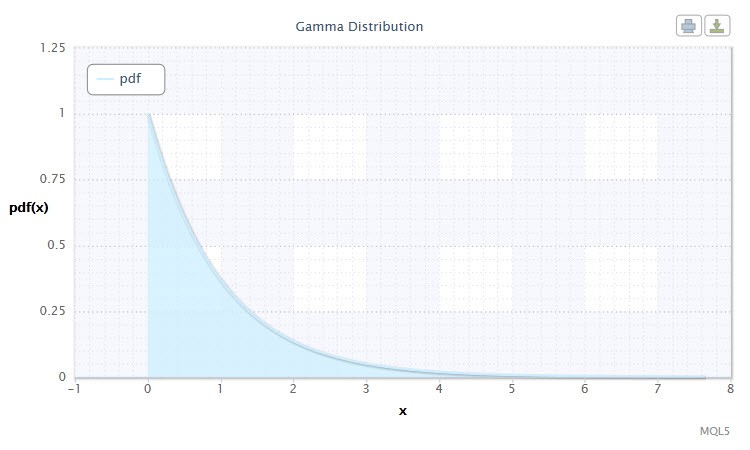
Şekil 8. Gama dağılımı yoğunluğu Gam(1,1).

Bunun notasyonu aşağıdaki biçime sahiptir: X ~ Gam (α,β), olduğunda:

X rastgele bir değişkendir;
α şekil parametresidir (0<α);
β ölçek parametresidir (0<β).

Rastgele değişken X'in geçerli aralığı: 0 ≤ X ≤ +∞.

CGammadist sınıf tanımlı varyantta aşağıdaki gibi görünür:

//+------------------------------------------------------------------+
//|                Gamma Distribution class definition               |
//+------------------------------------------------------------------+
class CGammadist : CGamma // CGamma class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous scale parameter  (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CGammaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CGammadist()
     {
      setCGammadist();
     }
   void setCGammadist(double Alph=1.0,double Bet=1.0)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Gamma Distribution!");
      fac=alph*log(bet)-gammln(alph);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0.) Alert("bad x in Gamma Distribution!");
      return exp(-bet*x+(alph-1.)*log(x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Gamma Distribution!");
      return gammp(alph,bet*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Gamma Distribution!");
      return invgammp(p,alph)/bet;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Gama dağılım sınıfı, tamamlanmamış gama işlevini açıklayan CGamma sınıfından türemiştir.

CGamma sınıfı aşağıdaki gibitanımlanır:

//+------------------------------------------------------------------+
//|            Incomplete Gamma Function class definition            |
//+------------------------------------------------------------------+
class CGamma : public CGauleg18
  {
private:
   int               ASWITCH;
   double            Eps,
   Fpmin,
   gln;
public:
   //+------------------------------------------------------------------+
   //| CGamma class constructor                                         |
   //+------------------------------------------------------------------+
   void CGamma()
     {
      int aswi=100;
      setCGamma(aswi,EPS,FPMIN);
     };
   void setCGamma(int aswi,double eps,double fpmin) //CGamma set-method
     {
      ASWITCH=aswi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            gammp(const double a,const double x); //incomplete gamma function
   double            gammq(const double a,const double x); //incomplete gamma function Q(a,x)
   void              gser(double &gamser,double a,double x,double &gln); //incomplete gamma function P(a,x)
   double            gcf(const double a,const double x); //incomplete gamma function Q(a,x)
   double            gammpapprox(double a,double x,int psig); //incomplete gamma by quadrature
   double            invgammp(double p,double a); //inverse of incomplete gamma function
  };
//+------------------------------------------------------------------+

Hem CGamma sınıfı hem de CBeta sınıfıtemel sınıf olarak CGauleg18'e sahiptir.

2.1.9 Beta Dağılımı

Şimdi beta dağılımını gözden geçirelim.

Olasılık teorisi ve istatistikte, beta dağılımı kesinlikle sürekli dağılımlardan oluşan iki parametreli bir ailedir. Değerleri sınırlı bir aralıkta tanımlanan rasgele değişkenleri tanımlamak için kullanılır. Yoğunluk aşağıdaki gibi tanımlanır:

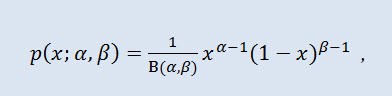
burada B beta işlevidir, α 1. şekil parametresidir (0<α), β 2. şekil parametresidir (0<β).

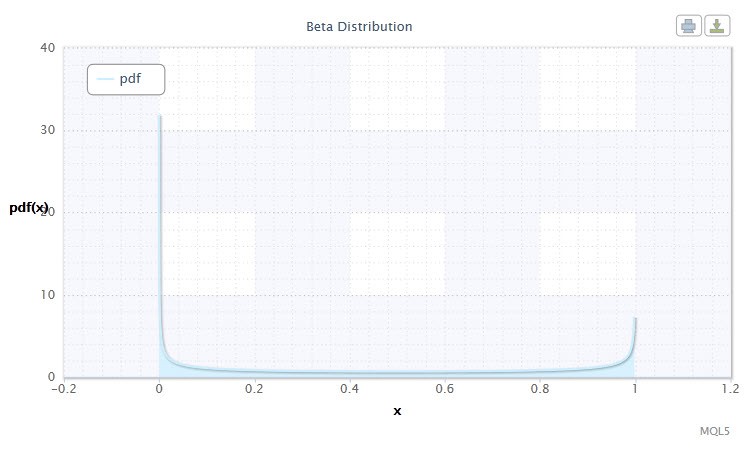
Şekil 9. Beta dağılım yoğunluğu Beta(0.5,0.5)

Bunun notasyonu aşağıdaki biçime sahiptir: X ~ Beta (α,β), olduğunda:

X rastgele bir değişkendir;
α 1. şekil parametresidir (0<α);
β 2. şekil parametresidir (0<β).

Rastgele değişken X'in geçerli aralığı: 0 ≤ X ≤ 1.

CBetadist sınıfı bu dağılımı aşağıdaki şekilde açıklar:

//+------------------------------------------------------------------+
//|                Beta Distribution class definition                |
//+------------------------------------------------------------------+
class CBetadist : CBeta // CBeta class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous shape parameter (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CBetadist class constructor                                      |
   //+------------------------------------------------------------------+
   void  CBetadist()
     {
      setCBetadist();
     }
   void setCBetadist(double Alph=0.5,double Bet=0.5)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Beta Distribution!");
      fac=gammln(alph+bet)-gammln(alph)-gammln(bet);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0. || x>=1.) Alert("bad x in Beta Distribution!");
      return exp((alph-1.)*log(x)+(bet-1.)*log(1.-x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0. || x>1.) Alert("bad x in Beta Distribution");
      return betai(alph,bet,x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>1.) Alert("bad p in Beta Distribution!");
      return invbetai(p,alph,bet);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.10Laplace Dağılımı

Bir diğer dikkat çekici sürekli dağılım, Laplace dağılımıdır (çift üstel dağılım).

Olasılık teorisindeki Laplace dağılımı (çift üstel dağılım), olasılık yoğunluğunun olduğu rastgele bir değişkenin sürekli dağılımıdır:

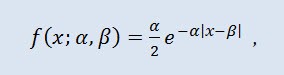
Burada α konum parametresi (-∞ ≤ α ≤ +∞), β ölçek parametresi (0<β).

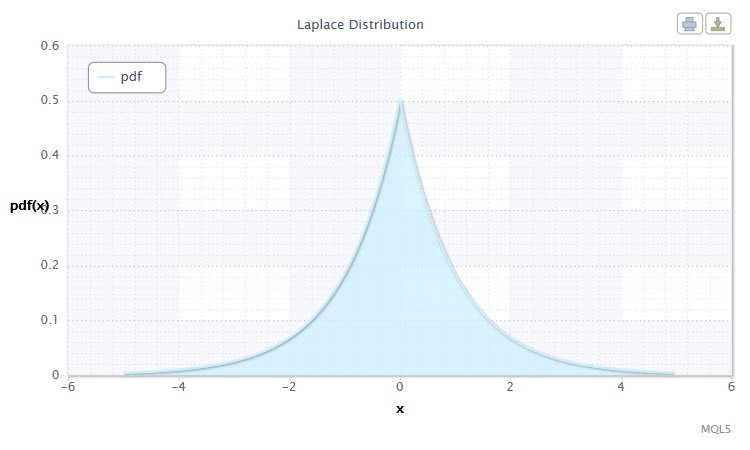
Şekil 10. Laplace dağılımıyoğunluğu Lap(0,1)

Bunun notasyonu aşağıdaki biçime sahiptir: X ~ Lap (α,β), olduğunda:

X rastgele bir değişkendir;
konum parametresi (-∞ ≤ α ≤ +∞) α);
β ölçek parametresidir (0<β).

Rastgele X değişkeninin geçerli aralığı: -∞ ≤ X ≤ +∞.

Bu dağılımın amaçları doğrultusundaCLaplacedist sınıfı aşağıdaki gibi tanımlanmıştır:

//+------------------------------------------------------------------+
//|                 Laplace Distribution class definition            |
//+------------------------------------------------------------------+
class CLaplacedist
  {
public:
   double            alph;   //location parameter (α)
   double            bet;    //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLaplacedist class constructor                                   |
   //+------------------------------------------------------------------+
   void  CLaplacedist()
     {
      alph=.0;               //default parameter α
      bet=1.;                //default parameter β
      if(bet<=0.) Alert("bad bet in Laplace Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-fabs((x-alph)/bet))/2*bet;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double temp;
      if(x<0)
         temp=0.5*exp(-fabs((x-alph)/bet));
      else
         temp=1.-0.5*exp(-fabs((x-alph)/bet));
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      double temp;
      if(p<0. || p>=1.) Alert("bad p in Laplace Distribution!");
      if(p<0.5)
         temp=bet*log(2*p)+alph;
      else
         temp=-1.*(bet*log(2*(1.-p))+alph);
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Bu nedenle, MQL5 kodunu kullanarak on sürekli dağılım için 10 sınıf oluşturduk. Bunların dışında, belirli işlev ve yöntemlere ihtiyaç olduğu için tamamlayıcı olan bazı sınıflar oluşturuldu (örneğin CBeta ve CGamma).

Şimdi ayrık dağılımlara devam edelim ve bu dağılım kategorisi için birkaç sınıf oluşturalım.

2.2.1 Binom Dağılımı

Şimdi binom dağılımı ile başlayalım.

Olasılık teorisinde, binom dağılımı, her birinde başarı olasılığının eşit olduğu bir dizi bağımsız rastgele deneydeki başarı sayısının dağılımıdır. Olasılık yoğunluğu aşağıdaki formülle verilmiştir:

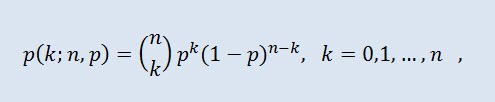
burada (n k) binom katsayısıdır, n deneme sayısıdır (0 ≤ n), p başarı olasılığıdır (0 ≤ p ≤1).

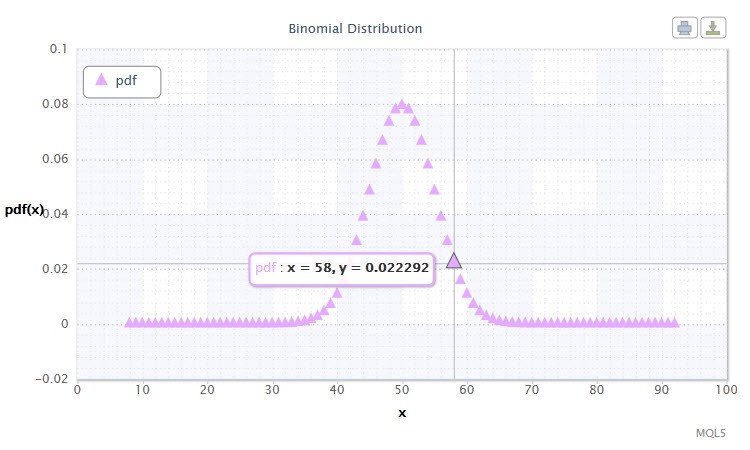
Şekil 11. Binom dağılımı yoğunluğu Bin(100,0,5).

Bunun notasyonu aşağıdaki biçime sahiptir: k ~ Bin (n,p), olduğunda:

k rastgele bir değişkendir;
n deneme sayısıdır (0 ≤ n);
p başarı olasılığıdır (0 ≤ p ≤1).

Rastgele değişken X'in geçerli aralığı: 0 veya 1.

Rastgele X değişkeninin olası değerleri size bir şey gösteriyor mu? Gerçekten de, bu dağılım ticaret sistemindeki kazanma (1) ve kayıp (0) anlaşmalarının toplamını analiz etmemize yardımcı olabilir.

СBinomialdist sınıfını aşağıdaki gibi oluşturalım:

//+------------------------------------------------------------------+
//|               Binomial Distribution class definition             |
//+------------------------------------------------------------------+
class CBinomialdist : CBeta // CBeta class inheritance
  {
public:
   int               n;      //number of trials
   double            pe,     //success probability
   fac;                      //factor
   //+------------------------------------------------------------------+
   //| CBinomialdist class constructor                                  |
   //+------------------------------------------------------------------+
   void              CBinomialdist()
     {
      setCBinomialdist();
     }
   void setCBinomialdist(int N=100,double Pe=0.5)//default parameters n and pe
     {
      n=N; pe=Pe;
      if(n<=0 || pe<=0. || pe>=1.) Alert("bad args in Binomial Distribution!");
      fac=gammln(n+1.);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k>n) return 0.;
      return exp(k*log(pe)+(n-k)*log(1.-pe)+fac-gammln(k+1.)-gammln(n-k+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k==0) return 0.;
      if(k>n) return 1.;
      return 1.-betai((double)k,n-k+1.,pe);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int k,kl,ku,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Binomial Distribution!");
      k=fmax(0,fmin(n,(int)(n*pe)));
      if(p<cdf(k))
        {
         do
           {
            k=fmax(k-inc,0);
            inc*=2;
           }
         while(p<cdf(k));
         kl=k; ku=k+inc/2;
           } else {
         do
           {
            k=fmin(k+inc,n+1);
            inc*=2;
           }
         while(p>cdf(k));
         ku=k; kl=k-inc/2;
        }
      while(ku-kl>1)
        {
         k=(kl+ku)/2;
         if(p<cdf(k)) ku=k;
         else kl=k;
        }
      return kl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int k)
     {
      return 1.-cdf(k);
     }
  };
//+------------------------------------------------------------------+

2.2.2 Poisson Dağılımı

İncelenen bir sonraki dağılım, Poisson dağılımıdır.

Poisson dağılımı, bu olayların sabit bir ortalama yoğunlukta ve birbirinden bağımsız olarak gerçekleşmesi koşuluyla, belirli bir süre boyunca meydana gelen bir dizi olayla temsil edilen rastgele bir değişkeni modeller. Yoğunluk aşağıdaki formu alır:

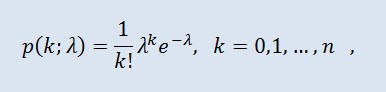
k! olan durumda faktöryel, λ konum parametresidir (0 < λ).

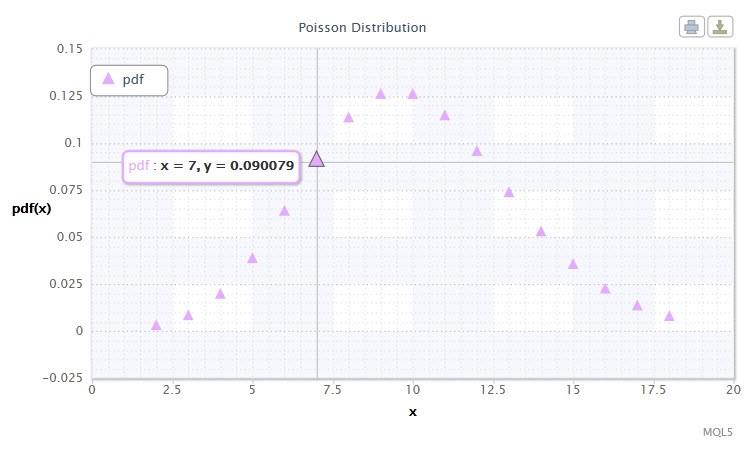
Şekil 12. Poisson dağılım yoğunluğu Pois(10).

Bunun notasyonu aşağıdaki biçime sahiptir: k ~ Pois(λ), burada:

k rastgele bir değişkendir;
φ konum parametresidir (0 < λ).

Rastgele değişken X'in geçerli aralığı: 0 ≤ X ≤ +∞.

Poisson dağılımı, risk derecesini tahmin ederken önemli olan "nadir olaylar yasasını" açıklar.

CPoissondist sınıfı bu dağılımın amaçlarına hizmet edecektir:

//+------------------------------------------------------------------+
//|               Poisson Distribution class definition              |
//+------------------------------------------------------------------+
class CPoissondist : CGamma // CGamma class inheritance
  {
public:
   double            lambda;   //location parameter (λ)
   //+------------------------------------------------------------------+
   //| CPoissondist class constructor                                   |
   //+------------------------------------------------------------------+
   void CPoissondist()
     {
      lambda=15.;
      if(lambda<=0.) Alert("bad lambda in Poisson Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      return exp(-lambda+n*log(lambda)-gammln(n+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      if(n==0) return 0.;
      return gammq((double)n,lambda);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int n,nl,nu,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Poisson Distribution!");
      if(p<exp(-lambda)) return 0;
      n=(int)fmax(sqrt(lambda),5.);
      if(p<cdf(n))
        {
         do
           {
            n=fmax(n-inc,0);
            inc*=2;
           }
         while(p<cdf(n));
         nl=n; nu=n+inc/2;
           } else {
         do
           {
            n+=inc;
            inc*=2;
           }
         while(p>cdf(n));
         nu=n; nl=n-inc/2;
        }
      while(nu-nl>1)
        {
         n=(nl+nu)/2;
         if(p<cdf(n)) nu=n;
         else nl=n;
        }
      return nl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int n)
     {
      return 1.-cdf(n);
     }
  };
//+=====================================================================+

Tüm istatistiksel dağılımları bir makale içinde düşünmek açıkça imkansızdır ve muhtemelen gerekli bile değildir. Kullanıcı, istenirse, yukarıda belirtilen dağılım galerisini genişletebilir. Oluşturulan dağılımlar Distribution_class.mqh dosyasında bulunabilir.

3. Dağılım Grafikleri Oluşturma

Şimdi dağılımlar için oluşturduğumuz sınıfların gelecekteki çalışmalarımızda nasıl kullanılabileceğini görmemizi öneriyorum.

Bu noktada, yine OOP'yi kullanarak, kullanıcı tanımlı parametre dağılımlarını işleyen ve bunları ekranda görüntüleyen CDistributionFigure sınıfını oluşturdum"HTML'de Grafikler ve Diyagramlar"makalesinde açıklanan yollarla .

//+------------------------------------------------------------------+
//|           Distribution Figure class definition                   |
//+------------------------------------------------------------------+
class CDistributionFigure
  {
private:
   Dist_type         type;  //distribution type
   Dist_mode         mode;  //distribution mode
   double            x;     //step start
   double            x11;   //left side limit
   double            x12;   //right side limit
   int               d;     //number of points
   double            st;    //step

public:
   double            xAr[]; //array of random variables
   double            p1[];  //array of probabilities
   void              CDistributionFigure();  //constructor 
   void              setDistribution(Dist_type Type,Dist_mode Mode,double X11,double X12,double St); //set-method
   void              calculateDistribution(double nn,double mm,double ss); //distribution parameter calculation
   void              filesave(); //saving distribution parameters
  };
//+------------------------------------------------------------------+

Uygulama atlanma. Bu sınıfın Dist_type ve buna bağlı olarak Dist_mode ilgili tür ve mod gibi veri üyelerine sahip olduğunu unutmayın. Bu tipler, incelenmekte olan dağılımların ve türlerinin numaralandırmalarıdır.

Bu yüzden, sonunda bazı dağılımların bir grafiğini oluşturmaya çalışalım.

Sürekli dağılımlar için continuousDistribution.mq5 komut dosyası yazdım, anahtar satırları aşağıdaki gibi:

//+------------------------------------------------------------------+
//|                     Input variables                              |
//+------------------------------------------------------------------+

input Dist_type dist;  //Distribution Type
input Dist_mode distM; //Distribution Mode
input int nn=1;        //Nu
input double mm=0.,    //Mu
            ss=1.;    //Sigma
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//(Normal #0,Lognormal #1,Cauchy #2,Hypersec #3,Studentt #4,Logistic #5,Exponential #6,Gamma #7,Beta #8 , Laplace #9)
   double Xx1,      //left side limit
          Xx2,     //right side limit          
          st=0.05; //step
   if(dist==0) //Normal
     {
      Xx1=mm-5.0*ss/1.25;
      Xx2=mm+5.0*ss/1.25;
     }
   if(dist==2 || dist==4 || dist==5) //Cauchy,Studentt,Logistic
     {
      Xx1=mm-5.0*ss/0.35;
      Xx2=mm+5.0*ss/0.35;
     }
   else if(dist==1 || dist==6 || dist==7) //Lognormal,Exponential,Gamma
     {
      Xx1=0.001;
      Xx2=7.75;
     }
   else if(dist==8) //Beta
     {
      Xx1=0.0001;
      Xx2=0.9999;
      st=0.001;
     }
   else 
     {
      Xx1=mm-5.0*ss;
      Xx2=mm+5.0*ss;
     }
//---
   CDistributionFigure F;        //creation of the CDistributionFigure class instance 
   F.setDistribution(dist,distM,Xx1,Xx2,st);
   F.calculateDistribution(nn,mm,ss);
   F.filesave();
   string path=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\Distribution_function.htm";
   ShellExecuteW(NULL,"open",path,NULL,NULL,1);
  }
//+------------------------------------------------------------------+

Ayrık dağılımlar için discreteDistribution.mq5 komutdosyası yazıldı.

Cauchy dağılımı için standart parametrelerle komut dosyasını çalıştırdım ve aşağıdaki videoda gösterildiği gibi aşağıdaki grafiği aldım.

Sonuç

Bu makalede, MQL5'te de kodlanmış rastgele bir değişkenin birkaç teorik dağılımı tanıtılmıştır. Piyasa ticaretinin tek başına ve dolayısıyla bir ticaret sisteminin çalışmasının temel olasılık yasalarına dayanması gerektiğine inanıyorum.

Ve bu makalenin ilgili okuyucular için pratik bir değere sahip olacağını umuyorum. Bu konuda, kendi açımdan, daha fazla konuya değineceğim ve istatistiksel olasılık dağılımlarının olasılık modeli analizinde nasıl kullanılabileceğini göstermek için pratik örnekler vereceğim.

Dosyakonumu:

#	Dosya	Yol	Açıklama
1	Distribution_class.mqh	%MetaTrader%\MQL5\Include	Dağılım sınıfları galerisi
2	DistributionFigure_class.mqh	%MetaTrader%\MQL5\Include	Dağılımların grafik görüntüleme sınıfları
3	continuousDistribution.mq5	%MetaTrader%\MQL5\Scripts	Sürekli dağılım oluşturma komut dosyası
4	discreteDistribution.mq5	%MetaTrader%\MQL5\Scripts	Ayrık bir dağılım oluşturma komut dosyası
5	dataDist.txt	%MetaTrader%\MQL5\Files	Dağılım görüntüleme verileri
6	Distribution_function.htm	%MetaTrader%\MQL5\Files	Sürekli dağılım HTML grafiği
7	Distribution_function_discr.htm	%MetaTrader%\MQL5\Files	Ayrık dağılım HTML grafiği
8	exporting.js	%MetaTrader%\MQL5\Files	Grafik aktarmak için Java komut dosyası
9	highcharts.js	%MetaTrader%\MQL5\Files	JavaScript kitaplığı
10	jquery.min.js	%MetaTrader%\MQL5\Files	JavaScript kitaplığı

Literatür:

K. Krishnamoorthy. Handbook of Statistical Distributions with Applications, Chapman and Hall/CRC 2006.
W.H. Press, et al. Numerical Recipes: The Art of Scientific Computing, Third Edition, Cambridge University Press: 2007. - 1256 pp.
S.V. Bulashev Statistics for Traders. - M.: Kompania Sputnik +, 2003. - 245 pp.
I. Gaidyshev Data Analysis and Processing: Special Reference Guide - SPb: Piter, 2001. - 752 pp.: ill.
A.I. Kibzun, E.R. Goryainova — Probability Theory and Mathematical Statistics. Basic Course with Examples and Problems
N.Sh. Kremer Probability Theory and Mathematical Statistics. M.: Unity-Dana, 2004. — 573 pp.

MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/271

Ekli dosyalar |

ZIP indir

distribution_class.mqh (108.26 KB)

continuousdistribution.mq5 (2.45 KB)

discretedistribution.mq5 (2.01 KB)

distribution_function.zip (59.99 KB)

distributionfigure_class.mqh (19.68 KB)

Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.

Bu yazarın diğer makaleleri

Tartışmaya git

Kaynak Kodun İzlenmesi, Hata Ayıklanması ve Yapısal Analizi

Yürütülen bir kodun yapısını oluşturma ve izleme sorunlarının tamamı, ciddi zorluklar olmadan çözülebilir. Bu olasılık, MQL5 dilinin yeni özelliği - karmaşık veri türlerinin (yapılar ve sınıflar) otomatik olarak oluşturulması ve yerel kapsam dışına çıkarken bunların ortadan kaldırılması nedeniyle MetaTrader 5'te ortaya çıkmıştır. Makale, metodolojinin ve hazır aracın açıklamasını içerir.

Doğrusal Regresyon Örneğiyle 3 Gösterge Hızlandırma Yöntemi

Makale, gösterge hesaplama algoritmaları optimizasyonu yöntemlerini ele alır. Herkes kendi ihtiyaçlarına en uygun yöntemi bulacaktır. Burada üç yöntem açıklanmıştır. Bunlardan biri oldukça basittir, bir sonraki ise sağlam bir matematik bilgisi gerektirir ve sonuncusu ise biraz zeka gerektirir. Göstergeler veya MetaTrader5 terminal tasarım özellikleri, açıklanan yöntemlerin çoğunu gerçekleştirmek için kullanılır. Yöntemler oldukça evrenseldir ve sadece doğrusal regresyon hesaplamasının hızlandırılması için değil, aynı zamanda diğer birçok gösterge için de kullanılabilir.

İstatistiksel Tahminler

Matematiksel model ve yöntemlerin çoğu farklı varsayımlara dayandığı için bir dizinin istatistiksel parametrelerinin tahmini çok önemlidir. Örneğin, dağılım yasasının normalliği veya ayrılma değeri veya diğer parametreler. Bu nedenle, zaman serilerini analiz ederken ve tahmin ederken, ana istatistiksel parametreleri hızlı ve net bir şekilde tahmin etmeye izin veren basit ve kullanışlı bir araca ihtiyacımız var. Makale, rastgele bir dizinin en basit istatistiksel parametrelerini ve görsel analizinin çeşitli yöntemlerini kısaca açıklamaktadır. Bu yöntemlerin MQL5'te uygulanmasını ve Gnuplot uygulamasını kullanarak hesaplama sonuçlarının görselleştirilmesi yöntemlerini sunar.

Fiyat Korelasyonunun İstatistiksel Verilerine Dayalı Sinyalleri Filtreleme

Geçmişteki fiyat davranışı ile gelecekteki eğilimleri arasında herhangi bir ilişki var mı? Fiyat neden bugün önceki günkü hareketinin karakterini tekrarlıyor? İstatistikler, fiyat dinamiklerini tahmin etmek için kullanılabilir mi? Bir cevabı var ve olumlu. Herhangi bir şüpheniz varsa, o zaman bu makale tam size göre. MQL5'te bir ticaret sistemi için çalışan bir filtrenin nasıl oluşturulacağını anlatacağım ve fiyat değişikliklerinde ilginç bir model ortaya çıkaracağım.