기고글 토론 "패턴 검색에서 무자비 대입 방식(6부): 주기적 최적화"

[MetaQuotes]

새로운 기고글 패턴 검색에서 무자비 대입 방식(6부): 주기적 최적화 가 게재되었습니다:

이 기사에서는 MetaTrader 4 및 5 거래에서 자동화 체인 전체를 닫을 수 있을 뿐만 아니라 훨씬 더 흥미로운 작업을 할 수 있게 해준 개선 사항의 첫 번째 부분을 보여드리겠습니다. 이제부터는 이 솔루션을 사용하면 EA를 생성하고 최적화하는 것을 완전히 자동화할 수 있을 뿐만 아니라 효과적인 트레이딩 구성을 찾는 데 드는 인건비를 최소화할 수 있습니다.

전체 아이디어에서 가장 중요한 요소는 터미널과 내 프로그램 간의 상호 작용 시스템입니다. 실제로 이것은 고급 최적화 기준을 갖춘 순환 최적화 프로그램입니다. 가장 중요한 것은 이전 섹션에서 다루었습니다. 전체 시스템이 작동하려면 먼저 MetaTrader 5 터미널 중 하나인 호가 소스가 필요합니다. 이전 글에서 이미 설명했듯이 호가는 내게 편리한 형식으로 파일에 기록됩니다. 이것은 언뜻 보기에 다소 이상하게 작동하는 EA를 사용하여 수행됩니다:

EA의 기능에 저만의 독특한 체계를 사용하는 것은 꽤 흥미롭고 유익한 경험이었습니다. 다음은 제가 해결해야했던 문제의 데모 일뿐이지만 이 모든 것은 EA 거래에도 사용될 수 있습니다: 

작성자: Evgeniy Ilin

[fxsaber]

формулы 2

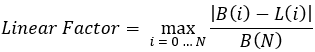
이 공식 안에 무엇이 있는지 이해해 봅시다:

• N - 전체 백테스트 또는 트레이딩 구간에서 완전히 개설 및 청산된 거래 포지션의 수입니다.
• B(i) - 해당 청산된 포지션 "i" 이후의 잔고 라인 값입니다.
• L(i) - 0에서 가장 최근 잔고 지점(최종 잔고)까지 그려진 선입니다.

거의 샤프에 가까운 것 같습니다:

//--- 주식 배열에서 증분의 로그를 계산합니다.
   for(int i = 1; i < m_bars_counter; i++)
     {
      //--- 에퀴티가 변경된 경우에만 추가
      if(m_equities[i] != prev_equity)
        {
         log_return = MathLog(m_equities[i] / prev_equity); // 증분 로그
         aver += log_return;            // 증분 평균 로그
         AddReturn(log_return);         // 증분에서 로그 배열 채우기
         counter++;                     // 수익률 카운터
        }
      prev_equity = m_equities[i];
     }
//--- 샤프 비율을 계산할 값이 충분하지 않으면 0을 반환합니다.
   if(counter <= 1)
      return(0);
//--- 증분 로그의 평균 값
   aver /= counter;
//--- 표준 편차 계산
   for(int i = 0; i < counter; i++)
      std += (m_returns[i] - aver) * (m_returns[i] - aver);
   std /= counter;
   std = MathSqrt(std);
//--- 현재 시간대의 샤프 비율
   double sharpe = aver / std;

[Evgeniy Ilin]

fxsaber #:

거의 샤프에 가까운 것 같아요:

비슷한 점이 있지만 언뜻 보기에는 비슷합니다. 모두가 대차 대조표 성장 모델을 그리워합니다. 잔액 성장의 기울기가 지속적으로 하락하는 경우 (잔액 곡선의 두 번째 미분이 음수 인 경우) 곧 음수가 될 수 있으므로 이러한 모델은 바람직하지 않습니다. 요점은 그래픽적으로 가장 유망해 보이는 곡선을 선택하는 것입니다.

[fxsaber]

Evgeniy Ilin #:

유사점이 있지만 언뜻 보기에는 비슷합니다. 모두가 균형 성장 모델을 그리워합니다. 균형 성장의 기울기가 지속적으로 하락하는 경우 (균형 곡선의 두 번째 미분이 음수 인 경우) 이러한 모델은 곧 마이너스 영역으로 들어갈 수 있으므로 바람직하지 않습니다. 요점은 그래픽적으로 가장 유망해 보이는 곡선을 선택하는 것입니다.

하강 곡선에 대한 샤프 알고리즘은 음수 값을 제공합니다. 나는 비유를 위해서만 당신에게 주었고, 샤프에 대해 논의 할 필요가 없습니다....

내 경험의 예.

• 기준 "아름다운 곡선"-OOS를 통과하지 못합니다.
• 기준 "추악한 곡선"-곡선 자체가 아름다운 것으로 판명 된 반면 OOS를 통과합니다.
• 수수료 없음 - OOS를 통과하지 못함.
• 커미션이 설정됨 - OOS를 통과합니다.

즉, 최적화가 아름다움을 위한 것이라면 피팅 요소가 높다는 것이 밝혀졌습니다. 가치 있는 무언가를 발견하면 아름답게 보입니다.

그래서 저는 아름다움을 직접 찾지 않습니다. 저는 거래 수와 TS 코어의 알고리즘에 더 의존합니다. 목표는 아름다움 기준 없이 아름다움을 얻는 것입니다. 일반적으로이 변형은 OOS를 통과합니다.

ZY 수수료가있는 변형이 더 흥미 롭습니다 (그러나 일반적으로 그 반대 : 수수료 감소-패턴을 찾을 확률이 더 높음). 실제로 트랜잭션 수(통계적 유의성)는 감소하지만 검색 성공 확률은 증가합니다.

[Evgeniy Ilin]

fxsaber #:

하향 곡선에 대한 샤프 알고리즘은 음수 값을 생성합니다. 이것은 단지 비유를 위한 것이므로 샤프에 대해 논의할 필요가 없습니다.....

제 경험에서 나온 예시입니다.

• "아름다운 곡선" 기준 - OOS를 통과하지 못합니다.
• "추악한 곡선" 기준 - OOS를 통과하지만 곡선 자체는 아름답습니다.
• 수수료 없음 - OOS를 통과하지 못함.
• 커미션 설정 - OOS를 통과합니다.

즉, 최적화가 아름다움을 위한 것이라면 피팅 요소가 높다는 것이 밝혀졌습니다. 가치 있는 무언가를 발견하면 아름답게 보입니다.

그래서 저는 아름다움을 직접 찾지 않습니다. 저는 거래 수와 TS 코어의 알고리즘에 더 의존합니다. 목표는 아름다움 기준 없이 아름다움을 얻는 것입니다. 일반적으로이 변형은 OOS를 통과합니다.

ZY 수수료가있는 변형이 더 흥미 롭습니다 (그러나 일반적으로 그 반대 : 적은 수수료-패턴을 찾을 확률이 더 높음). 실제로 트랜잭션 수(통계적 유의성)는 감소하지만 검색 성공 확률은 증가합니다.

하지만 여전히 한계가 있다는 것은 분명합니다. 예를 들어 저는 이렇게 행동합니다:

• 필요한 최소 기대치를 핍으로 설정합니다(스프레드만 고려하고 수수료와 스왑도 대략적으로 추가합니다).
• 필요한 최소 거래 횟수를 설정하는데, 고려되는 구간 길이를 고려하여 필요한 최소 거래 횟수를 설정합니다.
• 곡선 매칭 계수를 조정합니다.

스프레드 내부에서 무언가를 찾는 것은 의미가 없습니다 ). 거래는 거의 없을 것이며, 그것은 사실이며, 아무것도 할 수 없습니다. 모든 곳에 피팅이 있으며 문제는 알고리즘 자체에주의를 기울이지 않고 최소화하는 방법입니다. 방법이 있습니다. 곡선 추정없이 우리는 알고리즘이 처음에는 그랄이라는 사실에만 의지 할 수 있습니다. 나는 그것없이하는 방법, 방법이 있지만 여기에 그런 것을 쓰는 것이 두렵습니다 ))).

[fxsaber]

Evgeniy Ilin #:

여전히 한계가 있다는 것은 분명합니다. 이것이 제가 운영하는 방식입니다:

• 필요한 최소 매트 기대치를 포인트로 설정합니다(스프레드만 고려하고 수수료와 스왑도 대략적으로 추가합니다).

저는 그렇게 하지 않습니다. 시장 규칙성은 브로커의 거래 조건에 의존하지 않습니다. 저는 이런 방식을 선호합니다.

트레이딩, 자동매매 시스템 및 테스트 트레이딩 전략에 관한 포럼

트레이딩의 머신러닝: 이론, 패턴, 실전 및 알고리즘 트레이딩

FXSABER, 2023.08.19 11:10 AM

가장 높은 잠재 수익으로 선택할 수 있는 과거 데이터 브로커. 예를 들어 EURUSD_Broker1의 잠재 수익이 EURUSD_Broker2보다 높습니다. 그러면 EURUSD_Broker1을 선택합니다.

메이저와 크로스 모두 스캘핑이 가능합니다. 하지만 전부는 아닙니다. 각각에 대해 훈련하고 결과를 확인하십시오. 대략적으로 말하면 그것이 제가하는 일입니다.

즉, "바위 속의 금"의 농도가 더 높은 곳을 검색하는 것이 논리적입니다.

• 해당 지역의 길이를 고려하여 필요한 최소 거래 횟수를 설정합니다.

예, 이것은 유전학이 막 다른 골목으로 가지 않도록하는 일종의 도움입니다.

• 곡선 맞춤 계수를 조정합니다.

제가 일부러 하지 않는 작업입니다. 예를 들어 TS가 PF>2.5를 생성하도록 훈련할 수 있습니다. 적절한 수의 거래를 하면 거의 자동으로 아름다운 커브를 생성합니다. 저는 연습을 많이 시작하지 않았습니다. 하지만 연구용으로는 항상 흥미롭습니다.

스프레드 안에서 무언가를 찾는 것은 의미가 없습니다 ). 거래는 거의 없을 것이며, 사실이며, 당신은 그것으로 아무것도 할 수 없습니다. 모든 곳에 피팅이 있으며 문제는 알고리즘 자체에주의를 기울이지 않고 최소화하는 방법입니다. 방법은 있습니다. 곡선 추정없이 우리는 알고리즘이 처음에는 그랄이라는 사실에만 의지 할 수 있습니다. 나는 그것없이하는 방법, 방법이 있지만 여기에 그런 것을 쓰는 것이 두렵습니다 ))).

나는 TS와 확산의 연결을 이해하지 못합니다.

[Evgeniy Ilin]

• Например, можно обучить ТС, чтобы выдавал PF>2.5. При должном количестве сделок это почти автоматом выдаст красивую кривую

아름답지만 모양이 다를 수 있으며 가능한 전진은 모양에 따라 다릅니다. 적어도 작동하는 설정을 찾을 확률이 높아집니다. 2.5의 이익 계수는 매우 뚱뚱하고 1.5는 꽤 많다고 말하고 싶습니다 )) 피팅시 이러한 숫자는 일반적으로 발생합니다. 더 많은 설정을 버림으로써 나머지 설정에 더 많은 가중치를 두는 방법과 같습니다 (제 기준을 의미합니다). 저는 일반적으로 로봇 공학에서 알고리즘보다 애드온에 의해 주요 작업이 수행되고 알고리즘에 거의 의존하지 않는 흥미로운 패러다임에 도달했습니다. 여기서 특정 설정의 중요성을 높이는 모든 기준은 가치가 있습니다. 결국, 총체적으로 그들은 각각 자신의 수준에서 작동합니다.

나머지에 동의합니다.

.

• TS와 스프레드의 연관성을 이해하지 못합니다 .

스캘핑을하는 경우 예, 여기서는 입찰가를 사용하고 규칙적으로 스프레드에서 수레를 요청합니다. 그러나 틱은 많은 사람들에게 다르며 많은 사람들이 그것에 달려 있습니다 ). 요점은 예를 들어 브로커를 변경할 때 신호에 영향을 미치지 않도록 스프레드를 무시하는 것처럼 스프레드가 한 포인트 거래의 평균 크기보다 가능한 한 작았다는 것입니다 (예를 들어, 이것은 내 환상입니다).

[fxsaber]

Evgeniy Ilin #:
아름답지만 모양이 다르며 모양에 따라 가능한 전진이 달라집니다.

MaxBalance 기준(아름다움이 아닌)으로 찾은 커브의 예입니다.

[Anatoli Kazharski]

fxsaber #:

(예쁘기 기준이 아닌) MaxBalance 기준으로 찾은 커브의 예입니다.

이런 방식으로 많은 커브가 선택되는 것을 보면 흥미로울 것입니다("아름다움이 아닌" MaxBalance 기준).

[fxsaber]

Anatoli Kazharski #:

이런 식으로 많은 커브가 선택되는 것을 보는 것은 흥미로울 것입니다("예뻐서가 아닌" MaxBalance 기준).

이것은 해당 옵트 파일의 여섯 번째 결과입니다. 처음 다섯 개는 더 나빠 보입니다.

입력 파라미터 세트가 서로 가깝지 않도록 적은 수의 GA 패스를 수행합니다.

[fxsaber]

아래에서 거래 횟수를 제한하는 MaxBalance 기준이 항상 샘플에서 아름다운 곡선을 제공 할 때 TS를 구축하는 몇 가지 접근 방식이 있다는 인상을 받았습니다. 이 경우 이러한 TS는 OOS에서 완전한 손실이 있더라도 합리적인 것으로 간주 될 수 있습니다. 그러나 이 기사에서 샤프, R^2 또는 기준으로 아름다움을 검색하는 것은 의심스러운 것 같습니다. 아마도 나는 틀렸을 것입니다.