私たちのファンページに参加してください
- ビュー:
- 1108
- 評価:
- パブリッシュ済み:
-
このコードに基づいたロボットまたはインジケーターが必要なら、フリーランスでご注文ください フリーランスに移動
簡単に言うと、これは、確率密度関数を使用して係数と平均を計算している一種の加重平均(または、呼び方によってはデジタルフィルタ)です。PDFの簡単な説明は次のとおりです。
連続確率変数の確率理論、確率密度関数(probability density function、PDF)、密度とは関数です。この関数のサンプル空間(任意の変数によって取られる可能な値の集合)内の任意の与えられたサンプル(または点)の値は確率変数の値がそのサンプルに等しくなる相対尤度を提供するものとして解釈することができます。言い換えれば、任意の特定の値をとる連続確率変数の絶対尤度は(無限の可能な値があるため)0ですが、2つの異なるサンプルにおけるPDFの値を使用して、確率変数の任意の特定の描画において、確率変数が他のサンプルと比較して1つのサンプルに等しくなる可能性がどれほど高いかを推測することができます。
より詳しくはhttps://en.wikipedia.org/wiki/Probability_density_functionでご覧になれます。
この指標には通常のオプションセットがあります。レベルは3種類です。
- 浮動
- 分位数
- またはレベルなし(「オンスロープ」モードに切り替わるとき)
色(およびアラート)の選択肢は下記です。
- 外側レベルの交差
- 中間レベルの交差
- 勾配の変化
指標は通常の価格と平均足の価格を備えており、多時間軸です。
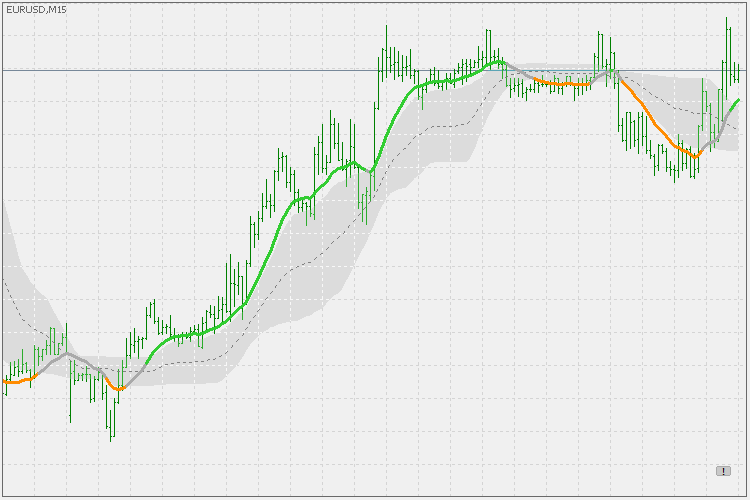
あいまいになるのは、分散と平均パラメータです。
一般に、どちらもPDFmaの「スピード」に影響しています。分散は0から1までの範囲で使用できます。分散が小さければ小さいほど、PDFmaはより速く(そして滑らかに)なります(下の例では、緑の値に分散1、橙色の値に分散0.5を使用しています)。
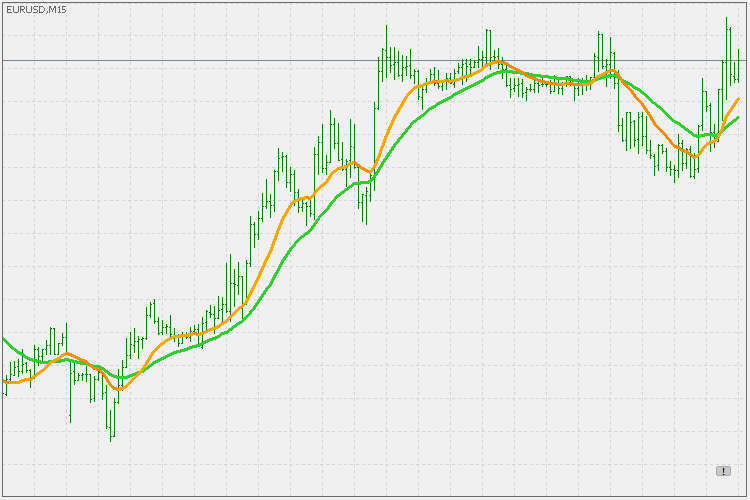
平均は、-1から1の範囲の値を使用する点を除いて同じです。下の例の緑は平均値1を使用し、橙色は平均-1を使用しています。
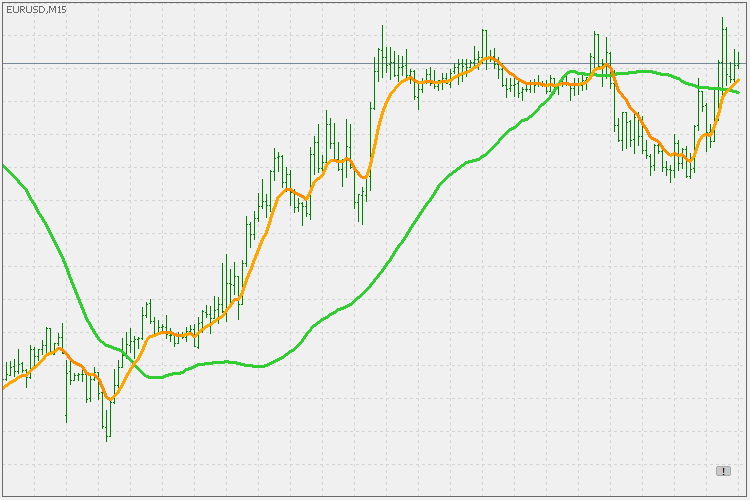
いずれにせよ、このタイプのフィルタ/平均を実験する余地は十分にあります。
MetaQuotes Ltdによって英語から翻訳されました。
元のコード: https://www.mql5.com/en/code/17188
 CashMachine 5min
CashMachine 5min
このエキスパートアドバイザーには、iDeMarker(DeMarker、DeM)とiStochastic(ストキャスティクス)指標が使用されます。利益を保護するためには3つの仮想レベルがあります。
 再帰的な(二重)平滑化されたストキャスティクス
再帰的な(二重)平滑化されたストキャスティクス
この再帰的な(二重)平滑化されたストキャスティクスは、深さ15までの二重平滑化されたストキャスティクスの計算を可能にします。