Derivative - MetaTrader 5のためのインディケータ

数学におけるデリバティブの値の計算は、次の簡単な式によって行われます。

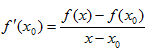, (1)

ここでは、

• x0 — 引数の現在の値
• x — チャートの右側の引数の値
• f(x0) — x0ポイントでの関数の値
• f(x) — хポイントでの関数の値

オリジナルの定義では、xとx0派生する差は、ゼロに向かっていて、つまり極限関数(limit)が使われています。(1)の式を用いて、直接微分を避けながら導関数の近似値を算出することができます。

価格チャートに応じ、x0は現在のバー、またxはいくつかのチャート期間の後に形成される今後のバーです。同様に、f(x0)は現在のバーの価格値、またf(x)は今後のバーの価格値です。すると、(1)の式にf(x0)とf(x)という2つの不明なものが含まれていることがわかります。同じ2つの未知数を含む、追加の式がない為、この場合には方程式の解(1)は存在しません。

f'(x0)導関数を発見することができるように、f(x)とf(x0)として既知の値を入れる必要があります。この為にx0として現在のバーから左にある点を採用する必要があります。現在のバーはxです。その結果、 f(x0)とf(x)が特定の値になります。（xとx0のポイントの価格はチャート上に見える価格値に相応します。）

しかし、計算された値は、デリバティブの助けを借りずに価格の上昇または下落を判断することができるトレーダーによく知られている領域を特色づけるものです。この場合、有用な情報は、単純にデリバティブの値ではなく、隣接するバーでの2つのデリバティブの値の比較です。この時、もし計算された値の符号が異なる場合、価格は極値を介して移行し、極値のタイプは符号の組み合わせによって容易に明確になります。負の数値から正の数値への移行は最少値、また正から負への移行は最大値です。

導関数の計算の原理は、インディケータDerivativeに実装されています。結果、テストするバーとパラメータで『遅延』の設定をしたバーのいくつかの数から離れたバーとの間の価格の差を反映しています。

インディケータを使用する最も簡単な方法としては、ゼロラインとの交差が下から上に起こった場合は買い、上から下に起こった場合は売りとなります。

一番初めにこのインディケータがMQL4で実装され、mql5.comのCode Baseに掲載されたのは、2015年9月9日です。

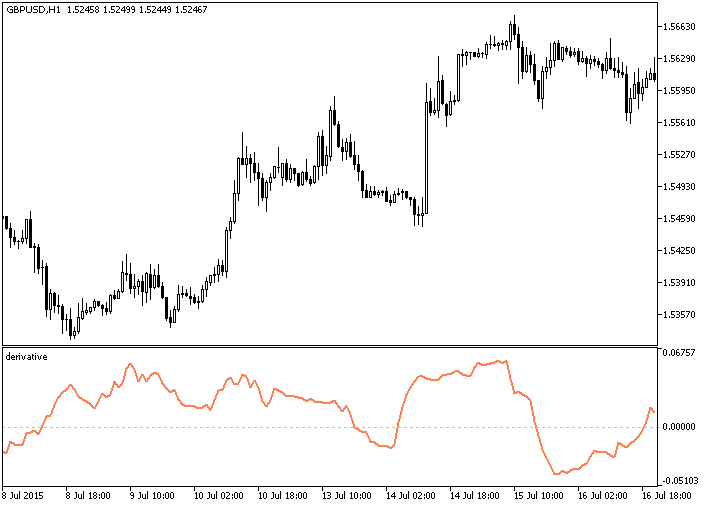
画像1インディケータ Derivative