Los bosques aleatorios predicen las tendencias

Introducción

En un principio, el objetivo de la construcción del sistema era predecir el comportamiento de un cierto instrumento de mercado, por ejemplo, una pareja de divisas. Los objetivos de la predicción pueden ser diversos, no nos limitamos a predecir tendencias, sino más concretamente a predecir el crecimiento («longs») o las caídas («shorts») de los valores de las cotizaciones de una pareja de divisas.

Normalmente, para resolver los problemas de la predicción, el trader toma el gráfico de una pareja de divisas, dibuja una cierta cantidad de indicadores e intenta encontrar una cierta combinación, un patrón que tendrá capacidades predictivas.

En este artículo vamos a estudiar la elección automática de patrones y su valoración preliminar con la ayuda del paquete Rattle del sistema de análisis estadístico R.

1. Sobre Rattle

En calidad de instrumento de predicción del comportamiento de las parejas de divisas, elegiremos el sistema R, que encaja de manera ideal en las tareas de predicción en los mercados financieros y, en particular, para las predicciones del comportamiento de las parejas de divisas. Además, R se mantiene, ante todo, como un lenguaje de programación para los estadistas cualificados, quedando fuera del alcance muchos traders. La complejidad del mismo R se agrava por el hecho de que los instrumentos para la predicción son muy numerosos y están dispersos por los muchos paquetes que, propiamente, constituyen la funcionalidad básica de R.

Rattle (the R Analytical Tool To Learn Easily) une la multitud de paquetes R, que son importantes para la construcción de sistemas comerciales, pero cada uno por separado no son fáciles de usar para los principiantes. No es necesario comprender R para comenzar con Rattle. Pero el resultado del trabajo con Rattle será un código en R, que puede ser utilizado al construir un sistema comercial real. Pero en esta etapa no será necesario tener conocimientos de R.

En cualquier caso, Rattle es un instrumento insustituible en la etapa en la que se proyecta el sistema comercial, y también permite incluso a los principiantes ver rápidamente los resultados de esta u otra idea y obtener una valoración.

Rattle (Williams, 2009) es un sistema operativo gratuito con un código fuente abierto, creado en el marco del paquete estadístico del sistema operativo R (Grupo de trabajo de Desarrollo R, 2011). Como sistema operativo gratuito, el código fuente de Rattle y R están disponible sin limitaciones. El código fuente de Rattle está escrito en el lenguaje С y está permitido a todos (y se fomenta) mirar el código fuente con motivos educativos, para comprenderlo, comprobarlo y ampliarlo.

2. Descripción de los datos de origen

En la base de los cálculos realizados para el artículo yace un conjunto de datos que contiene cotizaciones de seis parejas de divisas EURUSD, GBPUSD, USDCHF, USDJPY, EURGBP, USDCAD con precios de cierre en el marco temporal Н1 en el periodo comprendido desde 10.01.2011 a 24.12.2013, para un total por encima de las 18 mil barras, lo que es suficiente para generar confianza en los cálculos realizados. En base a las parejas de divisas indicadas fue creado un conjunto de datos que se usaba para buscar patrones que pudiesen predecir las posiciones «short-long» (largas-cortas).

El conjunto de datos con las cotizaciones fuente se encuentra en el anexo al artículo con el nombre kot60_110101_131231_UA.txt.

2.1. Creación de una variable objetivo

El primer paso en el proceso es decidir qué es lo que queremos predecir. A pesar del crecimiento aparente, la elección de un objetivo de predicción y de los datos que materializan este objetivo en forma de un conjunto de cifras, tiene un carácter elemental.

Recurrimos a la idea de predecir una tendencia. Esta idea se apoya en el deseo de comerciar con tendencias.

De la definición de tendencia: «la tendencia es creciente si el precio siguiente es mayor que el precio anterior» y al contrario para la tendencia decreciente. De la deficinición se deduce que es necesario predecir el precio de la pareja de divisas. Era de 1.3500 para eurusd, se ha predicho 1.3550, es una tendencia creciente, así que compramos.

Pero las órdenes básicas son las órdenes «comprar» y «vender», y lo que se ha predicho es la magnitud del precio. La magnitud del precio se usa, por ejemplo, en los sistemas comerciales para la ruptura de un nivel. Para realizar un plan de comercio con tendencias será necesario llevar a cabo algunas acciones adicionales sobre comparaciones de precios. Además, ¡parece obvio que no estamos prediciendo que teníamos intención de comerciar!

Por eso, si se había planeado un sistema comercial de tendencia, entonces el modelo deberá predecir la tendencia directamente. Los tendencias deben estudiar el modelo, la variable objetivo debe tomar solo dos valores «comprar» y «vender» o en forma codificada (categórica) «1» y «-1».

La diferencia de los modelos que usan un conjunto de datos de origen para el cálculo de la futura amplitud del precio de un activo financiero, y los modelos que atribuyen el conjunto de datos de origen a una cierta clase, es elemental. El primer tipo pertenece a los modelos regresivos, y el segundo tipo de modelos pertenece a los modelos de clasificación.

Según los modelos de predicción de tipo regresivo se calcula el valor de una cierta magnitud en el futuro, y cuando este futuro acontece, entonces tendremos el valor de hecho de esta magnitud predicha.

Según los modelos de predicción de tipo clasificatorio, se calcula la clase a la que pertenecerá el conjunto de los datos de origen que llega en el momento de la predicción. En calidad de ellas tomaremos dos clases, «long» y «short». Como en cualquier otro modelo de tipo clasificatorio, estas dos clases no tienen una magnitud concreta, «long» no se puede comparar con «short». Aunque para mayor comodidad codifiracaremos en lo sucesivo «long» como «1» y short como «0», no significa que «long» sea más que «short». Para hacer hincapié en esta circunstancia en R y, propiamente dicho, en Rattle para tales variables cualitativas, existe un tipo especializado, las variables categóricas (nominales).

Las «long» y las «short» en calidad de variables objetivo se diferencian de las variables independientes descritas más abajo, en que, en general, no existen. Esta circunstancia concuerda bastante bien con el hecho de que hayamos decidido predecir un futuro que ahora no existe. Sin embargo, podemos representar perfectamente las tendencias sobre datos históricos, dado que en el pasado, el futuro para nostros es una cuestión totalmente abierta.

Para determinar tendencias en base a los datos históricos, se usa el indicador ZigZag, un indicador magnífico en base a datos históricos y nada fiable en el gráfico real: siempre reescribe el último eslabón, y a veces hasta el anterior. Pero en base a los datos históricos, no existe dinámica alguna, por eso se pueden representar tendencias muy bonitas con ayuda de este indicador.

Para construir la variable objetivo, se usa ZigZag con un parámetro «distancia entre virajes» igual a 0.0035 dólares. En la fig. 1 se muestra el resultado.

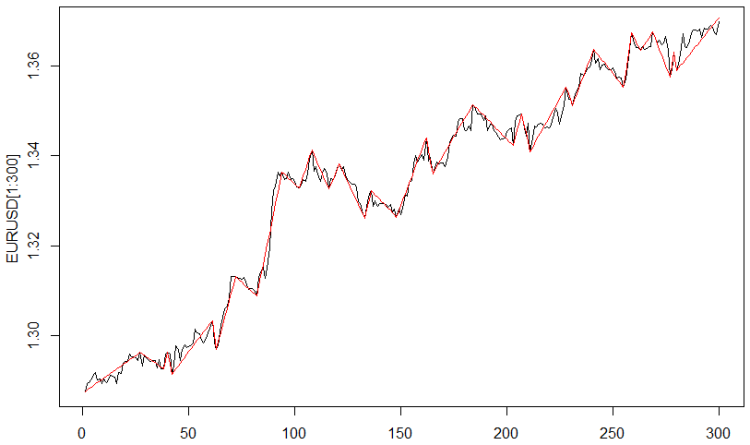
Fig. 1. Indicador ZigZag

Solo queda transformar los valores de los indicadores en una magnitud categórica, en la que long = 1, y «short» = 0.

El resultado se muestra en la fig. 2.

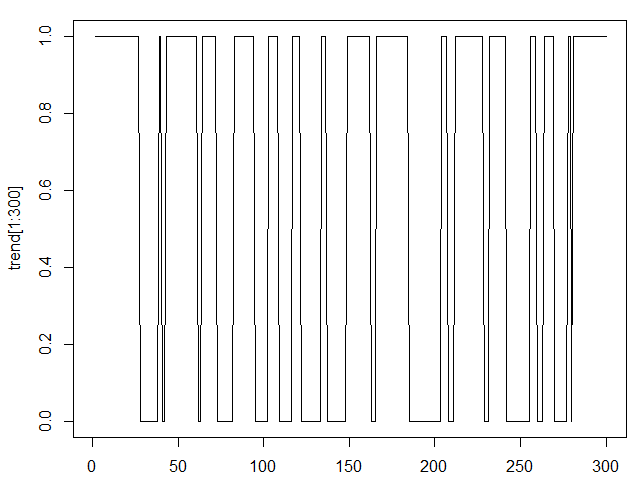
Fig.2. Indicador ZigZag en forma de categoría

Y la última operación con una variable de objetivo. Desplazamos el indicador ZigZag a la izquierda, como resultado de ello tenemos que a la barra actual le corresponde el valor futuro del indicador ZigZag. En este artículo se ha realizado un desplazamiento de una unidad, lo que se corresponde con la predicción de un paso adelante, para los datos utilizados es de una hora hacia adelante.

Se puede realizar un desplazamiento de una cantidad de barras mayor, lo cual se corresponderá con la predicción de una mayor cantidad de barras. Hago notar la diferencia de este enfoque con los modelos de pronóstico, en los que para el pronóstico del valor siguiente necesariamente se usa siempre el valor anterior, es decir, para el pronóstico de dos horas adelante se utilizará el pronóstico de una hora adelante, lo que provocará la simulación de un error de pronóstico.

Los modelos presentados en este artículo y los modelos clasificatorios en general, no poseen propiedades de acumulación de error de pronóstico. En los modelos de clasificación, el pronóstico de dos barras por delante tendrá su propio error de predicción, que no está relacionado en forma alguna con el error de prediccón de una barra por delante.

2.2. Creación de variables independientes

Las variables independientes, predictoras en lo sucesivo, son independientes en el sentido de que entran en el modelo desde fuera, son variables externas y mesurables, o variables calculadas en base a estas variables externas. Por ejemplo, cualquier dato económico, financiero, incluyendo las cotizaciones de las parejas de divisas, es una variable independiente, ya que sus valores se forman como resultado de la actividad de los sujetos en el mercado. A esta misma categoría de variables pertenecen también los indicadores del análisis técnico, que se calculan en base a las cotizaciones.

La elección de las variables independientes es no menos importante que la elección de la variable objetivo. Lo que es más, precisamente la elección de las variables independientes determina el éxito del modelado. La mayor parte del tiempo invertido en el desarrollo de modelos se gasta precisamente en el análisis y la elección del conjunto de variables independientes.

A la definición de predictoras, se ajustan las variables del archivo fuente kot60_110101_131231_UA, en el que se contienen seis cotizaciones de parejas de divisas, así como la fecha y la hora.

Las dos últimas magnitudes son muy interesantes en el plano metódico. Los intentos de usar las fechas y las horas en los sistemas comerciales se dan siempre, pero en nuestros modelos la consideración de cierta información oculta sobre la independencia de las cotizaciones de la hora del día y el día de la semana puede ser expuesta con los modelos de clasificación de manera automática. Lo único, eso sí, es que resulta imprescindible transformar estas dos variables al aspecto categórico: la hora como una categoría con 24 niveles, y la fecha en una variable categórica con cinco niveles, que corresponderán al día de la semana.

Aparte de los predictores de origen ya presentes, crearemos predictores adicionales, que, en mi opinión, descubren la presencia de tendencias en las cotizaciones de origen. Estos predictores adicionales los crearemos con la ayuda de indicadores ampliamente conocidos.

Aplicaremos los siguientes indicadores: la media móvil con los periodos 5,10 y 15; MACD(12,26,9), RSI con periodos 14,21,28. Además, utilizaremos el incremento de las cotizaciones y de las medias móviles. Todas estas transformaciones las aplicaremos a cada una de las seis cotizaciones de las parejas de divisas.

Entre las variables independientes incluiremos el propio indicador ZigZag, como ayuda auxiliar. Para construir los modelos, naturalmente, no se va a utilizar, ya que su valor en la última barra de la derecha resulta desconocido.

De esta forma se han creado 88 variables independientes, más una variable objeto y más una variable auxiliar (ZigZag). La cantidad de datos según cada una de las variables es igual a 18083.

Este conjunto de variables al completo está realizado en forma de zona de trabajo de R y está disponible en el anexo al artículo bajo el nombre TC.RData. Se puede utilizar este conjunto de datos de la siguiente forma:

• cargamos R;
• cargamos la biblioteca Rattle;
• la pestaña Archivo/Zona de trabajo;
• buscamos en el disco el archivo TC.RData y lo cargamos.

3. Análisis intelectual de los datos de origen

El paquete Rattle propone un conjunto de medios para el procesamiento perliminar, a veces denominado intelectual, de los datos: data mining es un término en inglés ampliamente extendido.

3.1. Introducción y visión preliminar

Veamos ciertas posibilidades que se harán disponibles tras la ejecución de las acciones enumeradas antes de este capítulo, más arriba.

Como resultado tendremos la imagen mostrada en la fig. 3.

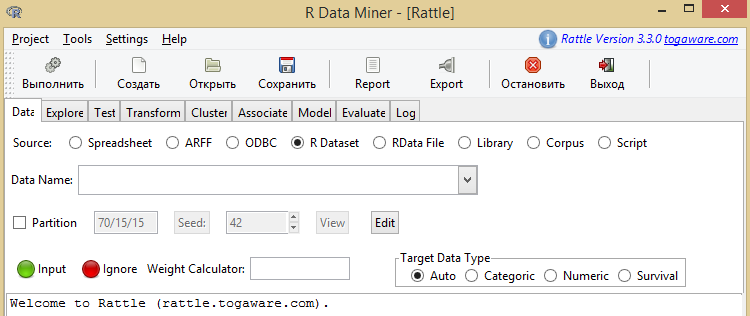
Dib.3. Pantalla inicial de Rattle

La construcción de modelos en Rattle se corresponde con el movimiento desde la pestaña Data a la pestaña Log.

La primera pestaña Rattle – Data, como reza su nombre «Datos», permite cargar los datos con los que se podrá llevar a cabo la manipulación en lo sucesivo.

A nosotros nos interesan dos botones: Spreadsheets y R Dataset.

El botón Spreadsheets permite cargar los archivos con formato Excel. El lector que tenga deseo de comprobar sus ideas, puede preparar su propio archivo Excel y usar las posibilidades de Rattle.

Para repetir las acciones descritas en el artículo o cualquier acción adicional con un archivo claramente exesivo, anexo al artículo, hay que pulsar el botón R Dataset. Este botón carga el archivo en formato R, llamado «Espacio de trabajo» o «Archivo de trabajo». Tienen una extensión en el disco .RData. Este archivo debe cargarse en R, después de lo cual se encontrará disponible mediante este botón.

Cargamos nuestro archivo preparado de antemano y obtenemos la parte superior de la imagen en la fig. 4 y la parte inferior en la fig. 5.

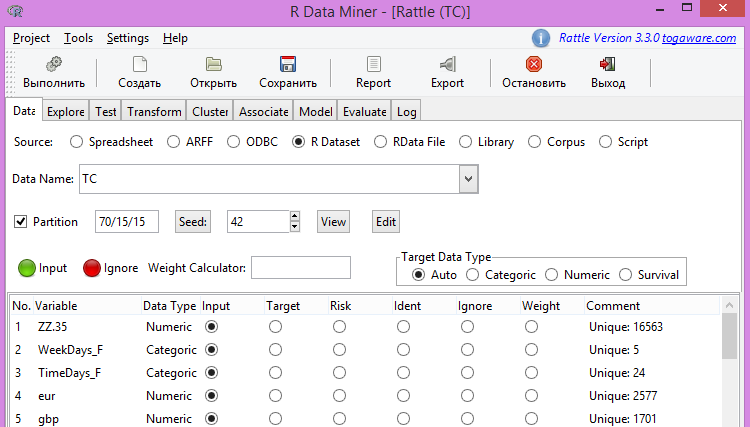
Fig.4. Parte superior del archivo fuente

Fig.5. Parte inferior del archivo fuente

3.2. Correlación entre la variable objetivo y la variable independiente

Observación. El botón «Ejecutar» juega un papel determinante: al principio se prepara la acción, pero no se lleva a cabo. Para que cualquier función se ejecute, es necesario pulsar el botón «Ejecutar». Es imprescindible hacerlo en todas partes al preparar las acciones indicadas en este archivo.

En la fig. 4 se puede ver la lista de variables, sus características, así como el papel de estas variables en sus usos. Dado que no es nuestra intención, y en principio no podemos utilizar el indicador ZigZag en los modelos, entonces, antes de construir los modelos, lo marcaremos con Ignore - ignorar.

Las variables restantes, en nuestro caso, se usan como variables de entrada, excepto la última variable, que se usa como variable objetivo - Target.

Un valor importante a la hora de fundamentar el nivel de confianza por los resultados de la modelación lo juega el botón Partition, con la ayuda del cual el conjunto de datos fuente puede ser dividido en tres partes, o no ser dividido en absoluto. En este lugar se indican las proporciones del conjunto de datos que son usados para el entrenamiento del modelo (Training), la comprobación del modelo (Validation) y el testado del modelo (Testing).

En el campo siguiente se indica el número inicial para el contador de cifras semialeatorio. El sentido de todo esto reside en lo siguiente: por ejemplo, un 70% de los datos de origen, que son compuestos en el conjunto de datos de entrenamiento, se eligen del conjunto de datos fuente de una manera aleatoria. Como resultado de esto, las dos partes restantes de un 15% (al igual que en nuestro caso) también representan una secuencia aleatoria de barras.

Por eso, modificando Seed, podemos obtener del conjunto de datos fuente una cantidad aleatoria de conjuntos de datos de entrenamiento y y de otro tipo.

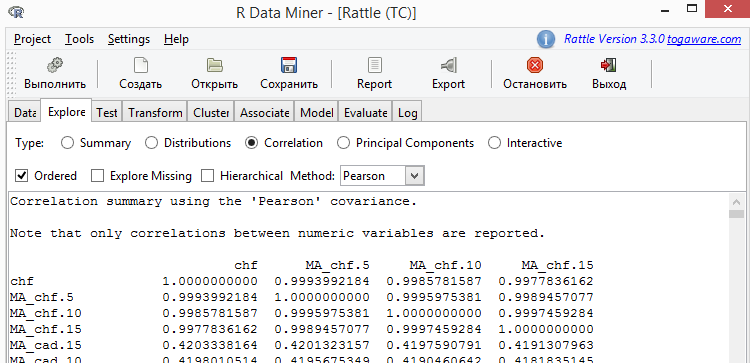
Fig.6. Correlación de las variables

En el recuadro obtenido, cuyas dimensiones son bastante considerables, encontramos una columna con el encabezado ZZ.35, a partir del cual se ha seleccionado el extracto mostrado en el recuadro de más abajo.

Variable	ZZ.35
RSI_cad.14	-0.0104122177
JPY.dif2	-0.0088412685
EUR.dif3	-0.0052379279
CHF.dif3	-0.0049692265
GBP.dif3	-0.0047409208
GBP.dif1	0.0044691430
MA_cad.15.dif1	-0.0039004722
JPY.dif1	-0.0023831247
GBP.dif2	-0.0015356091
EUR.dif2	-0.0013759749
CHF.dif2	-0.0012447101
EUR.dif1	0.0005863149
MA_cad.10.dif1	0.0023981433
CHF.dif1	0.0024543973
MA_gbp.5.dif1	0.0043757197
MA_cad.5.dif1	0.0075424397
MA_gbp.10.dif1	0.0094964069
EURGBP.dif1	0.0095990416
CAD.dif1	0.0110571043

Recuadro 1.  Correlación de variables

Podemos ver que una lista bastante grande de variables tiene una correlación con ZZ.35 menor a 0.01. Y la magnitud de una correlación, menor a 0.1, no permite extraer ninguna conclusión sobre la influencia de variables independientes en la variable objetivo.

En esta etapa destacamos este hecho y lo utilizaremos según las circunstancias para valorar los modelos.

En los modelos de clasificación, el nivel de influencia de los predictores en la variable objetivo juega un papel extremadamente importante. Se considera que con una magnitud pequeña de correlación el predictor correspondiente se se muestra como ruido en el modelo, lo que provoca su reentrenamiento. Entendemos por reentrenamiento del modelo un estado suyo en el que el modelo comienza a tener en cuenta información poco relevante para la variable objetivo y los predictores.

No existen recomendaciones en lo que respecta a la magnitud de la correlación. Normalmente se usa el número mágico para la estadística, el 5%. Pero, en principio, esto no resulta fiable. La cuestión es que la eliminación de los indicadores que para los modelos son ruido, provoca una reducción del error de predicción. Y la eliminación del predictor que no es ruido para el modelo, provoca el aumento del error de predicción. Así que la lista mínima de predictores útiles para el modelo se establece de manera experimental.

3.3. Escalado

Algunos modelos, por ejemplo, las máquinas de vectores de apoyo SVM, son demasiado sensibles al diferente escalado de los predictores, refieriéndonos con ello a lo siguiente. Por ejemplo, la pareja de divisas EURUSD tiene una variabilidad de datos en los límites de 0.5, la pareja de divisas USDJPY tiene una variabilidad de varias décimas de unidad. Para evitar un escalado diferente de los predictores, estos son transformados en la pestaña Transform en una sola escala, que es lo preferible cuando la fluctuación de todos los predictores tienen lugar en el diapasón [0-1].

Para llevar a cabo el escalado, introducimos Transform/Rescale/Scale [0-1]. A continuación, establecemos todas las variables y pulsamos, como siempre, «Ejecutar».

3.4. Transformación en tipo categórico

La transformación en tipo categórico permite transformar el valor de la variable numérica en un factor de varios niveles. Entre nuestros predictores, existe un candidato claro a ser transformado en un factor multinivel, se trata del indicador RSI, que, como se considera, teniendo en cuenta sus valores más cerca del cero o del 100 muestra el viraje de la tendencia.

Para llevar a cabo la transformación de los valores del indicador RSI en una forma categórica, introducimos: Transform/Recode/KMeans, en este caso, la cantidad de niveles de los factores se establecerá como igual a 8. Marcamos todos los indicadores RSI y, como siempre, pulsamos «Ejecutar».

Bien, marcamos en la pestaña Data la variable ZZ.35 como Ignore y podemos pasar a la construcción de los modelos.

4. Algoritmo general del modelo de clasificación

En Rattle están disponibles los siguientes modelos:

• modelo de clasificación en forma de árbol (Tree);
• modelo de bosque aleatorio (forest);
• modelo de árboles intensificado (ada);
• modelo de máquina de vectores de apoyo (SVM);
• modelos lineales generalizados (glm);
• modelo de redes neuronales (NNET).

A pesar de la diferencia sustancial de los modelos de clasificación, y no solo de los disponibles en Rattle, todos tienen rasgos comunes, que consisten en lo siguiente.

Se toma un conjunto de entrenamiento, que consta de líneas (en nuestro caso 18030), que contienen los valores de los predictores (88, en nuestro caso) y el valor de la variable objetivo – «long» o «short» en nuestro ejemplo.

Cualquiera de los algoritmos de clasificación resuelve la tarea siguiente: separar la combinación de los valores de los predictores a los que corresponde «long» de la combinación de los valores de los predictores a los que corresponde «short». Esta es la etapa de entrenamiento del modelo.

A continuación viene la etapa de comprobación del modelo.

Tomamos otro conjunto de datos, y como recordamos, hemos dividido el conjunto de datos fuente en tres partes, y se comprueban las combinaciones de los predictores que se compararon con aquellos que que fueron obtenidos en la etapa de entrenamiento. Para cada combinación de los predictores se muestran apreciaciones sobre la pertenencia a «longs» o «shorts». Dado que en el conjunto de datos de prueba son conocidos estos valores, entonces se compara el resultado de la predicción con un hecho. La correspondencia de «longs-shorts» reales con lo predicho es lo que da el error de predicción.

Si el resultado no nos conviene, podemos volver a la etapa de análisis intelectual de los datos, con el objeto de mejorar el resultado. Por desgracia, esta cualidad de esta etapa se ve determinada prácticamente en su totalidad por la expriencia del trader. Se llevan a cabo los cambios del cojunto de datos fuente, y de nuevo se ejecuta la modelación.

Si los resultados en el conjunto de datos de entrenamiento y comprobación nos parecen adecuados, entonces comprobamos de nuevo el modelo sobre el conjunto de datos que aún no ha sido usado, el conjunto de datos de prueba.

La calidad de los modelos no consiste solo en lo pequeño que sea el error de predicción, sino también en las pequeñas divergencias en la magnitud de este error en los diferentes conjuntos de datos, esto nos habla de la fiabilidad del modelo y la ausencia de reentrenamiento, en el argot de los traders se llaman ajustes superiores.

En el artículo vamos a estudiar solo uno de los modelos, el modelo de bosque de árboles aleatorios, llamado de modo abreviado «bosque aleatorio».

5. Modelo de bosque aleatorio

5.1. Breve panorámica

El algoritmo de trabajo del trader se puede representar de la siguiente forma: se toma la cotización de una pareja de divisas, se le aplica un cierto conjunto de indicadores y, según la totalidad de los valores de la cotización y los indicadores, se toma una decisión comercial.

Al sencillísimo sistema comercial «Media móvil», en el que se compra cuando el precio actual es mayor a la media móvil, y se vende si es menor, se le pueden añadir condiciones adicionales, por ejemplo, los valores del indicador RSI. Como resultado, el trader obtiene un árbol de decisiones, en cuyas hojas se encuentran los valores de la cotización de la pareja de divisas, los valores de la media móvil y los valores del indicador RSI, y en sus raíces tiene dos valores de «comprar-vender».

El proceso descrito de construcción del árbol de decisiones está automatizado en el modelo de árboles de clasificación. Como resultado, se obtiene un árbol, en el argot de los traders, un patrón.

El algoritmo de un árbol por separado no puede producir modelos exactos, porque la variedad provoca una inestabilidad que se puede observar al crear árboles de decisiones por separado.

El lector puede comprobar por sí mismo esta afirmación, con ayuda de Rattle, utilizando el modelo Tree, que realiza el algoritmo descrito de construcción del árbol.

La idea del modelo del bosque de árboles aleatorios reside en la inclusión en la composición del modelo, no solo de un árbol clasificatorio (ni un patrón), sino de muchos árboles. Como resultado, los bosques aleatorios tienen tendencia a poseer una alta resistencia ante los cambios en los datos, se muestran muy resistentes al ruido (es decir, a las variables que tienen una pequeña influencia en la variable objetivo).

La aleatoriedad utilizada por el algoritmo del bosque aleatorio se manifiesta en la elección, tanto de la línea del recuadro (de observaciones), como de los indicadores. Precisamente esta aleatoriedad determina la significativa resistencia al ruido, a las irrupciones y el reentrenamiento, si lo comparamos con otros clasificadores con forma de árbol.

La aleatoriedad, asimismo, determina una capacidad calculatoria significativa. En la creación de un árbol de decisiones suelto, el desarrollador del modelo puede elegir una multitud aleatoria de observaciones, disponibles en el conjunto de datos de entrenamiento. Además, en cada nudo del proceso de creación del árbol de decisiones se examina solo una pequeña parte de todas las variables disponibles al determinar la mejor división del conjunto de datos. Esto provoca una disminución significativa de las exigencias a las potencias del cálculo.

En conclusión, podemos decir que el bosque aleatorio es una buena elección para construir los modelos, por una serie de motivos. Con frecuencia es necesario un pequeño procesado preliminar de los datos, dado que los datos no deben estar normalizados, y la aproximación a las irrupciones es flexible. Se pueden evitar las exigencias en la elección de variables, porque el algoritmo elige por sí mismo las variables de manera efectiva. Dado que se crea una gran cantidad de árboles, utilizando dos niveles de aleatoriedad (de observación y predictores), entonces cada árbol es un modelo independiente efectivo, y el modelo resultante no es proclive al reentrenamiento sobre el conjunto de datos de entrenamiento.

Los algoritmos de los bosques aleatorios con frecuencia crean de 100 a 500 árboles. Al componer el modelo final, las decisiones tomadas por cada uno de los árboles se unen mediante el procesado de los árboles como iguales. La decisión final en el conjunto de los árboles será la decisión que se tome en la mayor parte de los árboles constituyentes del grupo. Incluso si 51 de estos 100 árboles indican «long», se tomará la decisión de «long», aunque, posiblemente, con menor seguridad.

5.2. Algoritmo

5.2.1. Formación del extracto del conjunto de datos

El algoritmo de formación del árbol aleatorio crea muchos árboles de decisiones, utilizando un concepto, llamado agregación bootstrap (bagging es la abreviatura de bootstrap aggregation), para introducir la aleatoriedad en el proceso de formación del extracto. La agregación bootstrap es la idea de reunir el extracto aleatorio de observaciones en un casillero. En el orden aleatorio se crean muchos casilleros de las observaciones elegidas, obtenidas de las observaciones de origen en el conjunto de datos fuente.

La selección para el casillero se hace mediante sustitución, lo que significa que una observación por separado tiene oportunidad de aparecer múltiples veces en un casillero concreto. Con frecuencia, el volumen del extracto es el mismo que un conjunto completo de datos, y en la práctica, resulta que casi dos tercios de las observaciones serán incluidas en los casilleros (con repeticiones) y un tercio no será tenido en cuenta. Después, cada casillero de observaciones se usa como conjunto de datos de entrenamiento para crear un árbol de decisiones, y las observaciones que no han sido tenidas en cuenta pueden ser utilizadas como extracto independiente para la valoración de datos.

5.2.2. Formación del conjunto de predictores

El segundo elemento básico de la aleatoriedad concierne a la elección de predictores para la división del conjunto de datos. A cada paso en la creación de un nudo de decisión (es decir, en cada punto de división del árbol), se elige un conjunto de predictores aleatorio y, por lo común, pequeño. Solo se examinan los predictores elegidos a la hora de elegir en el punto de división. Para cada nudo en la creación del árbol de decisiones se examina un conjunto aleatorio diferente de predictores.

5.2.3. Aleatoriedad

Mediante la formación de conjuntos aleatorios, tanto de datos, como de variables, se obtienen árboles de decisiones que poseen, en virtud de una finalidad definida, diferentes orientaciones con capacidad resolutiva para diversas multitudes de datos. Precisamente este cambio permite considerar este conjunto de árboles como una presentantación del equipo de expertos colaboradores, con un peritaje distinto dará una predicción «mejor».

La formación de extractos también presupone otra ventaja significativa, la efectividad de cálculo. Estudiando solo una pequeña parte de la cantidad total de predictores, al estudiar la cuestión de la división, se reducen significativamente los volúmenes de cálculos requeridos.

Al crear cada árbol de decisiones, el algoritmo de formación del árbol aleatorio normalmente no va a romper el árbol de decisiones. Se considera que el bosque aleatorio de árboles sobreajustados puede dar un modelo muy bueno, que se cumpla bien en base a los nuevos datos.

5.2.4. Cálculo en conjunto

En el despliegue de muchos árboles de decisiones como un modelo solo, cada árbol tiene el mismo peso en el proceso final de toma de decisiones. Simplemente, es la mayoría la que dicta el resultado. Por eso el 51% de las particiones y el 99% de las particiones dan una misma clase, por ejemplo, de «longs».

Los resultados de los cálculos presentados por Rattle son parciales: el usuario obtiene solo el resultado en forma de clase. Al usar el modelo en R se hacen accesibles los resultados en forma de probabilidad de clase.

5.3. Construcción del modelo de árbol casual

Para construir el modelo es necesario introducir Model/Forest , después comenzará el cómputo del modelo, que ocupará varios minutos para nuestros datos de origen.

Dividiré el resultado del cálculo en varias partes y lo comentaré.

Veamos los resultados mostrados en la fig. 7.

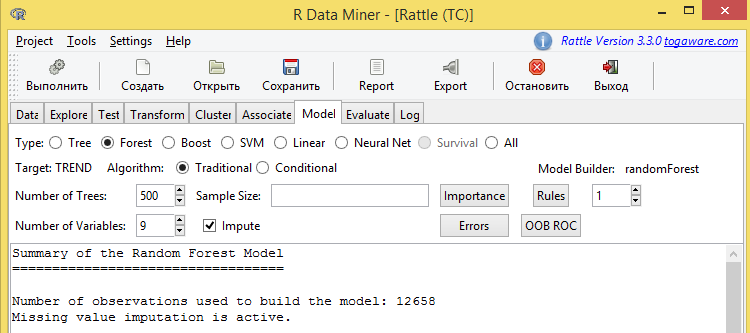
Fig.7. Parte superior de los resultados del ajuste del modelo del bosque aleatorio

Destacaremos cierta información en esta imagen.

Variable objetivo – TREND.

Durante la construcción del modelo se crearon 500 árboles. Al producirse la división en cada nudo del árbol se usaron 9 predictores (variables). Además de esto, a nosotros nos resultan de gran interés los botones Errors (Errores) y OOB ROC.

A continuación, se muestra la información sobre el error de predicción, que tiene el aspecto que sigue:

OOB estimate of error rate: 15.97%

Confusion matrix:

	0	1	class.error
0	4960	1163	0.1899396
1	858	5677	0.1312930

Recuadro 2. Matriz de conjugación (de errores) para el conjunto de entrenamiento

La transmisión es la siguiente: Magnitud del error de valoración fuera del casillero: 15.97%.

El error de predicción obtenido es a todas luces considerable. Es importante precisar cómo se ha obtenido, precisamente: «fuera del casillero». El asunto es que, para construir el modelo no se usó todo el conjunto de datos de entrenamiento que, a su vez, consituye un 70% del conjunto de datos de origen. Para construir el modelo se usó aproximadamente el 60% del conjunto de datos de entrenamiento, y el 40% quedó sin utilizar. Este 40% precisamente es llamado «Out of bag» - fuera del casillero. Precisamente en base a estos datos se ha obtenido el error de predicción, un 15.97%.

Siguamos con el texto.

La matriz de conjugación, aún no llamada matriz de errores, se lee del modo siguiente. 

La línea superior es la predicción de «shorts» y «longs». A la izquierda, a un lado, están las «shorts» y «longs» reales, obtenidas del indicador ZigZag para los datos históricos.

La magnitud 4960 con las coordenadas (0,0) es la cantidad de «shorts» que fueron correctamente predichas. La siguiente magnitud, 1163, es la cantidad de «shorts» que fueron predichas como «longs».

La magnitud 858 con las coordenadas (1,0), es la cantidad de «longs» que fueron predichas como «shorts». La magnitud 5677, es la cantidad de «longs» correctamente predichas.

A continuación vienen los resultados del modelado.

Mostraré varias líneas del recuadro grande, en el que se enumeran todas las variables del modelo. Se trata de un recuadro sobre la "importancia" de las variables.

	0	1	MeanDecreaseAccuracy	MeanDecreaseGini
MA_eur.5.dif1	42.97	41.85	54.86	321.86
EUR.dif3	37.21	46.38	51.80	177.34
RSI_eur.14	37.70	40.11	50.75	254.61
EUR.dif2	24.66	31.64	38.24	110.83
MA_eur.10.dif1	22.94	25.39	31.48	193.08
CHF.dif3	22.91	23.42	30.15	73.36
MA_chf.5.dif1	21.81	23.24	29.56	135.34

Recuadro 3. Importancia de las variables dentro del modelo de bosque aleatorio.

El recuadro contiene varias valoraciones de la importancia de las variables. Por «importancia» entendemos el nivel de influencia de una variable concreta sobre la variable objetivo. Cuanto mayor sea la magnitud de la valoración, «más importante» será la variable correspondiente.

La información de este recuadro se usa para excluir del modelo las variables menos importantes. Como sucede en general en la estadística, al igual que en la clasificación en concreto, se considera que cuanto más simple sea el modelo, mejor será, se entiende que no por la pérdida de precisión del modelo, por supuesto.

Lo último que resulta de interés en la pestaña Model es el botón Errors. Lo pulsamos, obteniendo la fig.8.

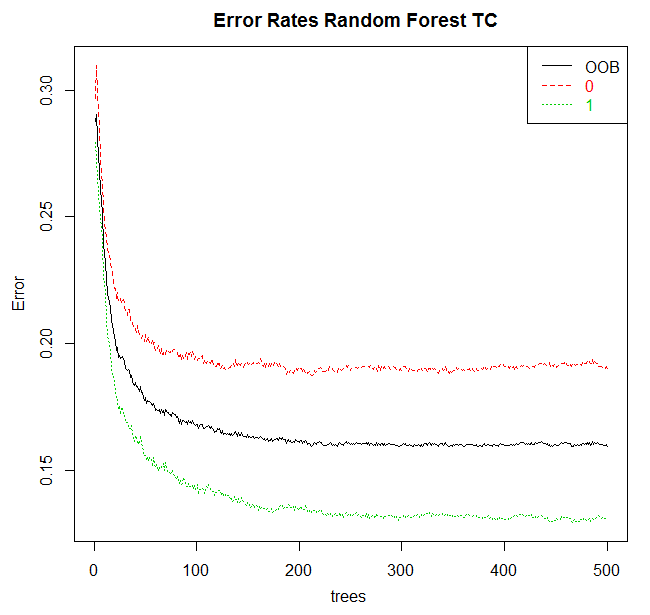
Dib.8. Dependencia del error de modelado con respecto a la cantidad de árboles

6. Eficiencia de los modelos

La valoración de la eficacia de los modelos se realiza en la pestaña Evaluate, en la que Rattle proporciona acceso al conjunto de opciones para la valoración de la efectividad de los modelos.

De toda la lista de opciones presentadas de valoración de la efectividad de los modelos, nos detendremos en Error Matrix (matriz de errores), que en la pestaña anterior era la matriz de conjugación.

Al pasar de la pestaña Model a la pestaña Evaluate, el último de los modelos creados será cancelado automáticamente mediante una etiqueta. Esto se corresponde con la manera general de comportarse de Rattle: creamos y ajustamos el modelo, después investigamos su efectividad, trasladándonos a la pestaña Evaluate.

Para valorar el modelo es imprescindible indicar el conjunto de datos sobre el que hay que realizar la valoración. La siguiente línea de las opciones dentro del interfaz Rattle muestra el conjunto de las fuentes de datos alternativas.

Las primeras cuatro opciones para Data corresponden a la división del conjunto de datos indicado en la pestaña Data. Las opciones son Training (entrenamiento), Validation (comprobación), Test (testado) y Full (conjunto completo). El concepto de la división del conjunto de datos en los conjuntos de entrenamiento/comprobación/testado se ha discutido con anterioridad.

La primera opción (pero no la mejor variante) debe valorar el modelo sobre el conjunto de datos de entrenamiento. Por lo general, esta no es una buena idea. El problema con la valoración del modelo sobre el conjunto de datos de entrenamiento consiste en que el modelo fue creado en este mismo conjunto de datos. El modelo debe ejecutarse muy bien sobre el conjunto de datos de entrenamiento, porque nos hemos esforzado especialmente en ello. Pero el modelo se ejecutará siempre en base a datos antes desconocidos.

Es impresindible adoptar un enfoque que posibilite una ejecución buena del modelo en base a datos nuevos y desconocidos de antemano. En este caso, obtenemos una clasificación real de los errores del modelo, que reflejará la diferencia de predicción según los modelos y los datos reales. Esta clasificación de errores sobre un conjunto desconocido, y no una clasificación de errores sobre el conjunto de datos de entrenamiento, dará una mejor valoración de la efectividad del modelo.

Utilizamos el conjunto de datos de Validation (Comprobación) para comprobar la efectividad del modelo al crearlo y ajustarlo. De esta forma, tras crear un modelo, se comprobará la efectividad según ese conjunto de datos de comprobación. A continuación se pueden cambiar algunas opciones de los ajustes para la creación de un modelo. Comparamos el nuevo modelo con el viejo, basando su efectividad en el conjunto de datos de comprobación. En este sentido, el conjunto de datos de comprobación se usa durante el proceso de modelado, para crear el modelo definitivo. Por consiguiente, tendremos todavía una valoración desubicada de la efectividad definitiva de nuestro modelo, si nos fiamos del conjunto de datos de comprobación para esta medida.

El conjunto de datos Test (Testado), es el conjunto de datos definitivo, que no se ha usado en absoluto durante la creación del modelo. En cuanto hemos identificado el «mejor» modelo basado en los conjuntos de datos de entrenamiento y comprobación, entonces podemos valorar la efectividad del modelo en el conjunto de datos de testado. Se trata de la valoración de la efectividad esperada sobre cualquier conjunto de datos nuevos. La cuarta operación utiliza para la valoración del modelo el conjunto de datos Full (Todo el conjunto, es la unión de los conjuntos de los datos de entrenamiento, comprobación y testado). Esto, como se puede notar, no es más que una curiosidad, y no proporciona una efectividad definitiva.

Otra posibilidad disponible como fuente de datos, se proporciona mediante la introducción de extractos. Estará disponible si se elige la opción Score como tipo de valoración. En este caso se desplegará una ventana para introducir ciertos datos adicionales.

La matriz de errores (de conjugación) se usa para predecir la variable objetivo categórica.

La matriz de errores (Error Matrix) muestra los resultados reales contra los resultados predichos. Se muestran dos recuadros: el primero muestra los resultados cuantitativos, el segundo recuadro muestra los resultados en tanto por ciento.

En Rattle la matriz de errores se encuentra en la pestaña Evaluate. Pulsando el botón «Ejecutar» se ejecuta el modelo elegido sobre el conjunto de datos indicado para la predicción del resultado para cada una de las observaciones en este conjunto de datos. Las predicciones se comparan con las observaciones reales.

En la fig. 9 se muestra la matriz de errores para el modelo de bosque aleatorio calculado con anterioridad.

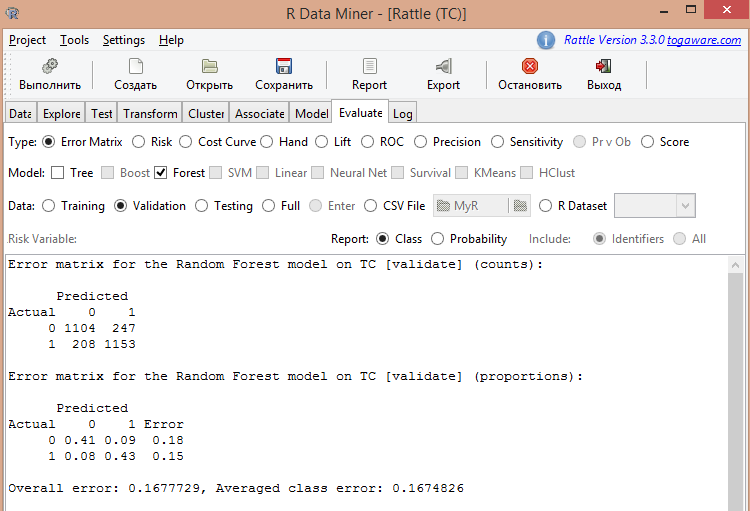
Fig.9. Resultado de la valoración del modelo de bosque aleatorio

Como podemos ver en la imagen, el error medio constituye un 0.167, es decir, el 16.7%. En la etapa de entrenamiento se obtuvo un error de predicción igual al 15.97%. Se pueden considerar estas magnitudes como iguales.

Realicemos los cálculos para el conjunto de datos de testado. Obtenemos el siguiente resultado:

Error matrix for the Random Forest model on TC [test] (counts):

	Predicted	Predicted
Actual	0	1
0	1016	256
1	193	1248

 Recuadro 4. Matriz de errores para el modelo de bosque aleatorio en magnitudes absolutas (conjunto de prueba)

Error matrix for the Random Forest model on TC [test] (proportions):

	Predicted	Predicted
Actual	0	1	Error
0	0.37	0.09	0.20
1	0.07	0.46	0.13

Recuadro 5. Matriz de errores para el modelo de bosque aleatorio en magnitudes relativas (conjunto de prueba)

Overall error: 0.1654994, Averaged class error: 0.1649244

El error de predicción es igual a 16.4%.

Las tres cifras obtenidas son aproximadamente iguales, lo cual habla de un resultado de modelado asumible.

Hay que destacar, por otra parte, que la efectividad de los modelos que calcula Rattle debe ser comprobada obligatoriamente en el simulador de los terminales МetaТrader 4 o MetaTrader 5. Después, como viene siendo habitual, en la demo cuenta y la cuenta real con lotes pequeños. Solo después de esto se podrá llegar a conclusiones definitivas sobre el modelo.

7. Mejora del modelo

Más arriba, al investigar la correlación de la pseudo variable objetivo ZZ.35 con los predictores, resultó que una cantidad significativa de predictores se muestra débilmente correlacionada con la variable objetivo.

Eliminamos aquellos predictores que tengan un coeficiente de correlación menor a 0.01. Para ello, en la pestaña Data marcamos los predictores correspondientes como ignorados (Ignore)   y repetimos el cálculo del modelo de bosque aleatorio en la pestaña Model.

Obtenemos los resultados siguientes:

• Error de predicción fuera del casillero = 15.77%;
• Error de predicción en el conjunto de datos de comprobación = 15.67%;
• Error de predicción en el conjunto de datos de testado = 15.77%.

Aunque el error haya disminuido considerablemente, pero, lo que es más importante, haya disminuido la brecha entre errores de predicción en distintos conjuntos de datos, nuestro modelo es estable.

Se puede continuar eliminando predictores, guiándose por el recuadro de correlaciones. Además, es posible intentar mejorar la efectividad del modelo (disminuir el error de predicción), utilizando la información del recuadro de importancia de los predictores, que se ha obtenido al calcular el modelo.

En cualquier caso, el proceso de exclusión de los predictores debe continuarse hasta que la eliminación de los predictores no provoque un empeoramiento en la efectividad del modelo. En esta etapa ya se podrá parar, ya que dispondrá usted de un modelo mínimo, pero efectivo para un conjunto concreto de predictores.

8. Uso del modelo en el terminal MetaTrader 4

En teoría, podemos imaginarnos la siguiente organización del comercio en bolsa utilizando Rattle. Los datos de entrada para Rattle son preparados en forma de archivo Excel por un cierto instrumento externo para un periodo de un día o más. Al cerrar la bolsa, el trader obtiene los precios necesarios, los introduce en un archivo de origen, hace en unos pocos minutos una predicción para el día siguiente y antes de la apertura de los movimientos de la bolsa ya tiene un pronóstico para el día completo.

No logrará comerciar dentro del día sin el terminal МetaТrader 4 o su análogo.

Para organizar el comercio automático o semiatomático utilizando Rattle se necesitará:

• un modelo entrenado de antemano, que haya sido guardado en forma de espacio de trabajo R;
• una biblioteca de interacción del terminal y R;
• el código en R, que transmite la porción de turno de datos al modelo, obtiene el resultado y envía el resultado del modelado de vuelta al terminal.

El entrenamiento de uno de los seis modelos disponibles en Rattle, como se ha visto arriba. La cantidad de modelos de clasificación disponibles en R se acerca a los 150, pero para su uso, Rattle es inútil.

La biblioteca de interacción de R y del terminal МetaТrader 4 se encuentran en CodeBase: mt4R for new MQL4.

El código en R, que corresponde al modelo entrenado, está disponible en el registro (pestaña Log). Todas las acciones que se llevaron a cabo al crear el modelo, son protocolizadas en forma de código en R, que es lo que se debe usar en el comercio real.

Conclusión

El artículo le resultará útil tanto a los principiantes, como a los traders experimentados, para la valoración preliminar y la elección de un modelo de sistema comercial.

Al utilizar Rattle, el principal problema intelectual en la construcción del sistema comercial es la elección de la variable objetivo y de los predictores imprescindibles para dicha variable objetivo. Los traders experimentados ya llevan su buen tiempo trabajado en esta esfera, y a los principiantes, Rattle les ayudará a adquirir la experiencia necesaria.