Redes neuronales: así de sencillo (Parte 31): Algoritmos evolutivos

Contenido

• Introducción
• 1. Principios básicos para construir el algoritmo
• 2. Aplicación usando MQL5
• 3. Simulación
• Conclusión
• Enlaces
• Programas usados en el artículo.

Introducción

Seguimos analizando los métodos sin gradiente para la optimización de modelos. La principal ventaja de los métodos de optimización de esta clase es la capacidad de optimizar modelos que no pueden optimizarse usando métodos de gradiente. Hablamos de las tareas en las que no resulta posible determinar la derivada de la función del modelo o su cálculo se complica por algunos factores. En el artículo anterior, nos familiarizamos con el algoritmo de optimización genética. Si el lector recuerda, la idea del algoritmo genético se toma de las ciencias naturales. Cada peso del modelo está representado por un gen aparte en el genoma del modelo. El proceso de optimización valora una determinada población de modelos inicializados aleatoriamente. La población tiene una "vida útil" finita, y al final de la época, se seleccionan los "mejores" representantes de la población, que darán "descendencia" para la próxima época. Para cada individuo (modelos en la nueva población), se eligen un par de "padres" al azar, y los "genes de los padres" también se heredan aleatoriamente.

1. Principios básicos para construir el algoritmo

Como podemos ver, existe mucha aleatoriedad en el algoritmo de optimización genética anteriormente analizado. Sí, seleccionamos a propósito a los mejores representantes de cada población, pero al mismo tiempo, la mayor parte de la población es eliminada. Es decir, si ejecutamos completamente toda la población en cada época, realizaremos una gran cantidad de trabajo "vacío". Además, el desarrollo de nuestra población de modelos de una época a otra en la dirección necesaria dependerá en gran medida del factor de azar, y nada nos garantiza un movimiento orientado hacia la meta.

Si recordamos el método de descenso de gradiente, en cada iteración nos movemos hacia el antigradiente de forma premeditada. De esta forma, minimizaremos el error del modelo, y la formación del modelo avanzará en la dirección requerida. Obviamente, para aplicar el método de descenso de gradiente, necesitaremos determinar de forma analítica la derivada de la función en cada iteración,

pero, ¿y si no tenemos esa oportunidad? ¿Podremos combinar ambos enfoques de alguna manera?

Primero debemos recordar el significado geométrico de la derivada de una función. La derivada de una función caracteriza la tasa de cambio del valor de la función en un punto determinado, y se define como el límite de la razón de cambio en el valor de la función respecto al cambio en su argumento cuando el cambio en el argumento tiende a "0". Obviamente, si tal límite existe.

Esto significa que además de la derivada analítica, podremos encontrar alguna aproximación de la misma de forma experimental. Para determinar experimentalmente la derivada de una función con respecto al argumento x, necesitaremos modificar ligeramente el valor del parámetro x en igualdad de condiciones, y calcular el valor de la función. La razón de cambio en el valor de la función respecto al cambio en el argumento nos ofrecerá un valor aproximado de la derivada.

Como nuestros modelos no son lineales, para obtener una mejor definición de la derivada de manera experimental, le recomendamos realizar las siguientes 2 operaciones para cada argumento. En el primer caso, añada un cierto valor, y en el segundo caso, reste ese mismo valor. El valor medio de las dos operaciones nos dará una aproximación más precisa del valor de la derivada de nuestra función con respecto al argumento analizado en un punto concreto.

Debemos decir que con frecuencia se usa un enfoque similar al evaluar la corrección de la derivación de un modelo derivado analítico. Los algoritmos evolutivos también se basan en la explotación de dicha propiedad. La idea principal de las estrategias de optimización evolutiva consiste en utilizar gradientes obtenidos experimentalmente para determinar la dirección de optimización de los parámetros del modelo,

pero, como podemos ver fácilmente, el principal problema al usar gradientes experimentales es la necesidad de realizar una gran cantidad de operaciones. Solo para determinar la influencia de un parámetro en el resultado del modelo, necesitaremos hacer 3 pasadas directas del modelo con los mismos datos iniciales. Como consecuencia, un aumento en el número de parámetros del modelo se verá acompañado de un aumento de 3 veces en el número de iteraciones.

Esto no nos conviene, y debemos hacer algo al respecto.

Por ejemplo, podemos cambiar no un parámetro, sino, digamos, dos, pero en este caso, ¿cómo determinaremos la influencia de cada uno de ellos? ¿Y cómo cambiaremos los parámetros seleccionados? ¿De forma sincrónica o no? ¿Y si la influencia de los parámetros seleccionados en el resultado no es la misma? ¿Y si necesitan ser cambiados con distinta intensidad?

Obviamente, podemos ignorar todas estas preguntas y decir que los procesos que ocurren dentro del modelo no son importantes para nosotros. Necesitamos conseguir un modelo que cumpla con nuestros requisitos, aunque puede que no sea óptimo. Al final, el concepto de optimalidad supone el máximo cumplimiento posible de todos los requisitos presentados.

En este caso, podemos ver el modelo y el conjunto de sus parámetros como un todo único. Podemos utilizar algún algoritmo y cambiar todos los parámetros del modelo a la vez. El algoritmo usado para cambiar los parámetros puede ser cualquiera, incluida la distribución aleatoria.

El impacto de los cambios lo evaluaremos de la única manera disponible: probando el modelo con la muestra de entrenamiento. Si el nuevo conjunto de parámetros puede mejorar el resultado anterior, entonces lo aceptaremos. Si el resultado es peor que el anterior, lo rechazaremos y volveremos al conjunto de parámetros anterior, repitiendo el ciclo para los nuevos parámetros una y otra vez.

¿No le recuerda esto a un algoritmo genético? ¿Y dónde está la estimación del gradiente experimental que discutimos anteriormente?

Vamos a acercarnos aún más al algoritmo genético. De la misma forma, tomaremos una población completa de modelos, cuya efectividad se probará en algún conjunto finito de entrenamiento. Solo que en este caso utilizaremos para todos los valores parámetros que tienen un valor cercano, en contraste con el algoritmo genético, en el que cada modelo era un individuo determinado creado aleatoriamente. De hecho, tomaremos un modelo y añadiremos algo de ruido aleatorio a sus parámetros. Precisamente el uso de ruido aleatorio nos permitirá obtener una población en la que no habrá un solo modelo idéntico, pero una pequeña cantidad de ruido nos permitirá obtener los resultados de todos los modelos en el mismo subespacio con una pequeña desviación, y esto significa que los resultados de los modelos serán comparables.

   donde w' - parámetros del modelo en la población;
         w - parámetros del modelo original;
         ɛ - ruido aleatorio.

Podemos evaluar el rendimiento de cada modelo de la población usando una función de pérdida o un sistema de recompensa. La elección será nuestra y dependerá en gran medida del planteamiento del problema. Al mismo tiempo, tendremos en cuenta la política de optimización. Minimizaremos la función de pérdida y maximizaremos la recompensa total. En la parte práctica de este artículo, maximizaremos la recompensa total, de forma similar a la resolución del problema de aprendizaje por refuerzo.

Después de probar el funcionamiento de la nueva población con la muestra de entrenamiento, deberemos determinar cómo optimizar los parámetros del modelo original. Aquí podremos sumergirnos en las matemáticas de las operaciones e intentar deducir de alguna manera la influencia de cada parámetro en el resultado. En este caso, además, utilizaremos una serie de suposiciones, pero antes hemos acordado considerar el modelo como un todo, y esto significa que el conjunto completo de ruido añadido en cada modelo de población individual se podrá valorar usando la recompensa total resultante durante la prueba del rendimiento del modelo con la muestra de entrenamiento. Por consiguiente, añadiremos a los parámetros del modelo original la media ponderada del ruido del parámetro correspondiente de todos los modelos de la población, y ponderaremos los valores de ruido con la recompensa total. Y, obviamente, multiplicaremos la media ponderada resultante por el coeficiente de aprendizaje del modelo. La fórmula para actualizar los parámetros del modelo se muestra a continuación. Como podemos ver, la fórmula presentada es muy similar a la fórmula que se utiliza para actualizar los pesos al usar el descenso de gradiente.

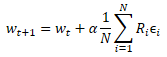
Precisamente este modelo evolutivo de optimización de modelos fue propuesto por el equipo de OpenAI en septiembre de 2017 en el artículo "Evolution Strategies as a Scalable Alternative to Reinforcement Learning". En dicho artículo, el algoritmo propuesto se considera como una alternativa a los métodos de Q-learning y Policy Gradient previamente analizados. El algoritmo propuesto, además, muestra su viabilidad y productividad, demostrando tolerancia a la frecuencia de acción y las recompensas retrasadas. Además, el método de escalado de algoritmos propuesto por los autores permite aumentar la velocidad de resolución del problema con una dependencia casi lineal gracias a la implicación de recursos informáticos adicionales. Entonces, usando más de mil computadoras en paralelo, lograron resolver el problema del caminar tridimensional humanoide en solo 10 minutos. No obstante, no vamos a considerar el problema del escalado en nuestro artículo.

2. Implementación usando MQL5

Tras considerar los aspectos teóricos del algoritmo, vamos a pasar a la parte práctica de nuestro artículo, en la que analizaremos la implementación del algoritmo propuesto usando las herramientas de MQL5. Debemos decir de inmediato que no implementaremos un algoritmo 100% original. Hemos realizado algunos cambios, preservando totalmente la idea del algoritmo. En particular, a los autores se les propuso utilizar un algoritmo codicioso para elegir una acción. En este punto, hemos dejado el algoritmo probabilístico para elegir una acción. Además, hemos añadido parámetros de mutación similares al algoritmo genético. El algoritmo original no usaba mutación.

Para implementar el algoritmo, crearemos una nueva clase de red neuronal CNetEvolution como sucesora de la clase de modelo de algoritmo genético. La herencia se realizará de forma no pública, por ello, deberemos redefinir todos los métodos utilizados. A primera vista, la herencia pública podría salvarnos de redefinir algunos métodos que simplemente redirigiremos a los métodos de la clase padre, pero la herencia no pública bloqueará el acceso a los métodos no usados. Esto resulta más útil al sobrecargar los métodos. Entonces el usuario no verá los métodos sobrecargados de las clases principales, lo cual evitará confusiones innecesarias.

class CNetEvolution : protected CNetGenetic
  {
protected:
   virtual bool      GetWeights(uint layer) override;

public:
                     CNetEvolution() {};
                    ~CNetEvolution() {};
   //---
   virtual bool              Create(CArrayObj *Description, uint population_size) override;
   virtual bool              SetPopulationSize(uint size) override;
   virtual bool              feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) override;
   virtual bool              Rewards(CArrayFloat *rewards) override;
   virtual bool              NextGeneration(float mutation, float &average, float &mamximum);
   virtual bool              Load(string file_name, uint population_size, bool common = true) override;
   virtual bool              Save(string file_name, bool common = true);
   //---
   virtual bool              GetLayerOutput(uint layer, CBufferFloat *&result) override;
   virtual void              getResults(CBufferFloat *&resultVals);
  };

En el cuerpo de una nueva clase, no declararemos los nuevos ejemplares de la clase. Además, no declararemos ninguna variable interna: nos bastará con usar los objetos y variables de las clases padres. Por consiguiente, tanto el constructor como el destructor de la clase permanecerán vacíos.

Observe aquí que no estamos creando objetos para almacenar los pesos del modelo original antes de añadir el ruido, y esto también supone una desviación respecto al algoritmo original. Pero volveremos a este tema durante la implementación.

A continuación, vamos a analizar el método para crear la población de modelos Create. En los parámetros, el método obtiene el array dinámico de la descripción del modelo y el tamaño de la población, de forma similar al método de la clase padre. La funcionalidad principal la implementaremos con la ayuda del método de la clase padre. Para hacer esto, solo necesitaremos llamarlo y transmitirle los parámetros obtenidos.

No olvidemos que en el método de la clase de algoritmo genético CNetGenetic::Create creamos una población de modelos con la misma arquitectura y coeficientes de peso aleatorios. Ahora necesitaremos crear una población similar. Solo los parámetros de nuestros modelos deberán encontrarse cerca. Para hacerlos así, llamaremos al método NextGeneration, del cual hablaremos un poco más adelante.

Luego comprobaremos el resultado de las operaciones en cada paso, y al final del método, retornaremos el resultado lógico de las operaciones.

bool CNetEvolution::Create(CArrayObj *Description, uint population_size)
  {
   if(!CNetGenetic::Create(Description, population_size))
      return false;
   float average, maximum;
   return NextGeneration(0,average, maximum);
  }

Ya mencionamos el método NextGeneration anteriormente. Así que no pospondremos para más adelante lo que podemos hacer ahora mismo: vamos a ver su algoritmo. La funcionalidad de este método resulta similar a la funcionalidad del método de la clase padre del mismo nombre, pero, como hemos mencionado anteriormente, existen ciertos detalles asociados con los requisitos del algoritmo.

En los parámetros, el método obtiene la probabilidad de mutación y dos variables donde escribiremos el valor de la recompensa media y máxima.

En el cuerpo del método, almacenaremos directamente los valores de recompensa requeridos y limitaremos el valor máximo de la mutación. La limitación del valor máximo de mutación se debe al deseo de obtener un modelo entrenado. De hecho, con un valor sobreestimado de la mutación, en cada iteración generaremos parámetros aleatorios del modelo, independientemente de los resultados conseguidos. Como consecuencia, nuestra población constará continuamente en modelos aleatorios no entrenados.

bool CNetEvolution::NextGeneration(float mutation, float &average, float &maximum)
  {
   maximum = v_Rewards.Max();
   average = v_Rewards.Mean();
   mutation = MathMin(mutation, MaxMutation);

Ahora vamos a trabajar un poco en la preparación de la base para actualizar los pesos del modelo. Como hemos mencionado en la parte teórica del presente artículo, la medida para ponderar el valor del ruido al actualizar los parámetros será la recompensa total de un modelo individual en el conjunto de entrenamiento, pero dependiendo de la política de recompensas utilizada, la recompensa total podrá ser positiva o negativa, y con un alto grado de probabilidad nos veremos en una situación en la que las recompensas totales de todos los miembros de la población tendrán el mismo signo. Todos positivos o todos negativos.

Al mismo tiempo, no todas las adiciones de ruido a los parámetros del modelo tendrán un efecto positivo o negativo. En este caso, la influencia positiva de algunos componentes se extinguirá por la influencia negativa de otros. En el mejor de los casos, esto ralentizará nuestro progreso en la dirección correcta, y en el peor de los casos, provocará el entrenamiento del modelo en la dirección opuesta. Para minimizar la influencia de este efecto, escribiremos la diferencia entre la recompensa total de un modelo en particular y la recompensa total promedio de toda la población en el vector de probabilidad v_Probability .

Este paso está relacionado con la suposición de que el ruido que estamos añadiendo pertenece a la distribución normal. Esto significa que la recompensa total del modelo original estará aproximadamente en el medio de la distribución total de las recompensas totales de la población, y después de calcular la diferencia, los modelos con un nivel de recompensa total por debajo del promedio obtendrán una probabilidad negativa, y cuanto menor sea la recompensa total del modelo, más negativa será su probabilidad. Asimismo, los modelos con la recompensa total más alta también recibirán la probabilidad positiva más alta. ¿Y qué nos aporta esto desde un punto de vista práctico? Si el ruido añadido ha tenido un efecto positivo, multiplicarlo por una probabilidad positiva dará como resultado una desviación en el coeficiente de ponderación en la misma dirección. Entonces, dirigimos el entrenamiento del modelo en la dirección necesaria. Si el ruido añadido ha tenido un impacto negativo, al multiplicarlo por una probabilidad negativa, cambiaremos la dirección de la desviación del coeficiente de ponderación del negativo obtenido al positivo esperado, y, nuevamente, dirigiremos el entrenamiento de nuestro modelo hacia la maximización de la recompensa total.

Además, según el algoritmo original, los parámetros del modelo se corregirán en el promedio ponderado del ruido. Por lo tanto, también normalizaremos el vector de probabilidades obtenido de tal forma que la suma de los valores absolutos de todos sus elementos sea igual a "1".

   v_Probability = v_Rewards - v_Rewards.Mean();
   float Sum = MathAbs(v_Probability).Sum();
   if(Sum == 0)
      v_Probability[0] = 1;
   else
      v_Probability = v_Probability / Sum;

Después de determinar los coeficientes de actualización del modelo que hemos escrito en el vectorv_Probability, procederemos a realiza el ciclo de iteración sobre las capas del modelo. Precisamente en el cuerpo de este ciclo formaremos los parámetros de los modelos de la nueva población.

En el cuerpo del ciclo, primero obtendremos el puntero al array dinámico de los objetos de la capa actual, e inmediatamente verificaremos la validez del puntero al objeto que hemos obtenido. Asimismo, comprobaremos el tamaño del array dinámico. Este deberá coincidir con el tamaño de la población establecido. Si el tamaño de la población resulta insuficiente, llamaremos al método CreatePopulation para crear modelos adicionales. No debemos olvidar que aquí estamos usando el método de la clase padre sin cambios. 

   for(int l = 1; l < layers.Total(); l++)
     {
      CLayer *layer = layers.At(l);
      if(!layer)
         return false;
      if(layer.Total() < (int)i_PopulationSize)
         if(!CreatePopulation())
            return false;

Después de eso, llamaremos al método GetWeights, que creará los parámetros actualizados de la capa del modelo actual en las matrices m_Weights y m_WeightsConv . Analizaremos el algoritmo del método en sí más adelante.

      if(!GetWeights(l))
         return false;

Ahora que hemos actualizado los parámetros de nuestro modelo, podemos empezar a rellenar la población. Para ello, creamos un ciclo anidado con un número de iteraciones igual al tamaño de la población.

En el cuerpo del ciclo, obtendremos el puntero al objeto de neurona actual de la capa neuronal analizada, y comprobaremos directamente la validez del puntero resultante. Luego obtendremos el puntero al objeto de matriz de pesos.

      for(uint i = 0; i < i_PopulationSize; i++)
        {
         CNeuronBaseOCL* neuron = layer.At(i);
         if(!neuron)
           return false;
         CBufferFloat* weights = neuron.getWeights();

Si el puntero de la matriz de pesos resultante es válido, comenzaremos a trabajar con él. Aquí crearemos otro ciclo anidado que iterará sobre los elementos de la matriz de pesos.

En el cuerpo del ciclo, primero verificaremos la probabilidad de usar una mutación y, de ser necesario, generaremos un número aleatorio. Si el número aleatorio generado es menor que la probabilidad de mutación, escribiremos un coeficiente de peso aleatorio en el elemento actual de la matriz, y luego pasaremos a la siguiente iteración del ciclo. Utilizaremos aproximadamente el mismo enfoque en el algoritmo genético.

         if(!!weights)
           {
            for(int w = 0; w < weights.Total(); w++)
              {
               if(mutation > 0)
                 {
                  int err_code;
                  float random = (float)Math::MathRandomNormal(0.5, 0.5, err_code);
                  if(mutation > random)
                    {
                     if(!weights.Update(w, GenerateWeight((uint)m_Weights.Cols())))
                       {
                        Print("Error of update weights");
                        return false;
                       }
                     continue;
                    }
                 }

Si vamos a actualizar el peso actual, primero verificaremos su valor actual. Si es necesario, reemplazaremos el número no válido con un coeficiente de peso aleatorio,

               if(!MathIsValidNumber(m_Weights[0, w]))
                 {
                  if(!weights.Update(w, GenerateWeight((uint)m_Weights.Cols())))
                    {
                     Print("Error of update weights");
                     return false;
                    }
                  continue;
                 }

y al final de la iteración del ciclo anidado, añadiremos ruido al peso actual.

               if(!weights.Update(w, m_Weights[0, w] + GenerateWeight((uint)m_Weights.Cols())))
                 {
                  Print("Error of update weights");
                  return false;
                 }
              }
            weights.BufferWrite();
           }

Después de añadir ruido a todos los elementos de la matriz de pesos del elemento actual de la población, transmitiremos los parámetros actualizados a la memoria del contexto OpenCL.

Si es necesario, repetiremos las iteraciones descritas anteriormente para la matriz de pesos de la capa convolucional.

         if(neuron.Type() != defNeuronConvOCL)
            continue;
         CNeuronConvOCL* temp = neuron;
         weights = temp.GetWeightsConv();
         for(int w = 0; w < weights.Total(); w++)
           {
            if(mutation > 0)
              {
               int err_code;
               float random = (float)Math::MathRandomNormal(0.5, 0.5, err_code);
               if(mutation > random)
                 {
                  if(!weights.Update(w, GenerateWeight((uint)m_WeightsConv.Cols())))
                    {
                     Print("Error of update weights");
                     return false;
                    }
                  continue;
                 }
              }

            if(!MathIsValidNumber(m_WeightsConv[0, w]))
              {
               if(!weights.Update(w, GenerateWeight((uint)m_WeightsConv.Cols())))
                 {
                  Print("Error of update weights");
                  return false;
                 }
               continue;
              }

            if(!weights.Update(w, m_WeightsConv[0, w] + GenerateWeight((uint)m_WeightsConv.Cols())))
              {
               Print("Error of update weights");
               return false;
              }
           }
         weights.BufferWrite();
        }
     }

Las iteraciones se repiten para todos los elementos de la secuencia.

Al final del método, restableceremos el vector de acumulación de la recompensa total y finalizaremos el método.

   v_Rewards.Fill(0);
//---
   return true;
  }

Siguiendo la cadena de llamadas a los métodos, a continuación veremos el método GetWeights, al que llamaremos desde el método anterior. El propósito de este método consiste en actualizar los parámetros del modelo que estamos optimizando. Conviene recordar que la clase principal del algoritmo genético CNetGenetic que estamos usando tenía un método con el mismo nombre para descargar los parámetros de una capa neuronal de todos los modelos de población. Posteriormente, utilizaremos la matriz resultante para crear una nueva población. Aquí seguiremos la misma lógica, solo que el contenido cambiará ligeramente según el algoritmo de optimización utilizado.

En los parámetros, el método obtendrá el número ordinal de la capa neuronal cuya matriz de parámetros deseamos crear. En el cuerpo del método, verificaremos la presencia de un vector de probabilidad formado usando los representantes de la población al actualizar los parámetros del modelo, y llamaremos al método homónimo de la clase padre. No se olvide de controlar el proceso de ejecución de las operaciones.

bool CNetEvolution::GetWeights(uint layer)
  {
   if(v_Probability.Sum() == 0)
      return false;
   if(!CNetGenetic::GetWeights(layer))
      return false;

Una vez completadas las operaciones del método de la clase padre, esperaremos a que las matrices m_Weights y m_WeightsConv contengan los coeficientes de peso de la capa neuronal analizada de todos los modelos de población.

Tenga en cuenta que las matrices contienen los coeficientes de peso, y para actualizar los parámetros del modelo, necesitaremos los valores de ruido añadido y los parámetros del modelo original.

Procederemos de forma similar a configurar la recompensa. Ya sabemos que el ruido tiene una distribución normal, mientras que cada parámetro de los modelos de población supone la suma del parámetro correspondiente del modelo original y el ruido. Estamos suponiendo que los parámetros del modelo original se encuentran en mitad de la distribución de los parámetros correspondientes de los modelos de población. Entonces podremos usar el vector de valores promedio de los parámetros de población correspondientes.

   if(m_Weights.Cols() > 0)
     {
      vectorf mean = m_Weights.Mean(0);

Así, restando el vector de valores promedio a la matriz de parámetros de los modelos de población, podremos obtener la matriz requerida de ruido añadido.

      matrixf temp = matrixf::Zeros(1, m_Weights.Cols());
      if(!temp.Row(mean, 0))
         return false;
      temp = (matrixf::Ones(m_Weights.Rows(), 1)).MatMul(temp);
      m_Weights = m_Weights - temp;

Usando el mismo enfoque para determinar el ruido añadido y las probabilidades de su uso en la actualización de los coeficientes de peso del modelo, obtendremos valores comparables, y luego podremos usar la fórmula anterior para actualizar los parámetros del modelo. Después de ello, solo tendremos que transmitir los valores obtenidos a la matriz correspondiente.

      mean = mean + m_Weights.Transpose().MatMul(v_Probability) * lr;
      if(!m_Weights.Resize(1, m_Weights.Cols()))
         return false;
      if(!m_Weights.Row(mean, 0))
         return false;
     }

De ser necesario, repetiremos las operaciones para la segunda matriz.

   if(m_WeightsConv.Cols() > 0)
     {
      vectorf mean = m_WeightsConv.Mean(0);
      matrixf temp = matrixf::Zeros(1, m_WeightsConv.Cols());
      if(!temp.Row(mean, 0))
         return false;
      temp = (matrixf::Ones(m_WeightsConv.Rows(), 1)).MatMul(temp);
      m_WeightsConv = m_WeightsConv - temp;
      mean = mean + m_WeightsConv.Transpose().MatMul(v_Probability) * lr;
      if(!m_WeightsConv.Resize(1, m_WeightsConv.Cols()))
         return false;
      if(!m_WeightsConv.Row(mean, 0))
         return false;
     }
//---
   return true;
  }

Podrá encontrar el código completo de todos los métodos y clases en el archivo adjunto.

Arriba hemos analizado el algoritmo de los métodos que han sido modificados para organizar el algoritmo evolutivo. Para implementar la funcionalidad completa de la clase, aún necesitaremos redefinir los métodos para redirigir el flujo a los métodos correspondientes de la clase principal. No olvide que esta es una medida necesaria para la herencia no pública.

bool CNetEvolution::SetPopulationSize(uint size)
  {
   return CNetGenetic::SetPopulationSize(size);
  }

bool CNetEvolution::feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true)
  {
   return CNetGenetic::feedForward(inputVals, window, tem);
  }

bool CNetEvolution::Rewards(CArrayFloat *rewards)
  {
   if(!CNetGenetic::Rewards(rewards))
      return false;
//---
   v_Probability = v_Rewards - v_Rewards.Mean();
   v_Probability = v_Probability / MathAbs(v_Probability).Sum();
//---
   return true;
  }

bool CNetEvolution::GetLayerOutput(uint layer, CBufferFloat *&result)
  {
   return CNet::GetLayerOutput(layer, result);
  }

void CNetEvolution::getResults(CBufferFloat *&resultVals)
  {
   CNetGenetic::getResults(resultVals);
  }

Para completar el trabajo en la clase, solo deberemos redefinir los métodos para trabajar con archivos. En primer lugar, tendremos que decidir qué método usaremos para guardar el modelo. Como ya habrá notado, más arriba no hemos guardado un modelo aparte con los parámetros actualizados. Solo hemos actualizado los parámetros para construir una nueva población. Sin embargo, para guardar el modelo entrenado, deberemos elegir solo uno, y aquí resulta bastante lógico conservar el modelo con el mejor resultado. Entre los métodos de la clase padre, ya tenemos uno, así que redirigiremos el flujo de operaciones hacia él.

bool CNetEvolution::Save(string file_name, bool common = true)
  {
   return CNetGenetic::SaveModel(file_name, -1, common);
  }

Bien, ya hemos resuelto el problema del almacenamiento del modelo. Vamos a pasar al método de carga del modelo preentrenado. La situación es similar, pero con un matiz: durante el proceso de entrenamiento, no guardamos a la población completa, sino solo al modelo con los mejores resultados. En consecuencia, después de cargar dicho modelo, necesitaremos crear una población de un tamaño determinado. Hemos previsto dicha posibilidad en el método para cargar la clase padre, pero allí se crea una población de modelos con parámetros absolutamente aleatorios, y nosotros necesitamos crear una población alrededor de un modelo con la adición de ruido. Por lo tanto, primero llamaremos al método de carga de datos del modelo de la clase padre, que creará la funcionalidad y la población del tamaño necesario, y luego reiniciaremos el vector de recompensas totales y llamaremos al método NextGeneration anteriormente analizado, en el que se creará una nueva población con las características necesarias.

bool CNetEvolution::Load(string file_name, uint population_size, bool common = true)
  {
   if(!CNetGenetic::Load(file_name, population_size, common))
      return false;
   v_Rewards.Fill(0);
   float average, maximum;
   if(!NextGeneration(0, average, maximum))
      return false;
//---
   return true;
  }

Probablemente, aquí debamos prestar atención a un punto que no hemos aclarado antes. ¿Cómo separará nuestro nuevo método de generación de población el modelo cargado de los modelos rellenados con pesos aleatorios? De hecho, este problema se resuelve de forma bastante simple. En el método de la clase principal, el modelo cargado se colocará en la población con índice "0", y se le añadirán modelos con parámetros aleatorios. Para determinar la probabilidad de usar el ruido añadido, usaremos el vector de recompensa total de los modelos, que, muy prudentemente, hemos puesto a cero antes de llamar al método para crear una nueva población. Por ello, en el cuerpo del método NextGeneration, al determinar las probabilidades, también obtendremos un vector de valores cero, y la suma de los valores del vector será "0". En este caso, determinaremos el 100% de probabilidad de uso solo del modelo con el índice "0" (cargado del archivo) para formar la base de parámetros de los modelos de la nueva población. Además, la probabilidad de usar los parámetros de los modelos aleatorios será "0". Por consiguiente, la nueva población se construirá en torno al modelo cargado desde el archivo.

bool CNetEvolution::NextGeneration(float mutation, float &average, float &maximum)
  {
.............
.............
.............
   v_Probability = v_Rewards - v_Rewards.Mean();
   float Sum = MathAbs(v_Probability).Sum();
   if(Sum == 0)
      v_Probability[0] = 1;
   else
      v_Probability = v_Probability / Sum;
.............
.............
.............
  }

Ya hemos revisado el algoritmo de todos los métodos de la nueva clase CNetEvolution, así que podemos proceder al entrenamiento del modelo, cosa que realizaremos en la siguiente sección de este artículo.

3. Simulación

Para entrenar el modelo, hemos creado el experto "Evolution.mq5" usando como base el experto del artículo anterior. Hemos mantenido sin cambio todos los parámetros y configuraciones del asesor. En principio, bastará con cambiar la clase de objeto en el asesor de entrenamiento del modelo con el algoritmo genético, y podremos entrenar los nuevos modelos con el algoritmo evolutivo.

Vamos a detenernos un poco en el procedimiento para crear un nuevo modelo. Si recuerda, después de crear la herramienta para el Transfer-Learning en los artículos [7] y [8], no especificamos la arquitectura del modelo en el código del asesor. Esto nos permitirá experimentar con diferentes modelos sin tener que realizar cambios en el código del asesor.

Para crear un nuevo modelo, ejecutaremos la herramienta "NetCreator" creada anteriormente. No estamos usando el lado izquierdo de la herramienta, ni tampoco cargando ningún modelo previamente entrenado, ya que estamos creando un modelo completamente nuevo, 

y sabemos que durante el entrenamiento, suministramos a la entrada del modelo 12 parámetros de descripción para cada vela. Al mismo tiempo, planeamos analizar los datos históricos a una profundidad de 20 velas. En consecuencia, el tamaño de la capa de datos inicial será de 240 neuronas (12 * 20). Como capa de datos de entrada, usaremos una capa neuronal completamente conectada sin utilizar ninguna función de activación. A continuación, introduciremos los parámetros de la primera capa en la parte central de nuestra herramienta y presionaremos el botón "ADD LAYER". Como resultado de esta operación, aparecerá la descripción de la primera capa neuronal en el bloque derecho de nuestra herramienta.

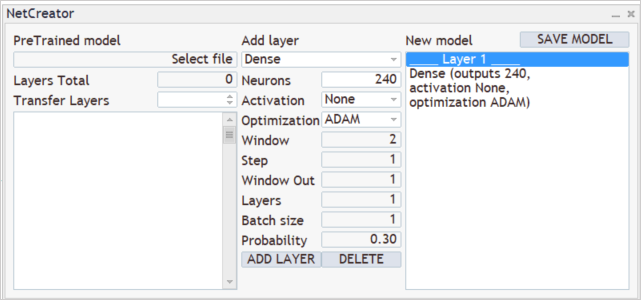
Después viene el proceso de creación de la arquitectura de nuestro modelo. Por ejemplo, queremos que nuestro modelo analice patrones de 3 velas adyacentes. Para hacer esto, añadiremos una capa convolucional con un tamaño de ventana analizada de 36 neuronas (12 * 3). El paso de desplazamiento de la ventana analizada se establecerá en 12 neuronas, lo cual se corresponde con el número de elementos en la descripción de una vela. Para darle más libertad de acción al modelo, crearemos 12 filtros para el análisis de patrones. Como función de activación, utilizaremos una tangente hiperbólica que nos permitirá separar lógicamente los patrones alcistas y bajistas, y al mismo tiempo, la salida de la capa neuronal se normalizará dentro del rango de la función de activación.

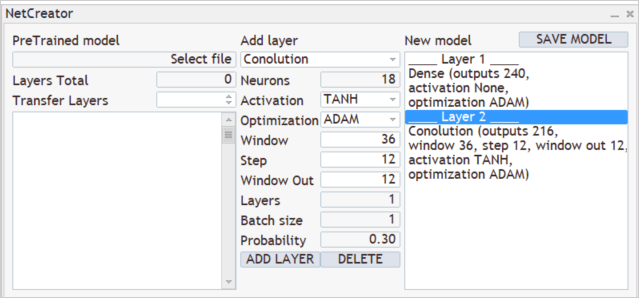
No debemos olvidar que la capa convolucional creada retornará primero una secuencia con todos los elementos de un filtro, y luego de otro, lo cual podemos comparar con una matriz en la que cada fila se corresponde con un filtro separado, mientras que los elementos de la fila representan el resultado del funcionamiento de filtro en toda la secuencia de datos de origen.

A continuación, analizaremos los resultados de los filtros sobre la capa convolucional creada, y construiremos una cascada de 3 capas convolucionales, cada una de las cuales analizará los resultados de la capa convolucional anterior. Las 3 capas tendrán las mismas características. Analizarán las 2 neuronas adyacentes en incrementos de 1 neurona. También se utilizarán 2 filtros en cada capa para el análisis.

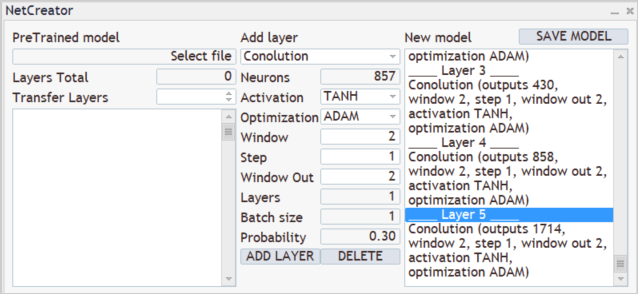
Como podemos ver, gracias a que usamos un paso pequeño para la ventana de datos analizados, además de varios filtros, el tamaño del vector de resultados aumentará de una capa a otra. Por lo general, las capas de submuestreo se usan para reducir la dimensionalidad. Con su ayuda, podemos promediar el valor en la salida de los filtros o tomar el valor máximo. En este caso, no los hemos usado con la esperanza de guardar la mayor cantidad de información útil posible.

Las capas convolucionales efectúan una especie de preparación de los datos iniciales, destacando algunos patrones en ellos, y cuantas más capas convolucionales haya, más patrones complejos podrá resaltar el modelo. Sin embargo, no debemos concentrarnos en modelos excesivamente profundos, ya que esto complicará el proceso de aprendizaje. Sí, los métodos analizados sin gradiente de optimización del modelo no están sujetos a los problemas de explosión y desvanecimiento del gradiente, pero, ¿realmente necesitamos redes profundas para resolver sus problemas? Experimente con diferentes opciones y determine el efecto del aumento del modelo en el resultado final. Notará que, en algún momento, añadir nuevas capas no cambiará el resultado, pero requerirá recursos adicionales para optimizar el modelo.

Los resultados de las capas neuronales convolucionales los procesaremos con un perceptrón completamente conectado de 3 capas con 500 neuronas cada una. En ellos también hemos utilizado la tangente hiperbólica como función de activación. Le sugerimos que ponga a prueba el funcionamiento de varias funciones de activación y compare el resultado.

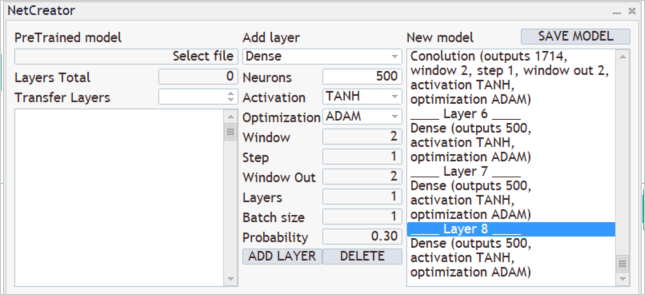
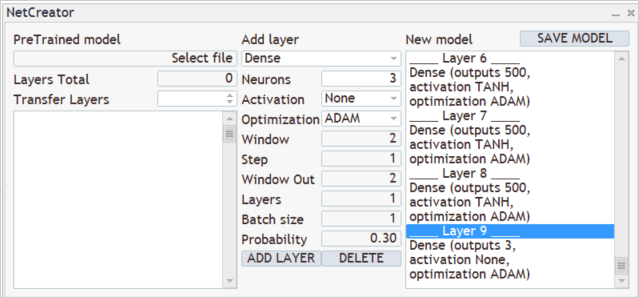
A la salida de nuestro modelo, queremos obtener la distribución de la probabilidad de 3 acciones: compra, venta, espera. Para hacer esto, crearemos otra capa completamente conectada de 3 neuronas, pero esta vez sin utilizar la función de activación.

Creando el nuevo modelo. Paso 5titlealtCreando el nuevo modelo. Paso 5alt

Y trasladaremos el resultado a la región de probabilidades utilizando la capa SoftMax.

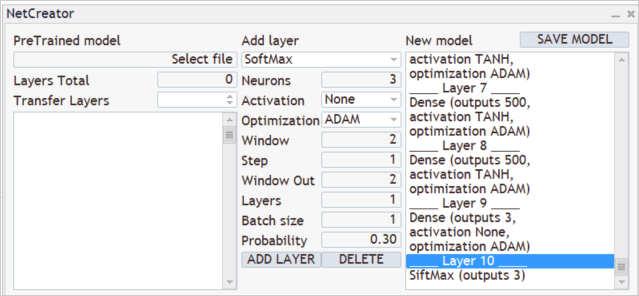
Con esto, podemos dar por finalizada la creación del nuevo modelo. Solo tenemos que guardarlo con el nombre del archivo al que accederá nuestro asesor. La funcionalidad de guardado del modelo se iniciará presionando la tecla "SAVE MODEL".

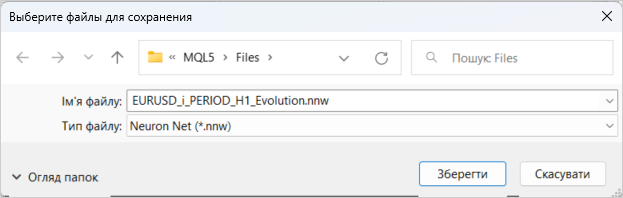
El entrenamiento del nuevo modelo, como antes, se realizará usando los datos históricos de los últimos 2 años del instrumento EURUSD y el marco temporal H1. Ya hemos descrito el proceso de entrenamiento del modelo más de una vez en los artículos de esta serie, así que no nos detendremos en él.

Es interesante que durante la optimización del modelo, el gráfico de la dinámica del error total ha mostrado una dinámica abrupta.

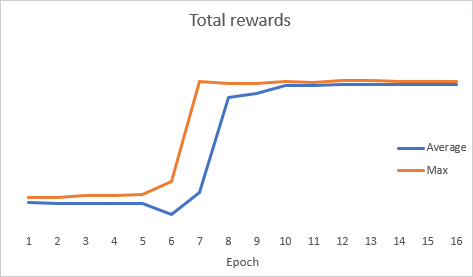
Después de la optimización, hemos probado el modelo en el simulador de estrategias, Para probar el modelo, hemos utilizado el asesor Evolution-test.mq5, que es una copia exacta del asesor usado varios artículos atrás. Los cambios han afectado solo al nombre del archivo del modelo cargado. Podrá encontrar el código completo del asesor en el archivo adjunto.

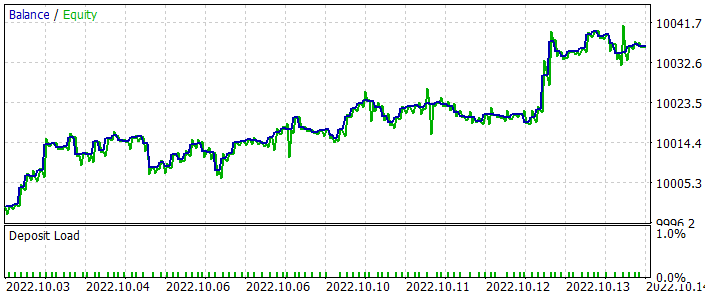
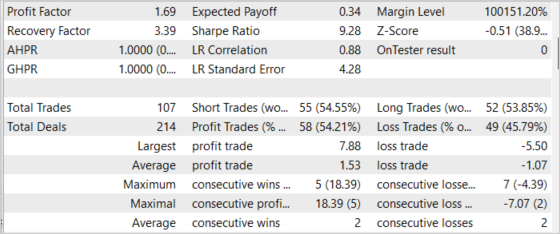
Hemos realizado pruebas para el periodo de las últimas 2 semanas no incluidas en la muestra de entrenamiento. Es decir, las pruebas se han realizado en condiciones lo más próximas posibles a las reales. Los resultados de las pruebas han mostrado la viabilidad del enfoque propuesto. En el gráfico a continuación, podemos ver la dinámica de aumento del balance. En general, hemos realizado 107 transacciones durante el periodo de prueba. De estas, casi el 55% han sido rentables. Sí, la proporción de operaciones rentables respecto a operaciones perdedoras está próxima a 1:1, pero la operación ganadora promedio es un 43% más alta que la operación perdedora promedio, lo cual en general ha ofrecido un factor de beneficio de 1,69, mientras que el factor de recuperación ha llegado a 3,39.

Conclusión

En este artículo, nos hemos familiarizado con otro método de optimización sin gradiente: el algoritmo evolutivo. Asimismo, hemos creado una clase para implementar este algoritmo. La eficacia del algoritmo analizado ha sido confirmada mediante la optimización del modelo y la prueba de los resultados de optimización en el simulador de estrategias. Los resultados de la prueba han mostrado la posibilidad de que el asesor obtenga beneficios. Sin embargo, debemos señalar que las pruebas se han realizado en un intervalo de tiempo corto, y esto no garantiza el beneficio a largo plazo.

El modelo y el asesor experto integrados en el artículo tienen como cometido únicamente mostrar el funcionamiento de la tecnología. Antes de utilizarlos en cuentas reales, el usuario deberá introducir configuraciones y optimizaciones adicionales. 

Enlaces

1. Redes neuronales: así de sencillo (Parte 26): Aprendizaje por refuerzo
2. Redes neuronales: así de sencillo (Parte 27): Aprendizaje Q profundo (DQN)
3. Redes neuronales: así de sencillo (Parte 28): Algoritmo de gradiente de políticas
4. Redes neuronales: así de sencillo (Parte 29): Algoritmo actor-crítico con ventaja (Advantage actor-critic)
5. Natural Evolution Strategies
6. Evolution Strategies as a Scalable Alternative to Reinforcement Learning
7. Redes neuronales: así de sencillo (Parte 23): Creamos una herramienta para el Transfer Learning
8. Redes neuronales: así de sencillo (Parte 24): Mejorando la herramienta para el Transfer Learning

Programas usados en el artículo.

#	Nombre	Tipo	Descripción
1	Evolution.mq5	Asesor	Asesor para la optimización de modelos
2	NetEvolution.mqh	Biblioteca de clases	Biblioteca para organizar el algoritmo evolutivo
3	Evolution-test.mq5	Asesor	Asesor Experto para probar modelos en el Simulador de Estrategias
4	NeuroNet.mqh	Biblioteca de clases	Biblioteca para organizar modelos de redes neuronales
5	NeuroNet.cl	Biblioteca	Biblioteca de código OpenCL para organizar modelos de redes neuronales