From Novice to Expert: Implementation of Fibonacci Strategies in Post-NFP Market Trading

Contents

• Introduction
• Implementation Strategy
• Results
• Conclusion
• Key Lessons
• Attachments

Introduction

Missing the exact moment of a major economic announcement—such as the NFP (Non-Farm Payroll)—often triggers FOMO (Fear of Missing Out). This typically happens because traders rush to catch the movement even when it has already ended. In most cases, the initial spike lasts less than a minute, moving many pips in the market’s favored direction. Entering late in such situations is extremely risky, as the surge is already complete and the price can quickly reverse, leading to significant losses.

Professional traders, however, do not chase these spikes. Instead, they either prepare in advance for early, safer entries or wait patiently for the market to retrace and provide new opportunities at well-calculated entry levels. Their edge lies in understanding Fibonacci retracement principles and mastering the discipline of waiting until the right conditions are established.

In this discussion, we will address the challenges of trading after news-driven spikes by applying Fibonacci principles in an algorithmic way. To set the foundation, the next section will briefly introduce Fibonacci for those new to the concept, before we proceed to the design and implementation of the strategy.

A Brief Look at Fibonacci Retracement

Pioneered by the Italian mathematician Leonardo Bonacci (commonly known as Fibonacci) many centuries ago, the Fibonacci sequence has become one of the most influential tools in modern technical analysis. In mathematics, the sequence is simple: each number is the sum of the two preceding numbers (1, 1, 2, 3, 5, 8, 13, …). Yet its appearance in nature, architecture, and even human behavior has fascinated scholars for generations.

In financial markets, the Fibonacci sequence is applied through Fibonacci retracement levels—a method traders use to identify potential reversal or continuation zones during market corrections. The most commonly used retracement ratios are 23.6%, 38.2%, 50%, 61.8%, and 78.6%, each derived from relationships within the Fibonacci sequence. These levels act as psychological markers where traders anticipate price reactions, either pausing, bouncing, or reversing.

The principle behind retracement is that markets never move in a straight line. After a strong upward or downward move, prices typically pull back before resuming their trend. Fibonacci retracement provides a framework for measuring the likely depth of such pullbacks. For example a:

• 38.2% retracement often suggests a shallow pullback in a strong trend.
• 50% retracement (though not a true Fibonacci number) is widely used as a midpoint correction.
• 61.8% retracement, known as the “golden ratio,” is considered the most critical level where major reversals often occur.

In trading practice, Fibonacci levels are rarely used in isolation. They become more powerful when combined with price action, support and resistance, moving averages, or event-driven market behavior—such as retracements that occur shortly after major news spikes.

In this strategy, our focus is on post-NFP trading, where Fibonacci retracement helps filter out the noise of the initial spike and guides traders toward structured, higher-probability entry points. Instead of succumbing to FOMO, the trader learns to “wait for the pullback” and enter at more sustainable levels. There is a wealth of information on Fibonacci available on the MQL5 Community platform for further reading.

Accessibility on MetaTrader 5 Terminal

In the default MetaTrader 5 interface, the charting toolbox is prioritized and immediately available — the most commonly used analytical objects are preloaded and can be dragged directly onto the chart. Drawing tools (such as the Fibonacci retracement object) have draggable vertices that you can place on swing points to display price levels visually. Traders use these objects both to review how price reacted to levels in the past and to project likely reaction zones for future retracements.

Practical tips:

• Drag the tool onto a clear swing high and swing low (or vice-versa) to anchor the retracement to meaningful reference points.
• Use the object’s vertex handles to fine-tune the placement so the levels align with candle closes or wicks, depending on your preferred rule.
• Save commonly used templates or profiles so your preferred Fibonacci settings and chart layout are instantly accessible across charts.

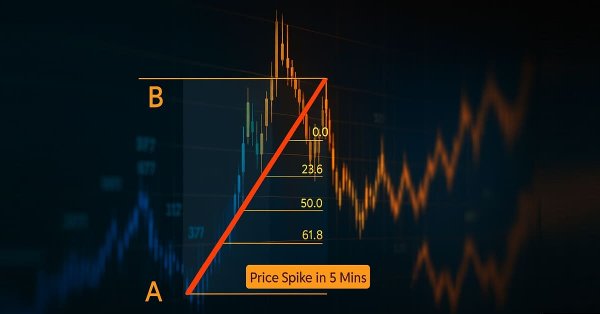
See Figure 1 below, which shows the Fibonacci retracement drawn on the chart.

Figure 1. Drawing the Fibonacci Retracement Tool on MetaTrader 5 Terminal

Concept study using the September 5, 2025, Non-Farm Payroll announcement:

A manual review of the price action after the NFP announcement on September 5, 2025, supports the idea that Fibonacci retracement levels can meaningfully guide post-event entries. The attached illustrations use the Fibonacci Retracement tool to highlight how price tested and respected specific levels after the initial spike, which helps distinguish high-probability re-entry zones from noise.

These observations allow us to design more disciplined order placement and risk-management rules anchored to the retracement bands and the nearest reference prices (pre-spike baseline and spike extremum). For clarity, I analyzed three currency-pair charts that include the US dollar, because USD pairs tend to exhibit stronger, more consistent movement around major U.S. economic releases.

Our study draws on the most recent NFP releases available at the time of writing. For the case study, we analyzed three USD-centric pairs — GBP/USD, USD/JPY, and EUR/USD — before transforming the idea into an algorithm. Below are chart screenshots that illustrate how the technique performs in each example.

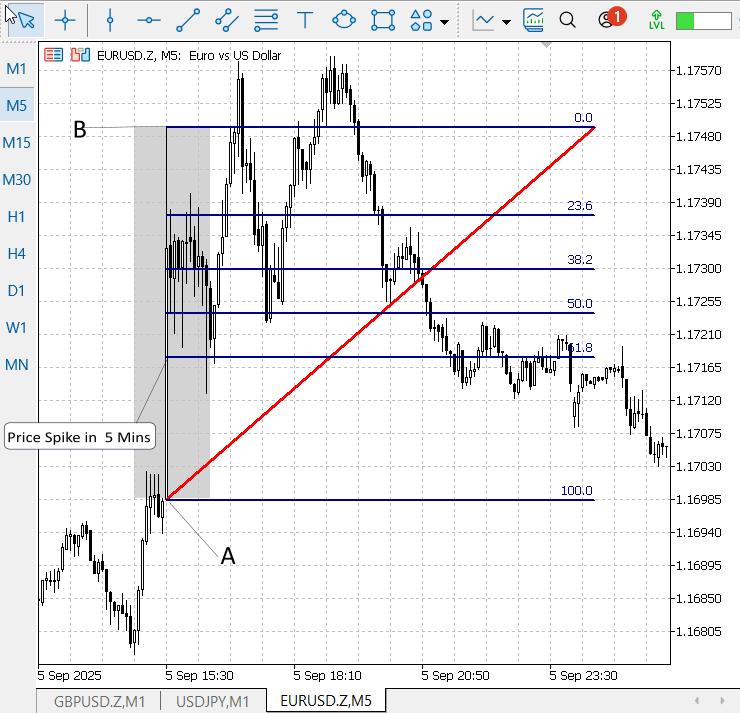
Figure 2. EURUSD, M5, Price Action after NFP Announcement

In Figure 2 (EUR/USD, M5), price clearly respects the laws of retracement. Markers A and B denote the pre-spike baseline and the spike extremum created by the NFP announcement. The Fibonacci retracement was drawn from A (baseline) to B (spike high) for the first M5 candle following the release. Price subsequently pulled back to test the Fibonacci bands, and the retracement levels are visibly respected—in this example, the 50% level was reached and acted as a meaningful reaction point. Price moved back to test the 61.8% Fibonacci retracement and even pushed slightly past that band—though it did not retrace all the way to the baseline (100%). After that shallow overshoot, momentum returned, and the market produced a new high that exceeded the original spike extremum, confirming bullish continuation.

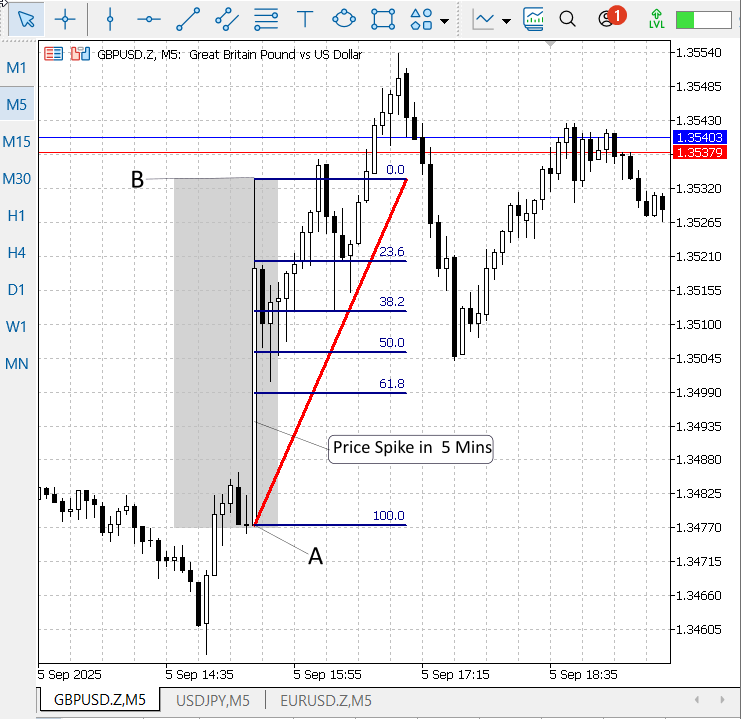
Figure 3. GBPUSD, M5, Price Action after NFP Announcement.

EUR/USD is strongly correlated with GBP/USD, and GBP/USD exhibited a similar—though not identical—bullish response to the announcement. Figure 3 (above) shows GBP/USD with the same Fibonacci overlay used in Figure 2, illustrating how price reacted to the news on that pair and reinforcing the cross-pair consistency of the retracement behavior.

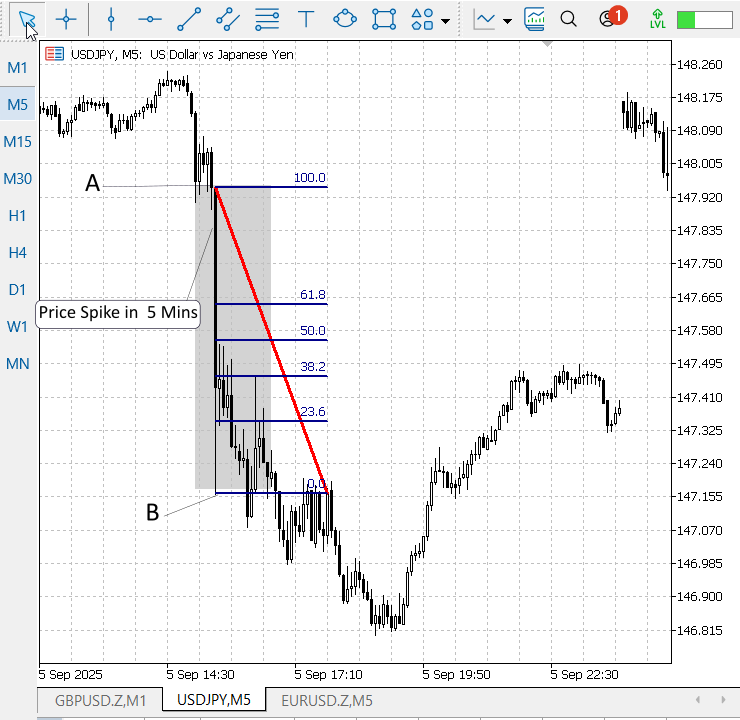
Figure 4. USDJPY, M5, Price Action after NFP Announcement

Figure 4 (USD/JPY) shows a clear bearish reaction to the NFP release. After the initial down-spike (points A→B), price pulled back to roughly the 50% Fibonacci retracement level before resuming its decline and making new lows. Taken together, the three charts (EUR/USD, GBP/USD, and USD/JPY) demonstrate a consistent probability that price will retrace into Fibonacci zones after a news spike — even when the direction differs between pairs.

Implication & high-level approach (before coding)

With the three examples (EUR/USD, GBP/USD, and USD/JPY) in mind, we can define a compact, high-level plan to turn the idea into an algorithm:

Definitions

• P_base — the pre-spike baseline (price where the rapid move originated).
• P_spike — the spike extremum (highest price for a bullish spike, lowest for a bearish spike).
• Spike direction — bullish if P_spike > P_base (up-spike); bearish if P_spike < P_base (down-spike).

Entry logic (both directions)
1. Draw Fibonacci retracement levels between P_base and P_spike after the first completed reference candle following the event. 2. Wait for a structured retracement into the target zone (for example, 38.2–61.8%) with your chosen confirmation (candle close, wick rejection, tick-volume normalization, etc.). 3. For a bullish spike (price spiked up and then retraced):

• Entry: go long when price retraces into the chosen Fib zone and confirmation is observed.
• Take Profit (TP): primary TP at P_spike (the spike extremum). Secondary/extended TPs may use Fib extensions or ATR multiples.
• Stop Loss (SL): place SL at or just below P_base (the spike base / origin of the rapid move). Add a small buffer (e.g., spread + X pips) to avoid being stopped by micro-noise.

4. For a bearish spike (price spiked down and then retraced):

• Entry: go short when price retraces into the chosen Fib zone and confirmation is observed.
• TP: primary TP at P_spike (the low extremum of the down-spike).
• SL: Place SL at or just above P_base (the origin of the rapid down move), with a small buffer.

Why this mapping?

• Using P_spike as TP aligns the trade objective with the most recent demonstrable extreme — we’re trying to capture the re-test of the spike extremum (the “return to the spike”).
• Using P_base as SL uses the point of origin of the rapid move as the logical invalidation: if price traverses back past the origin, the post-spike re-entry thesis is broken.

Practical adjustments & risk controls

We will buffer the SL by a small fixed amount (e.g., a few pips or spread × 1.5) and calculate lot size from account risk % × distance (SL—entry) to keep absolute risk small (target 0.5%). If P_base is too distant, we will offer an alternative tighter SL (next Fib or ATR(5m) × factor) as a selectable parameter. The EA will support partial exits at P_spike, trailing of the remaining position, automatic cancellation of stale limit orders after M minutes, and an optional correlated-pair confirmation toggle.

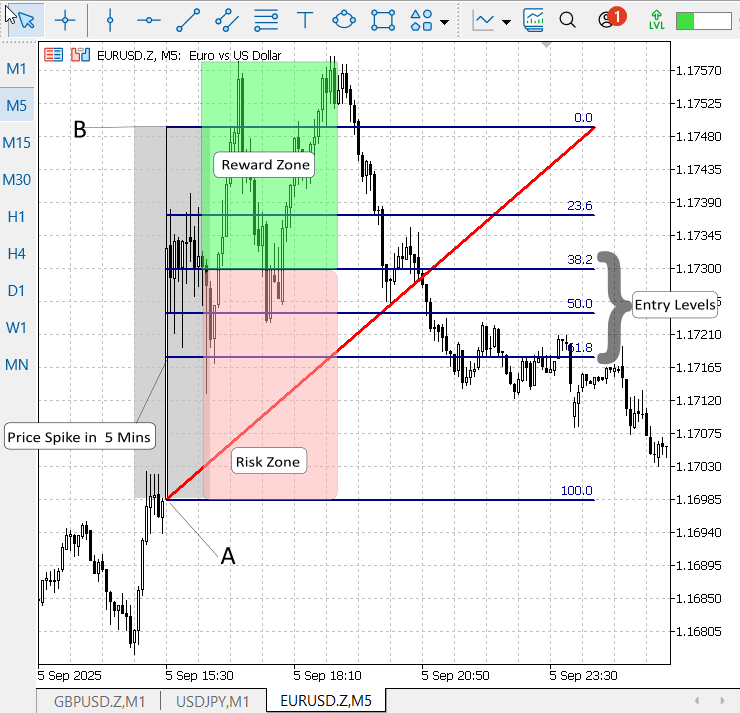
Figure 5. Visual overview of the post-NFP Fibonacci re-entry strategy

Figure 5 (above) is a conceptual visualization of the strategy. For a bullish setup, place the stop-loss just below point A (the spike base) and the take-profit above point B (the spike extremum); for a bearish setup, its  stop-loss above A and take-profit below B (typical example Figure 4 USDJPY). Add a small buffer to the stop-loss (for example, a few pips or spread × 1.5) to reduce noise-driven stop-outs.

Edge cases

If the price fully retraces to 100% (i.e., back to P_base) and then continues beyond, consider cancelling the original thesis — the retrace completed, and the move may be reversing.

If the spike direction is unclear or the swing span < minimum bars/pips, abort the trade (too noisy).

Implementation Strategy

To simplify the development process, I implemented a dedicated class header in MetaEditor 5 responsible for managing Nonfarm Payrolls (NFP) announcement timestamps and converting them correctly between Eastern Time (ET), UTC, and the broker’s server time. This header centralizes DST handling, ET offset calculation, and conversion utilities so other modules remain timezone-agnostic.

Using that header, I developed an Expert Advisor that:

• Detects the first M5 candle that closes after the NFP release,
• Draws a Fibonacci retracement anchored to that candle,
• Deploys pending orders at the 38.2%, 50.0%, and 61.8% levels.
• Applies robust broker checks (minimum stop distances, normalization, expiration), and
• Manages the lifecycle of chart objects and pending orders (cleanup on fills or expiry).

In the next two steps, we will produce detailed, developer-friendly explanations of the code: first the NFPTimeManager header (design decisions, APIs, DST & timezone logic), then the EA (data flow, order management, and safety checks). These explanations will show how the system was designed, implemented, and tested in MQL5.

Step 1: NFPTimeManager header

1.1. File header and metadata

This file begins with a standard header block and MQL5 #property attributes. The header documents authorship and versioning so other developers (or future you) immediately understand the file’s purpose and provenance. The properties let the MQL5 build system show metadata in MetaEditor 5.

//+------------------------------------------------------------------+ 
//|                                               NFPTimeManager.mqh  |
//|                        Copyright 2025, Clemence Benjamin  |
//|                                       https://www.mql5.com/en/users/billionaire2024/seller|
//+------------------------------------------------------------------+
#property copyright "Clemence Benjamin"
#property version   "1.0"

1.2. Class declaration and private timezone fields

We encapsulate all NFP-related utilities inside a CNFPTimeManager class. Two private integer fields track the optional trader timezone and the broker/server timezone; keeping these internal makes conversion functions deterministic and avoids scattering timezone logic across the codebase.

class CNFPTimeManager
{
private:
   int      m_traderTimeZone; // Trader time zone offset from UTC (hours) - optional
   int      m_serverTimeZone; // Server time zone offset from UTC (hours)

1.3. GetETOffset — computing Eastern Time offset with DST

NFP is released at a fixed local ET time (08:30 ET). GetETOffset computes whether a given date uses Eastern Standard Time (UTC−5) or Eastern Daylight Time (UTC−4). It uses U.S. DST rules (2nd Sunday March to 1st Sunday November) and returns the integer UTC offset. This keeps calendar math correct across seasons.

   // returns ET offset (-4 for EDT, -5 for EST) for a given datetime (trader time context)
   int GetETOffset(datetime time)
   {
      MqlDateTime dt;
      TimeToStruct(time, dt);
      int year = dt.year;

      // DST: 2nd Sunday of March to 1st Sunday of November (US rules)
      datetime dst_start = GetNthDayOfWeek(year, 3, 0, 2); // 2nd Sunday of March
      datetime dst_end   = GetNthDayOfWeek(year, 11, 0, 1); // 1st Sunday of November
      // Note: We interpret the DST boundaries as local US/Eastern dates at 02:00 local time,
      // but for our purpose using whole-day thresholds is acceptable (NFP at 8:30 ET).
      if(time >= dst_start && time < dst_end)
         return -4; // EDT
      return -5;    // EST
   }

1.4. GetNthDayOfWeek — robust monthly calendar math

Calendar arithmetic like “second Sunday of March” can be surprisingly error-prone. GetNthDayOfWeek builds the date for the 1st of the month, finds that day’s weekday, and calculates the offset to the requested N-th weekday. The function returns an exact datetime for the requested occurrence and is reused by DST and NFP timestamp calculations.

   // correctly compute the N-th day_of_week (0=Sunday..6=Saturday) in given month/year
   datetime GetNthDayOfWeek(int year, int month, int day_of_week, int n)
   {
      MqlDateTime dt;
      // build date for the 1st of month
      dt.year = year;
      dt.mon  = month;
      dt.day  = 1;
      dt.hour = 0;
      dt.min  = 0;
      dt.sec  = 0;
      datetime first = StructToTime(dt);
      MqlDateTime dt2;
      TimeToStruct(first, dt2);
      int dow_first = dt2.day_of_week; // 0..6
      int delta = (day_of_week - dow_first + 7) % 7;
      int days_to_nth = delta + (n - 1) * 7;
      return first + days_to_nth * 86400;
   }

1.5. Constructor and timezone setters

A short constructor initializes timezone fields to zero. Two public setters allow calling code to explicitly set a trader timezone or the server timezone if automatic detection is not desired or if you need to override detection for testing or remote servers.

public:
   CNFPTimeManager()
   {
      m_traderTimeZone = 0;
      m_serverTimeZone = 0;
   }

   // set trader timezone if you need to convert between trader/local and server
   void SetTraderTimeZone(int timezone_hours)
   {
      m_traderTimeZone = timezone_hours;
   }

   void SetServerTimeZone(int timezone_hours)
   {
      m_serverTimeZone = timezone_hours;
   }

1.6. DetectServerTimeZone and GetServerTime — server-awareness helpers

DetectServerTimeZone is a convenience that compares TimeCurrent() (server time) to TimeLocal() (local machine time) and stores the integer hour offset. GetServerTime simply wraps TimeCurrent() so other modules call a single source for the server’s current timestamp.

   // attempt to auto-detect server timezone (difference between server and local)
   int DetectServerTimeZone()
   {
      datetime local = TimeLocal();
      datetime server = TimeCurrent();
      int offset_seconds = (int)(server - local);
      int offset_hours = offset_seconds / 3600;
      m_serverTimeZone = offset_hours;
      return offset_hours;
   }

   datetime GetServerTime()
   {
      return TimeCurrent();
   }

1.7. GetNFPTimestampTrader — NFP wall-clock time in ET

This method returns a datetime that represents the NFP event at 08:30 ET on the first Friday of a given month/year. The function works in “trader time” terms (ET wall-clock) and will be converted to server time separately. This separation of concerns keeps the function simple and predictable.

   // NFP candidate time in trader (ET) zone: first Friday of month at 08:30 ET
   datetime GetNFPTimestampTrader(int year, int month)
   {
      // first Friday (5) of the month
      datetime first_friday = GetNthDayOfWeek(year, month, 5, 1);
      MqlDateTime dt;
      TimeToStruct(first_friday, dt);
      dt.hour = 8; dt.min = 30; dt.sec = 0;
      return StructToTime(dt); // this is in server timescale semantics but represents the ET timestamp
   }

1.8. TraderETtoServer — convert ET timestamp to server time

This is the critical conversion function: it takes an ET wall-clock timestamp (e.g., 2025-09-05 08:30 ET), computes whether ET was on DST, converts that to UTC, then shifts to the configured server timezone. The result is the absolute server-time moment to which the EA should align scheduling and bar indexing.

   // Convert a trader ET timestamp to server absolute time using ET offset and server tz
   datetime TraderETtoServer(datetime nfp_trader_time)
   {
      int et_offset = GetETOffset(nfp_trader_time); // UTC offset for ET at that date (-4/-5)
      // nfp_trader_time is interpreted in ET (i.e., wall-clock ET). To get UTC we add -ET offset:
      // UTC = ET - ET_offset_hours
      // Server local = UTC + server_tz
      int server_tz = m_serverTimeZone;
      datetime nfp_server_time = nfp_trader_time - et_offset * 3600 + server_tz * 3600;
      return nfp_server_time;
   }

1.9. GetNextNFPServerTime and GetLastNFPServerTime — forward/backward search

These helpers search forward (next) or backward (most recent) for an NFP server timestamp, scanning up to 13 months. They convert the ET candidate to server time and compare with TimeCurrent(). The functions are safe for edge cases around year boundaries because they correctly increment or decrement month/year.

   // Return the next NFP server datetime strictly greater than now (search up to 13 months)
   datetime GetNextNFPServerTime()
   {
      datetime server_time = GetServerTime();
      MqlDateTime sd; TimeToStruct(server_time, sd);
      int year = sd.year, month = sd.mon;
      for(int i=0;i<13;i++)
      {
         datetime nfp_trader = GetNFPTimestampTrader(year, month);
         datetime nfp_server = TraderETtoServer(nfp_trader);
         if(nfp_server > server_time) return(nfp_server);
         month++; if(month>12){ month=1; year++; }
      }
      return(0);
   }

   // Return most recent NFP server datetime <= now (search backwards)
   datetime GetLastNFPServerTime()
   {
      datetime server_time = GetServerTime();
      MqlDateTime sd; TimeToStruct(server_time, sd);
      int year = sd.year, month = sd.mon;
      for(int i=0;i<13;i++)
      {
         datetime nfp_trader = GetNFPTimestampTrader(year, month);
         datetime nfp_server = TraderETtoServer(nfp_trader);
         if(nfp_server <= server_time) return(nfp_server);
         month--; if(month<1){ month=12; year--; }
      }
      return(0);
   }

1.10. IsNFPEventActive — quick activity window check

A simple boolean helper tests whether the most recent NFP is within a configurable time window (± by default one hour). It’s useful when you want code to behave differently during the NFP window (e.g., pause trading or log events).

   // Detect if an NFP event is currently within ±window_seconds of server time (default ±3600s)
   bool IsNFPEventActive(int window_seconds = 3600)
   {
      datetime server_time = GetServerTime();
      datetime last_nfp = GetLastNFPServerTime();
      if(last_nfp == 0) return(false);
      if(MathAbs((long)(server_time - last_nfp)) <= window_seconds) return(true);
      return(false);
   }

1.11. FirstM5OpenAfterNFP — map event time to M5 open

Trading logic reacts to the first M5 candle close after NFP. This utility returns the M5 open time that contains the event (its close is the first close after the timestamp). We use simple floor arithmetic (timestamp / 300 * 300) so it is fast and unambiguous.

   // Utility: compute the M5 open time for the bar that contains the NFP or the first bar after it.
   // Returns the M5 open time for the bar whose close is the first > nfp_server_time.
   datetime FirstM5OpenAfterNFP(datetime nfp_server_time)
   {
      if(nfp_server_time <= 0) return(0);
      // PeriodSeconds for M5 = 300
      int period = PERIOD_M5;
      int psec = 60 * 5;
      // floor open time:
      long open_floor = (long)(nfp_server_time / psec) * psec;
      // if the event falls exactly at an open boundary, then the bar with open=open_floor is the one that includes event
      // its close = open_floor + psec -> that is the first close after event
      return (datetime)open_floor;
   }

1.12. GetM5BarIndexByOpenTime — convert open time to bar index

Finally, this convenience wraps iBarShift to return the M5 series bar index (0-based from the current bar) for a given M5 open time. It returns -1 if no exact match is found. This function is handy when the EA needs to call CopyRates or index into historical bars.

   // Convenience: compute the M5 bar index (iBarShift) for an M5 open time (exact match)
   int GetM5BarIndexByOpenTime(string symbol, datetime m5_open_time)
   {
      if(m5_open_time <= 0) return(-1);
      // prefer exact match - returns index where rates[].time == m5_open_time
      int idx = iBarShift(symbol, PERIOD_M5, m5_open_time, true);
      return idx; // -1 if not found
   }
};

Step 2:  Post-NFP Fibonacci Trader EA

2.1. File header, includes, and inputs 

This top block declares the EA’s metadata and imports the trading helper and the NFPTimeManager header. All the input lines are the knobs you expose to the trader: colours, naming, whether the EA autoplaces orders, the lot size, buffers for SL/TP, strictness, and how long the fib should live. Keep these values simple when testing (demo) and tune per symbol later.

//+------------------------------------------------------------------+
//|             Post-NFP Fibonacci Trader EA                        |
//|  Post-NFP fib + pending orders with robust SL/TP buffer & object |
//|  lifecycle: destroy object when any order fills OR after expiry  |
//+------------------------------------------------------------------+
#property copyright "Clemence Benjamin"
#property version   "1.0"
#property strict

#include <Trade\Trade.mqh>
#include <NFPTimeManager.mqh>

// --- visual / fib inputs
input color  InpFiboColor = clrDodgerBlue;
input string InpPrefix = "FIBO_NFP_";
input bool   InvertFiboOrientation = true;
input bool   InpRayRight = true;

// Trading inputs
input double InpLots = 0.01;
input int    InpSlippage = 10;
input ulong  InpMagic = 123456;
input int    InpOrderExpirationMinutes = 0;
input bool   InpAutoPlaceOrders = true;
input bool   InpRequireStrictSLAt100 = false; // strict mode
input double InpSLBufferPoints = 20.0; // SL moved away from 100% by this many points
input double InpTPBufferPoints = 20.0; // TP moved away from 0% by this many points
input int    InpFibExpiryHours = 3;    // how many hours before fib auto-deletes

2.2. Global state — where runtime data is stored

These globals hold the live state the EA needs between calls: the fib anchors, whether the original bar was bullish, tracked pending tickets, the current fib object name and its creation time (for expiry), the fixed fib levels, and M5 bookkeeping. They are declared by the developer and updated at runtime.

// --- internal
CTrade trade;
CNFPTimeManager nfpManager;

double g_price0 = 0.0;
double g_price100 = 0.0;
bool   g_fibBullish = false;

ulong g_pendingTickets[];                  // tracked pending tickets
string g_currentFibName = "";              // current fib object name
datetime g_fibCreateTime = 0;              // server time when fib created

static const double S_levels[] = {38.2, 50.0, 61.8};

datetime lastM5Open = 0;
datetime lastProcessedNFP = 0;

2.3. OnInit() — initial setup and linking to the NFP header

When the EA attaches, OnInit detects the server timezone using the header (so ET server conversions are correct), configures CTrade defaults (magic number and slippage), clears any previous ticket array memory, and records the current M5 open time. This prepares the EA to detect the next M5 close after NFP.

int OnInit()
{
   // initialize NFP manager tz
   int detected = nfpManager.DetectServerTimeZone();
   PrintFormat("EA: Detected server timezone UTC%+d", detected);

   trade.SetExpertMagicNumber(InpMagic);
   trade.SetDeviationInPoints(InpSlippage);

   ArrayFree(g_pendingTickets);

   // initialize last M5 open time
   MqlRates r[];
   if(CopyRates(_Symbol, PERIOD_M5, 0, 1, r) == 1) lastM5Open = r[0].time;
   else lastM5Open = 0;

   Print("EA: Initialized v1.50 — monitoring NFP, will create fib on first M5 close after NFP.");

   return(INIT_SUCCEEDED);
}

2.4. OnDeinit() — shutdown and cleanup

OnDeinit makes sure the EA leaves no orphaned pending orders or chart objects when removed. It cancels any tracked pending orders, deletes the current fib (if present), and frees the ticket array. This is an important housekeeping step for safe testing and live use.

void OnDeinit(const int reason)
{
   // cleanup: cancel tracked pending orders and delete fib
   CancelExistingPendingOrders();
   DeleteCurrentFibIfExists();
   ArrayFree(g_pendingTickets);
}

2.5. OnTradeTransaction() — detect fills and react immediately

This callback listens to trade system events. When a deal is added (a fill), the EA checks whether the filled order matches one of its tracked pending tickets. If yes, it deletes the fib and cancels remaining pending orders (and clears its ticket list). It also removes tickets from tracking if they are deleted externally. This ensures the visual fib and tracked pending orders stay synchronized with actual trades.

void OnTradeTransaction(const MqlTradeTransaction &trans, const MqlTradeRequest &request, const MqlTradeResult &result)
{
   // We care about deals added (fills) and order deletions possibly made externally
   if(trans.type == TRADE_TRANSACTION_DEAL_ADD)
   {
      ulong orderTicket = trans.order;
      if(orderTicket == 0) return;

      for(int i = ArraySize(g_pendingTickets)-1; i >= 0; i--)
      {
         if(g_pendingTickets[i] == orderTicket)
         {
            PrintFormat("EA: Detected fill for tracked order %I64u -> destroying fib and cancelling remaining pending orders.", orderTicket);
            ArrayRemove(g_pendingTickets, i);
            CancelExistingPendingOrders();
            DeleteCurrentFibIfExists();
            ArrayFree(g_pendingTickets);
            return;
         }
      }
   }
   else if(trans.type == TRADE_TRANSACTION_ORDER_DELETE)
   {
      ulong orderTicket = trans.order;
      if(orderTicket == 0) return;
      for(int i = ArraySize(g_pendingTickets)-1; i>=0; i--)
      {
         if(g_pendingTickets[i] == orderTicket)
         {
            ArrayRemove(g_pendingTickets, i);
            PrintFormat("EA: Tracked order %I64u was deleted externally — removed from internal list.", orderTicket);
            break;
         }
      }
   }
}

2.6. OnTick() — heartbeat logic: expiry check and M5-close trigger

OnTick runs every market tick. It performs two core checks: (A) if the current fib exists and its lifetime (e.g., 3 hours) expired — delete it and cancel pending orders; (B) detect when a new M5 bar opens (the previous M5 closed). On that M5-close event it asks the header for the last NFP server time, verifies whether the closed M5 is the first M5 after NFP, and if so calls the fib + order placement routines. This design ensures the fib anchors to a completed M5 candle after the NFP release.

void OnTick()
{
   // 1) Check for fib expiry by time
   if(StringLen(g_currentFibName) > 0 && g_fibCreateTime > 0)
   {
      datetime now = TimeCurrent();
      if(now >= (datetime)(g_fibCreateTime + InpFibExpiryHours * 3600))
      {
         PrintFormat("EA: Fib '%s' expired after %d hours -> deleting object and cancelling pending orders.",
                     g_currentFibName, InpFibExpiryHours);
         CancelExistingPendingOrders();
         DeleteCurrentFibIfExists();
      }
   }

   // 2) Detect M5 new bar open (previous M5 bar closed)
   MqlRates m5rt[];
   if(CopyRates(_Symbol, PERIOD_M5, 0, 1, m5rt) != 1) return;
   datetime currentM5Open = m5rt[0].time;
   if(currentM5Open == lastM5Open) return;

   // previous M5 open is the bar that just closed
   datetime prevOpen = lastM5Open;
   lastM5Open = currentM5Open;

   // find last NFP server time (the release to react to)
   datetime lastNFP = nfpManager.GetLastNFPServerTime();
   if(lastNFP == 0) return;

   // if already processed this NFP skip
   if(lastProcessedNFP == lastNFP) return;

   // compute bar open floor (M5) that contains the event
   int psec = 60*5;
   long floorOpen = (long)(lastNFP / psec) * psec;
   datetime firstM5OpenAfterNFP = (datetime)floorOpen;

   // we want prevOpen == firstM5OpenAfterNFP (i.e. the bar that closed is that target)
   if(prevOpen != firstM5OpenAfterNFP) return;

   // find M5 index of that open time
   int m5Index = iBarShift(_Symbol, PERIOD_M5, prevOpen, true);
   if(m5Index < 0)
   {
      PrintFormat("EA: Could not find M5 index for open time %s", TimeToString(prevOpen, TIME_DATE|TIME_MINUTES));
      return;
   }

   // update fib using that M5 bar and create pending orders
   if(!UpdateFibFromM5Bar(m5Index)) { Print("EA: UpdateFibFromM5Bar failed."); return; }
   if(InpAutoPlaceOrders) PlaceOrRefreshPendingOrders();

   // mark processed
   lastProcessedNFP = lastNFP;
   PrintFormat("EA: Processed NFP at %s (server time). Used M5 open %s as anchor.",
               TimeToString(lastNFP, TIME_DATE|TIME_MINUTES), TimeToString(prevOpen, TIME_DATE|TIME_MINUTES));
}

2.7. UpdateFibFromM5Bar() — read M5 bar, compute anchors, draw the fib

This function reads the chosen M5 bar with CopyRates, determines whether that candle was bullish or bearish (close vs open), computes the 0% and 100% anchors according to your mapping, optionally inverts them for visual preference, stores them for trading, removes old prefix objects, and creates a uniquely named OBJ_FIBO covering exactly that candle. It records the creation time for expiry logic.

bool UpdateFibFromM5Bar(int m5Index)
{
   if(m5Index < 0) return(false);

   MqlRates r[];
   int copied = CopyRates(_Symbol, PERIOD_M5, m5Index, 1, r);
   if(copied != 1)
   {
      PrintFormat("EA: CopyRates for M5 index %d failed (copied=%d).", m5Index, copied);
      return(false);
   }

   double bar_high = r[0].high;
   double bar_low  = r[0].low;
   double bar_open = r[0].open;
   double bar_close= r[0].close;
   datetime bar_time = r[0].time;

   bool bullish = (bar_close > bar_open);
   g_fibBullish = bullish;

   // user's mapping:
   double price0 = bullish ? bar_high : bar_low;   // 0% anchor
   double price100= bullish ? bar_low  : bar_high; // 100% anchor

   if(InvertFiboOrientation) { double t = price0; price0 = price100; price100 = t; }

   // store anchors for trading
   g_price0 = price0;
   g_price100 = price100;

   // delete any existing prefix objects to avoid clutter
   int tot = ObjectsTotal(0);
   for(int i = tot-1; i >= 0; i--)
   {
      string nm = ObjectName(0, i);
      if(StringFind(nm, InpPrefix) == 0) ObjectDelete(0, nm);
   }

   // create a unique name for this fib
   g_currentFibName = InpPrefix + _Symbol + "_" + IntegerToString((int)bar_time);
   bool created = ObjectCreate(0, g_currentFibName, OBJ_FIBO, 0, bar_time, price0, (datetime)(bar_time + PeriodSeconds(PERIOD_M5)), price100);
   if(!created)
   {
      PrintFormat("EA: Failed to create Fibo '%s' (err=%d)", g_currentFibName, GetLastError());
      g_currentFibName = "";
      return(false);
   }

   ObjectSetInteger(0, g_currentFibName, OBJPROP_COLOR, InpFiboColor);
   ObjectSetInteger(0, g_currentFibName, OBJPROP_RAY_RIGHT, InpRayRight ? 1 : 0);
   ObjectSetInteger(0, g_currentFibName, OBJPROP_SELECTABLE, true);
   ObjectSetInteger(0, g_currentFibName, OBJPROP_HIDDEN, false);

   string desc = bullish ? "Fibo anchored to bullish M5 bar" : "Fibo anchored to bearish M5 bar";
   if(InvertFiboOrientation) desc += " (inverted)";
   if(InpRayRight) desc += " (ray-right)";
   ObjectSetString(0, g_currentFibName, OBJPROP_TEXT, desc);

   g_fibCreateTime = TimeCurrent();

   PrintFormat("EA: Drew Fibo '%s' on M5 index %d (open=%s) high=%.5f low=%.5f",
               g_currentFibName, m5Index, TimeToString(bar_time, TIME_DATE|TIME_MINUTES), bar_high, bar_low);

   return(true);
}

2.8. DeleteCurrentFibIfExists() — single place to remove the fib

A tiny helper that deletes the current fib object if it exists and clears the EA’s state about it. Centralizing deletion reduces duplication and avoids subtle bugs where the name is not cleared.

void DeleteCurrentFibIfExists()
{
   if(StringLen(g_currentFibName) == 0) return;
   if(ObjectFind(0, g_currentFibName) >= 0)
   {
      ObjectDelete(0, g_currentFibName);
      PrintFormat("EA: Deleted fib object '%s'.", g_currentFibName);
   }
   g_currentFibName = "";
   g_fibCreateTime = 0;
}

2.9. CancelExistingPendingOrders() — track-and-clean strategy

The EA tracks tickets it creates in g_pendingTickets. This routine iterates that list and calls trade.OrderDelete for each ticket. Using tracked tickets is safer than deleting by symbol or comment because it targets only orders created in the current EA run (unless you later add persistence).

void CancelExistingPendingOrders()
{
   if(ArraySize(g_pendingTickets) == 0) return;

   for(int i = ArraySize(g_pendingTickets)-1; i >= 0; i--)
   {
      ulong ticket = g_pendingTickets[i];
      if(ticket == 0) { ArrayRemove(g_pendingTickets, i); continue; }
      bool del = trade.OrderDelete(ticket);
      if(!del) PrintFormat("EA: Failed to delete pending ticket %I64u (err=%d)", ticket, GetLastError());
      else PrintFormat("EA: Deleted pending ticket %I64u", ticket);
      ArrayRemove(g_pendingTickets, i);
   }
}

2.10. PlaceOrRefreshPendingOrders() — computing entries, SL/TP, and placing orders (the trading core)

This is the trading heart. For each fib level (38.2, 50, 61.8) it:

• Computes the entry price by linear interpolation between g_price0 and g_price100.
• Computes desired SL and TP anchored at 100% and 0% respectively, then moves them away from the entry by InpSLBufferPoints / InpTPBufferPoints depending on whether the original M5 bar was bullish or bearish. (This ensures SL is below 100% and TP above 0% for bullish cases — and mirrored for bearish.)
• Normalizes prices to symbol digits.
• Queries broker limits (SYMBOL_TRADE_STOPS_LEVEL, SYMBOL_POINT) and enforces minimal stop/pending distances. If necessary, it adjusts SL/TP (or skips the level when strict mode is enabled).
• Decides per-level whether a BUY_LIMIT (entry below market) or SELL_LIMIT (entry above market) is appropriate, places the pending order using CTrade with expiration/time type if configured, logs success/failure, and stores the ticket for cleanup.

This approach minimizes broker rejections and keeps price relationships logically correct.

void PlaceOrRefreshPendingOrders()
{
   // clear previously tracked tickets first
   CancelExistingPendingOrders();

   if(g_price0 == 0.0 || g_price100 == 0.0)
   {
      Print("EA: anchors not set - skipping placement");
      return;
   }

   trade.SetExpertMagicNumber(InpMagic);
   trade.SetDeviationInPoints(InpSlippage);

   double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
   double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
   double point = SymbolInfoDouble(_Symbol, SYMBOL_POINT);

   long stops_level = 0;
   if(!SymbolInfoInteger(_Symbol, SYMBOL_TRADE_STOPS_LEVEL, stops_level)) stops_level = 0;
   double min_stop_distance = (double)stops_level * point;
   if(min_stop_distance < point) min_stop_distance = point;
   double min_pending_distance = min_stop_distance;

   // compute buffer values in price units (points * point)
   double sl_buffer_price = InpSLBufferPoints * point;
   double tp_buffer_price = InpTPBufferPoints * point;

   ENUM_ORDER_TYPE_TIME place_time_type = (InpOrderExpirationMinutes > 0) ? ORDER_TIME_SPECIFIED : ORDER_TIME_GTC;
   datetime place_expiration = (InpOrderExpirationMinutes > 0) ? (TimeCurrent() + InpOrderExpirationMinutes * 60) : 0;

   int digits = (int)SymbolInfoInteger(_Symbol, SYMBOL_DIGITS);
   int levelsCount = ArraySize(S_levels);

   for(int i=0;i<levelsCount;i++)
   {
      double pct = S_levels[i] / 100.0;
      double entry = g_price0 + pct * (g_price100 - g_price0);
      // base desired SL and TP anchored at 100% and 0%
      double sl_desired = g_price100;
      double tp_desired = g_price0;

      // Apply buffers depending on the original fib bullish/bearish orientation
      if(g_fibBullish)
      {
         sl_desired = (g_price100 - sl_buffer_price);
         tp_desired = (g_price0 + tp_buffer_price);
      }
      else
      {
         sl_desired = (g_price100 + sl_buffer_price);
         tp_desired = (g_price0 - tp_buffer_price);
      }

      // normalize values
      entry = NormalizeDouble(entry, digits);
      sl_desired = NormalizeDouble(sl_desired, digits);
      tp_desired = NormalizeDouble(tp_desired, digits);

      // decide pending type by comparing entry price with market and min_pending_distance
      bool wantBuy = false, wantSell = false;
      if(entry <= (ask - min_pending_distance)) wantBuy = true;
      else if(entry >= (bid + min_pending_distance)) wantSell = true;
      else
      {
         PrintFormat("EA: Skipping level %.2f: entry(%.5f) too close to market (Ask=%.5f Bid=%.5f) min_pending_dist=%.5f",
                     S_levels[i], entry, ask, bid, min_pending_distance);
         continue;
      }

      ENUM_ORDER_TYPE otype = (wantBuy ? ORDER_TYPE_BUY_LIMIT : ORDER_TYPE_SELL_LIMIT);
      bool adjusted = false;

      // Validate/adjust stops unless strict mode requested
      if(otype == ORDER_TYPE_BUY_LIMIT)
      {
         // For BUY_LIMIT we need sl < entry < tp
         if(!(sl_desired < entry - min_stop_distance))
         {
            if(InpRequireStrictSLAt100)
            {
               PrintFormat("EA: Strict mode: skipping level %.2f because SL would be adjusted (desired SL %.5f not < entry-%.5f).",
                           S_levels[i], sl_desired, (entry - min_stop_distance));
               continue;
            }
            double old = sl_desired;
            sl_desired = NormalizeDouble(entry - min_stop_distance, digits);
            adjusted = true;
            PrintFormat("EA: Adjusted SL BUY level %.2f old=%.5f -> new=%.5f", S_levels[i], old, sl_desired);
         }
         if(!(tp_desired > entry + min_stop_distance))
         {
            if(InpRequireStrictSLAt100)
            {
               PrintFormat("EA: Strict mode: skipping level %.2f because TP would be adjusted (desired TP %.5f not > entry+%.5f).",
                           S_levels[i], tp_desired, (entry + min_stop_distance));
               continue;
            }
            double old = tp_desired;
            tp_desired = NormalizeDouble(entry + min_stop_distance, digits);
            adjusted = true;
            PrintFormat("EA: Adjusted TP BUY level %.2f old=%.5f -> new=%.5f", S_levels[i], old, tp_desired);
         }
      }
      else // SELL_LIMIT
      {
         // For SELL_LIMIT we need tp < entry < sl
         if(!(sl_desired > entry + min_stop_distance))
         {
            if(InpRequireStrictSLAt100)
            {
               PrintFormat("EA: Strict mode: skipping level %.2f because SL would be adjusted (desired SL %.5f not > entry+%.5f).",
                           S_levels[i], sl_desired, (entry + min_stop_distance));
               continue;
            }
            double old = sl_desired;
            sl_desired = NormalizeDouble(entry + min_stop_distance, digits);
            adjusted = true;
            PrintFormat("EA: Adjusted SL SELL level %.2f old=%.5f -> new=%.5f", S_levels[i], old, sl_desired);
         }
         if(!(tp_desired < entry - min_stop_distance))
         {
            if(InpRequireStrictSLAt100)
            {
               PrintFormat("EA: Strict mode: skipping level %.2f because TP would be adjusted (desired TP %.5f not < entry-%.5f).",
                           S_levels[i], tp_desired, (entry - min_stop_distance));
               continue;
            }
            double old = tp_desired;
            tp_desired = NormalizeDouble(entry - min_stop_distance, digits);
            adjusted = true;
            PrintFormat("EA: Adjusted TP SELL level %.2f old=%.5f -> new=%.5f", S_levels[i], old, tp_desired);
         }
      }

      // final relation sanity
      bool valid = true;
      if(otype == ORDER_TYPE_BUY_LIMIT) valid = (sl_desired < entry && tp_desired > entry);
      else valid = (sl_desired > entry && tp_desired < entry);
      if(!valid)
      {
         PrintFormat("EA: Skipping level %.2f due to invalid final SL/TP relation entry=%.5f SL=%.5f TP=%.5f",
                     S_levels[i], entry, sl_desired, tp_desired);
         continue;
      }

      // build order comment
      string comment = InpPrefix + DoubleToString(S_levels[i], 2);

      // Place pending with proper signature (includes time type and expiration)
      bool placed = false;
      if(otype == ORDER_TYPE_BUY_LIMIT)
         placed = trade.BuyLimit(InpLots, entry, _Symbol, sl_desired, tp_desired, place_time_type, place_expiration, comment);
      else
         placed = trade.SellLimit(InpLots, entry, _Symbol, sl_desired, tp_desired, place_time_type, place_expiration, comment);

      if(!placed)
      {
         int err = GetLastError();
         PrintFormat("EA: Failed to place %s at %.5f (lvl %.2f) err=%d ret=%d",
                     (otype==ORDER_TYPE_BUY_LIMIT ? "BUY_LIMIT":"SELL_LIMIT"),
                     entry, S_levels[i], err, (int)trade.ResultRetcode());
      }
      else
      {
         ulong ticket = trade.ResultOrder();
         PrintFormat("EA: Placed %s ticket=%I64u lvl=%.2f entry=%.5f SL=%.5f TP=%.5f adjusted=%s",
                     (otype==ORDER_TYPE_BUY_LIMIT ? "BUY_LIMIT":"SELL_LIMIT"),
                     ticket, S_levels[i], entry, sl_desired, tp_desired, (adjusted ? "yes":"no"));

         // track ticket for cleanup and fill detection
         ArrayResize(g_pendingTickets, ArraySize(g_pendingTickets) + 1);
         g_pendingTickets[ArraySize(g_pendingTickets)-1] = ticket;
      }
   } // levels loop
}

2.11. How the EA uses the NFPTimeManager header — simple call points

The header does the heavy date/time work: the EA calls DetectServerTimeZone() in OnInit() to set up conversion, and GetLastNFPServerTime() each M5 close to find the server-time moment of the most recent NFP. Using that timestamp, the EA computes the first M5 open after NFP and reacts when that M5 closes. This keeps the EA’s core logic clean and timezone-safe.

// example header calls in OnInit/OnTick
int detected = nfpManager.DetectServerTimeZone();
datetime lastNFP = nfpManager.GetLastNFPServerTime();

Results

With the NFPTimeManager class the EA reliably identifies the Nonfarm Payrolls (NFP) release even on historical data, allowing us to run and validate the strategy in the Strategy Tester after a successful compilation. Below are animated images that illustrate the test process in the Strategy Tester.

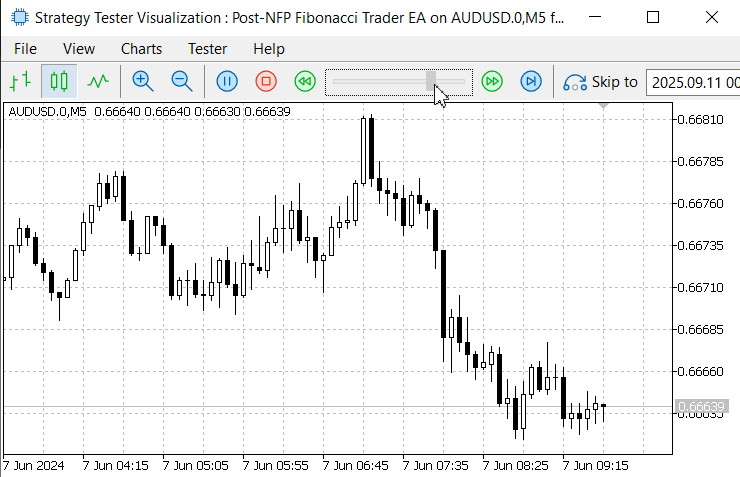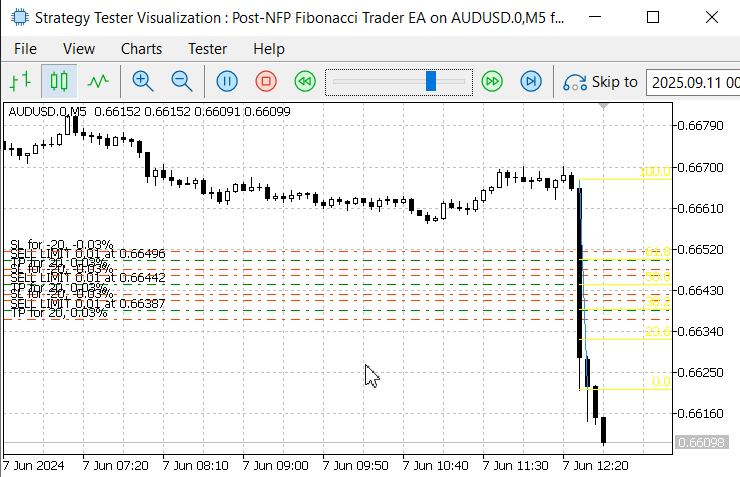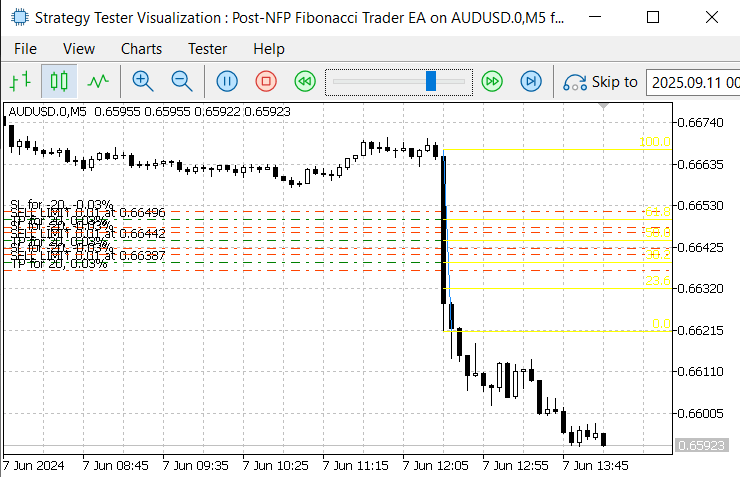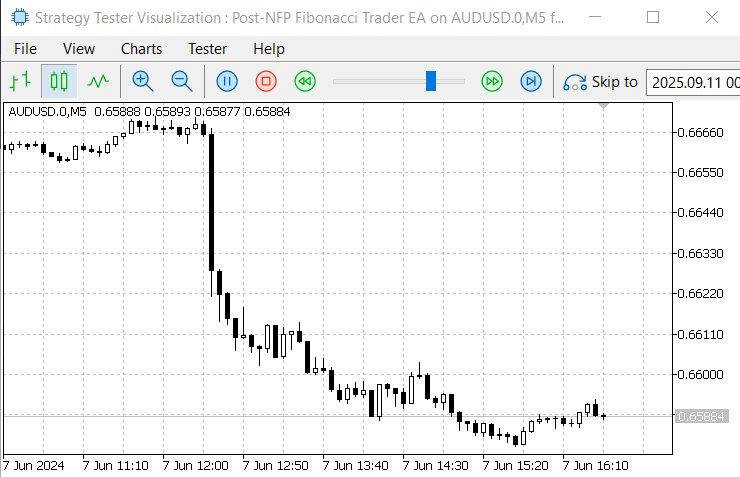
Figure 6. June 7, 2024, NFP Announcement

In Figure 6, during the June 7, 2024 NFP announcement, the EA successfully detected the event day and correctly aligned the NFP release time with the local server time, as confirmed in the Strategy Tester. The Fibonacci retracement tool was plotted and executed as designed. However, the pending orders were not triggered because the retracement was too shallow and failed to reach the entry levels.

Another issue observed was the incorrect placement of stop-loss and take-profit values on the pending orders, which did not fully align with our intended specification. This can be corrected either in the code or through input parameter adjustments.

Despite these limitations, the most important outcome is that the EA was able to detect the event, map the time zones accurately, and automate Fibonacci placement. These achievements are a strong foundation, and further refinements can be made in future iterations. Below is another image for the November 1, 2024 event.

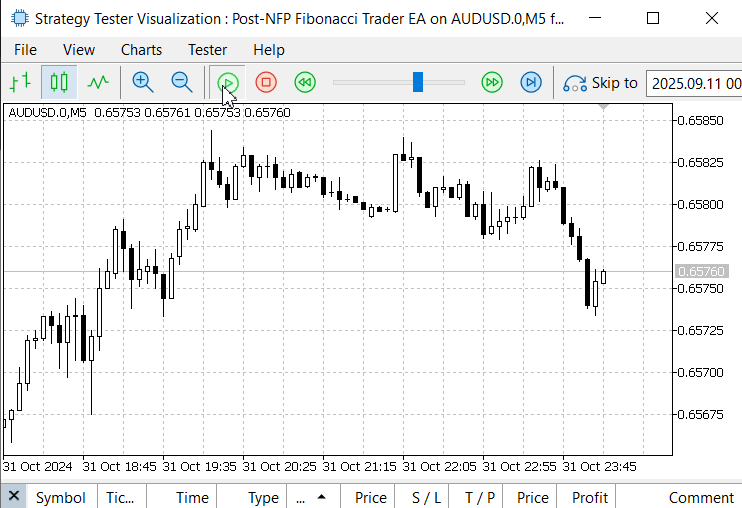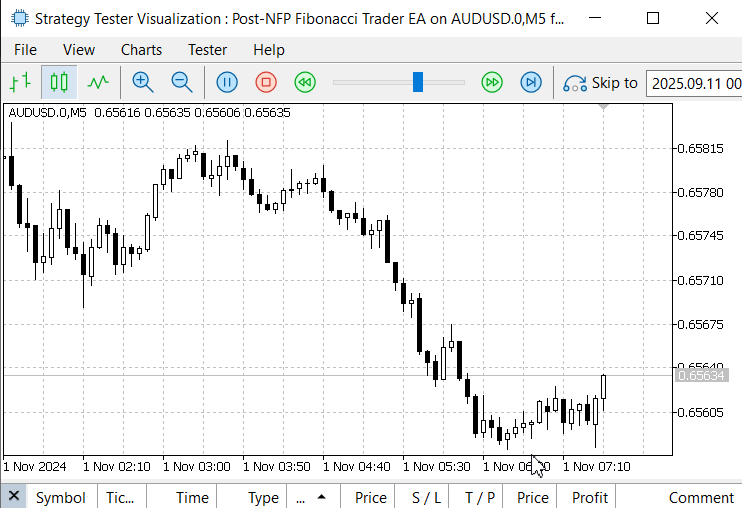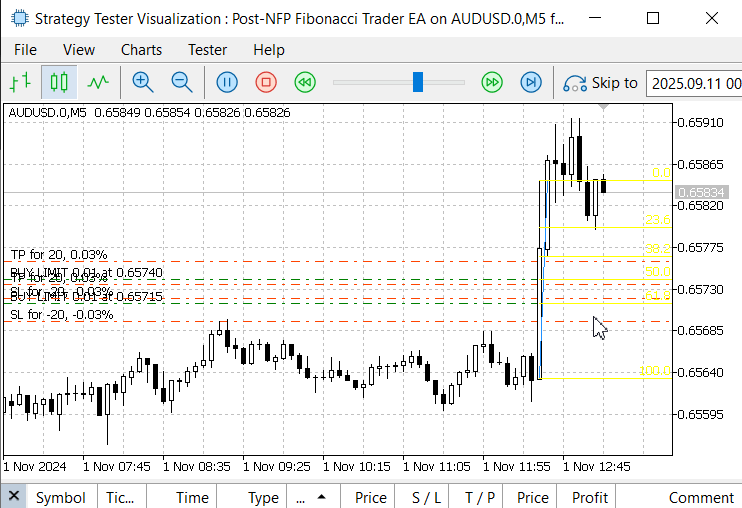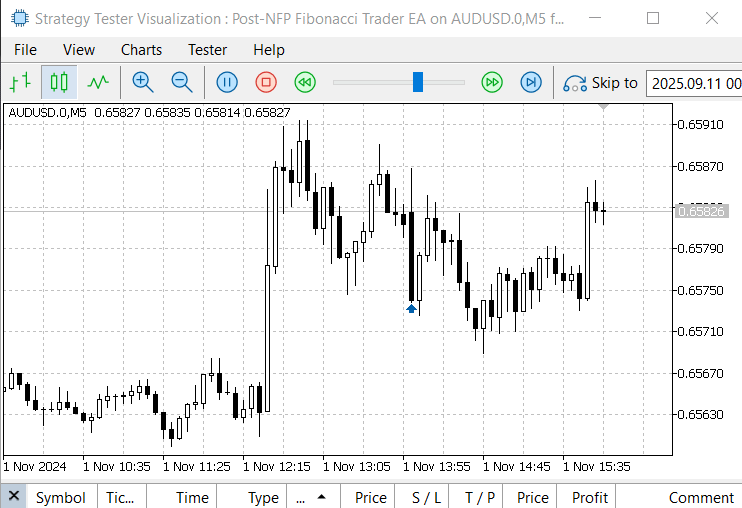
Figure 7. November 1, 2024, NFP Announcement

Conclusion

The Fibonacci retracement tool can be algorithmically applied to trade Non-Farm Payroll (NFP) events with a structured, rules-based approach. Instead of chasing the initial spike, this method navigates the market a few minutes after the release—during the natural correction phase. Conceptually, between 30% and 60% of the original five-minute price spike can be captured as profit even if a trader missed the first move. This is made possible by referencing Fibonacci ratios, which map the full extent of the spike as 100% and provide precise retracement levels for trade placement.

Among these, the 38.2% Fibonacci level often shows the highest probability of generating a gain comparable to 38.2% size of the initial spike. However, it is important to note that the market does not always respect this behavior, and no setup is guaranteed. Our testing showed promising results in multiple scenarios, though the approach should be treated as a structured probability, not a certainty.

In this study, we did not conduct extensive performance analytics on the EA but focused on demonstrating the concept through practical simulations in the Strategy Tester. The prototype has room for refinement and optimization—whether through enhanced order management, statistical validation, or adaptation to other currency pairs and non-news trading contexts.

Equally valuable were the lessons learned in building the strategy: starting from scratch, applying modularization to keep the code clean and reusable, and thinking forward to advanced extensions. This is a foundation to build upon, and with further development, it can evolve into a more powerful and flexible trading tool.

We welcome your thoughts and feedback in the comments section below. Furthermore, please see the attached source documents and review our key lessons summary table for practical takeaways.

Key Lessons

Key Lesson	Description:
Modularize logic	Split functionality into small, focused units (classes or functions). Example: a dedicated NFPTimeManager for time/DST logic keeps the EA core readable and reusable.
Handle timezones & DST explicitly	Convert event times (ET) into server time using deterministic rules. Mistakes here will misalign anchors on historical tests and live runs—so centralize and test this logic.
Anchor to closed bars	Always base calculations on completed candles (e.g., the first M5 that closed after NFP). This avoids intrabar recalculation instability and makes results reproducible in the Strategy Tester.
Respect broker limits	Query SYMBOL_TRADE_STOPS_LEVEL, SYMBOL_POINTand SYMBOL_DIGITS at runtime and validate SL/TP/pending distances to avoid rejected orders.
Normalize prices & use correct precision	Always normalize entry, SL and TP to the symbol's digits. Small rounding errors easily cause broker rejections.
Design safe fallback behaviours	Provide strict vs adaptive modes: either skip levels that require stop changes (strict) or automatically adjust stops to comply with broker rules (adaptive). Log both decisions.
Use robust order placement APIs	Use CTrade helper methods with the correct signatures (including expiration/time type) to avoid later modifications and reduce error handling complexity.
Track and manage your own tickets	Keep an internal list of created tickets so the EA can reliably cancel or monitor only the orders it created (avoid deleting unrelated user orders).
Object lifecycle & UI cleanliness	Give chart objects short unique names (e.g., fib_SYMBOL_YYMMDDhhmm), store verbose info in OBJPROP_TEXT, and delete objects when orders fill or expire.
Use OnTradeTransaction for fills	Detect fills and external deletions with trade-transaction events to react immediately (clean-up, logging) and avoid polling-based delays.
Verbose logging for traceability	Log every key action (create, adjust, skip, place, fail, delete). Clear logs are essential for debugging, backtests, and regulatory/audit purposes.
Test in Strategy Tester & demo first	Validate logic on historical NFP dates in the Strategy Tester (deterministic) and then run on a demo account. Use deterministic anchors (closed bars) for reproducible tests.

Attachments

File name	Version	Description
NFPTimeManager.mqh	1.0	DST-aware time utility class that centralizes all Nonfarm Payroll (NFP) timestamp calculations and conversions between Eastern Time (ET), UTC, and the broker/server time. Key functions include detection of server time zone, calculation of the NFP wall-clock (first Friday 08:30 ET), ET server conversion, retrieval of the most recent/next NFP server timestamp, and helpers to map NFP moments to M5 open times and bar indices. Designed for reuse and unit testing so the EA remains timezone-agnostic.
Post-NFP Fibonacci Trader EA.mq5	1.0	Full Expert Advisor that uses the NFPTimeManager to detect the first M5 candle close after an NFP release, draws a Fibonacci retracement anchored to that candle, and places pending orders at 38.2%, 50% and 61.8% retracement levels. Features include SL/TP buffers, strict vs adaptive stop handling, broker-limit validation (SYMBOL_TRADE_STOPS_LEVEL, SYMBOL_POINT, digits), ticket tracking, automatic cleanup (on fill or after configurable expiry), and verbose logging for traceability. Configurable via inputs; tested in the Strategy Tester and demo environment.