Monte Carlo Permutation Tests in MetaTrader 5

Introduction

Aleksey Nikolayev, wrote an interesting article titled, "Applying the Monte Carlo method for optimizing trading strategies". It describes a method of permutation testing where a sequence of trades from a test are randomly commuted. The author briefly mentions another type of permutation test, where the sequence of price data is randomly changed and the performance of a single Expert Advisor (EA) is compared against performance attained when tested on numerous other  sequence variations of the same price series.

In my opinion the author wrongly suggested that there was no way to conduct such a test on an arbitrary EA using MetaTrader 5. At least not entirely. Therefore, in this article we will demonstrate a permutation test involving randomly permuted price data using MetaTrader 5. We will present code for permuting price series , as well as a script that automates the initial steps when preparing to conduct a permutation test of a complete EA.

Permutation testing overview

To put it succinctly, the type of permutation test we will describe involves selecting a sample of price data. It is preferable that the test to be conducted, is done out of sample. After running a test on this price series, we make a note of whatever performance criteria we may be interested in measuring. Then we randomly change the sequence of the original price series, test the EA and note the performance.

We do this many times over, each time permuting the price series and recording the resulting performance criteria we noted for other tests. This should be done at least a hundred times, ideally, thousands. The more times we permute and test , the more robust the results will be. But, hold on, what do we expect our results to reveal about the EA being tested?

Value of conducting permutation tests

When a number of iterative tests have been conducted, we end up with a collection of performance figures from each permutation. It does not matter what performance figure we use, it could be the Sharpe Ratio, profit factor or simply the resulting balance or net profit. Suppose 99 permutations have been conducted, 100 inclusive of the original unpermuted test. We have 100 performance figures to compare.

The next step is to enumerate the number of times the performance figure for the unpermuted test was surpassed and present this number as a fraction of the tests conducted, in this instance being 100. This fraction is the probability of obtaining the result of the unpermuted test or better, by chance, if the EA had no profit potential at all. In statistics, it is referred to as a p-value and is the result of conducting a hypothesis test.

Continuing with our hypothetical permutation test of 100 iterations, it came to be that exactly 29 permuted performance figures were better than the benchmark unpermuted test. We get a p-value of 0.3, i.e. 29+1/100. It means there is a probability of 0.3 that a money losing EA would have obtained similar or better performance as observed from the unpermuted test operation. Such a result may seem encouraging, but what we want are p-values as close to zero as possible something in the range of 0.05 and under.

The complete formula is given below:

z+1/r+1

Where r is the number of permutations done and z is the total number of permuted tests with better performance. To conduct the test properly, the permutation procedure is important.

Permuting price series

To permute a collection of data correctly we have to make sure that every possible sequence variation is equally likely. This requires a uniformly distributed random number between 0 and 1 to be generated. The mql5 standard library provides a tool that satisfies this need in the statistics library. Using it we can specify the range of values demanded.

//+------------------------------------------------------------------+
//| Random variate from the Uniform distribution                     |
//+------------------------------------------------------------------+
//| Computes the random variable from the Uniform distribution       |
//| with parameters a and b.                                         |
//|                                                                  |
//| Arguments:                                                       |
//| a           : Lower endpoint (minimum)                           |
//| b           : Upper endpoint (maximum)                           |
//| error_code  : Variable for error code                            |
//|                                                                  |
//| Return value:                                                    |
//| The random value with uniform distribution.                      |
//+------------------------------------------------------------------+
double MathRandomUniform(const double a,const double b,int &error_code)
  {
//--- check NaN
   if(!MathIsValidNumber(a) || !MathIsValidNumber(b))
     {
      error_code=ERR_ARGUMENTS_NAN;
      return QNaN;
     }
//--- check upper bound
   if(b<a)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }

   error_code=ERR_OK;
//--- check ranges
   if(a==b)
      return a;
//---
   return a+MathRandomNonZero()*(b-a);
  }

Shuffling price data has unique demands. First we cannot simply change the position of a price value around as this will disturb the temporal relations characteristic of financial timeseries. So instead of actual prices we will permute price changes. By first log transforming prices before differencing, we minimize the influence of variations in raw price differences.

Using this method, we have to hold back the first price value and exclude it from the permutation. When the series is reconstructed, the result will be the preservation of the trend present in the original price sequence. The only variation being the internal price movements between the same first and last price of the original series.

Before actually permuting the price series we have to decide what data we will use. In MetaTrader 5, chart data is displayed as bars that are constructed from tick data. Permuting a single price series is a lot easier than permuting bar information. So we will use tick data. Using ticks brings up a number of other complications as well, since ticks include other information besides raw prices. There is information about volume, time and tick flags.

Firstly, time and tick flag information will be left untouched so our permutation routine should not alter this information. We are interested in only the bid, ask and volume. The second complication comes from the possibility of anyone of these values being zero, which will cause problems when applying a log transformation to them. To demonstrate how to get over these challenges let's look at some code.

Implementation of tick permutation algorithm

The CPermuteTicks class contained in the include file PermuteTicks.mqh implements our tick permutation procedure. Inside PermuteTicks.mqh, we include Uniform.mqh from the standard library to gain access to a utility that outputs uniformly generated random numbers within a set range. The subsequent defines specify this range, be careful if you feel the need to change these values, ensure that minimum is actually less than the maximum threshold.

//+------------------------------------------------------------------+
//|                                                 PermuteTicks.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Stat\Uniform.mqh>
//+-----------------------------------------------------------------------------------+
//| defines: representing range of random values from random number generator         |
//+-----------------------------------------------------------------------------------+
#define MIN_THRESHOLD 1e-5
#define MAX_THRESHOLD 1.0

The CMqlTick structure represents corresponding members of the built in MqlTick structure that the class will manipulate. Other tick information will not be touched.

//+------------------------------------------------------------------+
//| struct to handle tick data to be worked on                       |
//+------------------------------------------------------------------+
struct CMqlTick
  {
   double            ask_d;
   double            bid_d;
   double            vol_d;
   double            volreal_d;
  };

The CPermuteTicks class has 3 private array properties that store: first the original ticks kept in m_ticks, second are the log transformed ticks kept in m_logticks, lastly there are the differenced ticks collected in m_differenced.

//+------------------------------------------------------------------+
//| Class to enable permutation of a collection of ticks in an array |
//+------------------------------------------------------------------+
class CPermuteTicks
  {
private :
   MqlTick           m_ticks[];        //original tick data to be shuffled
   CMqlTick          m_logticks[];     //log transformed tick data of original ticks
   CMqlTick          m_differenced[];  //log difference of tick data
   bool              m_initialized;    //flag representing proper preparation of a dataset
   //helper methods
   bool              LogTransformTicks(void);
   bool              ExpTransformTicks(MqlTick &out_ticks[]);

public :
   //constructor
                     CPermuteTicks(void);
   //desctrucotr
                    ~CPermuteTicks(void);
   bool              Initialize(MqlTick &in_ticks[]);
   bool              Permute(MqlTick &out_ticks[]);
  };

m_initialized is a boolean flag that signals a successful preprocessing operation before permutations can be done.

To use the class, a user would have to call the Initialize() method after creating an instance of the object. The method requires an array of ticks that are to be permuted. Inside the method, inaccessible class arrays are resized and LogTranformTicks() is enlisted to transform the tick data. It is done by making sure to avoid zero or negative values, replacing them with 1.0. Once a permutation is done and log transformed tick data is returned to its original domain by the ExpTransformTicks() private method.

//+--------------------------------------------------------------------+
//|Initialize the permutation process by supplying ticks to be permuted|
//+--------------------------------------------------------------------+
bool CPermuteTicks::Initialize(MqlTick &in_ticks[])
  {
//---set or reset initialization flag  
   m_initialized=false;
//---check arraysize
   if(in_ticks.Size()<5)
     {
      Print("Insufficient amount of data supplied ");
      return false;
     }
//---copy ticks to local array
   if(ArrayCopy(m_ticks,in_ticks)!=int(in_ticks.Size()))
     {
      Print("Error copying ticks ", GetLastError());
      return false;
     }
//---ensure the size of m_differenced array
   if(m_differenced.Size()!=m_ticks.Size()-1)
      ArrayResize(m_differenced,m_ticks.Size()-1);
//---apply log transformation to relevant tick data members
   if(!LogTransformTicks())
     {
      Print("Log transformation failed ", GetLastError());
      return false;
     }
//---fill m_differenced with differenced values, excluding the first tick
   for(uint i=1; i<m_logticks.Size(); i++)
     {
      m_differenced[i-1].bid_d=(m_logticks[i].bid_d)-(m_logticks[i-1].bid_d);
      m_differenced[i-1].ask_d=(m_logticks[i].ask_d)-(m_logticks[i-1].ask_d);
      m_differenced[i-1].vol_d=(m_logticks[i].vol_d)-(m_logticks[i-1].vol_d);
      m_differenced[i-1].volreal_d=(m_logticks[i].volreal_d)-(m_logticks[i-1].volreal_d);
     }
//---set the initilization flag
   m_initialized=true;
//---
   return true;
  }

To output permuted ticks, the aptly named method Permute() should be called. It has a single parameter requirement of a dynamic MqlTick array, where the permuted ticks will be placed. This is where the tick shuffling procedure is located, inside a while loop that swaps the position of a differenced tick value depending on the random number generated at each iteration.

//+------------------------------------------------------------------+
//|Public method which applies permutation and gets permuted ticks   |
//+------------------------------------------------------------------+
bool CPermuteTicks::Permute(MqlTick &out_ticks[])
  {
//---zero out tick array  
   ZeroMemory(out_ticks);
//---ensure required data already supplied through initialization
   if(!m_initialized)
     {
      Print("not initialized");
      return false;
     }
//---resize output array if necessary
   if(out_ticks.Size()!=m_ticks.Size())
      ArrayResize(out_ticks,m_ticks.Size());
//---
   int i,j;
   CMqlTick tempvalue;

   i=(int)m_ticks.Size()-1;
   
   int error_value;
   double unif_rando;

   ulong time = GetTickCount64();

   while(i>1)
     {
      error_value=0;
      unif_rando=MathRandomUniform(MIN_THRESHOLD,MAX_THRESHOLD,error_value);
      if(!MathIsValidNumber(unif_rando))
        {
         Print("Invalid random value ",error_value);
         return(false);
        }
      j=(int)(unif_rando*i);
      if(j>=i)
         j=i-1;
      --i;
//---swap tick data randomly
      tempvalue.bid_d=m_differenced[i].bid_d;
      tempvalue.ask_d=m_differenced[i].ask_d;
      tempvalue.vol_d=m_differenced[i].vol_d;
      tempvalue.volreal_d=m_differenced[i].volreal_d;

      m_differenced[i].bid_d=m_differenced[j].bid_d;
      m_differenced[i].ask_d=m_differenced[j].ask_d;
      m_differenced[i].vol_d=m_differenced[j].vol_d;
      m_differenced[i].volreal_d=m_differenced[j].volreal_d;

      m_differenced[j].bid_d=tempvalue.bid_d;
      m_differenced[j].ask_d=tempvalue.ask_d;
      m_differenced[j].vol_d=tempvalue.vol_d;
      m_differenced[j].volreal_d=tempvalue.volreal_d;
     }
//---undo differencing 
   for(uint k = 1; k<m_ticks.Size(); k++)
     {
      m_logticks[k].bid_d=m_logticks[k-1].bid_d + m_differenced[k-1].bid_d;
      m_logticks[k].ask_d=m_logticks[k-1].ask_d + m_differenced[k-1].ask_d;
      m_logticks[k].vol_d=m_logticks[k-1].vol_d + m_differenced[k-1].vol_d;
      m_logticks[k].volreal_d=m_logticks[k-1].volreal_d + m_differenced[k-1].volreal_d;
     }
//---copy the first tick  
   out_ticks[0].bid=m_ticks[0].bid;
   out_ticks[0].ask=m_ticks[0].ask;
   out_ticks[0].volume=m_ticks[0].volume;
   out_ticks[0].volume_real=m_ticks[0].volume_real;
   out_ticks[0].flags=m_ticks[0].flags;
   out_ticks[0].last=m_ticks[0].last;
   out_ticks[0].time=m_ticks[0].time;
   out_ticks[0].time_msc=m_ticks[0].time_msc;     
//---return transformed data
   return ExpTransformTicks(out_ticks);
  }
//+------------------------------------------------------------------+

Once all iterations have been completed, the m_logticks array is rebuilt by undoing the differencing using permuted m_differenced tick data. Finally, the sole argument to the Permute() method is filled with m_logtick data returned to its original domain,  with time and tick flag information copied from the original tick series.

//+-------------------------------------------------------------------+
//|Helper method applying log transformation                          |
//+-------------------------------------------------------------------+
bool CPermuteTicks::LogTransformTicks(void)
  {
//---resize m_logticks if necessary  
   if(m_logticks.Size()!=m_ticks.Size())
      ArrayResize(m_logticks,m_ticks.Size());
//---log transform only relevant data members, avoid negative and zero values
   for(uint i=0; i<m_ticks.Size(); i++)
     {
      m_logticks[i].bid_d=(m_ticks[i].bid>0)?MathLog(m_ticks[i].bid):MathLog(1e0);
      m_logticks[i].ask_d=(m_ticks[i].ask>0)?MathLog(m_ticks[i].ask):MathLog(1e0);
      m_logticks[i].vol_d=(m_ticks[i].volume>0)?MathLog(m_ticks[i].volume):MathLog(1e0);
      m_logticks[i].volreal_d=(m_ticks[i].volume_real>0)?MathLog(m_ticks[i].volume_real):MathLog(1e0);
     }
//---
   return true;
  }

//+-----------------------------------------------------------------------+
//|Helper method undoes log transformation before outputting permuted tick|
//+-----------------------------------------------------------------------+
bool CPermuteTicks::ExpTransformTicks(MqlTick &out_ticks[])
  {
//---apply exponential transform to data and copy original tick data member info
//---not involved in permutation operations
   for(uint k = 1; k<m_ticks.Size(); k++)
     {
      out_ticks[k].bid=(m_logticks[k].bid_d)?MathExp(m_logticks[k].bid_d):0;
      out_ticks[k].ask=(m_logticks[k].ask_d)?MathExp(m_logticks[k].ask_d):0;
      out_ticks[k].volume=(m_logticks[k].vol_d)?(ulong)MathExp(m_logticks[k].vol_d):0;
      out_ticks[k].volume_real=(m_logticks[k].volreal_d)?MathExp(m_logticks[k].volreal_d):0;
      out_ticks[k].flags=m_ticks[k].flags;
      out_ticks[k].last=m_ticks[k].last;
      out_ticks[k].time=m_ticks[k].time;
      out_ticks[k].time_msc=m_ticks[k].time_msc;
     }
//---
   return true;
  }

We now have an algorithm to handle price series permutations, this is only half the battle so to speak, we still have to do the test.

Permutation test procedure

The permutation test procedure will leverage two features of the MetaTrader 5 terminal. The first being the ability to create custom symbols and specify their properties. The second is the ability to optimize EA's according to enabled symbols in the Market Watch List. So there are at least two more steps to the whole process.

We can permute ticks, and create custom symbols, putting this together we can generate custom symbols based on any existing symbol. With each custom symbol being specified with a unique permutation of ticks for the symbol used as a basis. Creating  symbols can be done manually, then again why would we punish ourselves when we could automate the entire task of symbol creation, and addition of permuted ticks.

The script PrepareSymbolsForPermutationTests does exactly this. Its user specified inputs allow setting a base symbol, the date range of ticks from the base symbol to be used in the permutations, the number of required permutations which corresponds with the number of custom symbols that will be created and an optional string identifier that will be appended to the names of the new custom symbols.

//+------------------------------------------------------------------+
//|                            PrepareSymbolsForPermutationTests.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<GenerateSymbols.mqh>
#property script_show_inputs
//--- input parameters
input string   BaseSymbol="EURUSD";
input datetime StartDate=D'2023.06.01 00:00';
input datetime EndDate=D'2023.08.01 00:00';
input uint     Permutations=100;
input string   CustomID="";//SymID to be added to symbol permutation names
//---
CGenerateSymbols generateSymbols();
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   if(!generateSymbols.Initiate(BaseSymbol,CustomID,StartDate,EndDate))
       return;
//---
   Print("Number of newly generated symbols is ", generateSymbols.Generate(Permutations));
//---          
  }
//+------------------------------------------------------------------+

The script automatically creates symbol names using the base symbol name, with an enumeration at the end. The code that does all this is enclosed in GenerateSymbols.mqh which contains the definition of the CGenerateSymbols class. The class definition relies on two other dependencies: NewSymbol.mqh which contains the definition of the CNewSymbol class adapted from code in the article "MQL5 Cookbook: Trading strategy stress testing using custom symbols".

//+------------------------------------------------------------------+
//| Class CNewSymbol.                                                |
//| Purpose: Base class for a custom symbol.                         |
//+------------------------------------------------------------------+
class CNewSymbol : public CObject
  {
   //--- === Data members === ---
private:
   string            m_name;
   string            m_path;
   MqlTick           m_tick;
   ulong             m_from_msc;
   ulong             m_to_msc;
   uint              m_batch_size;
   bool              m_is_selected;
   //--- === Methods === ---
public:
   //--- constructor/destructor
   void              CNewSymbol(void);
   void             ~CNewSymbol(void) {};
   //--- create/delete
   int               Create(const string _name,const string _path="",const string _origin_name=NULL,
                            const uint _batch_size=1e6,const bool _is_selected=false);
   bool              Delete(void);
   //--- methods of access to protected data
   string            Name(void) const { return(m_name); }
   bool              RefreshRates(void);
   //--- fast access methods to the integer symbol properties
   bool              Select(void) const;
   bool              Select(const bool select);
   //--- service methods
   bool              Clone(const string _origin_symbol,const ulong _from_msc=0,const ulong _to_msc=0);
   bool              LoadTicks(const string _src_file_name);
   //--- API
   bool              SetProperty(ENUM_SYMBOL_INFO_DOUBLE _property,double _val) const;
   bool              SetProperty(ENUM_SYMBOL_INFO_INTEGER _property,long _val) const;
   bool              SetProperty(ENUM_SYMBOL_INFO_STRING _property,string _val) const;
   double            GetProperty(ENUM_SYMBOL_INFO_DOUBLE _property) const;
   long              GetProperty(ENUM_SYMBOL_INFO_INTEGER _property) const;
   string            GetProperty(ENUM_SYMBOL_INFO_STRING _property) const;
   bool              SetSessionQuote(const ENUM_DAY_OF_WEEK _day_of_week,const uint _session_index,
                                     const datetime _from,const datetime _to);
   bool              SetSessionTrade(const ENUM_DAY_OF_WEEK _day_of_week,const uint _session_index,
                                     const datetime _from,const datetime _to);
   int               RatesDelete(const datetime _from,const datetime _to);
   int               RatesReplace(const datetime _from,const datetime _to,const MqlRates &_rates[]);
   int               RatesUpdate(const MqlRates &_rates[]) const;
   int               TicksAdd(const MqlTick &_ticks[]) const;
   int               TicksDelete(const long _from_msc,long _to_msc) const;
   int               TicksReplace(const MqlTick &_ticks[]) const;
   //---
private:
   template<typename PT>
   bool              CloneProperty(const string _origin_symbol,const PT _prop_type) const;
   int               CloneTicks(const MqlTick &_ticks[]) const;
   int               CloneTicks(const string _origin_symbol) const;
  };

The class helps to create new custom symbols based on existing ones. The last dependency required is of PermuteTicks.mqh which we have already encountered.

//+------------------------------------------------------------------+
//|                                              GenerateSymbols.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<PermuteTicks.mqh>
#include<NewSymbol.mqh>
//+------------------------------------------------------------------+
//| defines:max number of ticks download attempts and array resize   |
//+------------------------------------------------------------------+
#define MAX_DOWNLOAD_ATTEMPTS 10 
#define RESIZE_RESERVE 100
//+------------------------------------------------------------------+
//|CGenerateSymbols class                                            |
//| creates custom symbols from an existing base symbol's tick data  |
//|  symbols represent permutations of base symbol's ticks           |
//+------------------------------------------------------------------+
class CGenerateSymbols
{
 private:
   string         m_basesymbol;     //base symbol
   string         m_symbols_id;     //common identifier added to names of new symbols 
   long           m_tickrangestart; //beginning date for range of base symbol's ticks
   long           m_tickrangestop;  //ending date for range of base symbol's ticks
   uint           m_permutations;   //number of permutations and ultimately the number of new symbols to create
   MqlTick        m_baseticks[];    //base symbol's ticks
   MqlTick        m_permutedticks[];//permuted ticks;
   CNewSymbol    *m_csymbols[];     //array of created symbols
   CPermuteTicks *m_shuffler;       //object used to shuffle tick data
   
 public: 
   CGenerateSymbols(void);
   ~CGenerateSymbols(void);                      
   bool Initiate(const string base_symbol,const string symbols_id,const datetime start_date,const datetime stop_date);
   uint Generate(const uint permutations);
};

CGenerateSymbols has two member functions that a user needs to be aware of. The Initiate() method should be called first after object creation, it has 4 parameters that correspond with user inputs of the script already mentioned.

//+-----------------------------------------------------------------------------------------+
//|set and check parameters for symbol creation, download ticks and initialize tick shuffler|
//+-----------------------------------------------------------------------------------------+
bool CGenerateSymbols::Initiate(const string base_symbol,const string symbols_id,const datetime start_date,const datetime stop_date)
{
//---reset number of permutations previously done
 m_permutations=0;
//---set base symbol
 m_basesymbol=base_symbol;
//---make sure base symbol is selected, ie, visible in WatchList 
 if(!SymbolSelect(m_basesymbol,true))
  {
   Print("Failed to select ", m_basesymbol," error ", GetLastError());
   return false;
  }
//---set symbols id 
 m_symbols_id=symbols_id;
//---check, set ticks date range
 if(start_date>=stop_date)
   {
    Print("Invalid date range ");
    return false;
   }
 else
   {
    m_tickrangestart=long(start_date)*1000;
    m_tickrangestop=long(stop_date)*1000;
   }  
//---check shuffler object
   if(CheckPointer(m_shuffler)==POINTER_INVALID)
    {
     Print("CPermuteTicks object creation failed");
     return false;
    }
//---download ticks
   Comment("Downloading ticks");
   uint attempts=0;
   int downloaded=-1;
    while(attempts<MAX_DOWNLOAD_ATTEMPTS)
     {
      downloaded=CopyTicksRange(m_basesymbol,m_baseticks,COPY_TICKS_ALL,m_tickrangestart,m_tickrangestop);
      if(downloaded<=0)
        {
         Sleep(500);
         ++attempts;
        }
      else 
        break;   
     }
//---check download result
   if(downloaded<=0)
    {
     Print("Failed to get tick data for ",m_basesymbol," error ", GetLastError());
     return false;
    }          
  Comment("Ticks downloaded");  
//---return shuffler initialization result   
  return m_shuffler.Initialize(m_baseticks);        
}                      

The Generate() method takes as input the required number of permutations and returns the number of new custom symbols added to the Market Watch of the terminal.
The outcome of running the script will appear in the Expert's tab in the terminal.

//+------------------------------------------------------------------+
//| generate symbols return newly created or refreshed symbols       |
//+------------------------------------------------------------------+
uint CGenerateSymbols::Generate(const uint permutations)
{
//---check permutations
 if(!permutations)
   {
    Print("Invalid parameter value for Permutations ");
    return 0;
   } 
//---resize m_csymbols
  if(m_csymbols.Size()!=m_permutations+permutations)
    ArrayResize(m_csymbols,m_permutations+permutations,RESIZE_RESERVE);
//---
  string symspath=m_basesymbol+m_symbols_id+"_PermutedTicks"; 
  int exists;
//---do more permutations
  for(uint i=m_permutations; i<m_csymbols.Size(); i++)
      {
       if(CheckPointer(m_csymbols[i])==POINTER_INVALID)
              m_csymbols[i]=new CNewSymbol();
       exists=m_csymbols[i].Create(m_basesymbol+m_symbols_id+"_"+string(i+1),symspath,m_basesymbol); 
       if(exists>0)
          {
           Comment("new symbol created "+m_basesymbol+m_symbols_id+"_"+string(i+1) );
            if(!m_csymbols[i].Clone(m_basesymbol) || !m_shuffler.Permute(m_permutedticks))
                 break;
            else
                {
                 m_csymbols[i].Select(true);
                 Comment("adding permuted ticks");
                 if(m_csymbols[i].TicksAdd(m_permutedticks)>0)
                      m_permutations++;
                }              
          }
       else
          {
           Comment("symbol exists "+m_basesymbol+m_symbols_id+"_"+string(i+1) );
           m_csymbols[i].Select(true);
           if(!m_shuffler.Permute(m_permutedticks))
                 break;
           Comment("replacing ticks ");
           if(m_csymbols[i].TicksReplace(m_permutedticks)>0)
              m_permutations++;
           else
              break;   
          } 
     }   
//---return successful number of permutated symbols
 Comment("");
//--- 
 return m_permutations;
}

The next step is to run the optimization in the strategy tester, make sure to select the last optimization method and specify the EA to be tested. Start the test and find something to do for a while, as this will likely take a long time. When the strategy tester is done we have a collection of performance data that we can sink into.

An Example

Let's have a look at what doing all of this looks like by running a test using the bundled MACD Sample EA. The test will be run on the AUDUSD symbol with 100 permutations set in the script.

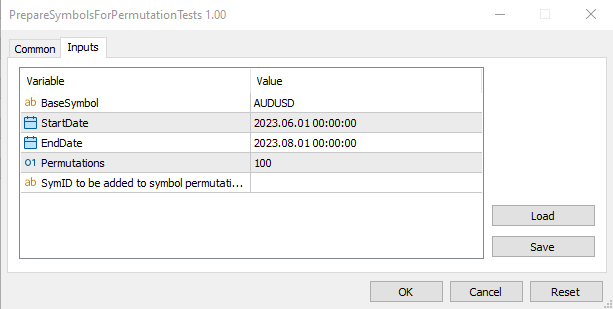
After running the script we have our 100 extra symbols based on the permuted ticks of a sample from the selected AUDUSD symbol.

Finally we run the optimization test.

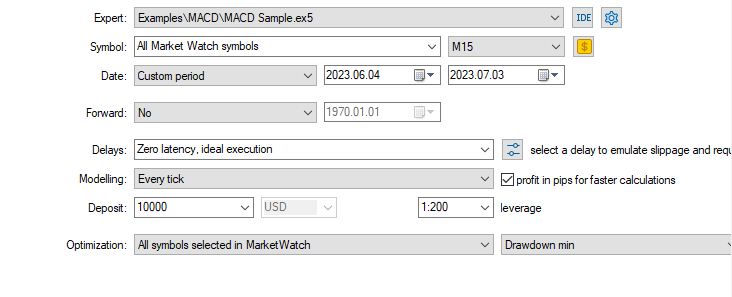
  The EA settings used are shown below.

The results from the test.

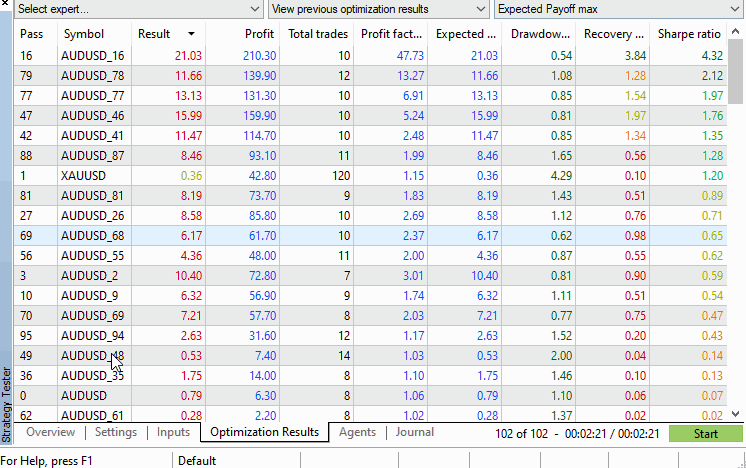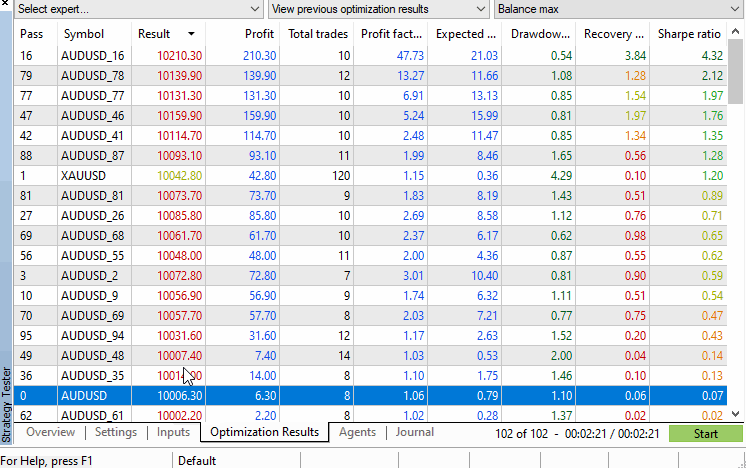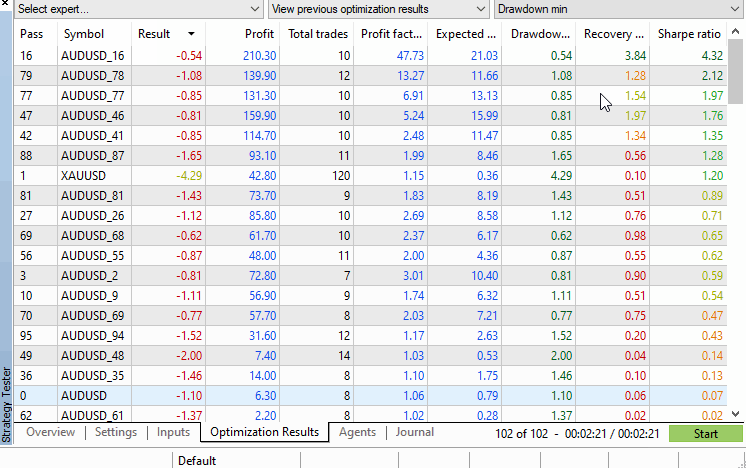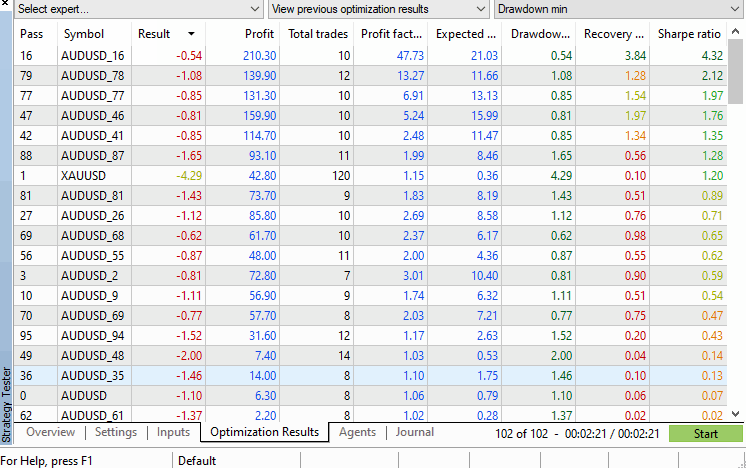
The strategy tester's results tab displays all the performance figures we may be interested in and arranges the symbols in descending order based on the selected performance criteria that can be selected by the dropdown menu in the top right corner of the tester window. From this view the p-value can be easily calculated manually, or if required automatically by processing the .xml file that can optionally be exported from the tester with a right click.

Using the example, we do not even have to run any calculations, as it can be seen that the original symbol's test figures are way down the results tab, with more than 10 permuted symbols clocking better performance. This indicates that the p-value is above 0.05.

Of course, the result of this test should be taken with a pinch of salt as the testing period chosen was very short. Users should select a test period that is much more substantial in length and representative of conditions likely to be encountered in real trading.

As already mentioned there are many options available for processing our results further in order to calculate the p-values. Any further operations will be centered on parsing the data from the xml file exported from the strategy tester. We will demonstrate how one may use a spread sheet application to process the file in a few clicks and keystrokes.

Obviously after exporting the file, make a note of where it is saved and open it using any spread sheet app. The graphic below shows use of the free OpenOffice Calc, where a new row at the bottom of the table was added. Before going any further, it would be wise to remove rows for symbols that should not be part of the calculations. Under each relevant corresponding column the  p-value is calculated using a custom macro. The formula of the macro references the permuted symbol's performance metrics (located in row 18 in the document shown) as well as that of the permuted symbols for each column.  The full formula for the macro is shown in the graphic.

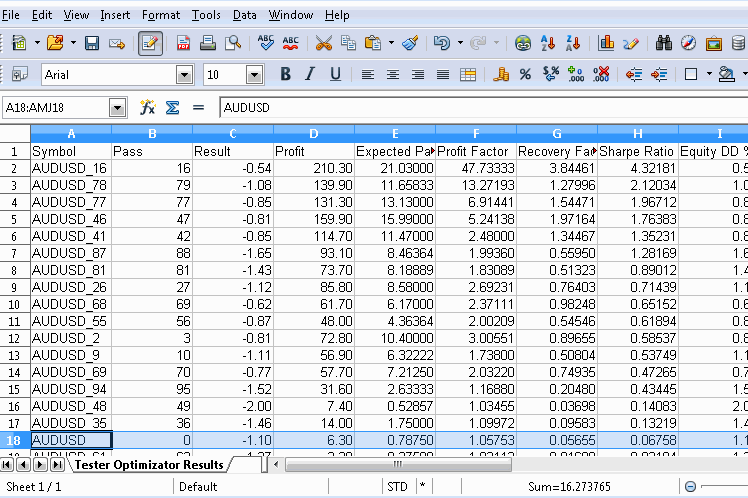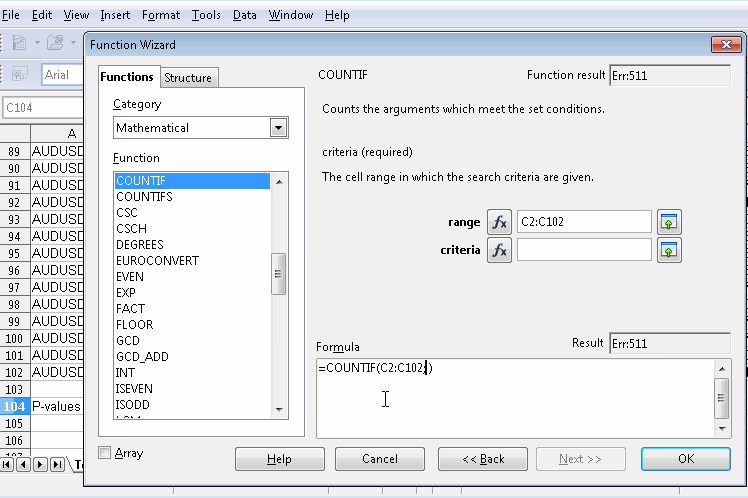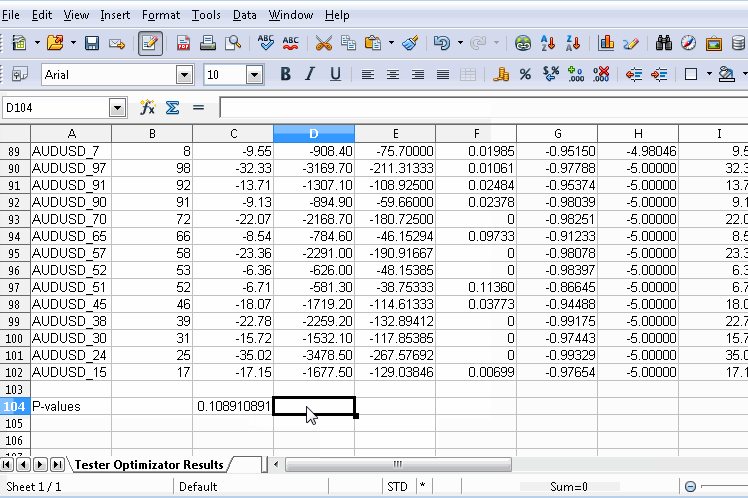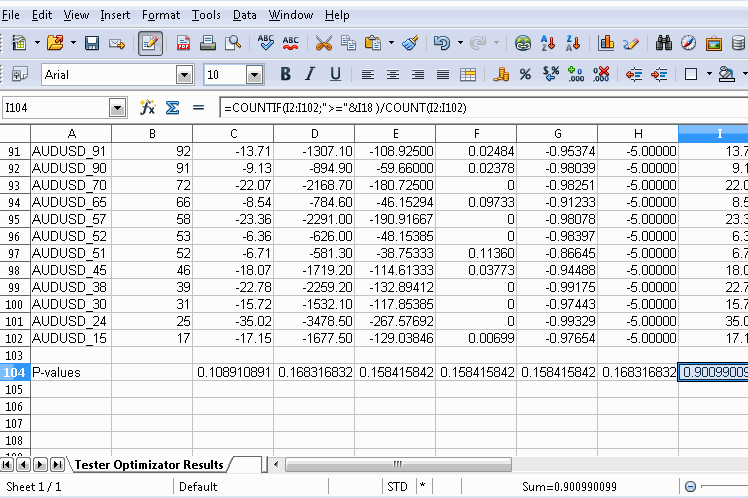
Besides using a spreadsheet application, we could use python, which has an abundance of modules for parsing xml files. If a user is proficient in mql5, it's possible to parse the files with a simple script as well. Just remember to pick an accessible directory when exporting the optimization results from the tester.

Conclusion

We have demonstrated that a permutation test can be applied to any EA, without access to the source code. Such a permutation test is invaluable as it applies fairly robust statistics that do not require making any assumptions about the distribution of any data involved. Unlike many other statistical tests used in strategy development.

The biggest drawback relates to the time and computer resources needed to conduct the test. It will require not only a powerful processor but also significant amounts of storage space. Generating new ticks and symbols will consume your free hard drive space. In my opinion anyone who is in the business of purchasing EAs should take note of this method of analysis, it takes time but it could also save you from making bad decisions that will cost you down the road.

Analysis that uses permuted price data can be applied in multiple ways.  We can use the method to analyze the behavior of indicators, as well as at different stages of strategy development. The possibilities are vast. Sometimes when developing or testing strategies it may seem that there is not enough data. Using permuted price series greatly multiplies the availability of data for testing. Source code of all mql5 programs described in the article are attached, i hope readers will find them useful.

FileName	Program Type	Description
GenerateSymbols.mqh	Include file	file contains definition of CGenerateSymbols class for generating symbols with ticks data permuted from a selected base symbol
NewSymbol.mqh	Include file	contains CNewSymbol class definition for creating custom symbols
PermuteTicks.mqh	Include file	defines the CPermuteTicks class for creating permutations of an array of tick data
PrepareSymbolsForPermutationTests.mq5	Script file	Script that automates the creation of custom symbols with permuted tick, in preparation of a permutation test