Uniformity Factor Indicator - Indikator für den MetaTrader 5

Hierbei handelt es sich um einen einfachen analytischen (nicht signalisierten, einmalig berechneten) Indikator, mit dem Sie die Hypothese testen können, dass die Preiszeitreihen einen "Random Walk" darstellen, insbesondere einen Gaußschen "Random Walk". Dies kann dazu beitragen, eine parametrische Umwandlung von Preisinkrementen in gleichmäßig verteilte, stabilere und vorhersehbarere Zeitreihen zu konstruieren, zumindest was die Volatilität angeht.

Wie Sie vielleicht wissen, wird die Strecke, die eine "Random Walk"-Variable nach N Schritten voraussichtlich zurücklegen wird, durch ihre Standardabweichung multipliziert mit sqrt(N) oder N^0,5 geschätzt.

Dieser Indikator berechnet die Statistik der "durchschnittlichen" Preisänderung (pro Balken) für vordefinierte Teilbereiche von Balken. Die "Mittelwertbildung" erfolgt über den Abstand (Anzahl der Balken bis zum gegebenen N) hoch F - ein Faktor, der von 0,1 bis 1 mit dem Schritt 0,1 aufgezählt wird.

Alle im aktuellen Chart verfügbaren Balken werden für die Erfassung der Statistiken in gleitenden Fenstern von bis zu N Balken verwendet.

Dann findet der Indikator die "regelmäßigste" gleichmäßige Verteilung der Statistiken unter den verschiedenen F's und zeigt ein Histogramm für diesen (als optimal angesehenen) Faktor an, normalerweise 0,5 oder 0,6. Jede Spalte des Histogramms ist das "durchschnittliche" Delta der Punkte pro Balken für die entsprechende Handelsdauer (Anzahl der Balken), wobei die "Mittelung" durch N^F erfolgt (bei F=1 erhalten Sie die Standardmittelung).

Der Indikator kann verschiedene Methoden zur automatischen Erkennung der "Regelmäßigkeit" (Flachheit) der statistischen Kurve verwenden:

• Minimum der Varianz;
• Minimum der Differenz zwischen den drei M's (Mittelwert, Median, Modus), als quadratischer Fehler;
• Minimum des Gini-Koeffizienten;

Die Kenntnis des optimalen Faktors kann nützlich sein für:

• Normalisierung der Eingabedaten (Preisänderungen) für neuronale Netze und andere Algorithmen des maschinellen Lernens;
• Schätzung einer ausreichenden Anzahl von Balken für die Zusammenstellung eines einzigen Eingangsvektors für die Analyse in Volatilitätshandelssystemen;
• Erkennung von Symbolen und/oder Zeitrahmen mit Anomalien (Nicht-Standard-F oder Singularität in der Verteilungskurve);

• Periode - maximaler Abstand in Balken (N), der für die Erfassung der Preisspannenstatistik verwendet wird, standardmäßig 200;
• Faktor - Exponent für die "Mittelwertbildung" über die Abstände, standardmäßig 0 - bedeutet automatische Erkennung, Sie können einen benutzerdefinierten Wert zwischen 0,0 und 1,0 für die Schätzung eingeben, zum Beispiel 0,525;
• Methode - eine der Methoden zur Schätzung der Homogenität: Varianz, Tripel_M, Gini;
• MaxBars - eine Begrenzung der Balken zur Berechnung der Statistiken, standardmäßig 0 - bedeutet alle verfügbaren Balken;

NB: Wenn Sie eine unbegrenzte Anzahl oder Hunderttausende von Balken im Diagramm verwenden, kann die Berechnung einige Zeit in Anspruch nehmen - wenn dies ein Problem darstellt, sollten Sie die Anzahl der Balken auf Zehntausende begrenzen.

Ausgaben

Der Indikator zeigt ein blaues Histogramm der durchschnittlichen Preisveränderung pro Balken für jeden Abstand im Bereich der Abstände (1..Periode) und für den ausgewählten Faktor der Gleichmäßigkeit.

Als zweites Histogramm (orange) wird zur Veranschaulichung auch eine kontinuierlich ansteigende Anzahl von Balken (Abstand) dargestellt.

Eine vollständige Tabelle der getesteten Faktoren und der entsprechenden Metriken der aktuellen Zeitreihe wird im Protokoll ausgedruckt.

XAGUSD.c D1, Max.Distance: 500, Bars: 2641
Factor: 0.4, Result: var(0.4) mmm(0.4) gini(0.4)*
    [factor]  [mean] [variance] [skewness] [kurtosis] [median]  [mode] [mmmse]  [gini]
[0]  0.10000 1.85217    0.21976   -0.87694    0.07751  1.95822 2.30853 0.33811 0.13930
[1]  0.20000 1.07575    0.04083   -1.12699    0.96219  1.12715 1.25786 0.13285 0.10093
[2]  0.30000 0.62887    0.00525   -1.54472    3.00927  0.64878 0.68616 0.04114 0.05943
[3]  0.40000 0.37043    0.00021   -2.90499   13.36923  0.37546 0.37502 0.00394 0.01753
[4]  0.50000 0.22015    0.00028    1.53459    1.38333  0.21532 0.21461 0.00426 0.03779
[5]  0.60000 0.13222    0.00064    1.98696    4.05157  0.12372 0.10902 0.01661 0.09162
[6]  0.70000 0.08041    0.00072    2.60714    8.60950  0.07122 0.05862 0.01551 0.15135
[7]  0.80000 0.04964    0.00065    3.39070   15.85717  0.04099 0.03149 0.01289 0.21637
[8]  0.90000 0.03119    0.00054    4.37643   27.17457  0.02359 0.01692 0.01018 0.28652
[9]  1.00000 0.02002    0.00044    5.57319   43.86448  0.01358 0.00909 0.00787 0.36126

Bildschirmfotos

Die folgenden Screenshots zeigen den Indikator auf 3 Zeitrahmen: D1, H1, M1.

Jeder Chart enthält 2 Instanzen des Indikators:

• Die obere Instanz ist für die automatische Erkennung von F durch Gini konfiguriert, und der gefundene Wert (einmal 0,4 und zweimal 0,5) wird im Titel angezeigt und mit einem Sternchen markiert;
• der untere Wert ist für den vordefinierten Wert F=0,6 konfiguriert;

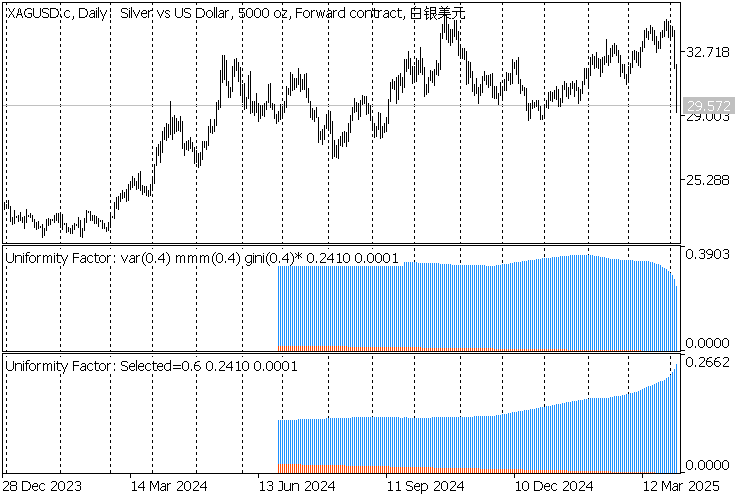
2 Indikatoren Gleichmäßigkeitsfaktor auf XAGUSD,D1

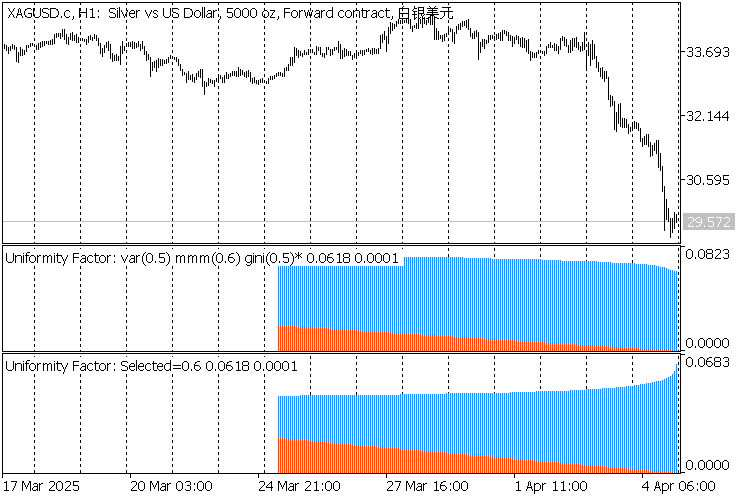
2 Indikatoren Gleichmäßigkeitsfaktor für XAGUSD,H1

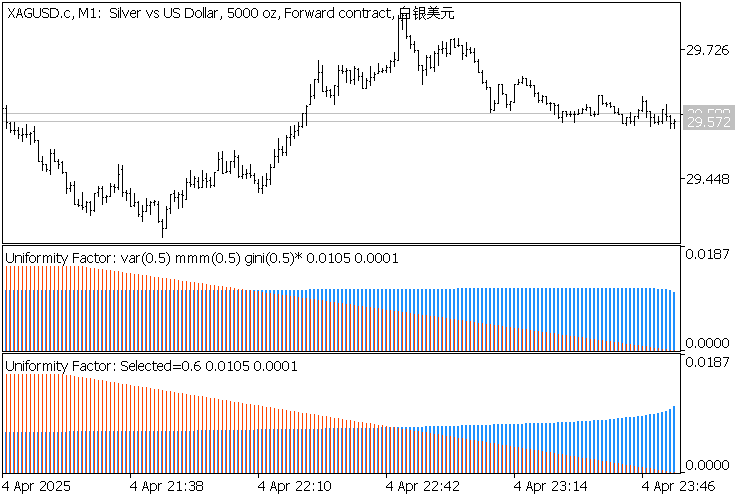
2 Indikatoren Gleichmäßigkeitsfaktor für XAGUSD,M1