Der Indikator CCI: Upgrade und neue Funktionen
Kurze Geschichte
Der Commodity Channel Index (CCI) ist jedem Händler bekannt. Er wurde von Donald Lambert entwickelt und erstmals 1980 in der Zeitschrift Commodities (jetzt Modern Trader) veröffentlicht. Seitdem hat dieser Indikator wohlverdienten Ruhm erlangt und ist bei den Händlern sehr beliebt geworden. Es ist Teil der Handelsplattform und wird sowohl im manuellen Handel als auch als Teil von automatisierten Handelssystemen verwendet.
Berechnungsalgorithmus
Die Berechnung des Indikators ist recht einfach und klar. Der Indikator zeigt an, wie stark der Kurs vom Durchschnittswert im Verhältnis zur mittleren absoluten Abweichung abweicht. Der Berechnungsalgorithmus kann wie folgt dargestellt werden. Der Zeitraum des Indikators betrage N Preise. Dann:
- Berechnen des EMA:
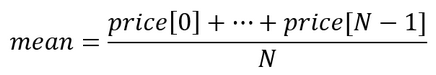
- Ermitteln der mittleren absoluten Abweichung
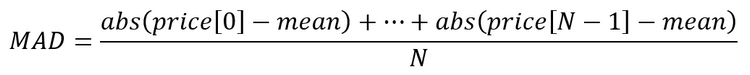
- Berechnen des Indikatorwerts
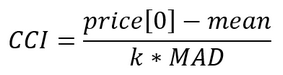
Im ursprünglichen Indikator ist der Korrekturfaktor k = 0,015. Er wird so gewählt, dass die Preisabweichung um 1,5*MAD gleich 100 Indikatoreinheiten ist. In diesem Fall beträgt die Abweichung um 3*MAD 200 Einheiten. (Interessanterweise ist der Wert des Normierungskoeffizienten k 66,6, wenn die Division durch die Multiplikation ersetzt wird)
Mögliche Algorithmusänderungen
Die Besonderheit des Indikators ist die Verwendung der mittleren absoluten Abweichung. Dieser Ansatz war zu Beginn der Computertechnologie durchaus gerechtfertigt, da die Berechnung der absoluten Abweichung weniger Rechenressourcen erforderte als die Berechnung der besser geeigneten Standardabweichung. Moderne Computer können das Quadrieren und Wurzel ziehen in einer angemessenen Zeitspanne bewältigen. Daher kann der Algorithmus zur Berechnung des Algorithmus wie folgt aussehen.
- Ermitteln der Summe von Zahlen:
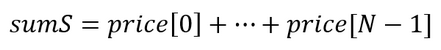
- Ermitteln der Summe der Quadrate:
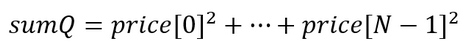
- Berechnen des Indikatorwerts:
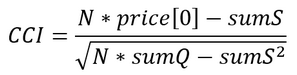
Ein solcher Algorithmus ist zwar genauer, aber immer noch nicht perfekt. Das Hauptproblem besteht darin, dass für die Schätzung der Durchschnittswerte und des quadratischen Mittelwerts eine ausreichend große Anzahl von Preisen (mindestens dreißig) erforderlich ist. Aber auch kurze Zeiträume können für den Handel genutzt werden. In der klassischen Version des CCI wird zum Beispiel ein Zeitraum von 14 Stichproben empfohlen.
Solche Situationen erfordern robuste statistische Methoden. Sie ermöglichen es, auch in sehr extremen Situationen, wie sie auf den Finanzmärkten häufig vorkommen, relativ stabile und zuverlässige Parameterschätzungen zu erhalten.
Schauen wir uns an, wie robuste Methoden funktionieren und vergleichen sie mit den klassischen Methoden. Nehmen wir zum Beispiel eine Zeitreihe mit drei Werten: p[0] = 1, p[1] = 3, p[2] = 8.
Dann reduziert sich der klassische Ansatz auf die folgenden Berechnungen:
- Mittelwert (1 + 3 + 8) / 3 = 4
- Absolute Abweichung (abs(1 - 4) + abs(3 - 4) + abs(8 - 4)) /3 = 2.67
- Untere und obere Grenze des Kanals 1,33 - 6,67
Rechnen wir nun mit der Standardabweichung:
- Mittelwert (1 + 3 + 8) / 3 = 4
- Die Standardabweichung: sqrt(((1 – 4)^2 + (3 – 4)^2 + (8 – 4)^2) / 3) = 2.94
- Untere und obere Grenze des Kanals 1,06 - 6,94
Robuste Schätzungen sind in den Berechnungen aufwendiger. Verwenden wir die Theil-Sen-Methode, um den Mittelwert zu schätzen. Zu diesem Zweck müssen zunächst alle Halbsummen der paarweise erfassten Zeitreihenwerte ermittelt werden. Die Anzahl dieser Paare lässt sich mit folgender Gleichung ermitteln: num=(N*(N-1)) / 2.
In diesem Fall ist der stabile Mittelwert gleich dem Median dieser Halbsummen. Um den Median zu ermitteln, müssen wir das Feld zunächst in aufsteigender Reihenfolge sortieren. Der Median entspricht dann dem Wert in der Mitte des Feldes. Um den Medianwert zu ermitteln, benötigen wir den Index des zentralen Elements, wenn die Größe der Matrix eine ungerade Zahl ist, und den Index von zwei zentralen Elementen, wenn die Größe der Matrix eine gerade Zahl ist. Dann ist der Median gleich dem Mittelwert dieser beiden Elemente.
Die Gleichungen für die Berechnung der Indizes in beiden Fällen ("Größe" ist die Anzahl der Elemente in der Matrix):
- Größe ungerader Zahl
Index = Größe / 2
- Größe gerader Zahl
Index1 = Größe / 2 - 1; Index2 = Größe / 2
Im Falle unseres Beispiels sieht das wie folgt aus:
hs1 = (1 + 3) / 2 = 2
hs2 = (1 + 8) / 2 = 4,5
hs3 = (3 + 8) / 2 = 5,5
Sortiert 2, 4.5, 5.5
- Mittelwert = 4,5
Kommen wir nun zur Abweichung. Wir müssen den Median zwischen den absoluten Werten der ursprünglichen Zeitreihe und ihrem Mittelwert finden.
d1 = abs(1 - 4,5) = 3,5
d2 = abs(3 - 4,5) = 1,5
d3 = abs(8 - 4,5) = 3,5
Sortiert 3.5, 1.5, 3.5
- Abweichung = 3,5
- Untere und obere Grenzen des Kanals 1 - 8
Vergleich zwischen klassischer und aktualisierter Indikatorversion
Lassen Sie uns diese Ansätze vergleichen. Bei normalen Berechnungen gingen die Minimal- und Maximalwerte der Zeitreihe über den Mittelwert +/- Abweichung hinaus. Im Falle einer robusten Schätzung passen alle Werte der ursprünglichen Reihe in diese Grenzen. Der Unterschied zwischen den drei Ansätzen ist offensichtlich, aber nur in unserem Beispiel. Nun wollen wir sehen, wie sich die verschiedenen Berechnungsmethoden bei realen Daten verhalten. Implementieren wir alle drei Algorithmen als einen separaten Indikator. Auf diese Weise können wir uns auch mit den Merkmalen der Berechnung der einzelnen Optionen vertraut machen.
Das Aussehen des Indikators hängt im Wesentlichen von zwei Variablen ab - der angewandten Preiskonstante und dem Zeitraum. In MQL5 kann die Preiskonstante bei der Definition der Indikatoreigenschaften festgelegt werden.
#property indicator_applied_price PRICE_TYPICAL
In MQL4 werde ich eine separate Funktion verwenden.
Der Indikator Zeitraum zeigt die Anzahl der in den Berechnungen verwendeten Kurswerte an.
input ushort iPeriod=14;//indicator period
Der Wert der Variablen sollte mindestens drei betragen. Beachten Sie, dass es bei kleinen Zeiträumen möglich ist, falsche (zu große) Werte zu erhalten.
Die Berechnung der klassischen CCI-Version für jeden i-ten Balken wird wie folgt durchgeführt. Zunächst wird der Wert des Stichprobenmittelwerts ermittelt.
double mean=0; //sample mean for(int j=0; j<iPeriod; j++) { mean=mean+price[i+j]; //sum up price values } mean=mean/iPeriod; //sample mean for the period
Nun ist es an der Zeit, die mittlere absolute Abweichung zu berechnen.
double mad=0; //mean absolute deviation for(int j=0; j<iPeriod; j++) { mad=mad+MathAbs(price[i+j]-mean); //sum up absolute difference values }
Wenn der Wert der mittleren absoluten Abweichung größer als Null ist, dann ist der Indikator gleich:
res=(price[i]-mean)*iPeriod/mad; Die Indikatorversion mit der Standardabweichung wird wie folgt berechnet. Zunächst müssen wir die Summen der Preise und ihre Quadrate ermitteln.
double sumS=0,//sum of prices sumQ=0;//sum of price squares for(int j=0; j<iPeriod; j++) { sumS=sumS+price[i+j]; sumQ=sumQ+price[i+j]*price[i+j]; }
Nun müssen wir den Nenner finden, der für die Berechnung des Indikators erforderlich ist.
double denom=MathSqrt(iPeriod*sumQ-sumS*sumS);
Wenn der Nenner größer als Null ist, ergibt sich folgendes Ergebnis:
res=(iPeriod*price[i]-sumS)/denom; Betrachten wir schließlich die Berechnungen mit den robusten Methoden. Zunächst müssen wir zwei Arrays vorbereiten, um die Zwischenergebnisse zu speichern. Ein Array dient zur Speicherung der Werte von Halbsummen, ein anderes zur Speicherung absoluter Differenzen.
double halfsums[],diff[]; Bereiten wir zunächst das Array mit den Halbsummen für die weitere Verwendung vor. Zu diesem Zweck müssen wir seine Größe definieren.
int size=iPeriod*(iPeriod-1)/2; //halfsums array size ArrayResize(halfsums,size); //set the array size
Nun wollen wir die Indizes der zentralen Elemente des Arrays ermitteln. Aus Gründen der Vielseitigkeit werde ich zwei Indizes verwenden. Wenn die Größe ungerade ist, stimmen diese Indizes überein, ansonsten sind sie unterschiedlich.
indx10=size/2; indx11=indx10; if(MathMod(size,2)==0) indx11=indx10-1;
Anschließend bereiten wir das Array diff vor. Seine Größe entspricht dem Zeitraum, für den der Indikator gilt. Die Elementindizes sind dieselben wie im vorherigen Fall.
ArrayResize(diff,iPeriod); indx20=iPeriod/2; indx21=indx20; if(MathMod(iPeriod,2)==0) indx21=indx20-1;
Nun ist es an der Zeit, mit der Berechnung der Indikatorwerte zu beginnen. Wir brauchen einen zusätzlichen Zähler, um das Feld mit Halbsummen zu füllen.
int cnt=0; //counter of array elements for(int j=iPeriod-2; j>=0; j--) { for(int k=iPeriod-1; k>j; k--) { halfsums[cnt]=(price[i+j]+price[i+k])/2; //half sum value cnt++; //increase the counter } }
Nach dem Füllen des Arrays sollte es sortiert werden. Die Werte aus der Mitte des Feldes sollten als Schätzwert für den Mittelwert verwendet werden.
ArraySort(halfsums); //sort the array double mean=(halfsums[indx10]+halfsums[indx11])/2; //robust mean
In der nächsten Phase ist eine robuste Schätzung der Standardabweichung zu ermitteln.
for(int j=0; j<iPeriod; j++) { diff[j]=MathAbs(price[i+j]-mean); } ArraySort(diff); double sd=(diff[indx20]+diff[indx21])/2; //robust standard deviation
Wenn die Standardabweichung größer als Null ist, dann ist der Indikatorwert gleich:
res=(price[i]-mean)/sd;
Jetzt können wir das Verhalten der verschiedenen Versionen des Indikators vergleichen. In einigen Fällen sehen die Indikatoren sehr ähnlich aus.
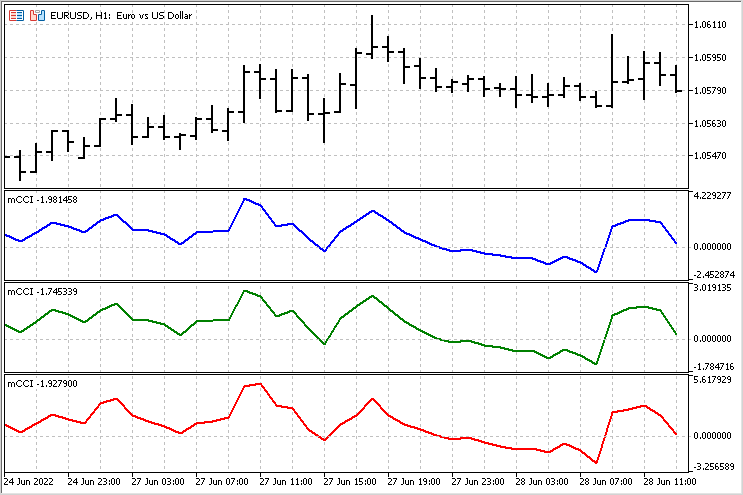
Aber es gibt auch Bereiche, in denen der Unterschied sehr deutlich ist.
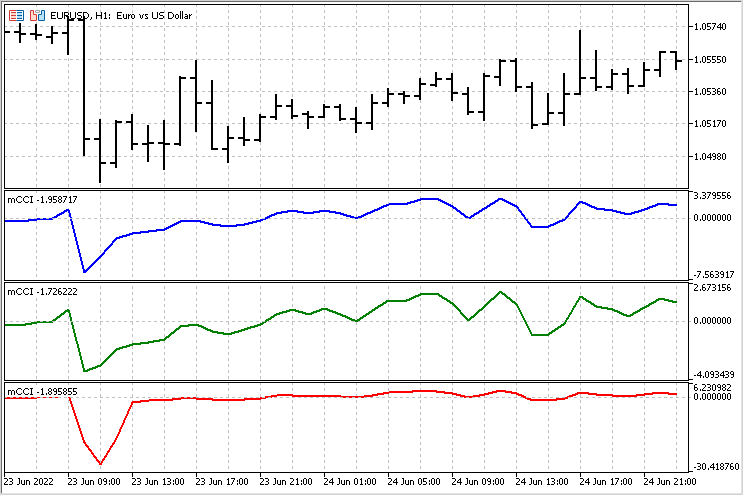
Ein kleiner Expert Advisor für den Vergleich der Indikatoren
Visuelle Vergleiche sind subjektiv und können zu falschen Schlussfolgerungen führen. Wir brauchen eine zuverlässigere Grundlage für unsere Schlussfolgerungen. Um alle Indikatorversionen zu testen, schreiben wir einen einfachen Expert Advisor. Weisen wir ihm dieselben Regeln für das Öffnen und Schließen von Positionen zu und vergleichen wir die Ergebnisse. Ich werde die folgenden Regeln anwenden - das Überschreiten eines bestimmten Niveaus öffnet eine Position in einer Richtung und schließt Positionen in der entgegengesetzten Richtung (falls vorhanden).
EA-Parameter:
- TypeInd - Indikatortyp (Klassisch, Quadratisch, Modern)
- RSI iPeriod — Periodenlänge des Indikators;
- iPrice - Indikatorpreis
- Level - Level, deren Überquerung verfolgt werden soll. Sein Wert von 150 entspricht dem Niveau von 100 im klassischen CCI.
Um den Test zu beschleunigen, wurde der Algorithmus zur Berechnung des Indikators in den EA verlagert. Die Indikatorwerte werden bei der Eröffnung eines neuen Balkens berechnet. Eine Kaufposition wird eröffnet, wenn der Indikatorwert den negativen Level nach oben überschreitet. Gleichzeitig werden die Verkaufspositionen geschlossen. Verkaufspositionen werden eröffnet (und Kaufpositionen werden geschlossen), wenn der Indikatorwert den positiven Level nach unten überschreitet.
Testparameter:
EURUSD-Paar
H1-Zeitrahmen
Zeitintervall - das Jahr 2021
iPeriode = 14
iPreis = PRICE_TYPICAL
Level = 150
Im Folgenden werden die Optionen für die Saldenkurve für alle drei Fälle vorgestellt.
TypeInd = Klassisch
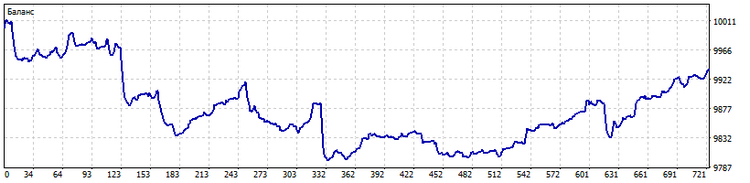
TypeInd = Quadratisch
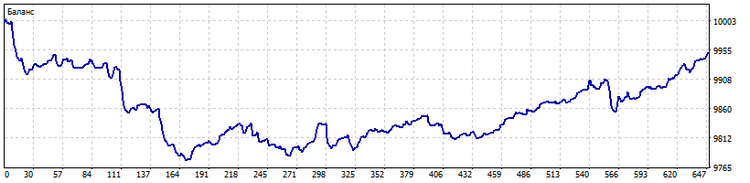
Wie wir sehen können, hat die Anwendung der Standardabweichung zu einem Rückgang der Anzahl der Geschäfte geführt, gefolgt von einem Rückgang der großen Verluste.
TypeInd = Modern
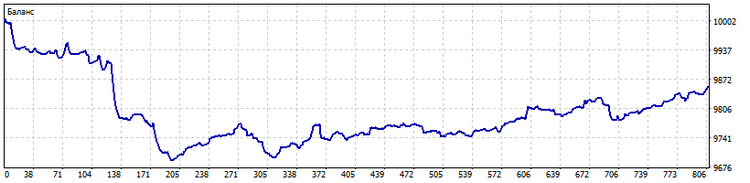
Durch die Verwendung robuster Schätzungen hat sich die Zahl der Abschlüsse erhöht, während die Zahl der großen Verluste noch weiter gesunken ist. Dies ist ein großer Vorteil für eine solche Indikatorversion.
Unabhängig davon sind die Regeln für die Eröffnung und Schließung von Positionen in allen Fällen stark verbesserungswürdig.
Indikatoränderung zur Schätzung eines Trends
Bei der sorgfältigen Beobachtung des CCI-Indikators (in jeder seiner Versionen) habe ich eine erstaunliche Entdeckung gemacht: Er kann sowohl positive als auch negative Werte annehmen. Ich weiß nicht, ob dies den Nobelpreis wert ist, aber MetaQuotes Ltd. sollte eine eigene Auszeichnung stiften. Ich habe sie definitiv verdient. Genug gescherzt.
Positive Indikatorwerte stehen für einen Aufwärtstrend, während negative Werte einen Abwärtstrend anzeigen. Schauen wir uns das im Detail an. Die Grundidee des neuen Indikators ist folgende: Wir summieren die Werte des CCI-Indikators vom Beginn eines Trends bis zu seinem Ende. Natürlich werden wir diese Bewegung mit den Mittelwerten vergleichen. Auf diese Weise können wir die Dauer der Trendbewegungen und deren Stärke beurteilen.
Die Version der Berechnungen mit robusten Schätzungen ist als Grundlage zu verwenden. Der einzige Unterschied besteht darin, dass wir die Summe der CCI-Indikatorwerte akkumulieren, nachdem sie das Nullniveau überwunden haben. Der Wert dieses kumulierten Betrags wird als Ausgabe verwendet. Die Durchschnittsbeträge für Aufwärts- und Abwärtstrends werden zum Vergleich getrennt berechnet. Das allgemeine Bild dieses Indikators sieht wie folgt aus.
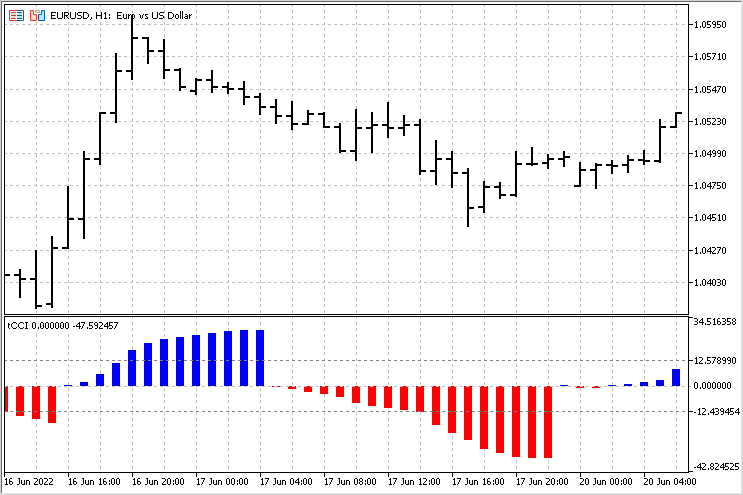
Mit diesem Indikator können wir den Beginn eines Trends, sein Ende und seine Stärke beurteilen. Die einfachste Strategie für diesen Indikator könnte wie folgt aussehen: Wenn der Trend über dem Durchschnitt lag (der Indikator hat das entsprechende Niveau überschritten), können wir erwarten, dass sich der Preis in die entgegengesetzte Richtung bewegt, wenn der Trend abgeschlossen ist.
Schlussfolgerung
Wie wir sehen, kann ein neuer Blick auf die technischen Indikatoren sehr nützlich sein. Kein einziger Indikator ist die endgültige Version - es besteht immer die Möglichkeit der Verfeinerung und Änderung für bestimmte Strategien. Beigefügte Dateien:
- mCCI - Indikator mit drei CCI-Versionen
- EA CCI - Handels-EA zum Vergleich verschiedener CCI-Versionen
- tCCI - Indikator, der die kumulierten Trendbeträge berechnet.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/11126
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Lernen Sie, wie man ein Handelssystem mit dem Awesome Oscillator entwickelt
Lernen Sie, wie man ein Handelssystem mit dem Awesome Oscillator entwickelt
 Erfahren Sie, wie Sie ein Handelssystem anhand des Relative Vigor Index entwickeln können
Erfahren Sie, wie Sie ein Handelssystem anhand des Relative Vigor Index entwickeln können
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Veröffentlichter Artikel CCI Indicator. Modernisierung und neue Möglichkeiten:
Autor: Aleksej Poljakov
Hallo, wo kann ich den mCCI-Indikator herunterladen, ich würde ihn gerne testen
Folgen Sie dem Link zum Artikel selbst. Alle Indikatoren sind unten auf der Seite angehängt
Die einfachste Ihrer Bedingungen ist die Losgröße. Hier gibt es vier Optionen - ein festes Lot, ein Lot für lineares, exponentielles oder exponentielles Wachstum der Einlage. Sie können noch ein hyperbolisches Wachstum hinzufügen, aber das ist nur etwas für Risikofreudige.
Aber alle anderen Bedingungen erfordern zusätzliche Forschung. Die Erstellung einer Bank von Filtern, mit denen ein Expert Advisor arbeiten könnte, ist keine leichte Aufgabe mehr. Es ist notwendig, die Möglichkeit vorzusehen, dass er mit dem Trend, gegen den Trend und in der Ebene arbeitet. Außerdem sollten die Filter im laufenden Betrieb umgeschaltet werden können. In einer solchen Situation wird auch die Auswahl des optimalen Stop-Loss und Take-Profit nicht einfach sein.