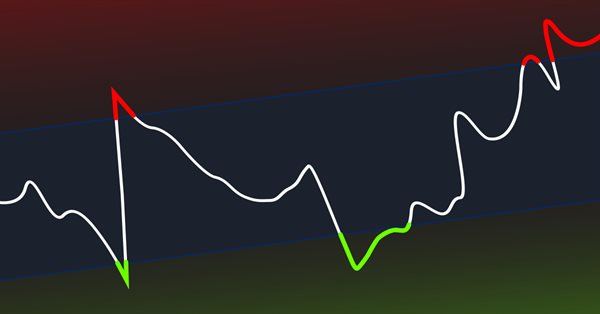
CCI 지표. 업그레이드 및 새로운 기능

역사 요약

CCI(Commodity Channel Index)는 모든 트레이더에게 친숙합니다. Donald Lambert가 개발했으며 1980년 잡지 Commodities(현재 –Modern Trader)에 처음 게재되었습니다. 그 이후로 이 지표는 명성을 얻었으며 거래자들 사이에서 매우 인기를 얻었습니다. CCI는 MetaTrader 거래 플랫폼 툴킷에 있습니다. 수동 거래와 자동 거래 시스템으로 사용됩니다.

계산 알고리즘

지표의 계산은 매우 간단하고 명확합니다. 지표는 평균 절대 편차와 관련하여 가격이 평균값에서 얼마나 벗어났는지를 보여줍니다. 계산 알고리즘은 다음과 같습니다. 지표의 기간을 N 가격 판독값으로 설정합니다. 그 다음에:

• mean 계산 

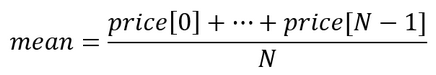
• 평균 절대 편차(mean absolute deviation) 찾기

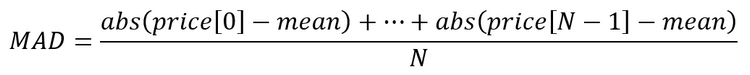
• 지표 값 계산

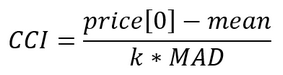
원래 지표에서 보정 계수 k = 0.015입니다. 1.5*MAD의 가격 편차가 100 지표 단위와 같도록 선택됩니다. 이 경우 3*MAD에 의한 편차는 200 단위입니다. (흥미롭게도 나눗셈을 곱셈으로 바꾸면 정규화 계수 k의 값은 66.6이 됩니다.)

가능한 알고리즘 변경

지표의 주목할 만한 특징은 평균 절대 편차를 사용한다는 사실입니다. 이 접근 방식은 컴퓨터가 발전하면서 절대 편차 계산이 더 적절한 표준 편차 계산에 비해 더 적은 계산 리소스를 필요로 했기 때문에 정당화되었습니다. 최신 컴퓨터는 합리적인 시간 내에 제곱 및 루팅을 처리할 수 있습니다. 따라서 계산 알고리즘은 다음과 같이 보일 것입니다.

• 숫자의 합 찾기:

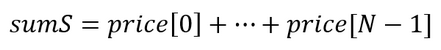
• 제곱합 구하기:

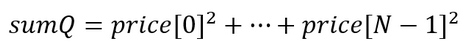
• 지표 값을 계산합니다.

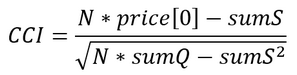
이러한 알고리즘은 더 정확하지만 완벽하지는 않습니다. 주요 문제는 평균 및 제곱 평균 제곱근 값을 추정하려면 충분히 많은 수의 가격 판독값(30개 이상)이 필요하다는 것입니다. 그러나 짧은 기간도 거래에 사용될 수 있습니다. 예를 들어 클래식 버전의 CCI에서는 14개 샘플 기간이 권장됩니다.

이러한 상황에는 강력한 통계 메서드가 필요합니다. 이를 통해 복잡한 금융 시장의 극한 상황에서도 안정적이고 신뢰할 수 있는 매개변수 추정치를 얻을 수 있습니다.

이제 사용 방법이 어떻게 작동하는지 살펴보고 기존 방법과 비교해 봅시다. 예를 들어 p[0] = 1, p[1] = 3, p[2] = 8의 세 가지 값의 시계열이 있다고 칩시다.

그런 다음 고전적인 접근 방식은 다음과 같은 간단한 계산입니다.

• 평균(Mean) (1 + 3 + 8) / 3 = 4
• 절대 편차(Absolute deviation)(abs(1 – 4) + abs(3 – 4) + abs(8 – 4)) /3 = 2.67
• 채널의 하한 및 상한 1.33 – 6.67 

이제 표준 편차를 사용하여 계산해 보겠습니다.

• 평균(Mean) (1 + 3 + 8) / 3 = 4
• 표준 편차 sqrt(((1 – 4)^2 + (3 – 4)^2 + (8 – 4)^2) / 3) = 2.94
• 채널의 하한 및 상한 1.06 – 6.94

강력한 추정을 위해서는 계산 비용이 더 많이 듭니다. Theil-Sen 방법을 사용하여 평균을 추정해 봅시다. 이렇게 하려면 먼저 쌍으로 취한 시계열 값의 모든 반합을 찾아야 합니다. 이러한 쌍의 수는 방정식: num=(N*(N-1)) / 2를 사용하여 얻을 수 있습니다.

이 경우 안정 평균(stable mean)은 이러한 반합의 중앙값(median)과 같습니다. 중앙값(median)을 찾으려면 먼저 배열을 오름차순으로 정렬해야 합니다. 그런 다음 중앙값은 배열 중앙에 있는 값에 해당합니다. 중앙값을 찾기 위해서는 배열의 크기가 홀수이면 중앙 요소의 인덱스가 필요하고, 배열의 크기가 짝수이면 두 개의 중앙 요소의 인덱스가 필요합니다. 그러면 median은 이 두 요소의 mean과 같습니다.

두 경우 모두 인덱스를 계산하기 위한 방정식('크기'는 배열의 요소 수임):

• size 홀수

Index = size / 2

• size 짝수

Index1 = size / 2 – 1; Index2 = size / 2

이 예의 경우 다음과 같이 표시됩니다.

hs1 = (1 + 3) / 2 = 2

hs2 = (1 + 8) / 2 = 4.5

hs3 = (3 + 8) / 2 = 5.5

정렬 2, 4.5, 5.5

• Mean = 4.5

이제 편차에 대해 알아봅니다. 원래 시계열의 절대값과 평균(mean) 사이의 중앙값(median)을 찾아야 합니다.

d1 = abs(1 – 4,5) = 3.5

d2 = abs(3 – 4,5) = 1.5

d3 = abs(8 – 4,5) = 3.5

정렬 3.5, 1.5, 3.5

• 편차 = 3.5
• 채널 1 – 8의 하한 및 상한

기존의 지표와 및 업그레이드된 지표 버전 비교

이러한 접근 방식을 비교해 봅시다. 정상적인 계산에서는 시계열의 최소값과 최대값이 평균(mean) +/- 편차를 넘어섰습니다. 강력한 추정을 할 경우 원래 계열의 모든 값이 이러한 경계에 맞습니다. 세 가지 접근 방식의 차이는 분명하지만 우리의 예에서만 그렇습니다. 이제 다양한 계산 방법이 실제 데이터에서는 어떻게 작동하는지 살펴보겠습니다. 세 가지 알고리즘을 각각의 별도의 지표로 구현해 보겠습니다. 이를 통해 각 옵션을 계산하는 기능에 익숙해질 수 있습니다.

지표가 그리는 것은 적용된 가격 상수와 기간이라는 두 가지 변수에 따라 크게 달라집니다. MQL5에서는 지표의 속성을 정의할 때 가격 상수를 설정할 수 있습니다.

#property indicator_applied_price PRICE_TYPICAL

MQL4에서는 저는 별도의 함수를 사용하겠습니다.

지표의 기간은 계산에 사용된 가격의 수를 보여줍니다.

input ushort iPeriod=14;//indicator period

변수 값은 3 이상이어야 합니다. 작은 기간의 경우 잘못된(너무 큰) 값을 얻을 수 있음을 명심하십시오.

각 i번째 막대에서 기존 CCI 버전의 계산은 다음과 같이 수행됩니다. 먼저 표본 평균(mean)의 값을 찾습니다.

double mean=0;                //sample mean
for(int j=0; j<iPeriod; j++)
   {
    mean=mean+price[i+j];     //sum up price values
   }
mean=mean/iPeriod;            //sample mean for the period

이제 평균 절대 편차(mean absolute deviation)를 계산할 시간입니다.

double mad=0;                          //mean absolute deviation
for(int j=0; j<iPeriod; j++)
   {
    mad=mad+MathAbs(price[i+j]-mean);  //sum up absolute difference values
   }

평균 절대 편차 값이 0보다 크면 지표는 다음과 같습니다:

res=(price[i]-mean)*iPeriod/mad;

표준 편차를 사용한 지표의 버전은 다음과 같이 계산됩니다. 먼저 가격의 합과 그 제곱을 찾아야 합니다.

double sumS=0,//sum of prices
       sumQ=0;//sum of price squares
for(int j=0; j<iPeriod; j++)
   {
    sumS=sumS+price[i+j];
    sumQ=sumQ+price[i+j]*price[i+j];
   }

이제 지표를 계산하는 데 필요한 분모를 찾아야 합니다.

double denom=MathSqrt(iPeriod*sumQ-sumS*sumS);

분모가 0보다 크면 결과는 다음과 같습니다:

res=(iPeriod*price[i]-sumS)/denom;

마지막으로 강력한 방법을 사용한 계산을 고려해 보겠습니다. 먼저 과정의 결과를 저장할 두 개의 배열을 준비해야 합니다. 한 배열은 반합의 값을 저장하는 것이고 다른 배열은 절대 차이를 저장하는 것입니다.

double halfsums[],diff[];

먼저 나중에 사용할halfsums배열을 준비합니다. 이를 위해 배열의 크기를 정의해 보겠습니다.

int size=iPeriod*(iPeriod-1)/2; //halfsums array size
ArrayResize(halfsums,size);     //set the array size

이제 배열의 중심 요소의 인덱스를 찾아봅시다. 다양성을 위해 두 가지 지수를 사용하겠습니다. size가 홀수인 경우 이러한 인덱스는 서로 일치하지만 그렇지 않으면 일치하지 않는 상태로 유지됩니다.

indx10=size/2;
indx11=indx10;
if(MathMod(size,2)==0)
   indx11=indx10-1;

그런 다음diff배열을 준비합니다. 이 배열의 크기는 지표 기간과 일치합니다. 요소 인덱스는 앞의 경우와 동일합니다.

ArrayResize(diff,iPeriod);
indx20=iPeriod/2;
indx21=indx20;
if(MathMod(iPeriod,2)==0)
   indx21=indx20-1;

이제 지표 값 계산을 시작할 때입니다. 반합으로 배열을 채우려면 추가 카운터가 필요합니다.

int cnt=0; //counter of array elements
for(int j=iPeriod-2; j>=0; j--)
   {
    for(int k=iPeriod-1; k>j; k--)
       {
        halfsums[cnt]=(price[i+j]+price[i+k])/2; //half sum value
        cnt++;                                   //increase the counter
       }
   }

배열을 채운 후에는 정렬해야 합니다. 배열의 중앙의 값을 평균(mean) 추정치로 사용해야 합니다.

ArraySort(halfsums);                               //sort the array
double mean=(halfsums[indx10]+halfsums[indx11])/2; //robust mean

다음 단계에서 표준 편차의 강력한 추정치를 찾아보시기 바랍니다.

for(int j=0; j<iPeriod; j++)
   {
    diff[j]=MathAbs(price[i+j]-mean);
   }
    
ArraySort(diff);
double sd=(diff[indx20]+diff[indx21])/2; //robust standard deviation

표준 편차가 0보다 크면 지표의 값은 다음과 같습니다.

res=(price[i]-mean)/sd;

이제 서로 다른 버전의 지표의 동작을 비교할 수 있습니다. 어떤 경우에는 지표가 매우 유사하게 보입니다.

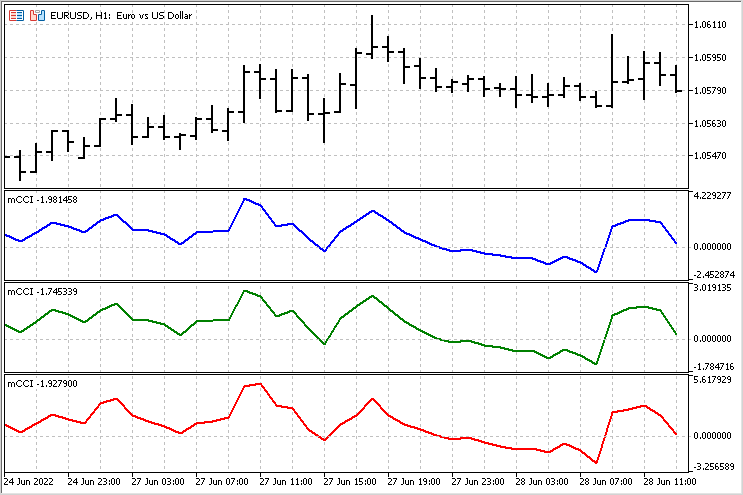
그러나 그 차이가 상당히 눈에 띄는 영역도 있습니다.

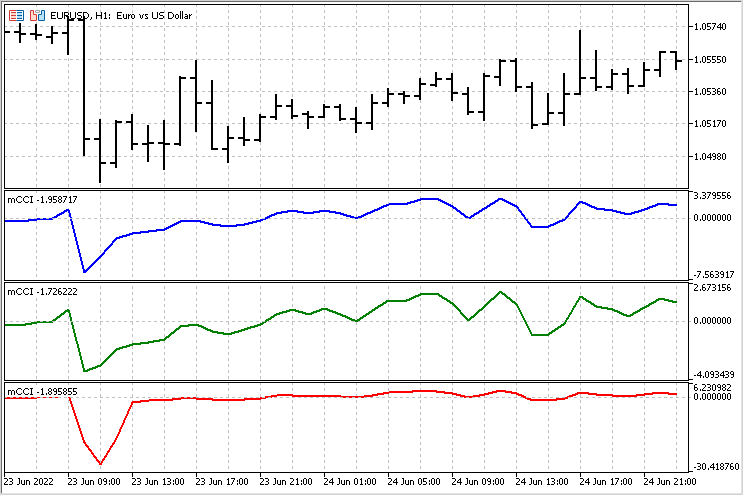
지표 비교를 위한 간단한 Expert Advisor

시각적 비교는 주관적이며 잘못된 결론으로 이어질 수 있습니다. 결론을 내리기 위해서는 더 신뢰할 수 있는 근거가 필요합니다. 모든 지표 버전을 평가하기 위해 간단한 Expert Advisor를 작성해 보겠습니다. 포지션에 진입하고 청산하는 데 동일한 규칙을 적용하고 결과를 비교해 봅시다. 저는 다음과 같은 규칙을 사용할 것입니다. 주어진 레벨을 교차하면 한 방향으로 포지션에 진입하고 반대 방향으로 포지션을 청산합니다(포지션이 있는 경우).

EA 매개변수:

• TypeInd- 지표 유형(클래식, 스퀘어, 모던)
• iPeriod- 지표 기간
• iPrice- 지표 가격
• 레벨- 교차점을 추적할 레벨 값 150은 원래의 CCI의 100 수준에 해당합니다.

테스트의 속도를 높이기 위해 지표 계산 알고리즘이 EA 내부로 이동되었습니다. 지표 값은 새로운 바가 열릴 때 계산됩니다. 지표 값이 음수 레벨 값을 상향 교차하면 매수 포지션에 진입합니다. 동시에 매도 포지션은 청산됩니다. 지표 값이 양수 수준 값을 하향 교차하면 매도 포지션으로 진입하고 매수 포지션이 청산됩니다.

테스트 매개변수:

EURUSD 쌍

H1 기간

시간 간격 – 2021년

iPeriod = 14

iPrice = PRICE_TYPICAL

레벨 = 150

세 가지 경우 모두에 대한 균형 곡선 옵션이 아래에 나와 있습니다.

TypeInd = Classical

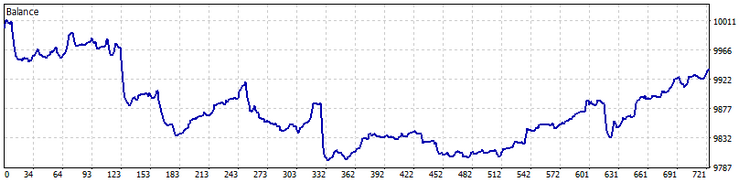
TypeInd = Square

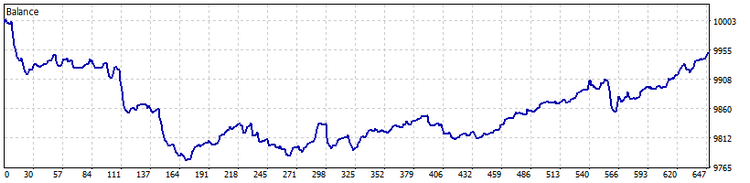
보시다시피 표준 편차를 적용하면 거래 건수가 감소하고 큰 손실도 감소했음을 확인할 수 있습니다.

TypeInd = Modern

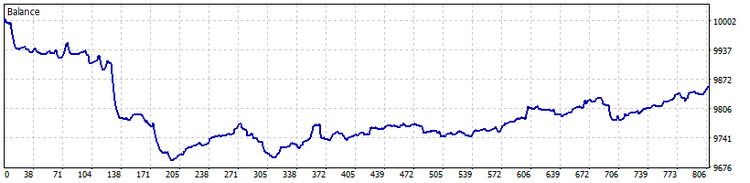
강력한 추정치를 사용하였고 이를 통해 거래 건수를 늘린 반면 큰 손실 건수는 훨씬 더 줄었습니다. 이것은 이 지표 버전의 뛰어난 이점입니다.

그럼에도 불구하고 포지션을 진입하고 청산하는 규칙은 어느 경우이든 개선이 필요합니다.

추세 추정을 위한 지표 수정

CCI 지표(모든 버전에서)를 주의 깊게 관찰하는 동안 저는 놀라운 발견을 했습니다. 이것이 노벨상을 받을 가치가 있는지는 모르겠지만 MetaQuotes Ltd는 어떤 상을 제정해야 합니다. 저는 충분히 그 상을 받을 자격이 있습니다. 농담입니다.

양수 지표 값은 상승 추세와 관련이 있고 음수 지표 값은 하락 추세와 관련이 있습니다. 이에 대해 더 자세히 살펴보겠습니다. 새로운 지표의 아이디어는 다음과 같습니다: 추세가 시작되는 순간부터 끝날 때까지 CCI 지표의 값을 합산합니다. 물론 이 움직임을 평균값(mean)과 비교할 것입니다. 이렇게 하면 추세의 움직임의 지속 시간과 강도를 평가할 수 있습니다.

강력한 추정치를 사용한 계산 버전이 기준으로 사용됩니다. 유일한 차이점은 0 레벨을 넘어선 후 CCI 지표 값의 합계를 누적한다는 것입니다. 이 누적된 금액의 값이 출력으로 사용됩니다. 상승 추세 및 하락 추세의 평균 금액은 비교를 위해 별도로 계산됩니다. 이 지표의 일반적인 그림은 다음과 같습니다.

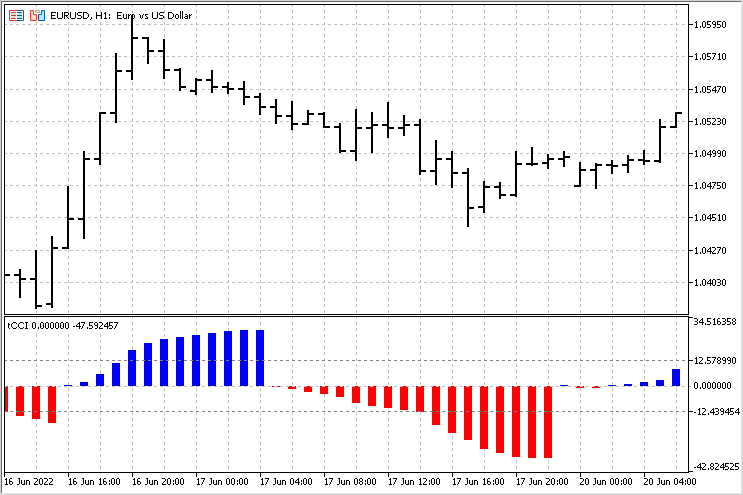
이 지표를 사용하여 추세의 시작, 끝 및 강도를 평가할 수 있습니다. 이 지표에 대한 가장 간단한 전략은 다음과 같을 수 있습니다 - 추세가 완료될 때 추세가 평균보다 높으면(지표가 해당 레벨을 넘어선 경우) 우리는 가격이 반대 방향으로 움직일 것으로 예상할 수 있습니다.

결론

보시다시피 기술 지표를 새롭게 보는 것은 매우 유용할 수 있습니다. 단일 지표가 최종 버전은 아닙니다. 특정 전략에 대한 개선 및 수정의 가능성은 항상 있습니다. 첨부 파일:

• mCCI— 세 가지 CCI 버전이 있는 지표
• EA CCI— 다른 CCI 버전 비교를 위해 거래하는 EA
• tCCI— 누적 추세 금액을 계산하는 지표