Entwicklung eines Replay Systems — Marktsimulation (Teil 15): Die Geburt des SIMULATORS (V) - RANDOM WALK
Einführung
In den letzten Artikeln dieser Reihe, in denen wir ein Replay System des Marktes entwickeln, haben wir gesehen, wie man simuliert, oder genauer gesagt, wie man eine Art virtuelle Simulation eines bestimmten Symbols erzeugt. Das Ziel ist es, die Bewegung so realitätsnah wie möglich zu gestalten. Obwohl wir von einem einfachen System, das dem des Strategietesters sehr ähnlich ist, zu einem sehr interessanten Modell gelangt sind, ist es uns noch nicht gelungen, ein Modell zu erstellen, das zu jedem Datensatz passt. Es muss dynamisch und gleichzeitig stabil genug sein, um viele mögliche Szenarien mit minimalem Programmieraufwand zu generieren.
Hier werden wir den Fehler aus dem Artikel „Entwicklung eines Replay-Systems — Marktsimulation (Teil 14) Geburt des SIMULATOR (IV)“ beheben Obwohl wir das Funktionsprinzip RANDOM WALK entwickelt haben, ist es für die Arbeit mit Werten aus einer vordefinierten Datei oder Datenbank nicht ganz ausreichend. Unser Fall ist ein Sonderfall: Die Datenbank gibt immer die Metriken an, die verwendet und befolgt werden müssen. Obwohl das RANDOM WALK-System, das wir zuvor erwogen und entwickelt haben, Bewegungen erzeugen kann, die denen auf einem realen Markt sehr ähnlich sind, ist es nicht für den Einsatz in einem Bewegungssimulator geeignet. Der Grund dafür ist, dass sie nicht den gesamten Bereich abdecken kann, der in allen Fällen abgedeckt werden muss. In sehr seltenen Fällen wird die gesamte Spanne vom Eröffnungskurs bis zum Höchst- oder Tiefstkurs vollständig abgedeckt, wobei sich die Richtung bei Erreichen einer der Grenzen vollständig ändert und das andere Extrem erreicht wird. Am Ende wird er wie von Geisterhand genau den Preis finden und stoppen, der für das Ende des Balkens festgelegt wurde.
Es mag unmöglich erscheinen, aber manchmal passiert es doch. Aber wir können uns nicht auf den Zufall verlassen. Gleichzeitig muss sie so zufällig wie möglich sein und innerhalb der zulässigen Grenzen liegen. Es sollte auch seine Funktion erfüllen - vollständige und umfassende Abdeckung aller Punkte der Balken. Wenn wir auf diese Weise denken und einige abstrakte mathematische Konzepte analysieren, können wir eine relativ attraktive Form des überwachten RANDOM WALK entwickeln. Zumindest was die Tatsache betrifft, dass alle interessanten Punkte und bestimmte Punkte erreicht werden.
Die Idee selbst ist einfach, wenn auch recht ungewöhnlich; ich werde nicht auf unnötige mathematische Details eingehen, um die Erklärung nicht zu verkomplizieren. Zusammen mit dem Code werden wir jedoch auch das Konzept betrachten, das verwendet wird, damit auch Sie es verstehen können, und diejenigen, die es verstehen, können sogar leichte Variationen von dem entwickeln, was ich vorstellen werde.
Verstehen der Idee und des Konzepts
Wenn Sie diese Artikelserie verfolgt haben, ist Ihnen vielleicht aufgefallen, dass wir zunächst experimentiert und versucht haben, ein System zu entwickeln, das alle Preisklassen abdecken kann. Dazu haben wir eine Technik verwendet, die derjenigen des Strategietesters sehr ähnlich ist. Diese Technik basiert auf der typischen Zickzack-Bewegung, die unter Marktbeobachtern weit verbreitet und bekannt ist. Für diejenigen, die damit nicht vertraut sind oder nicht wissen, worum es sich handelt, sei auf Abbildung 01 verwiesen, die die schematische Darstellung zeigt.
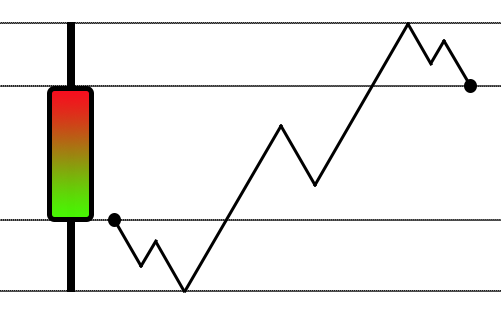
Abbildung 01 - Typische Zickzack-Bewegung
Obwohl eine solche Modellierung für den Strategietester geeignet ist, ist sie für das Replay/Simulationssystem nicht immer angemessen. Der Grund dafür ist einfach: Die Anzahl der Aufträge, die durch eine solche Simulation generiert werden, ist immer deutlich geringer als die tatsächliche Anzahl, aber das bedeutet nicht, dass das Modell ungültig ist, sondern nur, dass es für ein System wie das, das wir entwickeln wollen, nicht geeignet ist. Selbst wenn wir für die in Abbildung 01 gezeigte Bewegung einen Weg finden könnten, eine Anzahl von Tickets zu erzeugen, die der tatsächlich gehandelten entspricht, wäre die Bewegung selbst nicht komplex genug. Dies wäre lediglich eine Anpassung der echten Bewegung. Wir müssen dies anders umsetzen.
Wir müssen einen Weg finden, der so zufällig wie möglich ist, aber gleichzeitig den Code nicht verkompliziert. Denken Sie daran: Wenn die Komplexität des Codes zu schnell wächst, wird es bald unmöglich, ihn zu pflegen und zu korrigieren. Wir sollten uns immer bemühen, die Dinge so einfach wie möglich zu halten. Man könnte also meinen, wir könnten einfach zufällige Preiswerte generieren und so ein ausreichend hohes Maß an Komplexität simulieren, damit die Bewegung so realitätsnah wie möglich ist. Wir können es uns jedoch nicht leisten, jeden Preis oder jede Anzahl der generierten Tickets zu akzeptieren, wir müssen die Datenbank immer respektieren. Immer.
Wenn Sie sich die Datenbank ansehen, werden Sie feststellen, dass sie eine ganze Reihe nützlicher Informationen enthält. Abbildung 02 zeigt den typischen Inhalt einer Balkendatei. Einige Werte, die wirklich von Interesse sind, werden darin hervorgehoben.
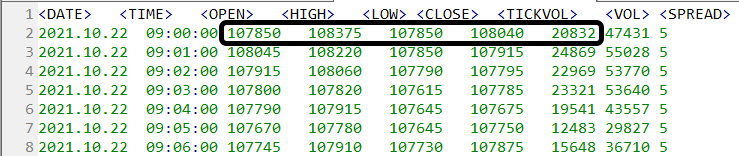
Abbildung 02 - Typischer Inhalt einer Datei mit 1-Minuten-Balken
Wenn wir diese Werte nehmen und völlig zufällige Preiswerte generieren, und ich betone, innerhalb der vorgegebenen Spanne bleiben, erhalten Sie eine völlig zufällige Art von Bewegung. Gleichzeitig wäre dieser Schritt selbst alles andere als bequem. Eine solche Bewegung kommt auf dem realen Markt nur selten vor.
Um zu sehen, was generiert wird, konvertieren wir die Dinge wieder in ein grafisches Format. Das Ergebnis einer völlig zufälligen Generierung von Preisen in einem bestimmten Bereich sieht folgendermaßen aus:
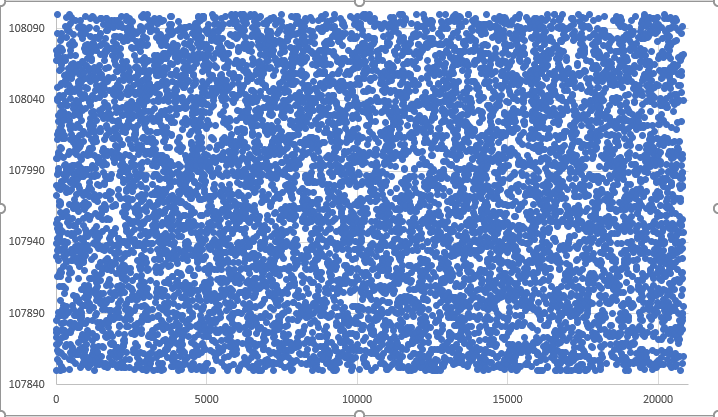
Abbildung 03 - Graphische Darstellung des Ergebnisses von völlig zufälligen Werten
Ein solches Diagramm lässt sich mit einer recht einfachen und gleichzeitig sehr effektiven Methode erstellen. Wir haben bereits gesehen, wie man das in Excel macht, sodass man ein Diagramm wie dieses erstellen kann. Auf diese Weise können Sie die Bewegung, die Sie erstellen, genauer analysieren, und zwar nur auf der Grundlage der Werte in der Datenbank. Es lohnt sich in der Tat, dies zu lernen, denn es ermöglicht eine schnellere Analyse von völlig zufälligen Werten. Ohne diese Ressource werden wir uns in der riesigen Datenmenge völlig verloren fühlen.
Wenn Sie wissen, wie man solche Diagramme erstellt, können Sie die Situation effizienter analysieren. Sie werden verstehen, dass das in Abbildung 03 dargestellte Diagramm aufgrund des hohen Grades an Zufälligkeit nicht ganz für unser System geeignet ist. Dann müssen wir nach einer Möglichkeit suchen, diese Zufälligkeit zumindest einzudämmen, um etwas zu schaffen, das einer echten Bewegung ähnlicher ist. Nach einer Weile werden Sie eine Methode entdecken, die oft in alten Videospielen verwendet wird, bei der sich die Spielfigur scheinbar zufällig durch das Spielgeschehen bewegt, aber in Wirklichkeit geschieht alles nach recht einfachen Regeln. Diese Methode findet sich auch in sehr beliebten und unterhaltsamen Mix-and-Match-Systemen wie dem Rubik's Cube (Abb. 04) oder sogar in 2D-Spielen wie 15 Puzzle, bei denen Schiebestücke sowohl zur Lösung des Problems als auch zum Mischen der Teile im Spiel verwendet werden (Abb. 05).

Abbildung 04 - Rubik's Cube - ein Beispiel für die RANDOM WALK Bewegung.

Abbildung 05 - 15 Puzzle: das einfachste RANDOM WALK System
Obwohl diese Spiele auf den ersten Blick nicht den Eindruck erwecken, dass sie RANDOM WALK verwenden, tun sie es tatsächlich. Aber nicht, um sie zu lösen, obwohl es möglich wäre, sie mit der RANDOM WALK-Methode zu lösen, auch wenn es viel länger dauern würde als mit geeigneteren Methoden. Um die Teile in scheinbar zufällige Positionen zu bringen, muss eine Formulierung mit RANDOM WALK verwendet werden. Danach versucht man, sie mit einer anderen Methode zu lösen, wie es ein Kind tut, indem man die Teile wieder an die richtige Stelle bringt. Dasselbe gilt für das System zur Erstellung von Tickets mit RANDOM WALK. Die Mathematik, die dem RANDOM WALK-Bewegungssystem zugrunde liegt, ist in allen Fällen dieselbe, sie ändert sich nicht.
In der Tat ändert sich nur das Richtungssystem, das wir verwenden werden. Versuchen Sie sich eine völlig sinnlose Bewegung vorzustellen, aber diese Bewegung findet im 3D-Raum statt und passt nicht in diese Mathematik. Um ehrlich zu sein, gibt es nur sehr wenige Fälle, in denen dies tatsächlich der Fall ist. In vielen dieser Fälle kann die Mathematik, die zur Beschreibung von RANDOM WALK herangezogen wird, die im Laufe der Zeit auftretenden Schwankungen erklären. Wendet man diese Mathematik auf das System „Preis x Zeit“ an, so erhält man ein Diagramm ähnlich dem in Abb. 06 dargestellten.
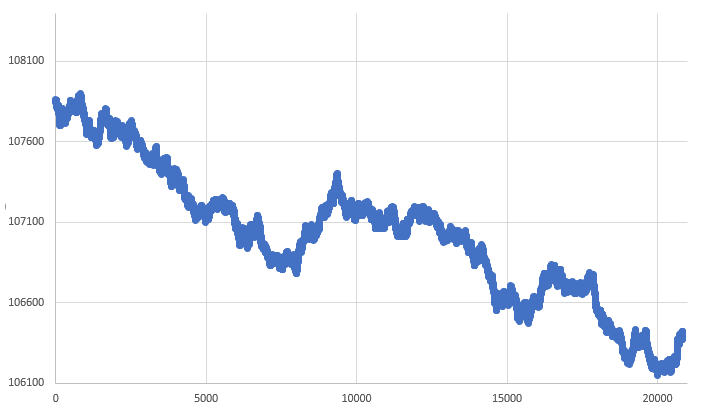
Abbildung 06 - RANDOM WALK von Preis x Zeit
Diese Art von Bewegung, die den gleichen Prinzipien wie die stochastischen Bewegungen folgt, ist der realen Bewegung, die der Markt normalerweise zeigt, sehr ähnlich. Lassen Sie sich jedoch nicht täuschen. Das obige Chart stellt keinen realen Vermögenswert dar. Er wird mit Hilfe eines Zufallszahlengenerators ermittelt: Zum vorherigen Preis wird eine Einheit addiert oder von ihm abgezogen, wodurch ein neuer Preis entsteht. Die Art und Weise, wie wir verstehen, ob wir addieren oder subtrahieren, hängt von der Regel ab, die wir verwenden. Man kann einfach sagen, dass jede zufällig erzeugte ungerade Zahl eine Addition und jede gerade Zahl eine Subtraktion bedeutet. Trotz ihrer Einfachheit ermöglicht es diese Regel, das gewünschte Ergebnis zu erzielen. Die Regel kann jedoch so abgeändert werden, dass jede zufällig erzeugte Zahl, die ein Vielfaches von 5 ist, eine Addition darstellt, andernfalls eine Subtraktion. Eine einfache Änderung dieser Regel führt zu einer völlig anderen Grafik. Sogar der Wert, der das Zufallsgenerierungssystem auslöst, verändert die Situation etwas.
Obwohl der Graph in Abb. 06 für ein völlig freies System geeignet ist, können wir ihn in einem Simulationssystem nicht verwenden. Der Grund dafür ist, dass wir die in der Datenbank angegebenen Werte beachten müssen, da diese uns explizite Ober- und Untergrenzen für die Erzeugung des RANDOM WALK vorgeben. Nachdem wir also Korrekturen vorgenommen haben, um die Einhaltung dieser Grenzwerte zu gewährleisten, gelangen wir von dem in Abb. 06 gezeigten Diagramm zu dem in Abb. 07 dargestellten Diagramm.
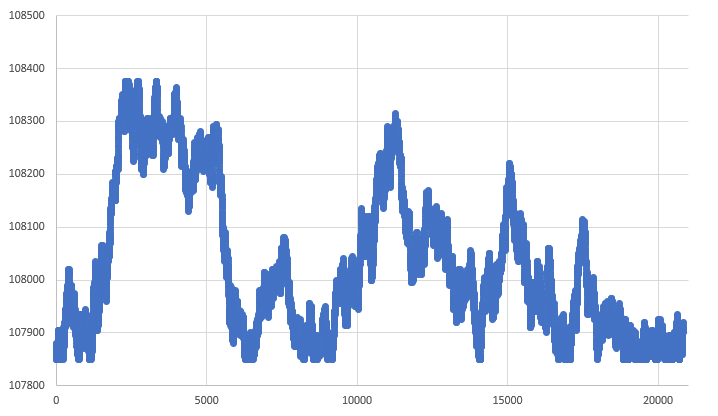
Abbildung 07 - RANDOM WALK innerhalb der Grenzen
Das System, das den in Abb. 07 gezeigten Graphen erzeugt, ist für die Verwendung in einem Simulator wesentlich besser geeignet. Hier haben wir eine Datenbank, die uns die Grenzen aufzeigt, innerhalb derer wir uns bewegen können. Tatsächlich gelingt es uns, mit ebenso einfacher Mathematik ein System zu schaffen, das ein akzeptables Maß an Komplexität enthält und gleichzeitig nicht völlig vorhersehbar ist, d. h. wir sind auf dem richtigen Weg. Bitte beachten Sie, dass sich in den Diagrammen von Abb. 01 bis zum Diagramm in Abb. 07 nur der Grad der Komplexität geändert hat. Oder besser gesagt, die Zufälligkeit im letzten Chart ist besser geeignet. Obwohl das in Abb. 01 gezeigte System für den Strategietester ausreicht, enthält das in Abb. 07 dargestellte Diagramm viel mehr Dinge, als für den Tester erforderlich sind. Für den Simulator sind diese Dinge jedoch von überragender Bedeutung.
Aber selbst mit dieser Steigerung der Komplexität, die in Schaubild 07 zu beobachten ist, ist sie für die Verwendung im Simulator noch nicht ganz ausreichend. Das Einzige, worüber wir uns bei der Verwendung des Systems sicher sein können, ist der Ausgangspunkt. In diesem Fall handelt es sich um den ERÖFFNUNGSPREIS. Es kann nicht garantiert werden, dass einer der anderen in der Datenbank angegebenen Punkte (CLOSE, MAXIMUM, MINIMUM) davon betroffen ist. Und das ist ein Problem, denn damit der Simulator wirklich brauchbar ist, müssen alle in der Datenbank angegebenen Punkte mit absoluter Sicherheit berührt werden.
Auf dieser Grundlage müssen wir irgendwie sicherstellen, dass aus dem Graphen in Abb. 07 ein Graph in Abb. 08 wird, bei dem wir absolute Sicherheit haben, dass diese Punkte zu einem bestimmten Zeitpunkt auch tatsächlich erreicht werden.
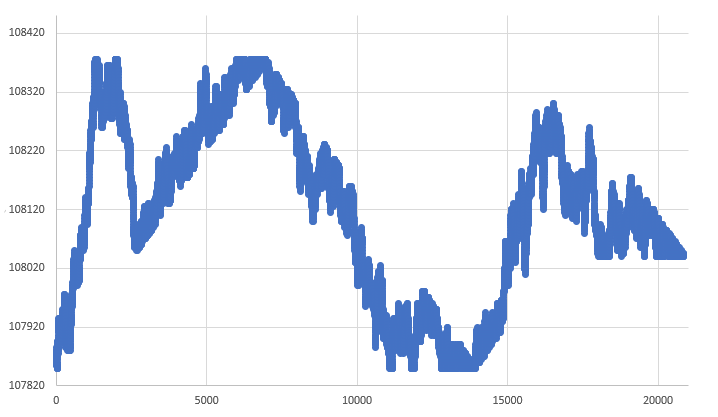
Abbildung 08 - Erzwungener RANDOM WALK
Diese Art von Veränderung erfordert nicht mehr als ein paar Anpassungen. Aber wenn Sie sich das Chart genau ansehen, können Sie deutlich erkennen, dass die Bewegung irgendwie gelenkt wird. Auch in diesem Fall kann man nicht umhin zu bemerken, dass wir einen RANDOM WALK haben, wenn auch nicht so natürlich, aber immer noch zufällig, wie man es bei einer stochastischen Bewegung erwarten würde. Nun möchte ich Ihre Aufmerksamkeit auf den folgenden Punkt lenken: Alle oben beschriebenen Diagramme verwenden dieselbe Datenbank. Sie ist in Abb. 02 dargestellt. Die beste Lösung ist jedoch die in Abb. 08 gezeigte, bei der wir eine Bewegung haben, die nicht so verwirrend und nicht so weit von der Datenbank entfernt ist wie in Abb. 03. In diesem Fall ähnelt alles dem, was beim Erstellen eines Balken passieren könnte.
Anhand der gezeigten Konzepte habe ich Sie wohl davon überzeugt, dass der Code in der im vorigen Artikel beschriebenen Phase nicht genau das ist, was wir im Simulator brauchen. Dies liegt daran, dass einige Punkte während des Zeitraums, in dem die Zufallsbewegung stattfand, möglicherweise nicht erreicht wurden. Was halten Sie von der Idee, diese Punkte nicht zwangsweise im Diagramm erscheinen zu lassen, sondern alles natürlicher zu gestalten?
Diesem Punkt werden wir im nächsten Thema nachgehen.
Erzwungener RANDOM WALK
Die Bezeichnung „forced random walk“ (erzwungene Zufallsbewegung) bedeutet nicht, dass wir eine Bedingung aufstellen werden. Wir werden die Bewegung jedoch in gewisser Weise einschränken, damit sie so natürlich wie möglich aussieht, aber dennoch ihren zufälligen Charakter beibehält. Es gibt noch ein Detail: Wir werden die Bewegung auf den Konvergenzpunkt ausrichten. Und das ist der Punkt, den Sie besuchen müssen. Wir erhalten also eine Kombination aus den Zahlen 01 und 07, und das ist doch sehr interessant, oder? In der Realität werden wir jedoch nicht den Pfad verwenden, der normalerweise wie in Abb. 01 dargestellt erstellt wird. Wir verfolgen einen etwas anderen Ansatz.
Um dies wirklich zu verstehen, schauen wir uns den Random-Walk-Code aus dem vorherigen Artikel an. Er ist unten aufgeführt:
inline void Simulation(const MqlRates &rate, MqlTick &tick[]) { #define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A))) long il0, max; double v0, v1; bool bLowOk, bHighOk; ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary); m_Ticks.Rate[++m_Ticks.nRate] = rate; max = rate.tick_volume - 1; v0 = 4.0; v1 = (60000 - v0) / (max + 1.0); for (int c0 = 0; c0 <= max; c0++, v0 += v1) { tick[c0].last = 0; tick[c0].flags = 0; il0 = (long)v0; tick[c0].time = rate.time + (datetime) (il0 / 1000); tick[c0].time_msc = il0 % 1000; tick[c0].volume_real = 1.0; } tick[0].last = rate.open; tick[max].last = rate.close; for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--) tick[macroRandomLimits(0, max)].volume_real += 1.0; bLowOk = bHighOk = false; for (int c0 = 1; c0 < max; c0++) { v0 = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? 1 : -1)); if (v0 <= rate.high) v0 = tick[c0].last = (v0 >= rate.low ? v0 : tick[c0 - 1].last + m_PointsPerTick); else v0 = tick[c0].last = tick[c0 - 1].last - m_PointsPerTick; bLowOk = (v0 == rate.low ? true : bLowOk); bHighOk = (v0 == rate.high ? true : bHighOk); } il0 = (long)(max * (0.3)); if (!bLowOk) tick[macroRandomLimits(il0, il0 * 2)].last = rate.low; if (!bHighOk) tick[macroRandomLimits(max - il0, max)].last = rate.high; for (int c0 = 0; c0 <= max; c0++) { ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray); m_Ticks.Info[m_Ticks.nTicks++] = tick[c0]; } #undef macroRandomLimits }
Wir müssen diesen Code, der oben hervorgehoben wurde, irgendwie ändern. Mit dem richtigen Ansatz können wir das System nach den Grundsätzen von RANDOM WALK verwalten und gleichzeitig den Pfadgenerierungsprozess kontrollieren. So werden wir alle vorgesehenen Punkte besuchen können. Denken Sie daran, dass der Anfangspunkt immer verwendet wird. Wir befassen uns also mit den anderen 3 Punkten: Hoch, Tief und Schlusskurs. Wir werden also Folgendes tun: Zuerst erstellen wir eine einfache Funktion, die den obigen Code ersetzt, aber auf eine viel interessantere Weise.
Um uns das Leben zu erleichtern, erstellen wir zunächst eine neue Funktion, die für die Erzeugung eines RANDOM WALK verantwortlich ist. Unten sehen Sie die erste Version.
inline long RandomWalk(long pIn, long pOut, const MqlRates &rate, MqlTick &tick[], int iMode) { double vStep, vNext, price, vHigh, vLow; vNext = vStep = (pOut - pIn) / ((rate.high - rate.low) / m_PointsPerTick); vHigh = rate.high; vLow = rate.low; for (long c0 = pIn, c1 = 0, c2 = 0; c0 < pOut; c0++, c1++) { price = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? -1 : 1)); price = tick[c0].last = (price > vHigh ? price - m_PointsPerTick : (price < vLow ? price + m_PointsPerTick : price)); switch (iMode) { case 0: if (price == rate.close) return c0; case 1: case 2: break; } if ((int)floor(vNext) < c1) { if ((++c2) <= 3) continue; vNext += vStep; if (rate.close > vLow) vLow += m_PointsPerTick); else vHigh -= m_PointsPerTick; } } return pOut; }
Nicht klar, was ich tue? Machen Sie sich keine Sorgen. Ich werde alles erklären. Wie bereits gesagt, ist dies die erste Version. Zunächst berechnen wir den Schritt, der notwendig ist, um einen Random Walk so auszuführen, dass er einen bestimmten Punkt erreicht. Wir speichern die Höchst- und Mindestwerte des Bereichs, in dem der Random Walk durchgeführt werden soll. Jetzt beginnt unsere Geschichte. Wir gehen nach dem Zufallsprinzip durch eine bestimmte Anzahl von Punkten, und bei jedem Schritt korrigieren wir die Situation, indem wir die zufällige Bewegung nicht blockieren, sondern sie in einen bestimmten Kanal lenken, aus dem sie nicht herauskommen kann. Er kann von Seite zu Seite oszillieren, verlässt aber auf keinen Fall den Kanal. Wenn wir uns im Nullmodus befinden, wird die Programmausführung angehalten, wenn der Zielpunkt erreicht ist. Dies ist wichtig, um eine größere Randomisierung zu gewährleisten. Keine Sorge, das wird später noch klarer werden.
Jetzt müssen wir noch etwas tun: Erinnern Sie sich, dass wir berechnet haben, wie lange es dauern würde, bis der Kanal reduziert ist? Es ist an der Zeit, mit der Schließung des Kanals zu beginnen. Der Kanal wird allmählich geschlossen, aber mit einem interessanten Detail. Wir werden sie nicht vollständig schließen. Wir belassen ein schmales Band, in dem der Preis seiner zufälligen Bewegung folgen kann, ähnlich wie bei Bollinger Bändern. Aber am Ende wird er praktisch an dem Punkt liegen, der als Endpunkt angegeben ist, d.h. am Schlusskurs. Dies geschieht in der Tat durch die Veränderung der Kanalgrenzen. Zuerst schließen wir den unteren Teil, und wenn wir den Austrittspunkt erreichen, beginnen wir mit dem Schließen des oberen Teils.
Auf die eine oder andere Weise wird der letzte Punkt praktisch zugänglich sein, aber wenn er nicht zugänglich ist, wird er sehr, sehr nahe am Ideal sein. Aber wo ist diese Funktion angesiedelt? Sie wird die alte Random-Walk-Methode ersetzen. Wir werden das, was in Abb. 01 passiert, mit dem kombinieren, was in Abb. 07 passiert. Das Ergebnis wird ein Bild sein, das Abb. 08 sehr ähnlich ist.
Hier ist die neue Simulationsfunktion.
inline void Simulation(const MqlRates &rate, MqlTick &tick[]) { #define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A))) long il0, max, i0, i1; bool b1 = ((rand() & 1) == 1); double v0, v1; MqlRates rLocal; ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary); m_Ticks.Rate[++m_Ticks.nRate] = rate; max = rate.tick_volume - 1; v0 = 4.0; v1 = (60000 - v0) / (max + 1.0); for (int c0 = 0; c0 <= max; c0++, v0 += v1) { tick[c0].last = 0; tick[c0].flags = 0; il0 = (long)v0; tick[c0].time = rate.time + (datetime) (il0 / 1000); tick[c0].time_msc = il0 % 1000; tick[c0].volume_real = 1.0; } tick[0].last = rate.open; tick[max].last = rate.close; for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--) tick[macroRandomLimits(0, max)].volume_real += 1.0; i0 = (long)(MathMin(max / 3.0, max * 0.2)); i1 = max - i0; rLocal = rate; rLocal.open = rate.open; rLocal.close = (b1 ? rate.high : rate.low); i0 = RandomWalk(1, i0, rLocal, tick, 0); rLocal.open = tick[i0].last; rLocal.close = (b1 ? rate.low : rate.high); RandomWalk(i0, i1, rLocal, tick, 1); rLocal.open = tick[i1].last; rLocal.close = rate.close; RandomWalk(i1, max, rLocal, tick, 2); for (int c0 = 0; c0 <= max; c0++) { ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray); m_Ticks.Info[m_Ticks.nTicks++] = tick[c0]; } #undef macroRandomLimits }
Der hervorgehobene Code-Teil ersetzt die alte Methode. Nun stellt sich eine wichtige Frage: Was macht der hervorgehobene Teil? Kannst Sie die Frage beantworten, indem Sie sich den Code ansehen?
Wenn Sie das verstehen können, gratuliere ich Ihnen herzlich! Wenn nicht, dann schauen wir uns diesen Code an.
i0 = (long)(MathMin(max / 3.0, max * 0.2)); i1 = max - i0; rLocal = rate; rLocal.open = rate.open; rLocal.close = (b1 ? rate.high : rate.low); i0 = RandomWalk(1, i0, rLocal, tick, 0); rLocal.open = tick[i0].last; rLocal.close = (b1 ? rate.low : rate.high); RandomWalk(i0, i1, rLocal, tick, 1); rLocal.open = tick[i1].last; rLocal.close = rate.close; RandomWalk(i1, max, rLocal, tick, 2);
Was umgesetzt wird, ist ein GROSSER Zickzackkurs, aber wie 🤔? Ich sehe es nicht 🥺! Wir werden Schritt für Schritt vorgehen. Zunächst berechnen wir den Grenzpunkt, an dem der erste Abschnitt des Zickzacks enden kann. Sobald dies geschehen ist, bestimmen wir sofort die Größe des dritten Zickzack-Segments. Ein Detail: Das erste Segment hat, anders als das dritte, keine feste Größe. Sie kann jeden Moment enden. Dieser Zeitpunkt wird durch das Random-Walk-Programm bestimmt. Da wir aber am Ende der ersten Stufe die zweite beginnen müssen, wird der von der Random-Walk-Funktion zurückgegebene Wert als Ausgangspunkt verwendet. Hier haben wir einen neuen Aufruf, um einen zweiten Random Walk zu erstellen. Klingt verwirrend?
Keine Sorge, wir schaffen das schon. Nun legen wir die Grenzen sowie die Eintritts- und Austrittspunkte des ersten Abschnitts des Random Walk fest. Wir rufen die Funktion zur Erstellung des Random Walk auf, die zurückkehrt, sobald sie den Endpunkt erreicht oder ihm so nahe wie möglich gekommen ist. Wir passen dann die Ein- und Ausstiegspunkte der nächsten Stufe wieder an. Rufen Sie die Funktion auf, um einen zufälligen Gang zu erzeugen, sodass die Bewegung von einem Ende zum anderen geht. Aber auch wenn diese Grenzen erreicht sind, kehrt die Funktion erst nach dem Besuch der angegebenen Anzahl von Positionen zurück. Danach bestimmen wir zum dritten und letzten Mal die Eintritts- und Austrittspunkte des Random Walk. Wir tätigen einen Anruf, der das letzte Segment bildet. Mit anderen Worten: Wir haben einen großen Zickzackkurs. Anstatt dass sich der Preis von einem Punkt zum anderen bewegt, schwankt er innerhalb der von uns festgelegten Grenzen 😁.
Wenn wir das oben beschriebene System ausführen, erhalten wir ein Diagramm, das dem in Abb. 08 gezeigten sehr ähnlich ist. Das ist sehr gut, wenn man bedenkt, wie einfach die oben beschriebene Methode ist, aber wir können das alles noch verbessern. Wenn Sie genau hinschauen, werden Sie feststellen, dass das in Abb. 08 gezeigte Diagramm Punkte aufweist, an denen der Preis gegen die Wand zu laufen scheint. Seltsamerweise geschieht so etwas manchmal auf dem realen Markt. Insbesondere, wenn eine der Parteien, Käufer oder Verkäufer, nicht zulässt, dass der Preis einen bestimmten Punkt überschreitet, kommt es zu der berühmten Auftragsschlacht im Auftragsbuch.
Wenn wir jedoch eine etwas natürlichere Bewegung im System erreichen wollen, müssen wir nicht die Simulationsfunktion selbst ändern, sondern nur die Ausführungsfunktion, die für die Erzeugung eines zufälligen Spaziergangs verantwortlich ist. Es gibt jedoch ein Detail in dieser ganzen Geschichte. Wir sollten nicht versuchen, eine neue Random-Walk-Methode zu entwickeln. Sie müssen nur eine Möglichkeit schaffen, die Begrenzungen ein- und auszuschalten, damit die Bewegung von selbst erfolgt. Wenn man es richtig macht, ist das Endergebnis viel natürlicher, als ob wir die Bewegung zu keinem Zeitpunkt gelenkt hätten.
Der erste Versuch, dies zu tun, besteht darin, eine Berührungskontrolle hinzuzufügen. Sobald dies geschieht, wird etwas Magisches beginnen. Hier ist also die neue Random-Walk-Methode - es handelt sich nicht um eine neue Methode, sondern nur um eine Anpassung der ursprünglichen Methode. Vergessen Sie nicht: Ich erkläre nur die neuen Teile 😉.
inline long RandomWalk(long pIn, long pOut, const MqlRates &rate, MqlTick &tick[], int iMode) { double vStep, vNext, price, vHigh, vLow; char i0 = 0; vNext = vStep = (pOut - pIn) / ((rate.high - rate.low) / m_PointsPerTick); vHigh = rate.high; vLow = rate.low; for (long c0 = pIn, c1 = 0, c2 = 0; c0 < pOut; c0++, c1++) { price = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? -1 : 1)); price = tick[c0].last = (price > vHigh ? price - m_PointsPerTick : (price < vLow ? price + m_PointsPerTick : price)); switch (iMode) { case 0: if (price == rate.close) return c0; break; case 1: i0 |= (price == rate.high ? 0x01 : 0); i0 |= (price == rate.low ? 0x02 : 0); vHigh = (i0 == 3 ? rate.high : vHigh); vLow = (i0 ==3 ? rate.low : vLow); break; case 2: break; } if ((int)floor(vNext) < c1) { if ((++c2) <= 3) continue; vNext += vStep; if (rate.close > vLow) vLow = (i0 == 3 ? vLow : vLow + m_PointsPerTick); else vHigh = (i0 == 3 ? vHigh : vHigh - m_PointsPerTick); } } return pOut; }
Jetzt haben wir eine völlig neue Situation. Deshalb müssen wir vermeiden, alte Grenzen zu überschreiten. Aber es gibt einen sehr subtilen Punkt. Wir haben eine neue Variable, die bei Null beginnt. In der Tat ist es wie ein Boolesches Ensemble. Was diese Variable bewirkt, ist unglaublich. Man muss also sehr vorsichtig sein, um das zu verstehen. Dieser Punkt ist sehr gut definiert und sehr interessant. Wenn wir uns im zweiten Segment des Zickzackkurses befinden, berührt der Kurs irgendwann das Hoch und dann das Tief. Bei jeder dieser Berührungen schreiben wir dann einen bestimmten Wert in unsere Variable. Was passiert, wenn wir eine Variable nicht als Bit-Einheiten, sondern als ein einziges Ganzes betrachten? Wir werden einen ganz bestimmten Wert erhalten. Dieser Wert kann null, eins, zwei oder drei sein.
Aber Moment mal, wie kann es drei 🤔 geben? Der Punkt ist, dass wir, wenn das Hoch berührt wird, eine boolesches ODER durchführen, bei der wir das kleinste Bit auf wahr setzen. Wenn das Tief berührt wird, führen wir die gleiche Operation durch, aber jetzt auf dem zweitkleinsten Bit. Das heißt, wenn das erste Bit bereits auf „true“ gesetzt ist und wir dann das zweite Bit auf „true“ setzen, gehen wir sofort von einem Wert von 1 zu einem Wert von 3 über, sodass der Zähler auf einen Wert von 3 steigt.
Es ist wichtig, diese Tatsache zu verstehen, da dies der Wert ist, den wir überprüfen werden. Anstatt 2 verschiedene boolesche Zahlen zu prüfen, wird ein Wert geprüft, der beide repräsentiert. Dies ist die Logik des Systems 😁. Wenn also der Wert 3 ist, dann haben wir eine Erweiterung der Grenzen, die verwendet werden kann. Oder, um es verständlicher auszudrücken, wenn wir diese Prüfung nicht durchführen würden, würden sich die Grenzen mit dem auf nur 3 mögliche Bewegungspositionen komprimierten Random Walk schließen. Aber auf diese Weise kann sich die Bewegung wieder natürlich entwickeln. Da die Grenzen erreicht sind, hat es keinen Sinn, die Bewegung weiter einzuschränken.
Die „Explosion“ findet an diesen Punkten statt. Wenn die Funktion dann versucht, die Grenzwerte zu reduzieren, ist sie nicht mehr in der Lage, dies zu tun. Jetzt wird der Zufallslauf entlang der gesamten Grenze stattfinden, was ihn viel natürlicher macht. Wenn wir nun das System mit derselben Datenbank laufen lassen, die wir ganz am Anfang des Artikels verwendet haben, erhalten wir ein Diagramm, das dem in Abb. 09 😊 sehr ähnlich ist.
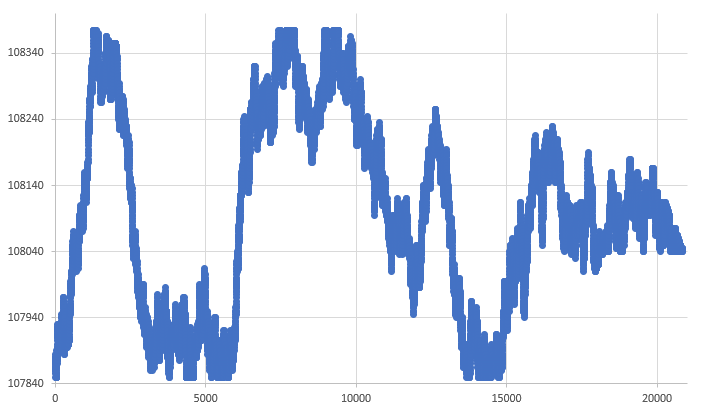
Abbildung 09 - Random Walk mit „Explosion“
Dieses Diagramm sieht viel natürlicher aus als das Diagramm in Abb. 08. Aber auch dieses letzte Diagramm, das perfekt zu sein scheint, hat noch einen Punkt, der nicht so natürlich ist. Er befindet sich im letzten Abschnitt. Achten Sie auf das Ende des Diagramms: Es sieht angesichts der Grenzen der möglichen Bewegung etwas unnatürlich aus. Diese Dinge verdienen es, in Ordnung gebracht zu werden, und das werden wir jetzt auch tun.
Um dieses Problem zu lösen, müssen wir der Funktion, die für den Random Walk verantwortlich ist, ein paar Zeilen hinzufügen. Nachstehend finden Sie die endgültige Fassung des Systems:
inline long RandomWalk(long pIn, long pOut, const MqlRates &rate, MqlTick &tick[], int iMode) { double vStep, vNext, price, vHigh, vLow; char i0 = 0; vNext = vStep = (pOut - pIn) / ((rate.high - rate.low) / m_PointsPerTick); vHigh = rate.high; vLow = rate.low; for (long c0 = pIn, c1 = 0, c2 = 0; c0 < pOut; c0++, c1++) { price = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? -1 : 1)); price = tick[c0].last = (price > vHigh ? price - m_PointsPerTick : (price < vLow ? price + m_PointsPerTick : price)); switch (iMode) { case 0: if (price == rate.close) return c0; break; case 1: i0 |= (price == rate.high ? 0x01 : 0); i0 |= (price == rate.low ? 0x02 : 0); vHigh = (i0 == 3 ? rate.high : vHigh); vLow = (i0 ==3 ? rate.low : vLow); break; case 2: break; } if ((int)floor(vNext) < c1) { if ((++c2) <= 3) continue; vNext += vStep; if (iMode == 2) { if ((c2 & 1) == 1) { if (rate.close > vLow) vLow += m_PointsPerTick; else vHigh -= m_PointsPerTick; }else { if (rate.close < vHigh) vHigh -= m_PointsPerTick; else vLow += m_PointsPerTick; } } else { if (rate.close > vLow) vLow = (i0 == 3 ? vLow : vLow + m_PointsPerTick); else vHigh = (i0 == 3 ? vHigh : vHigh - m_PointsPerTick); } } } return pOut; }
Es scheint etwas seltsam, aber sehen Sie sich Folgendes an: Wenn wir das erste und zweite Segment ausführen, wird der Code das tatsächlich genau so ausführen. Wenn wir zum dritten Segment übergehen, werden wir eine etwas andere Zahl haben.
Um eine Figur zu erhalten, die in der grafischen Analyse als SYMMETRISCHES DREIECK bezeichnet wird, müssen beide Seiten schrittweise reduziert werden. Aber es ist sehr wichtig zu verstehen, dass wir ein SYMMETRISCHES DREIECK oder ein ASYMMETRISCHES haben können. Je nachdem, ob der Ausgangspunkt gleich weit von den Extrempunkten entfernt ist, ergibt sich die Konstruktion eines symmetrischen Dreiecks. Wenn der Schluss- oder Ausstiegspunkt sehr nahe an einer der Begrenzungen liegt, ist das Dreieck asymmetrisch. Dazu werden wir abwechselnd Addition und Subtraktion verwenden. Dies geschieht vor allem an solchen Stellen. Die Methode des Umschaltens von Datenpunkten wird durch die Überprüfung des aktuellen Reduktionswertes realisiert.
Auf diese Weise erhalten wir ein endgültiges Diagramm, das dem in Abb. 10 gezeigten sehr ähnlich ist. Es ist unten aufgeführt:
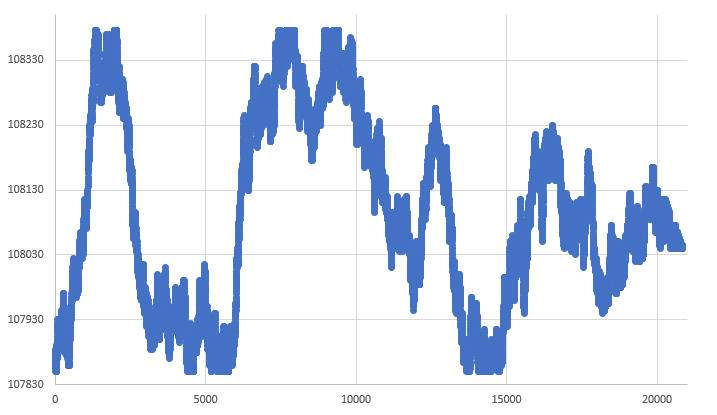
Abbildung 10 - Random-Walk-Diagramm eines 1-Minuten-Balkens
Das sieht viel natürlicher aus als jedes andere Chart, das wir bisher gesehen haben. Damit ist die Random-Walk-Basis abgeschlossen, und wir können zu den nächsten Schritten bei der Entwicklung unseres Replay-/Simulationssystems übergehen.
So können Sie nachvollziehen, wie sich das System derzeit verhält.
Der Anhang enthält den vollständigen Code in seinem derzeitigen Entwicklungsstand.
Schlussfolgerung
Man muss nicht unbedingt komplexe Mathematik verwenden, um Dinge zu erklären oder zu erschaffen. Als das Rad erfunden wurde, kannte man die Mathematik noch nicht, um den Radius auf der Grundlage des Wertes PI zu bestimmen. Wir haben lediglich die gewünschte Bewegung erreicht. In diesem Artikel habe ich gezeigt, dass einfache Mathematik, die in Kinderspielen verwendet wird, Bewegungen erklären und darstellen kann, die viele für unmöglich halten. Und sie verwenden immer wieder komplizierte mathematische Verfahren, obwohl die Lösung einfach ist. Versuchen Sie immer, die Dinge einfach zu gestalten.
Übersetzt aus dem Portugiesischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/pt/articles/11071
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.